SEM++: A particle model of cellular growth, signaling and migration

Abstract

We present a discrete particle method to model biological processes from the sub-cellular to the inter-cellular level. Particles interact through a parametrized force field to model cell mechanical properties, cytoskeleton remodeling, growth and proliferation as well as signaling between cells. We discuss the guiding design principles for the selection of the force field and the validation of the particle model using experimental data. The proposed method is integrated into a multiscale particle framework for the simulation of biological systems.

1 Introduction

Developmental processes such as embryogenesis, organ formation and tumor growth are orchestrated by multiscale bio-mechanical and chemical phenomena. In tumor-induced angiogenesis for instance, tip cell selection, sprout migration, proliferation of the stalk cells and the formation of lumen emerge as a result of such coordinated cell interactions [32, 39]. The phenotypic behavior of individual cells is determined by their response to a collection of stimuli from the surrounding environment, including mechanical and chemical signals provided by the extracellular matrix (ECM) and cells in their neighborhood. These processes can transform a homogeneous cell population to a heterogeneous one where individual cells interact in a coordinated way to give rise to a larger, hierarchical structure.

In this work, we consider eukaryotic animal cells of multicellular organisms as in the human body [1]. A conceptual sketch of a cell and its structural components is shown in Fig. 1. The interior of the cell is filled by the cytoplasm, a gel-like substance composed of 70–90 % water. Within the cytoplasm, the main structural components are the cell nucleus which occupies roughly 6 % of the cell and the cytoskeleton. The cytoskeleton is a highly dynamic network of different fibers (actin, intermediate filaments and microtubules). It determines the cell’s shape and drives locomotion. The cell membrane separates the cytoplasm from the surrounding environments and transmembrane receptors are used by cells to react to external stimuli. Those stimuli include chemical interactions with ligands, mechanical interactions with neighboring cells via cell-cell adhesion and mechanical interactions with the ECM via integrins. The ECM is the structure that occupies the extracellular space between cells. It is composed of a mixture of fibers (collagen, elastin and fibronectin) embedded inside a hydrated, gel-like substance.

Fig. 1

Conceptual sketch of a cell and its structural components: Black nucleus, red fibers, dark blue, yellow/purple organelles, light blue membrane, yellow/pink receptor, green/pink ligands. (Color figure online)

A variety of models have been proposed to model cells and biological tissues. In Fig. 2 we classify the models within two categories that aim to capture different length- and time-scales and different levels of detail. Continuum models ignore cell boundaries and consider larger regions of cells. Those regions are either identified by density fields like “number of cells per volume element” or by an interface surrounding the region of cells. Reaction–diffusion systems are commonly used to describe the evolution of a molecular entity through space but they can also model multi-cellular systems such as brain tumors [27, 60]. Single phase [17] and multiphase models [18, 34] treat tissues as a fluid-like material, while solid mechanics models [25, 28, 42, 55] treat tissues as an elastic solid governed by the corresponding continuum mechanics equations.

Fig. 2

Overview of cell-based and continuum models for biological tissues. Detailed models can capture single cells and subcellular details. Coarser models work with cell densities and collection of cells to reach larger length- and time-scales

Continuum models are well suited to capture the large-scale dynamics in growing tissue at the millimeter to centimeter range. However, the approximation of cells by a continuum density prohibits the exploration of single cell dynamic that give rise to important biological processes such as polarization, growth and adhesion. When cells are modeled at a continuum level, a single cell does not exist. The emergence of phenomena initiated by single cells, a result of mutation or phenotypic activation, can therefore not be studied in these models [31]. We wish to study such phenomena in computer simulations and we employ a cell-based model that can represent individual cells subject to mechanical stresses, migration, proliferation, cell-cell and cell-substrate adhesion and cell-cell mediated signaling.

In the field of cell-based modeling (see Fig. 2), we discriminate between grid-based and lattice-free particle methods. Cellular Automata are structured grids where every grid point represents a single cell [4, 15]. In single particle models each cell is represented by a particle which can freely move in space [5, 35, 49]. Cell vertex models represent cells with polygonal (2D) or polyhedral (3D) shapes which are evolved by minimizing an energy potential [16, 43]. They are valuable tools to study adhesion, surface tension and pressure driven cell arrangement as they explicitly capture cell size and shape, however, they are limited to represent polygonal cell shapes in closely packed epithelial layers. Cellular potts models (CPM) are derived from the Ising model of ferromagnetism [26] and have been used to study adhesion driven sorting in cell layers and various other developmental and pathological systems in biology [12, 23]. In CPM, a cell is defined as a set of lattice sites which are updated according to a Monte Carlo Metropolis algorithm to minimize an energy potential. They are not not time-dependent and describe equilibrium situations [5]. In the Immersed Boundary Cell Model each cell is represented by an elastic body and the immersed boundary method [50] is used to capture the interactions between the cells and a surrounding, incompressible, viscous fluid [53, 54].

The methods presented in this paper belong to the lattice-free methods and extend the subcellular element model (SEM) [45, 57]. In the SEM, cells are represented by an agglomeration of computational particles whose interactions are defined via short-range potentials. The potential function [57] models the viscoelastic properties of the cytoskeleton of isolated cells. Model parameters are non-dimensionalized to scale with the number of particles per cell and the mechanical stiffness and homotypic and heterotypic cell-cell adhesion are tunable via the intra-cellular and inter-cellular potential parameters respectively.

We present extensions to this model to account for actin polymerization based migration. We introduce a model for cell growth and proliferation driven by the cell-cycle and we propose extensions to model cell-cell mediated signaling processes that can determine the cell phenotype. We refine the structure of the cell to account for the explicit inclusion of subcellular organelles such as the nucleus. The cell membrane is explicitly traced to model membrane bound receptor mediated signaling cascades and its mechanical distinct properties from the cytoskeleton.

The proposed methods have been implemented in a standalone, object-oriented C++ framework that features thread-based parallelism. The implementation allows for modular extensions and fast prototyping of the model and integrates visualization capabilities for 2D simulations. Furthermore, we present an integration of the model into the LAMMPS framework [33, 51], a highly optimized parallel C++ library for the computation of particle interactions.

The article is structured as follows: First, we introduce the SEM and specify our extensions of it. Section 3 describes our implementation of the model. Applications of the model are shown in Sect. 4, followed by a brief summary.

2 Model and methods

We model cells as a collection of interacting particles, distinguishing particles in the interior as well as on the membrane of the cell. Intra- and intercellular interactions are modeled through parametrized pairwise forces. The model presented here is an extension based on the SEM [45, 57]. The model parameters of the extended SEM are summarized in Table 1. We consider SEM simulations in two or three dimensions.

Table 1 Model parameters of the extended SEM

2.1 The subcellular element model (SEM)

The SEM represents a cell by a collection of particles, the Subcellular elements (SCE), that interact via potential forces. The SCEs can be seen as a coarse-grained representation of a cell’s cytoskeleton. The Langevin equation of motion for the particle at position $\mathbf {y}_{\alpha _i}$ of SCE $\alpha$ of cell $i$ is given by

$$\begin{aligned} m {\ddot{\mathbf {y}}}_{\alpha _i} = \varvec{\xi }_{\alpha _i} - \eta {\dot{\mathbf {y}}}_{\alpha _i} + F^C(\mathbf {y}_{\alpha _i}) \end{aligned}$$

(1)

where $\varvec{\xi }_{\alpha _i}$ represents the thermal fluctuations and random cross-linking, polymerization and depolymerization events inside the cytoskeleton, $\eta$ is the viscous drag coefficient and $F^C(\mathbf {y}_{\alpha _i})$ are the pairwise forces on particle $\mathbf {y}_{\alpha _i}$.

The forces $F^C(\mathbf {y}_{\alpha _i})$ are derived from a modification of the empirical Morse potential, which has been used to model soft breakable bonds in polymers [11, 52]. The interaction potential between two particles at distance $r$ is given by

$$\begin{aligned} V(r) = u_0\,e^{2\rho \left( 1 - {r^2}/{r_{eq}^2}\right) } - 2\,u_0\,e^{\rho \left( 1-{r^2}/{r_{eq}^2}\right) }, \end{aligned}$$

(2)

where $u_0$ is the potential well depth, $\rho$ is a scaling factor and $r_{eq}$ is the equilibrium distance between two SCEs. The potential is repulsive for $r < r_{eq}$ to account for excluded volume effects and attractive for $r > r_{eq}$. To improve the computational performance of our implementation we define a cutoff $r_c = 2.5 r_{eq}$ and set a constant $V(r) = V(r_c)$ for $r > r_c$. We distinguish a potential function for the pairwise interaction between elements of the same cell $(V_{intra})$ and between particles of different cells $(V_{inter})$ by potential parameters $u_0^{intra}$ and $u_0^{inter}$ respectively. The $u_0^{intra}$ determines the interaction strength of the particles that model the cytoskeleton, whereas $u_0^{inter}$ is associated with the binding strength of receptor proteins that regulate cell-cell adhesion. Usually, we choose $u_0^{intra} > u_0^{inter}$. The pairwise forces $F^C(\mathbf {y}_{\alpha _i})$ are then computed as

$$\begin{aligned} F^C(\mathbf {y}_{\alpha _i})&= - \nabla _{\alpha _i} \sum _{{\beta _i}\ne {\alpha _i}} V_{intra}(|\mathbf {y}_{\alpha _i} - \mathbf {y}_{\beta _i}|) \nonumber \\&-\, \nabla _{\alpha _i} \sum _{j \ne i} \sum _{\beta _j} V_{inter}(|\mathbf {y}_{\alpha _i} - \mathbf {y}_{\beta _j}|). \end{aligned}$$

(3)

The noise term $\varvec{\xi }_{\alpha _i}$ is a vector of random variables $\xi ^m_{\alpha _i} (m=1,2\;\hbox {for}\; 2\hbox {D}, m=1,2,3 \; \hbox {for}\; 3\hbox {D})$ with mean zero and correlation

$$\begin{aligned} \langle \xi ^m_{\alpha _i}(t), \xi ^n_{\beta _j}(t') \rangle = 2 D \eta ^2 \delta _{i,j} \delta _{\alpha _i,\beta _j} \delta _{m,n} \delta (t-t'), \end{aligned}$$

(4)

where $D$ is the diffusion coefficient of the SCE, $m$ and $n$ are the vector components and $\delta$ denotes the Kronecker or Dirac delta function.

The cytoplasmic environment inside a cell is highly viscous. We can therefore assume over-damped motion $(m {\ddot{\mathbf {y}}}_{\alpha _i} \ll \eta {\dot{\mathbf {y}}}_{\alpha _i})$ [45], set $m {\ddot{\mathbf {y}}}_{\alpha _i} = 0$ and cast Eq. (1) into the framework of Brownian Dynamics

$$\begin{aligned} \eta {\dot{\mathbf {y}}}_{\alpha _i} = \varvec{\xi }_{\alpha _i} + F^C(\mathbf {y}_{\alpha _i}). \end{aligned}$$

(5)

The parameters for the model are computed given the radius $R_{cell}$ of a reference cell, the number of SCE per cell $N$, the stiffness $\kappa _0$ and the viscosity $\eta _0$ as

$$\begin{aligned} \begin{aligned} r_{eq}&= 2 R_{cell} (p_d/N)^{1/3},\ \eta = \eta _0/N,\\ \kappa&= \kappa _0 N^{-1/3} \left( 1 - \lambda N^{-1/3} \right) ,\ u_0 = \kappa r_{eq}^2 / (8\rho ^2), \end{aligned} \end{aligned}$$

(6)

where $p_d$ is the sphere close packing density and $\lambda = 0.75$ is a tuning coefficient for varying $N$ [57]. We set $p_d = \pi /(2\sqrt{3}) \approx 0.91$ for 2D and $p_d = \pi /(3\sqrt{2}) \approx 0.74$ for 3D simulations. We choose the stiffness $\kappa _0$ in the order of $10^{-3}\text {--}10^{-2}\;\hbox {N}\;\hbox {m}^{-1}$ and the viscosity $\eta _0$ in the order of $10^{-3}\text {--}10^{-2}\;\hbox {N}\;\hbox {s}\;\hbox {m}^{-1}$ [57]. Those values are derived from experimental measurements of the rheology of living cells [8, 14, 38, 62]. Sandersius et al. [57] conducted simulations to measure the viscoelastic properties of single cells subject to axial compression and stretching, showing good qualitative agreement with the experiments.

2.2 SEM++

The extensions of the proposed model include a modification of the potential function to increase adhesion between SCE, the polarization of cells, the smooth insertion and removal of SCE to model polymerization and depolymerization, the detection of cell membrane elements and a special SCE for the cell nucleus. These extensions are detailed below.

2.2.1 Potential functions

The potential function introduced in [57] (Eq. (2)) has been generalized here to allow for a dynamic shifting of the strength distributions of adhesion versus repulsion. The modified potential function is given by

$$\begin{aligned} V_m(r) = u_0\,e^{2\rho \left( 1 - {\tilde{r}(r)^2}/{r_{eq}^2}\right) } - \alpha \,u_0\,e^{\rho \left( 1-{\tilde{r}(r)^2}/{r_{eq}^2}\right) }. \end{aligned}$$

(7)

The potential parameters are the depth of the potential well $u_0$, the equilibrium distance $r_{eq} = r_{eq}(\alpha )$, the shifting parameter $\alpha$ and a scaling factor $\rho$. The specific case of $\alpha = 2$ recasts this potential into its original form (Eq. (2)). The magnitude of the force interacting in between different SCEs is then given by

$$\begin{aligned} F_m(r)&= -\delta _r V_m(r) = \frac{2 \tilde{r}(r) \rho u_0}{r^2_{eq}} \Big ( 2\,e^{2\rho \left( 1 - {\tilde{r}(r)^2}/{r_{eq}^2}\right) } \nonumber \\&- \alpha \,e^{\rho \left( 1-{\tilde{r}(r)^2}/{r_{eq}^2}\right) } \Big ) \end{aligned}$$

(8)

with the scaling function

$$\begin{aligned} \tilde{r}(r) = r \sqrt{1 - \log (2/\alpha )/\rho } \end{aligned}$$

(9)

to enforce $F(r_{eq}) = 0$.

The potential interaction defined above applies for both elements of the same cell (intra-cellular potential) and elements of different cells (inter-cellular potential). However, inter- and intra-cellular interactions are given by a different set of model parameters determining the interaction strength. The scaled profile of this modified force function for a set of different $\alpha$ values is depicted in Fig. 3.

Fig. 3

Potential force in 1D for different values of the shifting parameter $\alpha = 1, 2, 3, 4, 5, 6$, where the highest repulsive potential is realized with $\alpha = 1$ and the highest attractive potential for $\alpha = 6$. The remaining parameter values are set to $\rho = 2$ and $u_0 = 1$

2.2.2 Polarization

Polarity, the cells internal notion of direction, is induced by chemical and/or mechanical stimuli. In the context of this model, we do not consider any chemoattractant guiding cell motion. For migrating cells, we either directly assign a polarity vector to impose the direction of cell migration or we take the assumption that cell polarity is an observable property of the cell prescribed by its shape or elongation.

Fig. 4

Extracting cell polarity via the cell shape. Purple ellipse fitted to the cell shape with minor axis $A_{min}$ and major axis $A_{maj}$ defining two possible polarization directions $\mathbf {p}$ and ${\hat{\mathbf {p}}}$

Here, cell elongation is approximated by fitting an ellipse to the cell shape and extracting its major ($A_{maj}$) and minor ($A_{min}$) axes (see Fig. 4). The cell elongation can serve as a basis for polarity estimation. Cell polarity for cell $i$ is then imposed by the direction of the major axis: $\mathbf {p}_i = A_{maj}/|A_{maj}|$ . Given a polarity vector $\mathbf {p}_i$ per cell, we can further define the polar distance $p_{\alpha _i}$ of SCE $\alpha _i$ as the dot product of its distance from the cell center $\mathbf {y}_i$ and the polarization direction

$$\begin{aligned} p_{\alpha _i} = (\mathbf {y}_{\alpha _i} - \mathbf {y}_i) \cdot \mathbf {p}_i. \end{aligned}$$

(10)

2.2.3 Polymerization and depolymerization

Active, autonomous cell shape alteration and cell migration is the result of the assembly and disassembly of the cytoskeleton network via polymerization and depolymerization of actin filaments and microtubules. Although random polymerization events are accounted for in the noise term $\varvec{\xi }_{\alpha _i}$ of Eq. (5), this model does not qualify to capture the active dynamics of cytoskeleton remodeling in response to external stimuli.

We propose to model the building up and breaking down of the cytoskeleton via the explicit insertion and deletion of SCEs. In order to achieve a seamless, smooth and location independent insertion and removal of the selected elements for polymerization and depolymerization, we propose the introduction of a polymerization factor $\varphi _{\alpha _i}$ associated with each element. We define the time-interval for a polymerization event to occur as $T_p$.

The polymerization factor is defined by

$$\begin{aligned} \varphi _{\alpha _i}(t) = {\left\{ \begin{array}{ll} t/T_p, &{} t \le T_p,\\ 1, &{} t > T_p, \end{array}\right. } \end{aligned}$$

(11)

where $t$ denotes the time starting from the instant the element is inserted. For depolymerizing elements we use $1-\varphi _{\alpha _i}(t)$. For the interaction of element $\alpha _i$ with $\beta _j$, we consider two types of pairwise interactions $F_{p1}(r,\varphi )$ and $F_{p2}(r,\varphi )$ for polymerization and depolymerization respectively. Additionally, to the distance between the particles $r = |\mathbf {y}_{\alpha _i} - \mathbf {y}_{\beta _i}|$, we compute the polymerization interaction factor $\varphi = \varphi _{\alpha _i} \varphi _{\beta _j}$. The factor $\varphi$ scales the equilibration radius and for polymerization we cast Eq. (8) into the following form:

$$\begin{aligned} F_{p1}(r,\varphi ) = \frac{2 \tilde{r}(r) \rho u_0}{r^2_{eq}} \left( 2 E(r,\varphi )^2 - \alpha E(r,\varphi ) \right) \end{aligned}$$

(12)

with

$$\begin{aligned} E(r,\varphi ) = {\left\{ \begin{array}{ll} e^{\rho \left( 1-{\tilde{r}(r)^2}/{\left( \varphi r_{eq}\right) ^2}\right) }, &{} \varphi > 0,\\ 0, &{} \varphi = 0. \end{array}\right. } \end{aligned}$$

(13)

During depolymerization on the other hand, we wish to pull the surrounding SCEs towards the depolymerizing element. To this end, we modify Eq. (12) to amplify the adhesive part of the pairwise force as follows:

$$\begin{aligned} F_{p2}(r,\varphi )&= \frac{2 \tilde{r}(r) \rho u_0}{r^2_{eq}} \Big ( 2 E(r,\varphi )^2 \nonumber \\&- \left( \alpha + 8\left( 1-\varphi \right) \right) E(r,\varphi ) \Big ). \end{aligned}$$

(14)

Examples of the resulting force curves for varying values of $\varphi$ are shown in Fig. 5.

Fig. 5

Interaction force for different polarization coefficients $\varphi$. Left: Force for introducing an SCE as defined in Eq. (12). Right: Force for extracting an SCE as defined in Eq. (14). Curves are shown for values of $\varphi = 1(\textit{purple}), 0.9, .., 0.1(\textit{green})$. (Color figure online)

2.2.4 Cell membrane

We define the membrane of a cell to be represented by the outermost layer of SCEs enclosing all other SCEs of one cell. In order to detect the SCEs constituting the cell membrane, we introduce the membrane detection algorithms outlined below. In the proposed model, membrane particles are not explicitly and a priori tagged with this property but are instead identified by their SCE position within the cell. Living cells can be stretched or elongated to assume a membrane surface area six times its normal size. To account for this, in the proposed model, SCEs are integrated or removed from the membrane in a dynamic way, allowing the cell to change its surface area in response to stretching and compression. Mechanisms to limit the maximal membrane area by enforcing a membrane stiffness with respect to the cell surface area are subject of current investigations. Depending on the dimensionality of the model, we propose two different membrane detection algorithms for robustness and computational efficiency.

Fig. 6

Conceptual sketch of the membrane detection algorithm in 2D. a Dark elements denote the SCEs constituting the cell membrane, light elements are internal SCEs. b Neighbor elements of the SCE under consideration (dark element) are detected within a circle of radius $R_{2d}$. $\beta _{max}$ denotes the largest angular sector defined by the SCEs in the neighborhood of the SCE under consideration

Membrane detection in 2D models

For every SCE, we consider the elements of the same cell in its neighborhood defined by a circle of size $R_{2d}$. The neighborhood is then divided into angular sections defining the space between consecutive neighboring elements and the SCE under consideration. If the angle $\beta _{max}$ defining the largest of these sections exceeds a predefined threshold value $\beta ^{th}$, the element is considered part of the cell’s membrane. The membrane elements of cell $i$ are hereafter denoted by the subset $\alpha ^m_i$. We note that the algorithm works for both isolated and interacting cells. Furthermore, by taking the bisector of $\beta _{max}$, we get an estimate for the surface normal $\varvec{n}$ at the membrane element under consideration. A conceptual sketch of the membrane detection mechanism in 2D models is depicted in Fig. 6.

Membrane detection in 3D models

For every SCE, we count the elements in its neighborhood defined by a sphere of radius $R_{3d}$ belonging to the same cell $(N_{int})$ and to other cells $(N_{ext})$. For membrane elements, we expect to find a lower number of neighbor elements of the same cell $(N_{int})$. In the case of touching cells, we can identify membrane elements additionally by a high number of neighbor elements of a different cell. We set the threshold values for internal and external neighbor counts that determine membrane elements to $N_{int}^{th}$ and $N_{ext}^{th}$. We note that in an equilibrated setting, the internal neighbor count would be sufficient to identify the membrane elements. However, in the presence of a dynamic system where elements are introduced and removed locally, a threshold for external elements greatly improves the stability of the algorithm. A conceptual sketch of the membrane detection mechanism in 3D models is depicted in Fig. 7.

Fig. 7

Conceptual sketch of the membrane detection algorithm in 3D. a Thick outlined elements denote the SCEs constituting the cell membrane, light outlined elements are internal SCEs. b Neighbor elements (star) of the SCE under consideration (thick outline) are detected within a circle of radius $R_{3d}$. $N_{int}$ and $N_{ext}$, the number of neighboring elements belonging to the same cell (dark gray) and to another cell (light gray) are given for this example. (Color figure online)

Fig. 8

Interaction force of nucleus particle for different coefficients $\varphi$. Dashed lines represent the normal SCE potential force (Eq. (12)), solid lines represent the shifted nucleus potential force (Eq. (15)). Curves are shown for values of $\varphi = 1(\textit{purple}), 0.7, 0.4(\textit{green})$. (Color figure online)

2.2.5 Nucleus

The nucleus makes up around 5–10 % of a typical mammalian cell’s volume. Enclosed by the nuclear envelope, the nucleus is a compact structure isolated from the remaining cytoplasm. It has been observed experimentally that the nucleus behaves as a viscoelastic material similar to the cytoplasm, but with a 3–4 times increased stiffness and a viscosity of almost twice the magnitude measured in the cytoplasm [24]. Based on these differences in material properties and the size, we model the nucleus independently from the rest of the cell. Here, we approximate the ellipsoidal shape of the nucleus by a spherical nuclear element (NE) of radius $R_{nuc}$. As the choice of the specific interaction potential for the NE is empirical, in order to minimize the number of parameters, we maintain the same shape function and local support as introduced for the SCEs. We introduce a shifted version of the potential presented in Eq. (12) to account for the increased radius of the nucleus element. The resulting force is given as

$$\begin{aligned} F_{nuc}(r,\varphi ) = F_{p1}(n(r),\varphi ) \end{aligned}$$

(15)

with $n(r) = \max (r - n_{sft}, r_{min})$ and $n_{sft} = R_{nuc} - r_{eq}$. We note that the potential function is saturated inside $R_{nuc}$ at $F_{p1}(r_{min}, \varphi )$. In practice, we do not expect any SCEs to be located inside $R_{nuc}$. The nucleus potential can be faded in and out depending on parameter $\varphi$. This feature is used during cell proliferation to model nucleus disassembly and the segregation of chromosome material into two daughter nuclei during the M-phase (§4.3). The scaled profile of this force function for a set of different values of $\varphi$ is depicted in Fig. 8.

3 Implementation

The proposed methods have been implemented inside a C++ framework developed at the CSE Lab. The code explores object-oriented programming and thread level based parallelism of Intel’s TBB library. The object-oriented implementation allows for modular development and supports the adaptation and extension of existing methods. New concepts can easily be integrated and existing modules can be combined to assemble complex models. The flexibility of this framework is of key importance in developing novel methods and algorithms for cell-based models where the method of choice to model a certain phenomena is highly ambiguous. Often, the choice of one specific model over another is the result of an extensive validation and optimization process during which a number of implementations need to coexist.The framework integrates a GLUT based visualization engine that allows for direct visual feedback during development.The thread-based parallelism of the framework allows for efficient computations on multi-core architectures. However, it does not explore multi-processor parallelism or GPU based acceleration. Furthermore, the methods have not been subjected to extensive performance optimization.

To address this issue, we started to implement the core features of the extended SEM inside the LAMMPS framework [33, 51], a highly optimized parallel C++ library to conduct particle simulations in the field of MD on multi-node, multi-GPU clusters. In this way, limitations associated with the computational costs of individual-based models are addressed inside a highly efficient and thoroughly tested modeling framework for particle simulations that enables a boost in the modeled system size at almost no developmental cost. We evaluated a number of existing libraries used mainly for MD simulations including NAMD [44], Amber [3] and DESMOND [13]. Although performance is the main reason for integrating the SEM within these frameworks, the software needs to offer a set of key features to allow for this integration. Most MD frameworks are designed to be used at an interface level where the user provides scripts that drive the simulations. LAMMPS can in addition be used as a library, is very well documented and encourages the integration of new models directly inside the source code. An extension to the source code, especially the memory management, is essential to the integration of the SEM. Classic MD simulations usually keep the number of atoms (particles) fixed throughout the simulation, as they model a closed system. Simulating growth and death, however, demands the seamless insertion and deletion of elements in an efficient way. Of the different MD software we evaluated using these criteria, our results supported the selection of the LAMMPS framework as our platform of choice.

4 Applications

4.1 Cell stretching

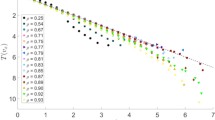
We performed simulations of creep response for single cells placed between two plates, modeling a related experimental study [14, 38]. In an in vitro experiment, a single cell is placed between two parallel, adhesive plates, one fixed and one movable in normal direction to the plate. A force is applied to the flexible plate and the strain of the cell is measured over time. In a computational setting, we initialize a cell between two adhesive walls (Lennard–Jones 9/3 wall potential) by continuously adding new SCEs at the center of the cell and then equilibrate the cell at its final size. This procedure initializes a quasi-random cell shape in a confined space between two plates (see Fig. 9). To exclude any far field effects of the wall potentials during cell stretching, we remove the walls and instead constrain the motion of the top and bottom layer of cells. The top layer is moved as a result of applying a stress $\sigma$ on the top wall while the bottom layer is kept fixed. In order to keep all wall particles in the same plane, the force applied on each top wall particle is calculated as $\mathbf {f} = {\hat{\mathbf {f}}} + \sigma \pi r^2_{eq}$, where ${\hat{\mathbf {f}}}$ is the average pairwise interaction force over all top layer elements. The simulation parameters are: $R_{cell} = 10\;\upmu \hbox {m},\; \kappa _0 = {5.0 \times 10^{-3}}\;{\hbox {N}\;\hbox {m}^{-1}},\; \eta _0 = {5.0 \times 10^{-3}}\;{\hbox {N}\;\hbox {s}\;\hbox {m}^{-1}},\; \rho =2$ and $\alpha =2$.

Fig. 9

Single cell growing between two fixed, adhesive plates. After equilibration, the bottom layer of SCEs are fixed while a force $\mathbf {f}$ is applied to the top row of SCEs. Bars at the top and bottom indicate the location of the plates. The small spheres show the distinct SCEs

Fig. 10

Comparison of simulations controlled by fixed diffusion coefficient $D$ (rough lines) and fixed temperature $T$ (smooth lines) subject to different applied stresses

Fig. 11

Influence of nucleus size on the creep response under different applied stresses. a $N = 1,000$ SCEs in reference cell without a nucleus. b $N = 8,000$ SCEs in reference cell without a nucleus

Cells are grown for ${200}\hbox { s}$ and relaxed for another ${100}\hbox { s}$ before the walls are removed. After removing the walls and assigning the wall layer particles, the system is relaxed for another ${4}\hbox { s}$. We perform creep response tests on the equilibrated system for applied stresses $\sigma$ of ${6.59}\;\hbox {Pa},\,{8.66}\;\hbox {Pa},\; {11.40}\;\hbox {Pa},\,{15.00}\;\hbox {Pa},\; {19.75}\;\hbox {Pa},\,{25.00}\;\hbox {Pa}$ and ${30.00}\;\hbox {Pa}$ for ${7}\;\hbox {s}$. The first five values for $\sigma$ correspond to simulation results reported in [57]. In order to capture recovery after the stress, we set $\sigma ={0}\hbox {Pa}$ for a period of ${4}\hbox { s}$ after the stretching.

Simulations of cells without a nucleus (see Fig. 10) are compared to simulations of cells including a nucleus element (see Fig. 11). We investigate cells with a nucleus of a size equivalent to 5, 10 and 20 % of the cells volume. To initialize the simulations including a nucleus, we remove SCE elements at the center of mass corresponding to the desired nucleus volume from the equilibrated cell holding no nucleus. We then introduce a nucleus element at the center of the cell and ramp up its polymerization parameter $\varphi$ over a time period of $T_p = {100}\hbox { s}$, followed by an additional equilibration period of ${10}\hbox { s}$. The nucleus potential parameters are set to the same values as for the SCE potential. We compare the creep response for cells with $N = 1,000$ and $N = 8,000$ elements. The system was integrated with Brownian Dynamics and Forward Euler time integration. The time steps during growth were set to $\varDelta t = {1.0 \times 10^{-3}}\hbox { s}$ and $\varDelta t = {2.5 \times 10^{-4}}\hbox { s}$ for $N = 1,000$ and $N = 8,000$ respectively. During the creep response test, a 10 times smaller $\varDelta t$ was used to ensure stability of the method. Additionally, we assessed two ways to control the random fluctuations during the creep response test: first with a constant diffusion coefficient $D = {1.6 \times 10^{-13}}\;\hbox {m}\;\hbox {s}^{-2}$ as reported in [57] and then with $D = k_B T / \eta$ computed with a fixed temperature of $T = {298}\hbox {K}$. We observe that the simulation results for a fixed diffusion coefficient D show more fluctuations in the strain curve. Otherwise, the creep response curves for a fixed temperature agree well with the results obtained for a bigger diffusion coefficient (Fig. 10). For large stresses, cells can be observed to rupture or undergo plastic deformations and are very sensitive to the level of discretization. We therefore consider to ignore the results obtained for stresses above ${19.75}\;\hbox {Pa}$.

Considering the simulation results in the absence and in the presence of a nucleus of varying size, we observe a viscoelastic creep response in all scenarios. In the presence of a large nucleus element, we observe a reduction in the observed deformation response. However, we find qualitative differences in the simulations corresponding to $N = 1,000$ SCEs and $N = 8,000$ SCEs (Fig. 11). Whereas the deformation is monotonically decreasing in the case where $N = 8,000$, for $N = 1,000$, we observe an increase in the observed deformation for a nucleus of 5 % volume before the deformation decreases for larger nuclei with respect to the reference case without a nucleus.

Sandersius and Newman introduced scaling formulas for the potential parameters and results are presented for cells composed of up to 1,000 elements [57]. Already in their work, the variations in the creep response was reported to increase with the number of elements per cell [57]. The large discrepancies in the simulation results obtained for cells with $N = 1,000$ and $N = 8,000$ elements suggest that the model parameter scalings for cells composed of even higher numbers of SCEs are not very accurate.

Fig. 12

Left to right: SEM simulation of cell migration via polymerization and depolymerization of the actin fiber network. Colors indicate polarization direction (pink front, green back). The membrane elements are marked by a black outline. The polymerization vector in this simulation is subject to random fluctuations (the image was adapted from [31]). (Color figure online)

In conclusion, these results suggest that inhomogeneities in the cytoplasm of the cell, as induced by a large organelle such as the nucleus, could have an important effect on the viscoelastic properties of the cell. We note, however, that the presence of a nucleus element does not change the response curve qualitatively. This effect could possibly be accounted for by adjusting the potential parameters. In the light of the presented results, the effect of a nucleus element on the creep response of cells under stress and the scaling behavior of the Subcellular Element Model for large numbers of elements per cell needs to be further investigated.

4.2 Cytoskeleton remodeling

Cytoskeleton remodeling in response to external mechanical and chemotactic stimuli can lead to alterations in the cell shape, structural reinforcement and migration, depending on the coordinating mechanisms that dictate the location of polymerization events. With the machinery for polymerization and depolymerization of distinct SCEs in place, we propose two different models for polymerization. We first introduce a polarity driven polymerization method that leads to directed cell migration. Secondly, we propose a density aware model for polymerization to account for the cell response to mechanical stimuli as a result of internal and external compression. We introduce the notion of a cytoskeleton density $d_{\alpha _i}$ at each element to be defined as the number of SCEs $\beta _j$ inside a defined neighborhood of radius $R_{dens}$. The density is further refined into the internal density $d^{int}_{\alpha _i}$, only considering neighborhood elements of the same cell $(i = j)$ and the external density $d^{ext}_{\alpha _i}$, only considering the neighborhood elements of different cells $(i \ne j)$.

Cell Migration (Polarity aware Polymerization) Cells can be observed to hold a persistence of direction in their migrative behavior [19]. In mesenchymal cell migration, the persistence of direction is a result of the polarization of the cell regulating the assembly and destruction of the actin cytoskeleton, in combination with orchestrated binding and unbinding of adhesion molecules of the cell membrane to the ECM. In the current model, focal adhesion sites are not explicitly modeled. In the 3D model, substrate adhesion is accounted for by introducing a wall potential force. Here, we employ a (9,3) LJ potential

$$\begin{aligned} V_w\left( r\right) =3\sqrt{3}\varepsilon \left[ \left( \frac{\sigma }{r} \right) ^9-\left( \frac{\sigma }{r}\right) ^3\right] , \end{aligned}$$

(16)

with $\varepsilon$ being the well depth and $\sigma$ the interaction length parameter. We determine the polarization distance $p_{\alpha _i}$ (Eq. (10)) of each element within cell $i$ and fit a normal distribution to the polarization distances $(\mathcal {N}(\mu _i, \sigma _i^2))$. From this distribution, we determine a threshold polarization $(\varPi _p)$ and depolarization $(\varPi _{dp})$ distance at the front and end of the cell as

$$\begin{aligned} \begin{aligned} \varPi _{dp}&= \mu _i-\pi _{dp}\sigma _i, \\ \varPi _{p}&= \mu _i+\pi _{p}\sigma _i, \\ \end{aligned} \end{aligned}$$

(17)

and randomly pick one element with $p_{\alpha _i} \ge \varPi _p$ and one element with $p_{\alpha _i} \le \varPi _{dp}$ for polymerization and depolymerization respectively. Polymerizing elements are inserted at the exact location of the identified element by the procedure proposed above. The smooth introduction of the element guarantees stability of this approach. In short, the proposed method suggests to remove an element at the cell’s trailing edge and introduce it at the leading front whilst keeping the cell’s integrity. Transport of depolymerized actin is not modeled implicitly, however, a balance between polymerized and depolymerized fibers is enforced as the events are coupled.

Fig. 13

3D simulation of cell migration in the SEM framework. Blue cell shape evolution, red polymerizing and depolymerizing elements. (Color figure online)

We present simulation results for single migrating cells in an in vitro environment in (Fig. 12, 2D) and (Fig. 13, 3D). Cell migration in the Subcellular Element Model has been considered before where cells are represented by single elements ($N = 1$) [46]. In this scenario, cell migration is realized by an advection velocity on the cell particle. Sandersius et al. [58, 59] have motivated coordinated polymerization as a driving mechanism in cell migration that resemble closely the model presented in this work.

Cell Reinforcement (Density aware Polymerization) Cells have been shown to react to external stimuli by mechanotaxis and cytoskeleton remodeling [29]. They do so in response to mechanical cues propagated by their environment, the extracellular matrix or migrating neighboring cells, in order to reinforce the stress fibers where needed or to evade highly populated tissue regions. We account for this behavior by including a mechanism to sense the cytoskeleton density at each element and coordinate the polymerization activity in response.

We investigate a number of different strategies to drive polymerization in response to pressure, including the location (at the membrane, internal, both), and the direction (low to high density, high to low density) of polymerization and the metric for density (internal $(d^{int}_{\alpha _i})$, external $(d^{ext}_{\alpha _i})$). Only two variations of these strategies show to be stable (maintain cell connectivity) for three interacting cells and a variety of parameters:

• 1 Only the internal density is considered and either all or only the membrane elements are subject to polymerization. Depolymerization happens at regions of low density and polymerization at regions of high density. This leads to a reinforcement of the cell in regions where it is compressed. This behavior is consistent with observations of cells reinforcing their actin network or basal lamina outside the cell in response to mechanical stress.

• 2 Only the external density is considered and only the cell membrane elements are subject to polymerization. This leads to a short migrative behavior of the cells to evade cell contact. This mechanism could initiate the polarization of the cell to migrate away from others.

Fig. 14

2D simulation of one migrating cell initially located to the right (a: white, b&c: orange) interacting with a second cell via cell-cell adhesion compared to experiments (d). The cell to the left is quiescent (a: red) or actively remodeling its cytoskeleton form regions of low to regions of high density as defined by $d_{\alpha _i}$ (b: blue) or $d^{int}_{\alpha _i}$ (c: blue). The last row shows an experimental observation of two living cells circling around each other (d). (Color figure online)

In Fig. 14, we report simulation results of cell migration subject to cell-cell adhesion. We observe one cell migrating along its major elongation axis subject to cell-cell adhesion forces exerted by a neighboring cell that is not migrating. For the non-migrating cell, we investigate three different scenarios: no active remodeling of the cytoskeleton (Fig. 14 a) and the two scenarios outlined above (Fig. 14 b,c). We find that with no active remodeling of the cytoskeleton in the non-migrating cell, the two cells loose contact very quickly. In contrast, if polymerization is active from low density to high density regions as defined by the metric $d_{\alpha _i}$, the cells remain in close contact and a circling pattern of the migrating cell around its neighboring cell can be observed. Such circling patterns are commonly observed in real cells. In Fig. 14 d, we show how two keratinocytes migrate on a collagen-coated substrate. The growth factor FGF7 was added to some of the cells to stimulate migration and the cells start circling around each other due to cell-cell adhesion [37]. The experimental images were provided by Michael Meyer from the Werner lab at ETH Zürich (HPL, Otto-Stern-Weg 7, 8093 Zürich, Switzerland).

From the simulations we observe that this behavior is very sensitive to the density sensing mechanism. Removing the external elements from the density estimation $(d^{int}_{\alpha _i})$ does not lead to the same behavior. These observations suggest that cytoskeleton remodeling plays a major role in cell-cell interactions observed during migration and pattern formation. Not only the processes that drive polymerization in the migrating cells but also the adhesion interactions and polymerization dynamics in neighboring cells can strongly influence and direct cell migration. It is therefore important for future works to carefully calibrate such migration models with experimental data. Data from wound healing assays [20, 40] or the growth of blood vessels in the mouse retina [41] could be used to fit parameters for the models and to quantify their uncertainties [6].

We note that the active reinforcement of the cell’s cytoskeleton has previously been addressed in the context of tissue stretching and during migration in epithelial like tissue sheets [59].

4.3 Growth and proliferation

The study of cellular growth and proliferation within the SEM framework has previously been proposed by Alt et al. [2]. The method suggests that at every time point, a subset of SCEs located in the center of the cell is allowed to duplicate with a small probability. For each duplicating element, a location at a distance $r_e$ from the element is selected. If the point is sufficiently far away from all neighboring elements, the new element is introduced at that location. Iterative equilibration of the potential forces will integrate the new element into the structure. Once a cell reaches an appropriate size, the cell is divided by a plane through the center of mass, perpendicular to the longest axis of the cell.

Here, we propose a refined model of cellular growth and proliferation that shares some common features with the method proposed in [2]. Having introduced a nucleus element, we can use this particle to store additional information about the cell, such as the cell cycle or its phenotype. We define three internal states for a cell: quiescent, migrating and proliferation. A cell undergoing proliferation can further reside in four states of the cell cycle: quiescent (G0, gap 0), growth (I, Interphase), nuclear division (M1, mitosis) and cytoplasmic division (M2, cytokinesis). Transition from one stage to the next are given by intervals $T_{G0},\,T_{I},\,T_{M1}$ and $T_{M2}$ sampled from a normal distribution with defined mean phase residence time $\mu _{G0,I,M1,M2}$ and standard deviation $\sigma _{G0,I,M1,M2}$.

• G0 After a cell division has occurred, the two daughter cells enter the quiescent state. The cells stay in the quiescent state to equilibrate for the time period $T_{G0}$ before the cells transit to the growth phase.

• I Cell growth is modeled via the duplication of SCEs at regular intervals over the time period $T_{I}$. The duplicating element is chosen at random and a new element is inserted at the exact location of the duplicated element. The polymerization factor is set to $\varphi _{\alpha _i}=0$ and ramped up to $\varphi _{\alpha _i}=1$ over the time interval $T_p={T_{i}}/{N}$. In this way we ensure that the location of insertion does not lead to any numerical instabilities and cell growth proceeds in a smooth manner. Variations to the proposed method to confine the region allowed for duplication to the center of the cell can easily be implemented.

• M1 When the cell has doubled in size, the cell cycle advances to the M1 phase where the nucleus breaks up into chromosomes which are divided to create two new nuclei. The nucleus is broken up by setting its polymerization factor $\varphi _{\alpha _i}=0$ and a second nucleus is introduced at the location of the original one. During the M1 and M2 phase, the nuclei elements take on the function of the two poles of the mitotic spindle. Over the time period $T_{M1}$, the two nuclei polymerization factors are ramped up. At the same time, the polymerization factor of the SCEs in the dividing cell is slightly increased to model swelling in size of the dividing cell [10]. Together, this leads to the separation of the two nuclei and the aggregation of SCEs around them. This way, the separation axis of the two nuclei, and accordingly the elongation of the cell is driven by the mechanical properties of the surrounding tissue.

• M2 After the two new nucleus elements have polymerized to attain their final size, the cell is split by assigning every SCE to the closest nucleus element inside the cell. The method does not depend on the introduction of a splitting plane and the orientation of cell division is driven by the mechanical properties of the surrounding tissue. Over the time period $T_{M2}$, the two new cells are equilibrated and the polymerization factor of the individual SCEs is smoothly decreased back to unity, reverting the swelling of the cell.

Fig. 15

3D simulation of cell proliferation. SCE elements are duplicated at regular time intervals until the number of SCEs per cell has doubled. Before cell division, a second nucleus element is introduced and cell division proceeds by assigning each SCE to its closest nucleus. Growth progression: bottom left to top right. Blue cell membrane, red nuclei. (Color figure online)

We would like to stress that in the context of cell proliferation, the polymerization factor is used to model phenomena different than actin polymerization. The observed swelling of cells during proliferation is not a result of increased polymerization, but a result of an increase in the intracellular osmotic pressure.

In the proposed simulation framework, the polymerization factor acts as a scaling coefficient to the potential function and thus can be used to model the swelling of the SCEs as a result of osmotic swelling. Likewise, as mentioned above, the nucleus elements take on the role of the mitotic spindle in phases M1 and M2. A 3D simulation result of the proliferation algorithm is shown in Fig. 15.

4.4 Juxtacrine signaling

Multicellular organisms depend on effective and robust communication channels in order to coordinate collective behavior during development, growth and pathology (e.g. tip cell selection during angiogenesis). In time, a number of different signaling channels have evolved to integrate mechanical, chemical, even electrical information form close and distant locations. Here, we focus on the chemical signaling of membrane bound ligand-receptor complexes acting between neighboring, physically touching cells, referred to as juxtacrine signaling [36].

The mechanism has been studied in the context of spatially heterogeneous pattern formation and gene expression. Stochastic simulations of pattern forming reaction–diffusion systems can be used to study the effect of noise at low molecule numbers [7, 9, 21, 22]. Here, we propose an implementation of juxtacrine signaling inside the extended SEM framework and study the influence of added noise and intrinsic noise as a result of the number of SCEs per cell.

Model of Juxtacrine Signaling The model studied here was presented for homogeneous systems in [47] and serves as a simple, generic model of juxtacrine signaling. The model consists of three membrane bound molecular entities per cell $i$: ligand $a_i$, receptor $f_i$ and the bound ligand-receptor complex $b_i$. It describes the basic dynamics of reversible ligand-receptor binding, internalization and production and decay of ligand and receptor molecules as

$$\begin{aligned} \begin{aligned} \frac{\partial a_i}{\partial t}&= -k_a a_i \langle f \rangle _i + k_d \langle b\rangle _i - d_a a_i + P_a(b_i), \\ \frac{\partial f_i}{\partial t}&= -k_a \langle a \rangle _i f_i + k_d b_i - d_f f + P_f(b_i), \\ \frac{\partial b_i}{\partial t}&= k_a \langle a \rangle _i f - k_d b_i - k_ib_i, \\ \end{aligned} \end{aligned}$$

(18)

where $k_a$ is the receptor-ligand binding association rate, $k_d$ is the disassociation rate, $k_i$ is the internalization rate and $d_a$ and $d_f$ are the the decay rates for ligand $a_i$ and receptor $f_i$ respectively.

In the original model, the notation $\langle \rangle$ indicates the average concentration over the neighboring cells, accounting for the fact that receptors of cell $i$ can only bind to ligands of the neighboring cells. The model implicitly assumes that ligand and receptor concentrations are distributed homogeneously on a cells’ membrane and that cells are arranged in a regular pattern, sharing an equal cell surface fraction with all neighboring cells. In the framework of SEM, these assumptions do not hold, as cell shape and position are not regular and fixed. We therefore define the operator $\langle \rangle$ as a weighted sum, accounting for the membrane fraction shared with each individual neighboring cells:

$$\begin{aligned} \langle x \rangle _i = \sum _{n\in \mathcal {N}_i}x_n f_{n,i}, \end{aligned}$$

(19)

where $\mathcal {N}_i$ is the set of neighboring cells of cell $i$ and $f_{n,i}$ is the fraction of the membrane area of cell $n$ in contact with cell $i$. Currently, this model assumes that ligands and receptors are homogeneously distributed on the membrane. However, the model could easily be extended to account for spatially heterogeneous distribution of molecules along the cell membrane.

The model includes a feedback mechanism that links the production rates of both the ligand $a_i$ and receptor $f_i$ to the bound receptor-ligand complex $b_i$. The feedback functions $P_a$ and $P_f$ are monotonically increasing, saturating Hill functions defined as

$$\begin{aligned} \begin{aligned} P_a(b)&= \frac{C_1^m b^m}{C_2^m + b^m}, \\ P_f(b)&= C_3 + \frac{C_4^n b^n}{C_5^n + b^n}, \end{aligned} \end{aligned}$$

(20)

with parameters $C_1,\ldots C_5$ and $n$. This model has been shown to produce spatial heterogeneous patterns in 1D and 2D systems [48] and the wavelength of the established patterns has been linked to the model parameters and the specific feedback functions $P_a$ and $P_f$ [47, 48, 61]. The influence of intrinsic noise arising from the stochastic treatment of the model and extrinsic, added noise to the deterministic set of ODEs, has been studied in [56]. They showed that this noise could have an accelerating effect on the patterning process.

Pattern quantification In order to measure progression during pattern formation, we define a metric that quantifies patterning at a certain point in time during simulation. Here, a pattern is characterized as a spatial inhomogeneity in some chemical species. Hence, we define the patterning intensity $I$ that sums up the concentration differences over each cell and its neighbors:

$$\begin{aligned} I=\sqrt{\sum _i \left( b_i - \bar{b}_i \right) ^2}, \end{aligned}$$

(21)

where $\bar{b}_i$ represents the average concentration of $b_i$ in neighboring cells defined as

$$\begin{aligned} \bar{b}_i=\frac{1}{\mathcal {N}}\sum _{n \in \mathcal {N}_i} b_n. \end{aligned}$$

(22)

Averaging weighted by the contact area with neighboring cells did not alter the observations made below.

We focus on the concentration of receptor-ligand complex $b$, as the complex induces the activation of a signaling pathway that could lead to migration, changes in morphology and gene expression. Note that the intensity $I$ is not normalized by the number of cells in the simulation and does not qualify to compare systems of different size. We do not consider the absolute magnitude of this function but are interested in its temporal evolution to determine when a pattern has stabilized (reached a constant value of $I$). A constant patterning intensity does not necessarily indicate a static pattern. Traveling or alternating patterns could also reflect a constant value of $I$.

Implementation details We determine the fraction of membrane protein $p$ of cell $j$ that is presented to cell $i$ as follows. For each membrane element $\alpha _i^m$ of cell $i$, we count the membrane elements $\beta _j^m$ of neighboring cells inside an interaction radius $r_m$ and store their number $N_{\alpha _i^m}$ on the membrane particle $\alpha _i^m$. We define the neighborhood of interacting elements around $\alpha _i^m$ as

$$\begin{aligned} \mathcal {N}_{\alpha _i^m} = \lbrace \beta _j^m | \left( i \ne j \right) \, \wedge ( \parallel \mathbf {y}_{\alpha _i^m} - \mathbf {y}_{\beta _j^m}\parallel \le r_m ) \rbrace . \end{aligned}$$

(23)

The amount of membrane bound protein $p$ that neighboring cells $j$ presents to cell $i$ is then calculated as

$$\begin{aligned} \langle p \rangle _i=\sum _{\alpha _i^m} \sum _{\beta _j^m \in \mathcal {N}_{\alpha _i^m}} \frac{N_{\beta _j^{m}}}{\sum _{\gamma _j^m} N_{\gamma _j^m}}p_j. \end{aligned}$$

(24)

Fig. 16

Conceptual sketch of the simulation domain and boundary conditions

Fig. 17

Time evolution of the intensity $I$ averaged over 19 simulations for different initial noise levels (0.01, 1, 5, 10 and 50 %). Cells are discretized with one SCE per cell

Results

All presented results are conducted in a periodic simulation domain containing 64 cells arranged in an eight by eight grid (see Fig. 16). The parameter values are set as proposed in [56]. All simulations are subject to the following initial conditions: $a={477.5}\;\hbox {mol}$, $f={1924.9}\;\hbox {mol}$ and $b={198.7}\;\hbox {mol}$, the steady state solution in the absence of any noise.

In a first set of simulations, each cell is discretized with only one SCE per cell. This removes any intrinsic noise in the system that might result from spatial inhomogeneities in cell contact areas of cells discretized with many elements. The cell conformation corresponds to the situation of a 2D regular, hexagonal grid. To initiate the pattern forming process, we add a defined amount of uniform multiplicative noise (0.01, 5, 10 and 50 %) and study the pattern forming dynamics. For each noise level, we ran 19 simulations and present the patterning intensity $I$ (see Fig. 17).

For all five investigated noise levels, we observe an initial steep increase of the intensity until a maximum level is reached, followed by a drop to about $80-85\%$ of the maximum. Thereafter, it rises again by $\sim 1\%$ and stabilizes. The steady state intensity represents the formation of a stable pattern and is located around the same level for all simulated noise levels, whereas the maximally attained intensity is slightly lower in the presence of $50\%$ noise as compared to the other noise levels. However, a striking difference can be seen in the transient phase during the beginning of the simulations. Whereas the slope of the intensity is similar for all simulated noise levels, they are shifted along the time axis with the maximum appearing earlier for higher simulated noise levels. This indicates that pattern formation in the studied system is faster as the initial noise level is increased, which is consistent with previous observations [56].

The observations above suggest that pattern formation in juxtacrine signaling networks that feature a feedback mechanism are not only dependent on noise but converge faster as the noise level increases. In multicellular tissues, intrinsic noise is present in the form of local variations in membrane bound protein expression and cell shape irregularity.

In the following, we want to investigate the influence of intrinsic noise inside the Subcellular Element Model on the pattern forming dynamics as a result of the number $N$ of SCEs per simulated cell. Moving from a one SCE per cell discretization to many SCEs per cell will brake the regularity of the neighbor contact areas and the cell positions and therefore introduce intrinsic noise in the signaling model at every simulated time step (not only at the beginning of the simulation). Here, we investigate five discretization levels with $N=10,25,50,75$ and $100$. Cells are initialized in a hexagonal grid configuration by placing all SCEs of a cell randomly around the cells center of mass. Before the simulation of the signaling network is started, SCE positions are fixed upon equilibration and the signaling levels are reset to the steady state initial conditions.

Fig. 18

Time evolution of the intensity $I$ averaged for 4 simulations. Results are shown for 5 different numbers of sub-cellular elements per cell

We report the evolution of the patterning intensity $I$ for a varying number of SCEs per cell in Fig. 18. We note that the intrinsic noise in the system is sufficient to initiate pattern formation in all five configurations and an intensity plateau is reached after 800 min. Again, all intensity curves show a steep initial increase until they reach a maximum intensity. For 25 and more SCEs per cell, the maximum is reached at around 400  min and the attained intensity maximum increases with the number of SCEs. After reaching the maximum in $I$, the intensity level decreases to stabilize at around 800 min. In contrast to the situation of one SCE per cell and different noise levels, the intensity functions for different numbers of SCEs do not collapse to the same value.From the presented results we deduce that higher numbers of SCEs lead to a higher intensity plateau. We also note that these steady state intensity levels are higher than what was observed for the single SCE case. The situation for 10 SCEs is markedly different from the other configurations. The characteristic peak in $I$ is not present and the intensity converges to a much higher value than what is observed for the other cases.

For higher numbers of SCEs (>25) we conclude that the intrinsic noise of the SEM and its variations due to cell resolution are different from what was observed for added initial noise simulations of single SCE cells. Cell resolution does not affect the speed of pattern formation but influences the observed intensity level. Comparing the time it takes to reach the maximal intensity, the simulations with many SCEs roughly correspond to the ones with a single SCE with 5 % added noise. The differences in the intensity plateau level could be a result of the intrinsic noise (a result of spatial contact inhomogeneities) that is continuously influencing the system as opposed to noise that is added at the beginning of the simulation.

5 Summary and outlook

In this work, we presented SEM++, an extension to the Subcellular Element Method [45, 57] that explicitly considers sub-cellular components such as the cell nucleus and the cell membrane. We introduce modifications to the potential functions of the Subcellular Elements that allow for polymerization and depolymerization as observed during migration and active cytoskeleton remodeling. SEM++ introduces a refined, unsupervised proliferation mechanism, actin polymerization driven cell migration and membrane protein mediated juxtacrine signaling.

SEM++ is implemented in an object-oriented, standalone C++ framework that allows for fast prototyping and model development. Furthermore, the methods have been integrated into the LAMMPS framework [33, 51] to benefit from its highly efficient and parallel implementation for particle simulations.

The model is well suited to resolve shape, structure and spatial interactions between cells. The computational elements inside the cell could further be used to model intra-cellular transport and signaling pathways operating in different locations of the cell. To accurately account for the extracellular milieu, the model needs to be extended or coupled to a model that captures the interaction of the cells with the surrounding ECM and can simulate signaling and transport processes inside the ECM. Since the method relies on discrete computational elements, it can readily be coupled to multiscale particle methods which can be used resolve the processes within the ECM [30].

Currently, the SEM does not consider directionality or heterogeneity inside a cell. The cytoskeleton of a cell is by no means a homogeneous network, as it is composed of oriented and elongated fiber bundles that are cross-linked to give the cell structure and shape. This could limit the application of the SEM in scenarios where cells at equilibrium assume an elongated shape, such as epithelial cells of the connective tissue or neurons. The introduction of spatially varying SCE potentials, elliptically shaped potential functions or fixed bonds in-between SCEs could address these limitations. Ongoing work focuses on the coupling of particle model with experimental data [20, 40, 41] and the quantification of uncertainties in the force field following related work of our group on Molecular Dynamics [6].