1 Introduction

Increasing electricity consumption is reflected in an increasing need to transmit higher and higher amounts of energy and a permanent expansion of existing transmission system. Land requirements and investments in a new part of transmission system can be greatly reduced by multi-circuit transmission lines on the same tower [1]. The lines can go side by side in their entire length or only in their part and transmission system becomes more and more interconnected. Line conductors on the same tower are placed close to each other, and currents flowing through them are affected by each other’s mutual impedances [2, 3]. Mutual impedances primarily depend on distances between conductors [4]. The distances are not the same between all conductors, and current unbalance arises in all affected lines [5]. Final value of unbalance can also be affected by other technical aspects such as the asymmetrical loads [6] or series compensation [7]. Unbalance is a complex problem of entire transmission system, and its reduction must also be solved in a complex way.

The problem is more obvious from Fig. 1a. There are symmetrically placed three phase conductors L1, L2 and L3 with mutual distance a, and one shield wire E above with unequal distances b and c. The mutual impedances between wires are dependent on these distances. If such a line is symmetrically loaded, symmetrically supplied, and the shield wires properly grounded through earth resistances, the phase currents are unbalanced.

Fig. 1
figure 1

Unbalance of transmission lines and its reduction

Full size image

In case of a simple transmission line, unbalance reduction can be achieved by classical method of transposition shown in Fig. 1b. While the shield wire is still in the same position (not drawn in Fig. 1b), the line is divided into three equal sections and phase conductors are alternated with each other. In each section, the current is induced into the shield wire but final summation along the entire line length is zero and the line loading is balanced.

In an interconnected system, transmission lines do not have to go side by side in their entire length, and a case depicted in Fig. 1c can occur. There are two transposed transmission lines T1 and T2. The lines go side by side on the same tower only for part of their length, and despite the fact that their transposition has been performed, the currents in both lines are also unbalanced.

Calculation simulations, analyses and reduction of the transmission lines current unbalance have been under research many times [3, 5, 7,8,9,10,11,12,13,14,15,16,17,18,19,20]. However, all the previous studies concern two parallel lines or multi-circuit transmission lines on the same tower of the point-to-point type, i.e. with a common sending and receiving end for all calculated lines. However, a real meshed transmission system has a much more complex configuration, where most lines go in parallel with another one for only a part of their length, the simplest case is in Fig. 1c. Considering this real topology brings an advanced level for the current unbalance calculation and the problem becomes much more complex.

For the current unbalance assessment, the unbalance factor is introduced in [1, 2], such as:

$$m_{f} = \left| {\frac{{\hat{I}_{0} }}{{\hat{I}_{1} }}} \right| \times 100\%$$
(1)

where mf is unbalance factor; \(\hat{I}_{0}\) is zero sequence current; \(\hat{I}_{1}\) is positive sequence current of one transmission line. High value of the factor can affect tripping of line protections [10, 19, 21] or increase the shield wire losses [11, 22,23,24,25,26]. Therefore a number of transmission system grid codes define its maximal allowed value, mainly for new lines constructions or reconstructions.

Due to aforementioned facts, transposition as a standard countermeasure may be a complex problem. A possible way of mf reduction is usually selecting the best solution from all the available ones but also considering economic aspects.

2 Calculation procedures

Unbalance factor mf of selected transmission line can be calculated by (1). In (1) zero sequence current \(\hat{I}_{0}\) and positive sequence current \(\hat{I}_{1}\) occur, hence all phase currents in selected transmission line must be calculated.

The presented methodology only calculates the current unbalance caused by transmission lines. The final current unbalance is affected by any load connected to the line, and the result is distorted. To get the line unbalance value, the symmetrical voltage source is connected to one side of the line, and the opposite side is short-circuited. The matrix equation for one section of n lines T1, T2, …, Tn placed on the same tower can be written as:

$$\left[ {\begin{array}{*{20}c} {\hat{\varvec{U}}_{T1} } \\ {\hat{\varvec{U}}_{T2} } \\ \vdots \\ {\hat{\varvec{U}}_{Tn} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1} } & {\hat{\varvec{Z}}_{T1,T2} } & \cdots & {\hat{\varvec{Z}}_{T1,Tn} } \\ {\hat{\varvec{Z}}_{T2,T1} } & {\hat{\varvec{Z}}_{T2,T2} } & \cdots & {\hat{\varvec{Z}}_{T2,Tn} } \\ \vdots & \vdots & {} & \vdots \\ {\hat{\varvec{Z}}_{Tn,T1} } & {\hat{\varvec{Z}}_{Tn,T2} } & \cdots & {\hat{\varvec{Z}}_{Tn,Tn} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T2} } \\ \vdots \\ {\hat{\varvec{I}}_{Tn} } \\ \end{array} } \right]$$
(2)

where \(\hat{\varvec{I}}_{T1} ,\hat{\varvec{I}}_{T2} , \ldots ,\hat{\varvec{I}}_{Tn}\) denote the current vectors for all currents in the line, i.e. phase conductors and shield wires as well; \(\hat{\varvec{U}}_{T1} ,\hat{\varvec{U}}_{T2} , \ldots ,\hat{\varvec{U}}_{Tn}\) denote voltage vectors; and for example, \(\hat{\varvec{Z}}_{T1,T2}\) denotes a sub-matrix respecting the mutual couplings between transmission lines T1 and T2. An example of the mutual coupling between the first and the last line T1 and Tn with one common shield wire can be written as:

$$\underbrace {{\left[ {\begin{array}{*{20}c} {\hat{U}_{L1} } \\ {\hat{U}_{L2} } \\ {\hat{U}_{L3} } \\ {\hat{U}_{E} } \\ \end{array} } \right]}}_{{\hat{\varvec{U}}_{T1} }} = \ldots + \underbrace {{\left[ {\begin{array}{*{20}c} {\hat{Z}_{L1,L1} } & {\hat{Z}_{L1,L2} } & {\hat{Z}_{L1,L3} } & {\hat{Z}_{L1,E} } \\ {\hat{Z}_{L2,L1} } & {\hat{Z}_{L2,L2} } & {\hat{Z}_{L2,L3} } & {\hat{Z}_{L2,E} } \\ {\hat{Z}_{L3,L1} } & {\hat{Z}_{L3,L2} } & {\hat{Z}_{L3,L3} } & {\hat{Z}_{L3,E} } \\ {\hat{Z}_{E,L1} } & {\hat{Z}_{E,L2} } & {\hat{Z}_{E,L3} } & {\hat{Z}_{E,E} } \\ \end{array} } \right]}}_{{\hat{\varvec{Z}}_{T1,Tn} }}\underbrace {{\left[ {\begin{array}{*{20}c} {\hat{I}_{L1} } \\ {\hat{I}_{L2} } \\ {\hat{I}_{L3} } \\ {\hat{I}_{E} } \\ \end{array} } \right]}}_{{\hat{\varvec{I}}_{Tn} }}$$
(3)

where \(\hat{I}_{L1} , \, \hat{I}_{L2} , \, \hat{I}_{L3}\) are phase currents; \(\hat{U}_{L1} , \, \hat{U}_{L2} , \, \hat{U}_{L3}\) are phase voltages of the symmetrical voltage source; \(\hat{U}_{E}\) is the shield wire voltage; \(\hat{I}_{E}\) is the shield wire current; and for example, \(\hat{Z}_{L1,L2}\) is mutual impedance between phases L1 and L2. If a continuous (or frequent) earthing of shield wire is assumed, its voltage is equal to zero, i.e. \(\hat{U}_{E} = 0\). In case of only one shield wire for all n transmission lines on the same tower, the dimension of full impedance matrix is \((3 + 1) \times n\). The reason for using n (virtual) shield wires is obvious in Fig. 2. There are two transmission lines T1 and T2 with one shield wire (in Fig. 2 blue-dashed).

Fig. 2
figure 2

Reason for using virtual shield wires and determination of voltage sources

Full size image

The system is described by three matrices \(\hat{\varvec{Z}}_{A}\), \(\hat{\varvec{Z}}_{B}\), and \(\hat{\varvec{Z}}_{C}\). Matrices \(\hat{\varvec{Z}}_{A}\) and \(\hat{\varvec{Z}}_{B}\) (dimensions are 4×4) are respectively used for sections A and B (consisting of one transmission line with one shield wire) where both lines go separately and matrix \(\hat{\varvec{Z}}_{C}\) (dimension is 7×7) is used for section C (consisting of two transmission lines with one shield wire) where both lines go side by side. The overall circuit matrix equation is as follows:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\hat{\varvec{U}}_{T1} } \\ {\hat{\varvec{U}}_{T2} } \\ \end{array} } \right] &= \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{A} } & {\mathbf{0}} \\ {\mathbf{0}} & {\hat{\varvec{Z}}_{B} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T2} } \\ \end{array} } \right] + \hat{\varvec{Z}}_{C} \left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T2} } \\ \end{array} } \right] \hfill \\ & = \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1}^{A} } & {\mathbf{0}} \\ {\mathbf{0}} & {\hat{\varvec{Z}}_{T2,T2}^{B} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T2} } \\ \end{array} } \right] \hfill \\& \quad + \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1}^{C} } & {\hat{\varvec{Z}}_{T1,T2}^{C} } \\ {\hat{\varvec{Z}}_{T2,T1}^{C} } & {\hat{\varvec{Z}}_{T2,T2}^{C} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T2} } \\ \end{array} } \right] \hfill \\ \end{aligned}$$
(4)

Since the dimensions of the first and the second matrices in (4) must be the same, one virtual shield wire must be added to section C.

3 Virtual shield wires construction

The original shield wire is divided into two parts, and thus virtual shield wires are obtained. The same current values must be carried by the virtual shield wires, and the position must also be the same as for the original one.

A new impedance matrix of section C must be formed by extension of the original matrix but the new must be equivalent to the original one. The original impedance matrix can be written as:

$$\left[ {\begin{array}{*{20}c} {\hat{\varvec{U}}_{L} } \\ 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{\varvec{A}}} & {\hat{\varvec{B}}} \\ {\hat{\varvec{C}}} & {\hat{D}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{L} } \\ {\hat{I}_{E} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{\varvec{A}}} & \hat{\varvec{C}}^{\text{T}} \\ {\hat{\varvec{C}}} & {\hat{D}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{L} } \\ {\hat{I}_{E} } \\ \end{array} } \right]$$
(5)

where \(\hat{\varvec{U}}_{L} = \left[ {\hat{U}_{L1} ,\hat{U}_{L2} ,\hat{U}_{L3} } \right]^{\text{T}}\) is the phase voltage vector; \(\hat{\varvec{I}}_{L} = \left[ {\hat{I}_{L1} ,\hat{I}_{L2} ,\hat{I}_{L3} } \right]^{\text {T}}\) is the phase current vector; \(\hat{\varvec{A}}\), \(\hat{\varvec{B}}\), \(\hat{\varvec{C}}\), \(\hat{D}\) denote sub-matrices of \(\hat{\varvec{Z}}_{C}\). The new two-shield-wires matrix equivalent to the original one can be written as follows:

$$\left[ {\begin{array}{*{20}c} {\hat{\varvec{U}}_{L} } \\ 0 \\ 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{\varvec{A}}^{{\prime }} } & {\hat{\varvec{B}}^{{\prime }} } & {\hat{\varvec{C}}^{{\prime }} } \\ {\hat{\varvec{D}}^{{\prime }} } & {\hat{E}^{{\prime }} } & {\hat{F}^{{\prime }} } \\ {\hat{\varvec{G}}^{{\prime }} } & {\hat{H}^{{\prime }} } & {\hat{I}^{{\prime }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{L} } \\ {\frac{{\hat{I}_{E} }}{2}} \\ {\frac{{\hat{I}_{E} }}{2}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{\varvec{A}}} & {\hat{\varvec{C}}^{\text {T}} } & {\hat{\varvec{C}}^{\text {T}} } \\ {\hat{\varvec{C}}} & {2\hat{D}} & 0 \\ {\hat{\varvec{C}}} & 0 & {2\hat{D}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{L} } \\ {\frac{{\hat{I}_{E} }}{2}} \\ {\frac{{\hat{I}_{E} }}{2}} \\ \end{array} } \right]$$
(6)

The current flowing through either new shield wire must be a half of the current flowing through the original wire, hence their self-impedance must be twice the original one. Since the position of new shield wires must be the same as for the original one, sub-matrices \(\hat{\varvec{B}}^{\prime }\) and \(\hat{\varvec{C}}^{\prime }\) must be equal to \(\hat{\varvec{C}}^{\text{T}}\) and sub-matrices \(\hat{\varvec{D}}^{\prime }\) and \(\hat{\varvec{G}}^{\prime }\) must be equal to \(\hat{\varvec{C}}\). The row equations with zero voltage in (5) and (6) can be written as:

$$0 = {\hat{\varvec{C}}}{\hat{\varvec{I}}}_{L} + {\hat{D}}{\hat{I}}_{E}$$
(7)
$$0 = {\hat{\varvec{C}}}{\hat{\varvec{I}}}_{L} + 2\hat{D}\frac{{\hat{I}_{E} }}{2} + \hat{F}^{\prime } \frac{{\hat{I}_{E} }}{2} \Rightarrow \hat{F}^{\prime } = 0$$
(8)
$$0 = {\hat{\varvec{C}}}{\hat{\varvec{I}}}_{L} + 2\hat{D}\frac{{\hat{I}_{E} }}{2} + \hat{H}^{\prime } \frac{{\hat{I}_{E} }}{2} \Rightarrow \hat{H}^{\prime } = 0$$
(9)

That means, equivalence of the new and the original matrices is maintained for a zero value of mutual impedances \(\hat{F}^{\prime }\) and \(\hat{H}^{\prime }\).

4 Voltage sources determination

Another challenge is a correct determination of voltage sources connected to the line ends in a meshed grid. The voltages must be chosen according to the required currents flowing through all considered lines (IW). Standardly these current loadings are supposed to be the nominal ones. Naturally these lines required currents must be considered as an average of the three phases for each line because of the unbalance. The task may be quite complicated. All conductors in the lines common sections are coupled by mutual impedances, and increasing the voltages of one transmission line results in changing the currents in all relevant lines. A correct supplying voltage setting can be found by an appropriately designed optimization. Equation (4) can be solved for known phase voltages of both lines \(\hat{\varvec{U}}_{T1}\) and \(\hat{\varvec{U}}_{T2}\), and currents vectors \(\hat{\varvec{I}}_{T1}\) and \(\hat{\varvec{I}}_{T2}\) can be found. The voltages in vectors \(\hat{\varvec{U}}_{T1}\) and \(\hat{\varvec{U}}_{T2}\) must be symmetrical with phasor magnitude Ui (root mean square value scale considered):

$$\left\{ {\begin{array}{*{20}l} {\hat{U}_{L1} = U_{i} } \hfill \\ {\hat{U}_{L2} = U_{i} \text{e}^{{ - \text{j}\frac{2\uppi }{3}}} } \hfill \\ {\hat{U}_{L3} = U_{i} \text{e}^{{\text{j}\frac{2\uppi }{3}}} } \hfill \\ {\hat{U}_{E} = 0} \hfill \\ \end{array} } \right.$$
(10)

Our task is to find the values of Ui (i = T1, T2) of both lines for the required average values of phase currents IT1W and IT2W, that is minimizing the following:

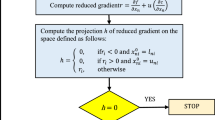
$$\Delta I_{i} = \frac{1}{3}\sum\limits_{m = 1}^{3} {\left| {\hat{\varvec{I}}_{i} \left( m \right)} \right|} - I_{iW} = I_{i} (U_{T1} , \, U_{T2} ) - I_{iW}$$
(11)

where ΔIi is called a defect, and the Ui for its sufficiently small value must be found. The task can be easily solved by Newton-Raphson method with diagram shown in Fig. 3.

Fig. 3
figure 3

Optimization process diagram

Full size image

The first step is to find the voltage estimations for k = 0 iteration, and create vector Uk. By solution of (4), the average currents of both lines IT1 and IT2 as functions of Uk can be found I(Uk) and used for calculation of defect ΔIk. In case the defect is sufficiently small (its maximum value is smaller than required δ), the procedure can be finished, and Uk are the voltages required. If the condition is not met, Jacobi functional matrix Jk must be constructed. The matrix is formed by partial derivatives as follows:

$$\left[ {\begin{array}{*{20}c} {\Delta I_{T1}^{k} } \\ {\Delta I_{T2}^{k} } \\ \end{array} } \right] = \underbrace {{\left[ {\begin{array}{*{20}c} {\frac{{\partial I_{T1} \left( {\varvec{U}^{k} } \right)}}{{\partial U_{T1} }}} & {\frac{{\partial I_{T1} \left( {\varvec{U}^{k} } \right)}}{{\partial U_{T2} }}} \\ {\frac{{\partial I_{T2} \left( {\varvec{U}^{k} } \right)}}{{\partial U_{T1} }}} & {\frac{{\partial I_{T2} \left( {\varvec{U}^{k} } \right)}}{{\partial U_{T2} }}} \\ \end{array} } \right]}}_{{\varvec{J}^{k} }}\left[ {\begin{array}{*{20}c} {\Delta U_{T1}^{k} } \\ {\Delta U_{T2}^{k} } \\ \end{array} } \right]$$
(12)

These derivatives easily can be calculated numerically with the surrounding of the point ξ to get Jacobi matrix as follows:

$$\left[ {\begin{array}{*{20}c} {\frac{{I_{T1} \left( {U_{T1\xi }^{k} ,U_{T2}^{k} } \right) - I_{T1} \left( {\varvec{U}^{k} } \right)}}{\xi }} & {\frac{{I_{T1} \left( {U_{T1}^{k} ,U_{T2\xi }^{k} } \right) - I_{T1} \left( {\varvec{U}^{k} } \right)}}{\xi }} \\ {\frac{{I_{T2} \left( {U_{T1\xi }^{k} ,U_{T2}^{k} } \right) - I_{T2} \left( {\varvec{U}^{k} } \right)}}{\xi }} & {\frac{{I_{T2} \left( {U_{T1}^{k} ,U_{T2\xi }^{k} } \right) - I_{T2} \left( {\varvec{U}^{k} } \right)}}{\xi }} \\ \end{array} } \right]$$
(13)
$$\left\{ \begin{aligned} U_{T1\xi }^{k} = U_{T1}^{k} + \xi \hfill \\ U_{T2\xi }^{k} = U_{T2}^{k} + \xi \hfill \\ \end{aligned} \right.$$
(14)

In the proposed method, the matrix is used to find the vector of voltage defects ΔUk, then a new value of voltages in k+1 iteration Uk+1 is found, and all procedure is repeated as shown in Fig. 3 until the condition max(ΔIk) ≤ δ is met.

Let’s consider a tower with z conductors labelled 1, 2, …, x, …, y, …, z. Diagonal elements in the impedance matrix in (3) for x-th conductor can be written as:

$$\hat{Z}_{x,x} = l_{v} \left( {R_{l} + R_{g} } \right) + R_{E} + \text{j}2\uppi l_{v} fL_{x,x}$$
(15)

where lv is length of corresponding line section; Rl is conductor resistance per kilometer; Rg is ground resistance per kilometer; RE is earthing resistance; f is system frequency; Lx,x is its self-inductance per kilometer. For the determination of Lx,x, several methods can be used (e.g. Carson’s method [27] or Rudenberg’s method [28]). In the Czech transmission system, the most commonly used method is Rudenberg’s method, which has been verified in many case studies. According to it, self-inductance can be expressed as:

$$L_{x,x} = 2 \times 10^{ - 4} \ln \left( {\frac{{D_{g} }}{{\xi_{1} r_{x} }}} \right)$$
(16)

where ξ1 is coefficient respecting nonuniform distribution of current in conductor cross-section; rx is conductor radius; Dg is depth of virtual conductor carrying current in the ground, and can be expressed as:

$$D_{g} = \frac{{0.178\sqrt {10^{7} \rho } }}{\sqrt f }$$
(17)

where ρ is ground resistivity. Ground resistance can be expressed e.g. according to [29] as:

$$R_{g} = 10^{ - 4} \uppi^{2} f$$
(18)

Non-diagonal elements of impedance matrix expressing mutual impedance between x-th and y-th conductor can be written as:

$$\hat{Z}_{x,y} = l_{v} R_{g} + R_{E} + {\text{j}}4\uppi l_{v} f \times 10^{ - 4} \ln \left( {\frac{{D_{g} }}{{d_{x,y} }}} \right)$$
(19)

where dx,y is distance between x-th and y-th conductor.

5 Case study of current unbalance calculation in meshed transmission system

Aforementioned calculation procedures are illustrated in the case study transmission system depicted in Fig. 4. The system consists of four interconnected transmission lines T1, T2, T3 and T4, and seven sections A, B, …, G described by matrices \(\hat{\varvec{Z}}_{A} , \, \hat{\varvec{Z}}_{B} ,\; \ldots ,\;\hat{\varvec{Z}}_{G}\). The sections consist of several sub-sections with different types of towers and phase arrangements. Each sub-section is described by its sub-matrix, and final matrices \(\hat{\varvec{Z}}_{A} , \, \hat{\varvec{Z}}_{B} ,\; \ldots ,\;\hat{\varvec{Z}}_{G}\) are summations of these sub-matrices. Sections A and B contain two shield wires and one transmission line (three-phase conductors), and sections C, D, E, F and G contain two shield wires and two transmission lines (six-phase conductors). Shield wires in sections C through G must be doubled (two virtual shield wires are created). Matrix dimension of \(\hat{\varvec{Z}}_{A} , \, \hat{\varvec{Z}}_{B} , { }\hat{\varvec{Z}}_{C} ,\;\hat{\varvec{Z}}_{D} ,\hat{\varvec{Z}}_{E} ,\hat{\varvec{Z}}_{F} ,\;\hat{\varvec{Z}}_{G}\) is 5×5, 5×5, 10×10, 10×10, 10×10, 10×10, 10×10, respectively. Voltage sources described by vectors \(\hat{\varvec{U}}_{T1} ,\; \, \hat{\varvec{U}}_{T2} ,\; \, \hat{\varvec{U}}_{T3}\) and \(\hat{\varvec{U}}_{T4}\) must be determined by optimization process, described in the previous chapter, according to the required line currents IT1W, IT2W, IT3W and IT4W. The voltage sources position (one of the two line ends) is determined by the required current flow direction.

Fig. 4
figure 4

Scheme of meshed transmission system

Full size image

The scheme can be described by:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\hat{\varvec{U}}_{T1} } \\ {\hat{\varvec{U}}_{T3} } \\ \end{array} } \right] = \hat{\varvec{Z}}_{F}^{{}} \left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ { - \hat{\varvec{I}}_{T4} } \\ \end{array} } \right] + \hat{\varvec{Z}}_{E}^{{}} \left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T2} } \\ \end{array} } \right] + \hat{\varvec{Z}}_{D}^{{}} \left[ {\begin{array}{*{20}c} { - \hat{\varvec{I}}_{T2} } \\ {\hat{\varvec{I}}_{T3} } \\ \end{array} } \right] + \hat{\varvec{Z}}_{C}^{{}} \left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T3} } \\ \end{array} } \right] \hfill \\ \, + \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{B}^{{}} } & {\mathbf{0}} \\ {\mathbf{0}} & {\hat{\varvec{Z}}_{A}^{{}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1}^{F} } & {\hat{\varvec{Z}}_{T1,T4}^{F} } \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ { - \hat{\varvec{I}}_{T4} } \\ \end{array} } \right] \hfill \\ \, + \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1}^{E} } & {\hat{\varvec{Z}}_{T1,T2}^{E} } \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ {\hat{\varvec{Z}}_{T3,T2}^{D} } & {\hat{\varvec{Z}}_{T3,T3}^{D} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - \hat{\varvec{I}}_{T2} } \\ {\hat{\varvec{I}}_{T3} } \\ \end{array} } \right] \hfill \\ \, + \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1}^{C} } & {\hat{\varvec{Z}}_{T1,T3}^{C} } \\ {\hat{\varvec{Z}}_{T3,T1}^{C} } & {\hat{\varvec{Z}}_{T3,T3}^{C} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T3} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1}^{B} } & {\mathbf{0}} \\ {\mathbf{0}} & {\hat{\varvec{Z}}_{T3,T3}^{A} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T3} } \\ \end{array} } \right] \hfill \\ \end{aligned}$$
(20)
$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\hat{\varvec{U}}_{T2} } \\ {\hat{\varvec{U}}_{T4} } \\ \end{array} } \right] = \hat{\varvec{Z}}_{G}^{{}} \left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T2} } \\ {\hat{\varvec{I}}_{T4} } \\ \end{array} } \right] + \hat{\varvec{Z}}_{F}^{{}} \left[ {\begin{array}{*{20}c} { - \hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T4} } \\ \end{array} } \right] + \hat{\varvec{Z}}_{E}^{{}} \left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T2} } \\ {\hat{\varvec{I}}_{T1} } \\ \end{array} } \right] + \hat{\varvec{Z}}_{D}^{{}} \left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T2} } \\ { - \hat{\varvec{I}}_{T3} } \\ \end{array} } \right] \hfill \\ \, = \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T2,T2}^{G} } & {\hat{\varvec{Z}}_{T2,T4}^{G} } \\ {\hat{\varvec{Z}}_{T4,T2}^{G} } & {\hat{\varvec{Z}}_{T4,T4}^{G} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T2} } \\ {\hat{\varvec{I}}_{T4} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ {\hat{\varvec{Z}}_{T4,T1}^{F} } & {\hat{\varvec{Z}}_{T4,T4}^{F} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - \hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T4} } \\ \end{array} } \right] \hfill \\ \, + \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T2,T2}^{E} } & {\hat{\varvec{Z}}_{T2,T1}^{E} } \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T2} } \\ {\hat{\varvec{I}}_{T1} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T2,T2}^{D} } & {\hat{\varvec{Z}}_{T2,T3}^{D} } \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T2} } \\ { - \hat{\varvec{I}}_{T3} } \\ \end{array} } \right] \hfill \\ \end{aligned}$$
(21)

The matrix equation forms can be chosen to the dimension 10 × 10 or 20 × 20. In Fig. 4 it is obvious only two transmission lines are affected, and size 10 × 10 is better to be used.

Equations (20) and (21) are solved to obtain the line currents \(\hat{\varvec{I}}_{T1} ,\; \, \hat{\varvec{I}}_{T2} ,\; \, \hat{\varvec{I}}_{T3}\) and \(\hat{\varvec{I}}_{T4}\). These currents are used to calculate \(\hat{I}_{1}\) and \(\hat{I}_{0}\) in each line and hence the unbalance factor mf from (1).

In the case study (part of the Czech 400 kV system was added with a new substation), the task was to find the lowest value of unbalance factor mf for vectors \(\hat{\varvec{I}}_{T1}\) and \(\hat{\varvec{I}}_{T3}\) with minimal costs and changes to the system. Since the reduction of unbalance was performed on the existing part of the system (there was only a small extension for the new substation), the transmission system operator suggested an appropriate place for possible transposition in section C, and the current unbalance reduction was achieved by changing the phase sequence arrangements in section C (by changing the matrix \(\hat{\varvec{Z}}_{C}\)). Technically, this requires to install two inverse transposition towers at the beginning and the end positions of section C. Generally, the current unbalance can be reduced by different topology changes or their combinations. The final suitable measure must satisfy transmission system operator requirements and economical and environmental aspects and depends on many aspects in real electrical system. This paper is primarily focused on the unbalance calculation and not on the measure design. Hence, the section C transposition should be understood only as an example with presented impacts on the unbalance factor.

The system examined is fairly complicated, and a clear way how to find the best current unbalance combination is calculating all possible phase sequence arrangements for lines T1 and T3 (however, we don’t discuss the technically most suitable solution). All possible phase sequences and their unbalance factors are mentioned in Table 1. The placements of phase conductor and ground wire on the tower correspond with Fig. 5.

Table 1 Unbalance factors of lines T1 and T3
Full size table
Fig. 5
figure 5

Phase placement in section C

Full size image

The maximum possible summary unbalance occurs for No. 11 (2.69% + 3.58% = 6.22%) and the minimum one for No. 28 (1.05% + 0.29% = 1.34%) but No. 14 (0.44% + 0.98% = 1.43%) is also possible for a better distribution of the factors on both lines. For all 36 possibilities, the equal current values obtained by aforementioned optimization process are calculated as required so that the current unbalances comparison is correct.

The calculations are influenced by several parameters. In (15), (17) and (19), earthing resistance RE and ground resistivity ρ occur. Sensitivity analysis of RE (with constant ρ = 100 Ωm) and ρ (with RE = 1 Ω) for transposition number 28 has been carried out and depicted in Fig. 6 and Fig. 7.

Fig. 6
figure 6

Sensitivity analysis of unbalance factor mf towards ground resistivity ρ

Full size image
Fig. 7
figure 7

Sensitivity analysis of unbalance factor mf towards earthing resistance RE

Full size image

The ρ value strongly depends on the soil type and the annual rainfall under all the transmission lines, and hence the average value must be considered. This value is usually one of the least known input data for line parameters calculations. Usually, a chosen value is used for the calculation even if the ground resistivity size can change significantly along the line. Its value affects all the matrix elements in (20) and (21). As shown in Fig. 6, the unbalance factor does not depend on the selected value of ρ significantly, so its imprecise value doesn’t result in technically wrong results.

The value of RE is usually provided by the system operator requirements but not always. The value affects all the matrix elements in (20) and (21) except for \(\hat{\varvec{Z}}_{E}\) and \(\hat{\varvec{Z}}_{C}\), and the final unbalance factor can strongly be influenced by the length of the appropriate section (RE value is not dependent on the line length). Shorter lines (T3 is the shortest one of all sections) can strongly be influenced by value of RE as depicted in Fig. 7.

6 Comparison with commonly used point-to-point calculation method

As mentioned in the introduction, commonly used point-to-point analyses of current unbalance have been under research many times [4,5,6, 15, 16, 18,19,20,21,22,23,24]. To show the differences and possible issues related to point-to-point method, the scheme of meshed transmission system from Fig. 4 was modified (reduced) to schemes (Scheme I and Scheme II) in Fig. 8a and Fig. 8b. Scheme I can be used for unbalance calculation of line T1, and similarly Scheme II can be used for unbalance calculation of line T3. The considered line is always added only by one other line on the same tower (double line) or with zero mutual couplings (different line corridors) to form one impedance matrix describing the reduced case. The line parallel with our considered one can be formed by partial sections of other lines from the original topology. These schemes allow us to simplify the calculations, and matrix equation with only one matrix is sufficient for calculations. For example, original matrix equations (20) and (21) can be modified for Scheme II as:

$$\left[ {\begin{array}{*{20}c} {\hat{\varvec{U}}_{T1} } \\ {\hat{\varvec{U}}_{T3} } \\ \end{array} } \right] = \left[ {\hat{\varvec{Z}}_{ABCD} } \right]\left[ {\begin{array}{*{20}c} {\hat{\varvec{I}}_{T1} } \\ {\hat{\varvec{I}}_{T3} } \\ \end{array} } \right]$$
(22)
$$\begin{aligned} \left[ {\hat{\varvec{Z}}_{ABCD} } \right] &= \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1}^{D} } & {\hat{\varvec{Z}}_{T1,T3}^{D} } \\ {\hat{\varvec{Z}}_{T3,T1}^{D} } & {\hat{\varvec{Z}}_{T3,T3}^{D} } \\ \end{array} } \right] \hfill \\&\quad + \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1}^{C} } & {\hat{\varvec{Z}}_{T1,T3}^{C} } \\ {\hat{\varvec{Z}}_{T3,T1}^{C} } & {\hat{\varvec{Z}}_{T3,T3}^{C} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\hat{\varvec{Z}}_{T1,T1}^{B} } & {\mathbf{0}} \\ {\mathbf{0}} & {\hat{\varvec{Z}}_{T3,T3}^{A} } \\ \end{array} } \right] \hfill \\ \end{aligned}$$
(23)
Fig. 8
figure 8

Modified schemes of meshed transmission system usable for point-to-point method

Full size image

Similar equation can also be constructed for Scheme I. Final results of calculations are shown in Table 2. These can be compared with results in Table 1. Differences ∆mf (defined in (24)) in total current unbalances for all transpositions are written in the last column of Table 2. In (24), unbalances obtained by modified schemes in Fig. 8 are labeled with *. We can see significant differences between the original and modified calculations to both polarities, which show high differences of both methods. That means if the common point-to-point method is used, finding the optimum transposition can be affected, and a wrong transposition may be selected.

Table 2 Unbalance factors of lines T1 and T3 calculated by Schemes I and II
Full size table
$$\Delta m_{f} = m_{f}^{*} (T1) - m_{f} (T1) + m_{f}^{*} (T3) - m_{f} (T3)$$
(24)

7 Conclusion

The paper presents a new methodology of the current unbalance calculation in meshed transmission systems. The meshed system consists of several sections with different phase arrangements, a different number of transmission lines on one tower, and a different number of shield wires. Some basic aspects of current unbalance have been mentioned in Sect. 1. As for calculations, several challenges described in Sect. 2 have been solved. Since it may be necessary to connect sections with a different number of shield wires, the virtual shield wires have been created to keep impedance matrix dimensions, and the correct values of line supplying voltage sources have been determined for the required average values of the line currents by an appropriately designed optimization process. The unbalance factors for all the possible phase arrangements in the selected section C have been calculated, and the best solution has been found. The aforementioned procedures have been demonstrated in a case study of part of Czech transmission system designed for a new 400 kV substation connection. The best calculated transposition in section C was used, and values of calculated unbalance factors have been verified after putting the substation into operation. The measurement has shown very good agreement with the calculated values with an error less than 8%. This is accepted as a very successful result taking into consideration a range of the line input parameters uncertainties. Finally, sensitivity analysis of the unbalance factor has been performed with view to the fact that the grounding input data is never easy to determine.

Meeting the minimum value of the current unbalance is one of the standard requirements of transmission system operators, and the current unbalance calculations are getting increasingly important in designing new parts of transmission systems.