Abstract
Compared to traditional point load forecasting, probabilistic load forecasting (PLF) has great significance in advanced system scheduling and planning with higher reliability. Medium term probabilistic load forecasting with a resolution to an hour has turned out to be practical especially in medium term energy trading and can enhance the performance of forecasting compared to those only utilizing daily information. Two main uncertainties exist when PLF is implemented: the first is the temperature fluctuation at the same time of each year; the second is the load variation which means that even if observed indicators are fixed since other observed external indicators can be responsible for the variation. Therefore, we propose a hybrid model considering both temperature uncertainty and load variation to generate medium term probabilistic forecasting with hourly resolution. An innovative quantile regression neural network with parameter embedding is established to capture the load variation, and a temperature scenario based technique is utilized to generate temperature forecasting in a probabilistic manner. It turns out that the proposed method overrides commonly used benchmark models in the case study.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Power load forecasting plays a core role in planning and scheduling of power system, for it not only reduces the costs of mismatching between generated power and actual demand, but also enhance the reliability of the whole system by eliminating the inadequate dispatching of energy. Among all literature introducing load forecasting techniques, most of them focus on point forecasting by generating fixed forecasting point at a specific moment in the future. Nevertheless, the power load is becoming cumulatively volatile with the growing fluctuation and uncertainty caused by natural and manual variation such as distributed renewable energy integration. As a result, forecasting approaches reflecting uncertainty on load are required by increasing number of decision-makers in the energy industry. Apparently, single-point prediction cannot represent the randomness appearing in load, and may sometimes invalidate the investment on power supply because of the sporadic gap between real and predicted values [1, 2].
Compared with point forecasting, probabilistic load forecasting describes the variation of the load by providing outputs in form of probability density function (PDF), confidential intervals, or quantiles of the distribution. It can be more suitable to confirm objective demands in system planning and energy trading, therefore being utilized in a wider range.
Literature on probabilistic load forecasting are relatively limited compare to traditional point forecasting. According to Hong and Fan [3], the combination of two or three of the following component can be utilized to generate probabilistic load forecasts: creating input scenario simulation, designing probabilistic models, and transforming point forecasts to probabilistic forecasts through post-processing. References [4,5,6] mainly utilized input scenario simulation, therefore, creating probabilistic forecasts. In [7], three basic input scenario generation methods, fix-date, shifted-date, bootstrap, were discussed, and an empirical study on these methods was established, measured by pinball loss.
Besides, more efforts have been devoted to generating probabilistic forecasting models. They can be summarized in following aspects: time series based, statistical regression based, sequence operation theory-based, and other machine learning method based. Fang [8] proposed a model based on chaotic time series. Sequence operation theory (SOT) was established by Kang [9], aiming to handle complicated probabilistic modeling. It has been utilized in modeling correlated stochastic variables [10] that can be used in generating probabilistic forecasts together with other statistic models. Statistical and other machine learning models were even more widely adopted in probabilistic forecasting like multiple linear regression [5, 11], quantile regression [12], gradient boosting [13], general addictive model (GAM) [14], kernel density estimation (KDE) [15], etc.
In addition, probabilistic forecasts according to post-processing are also proved to be effective. In Xie’s [6] and Mcsharry’s [16] studies, residual simulation was used to convert point forecasts to probabilistic forecasts. Liu [12] applied forecasting combination to optimize results, which tended to manifest a great boost in performance.
It can be concluded from the literature that probabilistic forecasting has a wide time scope from short-term to long term. Some of the works focused on short term probabilistic load forecasting [1, 17], whereas even more works were keen on medium and long term probabilistic load forecasting [4,5,6,7, 14, 15], because there is great significance in energy trading and system planning [3].
This paper offers a solution for long term probabilistic forecasting in terms of hourly loads, applying the combination of input variable scenario simulation and a probabilistic model to generate forecasts. Concretely, artificial neural network (ANN) is utilized as the basic structure capturing nonlinear relationships of variables. Although ANN was mentioned in some literature related to probabilistic load forecasting [7, 18], it was simply treated as model generating point forecasts, yet the uncertainty of outputs which can be described by the model itself was ignored. Thus, we innovatively refined the traditional ANN to an intricate model that can generate probabilistic forecasts. We first fed the model with multiple inputs generated by the scenario-based method. Then regularized loss resembling quantile regression as loss function to be optimized by ANN, and advanced optimization algorithms to avoid local minimum are adopted to describe the randomness of the load in an annual scope.
Besides, we also use the embedding, a technique mapping low dimensional variables into high dimensional space, which has been widely adopted in handling categorical variables in other neural-network scenarios [19, 20]. It is proved to achieve better results than other common techniques utilized in previous literature, like one-hot encoding. Altogether, It turns out that the proposed method overrides state-of-art benchmarks in medium term probabilistic load forecasting in the dataset described in the section of the case study.
It should be pointed out that some literature have already considered both uncertainties in the input scenarios and output variations. However, they either combined input scenarios and output residual simulation based on relatively statistical methodology [21], or traditional probabilistic statistical model [14]. Compared to these efforts, our method stands out in the fusing probabilistic outputs into a malleable non-linear network, which does not require setting up an extra combination of input variables and can capture the non-linear dependencies between input and output variables better due to its complex structure.
Our key original contributions can be summarized in two aspects compared to previous researchers:
-
1)
An ANN-based probabilistic forecasting model with regularized quantile optimization objective is proposed, considering both the randomness of inputs and the output variation described by a solid non-linear model.
-
2)
A novel embedding method is utilized to handle categorical input variables, manifesting potential effectiveness in enhancing the performance of load forecasting. It has strong malleability in other machine-learning related scenarios in the field of scheduling and operation for the power system.
-
3)
Dual uncertainties are considered based on the input fluctuation and load variation described by a robust non-linear model, which is relatively less considered in previous studies.
The rest of the paper is organized as follows: Sect. 2 introduces the overall objection and procedure of the proposed probabilistic load forecasting. Section 3, the core methodology in generating temperature scenario and describing load variation is proposed. Section 4 illustrates the evaluation criterion to qualify the performance of probabilistic forecasting and proposes several benchmark models for comparison. In Sect. 5, case study with data from ISO New England is established to verify the superiority of the proposed model. Finally, conclusions are drawn in Sect. 6.
2 Framework
The objection of probabilistic forecasting proposed in this paper is to generate hourly quantiles of probability density function (PDF) of annual hourly load utilizing information of one year and before. The overall procedure of probabilistic load forecasting can be summarized as follows. Figure 1 illustrates the procedure in a flow chart. It consists of five main steps: outliers detection, trend analysis, data normalization, probabilistic forecasting models training, and load variation and temperature uncertainty combination.
2.1 Outliers detection
Two steps are designed for outliers detection. The first step is a nave continuity-based method. It is hypothesized that the hourly load should not have a dual-side salutation at each point. So the anomalous criteria is set as:
\(E_t\) is anomalous point, if only
where \(E_{t-1}\) and \(E_{t+1}\) denote the load one hour before and after the time when \(E_{t-1}\) is recorded. This method can effectively capture temporary misreporting caused by error in auto measurement.
However, this nave method cannot capture outliers beyond the temporary false record. Thus, the multiple linear regression model (also Vanilla Model in [11]) is utilized as an outliers detector in the second stage. This method is firstly proposed and proved to be effective in [21]. The absolute percentage error (APE) is calculated after fitting the historical hourly load for each hourly load in training set. The original load observations in training set with APE values higher than 50% are considered as outliers and are replaced by values estimated by the outliers detector.
Besides, it should be stated that it is of great significance to apply nave outliers detection in the first place. Granted, the baseline model can be a panacea to detect and modify relatively sparse outliers, yet the model based method can be detrimentally affected when the amount anomalous load points increases. For example, in bus load forecasting, the amount of outliers appearing in the bus load data cannot be neglectable, therefore researchers have to utilize a nave method to clean the data in the first place. It can be concluded that applying nave outlier detection before other more advanced anomalous modification method is quite necessary, bringing robustness to the process of load forecasting as a whole.
2.2 Trend analysis
We extract the linear trend by simply adding linear variables ranging from 0 to 1 as inputs of the following regression model. The experiment results turn out that the forecasting model performs better considering linear trend than that without linear trend inputs.
2.3 Data normalization
Due to the scaling sensitivity of inputs fed into the neural network, we set the inputs in the same scale by normalizing temperature with a min-max scaler. The normalized features fall in the range of [0, 1], and is calculated with the following equation:
where \(I_{\text {norm}}\) denotes the normalized value of numerical input features; \(I_{\text {min}}\), \(I_{\text {max}}\) denote the lowest and highest values of all input features in this data set, respectively.
2.4 Training probabilistic forecasting models considering load cariation
The first stage of forecasting is training a regression model considering load variation, which is proposed as a quantile regression neural network (QRNN) in this paper, generating probabilistic results in the form of quantiles. Normalized hourly variables (temperature, day types etc.) act as training features whereas corresponding hourly loads are training labels, supervising the training process of QRNN. The training process iterates with fine tuning the parameters of the model, and it is terminated as long as the validation loss no longer decreases.
2.5 Combining temperature uncertainty in load forecasting on the basis of QRNN
Since QRNN is trained based on temporally simultaneous features, it cannot be utilized directly in forecasting one year ahead because some features, like hourly temperature in the next year, cannot be foreseen. So temperature uncertainty should be considered in real forecasting stage. The final results of load forecasting are generated by replacing the simultaneous temperature fed into QRNN with historical temperature scenarios.
3 Probabilistic load forecasting considering load variation and temperature uncertainty
In this section, formulation of the forecasting problem is illustrated, following the detailed description of the proposed model in this paper.
3.1 Problem formulation
As is mentioned in Sect. 2, to implement a probabilistic forecasting, we need to generate the PDF of the load for each hour. The distribution can be discretely manifested by a vector consisting of several quantiles of the PDF vector. Thus, the forecasting problem can be formulated as follows:
where \(\varvec{E}_{t} \in \mathbb {R}^{N_{\tau }}\) is the hourly power load vector at time t; \(N_{\tau }\) is the dimension of vector, which also means the number of quantiles \(\tau\); \(h(\cdot )\) denotes the general function mapping input variables to the output load, which in this paper \(h(\cdot )\) is established by QRNN; \(T_{t}\) refers to hourly temperature; \(Trend_{t}\) stands for the linear trend, ascending linearly from the first point to the last in the whole dataset; \(M_{t}\) (time mode) consists of four components, which can be formulated as:
where \(Hour_{t}, Weekday_{t}, Holiday_{t}, Month_{t}\) are categorical variables corresponding to time t.
3.2 Embedding technique for categorical variables
In a forecasting problem, categorical variables like the day type at moment t should be converted to numeric representations in order to fit the most numerical solved formulas. Most common techniques are direct numbering and one-hot encoding. Generally speaking, embedding is technique mapping 1-dimensional categorical variables to numerical features into high dimensional space. It is turned out that the categorical variables mapped by embedding technique capture more information of categorical variables than other common techniques due to its flexibility in output vector dimensions and the complexity of embedding parameters.
As is mentioned earlier, \(M_t^{}\) contains several categorical variables, each of which can be represented in higher-dimensional vectors. Concretely, in the first place, \(M_t\) is converted directly to numerical vector \(\varvec{m}_t^\text {T} \in \mathbb {R}^{4}\). For example, \(M_t\) contains {23:00, Tuesday, Not a Holiday, January} can be expressed as \([23, 2, 0, 1]^\text {T}\) in form of \(\varvec{M}_t\). Then, the embedded feature, which can also be called latent vector is defined by:
where \(\varvec{M}^{em}_{t} \in \mathbb {R}^{4 \times N_{em}}\) is the latent vector of time mode at moment t; \(\varvec{M}_{t}^{one-hot} \in \mathbb {R}^{4 \times N_{\text {max}}}\) is one-hot representation of \(\varvec{m}_t^\text {T}\), where \(N_{\text {max}}\) denotes the largest number of categories in elements of \(M_t\); \(\varvec{Q} \in \mathbb {R}^{N_{\text {max}} \times N_{em}}\) denotes the embedding parameter matrix, containing \(N_{\text {max}} \times N_{em}\) individual parameters, which can be learned and updated in the training process together with other parts of the neural network.
In order to connect to other parts of the network being discussed in following paragraph, \(\varvec{M}^{em}_{t}\) should be flattened to a vector by a flattening layer, then the final representation of categorical variables can be defined as:
where \(\varvec{m}^{em}_{t}\) is a vector of \(\mathbb {R}^{4N_{em}}\).
3.3 Quantile regression neural network
Artificial neutral network (ANN) has been proved to be suitable for regression problem with multiple features due to its complicated connection of variables and non-linear transformation through activation function [22]. Most commonly used ANN for regression problems utilize back propagation (BP) algorithm to update parameters by minimizing the loss between outputs of ANN \(\hat{y}\) and real value y, such as mean square error (MSE).
However, conventional neural network can only raise single output at a time, which is incompatible with the aim to forecast load in a probabilistic manner. Therefore, a neural network for probabilistic forecasting is proposed based on the fundamental structure of ANN. We name the proposed model as QRNN (quantile regression neural network). The idea is that QRNN can generate vectors consisting of quantiles of aimed PDF of hourly load by adjusting parameters in defined loss function. Three layers are constructed as the basic structure of QRNN. The first layer is the concatenation of flattened embedding feature \(\varvec{m}^{em}_{t}\), hourly temperature \(T_t\), and linear trend \(Trend_t\). The second layer is a fully connected layer with ReLU (Rectified Linear Units) as activation function, connecting to the third layer, with one hidden units as output. QRNN can be formulated as:
where \(f(\cdot )\) denotes the activation function; \(\varvec{W}\) and \(\varvec{b}\) are weights and bias to be learned; \(\hat{E}_t^{\tau }\) stands for \(\tau\)th quantile of the estimated load distribution.
Figure 2 demonstrates the overall structure of QRNN.
The parameters of the neutral network are learned by minimizing the loss function with back propagation. The loss function for training the neural network is defined as:
It consists of two parts. The first part of the lost function act as regularization preventing the QRNN from from overfitting. \(\Vert \cdot \Vert\) is the Frobenius norm. \(\lambda _1\), \(\lambda _2\), \(\lambda _3\) are parameters controlling the power of regularization to each parameters in the neural network. It shares the same idea with linear regression with regularization such as ridge regression [23], which is shown to achieve better performance than regression without adequate regularization. The second part accounts for minimizing the loss between real value and predicted value with respect to different given quantiles \(\tau\), where N stands for the number of samples fed into the network each time, \(E_t\) and \(\hat{E}_t^{\tau }\) are real value and predicted value corresponding to quantile \(\tau\) respectively.
By setting \(\tau\) as 1, 2, ..., \(N_{\tau }\), \(N_{\tau }\) forecasting results at time t, \(\hat{E}_t^{1}\), \(\hat{E}_t^{2}\), ..., \(\hat{E}_t^{N_{\tau }}\) are obtained through \(N_{\tau }\) QRNNs with different loss function. By concatenating these results, the estimation of \(\varvec{E}_{t}\) is obtained as \(\varvec{\widetilde{E}}_{t}\).
3.4 Combining temperature uncertainty on the basis of QRNN
It should be noted that \(\varvec{\widetilde{E}}_{t}\) indicates the variation of load knowing the exact simultaneous temperature beforehand. However, in a medium term forecasting problem, we cannot foresee the excessive annual horizon. As is acknowledged that temperature in a specific zone does not have similar pattern at the same moment for each year, the hourly temperature can be forecasted by the stacking temperatures at nearby moments in years before. Temperature scenario generation for temperature forecasting is proposed based on the aforementioned hypothesis and is proved to be effective in modeling the uncertainty of medium term hourly temperature [7].
To formulate the process, let \(T^{h}_{y, d}\) be the real temperature at hour h on the dth day of year y, then the temperature scenario can be represented as:
where \(\varvec{Ts}^{h}_{y, d}\) is the temperature scenario containing \((2n+1) m\) historical temperatures.
Then we replace \(T_t\) in (6) by elements in \(\varvec{Ts}^{h}_{y, d}\). As a result, the outputs of QRNN captures both temperature and load uncertainty. Final quantiles are generated according to empirical distribution constructed by these outputs.
4 Comparison and evaluation criteria
In this section, several evaluation criteria in the field of probabilistic forecasting are reviewed, and benchmark models for further comparison in case study will be proposed.
4.1 Evaluation criterion
Generally speaking, PDF of hourly loads provide maximum information on forecasting, yet it may not be practical to obtain the real PDF of real-world quantities and for most of the time, the real PDF are downsampled with sparse empirical results. Therefore, evaluation over simplified results should be considered to be more practical. As is discussed in [24], reliability, resolution, and sharpness are commonly used evaluation criteria for probabilistic forecasting. In [25], the author utilizes Prediction interval coverage probability (PICP) as an evaluation criterion, which is described to be a significant measure for the reliability of prediction intervals [25]. Nevertheless, PICP only considers the upper and lower bounds of the forecasting intervals, thus ignoring inner characteristics of the distribution. To balance the complexity caused by real PDF and potentially ignored information in interval-based measures like PICP, pinball loss function is presented as a sound evaluation criterion for load forecasting. It is defined as:
where \(E_t\), \(\hat{E}_t\) stand for real and estimated load at time t respectively; \(\tau\) is the targeted quantile of forecasting distribution. Actually, it is a similar representation of loss function in (7). Pinball loss considers the holistic contribution of forecasting results by integrating quantiles since quantiles are discrete and can be set to a feasible quantity, it can, therefore, simplifies the computing process. Moreover, it is obvious that a lower pinball loss indicates a better forecasting result. This is the criterion being used to evaluate the proposed method and benchmarks in this paper.
4.2 Benchmark models
Three benchmark models are discussed and utilized in performance evaluation. The first benchmark model is the multiple linear regression model (MLR) appeared as outliers detector. It is regarded as nave benchmark models in several probabilistic forecasting research [12, 14, 15]. The model is defined by:
where \(E_{t}\) denotes the hourly load; \(Month_t\), \(Weekday_t\), \(Hour_t\) are one-hot encodings of categorical variables; \(Trend_t\) denotes a linear trend component in all training data; \(T_t\) is the dry-bulb temperature.
In addition, a neural-network based model is introduced with (10) as optimizing target, we denote this model as MLP (multi-layer perceptron). This model act as a parallel with MLR since they all take in similar inputs and estimate parameters by optimizing the same objective (10), and merely consider temperature uncertainty. MLP has a similar structure with QRNN, yet it contains no embedding layers, only one hidden layer after the inputs are fed into the network, and ReLU as the activation function.
Except MLR and MLP as benchmark models, another benchmark model is proposed considering both uncertainties in temperature and load variation when inputs are fixed with linear quantile regression (LQR). To express load variation more directly, we train the quantile regression model separately on each hour and day type in order to connect hourly load directly with fixed temperature and its polynomials as the only inputs. For a specific hour and day type, the LQR model is given as:
where \(E_{t}^{\tau }\) is hourly load with quantile \(\tau\); \(T_{t}\) is corresponding temperature. The estimation of \(Y_{t,\tau }\) is calculated by minimizing (9).
Besides, it should be mentioned that \(T_t\) should be replaced by temperature scenarios in final forecasting for all of the three benchmark models, generating probabilistic forecasting results.
5 Case study
In this section, we demonstrate an experiment based on real world dataset. This section will be organized as follows. The proposed model is built up with Keras, an advanced deep learning library in Python, and benchmark models are built up with Scikit-Learn.
5.1 Introduction of dataset and experiment settings
The hourly load and corresponding weather information are obtained from the official website of ISO New England, which is accessible to the public. The data consists of 8 different zones in New England, US. We only utilize the time information (hour, week, month, year), load, and drybulb temperature in this case study. In our experiment, the data from 2004 to 2015 are selected as the combination of our training set, validation set, and test set.
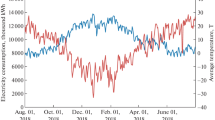
Figure 3 shows load variation and temperature uncertainty appeared in the recorded data. It can be concluded from Fig. 3a that even the temperature and other input variables are fixed, the load still appears to fluctuate. Besides, Fig. 3b indicates that temperature has great uncertainty at the same time of each year. Therefore, dual uncertainties should be considered to generate a more reasonable probabilistic forecasting intervals.
5.2 Procedures of proposed forecasting approach in the experiment
Above all, dual stage anomalous detection is implemented. Figure 4a demonstrate a anomalous measure record captured by the nave outliers detection method. Figure 4b shows the anomalous drop in load monitored by the model-based outliers detector.
Then training process on the training set is implemented by feeding normalized data described by (2) into QRNN. Concretely, seven years of hourly load and temperature from 2008 to 2014 serve as the training set, whereas 20% of the training set is randomly split as the validation set during each training epoch and stop training in advance by monitoring the validation loss. Concretely, when the validation loss does not decrease for 5 epochs, the training process is terminated. Besides, we tune the parameters: learning rate of the optimizer lr, the dimension of embedding layer \(N_{embedding}\), and regularization factors \(\lambda _1\), \(\lambda _2\), \(\lambda _3\) by minimizing the validation loss. Hourly data in 2015 are used for test of final forecasting performance. The outputs of QRNN are 9 quantile values \(\hat{E_{\tau }}\) estimated by minimizing (7), setting \(\tau\) from 0.1 to 0.9. Figure 5 shows the output intervals by QRNN with real temperature as an input. The interval implies the variation of the load even if the temperature is fixed.
In the second stage, as what has been declared in the last section, the uncertainty of temperature needs to be considered by giving a probabilistic forecast on the hourly temperature in 2015.
Temperature scenario based method demonstrated in Sect. 3 is proved to be more effective than other temperature forecasting techniques such as quantGAM [14] in this specific case study. Concretely, m and n in (8) are set to be 4 and 10 in the case study for all models. As a result, 90 temperature scenarios are generated and plugged into (6), and there will be 810 ultimate forecasting results. Final 9 quantiles are generated from the empirical distribution based on 810 results. Figure 6 shows the final results considering both load variation and temperature uncertainty.
5.3 Comparison and discussion
In this subsection, following crucial questions are about to be answered by making the corresponding comparison. Firstly, is a model combining output variation described by probabilistic model and temperature input uncertainty performs better than one only taking stochastic temperature scenarios into account? Secondly, can QRNN out perform other statistic models considering dual uncertainty? Thirdly, is embedding of categorical features beneficial for higher performance compared with traditional techniques like one-hot encoding? At the end, an overall comparison of forecasting performance is demonstrated between proposed models and three benchmark models.
Figure 7 shows three forecasting results of the same horizon. Apparently, three models underestimate the hourly load concordantly. Since QRNN captures both temperature uncertainty and load variation, the error is penalized by a greater forecasting interval, leading to the decrease in pinball loss, yet MLR without considering on load variation failed to compensate such error, therefore leading to a significant variance on this test day.
On the other hand, although LQR considers dual uncertainty as what has been illustrated in Sect. 4, the final forecasting results by LQR expressed in Fig. 7c indicates two main problems by simply modeling hourly load and temperature separately with nave linear quantile regression. Since the LQR model is trained separately when the hour and day types are fixed, loads are estimated independently and concatenated by the hour and dates to the final load series. This will lead to the discontinuity between hours, which can be detrimental to forecasting results due to the lack of smoothness. This argument actually undermines the “ training in separate hour” pattern in [14] since the load continuity within time is ignored. Besides, the forecasting interval is conspicuously widened. This can be explained that LQR only set temperature and its polynomials as inputs in the case study, which can lead to an overestimating problem because of scarcity in input feature types.
In addition, MLP is used as another benchmark model in final comparison. We use RMSprop as an optimizer for back-propagation of error for MLP. The number of perceptrons in the hidden layer can be treated as hyperparameter in this model, thus can be finetuned the till optimum. Only the best forecasting results are reported.
Table 1 shows the final forecasting pinball loss in 8 zones in New England by means of one proposed approach together with three benchmarks, and the maximum relative improvement (MaxRI) as well. With the fact that a lower pinball loss indicates a better probabilistic forecasting, QRNN overrides three benchmark models in 7 zones of 8 in total, yet it only underperforms 3.8% worser compared with the best model in this area. We can read the column of MaxRI that QRNN outperforms the benchmark models significantly. The relative improvements among all area reach 20% approximately, indicating the effectiveness of our proposed method against benchmarks in the case study.
In addition, MLR and MLP are parallel benchmarks as representatives of models considering the single uncertainty of temperature. The result turns out that they have similar performance in the case study, yet MLP performs slightly better since it has a higher capability in modeling non-linear effects and interactions between variables. Although LQR considers both load variation and temperature, the widened forecasting interval and discontinuity in load series may contribute to the high pinball loss.
To demonstrate the potential effectiveness of embedding toward categorical parameters, another comparison is conducted and the final results are shown in Table 2. It should be mentioned that the results of QRNN with embedding reported here are finetuned by adjusting embedding layers to minimize the validation loss. It can be concluded that compared to one-hot encoding, optimized parameter embedding can decrease the pinball loss and in other words, can better captures features of input variables in probabilistic forecasting.
Apart from that, in order to observe the forecasting performance in a more detailed time scope, we select a zone with QRNN as its best forecaster in 2015 and visualize the pinball loss with a bar chart in Fig. 8. Two main conclusions can be drawn from this figure. It is observed that QRNN does not perform best in March, April, May, September, even if the annual loss is low. However, there is a significant drop in pinball loss compared with single uncertainty-based models (MLP, MLR) in temperature extreme months, like February and August. It can be inferred that QRNN considering dual uncertainty can handle forecasting problem better than single uncertainty-based models because the load variation is more intense during temperature extreme period, so QRNN captures this characteristic better, leading to better performance in this period. On the other hand, the single uncertainty-based models are presented to achieve better performances when the temperature is mild since it is enough only taking temperature into account, while considering dual uncertainty may act as a conservative estimation by widening the forecasting interval.
6 Conclusion
In this paper, an innovative method on probabilistic load forecasting is proposed. By considering both input uncertainty and output variation, it turned out that the proposed QRNN model performs better than commonly used benchmark models. Besides, embedding techniques have shown potential in handling categorical inputs, which can enhance the overall performance of forecasting. Further studies can be conducted from multiple aspects, such as optimizing network structure with state-of-art techniques like deep neural networks and utilizing multi-temporal information to train the model, therefore mining more hidden information and enhance the performance of load forecasting.
References
Yang W, Kang C, Xia Q et al (2006) Short term probabilistic load forecasting based on statistics of probability distribution of forecasting errors. Autom Electr Power Syst 30(19):47–52
Li Z, Ye L, Zhao Y et al (2016) Short-term wind power prediction based on extreme learning machine with error correction. Prot Control Mod Power Syst 1(1):1–8
Hong T, Shu F (2016) Probabilistic electric load forecasting: a tutorial review. Int J Forecast 32(3):914–938
Hyndman RJ, Fan S (2010) Density forecasting for long-term peak electricity demand. IEEE Trans Power Syst 25(2):1142–1153
Hong T, Wilson J, Xie J (2014) Long term probabilistic load forecasting and normalization with hourly information. IEEE Trans Smart Grid 5(1):456–462
Xie J, Hong T, Laing T et al (2017) On normality assumption in residual simulation for probabilistic load forecasting. IEEE Trans Smart Grid 8(3):1046–1053
Xie J, Hong T (2016) Temperature scenario generation for probabilistic load forecasting. IEEE Trans Smart Grid. https://doi.org/10.1109/TSG.2016.2597178
Rengcun F, Zhou J, Zhang Y et al (2009) Short-term probabilistic load forecasting using chaotic time series. Journal of Huazhong University of Science and Technology (Natural Science Edition) 37(5):125–128
Kang C, Bai L, Xia Q et al (2002) Implement of probabilistic production cost simulation algorithm based on sequence operation theory. Proc CSEE 22(9):6–11
Zhang N, Kang C (2012) Dependent sequence operation for wind power outputs analyses. J Tsinghua Univ 52(5):704–709
Hong T, Wang P, Willis HL (2011) A naïve multiple linear regression benchmark for short term load forecasting. In: Proceedings of the 2011 IEEE power and energy society general meeting, Detroit, USA, 24–28 July 2011, pp 1–6
Liu B, Nowotarski J, Hong T (2017) Probabilistic load forecasting via quantile regression averaging on sister forecasts. IEEE Trans Smart Grid 8(2):730–737
Taieb SB, Hyndman RJ (2014) A gradient boosting approach to the Kaggle load forecasting competition. Int J Forecast 30(2):382–394
Gaillard P, Goude Y, Nedellec R (2016) Additive models and robust aggregation for GEFCom2014 probabilistic electric load and electricity price forecasting. Int J Forecast 32(3):1038–1050
Haben S, Giasemidis G (2016) A hybrid model of kernel density estimation and quantile regression for GEFCom2014 probabilistic load forecasting. Int J Forecast 32(3):1017–1022
McSharry PE, Bouwman S, Bloemhof G (2005) Probabilistic forecasts of the magnitude and timing of peak electricity demand. IEEE Trans Power Syst 20(2):1166–1172
Zhou J, Zhang Y, Li Q et al (2005) Probabilistic short-term load forecasting based on dynamic self-adaptive radial basis function network. Power Syst Technol 34(3):37–41
Ranaweera DK, Karady GG, Farmer RG (1996) Effect of probabilistic inputs on neural network-based electric load forecasting. IEEE Trans Neural Netw 7(6):1528–1532
Hong T, Wang P, Willis HL (2016) Deep neural networks for youtube recommendations. In: Proceedings of the 10th ACM conference on recommender systems, Boston, USA, 15–19 September 2016, pp 191–198
Li Y, Xu L, Tian F et al (2015) Word embedding revisited: a new representation learning and explicit matrix factorization perspective. In: Proceedings of 2015 international conference on artificial intelligence. Buenos Aires, Argentina, 25–31 June 2015, pp 3650–3656
Xie J, Hong T (2016) GEFCom2014 probabilistic electric load forecasting: an integrated solution with forecast combination and residual simulation. Int J Forecast 32(3):1012–1016
Lee D, Baldick R (2014) Short-term wind power ensemble prediction based on Gaussian processes and neural networks. IEEE Trans Smart Grid 5(1):501–510
Mcdonald GC (2010) Ridge regression. Wiley Interdiscip Rev Comput Stat 1(1):93–100
Hong T, Pinson P, Fan S et al (2016) Probabilistic energy forecasting: global energy forecasting competition 2014 and beyond. Int J Forecast 32(3):896–913
Wan C, Xu Z, Pinson P (2014) Probabilistic forecasting of wind power generation using extreme learning machine. IEEE Trans Power Syst 29(29):1033–1044
Acknowledgements
This work was supported by National Key R&D Program of China (No. 2016YFB0900100).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 7 December 2017
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
GAN, D., WANG, Y., YANG, S. et al. Embedding based quantile regression neural network for probabilistic load forecasting. J. Mod. Power Syst. Clean Energy 6, 244–254 (2018). https://doi.org/10.1007/s40565-018-0380-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-018-0380-x