Dynamic response and analysis of cracked beam subjected to transit mass

Abstract

In the existing research work, the dynamic response of a cracked cantilever beam with the presence of multiple transverse open cracks under a traversing mass has been discussed. The response of the traversing mass structure has been calculated at numerous mass magnitude and speed with random crack depth at different positions of cracks. The principal equation of motion of the structure subjected to moving mass has been developed and solved using Duhamel integral technique. The consequence of cracks in the structures along with moving mass has been examined. The effects of size and position of cracks on the structure during the movement of the traversing mass across the beam and the effects of speed on the dynamic response of the cracked beam have been investigated analytically and computationally. For the verifications of the numerical results, the laboratory tests have been conducted for the traversing mass-structural systems with various damage configurations of the structure. The results obtained from the numerical formulation have been compared with those of laboratory tests and converged well with the applied computational method.

Appendices

Appendix A

Crack analysis on the vibration characteristics of cantilever beam:

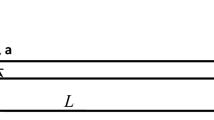
A cracked cantilever beam (Fig 9.) of length ‘L’, width ‘B’, thickness ‘H’ with multiple cracks of crack depth ‘$d_{1,2,3}$’, at distance of ‘$L_{1,2,3}$’ from the fixed end is considered for the analysis.

The analysis of the cracked beam is carried out as follows

• u(x, t) $=$ Longitudinal vibration displacement functions of the crack section

• y(x, t) $=$ Transverse vibration displacement functions of the crack section.

One can define the normalized function for the cracked structure with multiple cracks in normalized form as

$$\begin{aligned} \bar{{u}}_1 (\bar{{x}})= & {} A_1 \cos (\bar{{K}}_u \bar{{x}})+A_2 \sin (\bar{{K}}_u \bar{{x}}) \end{aligned}$$

(A-1)

$$\begin{aligned} \bar{{u}}_2 (\bar{{x}})= & {} A_3 \cos (\bar{{K}}_u \bar{{x}})+A_4 \sin (\bar{{K}}_u \bar{{x}}) \end{aligned}$$

(A-2)

$$\begin{aligned} \bar{{u}}_3 (\bar{{x}})= & {} A_5 \cos (\bar{{K}}_u \bar{{x}})+A_6 \sin (\bar{{K}}_u \bar{{x}}) \end{aligned}$$

(A-3)

$$\begin{aligned} \bar{{u}}_4 (\bar{{x}})= & {} A_7 \cos (\bar{{K}}_u \bar{{x}})+A_8 \sin (\bar{{K}}_u \bar{{x}}) \end{aligned}$$

(A-4)

$$\begin{aligned} y_1 (x)= & {} A_9 \cosh (\bar{{K}}_y \bar{{x}})+A_{10} \sinh (\bar{{K}}_y \bar{{x}})\nonumber \\&+A_{11} \cos (\bar{{K}}_y \bar{{x}})+A_{12} \sin (\bar{{K}}_y \bar{{x}}) \end{aligned}$$

(A-5)

$$\begin{aligned} y_2 (x)= & {} A_{13} \cosh (\bar{{K}}_y \bar{{x}})+A_{14} \sinh (\bar{{K}}_y \bar{{x}})\nonumber \\&+A_{15} \cos (\bar{{K}}_y \bar{{x}})+A_{16} \sin (\bar{{K}}_y \bar{{x}}) \end{aligned}$$

(A-6)

$$\begin{aligned} y_3 (x)= & {} A_{17} \cosh (\bar{{K}}_y \bar{{x}})+A_{18} \sinh (\bar{{K}}_y \bar{{x}})\nonumber \\&+A_{19} \cos (\bar{{K}}_y \bar{{x}}) +A_{20} \sin (\bar{{K}}_y \bar{{x}}) \end{aligned}$$

(A-7)

$$\begin{aligned} y_4 (x)= & {} A_{21} \cosh (\bar{{K}}_y \bar{{x}})+A_{22} \sinh (\bar{{K}}_y \bar{{x}})\nonumber \\&+A_{23} \cos (\bar{{K}}_y \bar{{x}}) +A_{24} \sin (\bar{{K}}_y \bar{{x}}) \end{aligned}$$

(A-8)

The normalized form may be expressed as

$\eta _{1,2,3} =L_{1,2,3} /L=$Relative location of cracks.

$$\begin{aligned} \bar{{x}}= & {} x/L,\bar{{u}}=u/L,\bar{{y}}=y/L,\bar{{t}}=t/L\\ \bar{{K}}= & {} \omega L/C_u , C_u =\left( {E/\rho } \right) ^{1/2}, \\ \bar{{K}}_y= & {} \left( {{\omega L}/{C_y }} \right) ^{1/2}, C_y =\left( {{EI}/m} \right) ^{1/2}, m=\rho A \end{aligned}$$

The different values of ‘$A' (A_i (i=1,24))$ can be determined from the different end conditions.

The different end conditions of the cantilever beam are as follows

$$\begin{aligned} \bar{{u}}_1 (0)=0,\bar{{y}}_1 (0)=0,\bar{{y}}_1 ^{\prime }(0)=0 \end{aligned}$$

(A-9)

At the free end $x=L$, then $\bar{{x}}=x/L=1$

$$\begin{aligned} \bar{{u}}_4 ^{\prime }(1)=0,\bar{{y}}_4 ^{{\prime }{\prime }}(1)=0,\bar{{y}}_4 ^{{\prime }{\prime }{\prime }}(1)=0 \end{aligned}$$

(A-10)

At the crack segment

$$\begin{aligned} \bar{{u}}_1 (\eta _1 )= & {} \bar{{u}}_2 (\eta _1 ), \bar{{u}}_2 (\eta _2 )=\bar{{u}}_3 (\eta _2 ), \bar{{u}}_3 (\eta _3 )=\bar{{u}}_4 (\eta _3 ) \nonumber \\\end{aligned}$$

(A-11)

$$\begin{aligned} \bar{{y}}_1 (\eta _1 )= & {} \bar{{y}}_2 (\eta _1 ), \bar{{y}}_2 (\eta _2 )=\bar{{y}}_3 (\eta _2 ), \bar{{y}}_3 (\eta _3 )=\bar{{y}}_4 (\eta _3 ) \nonumber \\\end{aligned}$$

(A-12)

$$\begin{aligned} \bar{{y}}_1 ^{{\prime }{\prime }}(\eta _1 )= & {} \bar{{y}}_2 ^{\prime \prime }(\eta _1 ),\bar{{y}}_2 ^{{\prime }{\prime }}(\eta _2 )=\bar{{y}}_3 ^{\prime \prime }(\eta _2 ),\bar{{y}}_3 ^{{\prime }{\prime }}(\eta _3 )=\bar{{y}}_4 ^{{\prime }{\prime }}(\eta _3 ) \nonumber \\\end{aligned}$$

(A-13)

$$\begin{aligned} \bar{{y}}_1^{{\prime }{\prime }{\prime }}(\eta _1 )= & {} \bar{{y}}_2 ^{{\prime } {\prime }{\prime }}(\eta _1 ), \bar{{y}}_2 ^{{\prime }{\prime }{\prime }}(\eta _2 )=\bar{{y}}_3 ^{{\prime }{\prime }{\prime }}(\eta _2 ), \bar{{y}}_3 ^{{\prime }{\prime }{\prime }}(\eta _3 )=\bar{{y}}_4 ^{\prime \prime \prime }(\eta _3 )\nonumber \\ \end{aligned}$$

(A-14)

At the first crack segment also

$$\begin{aligned} AE\frac{du_1 (L_1 )}{dx}= & {} K_{11} ^{1}\left[ {u_2 (L_1 )-u_1 (L_1 )} \right] \nonumber \\&+K_{12} ^{1}\left[ {\frac{dy_2 (L_1 )}{dx}-\frac{dy_1 (L_1 )}{dx}} \right] \end{aligned}$$

(A-15)

Similarly for the second and third crack sections, one can express

$$\begin{aligned} AE\frac{du_2 (L_2 )}{dx}= & {} K_{11} ^{2}\left[ {u_3 (L_2 )-u_2 (L_2 )} \right] \nonumber \\&+K_{12} ^{2}\left[ {\frac{dy_3 (L_2 )}{dx}-\frac{dy_2 (L_2 )}{dx}} \right] \end{aligned}$$

(A-16)

$$\begin{aligned} AE\frac{du_3 (L_3 )}{dx}= & {} K_{11} ^{3}\left[ {u_4 (L_3 )-u_3 (L_3 )} \right] \nonumber \\&+K_{12} ^{3}\left[ {\frac{dy_4 (L_3 )}{dx}-\frac{dy_3 (L_3 )}{dx}} \right] \end{aligned}$$

(A-17)

Equation (A-15) is for discontinuity due to axial deformation before and after the first crack.

Similarly due to the discontinuity of slope to the before and after of the first crack section, one can express

$$\begin{aligned} EI\frac{d^{2}y_1 (L_1 )}{dx^{2}}= & {} K_{21} ^{1}[u_2 (L_1 )-u_1 (L_1 )]\nonumber \\&+K_{22} ^{1}\left[ {\frac{dy_2 (L_1 )}{dx}-\frac{dy_1 (L_1 )}{dx}} \right] \end{aligned}$$

(A-18)

Similarly for the second and third crack sections, one can express

$$\begin{aligned} EI\frac{d^{2}y_2 (L_2 )}{dx^{2}}= & {} K_{21} ^{2}[u_3 (L_2 )-u_2 (L_2 )]\nonumber \\&+K_{22} ^{2}\left[ {\frac{dy_3 (L_2 )}{dx}-\frac{dy_2 (L_2 )}{dx}} \right] \end{aligned}$$

(A-19)

$$\begin{aligned} EI\frac{d^{2}y_3 (L_3 )}{dx^{2}}= & {} K_{21} ^{3}[u_4 (L_3 )-u_3 (L_3 )]\nonumber \\&+K_{22} ^{3}\left[ {\frac{dy_4 (L_3 )}{dx}-\frac{dy_3 (L_3 )}{dx}} \right] \end{aligned}$$

(A-20)

By inversing the compliance matrix, the local flexibility matrix element ‘$K_{ij}$’ may be determined.

One can determine the compliance matrix element by considering the strain energy at the crack location-

$$\begin{aligned} C_{ij} =\frac{\partial ^{2}}{\partial P_i \partial P_j }\int \limits _0^{d_1 } {J(a)dd} \end{aligned}$$

(A-21)

where $J(a)=$ Strain energy density function

$P_{i=1} =$Axial force, $P_{i=2}=$Bending moment

From the analysis of cracks, the dimensionless compliance factors can be given us using the following relations:

$$\begin{aligned} \bar{{C}}_{11}= & {} C_{11} \left( {\frac{BE}{2\pi }} \right) , \bar{{C}}_{12} =C_{12} \left( {\frac{BEH}{12\pi }} \right) ,\nonumber \\ \bar{{C}}_{22}= & {} C_{22} \left( {\frac{BH^{2}E}{72\pi }} \right) \hbox { and }\bar{{C}}_{12} =\bar{{C}}_{21} \end{aligned}$$

(A-22)

where B, H and E are the breadth, width and modulus of elasticity of the mild steel beam structure respectively.

The compliance matrix can be given as

$$\begin{aligned} C=\left( {{\begin{array}{ll} {C_{11} }&{} {C_{12} } \\ {C_{21} }&{} {C_{22} } \\ \end{array} }} \right) \end{aligned}$$

(A-23)

The inverse of compliance matrix will form the local stiffness matrix i.e.

$$\begin{aligned} K=\left( {{\begin{array}{ll} {K_{11} }&{} {K_{12} } \\ {K_{21} }&{} {K_{22} } \\ \end{array} }} \right) =\left( {{\begin{array}{ll} {C_{11} }&{} {C_{12} } \\ {C_{21} }&{} {C_{22} } \\ \end{array} }} \right) ^{-1} \end{aligned}$$

(A-24)

The stiffness matrix for first, second and third cracks can be given as:

$$\begin{aligned} {K}^{\prime }= & {} \left( {{\begin{array}{ll} {C_{11} ^{\prime }}&{} {C_{12} ^{\prime }} \\ {C_{21} ^{\prime }}&{} {C_{22} ^{\prime }} \\ \end{array}}} \right) ^{-1}=\left( {{\begin{array}{ll} {K_{11} ^{\prime }}&{} {K_{12} ^{\prime }} \\ {K_{21} ^{\prime }}&{} {K_{22} ^{\prime }} \\ \end{array}}} \right) \nonumber \\ {K}^{{\prime }{\prime }}= & {} \left( {{\begin{array}{ll} {C_{11} ^{\prime \prime }}&{} {C_{12} ^{{\prime }{\prime }}} \\ {C_{21} ^{\prime \prime }}&{} {C_{22} ^{{\prime }{\prime }}} \\ \end{array}}} \right) ^{-1}=\left( {{\begin{array}{ll} {K_{11} ^{\prime \prime }}&{} {K_{12} ^{{\prime }{\prime }}} \\ {K_{21} ^{\prime \prime }}&{} {K_{22} ^{{\prime }{\prime }}} \\ \end{array}}} \right) \nonumber \\ {K}^{{\prime }{\prime }{\prime }}= & {} \left( {{\begin{array}{ll} {C_{11} ^{\prime \prime \prime }}&{} {C_{12} ^{\prime \prime \prime }} \\ {C_{21} ^{\prime \prime \prime }}&{} {C_{22} ^{\prime \prime \prime }} \\ \end{array}}} \right) ^{-1}=\left( {{\begin{array}{ll} {K_{11} ^{\prime \prime \prime }}&{} {K_{12} ^{\prime \prime \prime }} \\ {K_{21} ^{\prime \prime \prime }}&{} {K_{22} ^{\prime \prime \prime }} \\ \end{array}}} \right) \end{aligned}$$

(A-25)

where ${K}^{\prime }$, ${K}^{{\prime }{\prime }}$ and ${K}^{{\prime }{\prime }{\prime }}$ are the stiffness matrix for first, second and third crack locations respectively.

For each of the stiffness matrix-$K_{12} =K_{21}$. For uncoupled case $K_{12} =K_{21} =0$, Where as for couple case $K_{12} =K_{21} \ne 0$

Appendix B

The Eigen functions are orthogonal not orthonormal. Applying the condition of orthonormality

$$\begin{aligned} \left\| {Y_n (x)} \right\|= & {} \left( {\int \limits _0^L {Y_n ^{2}} dx} \right) ^{1/2}=\left( \int \limits _0^{L_1 } Y_{n1} ^{2}dx+\int \limits _{L_1 }^{L_2 } {Y_{n2} ^{2}dx}\right. \nonumber \\&\left. +\int \limits _{L_2 }^{L_3 } {Y_{n3} ^{2}dx+\int \limits _{L_3 }^L {Y_{n4} ^{2}} } dx \right) ^{1/2}=1 \end{aligned}$$

(B-1)

To make the terms normalized in right part of Eq. (5), the constant coefficients A’s in Eq. 4a–d for Eigen functions should be replaced as

$$\begin{aligned} A= & {} \left( {1\Bigg /{\int \limits _0^{L_1 } {\left[ {\frac{Y_{n1} (x)}{A_{n1} }} \right] } ^{2}dx+\int \limits _{L_1 }^{L_2 } {\left[ {\frac{Y_{n2} (x)}{A_{n1} }} \right] } ^{2}dx}}\right. \nonumber \\&\left. +\int \limits _{L_2 }^{L_3 } {\left[ {\frac{Y_{n3} (x)}{A_{n1} }} \right] } ^{2}dx +\int \limits _{L_3 }^L {\left[ {\frac{Y_{n4} (x)}{A_{n1} }} \right] } ^{2}dx \right) ^{1/2} \end{aligned}$$

(B-2)

One can express the force between the beam and mass as-

$$\begin{aligned} f_m (x,t)=\left\{ {\begin{array}{ll} Mg, &{}x=\beta \\ 0, &{} x\ne \beta \\ \end{array}} \right\} \end{aligned}$$

(B-3)

Using the properties of Dirac delta function, one can express

$$\begin{aligned} f_m \left( {x,t} \right) =Mg\delta \left( {x-\beta } \right) \end{aligned}$$

(B-4)

The Fourier transformation of the function can be written as-

$$\begin{aligned} f_m \left( {x,t} \right) =\sum _{n=1}^\infty {A_n \sin \left( {\frac{n\pi }{L}x} \right) } \end{aligned}$$

(B-5)

Multiplying $\sin \left( {\frac{k\pi }{L}x} \right)$ on both sides of Eq. (B-5) and integrating it over the entire beam length, one can state the newly formed equation as-

$$\begin{aligned}&\int \limits _0^L {f_m \left( {x,t} \right) \sin \left( {\frac{k\pi }{L}x} \right) dx} \nonumber \\&\quad =\sum _{n=1}^\infty {A_n \int \limits _0^L {\sin \left( {\frac{n\pi }{L}x} \right) \sin \left( {\frac{k\pi }{L}x} \right) } dx} \end{aligned}$$

(B-6)

where $\hbox {n}, \hbox {k}=$ Number of the Eigen functions.

$$\begin{aligned} \int \limits _0^L {\sin \left( {\frac{n\pi }{L}x} \right) \sin \left( {\frac{k\pi }{L}x} \right) } dx=\left\{ {\begin{array}{ll} \frac{L}{2}, &{}n=k \\ 0, &{}n\ne k \\ \end{array}} \right\} \end{aligned}$$

(B-7)

Then

$$\begin{aligned}&A_{n=} \frac{2}{L}\int \limits _0^L {f_m (x,t)\sin \left( {\frac{n\pi }{L}x} \right) } dx \end{aligned}$$

(B-8)

$$\begin{aligned}&A_{n=} \frac{2Mg}{L}\int \limits _0^L {\delta (x-\beta )\sin \left( {\frac{n\pi }{L}x} \right) } dx \end{aligned}$$

(B-9)