Skip to main content
SpringerLink
Log in

Nonlinear modeling of an electrohydraulic actuation system via experiments and its characterization by means of neural network

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

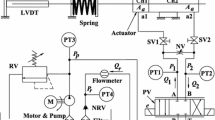
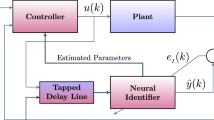
Abstract

The friction and end-cushioning effects in the actuator have been taken care in consideration in the modeling of the actuation method related to an electrohydraulic system. A much simpler friction model that retains all the features of the existing models has been developed for this purpose. In addition, a systematic experimental characterization procedure has been proposed that has been utilized in a supplementary manner for the development of the elaborate nonlinear system model. An artificial neural-network model has been constructed by training with experimental data keeping in mind the variation of discharge through the proportional valve with pressure and command signal. All the nonlinear subsystem models thus obtained have been incorporated simultaneously in MATLAB/SIMULINK to monitor the actuation dynamics. The variations of the theoretical and investigated (via experiments) displacements of the piston against different command signals have been found to be quite close to each other.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

A a :

Cross-sectional area of actuator piston, (m2)

A p :

Cross-sectional area of flow in pipe, (m2)

Cd :

Coefficient of discharge

C vi (i = 1–4):

Main-flow coefficient corresponding to the pressure drop ΔPi, (m3/(VPa1/2))

d b :

Actuator bore diameter, (m)

d c :

Cushion rod diameter, (m)

d o :

Cushion bush diameter, (m)

d r :

Actuator piston rod diameter, (m)

E :

Error between measured output value t k and the network predicted value y k

e f :

Feed forward voltage (V)

F f :

Frictional force (N)

f RV(Q s), f NRV(Q r):

Pressure-discharge characteristics for the relief valve and nonreturn valve, respectively, (Pa)

K s :

Spring constant, (N/m)

l b :

Inner length of actuator cylinder, (m)

l c :

Length of cushion rod, (m)

l l :

Lip length between cushion rod and actuator piston rod, (m)

l p−s :

Pipe length between pump delivery and the supply port of PV, (m)

l v1−a1 :

Pipe length between PV and chamber 1 of actuator, (m)

l v2−a2 :

Pipe length between PV and chamber 2 of actuator, (m)

l r−n :

Pipe length between NRV and the return port of PV, (m)

m a :

Moving mass of the actuator, (kg)

P A, P B :

Pressures at the two control ports A and B of the PV, respectively, (Pa)

P c1, P c2 :

Cushioning volume pressures in chambers 1 and 2, respectively, (Pa)

P n :

Pressures at the return port of PV and inlet to the NRV, respectively, (Pa)

P p :

Pressures at the pump exit and inlet to the PV, respectively, (Pa)

P Qdischarge :

Precision error of the discharge of the PV, (m3)

P Pp :

Precision error of exit pressure of pump, (bar)

P P1 :

Precision error of actuating pressure in chamber 1, (bar)

P Pr :

Precision error of return line, (bar)

P r :

Pressure of the return line to the tank, (Pa)

P 1, P 2 :

Piston-actuating pressures in chambers 1 and 2, respectively, (Pa)

Q a1, Q a2 :

Discharges through actuator control ports 1 and 2, respectively, (m3)

Q v1, Q v2 :

Discharges through ports v1 and v2, respectively, of PV, (m3)

S :

Stroke of the actuator, (m)

S Qdischarge :

Bias limit of the discharge of the PV, (m3)

S Pp :

Bias error of exit pressure of pump, (bar)

S P1 :

Bias error of actuating pressure in chamber 1, (bar)

S Pr :

Bias error of the return line to the tank, (bar)

t factor :

Coverage factor

\(V_{10} ,V_{20}\) :

Initial volumes in chambers 1 and 2, respectively, of the actuator, (m3)

U Pdischarge :

Total experimental uncertainty, (m3)

W :

Width of actuator piston, (m)

w ij :

Weights

y :

Displacement of actuator, (m)

β :

Bulk modulus of the oil, (Pa)

ρ :

Density of oil, (kg/m3)

ς:

Damping coefficient of the PV

NRV:

Nonreturn valve

NV:

Needle valve

LVDT:

Linear variable differential transformer

PT:

Pressure transducer

PV:

Proportional valve

RV:

Relief valve

SD:

Standard deviation

SV:

Shut-off valve

References

  1. Blackburn JF, Reethrop G, Shearer JL (1960) Fluid power control. The M.I.T Press, Cambridge

    Google Scholar 

  2. Merritt HE (1967) Hydraulic control systems. Wiley, New York

    Google Scholar 

  3. Precup RE, Rudas IJ, Tomescu ML, Tar JK (2008) Design and experiments for a class of fuzzy controlled servo systems. IEEE/ASME Trans Mechatron 13(1):22–35

    Article  Google Scholar 

  4. Kaddissi C, Kenne JP, Saad M (2000) Identification and real-time control of an electrohydraulic servo system based on nonlinear backstepping. IEEE/ASME Trans Mechatron 12:12–22

    Article  Google Scholar 

  5. Niksefat N, Sepehri N (2000) Design and experimental evaluation of a robust force controller for an electro-hydraulic actuator via quantitative feedback theory. Control Eng Pract 8(12):1335–1345

    Article  Google Scholar 

  6. Lee SY, Blackburn JF (1952) Contributions to hydraulic control; 1-steady-state axial forces on control valve pistons. Trans ASME 74(6):1005–1011

    Google Scholar 

  7. Wu D, Burton R, Schoenau G (2002) An empirical discharge coefficient model for orifice flow. Int J Fluid Power 3(3):13–19

    Article  Google Scholar 

  8. Mookherjee S, Acharyya S, Majumdar K, Sanyal D (2001) Static-performance based computer-aided design of a DDV and its sensitivity analysis. Int J Fluid Power 2:47–63

    Article  Google Scholar 

  9. Zhang H, Nikiforuk PN, Ukrainetz PR (1993) Neural adaptive control of MIMO electrohydraulic servosystem. In: Proc. 3rd int conf fluid power transmission contr., Hangzhou, pp 315–320

  10. de Wit CC, Olsson H, Astrom KJ, Lischinksy P (1995) A new model for control of systems with friction. IEEE Trans Autom Control 40(3):419–425

    Article  MathSciNet  Google Scholar 

  11. Owen WS, Croft EA (2003) The reduction of stick-slip friction in hydraulic actuators. IEEE/ASME Trans Mechatron 8(3):362–371

    Article  Google Scholar 

  12. Janocha H, Pesotski D, Kuhnen K (2008) FPGA-based compensator of hysteretic actuator nonlinearities for highly dynamic applications. IEEE/ASME Trans Mechatron 13:112–116

    Article  Google Scholar 

  13. Karnopp D (1985) Computer simulation of stick-slip friction in mechanical dynamic systems. Trans ASME J Dyn Syst Meas Control 107(1):100–103

    Article  Google Scholar 

  14. Yanada H, Sekikawa Y (2008) Modeling of dynamic behaviors of friction. Mechatronics 18(7):330–339

    Article  Google Scholar 

  15. Schwartz C, De Negri VJ, Climaco JV (2005) Modeling and analysis of an auto-adjustable stroke end cushioning device for hydraulic cylinders. J Braz Soc Mech Sci Eng VXXVII:415–425

    Article  Google Scholar 

  16. Marton L, Fodor S, Sepehri N (2011) A practical method for friction identification in hydraulic actuators. Mechatronics 21(1):350–356

    Article  Google Scholar 

  17. Rahmat MFA, Has Z, Husain AR, Md Sam Y, Ishaque K, Ghazaly R, Md Rozali S (2011) Modeling and controller design of an industrial hydraulic actuator system in the presence of friction and internal leakage. Int J Phys Sci 6(14):3502–3517

    Google Scholar 

  18. Guan C, Pan S (2008) Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters. Control Eng Pract 16(11):1275–1284

    Article  Google Scholar 

  19. Rahmat MFA, Md Rozali S, Abdul Wahab N, Has Z, Jusoff K (2010) Modeling and controller design of an electro-hydraulic actuator system. Am J Appl Sci 7(8):1100–1108

    Article  Google Scholar 

  20. Ghazali R, Sam YM, Rahmat MF, Jusoff K, Hashim AWIM (2011) Self-tuning control of an electro-hydraulic actuator system. Int J Smart Sens Intell Syst 4(2):189–204

    Google Scholar 

  21. Rahmat MFA, Abdul Wahab N, Has Z (2010) Application of draw wire sensor in position tracking of electro hydraulic actuator system. Int J Smart Sens Intell Syst 3(4):736–755

    Google Scholar 

  22. Shih KS, Li SHT, Tsai SH (2011) Novel adaptive fuzzy neural network controller for a class of certain non-linear systems. Proc I Mech Eng J Syst Control Eng 226:364–378

    Google Scholar 

  23. Knohl T, Unbehauen H (2000) Adaptive position control of electrohydraulic servo systems using ANN. Mechatronics 10(1):127–143

    Article  Google Scholar 

  24. Alfayad S, Ouezdou FB, Namoun F, Gheng G (2011) High performance integrated electro-hydraulic actuator for robotics. Part II: theoretical modeling, simulation, control & comparison with real measurements. Sens Actuators A 169(1):124–132

    Article  Google Scholar 

  25. Lippmann R (1987) An introduction to computing with neural nets. IEEE Acoust Speech Signal Process Mag 4(2):4–22

    Google Scholar 

  26. Rumelhart DE, Hinton G, Williams R (1986) Learning internal representations by backpropagating errors. In: Rumelhart DE, McClelland JL (eds) Parallel distributed processing: explorations in the microstructure of cognition, foundations, vol 1. MIT Press, Cambridge, pp 318–362

  27. Cybenko G (1989) Approximation by superpositions of a sigmoidal function. Math Control Signals Syst 2(4):303–314

    Article  MathSciNet  MATH  Google Scholar 

  28. Sarkar BK, Das J, Saha R, Mookherjee S, Sanyal D (2013) Approaching servoclass tracking performance by a proportional valve-controlled system. IEEE/ASME Trans Mechatron 18(4):1425–1430

    Article  Google Scholar 

  29. Mahato AC, Ghoshal SK, Samantaray AK (2017) Energy saving of a hydrostatic drive system by incorporating soft switch. J Braz Soc Mech Sci Eng 39(6):1929–1945

    Article  Google Scholar 

  30. Taylor J (1997) Introduction to error analysis, the study of uncertainties in physical measurements. University Science Books, New York

  31. Stern F, Muste M, Beninati ML, Eichinger WE (1999) Summary of experimental uncertainty assessment methodology with example (No. 406). IIHR Report

  32. Bezarra MA, Santelli RE, Oliveira EP, Villar LS, Escaleira LA (2008) Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 76(5):965–977

    Article  Google Scholar 

Download references

Acknowledgements

This work has been supported by AR&DB New Delhi and SAP-DRS of UGC New Delhi and Jadavpur University for equipment, and Prof. Dipankar Sanyal, Dr. Saikat Mookherjee, and Dr. Rana Saha of Mechanical Engineering Department, Jadavpur University, Kolkata for the help and valuable suggestions.

Author information

Authors and Affiliations

  1. Department of Mining Machinery Engineering, Indian Institute of Technology (ISM), Dhanbad, 826004, India

    J. Das & Santosh Kr. Mishra

  2. Department of Mechanical Engineering, Jadavpur University, Kolkata, 700032, India

    R. Saha, S. Mookherjee & D. Sanyal

Authors
  1. J. Das
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Santosh Kr. Mishra
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. R. Saha
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. S. Mookherjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. D. Sanyal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Santosh Kr. Mishra.

Additional information

Technical Editor: Jose A. dos Reis Parise.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Das, J., Mishra, S.K., Saha, R. et al. Nonlinear modeling of an electrohydraulic actuation system via experiments and its characterization by means of neural network. J Braz. Soc. Mech. Sci. Eng. 40, 58 (2018). https://doi.org/10.1007/s40430-018-0979-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-0979-x

Keywords

Search

Navigation