Abstract
Physiologically based pharmacokinetic modelling is well established in the pharmaceutical industry and is accepted by regulatory agencies for the prediction of drug–drug interactions. However, physiologically based pharmacokinetic modelling is valuable to address a much wider range of pharmaceutical applications, and new regulatory impact is expected as its full power is leveraged. As one example, physiologically based pharmacokinetic modelling is already routinely used during drug discovery for in-vitro to in-vivo translation and pharmacokinetic modelling in preclinical species, and this leads to the application of verified models for first-in-human pharmacokinetic predictions. A consistent cross-industry strategy in this application area would increase confidence in the approach and facilitate further learning. With this in mind, this article aims to enhance a previously published first-in-human physiologically based pharmacokinetic model-building strategy. Based on the experience of scientists from multiple companies participating in the GastroPlus™ User Group Steering Committee, new Absorption, Distribution, Metabolism and Excretion knowledge is integrated and decision trees proposed for each essential component of a first-in-human prediction. We have reviewed many relevant scientific publications to identify new findings and highlight gaps that need to be addressed. Finally, four industry case studies for more challenging compounds illustrate and highlight key components of the strategy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Linking of in-silico quantitative structure–property relationship models with physiologically based pharmacokinetic (PBPK) modelling is a powerful emerging technique, which is already being employed during early drug discovery. Combined with parameter sensitivity analyses, this can identify the compound properties most influencing systemic exposure and thus guide lead optimisation. |
The quality of first-in-human PBPK predictions is greatly improved when measured inputs are available for the most critical parameters. PBPK model verification in preclinical species, which has not always been included in assessments of first-in-human pharmacokinetic predictions, is critical to build confidence and improve accuracy. |
Uncertainty analysis is a key consideration to obtain maximal value from first-in-human PBPK predictions. |
1 Introduction
Physiologically based pharmacokinetic (PBPK) models represent the body as compartments parameterised based on physiology of tissues and organs including composition, volumes and blood flows [1]. Physiologically based pharmacokinetic models integrate this physiological description with compound-specific data to predict the pharmacokinetics of drugs, allowing simulation of the time course of drug concentrations in plasma and tissues. Here, we consider a PBPK model as a whole-body model describing systemic disposition linked to a mechanistic absorption model such as the advanced compartmental absorption and transit (ACAT) model [2]. The origin of PBPK modelling can be traced back to Teorell in 1937 [3, 4], but application of PBPK modelling in drug discovery, development and regulation came of age around 2006 [5]. The US Food and Drug Administration [6] and European Medicines Agency [7] have recently produced guidance documents on the appropriate use of PBPK models, and PBPK impacts on drug labels are increasingly common [8,9,10].
The majority of regulatory submissions including PBPK modelling have focused on drug–drug interactions and paediatric modelling [8, 10, 11]. However, a recent industry perspective on PBPK applications [12] highlighted diverse uses spanning pharmaceutical discovery and development from preclinical predictions to simulations of variability in different clinical populations, indicating the potential for expansion of regulatory applications [8]. At a 2014 meeting on PBPK modelling hosted by the US Food and Drug Administration, PBPK modelling for first-in-human (FIH) predictions was seen as mainly useful for drug developers [13]. However, PBPK modelling is increasingly used for regulatory purposes, and has been identified by the European Medicines Agency as a useful tool for assessing an appropriate starting dose for healthy volunteers [14]. The methods used and calculations on how doses and estimated exposure levels are determined, including methods for modelling such as PBPK modelling, should be included in the protocol and may be summarised in the investigator’s brochure [14].
Physiologically based pharmacokinetic models are a systems pharmacology approach that can act as a growing repository of knowledge on the pharmacokinetics of a new chemical entity or drug candidate [15], evolving to include new input data and mechanisms as scientific knowledge increases. This is of particular utility in preclinical development when PBPK modelling can be applied to predict clinical pharmacokinetics prior to FIH studies. A seminal paper from Jones et al. [16] first demonstrated that PBPK modelling, with verification of predictive performance first performed in preclinical species, is superior to empirical methods for predicting pharmacokinetics. Since then, several publications from industry groups have confirmed the superiority of PBPK modelling for this application [17,18,19] and many medium and large pharmaceutical companies are now routinely applying the approach as is clear from a recent cross-industry perspective [12].
Here, we have updated the strategy of Jones et al. [16] to include new knowledge and additional flow diagrams for each essential component of a FIH prediction. Although some information specific to GastroPlus is included and all the examples were conducted using GastroPlus, much of the information presented is generally applicable to PBPK modelling. The strategy has been updated based on a comprehensive review of subsequent publications and on the combined knowledge and experience of the authors who are all PBPK specialists and members of the GastroPlus User Group Steering Committee. Novel insights in the revised strategy include the use of quantitative structure–property relationship (QSPR) predictions as inputs for PBPK modelling prior to experimentation, integrating new Absorption, Distribution, Metabolism and Excretion (ADME) knowledge within the proposed decision trees and stressing the importance of considering uncertainty in predictions. The case studies described here highlight the application of the strategy and the importance of certain input parameters, such as the blood/plasma ratio (BPR), or model components, such as the tissue model, for molecules with challenging properties. We believe that a consistent PBPK strategy for FIH predictions, based on best practices and experience across companies, should increase the confidence of regulatory agencies in this application.
2 Model Building Strategy
The complexity of PBPK models, which include many adjustable parameters, mandates the definition of a consistent model building strategy and best practice guidance. Physiologically based pharmacokinetic models are used within numerous disciplines and by scientists with diverse backgrounds and thus a common approach covering various scenarios will facilitate regulatory evaluation.
Along with a consistent strategy, use of consistent physiological parameters and scaling factors allows a fair comparison between compounds, and some companies undergo internal harmonisation to ensure consistency. As an example of the possible range for a key parameter, liver blood flow has reported values in rats that include 47.2 [20], 55.2 [21] and 80 mL/min/kg [22]. The default PBPK models available within GastroPlus, include species-specific values for physiological parameters and scaling factors and thus encourage consistency.
2.1 Compound Assessment Using Quantitative Structure–Property Relationship plus Physiologically Based Pharmacokinetic Models
Although PBPK models require a large number of compound-specific inputs, many may be generated using QSPR models, enabling the use of PBPK models in early drug discovery before experimentation, potentially for virtual compounds. Although accurate prediction of pharmacokinetics using many properties predicted from a structure may be possible [23], it is not guaranteed [24] and verification with compounds from each chemical class has been recommended [25].
Combining QSPR predictions, for properties such as lipophilicity, acidity/basicity, clearance, solubility, permeability, binding to red blood cells and plasma proteins, with PBPK models for early simulations identifies gaps and major sensitivities, enabling a timely definition of essential experiments and prioritisation of fit-for-purpose resources to support model development and preclinical verification. Physiologically based pharmacokinetic modelling can be successfully applied in discovery with minimal data [26]. As compounds progress, models should be updated with more experimental data. Later, for FIH predictions, a comprehensive set of measured input data is generally required. Prediction accuracy is optimised by considering all available preclinical data [19], filling identified data gaps and verifying the preclinical PBPK model [18].
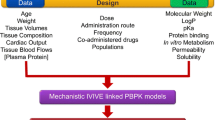
After integrating QSPR-predicted parameters into PBPK models (Fig. 1) to provide insights into compound properties and value-added experimentation, the in-vivo impact and interplay of compound properties within the physiological framework can be investigated via parameter sensitivity analysis (PSA). For example, for a basic compound, precipitation in the small intestine and binding to acidic phospholipids in tissues could both be critical. This can be explored by assessing the effect of predicted parameters for precipitation rate, intestinal solubility and the BPR, which affects the predicted tissue binding and thus the volume of distribution at steady state (Vss), on the predicted plasma concentration vs. time profile.
Compound assessment from structure using quantitative structure–property relationship (QSPR) plus physiologically based pharmacokinetic (PBPK) modelling [27, 30,31,32]. BCS Biopharmaceutics Classification System, BDDCS Biopharmaceutics Drug Disposition Classification System, BPR blood/plasma ratio, Dn dissolution number (the ratio of small intestine transit time/idealised dissolution time), ECCS Extended Clearance Classification System, Fup Fraction unbound in plasma, GI gastrointestinal, IVIVE in-vitro in-vivo extrapolation. 1[27], 2[31], 3[30], 4[32]
An initial QSPR plus PBPK assessment, as when combining ADMETPredictor™ with GastroPlus, will alert the modeller to the major challenges of modelling for a specific molecule. Thus, if the Biopharmaceutics Classification System (BCS) [27] class is predicted as I and II, mechanistic oral absorption modelling predictions may be straightforward, while class III and IV compounds may be more challenging [19, 28, 29]. Furthermore, the Extended Clearance Classification System framework [30], recently incorporated in ADMETPredictor™ Version 9.0, can predict whether a compound is predominantly cleared by renal elimination or if hepatic transporters may affect elimination. If hepatic metabolism by cytochrome P450 (CYP) 3A4 is predicted as the major elimination route, then the impact of intestinal metabolism on oral bioavailability should be considered and reaction phenotyping studies may be performed earlier.
2.2 Metabolism and Elimination
Physiologically based pharmacokinetic modelling requires quantitative understanding of the main mechanism(s) of drug clearance, and Fig. 2 presents a strategy for incorporating these routes. Predicting clearance during early discovery remains challenging [18, 26]; however, success was recently demonstrated by applying QSPR models within a chemical series [24, 26].
Physiologically based pharmacokinetic modelling strategy for elimination [42,43,44]. CLR renal clearance, CLR,u unbound renal clearance, ECCS Extended Clearance Classification System, Fup fraction unbound in plasma, GFR glomerular filtration rate, IVIVE in-vitro in-vivo extrapolation. 1[42], 2[43], 3[44]
The Extended Clearance Classification System can be a useful guide, and if the major elimination route is predicted as hepatic metabolism, then confidence in human predictions is higher if an in-vitro in-vivo extrapolation (IVIVE) can be established in preclinical species. The likelihood of a successful IVIVE is higher for compounds predominantly metabolised by CYP enzymes while non-CYP metabolism, although often captured qualitatively in hepatocyte models, remains more challenging [33]. The involvement of active uptake in hepatic clearance can be flagged by the Extended Clearance Classification System, and in such cases measurements in hepatocyte models may be useful [34] and human clearance predictions may be improved with cross-species empirical scaling factors [35]. More advanced hepatocyte models are also being explored with respect to improved IVIVE for more complex cases [36,37,38]. Renal [39, 40] and biliary [41] elimination involving active transport are also challenging to model mechanistically from in-vitro data, and, in general, prediction of human pharmacokinetics for transported molecules is difficult because absorption, distribution and elimination can all be affected [18].
However, there are encouraging developments. For renal secretion, measurements in organic anion transporter-transfected human embryonic kidney cells successfully predicted renal clearance of 31 diverse drugs [42] while a mechanistic model for passive tubular reabsorption was verified with a large dataset of drugs [43]. For hepatobiliary clearance, it was recently demonstrated that data from sandwich-cultured hepatocytes and a consistent IVIVE approach could predict in humans for 17 diverse drugs [44]. Furthermore, mechanistic IVIVE from the sandwich-cultured model, utilising transporter expression data in-vitro and in-vivo improved prediction for rosuvastatin in the rat [45]. It has also emerged that monkeys are a valuable model for the verification of hepatic disposition for transported molecules [44] particularly for substrates of the organic anion transporting polypeptide transporter [35]. Examples of complex PBPK models incorporating enzyme and transporter kinetics from in-vitro studies already exist and should become more common in the future as models evolve [46].
Irrespective of the mechanism, if preclinical verification of the clearance prediction can be demonstrated, this builds confidence in FIH pharmacokinetic predictions. When IVIVE is not successful in preclinical species it may be necessary to use empirical scaling factors for the human prediction (as for Compound 1 in Sect. 4.1) [47,48,49].
2.3 Distribution
Understanding tissue distribution is essential for PBPK modelling, and has been facilitated by mechanistic equations [1, 5]. Figure 3 presents a strategy for the distribution component of a PBPK model. GastroPlus defaults to the Lukacova [50] Kp (tissue-to-plasma partition coefficient) method, which builds on earlier work [51, 52], but other methods have been used [18, 24]. Whatever the method employed, the use of measured in-vitro input values for log P, pKa, Fup (fraction unbound in plasma), and BPR and verification in preclinical species are advisable to ensure accurate predictions (Fig. 3).
Physiologically based pharmacokinetic modelling strategy for distribution [17, 50, 53, 55]. BPR blood/plasma ratio, Fup fraction unbound in plasma, Kp tissue-to-plasma partition coefficient, SpecPStc specific in-vivo diffusional clearance per millilitre of tissue cell volume. 1[50], 2[55], 3[17], 4[53]
For molecules where passive processes dominate, distribution is often predictable using a standard perfusion-limited tissue model. See Compound 2 (Sect. 4.2) for an example that highlights the impact of measured BPR in predicting Vss for a basic compound.
However, for large compounds with slow passive diffusion through tissue membranes (as for Compound 4 in Sect. 4.4), permeability-limited tissue distribution models may be required, potentially including transporter kinetics. In other cases, measured input data for BPR have been empirically adjusted to match predictions to observed distribution [53]. The adjustment of BPR to account for phospholipid binding as well as lysosomal trapping of basic lipophilic compounds is currently an empirical fit and exploits the observation that acidic phospholipid content is highest in tissues with high lysosomal volumes [53]. Equations are emerging to describe the incorporation of lysosomal sequestration into Kp predictions [54] and may be included in future versions of GastroPlus.
When tissue partition equations are not predictive, quantitative whole-body autoradiography data, if reflective of the parent compound, may be used to estimate Kp values and adequately predict human pharmacokinetics from rat data [55]. Alternatively, animal Kp values can be scaled to human values, assuming unbound Kp values are identical and accounting for species differences in plasma protein binding [17].
2.4 Oral Absorption
Because oral absorption is a multifactorial process, preclinical verification of predictions is important to build confidence for FIH models. To focus on the accuracy of the absorption model when modelling preclinical species, intravenous data should be used to ensure the accuracy of disposition modelling. This can be achieved with a calibrated systemic PBPK model or a fitted compartmental pharmacokinetic model. It is also essential to have measured solubility data and, unless aqueous solubility is high enough to ensure complete and rapid dissolution, biorelevant media should be employed. For FIH, the use of in-vitro permeability data from an assay with an established conversion to in-vivo permeability is recommended [24]. Figure 4 provides a framework for assessing the various components impacting oral absorption.
Physiologically based pharmacokinetic modelling strategy for oral absorption [57, 58]. ASF absorption scale factors, BSSR bile salt solubilisation ratio, MPT mean precipitation time. a Other processes” transporters: efflux transporters can be incorporated in GastroPlus models with a simple method (e.g. adjusting permeability based on preclinical observations or in-vitro data) to more complex methods (e.g. specifically incorporating effects of transporters) [60,61,62]. 1[57], 2[58]
For lipophilic compounds, absorption is likely to be sensitive to the bile salt solubilisation ratio (BSSR) and thus minimally fasted-state simulated intestinal fluid (FaSSIF) and fed-state simulated intestinal fluid (FeSSIF) solubility data should be used to predict a BSSR, which can then be verified/optimised with oral data from preclinical species. The current GastroPlus model for bile salt solubilisation estimates the increase in in-vivo solubility relative to aqueous buffer solubility based only on the concentration of bile salts in the fasted and fed state media. If different BSSR estimates result from the use of either FaSSIF or FeSSIF data, this may indicate that effects other than simple bile salt solubilisation are involved [56]. In such cases, in-vivo verification in preclinical species should be used to assess the relevance of the BSSR estimates. Use of deconvoluted biorelevant gut solubility based on modelling in preclinical species is supported by good predictions for a compound set, including all BCS/Biopharmaceutics Drug Disposition Classification classes [19].
Generally, physiological parameters should not be fitted and default GastroPlus ACAT models should be used, although minor adjustments may occasionally be supported. For example, there is significant uncertainty associated with some model parameters such as the amount of fluid in the gastrointestinal tract [57]. For Compound 1 (BCS Class II), the inclusion of known variability in gastrointestinal tract fluid volumes and realistic formulation-specific particle size data was important for predicting absorption. Other examples of appropriate ACAT model adjustments include stomach transit time (which exhibits large inter-occasion variability), stomach pH (for patients taking proton pump inhibitors) or modification of effective permeability using built-in interspecies correlations. A thorough evaluation of species-specific verified ACAT models has yet to be published, although adjustment of the species-specific absorption scale factor has been reported with the use of the theoretical surface area-to-volume ratio (SA/V) model for dogs and the use of the Opt-logD SA/V Version 6.1 model with a colonic permeation rate set to match the small intestine for humans [58].
Ideally, preclinical oral pharmacokinetic data should cover human-relevant doses and formulations [19], so that confidence can be derived by the verification of formulation-specific models at relevant doses. The effect of food can be investigated pre-clinically and predicted for humans [59].
If a compound is thought to be metabolised by enzymes known to be active in the gut wall [63], then Fig. 5 provides a framework for assessing the impact on oral exposure. The aim of this diagram is to understand the potential risk of gut wall metabolism reducing exposures by leveraging data already generated for hepatic metabolism. High permeability may offset gut wall metabolism, and this can be investigated via a PSA. Initial studies of predicting intestinal metabolism focused on CYP3A4, possibly because of the utility of grapefruit juice studies in generating data to assess predictions [64]. An approach in GastroPlus incorporates metabolism into each compartment of the ACAT model. For compounds predominantly metabolised by CYP3A4, liver microsomal in-vitro clearance values were used to estimate the CYP3A4-mediated intestinal metabolism [65]. A similar strategy might prove useful for compounds metabolised by non-CYP gut wall enzymes such as UDP glucuronosyltransferases and sulfotransferases. However, such predictions for non-CYP enzymes are complicated by limited intestinal enzyme abundance data and in-vivo estimates of intestinal extraction, which are needed for verification of the approach. The strategy proposed in Fig. 5 tends towards under-prediction of the fraction of drug escaping gut wall metabolism and thus, when relevant gut wall extraction is predicted, alternative approaches to evaluate gut wall metabolism may be used in parallel to support decision making. Such an evaluation may include applying the strategy proposed by Peters et al. [63], which suggests factoring observations of gut wall metabolism in animal species, relevant in-vitro data on human intestinal metabolism and biopharmaceutical classification of the compound into evaluation of risk for a low fraction of drug escaping gut wall metabolism. In addition, compounds affected both by metabolism and active transport in the gut wall may benefit from empirical calibration of IVIVE scaling factors for metabolism and transport [62].
Physiologically based pharmacokinetic modelling strategy for assessing gut wall metabolism [65]. CLint hepatic intrinsic clearance, Fg fraction of drug escaping gut wall metabolism, Km concentration of substrate at half Vmax, Vmax maximum velocity or rate of enzyme catalyzed reaction. Note: Gut wall metabolism is often saturable, and thus if Vmax and Km parameters are available, evaluate saturation relative to dose
2.5 Uncertainty and Variability Analyses
While single simulations for the FIH dose prediction are often made, this approach limits the value achieved through PBPK modelling as it ignores uncertainty of inputs and variability in the simulated population. Considering both uncertainty and variability is important, particularly from a regulatory perspective [7]. When using PBPK for FIH dose projection, exploration of uncertainty is critical because of unknown factors at this stage, as highlighted with Compound 3 (Sect. 4.3).
A PSA can be used to determine the implications of key uncertainties [10], whether owing to limited data, lack of mechanistic understanding, inability to predict saturation of metabolism or absorption mechanisms, or a disconnect between in-vitro and in-vivo data. The European Medicines Agency encourages PSA to characterise the level of uncertainty in PBPK models [7, 66].
Uncertainties can be translated into PBPK model results and determine limits on what might be expected for clinical pharmacokinetics. Sometimes, focusing on a single critical model parameter is valuable. For example, clearance is often a sensitive parameter not known with great confidence, e.g. owing to disagreement between predicted clearance scaled from microsomes and hepatocytes, or between in-vitro and in-vivo clearance in preclinical species. One could give a range of predictions around the uncertain model parameter, or present a perceived most likely estimate and a worst-case scenario. It is important to clearly communicate what the range represents so that the information can be used appropriately.
Sometimes it may be important to convey uncertainty for multiple parameters, e.g. when both clearance and absorption predictions are uncertain. In this case, a three-dimensional PSA, the third dimension being the predicted pharmacokinetic parameter, presents the simulation results in a helpful manner to enable key decisions in the light of uncertainty.
For predicting variability, the population simulator tool in GastroPlus can be used to simulate a clinical trial by varying multiple (often physiological) model parameters within ranges defined by their estimated variability distributions. This powerful technique has been used for applications such as determining the implications of specific P450 genotypes/polymorphisms, understanding the range of expected drug–drug interactions, and simulating the effect of disease on pharmaokinetics in patients. However, simple approaches to understanding variability, e.g. comparing predicted pharmacokinetics in the fasted vs. fed state for a typical patient, or comparing predicted pharmacokinetics in a typical healthy subject and patient, can also be useful. Variability predictions may be most useful after human data are available to improve the PBPK models “top-down”.
For Compound 1 (see Sect. 4.1), a more thorough assessment of uncertainty and potential variability could have helped avoid a clinical protocol amendment to add additional sampling times. Figure 6 provides a checklist of input parameters that should be considered for uncertainty assessment. Only a subset of parameters from Fig. 6, dependent on compound properties, will be important (sensitive) in each specific PBPK model. Additionally, we have identified areas of opportunity (Table 1) that, if addressed, will improve PBPK modelling FIH predictions; these should also be considered in the context of uncertainty assessment.
Physiologically based pharmacokinetic modelling strategy for a potentially useful parameter sensitivity analysis (PSA) to be driven by the molecule properties and uncertainty evaluation. 3D three-dimensional, ADME Absorption, Distribution, Metabolism and Excretion, APL acidic phospholipid, ASF absorption scale factors, BCS Biopharmaceutics Classification System, BPR blood/plasma ratio, BSSR bile salt solubilisation ratio, Capt concentration of acidic phospholipids in tissue, CLint hepatic intrinsic clearance, FIH first-in-human, Fup fraction unbound in plasma, Km concentration of substrate at half Vmax, MPT mean precipitation time, PSA parameter sensitivity analysis, Peff effective permeability, SI small intestine, SolFactor solubility factor, Vmax maximum velocity or rate of enzyme catalyzed reaction
3 Materials and Methods
Simulations were conducted using GastroPlus (Simulations Plus Inc., Lancaster, CA, USA), and ADMETPredictor™ (Simulations Plus, Inc.) was used to predict physicochemical and biopharmaceutic properties. Software versions are recorded in Table 2 and specific settings within each case study. Input parameters necessary for a quality PBPK model for FIH PK prediction are summarised in Table 2.
The compounds have been selected to illustrate the application of the strategy and/or to highlight key components of the strategy, with their distinctiveness being stated in their respective titles. Compounds 1–3 are industry predictions and Compound 4 was based on literature data.
4 Case Studies
4.1 Compound 1: Empirical Physiologically Based Pharmacokinetic Model Factors from Preclinical Species Enable First-in-Human Prediction
Compound 1 is neutral and highly lipophilic (clogP > 5). The free fraction in plasma (< 0.1%) and aqueous solubility (< 1 µg/mL) were both too low for accurate quantification. These properties meant it was challenging to verify an IVIVE. However, medicinal chemistry had failed to identify active molecules with lower logP and preclinical in-vitro and in-vivo pharmacology was promising. Therefore, extrapolation of pharmacokinetics to estimate a clinical dose was conducted.
Similar Vss (between 1.5 and 3 L/kg) was seen in rats, dogs and monkeys and the predicted volumes using the Lukacova method [50] based on the physicochemical properties and assuming a Fup of 0.1% for all species, were in reasonable agreement with the observed data and predicted Vss of 3.2 L/kg in humans.
4.1.1 In-Vitro In-Vivo Extrapolation for Clearance Using Empirical Scaling Factors Verified with Preclinical Data
Scaling of in-vitro data to predict clearance should account for differences in binding in-vitro and in-vivo [70]. For Compound 1, binding could not be measured, and assuming that in-vitro free fraction was equivalent to Fup [25] resulted in a large over-prediction of clearance in the rat (~10-fold). Therefore, human clearance was predicted using an empirical scaling factor derived from the rat. To build confidence in this approach, in-vivo and in-vitro rat data for seven-lead optimisation compounds from the same structural class as the clinical candidate were used. Measured renal clearance was negligible for these compounds and it was assumed that the in-vivo systemic clearance, ranging from <1 to 35 mL/min/kg, represented hepatic metabolic clearance. Using the well-stirred liver model, compound-specific scaling factors were derived for both microsomal and hepatocyte intrinsic clearances. These scaling factors were then used to predict human clearance from intrinsic clearance values generated in human microsomes and hepatocytes. Predicted human hepatic clearances from hepatocytes and microsomes were in close agreement for all seven compounds (Fig. 7).
Consistency in human hepatic clearances scaled from human microsomal and hepatocyte intrinsic clearance when applying empirical scaling factors derived from rats. A modified well-stirred liver model (equation shown) with plasma and blood binding incorporated into an empirical scaling factor (SF) was used to scale the intrinsic clearances in microsomes and hepatocytes to in-vivo hepatic clearance (CL_rat) in rat. The compound-specific SF was estimated for microsomes (SF_m) and hepatocytes (SF_h). These SFs were then applied to scale intrinsic clearances measured in human microsomes and hepatocytes. The predicted hepatic clearances for the seven molecules were well correlated
The empirical scaling factor for Compound 1 was further verified by scaling of hepatocyte intrinsic clearances measured in dogs and monkeys. Predicted clearances of 0.6 mL/min/kg in the dog and 2.0 mL/min/kg in the monkey compared well with observed in-vivo values of 1.5 mL/min/kg and 1.8 mL/min/kg, respectively. Finally, scaling of human hepatocyte intrinsic clearance values predicted a mean hepatic clearance of 0.5 mL/min/kg (range: 0.2–0.7 mL/min/kg).
4.1.2 Solubility was Low and Absorption was Dose and Formulation Dependent
Predicting absorption for Compound 1 was challenging because of low solubility. Preclinical data showed decreasing bioavailability with increasing doses in the rat with an influence of formulation and feeding status. Absorption modelling for potential clinical dosage forms was supported by data from a formulation screening study in dogs, in which bioavailability ranged from 7% for a micronised tablet formulation in fasted dogs to 52% for a nano-suspension in fed dogs. Although the aqueous solubility was low (< 1 µg/mL), solubility was enhanced in biorelevant media, with a value of ~10 µg/mL in FaSSIF and ~35 μg/mL in FeSSIF. GastroPlus dog models for these formulations were developed by incorporating measured biorelevant solubility values and then optimising the dog absorption models to match exposure data for the formulations with two adjustments. First, the percentage of water in small and large intestine compartments was reduced to 10 and 0.1%, respectively, and second, the particle size was adjusted to 1 µm for the nano-suspension and 80 µm for the tablets. Regarding the change to the percentage water, such physiological model parameter changes (system parameter changes) made to match exposures for a particular drug are not recommended best practice. However, there is considerable uncertainty and ongoing debate over the relevant parameterisation of intestinal water volumes [71,72,73] and the parameterisation of the colonic model compartments is uncertain [74]. These optimised values were then transferred to the human absorption model to simulate possible clinical scenarios. Simulated fraction absorbed was only 11% for a 50-mg tablet in the fasted state, but increased to 41% in the fed state. Because of the predicted food effect, the first clinical study was conducted in the fed state.
4.1.3 Clinical Data show Importance of Conveying Uncertainty in Predicted Pharmacokinetics
In Fig. 8, the simulation for a 25-mg tablet dosed in the fed state is compared to clinical plasma exposures measured in the first six subjects dosed. Although maximum concentration was well predicted, there was more than a two-fold under-prediction of the area under the curve, and the observed half-life (10–14 days) was longer than expected (~3 days). Later in development, an intravenous microdose study was conducted; at 25 mg, the observed absolute bioavailability (30–40%) and Vss (3.7 L/kg) were close to the predicted values. However, systemic clearance at 0.18 mL/min/kg was slightly less than the predicted range of 0.2–0.7 mL/min/kg.
Predicted mean plasma concentrations (Plasma Conc.)for a 25-mg tablet (solid line) compared to measured concentrations in six healthy volunteers (symbols). The inset shows the same data on a log scale with measurements extending up to 60 days. The solid black line represents a mean clearance of 0.5 mL/min/kg, while the dotted lines show the range of clearance (0.2–0.7 mL/min/kg)
Despite the challenging properties of Compound 1, the pharmacokinetic prediction was good. However, as the phase I protocol had been designed considering only the mean prediction with a 3-day half-life, the planned sampling times did not allow adequate characterisation of pharmacokinetics, necessitating a protocol amendment. Consideration of uncertainty in clearance would have avoided this amendment, thus illustrating the importance of conveying uncertainty in predictions.
4.2 Compound 2: Impact of Blood/Plasma Ratio in Predicting Volume of Distribution at Steady State for a Basic Compound in a Retrospective Analysis
Based on QSPR and PBPK assessments, Compound 2 is a lipophilic base with high solubility and permeability (BCS Class I), metabolic elimination (ECCS) and a high Vss driven by binding to tissue acidic phospholipids. For bases, the BPR, used to estimate the association constant with acidic phospholipids, is likely to be a key input parameter for PBPK models. Using the Lukacova method for a 30-year-old 70-kg human, with QSPR compound-specific predicted inputs including BPR = 0.91, the predicted Vss is 3 L/kg. The PSA illustrated the sensitivity of BPR; for BPR = 0.55 (i.e. 1-haematocrit) the predicted Vss was 0.27 L/kg, and for an assumed higher BPR = 2, it was 13.1 L/kg.
4.2.1 High Volume of Distribution at Steady State and Species-Dependent Blood/Plasma Ratio
Pharmacokinetic data following intravenous administration were available in rats, rabbits, dogs, monkeys, minipigs and humans. These data enabled a retrospective isolation and assessment of the impact of BPR on predicted Vss. The comparison of simulated and observed profiles was made using the observed clearance from each species as input for the PBPK models. The Vss was predicted using the Lukacova method [50] with appropriate measured inputs for all species.
Compound 2 partitions more into the cellular fraction of blood than plasma for rats, rabbits and dogs (Table 3). The blood Vss, determined via a non-compartmental analysis from measured blood pharmacokinetics following intravenous administration is high in all species, but does not appear to be perfectly correlated with BPR, suggesting that Vss is driven by multiple processes. Fraction unbound in plasma is high across preclinical species except in monkeys, indicating species differences.
4.2.2 Tissue-to-Plasma Partition Coefficient Predictions for Physiologically Based Pharmacokinetic Models
Compound 2 lipophilicity was measured by two chromatographic methods: Chromatographic Hydrophobicity Index [75] using a C18 stationary phase and Immobilised Artificial Membrane [76] using chemically bonded phosphatidyl-choline to a silica surface. Both of these measurements can be converted to octanol/water logP equivalents and used as compound-specific inputs for the Lukacova method. The mean value of 4.2 from Chromatographic Hydrophobicity Index (2.9) and Immobilised Artificial Membrane (5.5) values was used. Measured basic pKa values of 8.96, 4.12 and 2.8 were the other compound-specific inputs.
For each species, PBPK models were built using actual bodyweights. Measured haematocrit values from the BPR assays were used if available, although values were consistent with default values in GastroPlus. Measured species-specific BPR and Fup were used in each PBPK model.
4.2.3 Assessment of Volume of Distribution at Steady-State Predictions
Using consistent lipophilicity and pKa values with species-specific BPR and Fup as inputs for the Lukacova method predicted the Vss within 60% of the observed values in all species except monkeys, where the Vss prediction error was approximately three-fold (Table 3). The same strategy successfully predicted the distribution in human (~ 20% overestimated).
The QSPR plus PBPK PSA for Compound 2 highlighted that BPR was a critical input parameter in the prediction of systemic distribution, which is likely owing to the interaction of the basic group with tissue acidic phospholipids. The Vss is large in all species, with the highest distribution in species with the highest BPR. This was adequately predicted using the Lukacova method with measured BPR as an input. The predicted distribution in monkeys was not predicted within the generally accepted two-fold range, illustrating the current reality of PBPK modelling within discovery, wherein a weight-of-evidence approach is needed. If most preclinical species (four out of five in this example) are accurately predicted, then this gives confidence in the human predictions and time is not spent attempting to determine why one species is an outlier. However, it is uncommon to have pharmacokinetic data in five preclinical species; smaller data sets may require further investigation of species discrepancies.
4.2.4 Power of Blood/Plasma Ratio
It is important to consider the BPR when studying pharmacokinetic properties [77]. The Lukacova method uses the BPR to estimate the association constant for bases with acidic phospholipids for each species, and thus predicts a range of association constants across the species owing to differences in BPR. Tissue-specific acidic phospholipid concentration data are only available for rats, dogs and humans [51, 78], which will have an impact on the predictions, although variability within species can be greater than between species.
In humans, tissue binding of Compound 2 is predicted to be driven solely by the interaction of the compound with neutral lipids and phospholipids, and modelling indicates the larger Vss measured in preclinical species is the result of additional binding to acidic phospholipids. Although the plausibility of species-specific differences in binding to acidic phospholipids has not been investigated for Compound 2, this example highlights the impact and thus the requirement of measuring BPR for compounds with basic centres to inform PBPK models. A recent publication, although critiquing some assumptions behind PBPK models, stated that Kps for bases are well predicted, possibly because of the use of BPR to calculate acidic phospholipid binding constants [79].
4.3 Compound 3: Challenging Lipophilic Weak Acid
Compound 3 is a lipophilic (clogP ~5) weak acid with low solubility, particularly in stomach acid (Table 2), presenting a challenge to in-vitro assays. Although Compound 3 is eliminated metabolically mainly through CYP3A4, the human clearance prediction was challenging because of its high metabolic stability. Physiologically based pharmacokinetic modelling was conducted prospectively to understand the compound’s pharmacokinetic properties and support the decision to move the compound into clinical development.
4.3.1 Low Clearance Expected in Humans but Uncertainty in Actual Estimate
Predicting clearance for acidic compounds by scaling in-vitro data is often challenging, and consideration of binding is important [70]. Hepatocytes provided one estimate of human clearance, but given the limitations of the in-vitro assays, single-species scaling based on monkeys [80] was also used for a range of predicted human clearance (i.e. 0.86–4.6 mL/min/kg, Table 4). Although the clearance prediction was uncertain, given the significant overestimation in two of three preclinical species using hepatocytes, there was confidence that human clearance would be low because of low clearance across preclinical species and stability in human hepatocytes.
4.3.2 Pragmatic Prediction of Distribution
Prediction of distribution was challenging as Vss exhibited 18-fold variability across preclinical species (0.25–4.5 L/kg). The Lukacova method [50] underestimated Vss across all preclinical species and this was mainly owing to an in silico-predicted acidic pKa value. A PSA showed that removing this acidic pKa from the calculation allowed the calculated Vss to be sensitive to other parameters, enabling improved consistency with observed data (Table 4). Consistent with the QSPR prediction of high binding, the in-vitro Fup was < 0.1% across species but could not be precisely determined in-vitro. It seemed likely that species differences in Vss were related to Fup differences. To determine Vss values consistent with observed values, a range of Fup = 0.01–0.1% was assumed. Thus, human Vss values from 0.48 to 3.6 L/kg were explored for human simulations.
4.3.3 In-Vitro vs. In-Vivo Differences in Biopharmaceutics Classification System Classification
The approach for Compound 3 included all species (rat, dog, and monkey), but for absorption modelling the focus was on the monkey because the formulation was similar to the one administered to humans. As expected from the in-silico pKa, solubility for the compound was low in simulated gastric fluid at a pH of 1 (< 0.05 µg/mL), but it was also low in FaSSIF (4.7 µg/mL). The microprecipitated bulk powder (MBP) formulation used in humans had improved solubility (~50 µg/mL in FaSSIF) (Table 2). Absorption modelling for monkey elucidated the importance of FaSSIF solubility data for the MBP formulation, without which the exposures at higher doses would have been significantly underestimated. Because of experience with the MBP formulation and its resulting supersaturation and improved formulation performance, solubility was not considered a key source of uncertainty in simulations for Compound 3 pharmacokinetics from the MBP formulation at the clinically relevant dose level.
The measured in-vitro permeability was low, but given the good absorption seen pre-clinically, the high in-silico permeability and the limitations of in-vitro data from low solubility, this in-vitro permeability was thought to be misleading. Therefore, the permeability for human pharmacokinetic predictions was increased based on comparison of simulations with rat and dog Oral pharmacokinetic data. Oral pharmacokinetic curves in the monkey initially overestimated observed exposures. A PSA was used to explore whether incomplete absorption through low permeability or gut extraction was more likely to be responsible for the over-predictions; the conclusion, supported by in-vitro reaction phenotyping data indicating CYP3A4 metabolism for Compound 3, was that gut extraction likely caused reduced Oral pharmacokinetic exposures in the monkey. Absorption modelling revealed that although this compound was a BCS Class IV based on in-vitro data, in-vivo behaviour of the enabling MBP formulation was consistent with that of a BCS Class I drug at clinically relevant doses.
For Compound 3, intestinal metabolism had to be considered because it is a CYP3A4 substrate in humans (Fig. 5). For the monkey, including intestinal metabolism in the PBPK model was important for predicting the pharmacokinetics. Because of its relatively high in-vivo permeability and metabolic stability, it was determined that gut extraction would be minimal in human. Intestinal metabolism due to CYP3A can be significant in the monkey, yet not relevant or less relevant to humans [81, 82]. GastroPlus was not used for the prediction of intestinal metabolism for this example, but its utility for this purpose has been demonstrated in preclinical species [83] and humans [65].
4.3.4 Importance of Verifying Physiologically Based Pharmacokinetic Models in Preclinical Species
First-in-human PBPK modelling can be applied without the important step of verifying the model in preclinical species, but confidence is lower. Assessing the in-vitro inputs against in-vivo pharmacokinetic profiles in preclinical species, and determining alternative parameters when in-vitro data were inconsistent with observed data, allowed a reasonably accurate human pharmacokinetic prediction for Compound 3 (Fig. 9).
Comparison of observed and predicted plasma concentrations (Cp) as a function of time for Compound 3. Open symbols represent values for individual subjects, closed x’s represent the median values, and the simulations are for the low clearance, low volume of distribution and high clearance, high volume of distribution cases for the first two dose levels (given in mg)
4.3.5 Uncertainty Assessment
For this example, clearance and Vss seemed uncertain, and high and low estimates were determined for each. However, running simulations for all possible combinations would have resulted in an unhelpfully large range of possible pharmacokinetic predictions. Additionally, it seemed likely that both clearance and Vss were linked to Fup (which could not be measured), given that Vss and CL were both high in the rat, and both low in the dog and monkey (Table 4). Therefore, two combinations of parameters were explored. Case 1 explored the combination of low clearance and low Vss due to a lower Fup (0.01%). Case 2 explored the combination of high clearance and high Vss due to a higher Fup (0.1%). Cases 1 and 2 are represented by the high and low curves in Fig. 9, respectively. Pharmacokinetic simulations for the two cases explored here approximately bracket the observed pharmacokinetic profiles, suggesting that for humans the actual fu value may be between the values of 0.01 and 0.1. Importantly, the PSA allowed exploration of a reasonable range of predictions, providing improved understanding of uncertainty and expected human pharmacokinetics along with increased confidence that efficacious exposures would be achieved in the clinic.
4.4 Compound 4: High Molecular Weight Compound with Expected Slow Passive Diffusion through Membranes
Based on the QSPR and PBPK assessments, Compound 4 has high molecular weight (> 1000 Da), reasonable solubility and low permeability (BCS Class III), and is mainly cleared by renal elimination (ECCS). It has moderate lipophilicity but owing to its large size and large number of ionisable groups, it is expected to have permeability-limited tissue distribution. A verified method for the prediction of tissue-specific permeability-surface area product (PStc) model parameters has not yet been established. For Compound 4, the specific PStc (PStc per milliliter of tissue cell volume) implemented in GastroPlus was determined from pharmacokinetic data in the rat and subsequently used to predict the FIH pharmacokinetics.
4.4.1 Determining Physiologically Based Pharmacokinetic Model Structure Based on Preclinical Studies
Compound 4 PK data following intravenous administration were available in the rat including concentrations in plasma [68, 84] and kidney homogenate [68]. These data were used to fit the specific PStc value and verify the prediction of systemic clearance from Fup and the glomerular filtration rate. The specific PStc was then used, along with physiological cell volumes in each tissue, to calculate PStc values for the remaining tissues. Active transport was not included in the model; only passive glomerular filtration and passive membrane diffusion were incorporated to account for tissue distribution and renal elimination. No other clearance mechanism was included.
Different strategies were explored to simulate distribution in the rat. A PBPK model with all perfusion-limited tissues (Kp values calculated with Poulin-extracellular method, equation 4 in [69]) reasonably simulated the plasma concentrations and matched the low Vss. This prediction assumed compound distribution only to extracellular tissue space with no diffusion through cell membranes. Although it provided a reasonable match to plasma concentrations, concentrations in kidney tissue were significantly under-predicted. Changing the model to all permeability-limited tissues and fitting the specific PStc enabled matching the compound concentrations in both plasma and kidney tissue (Fig. 10).
Plasma (black solid line, solid circles) and kidney (green dashed line, open triangles) concentrations for a 5-mg/kg (top) [84] and 100-mg/kg (bottom) [68] intravenous bolus injection simulated with a physiologically based pharmacokinetic model with all perfusion-limited (left) and all permeability-limited (right) tissues compared to measured concentrations (symbols) in the rat
4.4.2 Predicting Human Pharmacokinetics
Under the assumption that cell membrane composition is similar in different species, the specific PStc value (9.15 × 10−5 mL/s/mL cell volume) fitted against rat data was used with human physiology to accurately predict pharmacokinetics in humans [85] (Fig. 11). For comparison, human pharmacokinetics were also simulated using a perfusion-limited model (Kps from Poulin-extracellular method). Similar to the rat, a reasonable simulation of plasma concentrations was achieved. However, simulations of predicted kidney concentrations and the amount of drug secreted in urine were inaccurate with this simpler model. The simulated ratio of kidney and plasma concentrations after the ninth dose (1-hour infusions twice daily) was 0.12 for the perfusion-limited model but ranged from 12 to 153 across the dosing interval for the permeability-limited model. A measured Kp of 45.8 was reported in one subject with normal renal function following multiple-dose intravenous administration [86]; although the sampling time was not reported, the observed value falls within the range predicted by the permeability-limited model.
Plasma (black solid line, solid circles) and kidney (green dashed line) concentrations for a 1000-mg dose administered as 1-h intravenous infusion every 12 h [85] predicted with physiologically based pharmacokinetic models with all perfusion-limited (left) and all permeability-limited (right) tissues compared to measured plasma concentrations in healthy volunteers
The amount of drug excreted in urine after a 1-hour 1000-mg intravenous infusion in healthy volunteers was 85% within 24 hours and 91% within 72 h [87]. The perfusion-limited model predicted 100% of the dose secreted in urine within 24 hours, while the permeability-limited model predicted urinary elimination of 69% within 24 hours and 83% within 72 hours. Although total urinary elimination predicted by the permeability-limited model is lower than observed, the consistency with the observed trend for prolonged renal elimination suggests that mechanisms of distribution and elimination are captured more closely with this model.
5 Discussion and Conclusion
The case studies shown here illustrate the value of PBPK modelling to integrate multiple sources of data to improve the mechanistic understanding of the pharmacokinetic properties of a drug prior to FIH. For example, it can be challenging to parse the multiple mechanisms leading to incomplete bioavailability, and PBPK modelling has been a valuable tool for moving the scientific basis for this forward. If the input parameters are variable or uncertain, caution is required when interpreting results [88]. Physiologically based pharmacokinetic modelling allows the assessment of the implications of limitations in model inputs. The mechanistic basis of these models enables exploration of mechanistic questions such as whether co-administration with food or a CYP inhibitor is expected to increase exposures [89].
Many companies use PBPK modelling to predict human pharmacokinetics as their preferred method, and only resort to empirical approaches when PBPK modelling is not possible for some reason. Physiologically based pharmacokinetic modelling has been shown to be superior to empirical scaling [16, 18], but the benefits of the PBPK approach go beyond the accuracy of the prediction to include an improved mechanistic understanding. Physiologically based pharmacokinetic modelling, routinely applied for FIH pharmacokinetic predictions within pharmaceutical companies, requires an appropriate set of measured inputs that we define herein. The examples shown here were generated by different scientists working for different companies, and therefore reflect a diversity of methodologies. If more consistency can be used across the industry, the science of PBPK modelling may be advanced and confidence in the results may be improved
Physiologically based pharmacokinetic performance for human predictions was evaluated by the Pharmaceutical Research and Manufacturers of America [90] and they did not find a high degree of accuracy, especially for oral administration. However, this analysis suffered from severe limitations such as the use of in-vitro data from diverse company assays, use of a bespoke PBPK platform, and, importantly, no preclinical verification of compound-specific PBPK models prior to human predictions. Given the importance of assessing the ability to predict a compound’s pharmacokinetic properties in preclinical species and for appropriate mechanistic studies to inform model development as appropriate, it is not surprising that the Pharmaceutical Research and Manufacturers of America application of PBPK modelling resulted in poor predictions, particularly in comparison to other assessments that used industry best practice [16, 18]. Predicting human pharmacokinetics a priori is challenging, and if it is not possible to verify a compound-specific PBPK model in preclinical species then the confidence in the human pharmacokinetic predictions will be low.
A recent evaluation of bottom-up PBPK prediction by the Oral Biopharmaceutics Tools (OrBiTo) project highlighted that challenges still remain, and predictive performance declines with each layer of complexity from intravenous through oral solution to tablet [88]. This evaluation highlighted an increase in the uncertainty of predictions for modellers with < 5 years’ experience [88]. The proposed PBPK strategy herein for FIH pharmacokinetic predictions, based on a comprehensive review of recent literature and knowledge and best practices of experienced GastroPlus users, provides flow diagrams guiding through the layers of ADME complexities. Combining QSPR predictions with PBPK models from compound structure allows the assessment of risks based on compound type/properties [91], guides thinking and enables prioritisation of fit-for-purpose resources to support model development.
Applying the proposed PBPK strategy with integrated ADME PBPK decision trees across pharmaceutical companies will enable a true evaluation of PBPK modelling in drug discovery, overcoming the limitations of earlier analyses [88] while increasing the confidence of regulatory agencies in PBPK modelling for FIH pharmacokinetic predictions. The strategy uses an established PBPK platform and includes preclinical verification of PBPK models. To maximise the value achieved through PBPK modelling, PSAs are critical to explore uncertainties. Case studies for challenging compounds, with lipophilicity and Fup at the extremes of a previously published representative dataset [92], highlight the value that appropriate use of PBPK modelling can add to FIH predictions.
References
Poggesi I, Snoeys J, Van Peer A. The successes and failures of physiologically based pharmacokinetic modeling: there is room for improvement. Expert Opin Drug Metab Toxicol. 2014;10(5):631–5.
Agoram B, Woltosz WS, Bolger MB. Predicting the impact of physiological and biochemical processes on oral drug bioavailability. Adv Drug Deliv Rev. 2001;50(Suppl. 1):S41–67.
Teorell T. Kinetics of distribution of substances administered to the body. I. The extravascular modes of administration. Arch Int Pharmacodyn Ther. 1937;57:205–25.
Teorell T. Kinetics of distribution of substances administered to the body. II. The intravascular modes of administration. Arch Int Pharmacodyn Ther. 1937;57:226–40.
Rowland M, Peck C, Tucker G. Physiologically-based pharmacokinetics in drug development and regulatory science. Annu Rev Pharmacol Toxicol. 2011;51:45–73.
US FDA. Physiologically based pharmacokinetic analyses: format and content, guidance for industry. https://www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/UCM531207.pdf. Accessed 28 Apr 2018.
EMA. Guideline on the qualification and reporting of physiologically based pharmacokinetic (PBPK) modelling and simulation. http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2016/07/WC500211315.pdf. Accessed 28 Apr 2018.
Jamei M. Recent advances in development and application of physiologically-based pharmacokinetic (PBPK) models: a transition from academic curiosity to regulatory acceptance. Curr Pharmacol Rep. 2016;2(3):161–9.
Yoshida K, Budha N, Jin J. Impact of physiologically based pharmacokinetic models on regulatory reviews and product labels: frequent utilization in the field of oncology. Clin Pharmacol Ther. 2017;101(5):597–602.
Shebley M, Sandhu P, Emami Riedmaier A, Jamei M, Narayanan R, Patel A, et al. Physiologically based pharmacokinetic model qualification and reporting procedures for regulatory submissions: a consortium perspective. Clin Pharmacol Ther. 2018;104(1):88–110.
Luzon E, Blake K, Cole S, Nordmark A, Versantvoort C, Berglund EG. Physiologically based pharmacokinetic modeling in regulatory decision-making at the European Medicines Agency. Clin Pharmacol Ther. 2017;102(1):98–105.
Jones H, Chen Y, Gibson C, Heimbach T, Parrott N, Peters S, et al. Physiologically based pharmacokinetic modeling in drug discovery and development: a pharmaceutical industry perspective. Clin Pharmacol Ther. 2015;97(3):247–62.
Wagner C, Zhao P, Pan Y, Hsu V, Grillo J, Huang SM, et al. Application of physiologically based pharmacokinetic (PBPK) modeling to support dose selection: report of an FDA public workshop on PBPK. CPT Pharmacometrics Syst Pharmacol. 2015;4(4):226–30.
EMA. Guideline on strategies to identify and mitigate risks for first-in-human and early clinical trials with investigational medicinal products. https://www.ema.europa.eu/documents/scientific-guideline/guideline-strategies-identify-mitigate-risks-first-human-early-clinical-trials-investigational_en.pdf. Accessed 28 Nov 2018.
Andersen ME, Yang RSH, Clewell HJ III, Reddy MB. Introduction: a historical perspective of the development and applications of PBPK models. In: Reddy MB, Yang RSH, Clewell III HJ, Andersen ME, editors. Physiologically based pharmacokinetic modeling: science and applications. Hoboken: Wiley; 2005. p. 1–18.
Jones HM, Parrott N, Jorga K, Lavé T. A novel strategy for physiologically based predictions of human pharmacokinetics. Clin Pharmacokinet. 2006;45(5):511–42.
De Buck SS, Sinha VK, Fenu LA, Nijsen MJ, Mackie CE, Gilissen RA. Prediction of human pharmacokinetics using physiologically based modeling: a retrospective analysis of 26 clinically tested drugs. Drug Metab Dispos. 2007;35(10):1766–80.
Jones HM, Gardner IB, Collard WT, Stanley P, Oxley P, Hosea NA, et al. Simulation of human intravenous and oral pharmacokinetics of 21 diverse compounds using physiologically based pharmacokinetic modelling. Clin Pharmacokinet. 2011;50(5):331–47.
Zhang T, Heimbach T, Lin W, Zhang J, He H. Prospective predictions of human pharmacokinetics for eighteen compounds. J Pharm Sci. 2015;104(9):2795–806.
Hosseini-Yeganeh M, McLachlan AJ. Physiologically based pharmacokinetic model for terbinafine in rats and humans. Antimicrob Agents Chemother. 2002;46(7):2219–28.
Davies B, Morris T. Physiological parameters in laboratory animals and humans. Pharm Res. 1993;10(7):1093–5.
Peters SA. Appendices. In: Peters SA, editor. Physiologically-based pharmacokinetic (PBPK) modeling and simulations: principles, methods, and applications in the pharmaceutical industry. Hoboken: Wiley; 2012. p. 407–21.
Chaudhuri S, Bolger M, Lawless M, Balakrishnan A, Morrison J. Physiologically based pharmacokinetic modeling and simulation for drug candidate optimization and selection. AAPS News Magazine. 2016 Jun;15–8.
Hosea NA, Jones HM. Predicting pharmacokinetic profiles using in silico derived parameters. Mol Pharm. 2013;10(4):1207–15.
Parrott N, Paquereau N, Coassolo P, Lavé T. An evaluation of the utility of physiologically based models of pharmacokinetics in early drug discovery. J Pharm Sci. 2005;94(10):2327–43.
Daga PR, Bolger MB, Haworth IS, Clark RD, Martin EJ. Physiologically based pharmacokinetic modeling in lead optimization. 1. Evaluation and adaptation of GastroPlus to predict bioavailability of Medchem series. Mol Pharm. 2018;15(3):821–30.
Amidon GL, Lennernas H, Shah VP, Crison JR. A theoretical basis for a biopharmaceutic drug classification: the correlation of in vitro drug product dissolution and in vivo bioavailability. Pharm Res. 1995;12(3):413–20.
Gobeau N, Stringer R, De Buck S, Tuntland T, Faller B. Evaluation of the GastroPlus advanced compartmental and transit (ACAT) model in early discovery. Pharm Res. 2016;33(9):2126–39.
Hansmann S, Darwich A, Margolskee A, Aarons L, Dressman J. Forecasting oral absorption across biopharmaceutics classification system classes with physiologically based pharmacokinetic models. J Pharm Pharmacol. 2016;68(12):1501–15.
Varma MV, Steyn SJ, Allerton C, El-Kattan AF. Predicting clearance mechanism in drug discovery: Extended Clearance Classification System (ECCS). Pharm Res. 2015;32(12):3785–802.
Wu CY, Benet LZ. Predicting drug disposition via application of BCS: transport/absorption/elimination interplay and development of a biopharmaceutics drug disposition classification system. Pharm Res. 2005;22(1):11–23.
Jakubiak P, Wagner B, Grimm HP, Petrig-Schaffland J, Schuler F, Alvarez-Sánchez R. Development of a unified dissolution and precipitation model and its use for the prediction of oral drug absorption. Mol Pharm. 2016;13(2):586–98.
Argikar UA, Potter PM, Hutzler JM, Marathe PH. Challenges and opportunities with non-CYP enzymes aldehyde oxidase, carboxylesterase, and UDP-glucuronosyltransferase: focus on reaction phenotyping and prediction of human clearance. AAPS J. 2016;18(6):1391–405.
Harrison J, De Bruyn T, Darwich AS, Houston JB. Simultaneous assessment in vitro of transporter and metabolic processes in hepatic drug clearance: use of a media loss approach. Drug Metab Dispos. 2018;46(4):405–14.
De Bruyn T, Ufuk A, Cantrill C, Kosa RE, Bi YA, Niosi M, et al. Predicting human clearance of organic anion transporting polypeptide substrates using cynomolgus monkey: in vitro-in vivo scaling of hepatic uptake clearance. Drug Metab Dispos. 2018;46(7):989–1000.
Ramsden D, Tweedie DJ, Chan TS, Taub ME, Li Y. Bridging in vitro and in vivo metabolism and transport of faldaprevir in human using a novel cocultured human hepatocyte system. HepatoPac. Drug Metab Dispos. 2014;42(3):394–406.
Kratochwil NA, Meille C, Fowler S, Klammers F, Ekiciler A, Molitor B, et al. Metabolic profiling of human long-term liver models and hepatic clearance predictions from in vitro data using nonlinear mixed-effects modeling. AAPS J. 2017;19(2):534–50.
Kratochwil NA, Triyatni M, Mueller MB, Klammers F, Leonard B, Turley D, et al. Simultaneous assessment of clearance, metabolism, induction, and drug-drug interaction potential using a long-term in vitro liver model for a novel hepatitis B virus inhibitor. J Pharmacol Exp Ther. 2018;365(2):237–48.
Kunze A, Huwyler J, Poller B, Gutmann H, Camenisch G. In vitro-in vivo extrapolation method to predict human renal clearance of drugs. J Pharm Sci. 2014;103(3):994–1001.
Huang W, Isoherranen N. Development of a dynamic physiologically based mechanistic kidney model to predict renal clearance. CPT Pharmacometrics Syst Pharmacol. 2018;7(9):593–602.
Liu X, Chism JP, LeCluyse EL, Brouwer KR, Brouwer KL. Correlation of biliary excretion in sandwich-cultured rat hepatocytes and in vivo in rats. Drug Metab Dispos. 1999;27(6):637–44.
Mathialagan S, Piotrowski MA, Tess DA, Feng B, Litchfield J, Varma MV. Quantitative prediction of human renal clearance and drug-drug interactions of organic anion transporter substrates using in vitro transport data: a relative activity factor approach. Drug Metab Dispos. 2017;45(4):409–17.
Scotcher D, Jones C, Rostami-Hodjegan A, Galetin A. Novel minimal physiologically-based model for the prediction of passive tubular reabsorption and renal excretion clearance. Eur J Pharm Sci. 2016;94:59–71.
Kimoto E, Bi YA, Kosa RE, Tremaine LM, Varma MVS. Hepatobiliary clearance prediction: species scaling from monkey, dog, and rat, and in vitro-in vivo extrapolation of sandwich-cultured human hepatocytes using 17 drugs. J Pharm Sci. 2017;106(9):2795–804.
Ishida K, Ullah M, Toth B, Juhasz V, Unadkat JD. Successful prediction of in vivo hepatobiliary clearances and hepatic concentrations of rosuvastatin using sandwich-cultured rat hepatocytes, transporter-expressing cell lines, and quantitative proteomics. Drug Metab Dispos. 2018;46(1):66–74.
Nguyen HQ, Lin J, Kimoto E, Callegari E, Tse S, Obach RS. Prediction of losartan-active carboxylic acid metabolite exposure following losartan administration using static and physiologically based pharmacokinetic models. J Pharm Sci. 2017;106(9):2758–70.
Kadono K, Akabane T, Tabata K, Gato K, Terashita S, Teramura T. Quantitative prediction of intestinal metabolism in humans from a simplified intestinal availability model and empirical scaling factor. Drug Metab Dispos. 2010;38(7):1230–7.
Naritomi Y, Terashita S, Kimura S, Suzuki A, Kagayama A, Sugiyama Y. Prediction of human hepatic clearance from in vivo animal experiments and in vitro metabolic studies with liver microsomes from animals and humans. Drug Metab Dispos. 2001;29(10):1316–24.
Sayama H, Komura H, Kogayu M, Iwaki M. Development of a hybrid physiologically based pharmacokinetic model with drug-specific scaling factors in rat to improve prediction of human pharmacokinetics. J Pharm Sci. 2013;102(11):4193–204.
Lukacova V, Parrott N, Lavé T, Fraczkiewicz G, Bolger M, Woltosz W. General approach to calculation of tissue:plasma partition coefficients for physiologically based pharmacokinetic (PBPK) modeling. AAPS National Annual Meeting and Exposition; 16–20 Nov 2008; Atlanta (GA).
Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci. 2005;94(6):1259–76.
Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95(6):1238–57.
Samant TS, Lukacova V, Schmidt S. Development and qualification of physiologically based pharmacokinetic models for drugs with atypical distribution behavior: a desipramine case study. CPT Pharmacometrics Syst Pharmacol. 2017;6(5):315–21.
Assmus F, Houston JB, Galetin A. Incorporation of lysosomal sequestration in the mechanistic model for prediction of tissue distribution of basic drugs. Eur J Pharm Sci. 2017;109:419–30.
Xia B, Heimbach T, Lin TH, He H, Wang Y, Tan E. Novel physiologically based pharmacokinetic modeling of patupilone for human pharmacokinetic predictions. Cancer Chemother Pharmacol. 2012;69(6):1567–82.
Parrott NJ, Yu LJ, Takano R, Nakamura M, Morcos PN. Physiologically based absorption modeling to explore the impact of food and gastric pH changes on the pharmacokinetics of alectinib. AAPS J. 2016;18(6):1464–74.
Sutton SC. Role of physiological intestinal water in oral absorption. AAPS J. 2009;11(2):277–85.
Kesisoglou F. Use of preclinical dog studies and absorption modeling to facilitate late stage formulation bridging for a BCS II drug candidate. AAPS PharmSciTech. 2014;15(1):20–8.
Tistaert C, Heimbach T, Xia B, Parrott N, Samant T, Kesisoglou F. Food effect projections via physiologically based pharmacokinetic modeling: predictive case studies. J Pharm Sci. 2019;108(1):592–602.
Abuasal BS, Bolger MB, Walker DK, Kaddoumi A. In silico modeling for the nonlinear absorption kinetics of UK-343,664: a P-gp and CYP3A4 substrate. Mol Pharm. 2012;9(3):492–504.
Bolger MB, Lukacova V, Woltosz WS. Simulations of the nonlinear dose dependence for substrates of influx and efflux transporters in the human intestine. AAPS J. 2009;11(2):353–63.
Takano J, Maeda K, Bolger MB, Sugiyama Y. The prediction of the relative importance of CYP3A/P-glycoprotein to the nonlinear intestinal absorption of drugs by advanced compartmental absorption and transit model. Drug Metab Dispos. 2016;44(11):1808–18.
Peters SA, Jones CR, Ungell A-L, Hatley OJD. Predicting drug extraction in the human gut wall: assessing contributions from drug metabolizing enzymes and transporter proteins using preclinical models. Clin Pharmacokinet. 2016;55(6):673–96.
Yang J, Jamei M, Yeo KR, Tucker GT, Rostami-Hodjegan A. Prediction of intestinal first-pass drug metabolism. Curr Drug Metab. 2007;8(7):676–84.
Heikkinen AT, Baneyx G, Caruso A, Parrott N. Application of PBPK modeling to predict human intestinal metabolism of CYP3A substrates: an evaluation and case study using GastroPlus. Eur J Pharm Sci. 2012;47(2):375–86.
Zhao P. Report from the EMA workshop on qualification and reporting of physiologically based pharmacokinetic (PBPK) modeling and simulation. CPT Pharmacometrics Syst Pharmacol. 2017;6(2):71–2.
Butterfield JM, Patel N, Pai MP, Rosano TG, Drusano GL, Lodise TP. Refining vancomycin protein binding estimates: identification of clinical factors that influence protein binding. Antimicrob Agents Chemother. 2011;55(9):4277–82.
Kusama M, Yamamoto K, Yamada H, Kotaki H, Sato H, Iga T. Effect of cilastatin on renal handling of vancomycin in rats. J Pharm Sci. 1998;87(9):1173–6.
Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies. 1. Mechanism-based prediction of volume of distribution. J Pharm Sci. 2002;91(1):129–56.
Obach RS. Prediction of human clearance of twenty-nine drugs from hepatic microsomal intrinsic clearance data: an examination of in vitro half-life approach and nonspecific binding to microsomes. Drug Metab Dispos. 1999;27(11):1350–9.
Maharaj A, Fotaki N, Edginton A. Parameterization of small intestinal water volume using PBPK modeling. Eur J Pharm Sci. 2015;67:55–64.
Mudie DM, Murray K, Hoad CL, Pritchard SE, Garnett MC, Amidon GL, et al. Quantification of gastrointestinal liquid volumes and distribution following a 240 mL dose of water in the fasted state. Mol Pharm. 2014;11(9):3039–47.
Yu A, Jackson T, Tsume Y, Koenigsknecht M, Wysocki J, Marciani L, et al. Mechanistic fluid transport model to estimate gastrointestinal fluid volume and its dynamic change over time. AAPS J. 2017;19(6):1682–90.
Lennernas H. Regional intestinal drug permeation: biopharmaceutics and drug development. Eur J Pharm Sci. 2014;16(57):333–41.
Valko K, Du My C, Bevan C, Reynolds DP, Abraham MH. Rapid method for the estimation of octanol/water partition coefficient (log P(oct)) from gradient RP-HPLC retention and a hydrogen bond acidity term (zetaalpha(2)(H)). Curr Med Chem. 2001;8(9):1137–46.
Valko K, Du CM, Bevan CD, Reynolds DP, Abraham MH. Rapid-gradient HPLC method for measuring drug interactions with immobilized artificial membrane: comparison with other lipophilicity measures. J Pharm Sci. 2000;89(8):1085–96.
Hinderling PH. Red blood cells: a neglected compartment in pharmacokinetics and pharmacodynamics. Pharmacol Rev. 1997;49(3):279–95.
Rodgers T, Jones HM, Rowland M. Tissue lipids and drug distribution: dog versus rat. J Pharm Sci. 2012;101(12):4615–26.
Korzekwa K, Nagar S. On the nature of physiologically-based pharmacokinetic models: a priori or a posteriori? Mechanistic or empirical? Pharm Res. 2017;34(3):529–34.
Nagilla R, Ward KW. A comprehensive analysis of the role of correction factors in the allometric predictivity of clearance from rat, dog, and monkey to humans. J Pharm Sci. 2004;93(10):2522–34.
Komura H, Iwaki M. In vitro and in vivo small intestinal metabolism of CYP3A and UGT substrates in preclinical animals species and humans: species differences. Drug Metab Rev. 2011;43(4):476–98.
Akabane T, Tabata K, Kadono K, Sakuda S, Terashita S, Teramura T. A comparison of pharmacokinetics between humans and monkeys. Drug Metab Dispos. 2010;38(2):308–16.
Heikkinen AT, Fowler S, Gray L, Li J, Peng Y, Yadava P, et al. In vitro to in vivo extrapolation and physiologically based modeling of cytochrome P450 mediated metabolism in beagle dog gut wall and liver. Mol Pharm. 2013;10(4):1388–99.
Shimada I, Iwata C, Taga S, Teramachi H, Nomura M, Miyamoto K, et al. Enhanced renal clearance of vancomycin in rats with carcinogen-induced osteosarcoma. Anticancer Res. 2012;32(3):823–9.
Lodise TP, Drusano GL, Butterfield JM, Scoville J, Gotfried M, Rodvold KA. Penetration of vancomycin into epithelial lining fluid in healthy volunteers. Antimicrob Agents Chemother. 2011;55(12):5507–11.
Matzke GR, Zhanel GG, Guay DR. Clinical pharmacokinetics of vancomycin. Clin Pharmacokinet. 1986;11(4):257–82.
Nakashima M, Katagiri K, Oguma T. Phase I studies on vancomycin hydrochloride for injection. Chemotherapy. 1992;40(2):210–24.
Margolskee A, Darwich AS, Pepin X, Aarons L, Galetin A, Rostami-Hodjegan A, et al. IMI: oral biopharmaceutics tools project. Evaluation of bottom-up PBPK prediction success part 2: an introduction to the simulation exercise and overview of results. Eur J Pharm Sci. 2017;96:610–25.
Lave T, Parrott N, Grimm HP, Fleury A, Reddy M. Challenges and opportunities with modelling and simulation in drug discovery and drug development. Xenobiotica. 2007;37(10–11):1295–310.
Poulin P, Jones RDO, Jones HM, Gibson CR, Rowland M, Chien JY, et al. PHRMA CPCDC initiative on predictive models of human pharmacokinetics, part 5: Prediction of plasma concentration–time profiles in human by using the physiologically-based pharmacokinetic modeling approach. J Pharm Sci. 2011;100(10):4127–57.
Darwich AS, Margolskee A, Pepin X, Aarons L, Galetin A, Rostami-Hodjegan A, et al. IMI: oral biopharmaceutics tools project. Evaluation of bottom-up PBPK prediction success part 3: identifying gaps in system parameters by analysing in silico performance across different compound classes. Eur J Pharm Sci. 2017;96:626–42.
Margolskee A, Darwich AS, Pepin X, Pathak SM, Bolger MB, Aarons L, et al. IMI: oral biopharmaceutics tools project. Evaluation of bottom-up PBPK prediction success part 1: characterisation of the OrBiTo database of compounds. Eur J Pharm Sci. 2017;96:598–609.
Acknowledgements
The authors acknowledge the LinkedIn GastroPlus Users Group Steering Committee for their suggestions for this article, and in particular Siladitya Ray Chaudhuri for his valuable suggestions and Tycho Heimbach for his review of the manuscript. All in-vivo studies were conducted in accordance with local regulations for animal treatment.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
No funding was received for the preparation of this article. Simulations Plus paid the open access fee.
Conflict of Interest
Neil A. Miller, Micaela B. Reddy, Aki T. Heikkinen, Viera Lukacova and Neil Parrott are employees of GlaxoSmithKline R&D, Array BioPharma, Admescope Ltd, Simulations Plus, and Roche Pharma Research and Early Development, respectively, and may hold stock or stock options.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Miller, N.A., Reddy, M.B., Heikkinen, A.T. et al. Physiologically Based Pharmacokinetic Modelling for First-In-Human Predictions: An Updated Model Building Strategy Illustrated with Challenging Industry Case Studies. Clin Pharmacokinet 58, 727–746 (2019). https://doi.org/10.1007/s40262-019-00741-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40262-019-00741-9