Abstract
Background
Fetal antiretroviral exposure is usually derived from the cord-to-maternal concentration ratio. This static parameter does not provide information on the pharmacokinetics in utero, limiting the assessment of a fetal exposure–effect relationship.
Objective
The aim of this study was to incorporate placental transfer into a pregnancy physiologically based pharmacokinetic model to simulate and evaluate fetal darunavir exposure at term.
Methods
An existing and validated pregnancy physiologically based pharmacokinetic model of maternal darunavir/ritonavir exposure was extended with a feto-placental unit. To parameterize the model, we determined maternal-to-fetal and fetal-to-maternal darunavir/ritonavir placental clearance with an ex-vivo human cotyledon perfusion model. Simulated maternal and fetal pharmacokinetic profiles were compared with observed clinical data to qualify the model for simulation. Next, population fetal pharmacokinetic profiles were simulated for different maternal darunavir/ritonavir dosing regimens.
Results
An average (±standard deviation) maternal-to-fetal cotyledon clearance of 0.91 ± 0.11 mL/min and fetal-to-maternal clearance of 1.6 ± 0.3 mL/min was determined (n = 6 perfusions). Scaled placental transfer was integrated into the pregnancy physiologically based pharmacokinetic model. For darunavir 600/100 mg twice a day, the predicted fetal maximum plasma concentration, trough concentration, time to maximum plasma concentration, and half-life were 1.1, 0.57 mg/L, 3, and 21 h, respectively. This indicates that the fetal population trough concentration is higher or around the half-maximal effective darunavir concentration for a resistant virus (0.55 mg/L).
Conclusions
The results indicate that the population fetal exposure after oral maternal darunavir dosing is therapeutic and this may provide benefits to the prevention of mother-to-child transmission of human immunodeficiency virus. Moreover, this integrated approach provides a tool to prevent fetal toxicity or enhance the development of more selectively targeted fetal drug treatments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Fetal exposure to maternally administered medication is an important determinant of fetal drug toxicity or efficacy. Darunavir crosses the placenta and is frequently used in pregnancy. |
We can predict fetal exposure to darunavir, co-administered with ritonavir, by integrating human ex-vivo placental transfer and physiologically based pharmacokinetic modeling. |
The placental perfusion setup is a valuable experimental tool that can be integrated with physiologically based pharmacokinetic modeling to simulate fetal drug exposure to darunavir during pregnancy. Fetal darunavir trough concentration is just above the half-maximal effective concentration for wild-type human immunodeficiency virus and may benefit the prevention of mother-to-child transmission. |
The approach described in this study can be used to optimize maternal pharmacotherapy to prevent fetal toxicity or enhance the development of more selectively targeted fetal drug treatments. |
1 Introduction
Many women use medications during the course of their pregnancy for different reasons [1, 2]. For ethical and practical considerations, however, pregnant women are generally excluded from clinical studies [3,4,5]. Consequently, for the large majority of medications used during pregnancy, there is inadequate or no information on fetal exposure and safety. This imposes severe limitations on drug therapy during pregnancy as placental transfer potentially poses a threat to fetal well-being. However, it may allow drugs to be administered to the mother for therapeutic benefit of the fetus in utero.
Experimentally, fetal drug exposure remains difficult to quantify, as the fetus and placenta are not readily accessible for sampling until delivery. Sampling of umbilical cord blood and maternal blood at the time of delivery is an ethically acceptable and easily accessible method, allowing the calculation of a cord blood-to-maternal blood concentration ratio. Though a cord blood-to-maternal blood concentration ratio is a clinically useful index of relative fetal drug exposure, there is often large variability between mother-infant pairs owing to variability in the timing of the sample collection relative to the last maternal dose and it does not provide any information on the fetal concentration–time profile [6, 7]. Ex-vivo dual-side perfusion of a single human placental cotyledon has proven to be a clinically relevant model for studying placental transport of various endogenous compounds and xenobiotics [6]. Although this model gives a good estimate of placental transfer, it does not provide information on in-vivo fetal pharmacokinetics and exposure.
Physiologically based pharmacokinetic (PBPK) models may provide a solution. Such models incorporate pregnancy-induced changes in various physiological and anatomical parameters and represent a feasible approach for appropriate dose optimization in pregnant women [8]. A number of pregnancy PBPK (p-PBPK) models have been developed to predict the disposition of various drugs in pregnant women; however, these models are mainly related to maternal pharmacokinetics [9,10,11,12].
It remains a challenge to predict fetal drug exposure using p-PBPK models that include human placental transfer parameters. Various animal models have been used to study placental drug transfer, but data are of poor translational value because of interspecies variability in placental structure and hemodynamics [6, 13]. Very few p-PBPK models include actual human placental transfer parameters from ex-vivo placenta perfusion experiments [14, 15]. Such parameters are obtained by using intact placental tissue with corresponding hemodynamics and should include active as well as passive drug transfer processes.
Darunavir administered once daily (QD) or twice daily (BID), in combination with low-dose ritonavir (darunavir/ritonavir) is a preferred agent to be used in human immunodeficiency virus (HIV)-positive pregnant women [16]. In plasma, darunavir is approximately 94% protein bound, mainly to α-1-acid glycoprotein (AAG). Biotransformation is almost exclusively mediated by cytochrome P450 (CYP) 3A4. Clinically, darunavir is co-administered with the potent CYP3A4 inhibitor ritonavir, to reduce darunavir clearance and maintain higher plasma concentrations throughout the dosing interval [12]. Ritonavir is also known to have potent inhibitory effects on the efflux drug transporter, P-glycoprotein (P-gp), which in the intestine, may contribute to the increased darunavir bioavailability [17]. Recently, we reported on a whole-body p-PBPK model to describe the maternal pharmacokinetics of ritonavir-boosted darunavir in pregnancy [12]. Darunavir was considered a good candidate for further development of the p-PBPK model by including placental transfer and an in-utero compartmental structure because clinical data on its pharmacokinetics in pregnancy and cord blood concentrations are available [18].
In this study, the main focus was to develop a p-PBPK model to quantitatively predict fetal exposure to the antiretroviral compound, darunavir, co-administered with ritonavir. To achieve this, a previously developed p-PBPK model of darunavir [12] was extended by incorporating a feto-placental unit into the maternal model. Bi-directional placental transfer parameters for darunavir were determined using the ex-vivo, dual-sided, perfused isolated cotyledon model.
2 Methods
Maternal-to-fetal (MTF) transfer of darunavir has been previously studied with the ex-vivo cotyledon perfusion model [19]. In contrast to this study, we included ritonavir and evaluated MTF and fetal-to-maternal (FTM) placental darunavir transfer to account for the potential interaction with placental drug transporters [20]. In brief, placental transfer parameters for darunavir were determined using the ex-vivo, dually perfused, isolated cotyledon model. Next, the p-PBPK model of darunavir developed previously [12] was extended by a feto-placental unit including placental transfer based on ex-vivo data using Berkeley Madonna software (Berkeley Madonna Inc, California). After model parameterization, simulated maternal and fetal pharmacokinetic profiles were compared with observed clinical data.
2.1 Placenta Perfusion
The study was approved by the local Ethics Committee of Radboud University Medical Center, Nijmegen, the Netherlands (file number 2014-1397). The experimental setup and methodology were detailed previously [21]. The Electronic Supplementary Material provides more details and specifications on the ex-vivo placenta perfusions and bioanalyses.
2.2 Modeling
A full-body PBPK model comprising 13 tissue/organ compartments was built and coded in Berkeley Madonna syntax, Version 8.3.23.0 (http://www.berkeleymadonna.com/). The model was largely based on the darunavir/ritonavir p-PBPK model developed in Simcyp® Version 13 release 2 (Simcyp Limited, a Certara company, Sheffield, UK), and described previously for maternal darunavir pharmacokinetics [12]. All Berkeley Madonna codes are available upon request. No model fitting and/or parameter estimation was performed in the current study.
2.3 Physiologically Based Pharmacokinetic Model Development
Human physiological parameters were obtained from literature as well as from virtual populations of healthy volunteers and pregnant women implemented in Simcyp®. Physicochemical and in-vitro pharmacokinetic parameters of darunavir and ritonavir were obtained from literature [12].
First, a PBPK model was developed for darunavir in non-pregnant women for oral administration. The model was validated by comparing simulations with observed in-vivo PK profiles obtained after oral administration of standard dosages. Once the PBPK model was evaluated in the non-pregnant population, all drug-specific parameters were fixed and pregnancy-specific changes in physiological parameters were incorporated. Model performance was verified by comparing simulations with observed concentrations in pregnant women [22] as well as with the previously developed p-PBPK model of Colbers et al. [12]. The p-PBPK model was extended by incorporation of a feto-placental unit (Fig. 1). Simulated fetal plasma darunavir concentrations were compared with reported cord blood concentrations. Only population parameters were considered and individual variability was not included. We conducted sensitivity analyses to assess the impact of changes in feto-placental-related parameters on fetal plasma concentration–time profiles.
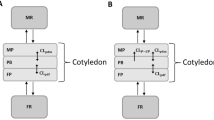
Final pregnancy physiologically based pharmacokinetic model including the feto-placental unit. EHR enterohepatic recirculation, fa fraction absorbed, CL af estimated clearance from amniotic fluid to fetal blood, CL fa estimated clearance from fetal blood to amniotic fluid, CL hepatic hepatic clearance, CL fm fetal-to-maternal placental clearance, CL mf maternal-to-fetal placental clearance, Q respective tissue/organ blood flow. The subscripts are denoted as follows: ad adipose, bo bone, br brain, he heart, ki kidney, lu lung, mu muscle, sk skin, sp spleen, gu gut, li liver, RoB rest of fetal body
Additionally, we explored the influence of different darunavir/ritonavir dosing regimens on fetal exposure. This was mainly done to illustrate its usefulness for assessing exposure–response relations. For this purpose, we assumed a minimum effective fetal plasma C trough of 0.55 mg/L. This is based on the half-maximal effective darunavir concentration for resistant HIV, a target frequently used in therapeutic drug monitoring [23].
3 Results
3.1 Ex-vivo Perfusion of Human Placental Cotyledon
A total of 15 placentas were collected from elective Caesarean sections (n = 8) and uncomplicated vaginal deliveries (n = 7). Six perfusions fulfilled the quality criteria for successful perfusion. On average, perfusion was started within 45 min of delivery; which is consistent with previous studies [24]. We conducted a perfusion experiment without placental tissue and found no indications for system adherence of darunavir and ritonavir (data not shown).
The concentration–time profiles of the FTM and MTF perfusion experiments are shown in Fig. 2a, c. Assuming that the amounts in the maternal, fetal, and placental compartments at each time point sum up to the total amount (100%) added at t = 0, the placental content was calculated (Fig. 2b, d). This was based on the absence of system adherence and the presumed absence of darunavir biotransformation in the perfused cotyledon. Sampling from the cotyledon over the course of the experiment was not feasible as it would have caused leakage. After each experiment, a cotyledon tissue sample was taken for bioanalyses (Fig. 2a, c). In the mass balance calculation, we accounted for volume and darunavir loss because of sampling. Darunavir did not accumulate in placental tissue. Bi-directional clearances were determined based on linear regression analysis of natural log-transformed darunavir concentrations in the closed reservoir after 60 min.
Darunavir concentration–time and mass-balance profiles in ex-vivo placenta perfusion. Placental transfer of darunavir in the presence of ritonavir over 150 or 180 min of perfusion. a Maternal-to-fetal transfer; data represent darunavir concentrations in the maternal reservoir (filled circles), maternal outflow (open circles), and fetal outflow (open triangles) after administration of darunavir/ritonavir (6/0.5 mg/L) to the maternal circulation at t = 0 min. b Maternal-to-fetal transfer; accumulation, and mass balance calculation (expressed as percentage of the initial maternal reservoir concentration) showing that tissue concentrations reach steady state at t = 60 min. c Fetal-to-maternal transfer; data represent darunavir concentrations in the fetal reservoir (filled triangles), fetal outflow (open triangles), and maternal outflow (open circles) after administration of darunavir/ritonavir (6/0.5 mg/L) to the fetal circulation at t = 0 min. Placental tissue concentrations at the end of the perfusion are shown as stars. d Fetal-to-maternal transfer; accumulation, and mass balance calculation (expressed as percentage of the initial fetal reservoir concentration) showing that tissue concentrations reach steady state at t = 60 min
The MTF and FTM cotyledon clearances were calculated as follows:
Ex-vivo cotyledon clearance
where CLcot represents the mean cotyledon clearance values, V is the volume of the perfusion reservoir, and k e is a placental elimination constant derived from the slope of the natural log concentration–time profile (MTF, R 2 = 0.994; FTM, R 2 = 0.976).
3.2 Development and Verification of a Darunavir/Ritonavir Physiologically Based Pharmacokinetic Model Model in Non-Pregnant Subjects
Time-based differential equations used to describe changes in drug concentrations in various organ compartments were as follows:
Maternal non-eliminating tissue compartments (perfusion limited)
Well-stirred liver model
where V, C li, C arterial, C sp, and C gu are volumes, drug concentrations in liver, arterial blood, spleen, and gut, respectively. The parameter Q denotes the respective blood flow in or out of the organ/tissue. CLhepatic, BP, and Kp are total hepatic clearance, blood-to-plasma ratio, and tissue-to-plasma partition coefficient, respectively. The subscripts ha, sp, gu, li, and t denote the hepatic artery, spleen, gut, liver, and tissue, respectively.
Absorption was defined by a one-compartment model with first-order absorption rate, ka. Drug administered in the dosing compartment (gut lumen) is absorbed into the gut wall, from which the drug is released into the portal circulation.
Perfusion-limited distribution kinetics was used for all non-eliminating tissues; hence, passive diffusion from plasma into tissue and homogenous distribution across the tissue mass was assumed. Tissue-to-plasma partition coefficients (Kp) used in this model were previously predicted by us in Simcyp®, using the Rodgers and Rowland method [12, 25]. Because a well-stirred liver model (perfusion-limited) resulted in substantial overestimation of darunavir exposure (in the absence of ritonavir) [12], a permeability-limited liver model including active uptake of the drug into the liver was used for the previous p-PBPK model of darunavir in pregnancy. In addition, empirical clinical data exist suggesting permeability-limited distribution into the eliminating tissues [26]. However, full parameterization of such a model requires data on activity and abundance of the drug transporters involved, which are currently not available. Because the scope of this work was mainly related to fetal pharmacokinetics, we used a simplified and refined well-stirred liver model against the background of their permeability-limited liver model, which includes active uptake of the drug into the liver. In refining the well-stirred liver model, we assumed that drug exchange in the liver is primarily driven by passive diffusion between plasma and the interstitial space; and that there is active transporter-mediated uptake of drug into the cell, in addition to passive diffusion. This leads to increased intracellular darunavir availability and thus, biotransformation.
Based on steady-state conditions, we derived the following equation:
where Cup is the unbound plasma concentration of drug, CuLi is the unbound drug concentration in the liver, and UF is an uptake ratio. The uptake parameter, UF, was estimated by fitting model simulations against the observed clinical data (darunavir/ritonavir 600/100 mg in non-pregnant adults) presented by Rittweger et al. (27). An optimal UF of 1.2 was estimated against the background of free plasma-to-tissue concentration ratio predicted in Simcyp® [12] and observed in vivo [28].
Systemic clearance of darunavir was considered to mainly occur via the liver; therefore, renal clearance was not included in the model [27]. Because enterohepatic recirculation of darunavir was a major determinant in modeling the interaction of darunavir with ritonavir in the existing p-PBPK model, and was suggested in a previous clinical study [29], an enterohepatic recirculation parameter was added to the current model as an empirical solution by visually fitting the simulated PK profile to the observed clinical data (non-pregnant). The enterohepatic recirculation was defined as a constant fraction of the modeled darunavir dose available for re-absorption from the gut lumen. This is based on the assumption that a small fraction of darunavir amount is excreted through biliary clearance to the gut lumen.
The darunavir-ritonavir drug–drug interaction model used includes both competitive and mechanism-based inhibition of CYP3A4 activity. A static ritonavir plasma concentration was used for inhibition. Different population ritonavir unbound steady-state C trough were used for BID and QD dosing, and for the pregnant and non-pregnant simulations [22]. Predicted PK profiles were in line with observed clinical data as well as with the simulated PK profiles by Colbers et al. (Fig. 3).
Simulation of maternal (non-pregnant) darunavir concentration–time profiles. Simulation of maternal (non-pregnant) darunavir pharmacokinetic profiles at steady state for darunavir/ritonavir (DRV/r) dosing regimens of a 600/100 mg twice daily (BID) and b 800/100 mg once daily (QD). These simulations are compared with previous physiologically based pharmacokinetic simulations [12], as well as observed clinical data [22]. conc. concentration
3.3 Development and Verification of a Darunavir/Ritonavir Physiologically Based Pharmacokinetic Model Model in Pregnant Subjects
After successful simulation of PK profiles in non-pregnant subjects, physiological parameters were modified to reflect changes in pregnancy, while keeping all drug-specific parameters constant. Physiological and metabolic changes (e.g., body weight and CYP enzyme activity) with gestational age were implemented using data and algorithms described previously [30]. Variations in protein binding during pregnancy as well as in the fetus at term were implemented in the model based on algorithms from Simcyp®, assuming the absence of changes in protein binding kinetics. Further details on model parameterization were described previously [12].
The PK profile of darunavir was simulated in pregnant women (gestational age = 38 weeks) for a steady-state situation of the clinical dosage regimens 600/100 mg BID as well as 800/100 mg QD. Visual inspection of the curves showed that the simulated PK profile was in line with observed clinical data as well as simulated PK profiles of Colbers et al. [12] (Fig. 4a, b). Based on this verification, we considered the model suitable for extension with a feto-placental unit to simulate fetal PK profiles.
Simulation of maternal and fetal darunavir concentration–time profiles. Simulation of maternal and fetal plasma darunavir pharmacokinetic profiles at steady state for darunavir/ritonavir (DRV/r) dosing regimens of a 600/100 mg twice daily (BID) and b 800/100 mg once daily (QD). Simulated fetal plasma darunavir concentrations compared with observed cord blood concentrations for the maternal doses of c 600/100 mg BID and d 800/100 mg OD. These simulations are compared with previous pregnancy physiologically based pharmacokinetic simulations [12], as well as observed clinical data [18, 22]. conc. concentration, GA gestational age
3.4 Incorporation of a Feto-Placental Unit
3.4.1 Scaling Ex-Vivo Cotyledon Darunavir Clearance to In-Vivo Placental Clearance
The ex-vivo cotyledon clearance of darunavir determined from the perfusion experiments was scaled to in-vivo placental clearance. Because darunavir displays a substantial degree of protein binding (94%) in plasma, it was necessary to assess the free darunavir fraction in the perfusion samples (containing 30 g/L albumin) to calculate an unbound cotyledon clearance. The mean, concentration-independent, protein-free fraction of darunavir in the perfusion medium was 16% ± 0.5% (n = 5). Second, the unbound cotyledon clearance was extrapolated to in-vivo cotyledon clearance, taking into account the respective protein-free fractions in maternal and fetal blood and the average number of cotyledons in a placenta (Table 1).
The equations used are as follows:Scaled placental clearance
where N cot denotes the average number of cotyledons per placenta, CLcot, mf is the MTF cotyledon clearance, CLcot, fm is the FTM cotyledon clearance, fuperf is the protein-free fraction in the perfusion medium, CLmf is in-vivo MTF placental clearance, CLfm is in-vivo FTM placental clearance, fup is the fraction unbound in maternal plasma, and fupF is the fraction unbound in fetal plasma.
Variations in protein binding in maternal and fetal blood were taken into account in this model. Fraction of unbound drug in maternal and fetal blood was predicted from algorithms available in Simcyp®, assuming the absence of changes in binding kinetics for AAG, the predominant binding protein for darunavir [12, 27]. However, fetal plasma AAG levels are appreciably lower than in the maternal circulation (fetal:maternal AAG ratio = 0.37) [6]. Predicting the darunavir fraction unbound in fetal plasma based on AAG as the primary binding protein and assuming an average fetal AAG level at term of 0.17 g/L [6], resulted in a predicted fupF of 0.22. This value is higher than the unbound fraction (fuperf) of 0.16 determined in the experimental placenta perfusion medium in the absence of AAG, but in the presence of albumin (30 g/L). This indicates that in vivo, albumin (33.5 g/L) may be more important in binding darunavir in the fetal circulation [31] relative to the low AAG levels. Therefore, predictions of the darunavir fraction unbound in the fetal circulation were based on albumin levels. The predicted fraction unbound in maternal and fetal blood were 0.12 and 0.27, respectively.
3.4.2 Fetal Physiologically Based Pharmacokinetics of Darunavir/Ritonavir
The placenta was considered as a barrier between maternal and fetal blood. The fetal compartment was split into fetal blood and rest of fetal body (Fig. 1). During late pregnancy, 20% of fetal cardiac output is distributed to the placenta, with the remaining 80% distributed to the rest of the fetal body (Q RoB; Fig. 1) [32]. Fetal tissues were lumped into one compartment. Tissue partitioning was based on reported adult V ss, assuming linearity between volume of distribution and body volume [12]. Although there may be differences in fetal V ss and adult V ss, no data are currently available to address such differences. Moreover, within-species V ss is usually well predicted by allometry [33].
Darunavir is also reported to distribute into amniotic fluid up to ~25% of maternal concentrations [34]. Although these data are limited, we assumed slow mass transfer (Table 1) from and into amniotic fluid to reach a steady-state amniotic concentration of about 25%. Mass transfer was assumed to be relatively slow compared with placental clearance because the processes of excretion and absorption into and from amniotic fluid are likely to be much slower than placental clearance.
Because of low abundance and activity of CYP3A enzymes in the placenta [35], it was assumed in this study that there was negligible placental metabolism of darunavir. Furthermore, in the presence of ritonavir, we would expect any remaining placental CYP metabolism to be completely inhibited. In addition, the relevance of fetal hepatic metabolism was assumed to be negligible and therefore not taken into account. Although large variability is reported, relative CYP3A4 gene expression was found to be 40,000 times higher in adults than in fetuses, whereas CYP3A7 expression was 5500 higher in fetuses than in adults [36]. It cannot be excluded that in utero other CYP450 enzymes (e.g., CYP3A7) may be involved in the biotransformation of darunavir. More research is needed to generate adequate data to be able to incorporate fetal hepatic metabolism into p-PBPK models in a mechanistic manner.
Darunavir disposition in the feto-placental unit was described as follows:
Fetal blood
Fetal body
Amniotic fluid
where CLmf denotes MTF placental clearance, CLfm is the FTM placental clearance, BPF is the fetal blood-to-plasma ratio, Q robF is the blood flow to the fetal body, V is the tissue volumes, C is the concentration, Q is the blood flow, KprobF is the fetal tissue partition coefficient, CLfa is the estimated clearance from fetal blood to amniotic fluid, CLaf is the estimated clearance from amniotic fluid to fetal blood, and robF is the rest of the fetal body. The subscripts amf, bloodF, and robF denote amniotic fluid, fetal blood, and rest of fetal body, respectively.
The parameters used to model the feto-placental unit are listed in Table 1. Simulated fetal plasma darunavir concentrations were comparable to observed cord blood concentrations (Fig. 4). From the observed clinical data, the median (range) ratio for darunavir cord plasma/maternal plasma was 0.2 (0.0–0.8) [22]. The simulated population fetal plasma-to-maternal plasma concentration ratio over a dosing interval is 0.30 (0.16–0.37).
3.5 Sensitivity Analysis
The results of the sensitivity analysis are shown in Fig. 5. Changes in fetal darunavir tissue partitioning affected the amplitude of the steady-state concentration-time profiles, which corresponds to changes in V ss. The steady-state fetal plasma concentration–time profiles were not affected by the extent of darunavir clearance from the amniotic fluid to fetal blood, mainly because clearance into and from amniotic fluid was substantially lower than placental clearance and partitioning into fetal tissue. This indicates that, as previously observed [14], within physiologically plausible ranges poorly informed assumptions made on partitioning into amniotic fluid do not influence the outcome of interest, i.e., fetal plasma concentrations. With regard to changes in fraction unbound in fetal plasma and MTF cotyledon clearance (parameterized proportionally), both substantially impact the fetal plasma concentrations. Therefore, precise (experimental) estimation and external validity of these parameters is essential.
Sensitivity analysis of feto-placental parameters. Sensitivity analysis of feto-placental parameters with respect to fetal plasma darunavir concentration–time profiles at steady state for darunavir/ritonavir dosing regimens of 600/100 mg twice daily. The parameters of interest include a fetal tissue partition coefficient), b amniotic fluid-to-fetal blood clearance, c fraction unbound in fetal plasma, and d maternal-to-fetal cotyledon clearance. conc. concentration
3.6 Exploratory Simulations of Fetal Exposure to Darunavir at Different Doses
Based on the assumed exposure–effect relationship for fetal antiviral activity, we conducted simulations to determine the optimal maternal dosing regimen with respect to fetal treatment outcomes. We simulated a dose range for both QD and BID maternal dosing (Fig. 6). These simulations indicate that the standard dosing regimens result in therapeutic exposure to darunavir. However, if HIV-positive women have developed (multiple) resistance to protease inhibitors, possibly even higher dosing regimens are optimal with regard to fetal benefit, especially in the case of high-risk situations, such as maternal HIV breakthrough at term.
Simulated fetal darunavir concentration-time profiles for several darunavir dosing regimens. Simulated fetal darunavir concentration–time profiles for several maternal darunavir doses for a once-daily (QD) dosing and b twice-daily (BID) dosing. The gray dashed lines represent the therapeutic target trough concentration. conc. concentration, DRV/r darunavir/ritonavir
4 Discussion
We developed a p-PBPK model for fetal drug exposure during pregnancy that allowed us to predict the fetal pharmacokinetics of ritonavir-boosted darunavir, at term. In this study we introduced a feto-placental unit in the model using bidirectional placental clearance parameters determined separately from an ex-vivo human cotyledon perfusion set-up.
To date, few p-PBPK models have simulated human fetal PK profiles by integrating ex-vivo human placental transfer parameters within a p-PBPK model. Two studies report placental transfer of two other antiretroviral treatments based on placental diffusion and placental elimination, using closed system, ex-vivo placental perfusion experiments and non-linear compartmental modeling [14, 15]. Although the derived physiological parameters can be used to simulate fetal pharmacokinetics, it is challenging to precisely identify all the required parameters using a one-way, closed-system perfusion setup [37].
The approach used in this study provides an alternative to integrating placental transfer into p-PBPK models. Bidirectional transfer parameters were determined separately, by performing MTF and FTM perfusion experiments. The placental clearances estimated from the current ex-vivo experiments can be considered as whole organ clearances and allowed inclusion of placental transfer as a single barrier, rather than a compartmental structure with corresponding flows, partitioning coefficients, and tissue volumes. In terms of future development of more mechanistic compartmental placental distribution models, for instance for in-vitro-to-in-vivo extrapolation of placental transfer data from passive permeability and placental active transport studies, this approach in PBPK modeling may provide a valuable starting point for verification steps.
With regard to the verification of simulated fetal exposure to drugs in general, hardly any information is available. Preclinical studies indicate substantial fetal darunavir exposure in rats, but extrapolation of these data to human pregnancy is challenging [38]. Umbilical cord-to-plasma concentration ratios in pregnant women taking darunavir/ritonavir were reported [22]. Such data allow a rough verification of the model by comparing simulated profiles with actual observed cord blood concentrations, as this is the closest proxy for fetal exposure clinically and ethically available [7]. The simulated fetal concentration–time profile corresponds with the range of observed cord blood concentrations, indicating that the developed darunavir PBPK model provides a good approximation of the fetal PK profile. The observed fetal plasma concentrations following darunavir 600 mg BID (Fig. 4c) show high variability. This can be misinterpreted as accumulation of the drug, which is unlikely under steady-state conditions. Caution is needed when interpreting concentration–time profiles based on one observation per subject, with a limited amount of subjects, which is also the reason why data-driven population pharmacokinetics is not an option in this case. Consequently, we looked at the range rather than the shape of these observed concentrations.
The observed FTM placental clearance in this study was higher than MTF placental clearance. One explanation could be that darunavir is a substrate for P-gp/ABCB1, an efflux transporter located at the apical surface of placental syncytiotrophoblast membrane. Darunavir efflux from trophoblasts into the maternal plasma could therefore result in relatively low MTF clearance. However, the experiment was conducted in the presence of ritonavir, which is known to inhibit P-gp, while also, P-gp functional expression is expected to be low in the term placentas used in this study because of reported gestational changes [39] Overall, the role of transporters in regulating passage across the placenta remains unclear [40, 41]. Because the system was operated under sink conditions, the higher FTM clearance can also be related by the higher flow rate in the maternal compartment, which maintains a steeper concentration gradient. Nevertheless, it is of note that the placental clearance parameters determined from this experimental set-up are based on physiological flows.
Because term placentas were used, the findings of this study are limited mainly to drug administration at term. Additionally, inferences on the impact of ritonavir concentrations on the darunavir placental transfer cannot be made. In general, human ex-vivo cotyledon perfusion experiments are limited to small numbers of term placentas. Studies over a large concentration range or with placentas from earlier stages of pregnancy are time consuming and generally less feasible [6]. More data on placental CYP450 expression, changes in hemodynamics, tissue composition, and active uptake and efflux transport may provide a better mechanistic basis for the description and prediction of the placental transfer processes. Placental transfer models could be developed that allow for the simulation of fetal PK profiles in early pregnancy and fetal exposure-response relationships, including drug–drug interactions.
Another interesting finding in this study was the observation that cotyledon clearance did not correlate in a linear manner with cotyledon weight. This is consistent with data from a previous study, possibly indicating that tissue volume is a poor indicator of membrane surface area [42]. Based on this observation, the cotyledon clearance was scaled per cotyledon assuming that with multiple perfusion experiments, the population clearance per cotyledon is approximated. Moreover, cutting the perfused part from the remainder of the placenta is not very precise; therefore, cotyledon weight was inappropriate to use for further calculations.
With regard to the prevention of mother-to-child transmission, vertical transmission of HIV from mothers with a low or undetectable viral load can occur [43]. Successful quantitative simulations of fetal exposure to antiretroviral treatments provide a good basis for administering antiretroviral agents for pre-exposure prophylaxis of the fetus, but the actual clinical relevance is still under debate [43]. Nevertheless, as shown by this study, p-PBPK models can be employed as tools to optimize maternal pharmacotherapy to prevent fetal toxicity or enhance the development of more selectively targeted, fetal drug treatments.
5 Conclusion
A p-PBPK model was developed to quantitatively predict fetal exposure at term to the protease inhibitor darunavir co-administered with ritonavir. By extending the existing maternal PBPK model with a feto-placental unit, in-vitro-to-in-vivo extrapolation was performed. If applied appropriately, the placental perfusion set-up is a valuable experimental tool that can be integrated with PBPK modeling to simulate fetal drug exposure during pregnancy.
References
Pisa FE, Casetta A, Clagnan E, Michelesio E, Vecchi Brumatti L, Barbone F. Medication use during pregnancy, gestational age and date of delivery: agreement between maternal self-reports and health database information in a cohort. BMC Pregnancy Childbirth. 2015;15:310.
Lupattelli A, Spigset O, Twigg MJ, Zagorodnikova K, Mardby AC, Moretti ME, et al. Medication use in pregnancy: a cross-sectional, multinational web-based study. BMJ Open. 2014;4(2):e004365.
Blehar MC, Spong C, Grady C, Goldkind SF, Sahin L, Clayton JA. Enrolling pregnant women: issues in clinical research. Womens Health Issues. 2013;23(1):e39–45.
Shields KE, Lyerly AD. Exclusion of pregnant women from industry-sponsored clinical trials. Obstet Gynecol. 2013;122(5):1077–81.
Mitchell AA, Gilboa SM, Werler MM, Kelley KE, Louik C, Hernandez-Diaz S, et al. Medication use during pregnancy, with particular focus on prescription drugs: 1976–2008. Am J Obstet Gynecol. 2011;205(1):51 e1–8.
Hutson JR, Garcia-Bournissen F, Davis A, Koren G. The human placental perfusion model: a systematic review and development of a model to predict in vivo transfer of therapeutic drugs. Clin Pharmacol Ther. 2011;90(1):67–76.
Zhang Z, Unadkat JD. Verification of a maternal-fetal physiologically based pharmacokinetic model for passive placental permeability drugs. Drug Metab Dispos. 2017;45(8):939–46.
Lu G, Abduljalil K, Jamei M, Johnson TN, Soltani H, Rostami-Hodjegan A. Physiologically-based pharmacokinetic (PBPK) models for assessing the kinetics of xenobiotics during pregnancy: achievements and shortcomings. Curr Drug Metab. 2012;13(6):695–720.
Gaohua L, Abduljalil K, Jamei M, Johnson TN, Rostami-Hodjegan A. A pregnancy physiologically based pharmacokinetic (p-PBPK) model for disposition of drugs metabolized by CYP1A2, CYP2D6 and CYP3A4. Br J Clin Pharmacol. 2012;74(5):873–85.
Ke AB, Nallani SC, Zhao P, Rostami-Hodjegan A, Isoherranen N, Unadkat JD. A physiologically based pharmacokinetic model to predict disposition of CYP2D6 and CYP1A2 metabolized drugs in pregnant women. Drug Metab Dispos. 2013;41(4):801–13.
Ke AB, Nallani SC, Zhao P, Rostami-Hodjegan A, Unadkat JD. Expansion of a PBPK model to predict disposition in pregnant women of drugs cleared via multiple CYP enzymes, including CYP2B6, CYP2C9 and CYP2C19. Br J Clin Pharmacol. 2014;77(3):554–70.
Colbers A, Greupink R, Litjens C, Burger D, Russel FG. Physiologically based modelling of darunavir/ritonavir pharmacokinetics during pregnancy. Clin Pharmacokinet. 2016;55(3):381–96.
Carter AM. Animal models of human placentation: a review. Placenta. 2007;28(Suppl. A):S41–7.
De Sousa Mendes M, Hirt D, Vinot C, Valade E, Lui G, Pressiat C, et al. Prediction of human fetal pharmacokinetics using ex vivo human placenta perfusion studies and physiologically based models. Br J Clin Pharmacol. 2016;81(4):646–57.
De Sousa Mendes M, Lui G, Zheng Y, Pressiat C, Hirt D, Valade E, et al. A physiologically-based pharmacokinetic model to predict human fetal exposure for a drug metabolized by several CYP450 pathways. Clin Pharmacokinet. 2017;56(5):537–50.
DHHS. Recommendations for use of antiretroviral drugs in pregnant HIV-1-infected women for maternal health and interventions to reduce perinatal HIV transmission in the United States [updated August 6, 2015]. Available from: http://aidsinfo.nih.gov/contentfiles/lvguidelines/perinatalgl.pdf. Accessed 12 July 2017.
Holmstock N, Annaert P, Augustijns P. Boosting of HIV protease inhibitors by ritonavir in the intestine: the relative role of cytochrome P450 and P-glycoprotein inhibition based on Caco-2 monolayers versus in situ intestinal perfusion in mice. Drug Metab Dispos. 2012;40(8):1473–7.
Stek A, Best BM, Wang J, Capparelli EV, Burchett SK, Kreitchmann R, et al. Pharmacokinetics of once versus twice daily darunavir in pregnant HIV-infected women. J Acquir Immune Defic Syndr. 2015;70(1):33–41.
Mandelbrot L, Duro D, Belissa E, Peytavin G. Placental transfer of darunavir in an ex vivo human cotyledon perfusion model. Antimicrob Agents Chemother. 2014;58(9):5617–20.
US Food and Drug Administration. Center for Drug Evaluation and Research: pharmacology review. Maryland: Silver spring; 2009.
Schalkwijk S, Greupink R, Colbers AP, Wouterse AC, Verweij VG, van Drongelen J, et al. Placental transfer of the HIV integrase inhibitor dolutegravir in an ex vivo human cotyledon perfusion model. J Antimicrob Chemother. 2016;71(2):480–3.
Colbers A, Molto J, Ivanovic J, Kabeya K, Hawkins D, Gingelmaier A, et al. Pharmacokinetics of total and unbound darunavir in HIV-1-infected pregnant women. J Antimicrob Chemother. 2015;70(2):534–42.
US Food and Drug Administration. Prezista label information. Maryland: Silver spring; 2014.
Mathiesen L, Mose T, Morck TJ, Nielsen JK, Nielsen LK, Maroun LL, et al. Quality assessment of a placental perfusion protocol. Reprod Toxicol. 2010;30(1):138–46.
Toh S, Mitchell AA, Louik C, Werler MM, Chambers CD, Hernandez-Diaz S. Antidepressant use during pregnancy and the risk of preterm delivery and fetal growth restriction. J Clin Psychopharmacol. 2009;29(6):555–60.
Yoshikado T, Maeda K, Furihata S, Terashima H, Nakayama T, Ishigame K, et al. A clinical cassette dosing study for evaluating the contribution of hepatic OATPs and CYP3A to drug-drug interactions. Pharm Res. 2017;34(8):1570–83.
Rittweger M, Arasteh K. Clinical pharmacokinetics of darunavir. Clin Pharmacokinet. 2007;46(9):739–56.
EMA. Prezista; summary of product characteristics 2014. Available from: http://www.ema.europa.eu/docs/en_GB/document_library/EPAR_-_Product_Information/human/000707/WC500041756.pdf. Accessed 12 July 2017.
Ter Heine R, Mulder JW, van Gorp EC, Wagenaar JF, Beijnen JH, Huitema AD. Intracellular and plasma steady-state pharmacokinetics of raltegravir, darunavir, etravirine and ritonavir in heavily pre-treated HIV-infected patients. Br J Clin Pharmacol. 2010;69(5):475–83.
Abduljalil K, Furness P, Johnson TN, Rostami-Hodjegan A, Soltani H. Anatomical, physiological and metabolic changes with gestational age during normal pregnancy: a database for parameters required in physiologically based pharmacokinetic modelling. Clin Pharmacokinet. 2012;51(6):365–96.
van den Akker CH, Schierbeek H, Rietveld T, Vermes A, Duvekot JJ, Steegers EA, et al. Human fetal albumin synthesis rates during different periods of gestation. Am J Clin Nutr. 2008;88(4):997–1003.
Kiserud T, Ebbing C, Kessler J, Rasmussen S. Fetal cardiac output, distribution to the placenta and impact of placental compromise. Ultrasound Obstet Gynecol. 2006;28(2):126–36.
Anderson BJ, Holford NH. Mechanism-based concepts of size and maturity in pharmacokinetics. Annu Rev Pharmacol Toxicol. 2008;48:303–32.
Else LJ, Taylor S, Back DJ, Khoo SH. Pharmacokinetics of antiretroviral drugs in anatomical sanctuary sites: the fetal compartment (placenta and amniotic fluid). Antivir Ther. 2011;16(8):1139–47.
Hakkola J, Pelkonen O, Pasanen M, Raunio H. Xenobiotic-metabolizing cytochrome P450 enzymes in the human feto-placental unit: role in intrauterine toxicity. Crit Rev Toxicol. 1998;28(1):35–72.
Betts S, Bjorkhem-Bergman L, Rane A, Ekstrom L. Expression of CYP3A4 and CYP3A7 in human foetal tissues and its correlation with nuclear receptors. Basic Clin Pharmacol Toxicol. 2015;117(4):261–6.
Mould DR, Upton RN. Basic concepts in population modeling, simulation, and model-based drug development. CPT Pharmacometrics Syst Pharmacol. 2012;1:e6.
US Food and Drug Administration. Center for Drug Evaluation and Research: pharmacology review: Prezista. Maryland: Silver spring; 2009.
Yau WP, Mitchell AA, Lin KJ, Werler MM, Hernandez-Diaz S. Use of decongestants during pregnancy and the risk of birth defects. Am J Epidemiol. 2013;178(2):198–208.
Staud F, Cerveny L, Ceckova M. Pharmacotherapy in pregnancy; effect of ABC and SLC transporters on drug transport across the placenta and fetal drug exposure. J Drug Target. 2012;20(9):736–63.
Joshi AA, Vaidya SS, St-Pierre MV, Mikheev AM, Desino KE, Nyandege AN, et al. Placental ABC transporters: biological impact and pharmaceutical significance. Pharm Res. 2016;33(12):2847–78.
Schroder H, Leichtweiss HP, Rachor D. Passive exchange and the distribution of flows in the isolated human placenta. Contrib Gynecol Obstet. 1985;13:106–13.
McCormack SA, Best BM. Protecting the fetus against HIV infection: a systematic review of placental transfer of antiretrovirals. Clin Pharmacokinet. 2014;53(11):989–1004.
Smith GC, Cameron AD. Estimating human fetal blood volume on the basis of gestational age and fetal abdominal circumference. BJOG. 2002;109(6):721–2.
Syme MR, Paxton JW, Keelan JA. Drug transfer and metabolism by the human placenta. Clin Pharmacokinet. 2004;43(8):487–514.
Acknowledgements
We thank all the women who donated placentas and the midwives who collected them. We thank Gerard Zijderveld for inclusion of participants, Nielka van Erp for supervision of the bioanalyses, and Noor van Ewijk-Beneken Kolmer for her help with the bioanalyses. We also are grateful for Khaled Abduljalil’s comments on an earlier version of the manuscript and Certara for the Simcyp Grant and Partnership Scheme grant allowing further research on this topic.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
This study was supported by Health ~ Holland, top sector Life Sciences & Health.
Conflict of interest
Stein Schalkwijk, Aaron O. Buaben, Jolien J.M. Freriksen, Angela P. Colbers, David M. Burger, Rick Greupink, and Frans G.M. Russel have no conflicts of interest directly related to this study.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Schalkwijk, S., Buaben, A.O., Freriksen, J.J.M. et al. Prediction of Fetal Darunavir Exposure by Integrating Human Ex-Vivo Placental Transfer and Physiologically Based Pharmacokinetic Modeling. Clin Pharmacokinet 57, 705–716 (2018). https://doi.org/10.1007/s40262-017-0583-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40262-017-0583-8