Abstract
Background and Objectives
Filgotinib (GLPG0634) is a selective inhibitor of Janus kinase 1 (JAK1) currently in development for the treatment of rheumatoid arthritis and Crohn’s disease. While less selective JAK inhibitors have shown long-term efficacy in treating inflammatory conditions, this was accompanied by dose-limiting side effects. Here, we describe the pharmacokinetics of filgotinib and its active metabolite in healthy volunteers and the use of pharmacokinetic–pharmacodynamic modeling and simulation to support dose selection for phase IIB in patients with rheumatoid arthritis.
Methods
Two trials were conducted in healthy male volunteers. In the first trial, filgotinib was administered as single doses from 10 mg up to multiple daily doses of 200 mg. In the second trial, daily doses of 300 and 450 mg for 10 days were evaluated. Non-compartmental analysis was used to determine individual pharmacokinetic parameters for filgotinib and its metabolite. The overall pharmacodynamic activity for the two moieties was assessed in whole blood using interleukin-6-induced phosphorylation of signal-transducer and activator of transcription 1 as a biomarker for JAK1 activity. These data were used to conduct non-linear mixed-effects modeling to investigate a pharmacokinetic/pharmacodynamic relationship.
Results
Modeling and simulation on the basis of early clinical data suggest that the pharmacokinetics of filgotinib are dose proportional up to 200 mg, in agreement with observed data, and support that both filgotinib and its metabolite contribute to its pharmacodynamic effects. Simulation of biomarker response supports that the maximum pharmacodynamic effect is reached at a daily dose of 200 mg filgotinib.
Conclusion
Based on these results, a daily dose range up to 200 mg has been selected for phase IIB dose-finding studies in patients with rheumatoid arthritis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Early clinical studies in healthy volunteers with the first selective Janus kinase 1 inhibitor, filgotinib, showed high exposure to an active metabolite that contributes to its overall pharmacodynamic effects. |
Dose-dependent pharmacodynamic activity of combined filgotinib and its metabolite was shown in whole blood from healthy volunteers following oral dosing of filgotinib. |
Pharmacokinetic/pharmacodynamic modeling and simulation show a maximal pharmacodynamic effect is achieved at daily dosing of 200 mg filgotinib, and this dose was selected as the highest in a phase IIB program in patients with rheumatoid arthritis. |
1 Background
Janus kinases (JAKs) are cytoplasmic tyrosine kinases that transduce cytokine signaling from membrane receptors to signal-transducer and activator of transcription (STAT) factors. Four JAK family members are known: JAK1, JAK2, JAK3, and TYK2. Most cytokines such as interleukins (ILs) and interferons (IFNs) that rely on JAKs for intracellular signal transduction recruit a JAK heterodimer to activate specific sets of STAT proteins. Upon receptor activation, JAK family members auto- and/or transphosphorylate each other, followed by phosphorylation of the STATs that then migrate to the nucleus to modulate transcription of effector genes [1].
This critical role in downstream signaling for cytokines makes JAKs attractive therapeutic targets for inflammatory diseases [2]. Xeljanz® (tofacitinib), approved in 2012 in the USA, was the first available JAK inhibitor for the treatment of moderate to severe rheumatoid arthritis (RA). Tofacitinib is a ‘pan-JAK inhibitor’, blocking JAK3 and JAK1 and to a lesser extent JAK2 [3]. Other JAK inhibitors with varying JAK selectivity profiles have already shown to be efficacious in RA [4]. The current data support that inhibition of JAK1 and/or JAK3 is beneficial in RA treatment. A large number of (pro) inflammatory cytokines are dependent upon JAK1. While inhibition of JAK2 and βc receptor-interacting family cytokines may contribute to the efficacy of JAK inhibitors in RA, there are concerns that this could cause anemia, and thrombocytopenia, by interfering with signaling through erythropoietin, thrombopoietin and colony-stimulating factors such as granulocyte-macrophage colony-stimulating factor [5, 6].
JAK1 is critical for the signal transduction of many type I and type II inflammatory cytokine receptors. Recent findings suggest that JAK1 inhibition might be largely responsible for the in vivo efficacy of JAK inhibitors in immune-inflammatory diseases [7]. Filgotinib (GLPG0634) was identified as a JAK1-selective inhibitor (half maximal inhibitory concentration (IC50): 629 nM or 267 ng/mL), displaying a 30-fold selectivity for JAK1- over JAK2-dependent signaling in human whole blood [8]. Preclinical studies showed that filgotinib dosing leads to the formation of a metabolite, resulting from the loss of the cyclopropyl carboxylic acid group (Fig. 1). This metabolite is active and exhibits a similar JAK1 selectivity profile as the parent compound albeit substantially less potent (IC50: 11.9 µM or 4,529 ng/mL) [9]. The formation of this metabolite is mediated via carboxylesterases.
This article presents the pharmacokinetics of filgotinib and its active metabolite after single and repeated dosing in healthy male volunteers. A population pharmacokinetic model was developed combining these data in healthy volunteers and those collected during a proof-of-concept study in patients with RA [10], with the aim of supporting dose selection for a phase IIB program. Data presented here demonstrate that the active metabolite is a ‘major metabolite’, as it has a substantially higher exposure than parent filgotinib and this higher exposure might compensate for its lesser potency. Therefore, pharmacokinetic/pharmacodynamic modeling and simulation in healthy volunteers were used to investigate the contribution of the active metabolite to the overall pharmacodynamic response.
2 Methods
Two phase I clinical trials (NCT01179581 and NCT01419990) and one phase IIa proof-of-concept study (NCT01384422) in patients with RA were conducted in accordance with accepted standards for the protection of subject safety and welfare and the principles of the Declaration of Helsinki and its amendments and were in compliance with Good Clinical Practice. Phase I protocols and informed consents were approved by the Ziekenhuis Netwerk Antwerpen Institutional Review Board (Belgium) and by local Ethical Committees from the Republic of Moldova for the study in patients. All healthy volunteers and patients with RA gave written informed consent prior to study initiation.
2.1 Trial Designs
The phase I studies were randomized, double-blind, placebo-controlled trials in healthy male volunteers (aged 40–60 years, body mass index: 18–30 kg/m2). Eligible volunteers were in good health with no clinically significant deviation from normal in terms of medical history, physical examinations, electrocardiograms, or clinical laboratory determinations. Volunteers were excluded from the study if they had a medical history of abnormal platelet function or a history of a current immunosuppressive condition. In the first study, filgotinib was administered as single doses from 10 mg up to repeated dosing of 200 mg per day, whereas in the second study, doses of 300 and 450 mg once daily were evaluated. Single doses of 10–200 mg filgotinib (or placebo) were taken by two panels of eight volunteers each, who received treatment as ascending doses in an alternating fashion among the two panels. Subsequently, separate cohorts of eight volunteers (six on filgotinib and two on placebo) received 25, 50, and 100 mg twice daily and 200, 300, and 450 mg once daily for 10 days. All doses were administered as capsules with 200 mL water. For practical reasons, treatments were administered after a standard breakfast (approximately 600 kcal). Drinks were standardized to at least 1,000 mL of mineral water per day.
The exposure to filgotinib and its metabolite was evaluated in 24 patients with moderate to severe RA and with insufficient response to methotrexate who received placebo or a total daily dose of 200 mg, either as a twice- or once-daily regimen (n = 12 per dose regimen). Three blood samples were collected for each patient over the 4-week study duration. All patients continued to use their therapy of methotrexate. None were receiving or had received biologic therapies. A summary with further details of the design features, including blood sampling scheduled is provided in Table 1.
Blood samples for pharmacokinetic assessments were collected in tubes containing lithium heparin as an anticoagulant to obtain plasma for the analysis of concentrations of filgotinib and its active metabolite. Within 30 min after blood collection, the plasma was separated in a refrigerated centrifuge (4–8 °C) for 10 min at approximately 1,500 g and stored at −20 °C until analysis.
Serial blood samples for pharmacodynamics (biomarker determination) were taken after the first and last dose in the multiple-dose phase I trials. Immediately after collection, the whole blood samples were submitted to ex vivo stimulation with IL-6 for assessment of STAT1 phosphorylation in CD4+ cells (inhibition of JAK1 activity) using flow cytometric analysis. Unstimulated control samples were prepared in parallel. Samples were stored at −20 °C until analysis, and then analyzed in batches.
2.2 Bioanalytical and Pharmacokinetic Assessments
Plasma concentrations of filgotinib and its active metabolite were determined simultaneously using a validated liquid-chromatography–mass spectrometry/mass spectrometry (LC–MS/MS) assay. To each 100-µL plasma sample, 20 µL of the internal standard (125 ng/mL deuterated filgotinib) and 400 µL of 2 % formic acid in water were added. Samples were centrifuged and the supernatant loaded onto a solid-phase extraction plate. After washing (400 µL 2 % acid formic in water followed by 400 µL of methanol:water 1:1, v/v), the samples were eluted (two times 300 µL 2 % ammonium hydroxide) and then evaporated to dryness at 40 °C under nitrogen. The extraction yield of filgotinib and its metabolite under these conditions was constant over the concentration range tested (3.00–750 ng/mL), 82.9–88.8 % for filgotinib and 83.7–87.5 % for its metabolite. The reconstituted samples (600 µL 2 % acetonitrile in water 20:80, v/v) were injected into a SCIEX API3000 LC-MS/MS equipped with a short, high-pressure liquid chromatography column. Filgotinib and its metabolite were detected in positive mode using multiple-reaction monitoring. Typical retention times were 1.3 and 0.7 min for filgotinib and its metabolite, respectively. Quantification was performed using peak area ratios and standard curves (with 1/Χ 2 least-squares quadratic regression) prepared from calibration standards. The lower limit of quantification for filgotinib and its metabolite was 1.00 ng/mL For both compounds, the between and within-run precision for quality controls expressed as a coefficient of variation (CV %) were not greater than 8.7 and 8.5 %, respectively, with deviations from nominal concentrations of no more than 12.0 %.
The plasma concentrations of filgotinib and its active metabolite were analyzed following a non-compartmental approach. The peak plasma concentrations (C max) and time to reach the C max (t max) were directly observed from the data. The terminal elimination rate constant (λ z) was determined by log-linear regression analysis of the elimination phase. The apparent terminal half-life calculated from \( t_{{ 1/ 2,\lambda_{\text{z}} }} \) = Ln2/λ z was reported only if more than three data points were used for linear regression to determine λ z with an adjusted R 2 value ≥0.900. The area under the plasma concentration-time curve (AUC) over 24 h (AUC0–24h), over the dosing interval (AUC0–t), and extrapolated to infinity (AUC0–∞) were determined using the linear up/log down trapezoidal rule method (WinNonLin®, version 5.3; Pharsight Corporation, Mountain View, CA, USA). The parent-metabolite ratio (R) was evaluated using AUC0–24h (for single dosing) or AUC0–t (for multiple dosing).
2.3 Bioassay and Pharmacodynamics Assessments
JAK1 inhibition was investigated using fluorescence-activated cell sorting analysis on blood samples from healthy volunteers after administration of filgotinib or placebo, after single dose (day 1) or at steady state (day 10), by measuring STAT1 phosphorylation (pSTAT1) in IL-6-stimulated blood. Measurements of IL-6-induced STAT1 phosphorylation were performed as described in van Rompaey et al. [8]. IL-6-induced pSTAT1 was reported as an individual percentage of pSTAT1-positive cells counted in CD4+ lymphocytes.
2.4 Statistical Analyses
For the pharmacokinetic analyses, the descriptive statistics analysis included arithmetic means and CVs for C max, AUC, and \( t_{{ 1/ 2,\lambda_{\text{z}} }} \), and medians and ranges for t max.
Dose proportionality and comparison of dosage regimen (100 mg twice daily vs 200 mg once daily) in healthy volunteers was tested on log–transformed filgotinib and its metabolite parameters (C max/dose, C t/dose, AUC/dose, \( t_{{ 1/ 2,\lambda_{\text{z}} }} \)) by means of a mixed-effect analysis of variance. The Wilcoxon–Mann–Whitney non-parametric test was used to assess the dose proportionality of t max.
Statistical inferential analyses were conducted using SAS® version 9.1 (SAS Institute Inc., Cary, NC, USA) at the 0.05 level of significance.
2.5 Population Pharmacokinetic and Pharmacokinetic/Pharmacodynamic Modeling
A population pharmacokinetic model was developed based on data from the two phase I studies including 56 male volunteers who received the filgotinib treatment within the dose range of 25–450 mg on at least one occasion (n = 6 per dose). Limited data from a proof-of-concept study during which 24 patients with RA were administered a total daily dose of 200 mg either as a twice- or once-daily regimen (n = 12 per dose regimen) [10] served to provide exposure data in female patients.
A pharmacokinetic/pharmacodynamic model using STAT phosphorylation data was developed based solely on data from the two phase I studies; no pharmacodynamic data were collected in patients with RA. To reduce the impact of samples near or below the limit of quantification, the 10-mg dose was excluded from the population pharmacokinetic. The values below the limit of quantification were approximately 5 % for filgotinib and less than 1 % for its metabolite. These values were not included in the population pharmacokinetic model. All analyses were performed in accordance with appropriate guidelines [11, 12]. The population pharmacokinetic and pharmacokinetic/pharmacodynamic models were developed by means of a non-linear mixed-effects modeling approach using NONMEM (version 7.1.2) [13]. The NONMEM model fitting used the first-order conditional estimation method with interaction. R software (version 2.15.1, 32 bit) was used for exploratory graphical analysis, for evaluation of goodness of fit, and model evaluation.
Following the identification of the structural model, covariates selected from differences between the three trials, were included in the pharmacokinetic and pharmacokinetic/pharmacodynamic models to assess the effect on model parameters either as centered power functions (continuous covariates: age, bodyweight) or as factors (binary covariates: sex, patient status: healthy volunteer vs RA patient). Covariates were selected based on statistical significance using an automated iterative forward addition (p = 0.01, corresponding to a change in NONMEM objective function value [ΔOFV] of −6.63 for 1 degree of freedom) and backward elimination (p = 0.001; ΔOFV of 10.8 for 1 degree of freedom) approach (scm tool in PsN 3.5.3).
Steady-state inhibition of pSTAT1 (inhibition of JAK1 activity) was simulated over 24 h for a typical male healthy volunteer of 75 kg following administration of 30, 50, 100, 200, and 300 mg once daily. The parameter uncertainty used for deriving the 90 % confidence interval on the simulated pSTAT1 inhibition was based on 1,000 bootstrap replicates of the pharmacokinetic and pharmacokinetic/pharmacodynamic models. The impact of dosing regimen on the pharmacodynamic response was investigated by comparing the simulated inhibition following treatment with 100 mg twice daily vs 200 mg once daily. Contribution of filgotinib and of its active metabolite to the simulated pharmacodynamic biomarker response was also investigated at each dose level.
3 Results
3.1 Non-Compartmental Pharmacokinetic Analysis
Mean plasma concentration–time profiles of filgotinib and its active metabolite in healthy volunteers are depicted in Fig. 2 and pharmacokinetic parameters are summarized in Tables 2 and 3.
3.2 Filgotinib
After single and repeated oral administration of filgotinib to healthy male volunteers, filgotinib was rapidly absorbed. The decrease in plasma concentrations displayed a biphasic profile (see Fig. 2a, c).
After single dosing, the exposure to filgotinib (both C max and AUC0–∞) increased dose proportionally within the 10- to 100-mg dose range (Table 2). At the highest single dose tested (200 mg), a slightly more than dose-proportional increase in exposure was observed and was not considered to be of clinical relevance.
After repeated dosing, steady state for filgotinib plasma concentrations was attained by day 2, regardless of the dose and dosing regimen (once or twice daily). At steady state after twice-daily administration, C max increased dose proportionally over the entire dose range while the exposure in terms of AUC showed a trend to increase more than dose proportionally (Table 3). As there were no changes in the apparent elimination half-life and absorption over the dose range from 25 to 100 mg twice daily, this minor deviation from dose proportionality is not expected to be clinically meaningful. Additionally, both C max and AUC0–t (exposure over the dosing interval i.e., 12 or 24 h) rose in proportion to the dose between 200 and 450 mg once-daily doses. At steady state for the 200-mg once-daily and 100-mg twice-daily regimens, the C max and AUC0–t for filgotinib increased in proportion to the dose whereas the apparent terminal half-life, and the accumulation ratio (R ac(AUC)) were essentially the same. These findings are in line with the dose-proportional pharmacokinetics of filgotinib.
Overall, the between-subject variability of AUC and C max at steady state was low to moderate (between-subject CV % range: 16–44 %).
3.3 Filgotinib’s Active Metabolite
After single dosing of filgotinib, plasma concentrations of its active metabolite were detected within 30 min and reached a maximum 3–5 h post-dose (Fig. 2b; Table 2). The metabolite plasma bioavailability parameters (C max and AUC0–24h) increased dose proportionally within the 10- to 200-mg dose range. The metabolite’s apparent terminal elimination half-life of approximately 20 h was constant following a single dose (Table 2).
After repeated dosing with filgotinib in healthy volunteers, the plasma elimination of the metabolite displayed a monophasic pattern with mean t1/2,λz ranging between 22 and 27 h, resulting in an average 2.0- and 3.9-fold accumulation of the metabolite after once- and twice-daily dosing with filgotinib, respectively (Table 3). Within the anticipated 50- to 200-mg therapeutic dose range, steady-state levels of the metabolite were achieved within 4 days. Overall, metabolite exposures were on average 16- to 20-fold higher than the exposures to filgotinib. A similar exposure difference for parent and metabolite was found in patients with RA [10].
At steady state in healthy volunteers, both C max and AUC0–t of the metabolite increased in proportion to the dose of filgotinib between 25 and 100 mg twice daily, as well as from 300 to 450 mg once daily (Table 3). The exposure observed at 200 mg once daily was within the same range as that obtained after 300 mg once daily. This finding could not be explained by a change in formation or elimination of the metabolite, because neither the t max nor the apparent elimination half-life was different from the two other doses tested as once-daily regimen (300 and 450 mg). In contrast, filgotinib showed dose proportionality within the 200- to 450-mg once-daily dose range.
At steady state after 200 mg once daily and 100 mg twice daily, the apparent elimination half-lives for the metabolite showed a slight though statistically significant difference (27.3 vs 22.5 h, p = 0.0292), that is of no clinical relevance, and which likely is owing to the low between-subject variability, as evidenced by the CV % on \( t_{{ 1/ 2,\lambda_{\text{z}} }} \) being below 18 %. Dose normalized exposure (AUC0–t) and parent-metabolite ratio after 200 mg once daily and 100 mg twice daily were similar, confirming the dose-proportional pharmacokinetics of the metabolite. As a reflection of the difference in the accumulation ratio, dose-normalized C max values were about 2-fold higher after twice-daily as compared with once-daily dosing. Overall, the between-subject variability of AUC0–t and C max of the metabolite at steady state was low (between-subject CV % <26 %).
3.4 Population Pharmacokinetic Model for Filgotinib and its Active Metabolite
The pharmacokinetic profiles were described by a combined two-compartment structural model component with oral absorption and linear elimination describing the pharmacokinetics of filgotinib, and a one-compartment model component with linear elimination for the metabolite (Fig. 3). At doses at and above 300 mg, a secondary pathway of elimination was included to describe the lower-than-expected observed metabolite exposure. This secondary pathway should not be seen as an actual mechanistic pathway, but rather as an empirical model component. Additional data would be needed to elucidate possible physiological mechanisms underlying the less-than-expected metabolite concentration at high doses.
Schematic for the combined structural model describing the pharmacokinetics of filgotinib and its active metabolite. CL P , CL M total filgotinib and metabolite clearance, respectively, FRAC fraction of filgotinib metabolized through secondary pathway of elimination, ka first-order absorption rate constant, Q filgotinib intercompartmental clearance, V C /F, V P /F, V M /F apparent filgotinib central, filgotinib peripheral, and metabolite volume of distribution, respectively
The development of the population pharmacokinetic model was based on a fixed-effects model including a complete conversion of filgotinib to its active metabolite and combined additive/proportional error models for both compounds. Including random effects on total plasma clearance and volume of distribution of both compounds (CLP/F, CLM/F, V C/F, and V M/F) resulted in a highly significant change in NONMEM OFV of −5,664. The OFV was further improved (by 184 points) by including the correlation between the additive and proportional error components of the two compounds. Adding a secondary pathway of elimination lowered the OFV by 67.6 points and led to a notable improvement in diagnostic plots. Removing the additive residual error component from the filgotinib model did not result in a statistically significant increase on OFV. Consequently, the residual variability on filgotinib was best described by a proportional error model, while a combined additive/proportional error model was retained to describe the residual variability of the metabolite.
Following the construction of the structural and statistical population pharmacokinetic model, a full model was developed by iteratively including statistically significant covariates (p = 0.01). The full covariate model included sex and body weight as covariates on the apparent clearance and volume of distribution of filgotinib and on the volume of distribution of the metabolite, subject status (patient vs healthy subject) as a covariate on filgotinib’s relative bioavailability, and age as a third covariate on the metabolite volume of distribution. Following backward elimination of covariates that did not reach the pre-defined significance level (p = 0.001), the final covariate model included body weight on the apparent clearance of filgotinib, patient status on the relative bioavailability, and sex on the apparent volume of distribution of filgotinib.
The final population pharmacokinetic model describing the pharmacokinetics of filgotinib and its metabolite is shown in Eq. 1:
Y P and Y M are the observed filgotinib and metabolite plasma concentrations based on the corresponding model predictions with multivariate normal proportional residual error. A, C P , C P, pred, and C M represent the model-predicted filgotinib amount in the absorption compartment, plasma and peripheral compartment filgotinib concentrations, and metabolite plasma concentration, respectively. V C /F, V P /F, and V M /F are the apparent volumes of distribution in the central and peripheral filgotinib compartments and the metabolite compartment, respectively, CLP/F, CLM/F, and Q/F are the total apparent filgotinib clearance, apparent metabolite clearance, and apparent inter-compartmental filgotinib clearance, respectively. FRAC represents the fraction of filgotinib that is cleared through the secondary pathway of elimination, and ka is the first-order absorption rate constant. ε P, prop and ε M, prop represent the unexplained residual variability defined as multivariate normal variables with variances \( \sigma_{\text{P,prop}}^{2} \) and \( \sigma_{\text{P,prop}}^{2} \), respectively. Cov(\( \sigma_{\text{P,prop}}^{2} \), \( \sigma_{\text{P,prop}}^{2} \)) represents the covariance between the residual error terms.
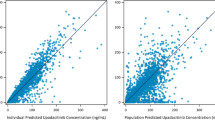
The estimated parameters for the final population pharmacokinetic model are provided in Table 4. All parameters were estimated with relative standard error (RSE) <50 %. Figure 4 shows goodness-of-fit plots based on the final population model of filgotinib and metabolite pharmacokinetics. Even if a small deviation from normality was observed, the residuals are acceptable (Fig. 4b). A number of samples are somewhat over-predicted (PRED/DV >10) by the model and appear below the diagonal in Fig. 4a. Most of these samples were taken shortly after dosing. This was judged acceptable, considering the low fraction of affected samples (6.5 % of filgotinib and 2.0 % of metabolite samples) and the limited data available in the absorption phase.
Goodness-of-fit assessment comparing observed filgotinib and metabolite concentrations with the corresponding population predictions (a) and Q–Q plot of conditional weighted residuals (b). Solid line shows line of unity. Residual-based diagnostics for pharmacokinetic model (c–f) with horizontal solid and dotted lines at zero and ±1.96, respectively. CWRES conditional weighted residuals
Apart from the diagnostics discussed above, the model selection was heavily based on mean observed and predicted time course plots stratified by dose and study. Figure 5 shows the mean time course plot for once-daily dosing at 200 mg.
Mean observed filgotinib (a) and metabolite (b) plasma concentration–time profiles after once-daily dosing at 200 mg. Small markers show the individual observed filgotinib and metabolite plasma concentrations on day 1 and 10 at 0.5, 1, 2, 3, 5, 8, and 12 h post-dose, with the mean (95 % confidence interval) shown with large markers (error bars). Thick solid lines show the corresponding mean population predictions based on the final population pharmacokinetic model
The appropriateness of the random-effects model was further assessed by visual predictive checks (not shown) and the model robustness and the validity of parametric uncertainty estimates were assessed by bootstrap (Table 4). These diagnostics indicated that the model is robust, that the parameter estimates represent a global minimum in the likelihood surface, and that the observed between-subject variability is adequately described by the developed pharmacokinetic model.
The distribution of individual-predicted filgotinib and active metabolite steady-state exposures increased proportionally with dose, and once- and twice-daily dosing at the same total daily dose (specifically: 100 mg twice daily vs 200 mg once daily) resulted in similar exposures. These findings are in good agreement with the conclusions drawn with non-compartmental pharmacokinetic analysis.
3.5 Population Pharmacokinetic/Pharmacodynamic Model
The relative inhibition of pSTAT1-positive cells observed in healthy volunteers was adequately described by a sequential direct-response model of predicted filgotinib and its metabolite plasma concentration. The drug effect on pSTAT1 inhibition was implemented as a sigmoid Emax model (Eq. 2).
Subscripts P and M refer to filgotinib and metabolite, respectively. C 0,P and C 0,M were the effective filgotinib and metabolite plasma concentrations normalized to the log-normally distributed, individual filgotinib and metabolite potencies, IC50,P and IC50,M, respectively. The predicted pSTAT1 response was defined relative to the normally distributed individual estimated baseline percentage of pSTAT1 positive cells following activation with IL-6, and the observed pSTAT1 response was described as the sum of the individual model predictions and residual unexplained variability described by a combined additive and proportional residual error model.
Including the sigmoidicity factor, H, led to a statistically significant change in NONMEM OFV of −21, corresponding to p < 0.001. The final model shown in Eq. 2 allows complete inhibition of the pSTAT1 response by either filgotinib or metabolite at sufficiently high exposures. Models based on incomplete inhibition due to the combined or individual effects of filgotinib or its metabolite were tested but did not result in statistically significant improvements of the model fit. The goodness-of-fit plots for the final population pharmacokinetic/pharmacodynamic model for filgotinib are shown in Fig. 6.
Goodness-of-fit assessment comparing observed pSTAT1 response to the corresponding population predictions (a) and Q–Q plot of conditional weighted residuals (b). Solid line shows line of unity. Residual-based diagnostics for the final model of pSTAT1 response (c–f) with horizontal solid and dotted lines show at zero and ±1.96, respectively. CWRES conditional weighted residuals
The estimated parameters for the pSTAT1 pharmacokinetic/pharmacodynamic model are provided in Table 5. All parameters were estimated with RSE <50 %. The appropriateness of the parametric confidence intervals was confirmed by a bootstrap validation of the model (Table 5). Figure 7 shows the model estimated relation between filgotinib and metabolite exposure and pSTAT1 response in a typical subject. The line segments in Fig. 7 indicate the filgotinib and metabolite concentrations leading to 50 % inhibition of the pSTAT1 response (293 and 1,686 ng/mL, respectively).
Estimated exposure-response relation between filgotinib (a) and metabolite (b) plasma concentrations and the proportion of pSTAT1-positive cells (95 % confidence interval). Vertical line segments indicate the filgotinib and metabolite concentrations leading to 50 % inhibition of the pSTAT1 signal compared with placebo
Of note is that conversely to filgotinib, the pre-dose concentrations of metabolite (C t) were above its IC50 from 100 mg once daily onwards (Table 3), suggesting the contribution of the metabolite to basal pSTAT1 inhibition.
3.6 Simulation of pSTAT1 Inhibition
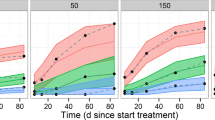
The simulated inhibition of pSTAT1 response in the typical subject (male healthy volunteer of 75 kg) at doses between 30 mg and 300 mg once daily and 100 mg twice daily with a 90 % confidence interval is shown in Fig. 8 and superposed on the predicted filgotinib and metabolite plasma concentration–time course. The impact of the peak filgotinib exposure compared with the sustained metabolite exposure is clearly visible in the simulated pharmacodynamic response. The response to once-daily doses between 30 mg and 50 mg and to 100 mg resulted in low and intermediate inhibition, respectively. Responses to higher doses appear to have reached a plateau with mean inhibition around 80 % predicted for both 200-mg and 300-mg total daily dose.
The model of pSTAT1 inhibition is a direct response model based on the individual predicted time courses of filgotinib and metabolite plasma concentrations. As such, the minimal inhibition at steady state is primarily determined by the sustained metabolite concentration, while the contribution from the more transient filgotinib exposure is predicted to be limited at the end of both once- and twice-daily dosing intervals. The maximal inhibition is determined by the C max of filgotinib adding to the inhibition caused by the sustained metabolite exposure. The simulated inhibition in terms of mean, minimum and maximum inhibition with 90 % confidence intervals over the course of the dosing interval are presented in Table 6. The corresponding hypothetical pSTAT1 inhibition following exposure to filgotinib or its major metabolite alone is summarized in Tables 7 and 8. It should be noted that the non-linearity of the exposure-response model (see Eq. 1) implies that the sum of responses shown in Table 6 does not (necessarily) equal the sum of responses shown in Tables 7 and 8.
4 Discussion
Pharmacokinetics and pharmacodynamics of filgotinib and its active metabolite were investigated in two phase I trials over a wide dose range (10–450 mg) and various dosing regimens (once and twice daily) in healthy male volunteers. Exposure to filgotinib and its metabolite were also evaluated in patients with RA, who were mostly female, by sparse sampling over a 4-week dosing period. Without pharmacodynamic assessments as in healthy volunteers, the patient data contributed to a limited extent to the model.
Filgotinib was extensively and rapidly absorbed after oral dosing in healthy volunteers. The filgotinib absorption profile was somewhat variable as shown by the relatively large range in t max values from 0.5 to 5.0 h within the 10- to 450-mg dose range. Taking into account the moderate variability in C max (28.9–42.0 %) within the anticipated therapeutic dose range (50- to 200-mg daily dose), this finding is not expected to be clinically relevant following repeated administrations of filgotinib.
The rate (C max) and the extent (AUC) of absorption of filgotinib increased dose proportionally over the 10- to 450-mg dose range. Consistent with the 6-h elimination half-life of filgotinib, there was no accumulation at steady state.
Filgotinib is metabolized to form a metabolite that is also active as a JAK1-selective inhibitor [9]. Therefore, its pharmacokinetic profile was evaluated in these early phase I trials. After filgotinib dosing, the metabolite concentrations reached a maximum within 3–5 h and then slowly decreased with an apparent elimination half-life of about 23 h leading to up to 4-fold accumulation after twice-daily dosing. The time to peak and the decline in plasma levels of the metabolite are much longer than those of filgotinib, suggesting that the elimination rather than the formation may be the rate-limiting step in the metabolite decline. As a consequence, the exposures to the active metabolite well exceed those of the parent compound filgotinib by a factor of 16–20 within the anticipated therapeutic dose range (50- to 200-mg daily dose), making it a ‘major metabolite’. Interestingly, this high exposure compensated for the lower potency of the metabolite and brought clinical exposures above whole blood IC50 values for inhibition of JAK1. It therefore supported the hypothesis that the metabolite may in fact contribute to the overall pharmacodynamics following treatment with filgotinib.
The pharmacokinetics of filgotinib and its major metabolite were found to be adequately described by the developed population pharmacokinetic model. The model was essentially constructed using data from healthy volunteers. The patient data used were limited to the exploration of the influence of some covariates on the pharmacokinetics of filgotinib, such as sex. While only male volunteers were included in the two phase I studies, the proof-of-concept study included 33/36 (92 %) female patients with RA [10]. This implies that sex is confounded with study and subject status, and as such, that the sex covariate included in the final population pharmacokinetic model on the filgotinib volume of distribution may represent a study or subject effect.
At doses of at least 300 mg once daily, a secondary pathway of elimination was included in the model to describe the observed data, in particular the plasma concentration of the metabolite. The pathway could not be described by available subject covariates, or nonlinear model components (e.g., saturation or induction). We have chosen not to speculate on potential physiologic mechanisms on this pathway and it has merely been included in the model as an empirical component. Additional investigations at high doses would be needed to substantiate this secondary pathway.
The exposure-pharmacodynamic response relationship in terms of the inhibition of pSTAT1 activation after stimulation with IL-6 was evaluated in these two phase I studies. The observed data were adequately described by a sigmoid Emax model for pSTAT1 inhibition, driven by the individual predicted time courses of filgotinib and metabolite plasma concentrations. The model predicted the exposure that would theoretically result in half-maximal inhibition of pSTAT1 response (IC50) at 293 ng/mL filgotinib and 1,686 ng/mL major metabolite. This corresponds to a relative potency of filgotinib vs its metabolite of approximately 3.8, which is in the same order of magnitude as the relative potency established in a rat collagen-induced arthritis model, in which the metabolite was found to be 10 times less potent than filgotinib [9]. The difference complicating the comparison of the ex vivo human clinical data and the in vitro data generated using a whole blood assay is that the potency estimates from the in vitro assays were based on separate potency assessments for filgotinib and its metabolite, while the corresponding estimates based on clinical data were derived from samples where both filgotinib and metabolite contribute to the overall pharmacodynamics. Despite this, the potencies determined with these two methods were similar for filgotinib (IC50 of 267 vs 293 ng/mL) and for its metabolite (IC50 of 4,529 vs 1,686 ng/mL) given the different methodologies used [9].
The pharmacodynamic effect was simulated in a typical subject by predicting exposures for filgotinib and metabolite based on the final population pharmacokinetic model, and the resulting pSTAT1 inhibition based on the developed pharmacokinetic/pharmacodynamic model. The simulations emphasized the individual contributions of filgotinib and metabolite to the pharmacodynamic effect: the sustained plasma concentration of the metabolite over time leads to a basal inhibition across the dosing interval, while the maximum inhibition coincided with the maximum predicted exposure of filgotinib. The simulations suggested that the response to doses between 30 mg and 100 mg once-daily results in low to intermediate inhibition of pSTAT1 activation, while the response was predicted to be similar following treatment with 200 and 300 mg once daily, and 100 mg twice daily, with a mean inhibition across the dosing interval of approximately 78 % (90 % confidence interval of 62–86 %).
5 Conclusion
After oral administration, exposure to filgotinib was dose proportional with an average elimination half-life of 6 h. A major metabolite was formed that showed JAK1 selectivity, with higher exposure but lower potency than filgotinib. The relatively long duration of JAK1 inhibition following filgotinib dosing suggests that the activity of this major metabolite contributes to the overall pharmacodynamics effects. Current modeling and simulation of the pSTAT1 dose-response relation (inhibition of JAK1 activity) support that the maximum pharmacodynamic response is reached at a daily dose of 200 mg filgotinib. A daily dose range from 50 to 200 mg is currently being evaluated in the DARWIN phase IIB program in patients with RA.
References
O’Shea JJ, Plenge R. JAK and STAT signaling molecules in immunoregulation and immune-mediated disease. Immunity. 2012;36:542–50.
O’Shea JJ, Kontzias A, Yamaoko K, Tanaka Y, Laurence A. Janus kinase inhibitors in autoimmune diseases. Ann Rheum Dis. 2013;72(Suppl. 2):111–5.
Ghoreschi K, Jesson M, Li X, Lee J, Ghosh S, Alsup J, Warner J, Tanaka M, Steward-Tharp S, Gadina M, Thomas C, Minnerly J, Storer C, LaBranche T, Radi Z, Dowty M, Head R, Meyer D, Kishore N, O’Shea J. Modulation of innate and adaptive immune responses by tofacitinib (CP-690,550). J Immunol. 2011;186:4234–43.
Vaddi K, Luchi M. JAK inhibition for the treatment of rheumatoid arthritis: a new era in oral DMARD therapy. Expert Opin Investig Drug. 2012;21:961–73.
Riese RJ, Krishnaswami S, Kremer J. Inhibition of JAK kinases in patients with rheumatoid arthritis: scientific rationale and clinical outcomes. Best Pract Res Clin Rheumatol. 2010;24:513–26.
Neubauer H, Cumano A, Müller M, Wu H, Huffstadt U, Pfeffer K. JAK2 deficiency defines an essential developmental checkpoint in definitive hematopoiesis. Cell. 1998;93:397–409.
Haan C, Rolvering C, Raulf F, Kapp M, Druckes P, Thoma G, Behrmann I, Zerwes H. Jak1 has a dominant role over Jak3 in signal transduction through γc containing cytokine receptors. Chem Biol. 2011;18:314–23.
Van Rompaey L, Galien R, Van der Aar E, Clement-Lacroix P, Nelles L, Smets B, Lepescheux L, Christophe T, Conrath K, Vandeghinste N, Vayssiere B, De Vos S, Fletcher S, Brys R, Van ’t Klooster G, Feyen J, Menet C. Preclinical characterization of GLPG0634, a selective inhibitor of JAK1 for the treatment of inflammatory diseases. J Immunol. 2013;191(7):3568–77.
Galien R, Vayssière B, De Vos S, Auberval M, Vandeghinste N, Dupont S, Clément-Lacroix P, Delerive P, Vanhoutte F, Brys R, Van der Aa A, Van Rompaey L, Van’t Klooster G. Analysis of the JAK1 selectivity of GLPG0634 and its main metabolite in different species, healthy subjects and rheumatoid arthritis patients. San Diego: American College of Rheumatology. Oct 2013 (Abstract no. 478).
Vanhoutte F, Mazur M, Van Der Aa A, Wigerinck P, Van’t Klooster G. Selective JAK1 inhibition in the treatment of rheulatoid arthritis: proof of concept with GLPG0634. Arthritis Rheum. 2012;64(Suppl. 10):2489.
U.S. Food and Drug Administration. Guidance for industry: population pharmacokinetics. Rockville: U.S. Food and Drug Administration; February 1999.
EMEA. Guideline on reporting the results of population pharmacokinetic analyses. London: EMEA; 2007 June.
Beal SL, Sheiner LB, Boeckmann AJ, Bauer RJ, editors. 1989–2009 NONMEM users guides. Icon Development Solutions, Ellicott City (MD): USA.
Acknowledgments
The authors acknowledge colleagues from Galapagos: Reginald Brys and René Galien for development of the biomarker assay, Nicolas Sabourault and Marc de Weer for drug substance and formulation development, and Christine Guerin for preclinical safety assessment as well as Drs. Eva Vets and Lien Gheyle and their trial teams from SGS Life Science Services Clinical Pharmacology Unit (Antwerp, Belgium) for conducting phase I trials, and Mrs. Ellen Vringer-Stokvis, Quotient BioResearch (Northamsponshire, UK) for plasma sample analysis.
AbbVie has provided funding to Galapagos for the development of filgotinib.
Conflict of interest
Florence Namour and Beatrice Vayssière are employees of Galapagos SASU; Annegret Van der Aa, Chantal Tasset, and Gerben Van’t Klooster are employees of Galapagos NV. Paul Matthias Diderichsen and Eugène Cox are employees of Quantitative Solutions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Namour, F., Diderichsen, P.M., Cox, E. et al. Pharmacokinetics and Pharmacokinetic/Pharmacodynamic Modeling of Filgotinib (GLPG0634), a Selective JAK1 Inhibitor, in Support of Phase IIB Dose Selection. Clin Pharmacokinet 54, 859–874 (2015). https://doi.org/10.1007/s40262-015-0240-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40262-015-0240-z