Effects of geometric optics in conformal Weyl gravity

Abstract

We have investigated effect of geometric optics as the rotation of polarization vector of light in spacetime of gravitational compact object in the fourth-order theory of conformal Weyl gravity. The Pineault–Roeder method is applied to the rotating Weyl metric, and analytical results are obtained in the limit of weak field and or slow rotation. For the photon traveling parallel to the symmetry axes from the equatorial plane to infinity, the rotation of the polarization plane depends on the Weyl parameter $\gamma$ on the contrary to the Kerr spacetime where there is no rotation of polarization plane for this case.

1 Introduction

Motivations for the more recent alternatives to general relativity (GR) are related to the construction of quantum gravity on one hand and, on the other hand, cosmological, associated with or replacing such constructs as “inflation”, “dark matter”, and “dark energy”. In the last century, scientists were surprised with the discovery of unexpected rotation curves [2, 14] for galaxies. Could there be more mass in the universe than we are aware of, or is the theory of gravity itself wrong? Among many theories of gravity, the theory of Conformal Weyl Gravity [4, 6] alternative to the standard second-order Einstein theory of gravity, which is a possible solution to current cosmological puzzles, such as dark matter and dark energy. Weyl gravity is a theory that is invariant under local conformal transformations:

$$\begin{aligned} g_{\mu \nu }(x)\rightarrow \Omega ^{2}(x)g_{\mu \nu }(x), \end{aligned}$$

(1)

where $\Omega (x)$ is a function on spacetime. This leads to the Weyl gravitational action given by the following:

$$\begin{aligned} I_\mathrm{W}= & {} -\alpha _g\int d^4x\,(-g)^{1/2}C_{\lambda \mu \nu \kappa } C^{\lambda \mu \nu \kappa }\nonumber \\= & {} -2\alpha _g\int d^4x\, (-g)^{1/2}\left[ R_{\mu \kappa }R^{\mu \kappa }-\frac{1}{3} (R^{\nu }_{\phantom {\nu }\nu })^2\right] , \end{aligned}$$

(2)

where $\alpha _g$ is dimensionless and the conformal Weyl tensor [17] $C_{\lambda \mu \nu \kappa }$ is defined by the following:

$$\begin{aligned} C_{\lambda \mu \nu \kappa }= & {} R_{\lambda \mu \nu \kappa } -\frac{1}{2}\left( g_{\lambda \nu }R_{\mu \kappa }- g_{\lambda \kappa }R_{\mu \nu }- g_{\mu \nu }R_{\lambda \kappa }+ g_{\mu \kappa }R_{\lambda \nu }\right) \nonumber \\&+\,\frac{1}{6}R^{\alpha }_{\phantom {\alpha }\alpha }\left( g_{\lambda \nu }g_{\mu \kappa }- g_{\lambda \kappa }g_{\mu \nu }\right) . \end{aligned}$$

(3)

From the variational principle, the action (2) leads to the following:

$$\begin{aligned} (-g)^{1/2}g_{\mu \alpha }g_{\nu \beta }\frac{\delta I_{ W}}{\delta g_{\alpha \beta }}=-2\alpha _{g} W_{\mu \nu }=-\frac{1}{2} T_{\mu \nu }, \end{aligned}$$

(4)

where $T_{\mu \nu }$ is energy momentum tensor, and

$$\begin{aligned} W_{\mu \nu } = 2C^{\alpha \ \ \beta }_{\ \mu \nu \ ;\beta \alpha } + C^{\alpha \ \ \beta }_{\ \mu \nu }R_{\alpha \beta }. \end{aligned}$$

(5)

In the fourth-order theory, there have been found exact solutions [7] of conformal Weyl gravity which generalize Kerr and Kerr–Newman solutions of GR. The vacuum solution of static spherically symmetric source for conformal gravity is given by the metric [6]:

$$\begin{aligned} \mathrm{d}s^2=-B(r)\mathrm{d}t^2+\frac{\mathrm{d}r^2}{B(r)}+r^2\left( \mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}\right) , \end{aligned}$$

(6)

where

$$\begin{aligned} B(r)=1- \frac{\beta (2-3\beta \gamma )}{r}-3\beta \gamma +\gamma r-kr^{2}, \end{aligned}$$

(7)

and $\beta , \gamma$, and k are integration constants and defined as follows: $\beta =\frac{GM}{c^2}\ (\hbox {cm})$ is geometrized mass, where M is the mass of the (spherically symmetric) source and G is the universal gravitational constant; and others $\gamma \ (\hbox {cm}^{-1})$ and $k\ (\hbox {cm}^{-2})$ are required by conformal gravity. The theory comes to the standard Schwarzschild solution ($\gamma =0=k$), and to the Schwarzschild–de Sitter ($\gamma =0$), as well as the term $-kr^{2}$, means a background De Sitter spacetime, which is important only over cosmological distances, while k has a very small value, the term $\gamma r$ becomes significant over galactic distance scales. In the review letter, [5] of Philip Mannheim has been discussed how gravitational theory can enable to be constructed candidate alternatives to the standard theory in which the dark matter and dark energy problems could then be resolved.

Moreover, in this paper, we study the effect of geometric optics as the rotation of polarization vector of light in the spacetime of rotating compact object in conformal Weyl gravity model.

This paper is organized as follows. In Sect. 2, it has been investigated the rotation of polarization vector using general Pienault–Roeder approach [12]. In Sect. 3, there have been considered two physical scenarios: in the first case, the source is in the equatorial plane, and the observer above the plane with $\theta < \pi /2$, which photons propagating parallel to and a distance b from the symmetry axis ($L=0$). In the second case, the source and the observer are in the symmetry axis ($\theta =0$), $r_{o} > r_{s}$. Section 5 summarizes the main results obtained.

Throughout, we use a space-like signature $(-,+,+,+)$. Greek indices run from 0 to 3 and Latin ones from 1 to 3.

2 Rotation of polarization vector of electromagnetic waves propagating in spacetime of compact object in conformal Weyl gravity

According to GR, gravitational field affects the propagation of electromagnetic fields. Nevertheless, one may use the geometrical optic approximation according to which light rays travel along the null geodesics and the polarization vector is parallelly propagated along them when the state of polarization is remained unaffected [8]. The purpose of this section is to analyze the effect of the parameter $\gamma$ of Weyl gravity on rotation of the polarization of a photon under the influence of the gravitational field of a rotating source in the fourth-order theory of conformal Weyl gravity. We assume that the external gravitational field of gravitating object in conformal fourth-order gravity is described by the rotating metric [3, 7, 10, 16], namely

$$\begin{aligned} \mathrm{d}s^2=&\left( bf-\bar{c}e\right) \left( \frac{\mathrm{d}x^2}{a}+\frac{\mathrm{d}y^2}{d}\right) \nonumber \\&+\frac{1}{bf-\bar{c}e}[d(b\,\mathrm{d}\phi -\bar{c}\,c\,\mathrm{d}t)^2- a(e\,\mathrm{d}\phi -f\,\mathrm{d}t)^2], \end{aligned}$$

(8)

which is the canonical Carter form of the metric, where

$$\begin{aligned} a(x)= & {} j^2+ux+px^2+vx^3-kx^4,\nonumber \\ d(y)= & {} 1+\bar{r}y-py^2+sy^3-j^2ky^4,\nonumber \\ b= & {} j^2+x^2,\quad e = j(1-y^2),\quad \bar{c} = j,\quad f =1, \end{aligned}$$

(9)

and $u,\ p,\ v,\ k,\ \bar{r}$, and s are constants satisfying the constraint $uv-\bar{r}s=0$. The angular momentum of the source is represented by j. The fourth-order Kerr solution includes the Kerr solution ($u=-2MG/c^2,\ p=1,\ v=\bar{r}=s=k=0$) and the Kerr–de Sitter solution ($u=2MG/c^2,\ p=1-kj^2,\ v=\bar{r}=s=0,\ k=\Lambda /3;\ \Lambda$ being the cosmological constant) as special cases.

Substituting for the functions in (9) with the choice $u=-2MG/c^2,\ p=1, \ v=\gamma$ in the metric (8) and then considering the weak filed ($u/r\ll 1$), slow rotation ($j/r\ll 1$) limits the above metric (8) in the Boyer–Lindquist coordinates ($x=r,\ y=\cos \theta$) which take the following form:

$$\begin{aligned} \mathrm{d}s^{2}=-B(r)\mathrm{d}t^{2}+\frac{\mathrm{d} r^2}{B(r)}+r^{2}\mathrm{d}\theta ^{2}+r^{2}\sin ^{2}\theta \mathrm{d}\phi ^{2}-2 \Omega r^{2}\sin ^{2}\theta \mathrm{d}t \mathrm{d}\phi , \end{aligned}$$

(10)

where $B(r)=(1-2M/r+\gamma r)$ is the lapse function, and $\Omega =\omega -j\gamma /r$, where $\omega =2Mj/r^{3}$ is the angular velocity of dragging inertial frames, $j=J/Mc$ is the specific angular momentum being equal to the total momentum J of the gravitating object per unit mass. In the paper,  [12] have been considered the applications of geometrical optics to the Kerr metric in the weak-field approximation ($j \ll M$) using Newman–Penrose formalism. Here, we applied this formalism to Weyl gravity.

The relationships between the tangent vector $k^{\mu }$ to the null congruence and the polarization vector $f^{\mu }$ is as follows:

$$\begin{aligned} k^{\mu }k_{\mu } = 0,\quad Dk^{\mu } = 0, \end{aligned}$$

(11)

and

$$\begin{aligned} k^{\mu } f_{\mu } = 0,\quad Df^{\mu }=0, \end{aligned}$$

(12)

where notation D denotes covariant derivative in the direction of the wave vector $k^{\mu }$.

The vector $m_{\mu }$

$$\begin{aligned} m^{\mu }=\frac{\sqrt{2}}{2}(a^{\mu }+ib^{\mu }), \end{aligned}$$

(13)

being relevant to the task considered here is from null tetrad $\left\{ e_{a\mu }\right\} =\left( m_{\mu },\bar{m}_{\mu },l_{\mu },k_{\mu }\right)$ adopted for the Newman–Penrose formalism [11].

Furthermore, the direction of vector $k^{\mu }$ is preserved under null rotations in the following way:

$$\begin{aligned}&k'^{\mu }=Ak^{\mu }, \end{aligned}$$

(14)

$$\begin{aligned}&m'^{\mu }=\mathrm{e}^{-i\chi }(m^{\mu }+Bk^{\mu }), \end{aligned}$$

(15)

$$\begin{aligned}&l'^{\mu } = A^{-1}(l^{\mu }+B\bar{m}^{\mu }+\bar{B}m^{\mu }+B\bar{B}k^{\mu }), \end{aligned}$$

(16)

where $A>0$ is positive, B is complex, and $\chi$ is real. When vector $k^{\mu }$ is tangent to the null congruence, the spin coefficient $\kappa \equiv -Dk_{\mu }m^{\mu }$ is zero [11]. Furthermore, assumption that the null tetrad has to propagate parallelly along the null congruence implies disappearance of other two spin coefficients: $\varrho =\pi =0$. Consequently, the plane spanned by vectors $k^{\mu }$ and $a^{\mu }$ can be identified with the polarization plane which is parallelly propagated in the direction of vector $k^{\mu }$, and, in turn, the polarization vector can be identified with the $a^{\mu }$ vector of the Newman–Penrose formalism.

The locally non-rotating frame (LNRF) [1] is orthonormal frame characterized by the one form $\omega ^{(0)} = \mathrm{e}^{\nu }\mathrm{d}t$, $\omega ^{(1)} = \mathrm{e}^{\lambda }\mathrm{d}r$, $\omega ^{(2)} = \mathrm{e}^{\mu }\mathrm{d}\theta$, and $\omega ^{(3)} = (\mathrm{d}\phi -\Omega \mathrm{d}t)\mathrm{e}^{\psi }$, and with the corresponding dual basis vectors:

$$\begin{aligned} \left\{ {e}_{a}^{ (\mu )}\right\} = \left\{ r^{(\mu )},\bar{r}^{(\mu )},q^{(\mu )},p^{(\mu )}\right\} . \end{aligned}$$

(17)

The concrete expressions for vectors $\mathrm{e}^{\nu }$, $\mathrm{e}^{\lambda }$, $\mathrm{e}^{\mu }$, and $\mathrm{e}^{\psi }$, the spacetime metric (10), are given by Eq. (42) in Appendix A. According to Pineault and Roeder [12] for an observer at rest in the orthonormal frame, the projection of vector $m^{\mu }$ on the LNRF is given by the following:

$$\begin{aligned} a_{+}^{\ (\mu )}= & {} \frac{1}{\sqrt{2}}\left\{ 0,-\frac{k^{(2)}}{k^{(0)}},1-K(k^{(2)})^{2},Kk^{(2)}k^{(3)}\right\} ,\end{aligned}$$

(18)

$$\begin{aligned} b_{+}^{\ (\mu )}= & {} \frac{1}{\sqrt{2}}\left\{ 0,-\frac{k^{(3)}}{k^{(0)}},-Kk^{(2)}k^{(3)}, 1-K(k^{(3)})^{2}\right\} , \end{aligned}$$

(19)

where $k^{(\mu )}$ is the projection of $k^{\mu }$ on the LNRF according to Eq. (41); $K=1/\left[ k^{(0)}\left( k^{(0)}+k^{(1)}\right) \right]$. A null rotation performed

$$\begin{aligned} m_{+}^{(\mu )}\rightarrow m^{(\mu )} = \mathrm{e}^{-i\chi } m_{+}^{(\mu )} \,\, , \end{aligned}$$

(20)

satisfies to the condition $\varrho =0$. Using this choice and considering the $\varrho$ coefficient as $\varrho \equiv Dm_{\mu }\bar{m}^{\mu }/2$, one can show that

$$\begin{aligned} D\chi =-2i\varrho _{+}. \end{aligned}$$

(21)

Expression (21) indicates the variation of the polarization vector in the $k^{\mu }$ direction, i.e., the congruence direction. The angle which we are going to obtain for the spacetime metric (10) is as follows:

$$\begin{aligned} D\chi= & {} -2i\varrho _{+} = \frac{k^{(3)}}{k^{(0)}+k^{(1)}}\bigg [\Gamma _{\ \ \ (2)(0)}^{(0)}k^{(0)}+ \Gamma _{\ \ \ (2)(1)}^{(1)}k^{(1)}\nonumber \\&+\,\Gamma _{\ \ \ (2)(2)}^{(1)}k^{(2)}+ \Gamma _{\ \ \ (2)(3)}^{(0)}k^{(3)}\bigg ] - \frac{k^{(2)}}{k^{(0)}+k^{(1)}}\nonumber \\&\times \bigg [\Gamma _{\ \ \ (3)(0)}^{(1)}k^{(0)}+\Gamma _{\ \ \ (3)(1)}^{(0)}k^{(1)}+\Gamma _{\ \ \ (3)(2)}^{(0)}k^{(2)}\nonumber \\&+\,\Gamma _{\ \ \ (3)(3)}^{(1)}k^{(3)} \bigg ]+\Gamma _{\ \ \ (3)(3)}^{(2)}k^{(3)}+\Gamma _{\ \ \ (3)(0)}^{(2)}k^{(0)}, \end{aligned}$$

(22)

where the quantities $\Gamma _{\ (\nu )(\gamma )}^{(\mu )}$ and $k^{(\mu )}$ are listed in Appendix B. Using the Eqs. (41) and (43), one can get expression for $D\chi$ in the first order in a as follows:

$$\begin{aligned} D\chi = - \frac{L \cos \theta }{r^{2} \sin ^{2}\theta } + \left( 3M + \frac{\gamma r^{2}}{2}\right) \frac{j \sin \theta }{r^2}\frac{\mathrm{d}\theta }{\mathrm{d}\lambda } + \mathcal {O}(j^2). \end{aligned}$$

(23)

The first term in the RHS of Eq. (23) is the Schwarzschild one being valid in the limit when $j\rightarrow 0$, and the second term contains the induced rotation of the polarization plane $\chi _p$, where

$$\begin{aligned} D\chi _{p}=\left( 3M + \frac{\gamma r^{2}}{2}\right) \frac{j \sin \theta }{r^2}\frac{\mathrm{d}\theta }{\mathrm{d}\lambda }. \end{aligned}$$

(24)

For an arbitrary trajectory, Eq. (24) can be integrated by introducing spherical coordinates $\psi$ which is an azimuthal angle (see [12]) in the plane of the orbit and $\alpha$ is the inclination angle of the orbital plane with respect to the equatorial plane. That is $\cos \theta =\sin \psi \sin \alpha$, and Eq. (24) becomes the following:

$$\begin{aligned} D\chi _{p}=-\left( 3M + \frac{\gamma r^{2}}{2}\right) \frac{j \sin \alpha }{r^2}\frac{\mathrm{d}(\sin \psi )}{\mathrm{d}\lambda }. \end{aligned}$$

(25)

The total change of polarization vector, taking into account Eq. (23) and the effect of dragging of inertial frames, is then

$$\begin{aligned} \Theta =\Delta \chi + \Delta \phi . \end{aligned}$$

(26)

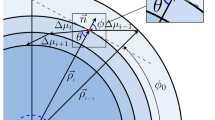
Here have been considered two physical scenarios, illustrated in Fig. 1. In the first case, the source is in the equatorial plane $(\theta =\alpha =\pi /2)$, and the observer above the plane with $\theta < \pi /2$, which photons propagating parallel to and a distance b from the symmetry axis ($L=0$). In the second case, the source and the observer are in the symmetry axis ($\theta =0$), $r_{o} > r_{s}$. The source and the observer are modeled by timelike curves $r=r_{s}$ and $r=r_{o}$, respectively.

Fig. 1

At top, the source and the observer are at distance b from the symmetry axis. At bottom, both source and observer are in the symmetry axis. The vector tangent to the null congruence and polarization vector are indicated by $\overrightarrow{k}$ and $\overrightarrow{a}$, respectively. The black hole, the source, and the observer are indicated by BH, S, and O, respectively

3 In particular case

3.1 Source in the black hole equatorial plane

In the first case, let the source be on the equatorial plane, and the observer is on the plane with $\theta < \pi /2$ (see Fig. 1, top panel). According to our consideration, we can write $\sin \psi =\sqrt{r^{2}-b^{2}}/r$, and Eq. (25) takes the following view:

$$\begin{aligned} D\chi _{p}=-\frac{j}{r^2}\left( 3M + \frac{\gamma r^{2}}{2}\right) \left( \frac{b^2}{r^2}\frac{1}{\sqrt{r^{2}-b^{2}}}\right) \frac{\mathrm{d} r}{\mathrm{d}\lambda }; \end{aligned}$$

(27)

that is

$$\begin{aligned} \int _{0}^{\chi }\mathrm{d}\chi _{p}=-\int _{b}^{r_{o}}\frac{6M+\gamma r^{2}}{2r^{4}}\cdot \frac{jb^{2}}{\sqrt{r^{2}-b^{2}}}\ \mathrm{d}r \,\, , \end{aligned}$$

(28)

where $D\chi _{p}=k^{1}\mathrm{d}\chi _{p}/\mathrm{d}r$ and $k^{1}=\mathrm{d}r/\mathrm{d}\lambda =\dot{r}$ (see Appendix A). Integrating Eq. (28), we have the variation between $a^{(\mu )}$ and $a_{+}^{\ (\mu )}$ along the null congruence:

$$\begin{aligned} \Delta \chi _{p}=-\frac{M j}{r_{o}}\left( \frac{1}{r_{o}^2}+\frac{2}{b^{2}}+\frac{\gamma }{2M}\right) \sqrt{r_{o}^{2}-b^{2}}. \end{aligned}$$

(29)

This result is the same obtained in Pineault and Roeder [12], since $\gamma =0$, and $r_{o}\rightarrow \infty$ ($\Delta \chi =-2Mj/b^2$).

The effect of dragging, $\Delta \phi$, is calculated using geodesic equations from A, as follows:

$$\begin{aligned} \Delta \phi= & {} \int _{\phi _{i}}^{\phi _{f}}\mathrm{d}\phi = \int _{b}^{r_{o}}\frac{j}{r^2}\frac{2M-\gamma r^{2}}{r-2 M+\gamma r^{2}}\sqrt{\frac{r^{3}-b^{2}(2 M-\gamma r^{2})}{r(r^{2}-b^{2})}}\,\mathrm{d}r \nonumber \\= & {} M j \left\{ \frac{2}{\sqrt{r_{o}^{2}-b^{2}}}\left( \frac{1}{r_{0}}+\frac{r_{o}}{b^{2}}\right) +\frac{\gamma }{\sqrt{r_{o}^{2}-b^{2}}}\left( 1-\frac{b^{2}}{r_{o}^2}\right) \right. \nonumber \\&+ \frac{\gamma }{b}\left( \arctan \frac{b}{\sqrt{r_{o}^{2}-b^2}}-\frac{\pi }{2}\right) +\frac{\gamma }{M}\log \frac{b}{r_{o}+\sqrt{r_{o}^{2}-b^2}} \Biggr \}. \end{aligned}$$

(30)

This result is the same obtained in [12], since $\gamma =0$, and $r_{o}\rightarrow \infty$ ($\Delta \phi =2Mj/b^2$). Then, we can assume that $r_{o}\rightarrow \infty$, following Pineault et al. Thus, the dragging, in this example, is as follows:

$$\begin{aligned} \Delta \phi = \int _{\phi _{i}}^{\phi _{f}}\mathrm{d}\phi = \left( \frac{2M}{b^{2}}-\frac{3M\pi \gamma }{2b}+\gamma \lim _{r_{o}\rightarrow \infty }\ln \frac{b}{r_{o}+\sqrt{r_{o}^{2}-b^{2}}}\right) j, \end{aligned}$$

(31)

and the variation between $a^{(\mu )}$ and $a_{+}^{(\mu )}$ along the congruence is as follows:

$$\begin{aligned} \Delta \chi = - \left( \frac{2M}{b^{2}}+\frac{\gamma }{2}\right) j. \end{aligned}$$

(32)

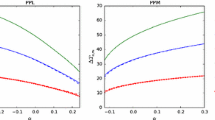
Consequently, the variation of the polarization vector is according to Eq. (26), in the first case, where observer and source are at a distance b from symmetry axis:

$$\begin{aligned} \Theta _{||} = \Delta \chi +\Delta \phi =-\frac{\gamma j}{2}\left( \frac{3M\pi }{b}+1\right) +\gamma \lim _{r_{o}\rightarrow \infty }\ln \frac{b}{r_{o}+\sqrt{r_{o}^{2}-b^{2}}}. \end{aligned}$$

(33)

When $\gamma =0$, it is coincided with the result by Pineault–Roeder’s work  [12].

3.2 Source and observer in the symmetry axis

In the second case (see Fig. 1, bottom panel), when the source and the observer are in the symmetry axis, $b=0$, $\theta =0$, and we have $\Delta \chi =0$. Then, Eq. (30) turns out to be the following:

$$\begin{aligned} \Theta _{\text {axis}}= & {} \Delta \phi = \int _{\phi _{i}}^{\varphi _{f}}\mathrm{d}\phi = \int _{r_{s}}^{r_{o}}\frac{j}{r^2}\frac{2M-\gamma r^{2}}{r-2 M+\gamma r^{2}}\mathrm{d}r \nonumber \\= & {} j \, \left[ M\left( \frac{1}{r_{s}^{2}}-\frac{1}{r_{o}^{2}}\right) -\gamma \left( 4M\left( \frac{1}{r_{s}}-\frac{1}{r_{o}}\right) -\ln \frac{r_{s}}{r_{o}}\right) \right] . \end{aligned}$$

(34)

Again, setting $\gamma =0$ with $r_{o}\rightarrow \infty$, we recover the Pineault–Roeder results.

4 Astrophysical implications

Now, we are going to get rough constraint on $\gamma$ parameter using some astrophysical data of blazar which is an active galactic nucleus with a relativistic jet directed very nearly towards Earth. Therefore, there are many observations of polarization of electromagnetic waves from distant quasars, but there is currently no practical method for measuring rotation of the polarization vector from astrophysical compact objects such quasars; here, we admit that, in the near future, scientist may detect kind effect by polarimeters with a high sensitivity which can measure polarization fraction at a few percent level and resolve polarization angle at a few degree level. For this purpose, we will admit the error of the measurement of this effect in the imaginary experiment being equal to $\approx 1\%$. As gravitational object, we take the well-known blazar 3C 273, which is located at 749 Mpc from us and has central black hole with mass measured a billion solar masses. Supposing that the correction due to Weyl gravity lies in the error bar, one can easily find the rough estimation of the upper limit of the Weyl parameter. For the purpose of the present discussion, the quasiclassical approximation is valid and the change of polarization vector

$$\begin{aligned} \Theta _{\text {axis}}=\Theta _{0} \pm \Delta \Theta , \end{aligned}$$

(35)

where $\Theta _{0}$ is the rotation of polarization plane in Kerr spacetime (see [12]). Comparison of the observational data of above blazar 3C 273 with our theoretical ones will help to obtain the rough estimation of the upper limit for the Weyl parameter as $\gamma \le 2\times 10^{-21} \mathrm {cm}^{-1}$.

5 Conclusion

In this paper, we have studied the rotation of polarization vector in the null congruence direction in the gravitational field of rotating massive object in conformal Weyl gravity using the Pineault–Roeder approach [12]. For the photon traveling parallel to the symmetry axes from the equatorial plane to infinity, the rotation of the polarization plane (33) depends on the Weyl parameter $\gamma$ on the contrary to the Kerr spacetime [12] where there is no rotation of polarization plane for this case. Here, if we admit that Weyl parameter $\gamma >0$ is positive, then, in this case, the polarization vector is counter-rotating with respect to the spin of the black hole as the angle in Eq. (33) would be negative.

To get the estimation for the value of Weyl parameter $\gamma$, one should compare the observational results with the theoretical results. In Ref. [6] has been gotten expression for integration constant in the theory as $\gamma \le 10^{-28} \mathrm{cm}^{-1}$ which was in good agreement with the observed galactic rotation curves without the need for dark matter. Regarding solar system experiments, in Ref. [13], there has been used CASSINI Doppler Datas and got an upper bound for Weyl parameter as $\gamma \sim 10^{-21}\mathrm{cm}^{-1}$. Authors of the Ref. [15] from the correction to geodetic effect obtained $\gamma \le 1.5\times 10^{-20} \mathrm{cm}^{-1}$. In the recent paper [3], there has been estimated lower limit for parameter $\gamma$ as $\gamma \le 2\times 10^{-20}\mathrm {cm}^{-1} \$ using the experimental results of Ref. [9] which was set on the Earth as central body on the precise measurement of the gravitational redshift by the interference of matter waves. Here, we estimated Weyl parameter as $\gamma \le 2\times 10^{-21} \mathrm{cm}^{-1}$ using some observational data of blazar in our quasiclassical approximation.

Appendices

Geodesics

Using the Hamilton–Jacobi equation for massless particle, one may easily find the equations of photons in the background spacetime described by metric (10) can be found in the form:

$$\begin{aligned} \dot{t}= & {} \frac{1}{1-\frac{2M}{r}+\gamma r}\left[ E-\frac{a L}{r^{2}}\left( \frac{2 M}{r}-\gamma r\right) \right] , \end{aligned}$$

(36)

$$\begin{aligned} \dot{r}= & {} \sqrt{\frac{E(-4 a M L+E r^{3}+2aLr^{2}\gamma )-K(r-2M+r^{2}\gamma )}{r^{3}}}, \end{aligned}$$

(37)

$$\begin{aligned} \dot{\theta }= & {} \frac{1}{r^2}\sqrt{K-L^{2}\text {cosec}^{2}\theta }, \end{aligned}$$

(38)

$$\begin{aligned} \dot{\varphi }= & {} \frac{1}{r^2}\left( \frac{j E(2 M-r^{2} \gamma )}{r-2 M r^{2} \gamma }+L\text {cosec}^{2}\theta \right) , \end{aligned}$$

(39)

where the dot means an ordinary derivative with respect to the affine parameter $\lambda$, and K is Carter’s constant.

For the equatorial orbits, K vanishes. The constants E and L are constants of motion related to the two Killing vector fields $\xi _{t}$ and $\xi _{\varphi }$ in the geometry with axial symmetry (10). That is

$$\begin{aligned} p_{t}=-E\quad \text{ and }\quad p_{\varphi } = L. \end{aligned}$$

(40)

Locally non-rotating frame

All physical quantities are indicated by parenthesis around the Greek indices in the locally non-rotating frame (LNRF). The components of the vector $k^{\mu }=\mathrm{d}x^{\mu }/\mathrm{d}\mu =\dot{x}^{\mu }$ which is tangent to the null congruence and its projections $k^{(\mu )}$ on the LNRF are as follows:

$$\begin{aligned} k^{(0)}= & {} \mathrm{e}^{\nu }k^{0}=\mathrm{e}^{\nu }\dot{t}, \nonumber \\ k^{(1)}= & {} \mathrm{e}^{\lambda }k^{1}=\mathrm{e}^{\lambda }\dot{r}, \nonumber \\ k^{(2)}= & {} \mathrm{e}^{\mu }k^{2}=\mathrm{e}^{\mu }\dot{\theta }, \nonumber \\ k^{(3)}= & {} \mathrm{e}^{\psi }(k^{3}-\Omega k^{0}) = \mathrm{e}^{\psi } (\dot{\phi } - \Omega \dot{t}). \nonumber \\ \end{aligned}$$

(41)

The functions $\nu ,\lambda ,\mu$ and $\psi$ are listed as following

$$\begin{aligned}&\mathrm{e}^{2\nu }=1-\frac{2M}{r}+\gamma r, \nonumber \\&\mathrm{e}^{2\lambda }=\left( 1-\frac{2M}{r}+\gamma r\right) ^{-1}\,,\nonumber \\&\mathrm{e}^{2\mu }= r^2, \nonumber \\&\mathrm{e}^{2\psi }=r^{2}\sin ^{2}\theta . \end{aligned}$$

(42)

The nonzero components of the connection projected on the LNRF: [1] are

$$\begin{aligned} \Gamma _{(1)(0)}^{(0)}= & {} \Gamma _{(0)(0)}^{(1)}=\partial _{r}\nu \mathrm{e}^{-\lambda }, \nonumber \\ \Gamma _{(2)(0)}^{(0)}= & {} \Gamma _{(0)(0)}^{(2)}=\partial _{\theta }\nu \mathrm{e}^{-\mu }, \nonumber \\ \Gamma _{(2)(1)}^{(1)}= & {} -\Gamma _{(1)(1)}^{(2)}=\partial _{\theta }\lambda \mathrm{e}^{-\mu }, \nonumber \\ \Gamma _{(2)(2)}^{(1)}= & {} -\Gamma _{(1)(2)}^{(2)}=-\partial _{r}\mu \mathrm{e}^{-\lambda }, \nonumber \\ \Gamma _{(3)(3)}^{(1)}= & {} -\Gamma _{(1)(3)}^{(3)}=-\partial _{r}\psi \mathrm{e}^{-\lambda }, \nonumber \\ \Gamma _{(3)(3)}^{(2)}= & {} -\Gamma _{(2)(3)}^{(3)}=-\partial _{\theta }\psi \mathrm{e}^{-\mu }, \nonumber \\ \Gamma _{(1)(3)}^{(0)}= & {} \Gamma _{(0)(3)}^{(1)}=\Gamma _{(3)(1)}^{(0)} = \Gamma _{(3)(0)}^{(1)} \nonumber \\= & {} \Gamma _{(0)(1)}^{(3)}=-\Gamma _{(1)(0)}^{(3)}=\frac{1}{2}\partial _{r}\Omega \mathrm{e}^{\psi -\nu -\lambda }, \nonumber \\ \Gamma _{(2)(3)}^{(0)}= & {} \Gamma _{(0)(3)}^{(2)}=\Gamma _{(3)(2)}^{(0)} =\Gamma _{(3)(0)}^{(2)} \nonumber \\= & {} -\Gamma _{(0)(2)}^{(3)}=-\Gamma _{(2)(0)}^{(3)}=\frac{1}{2}\partial _{\theta }\Omega \mathrm{e}^{\psi -\nu -\mu }. \end{aligned}$$

(43)