The Leverage of Demographic Dynamics on Carbon Dioxide Emissions: Does Age Structure Matter?

Abstract

This article provides a methodological contribution to the study of the effect of changes in population age structure on carbon dioxide (CO₂) emissions. First, I propose a generalization of the IPAT equation to a multisector economy with an age-structured population and discuss the insights that can be obtained in the context of stable population theory. Second, I suggest a statistical model of household consumption as a function of household size and age structure to quantitatively evaluate the extent of economies of scale in consumption of energy-intensive goods, and to estimate age-specific profiles of consumption of energy-intensive goods and of CO₂ emissions. Third, I offer an illustration of the methodologies using data for the United States. The analysis shows that per-capita CO₂ emissions increase with age until the individual is in his or her 60s, and then emissions tend to decrease. Holding everything else constant, the expected change in U.S. population age distribution during the next four decades is likely to have a small, but noticeable, positive impact on CO₂ emissions.

Introduction

Demographic trends and changes in economic production are major factors driving anthropogenic greenhouse gas emissions (e.g., O’Neill et al. 2001), which, in turn, are most likely responsible for the observed increase in average global temperatures over the last few decades (IPCC 2007). Although several demographic quantities are potentially important determinants of greenhouse gas emissions (e.g., O’Neill and Chen 2002; Schipper 1996), most models used to develop emissions scenarios explicitly consider only population size or, in a few cases, some aggregate measures of age structure (O’Neill 2005).

This article contributes to the study of the effect of changing population age structure on emissions of carbon dioxide (CO₂), the gas that accounts for most of the anthropogenic-driven greenhouse effect. I offer new methodological perspectives that bridge the gap between the literatures on IPAT-based approaches (e.g., Chertow 2001) and environmental input-output modeling (e.g., Hendrickson et al. 2006). I propose a model that can be interpreted as a generalization of the IPAT equation to a multisector economy with an age-structured population. The model provides a unified interpretation of previous IPAT-based studies of the effect of population age composition and economic structure on CO₂ emissions. It can also be seen as a static version of the general equilibrium model, with multiple dynasties of households, as suggested by Dalton et al. (2008). A major contribution of the article is the development of methods to estimate the life cycle profile of CO₂ emissions for individuals. The methodologies that I propose are applied to data for the United States, showing that the expected change in population age structure over the next four decades is likely to have a positive, but rather small, impact on CO₂ emissions, holding everything else constant.

Background

Two main approaches have been proposed to study the role played by population age structure in shaping the level of greenhouse gas emissions. The first approach originates from the conceptual framework provided by the so-called IPAT equation (Commoner 1972; Ehrlich and Holdren 1971, 1972). The second approach mostly relies on integrated energy-economic growth models, such as the Population-Environment-Technology model, that are calibrated with household demographic projections, input-output economic tables, and estimates of consumption expenditures, savings, labor supply, etc. (e.g., Dalton et al. 2008).

The IPAT equation is an accounting identity that was proposed in the early 1970s to conceptualize the multiplicative role of population size on measures of environmental disruption (Commoner 1972; Ehrlich and Holdren 1971, 1972). The identity decomposes environmental impact (I) into the product of population size (P), affluence (A), and technology (T):

$$ I = P \times A \times T, $$

(1)

where affluence is operationalized as per-capita income (Y/P), and technology is expressed as environmental impact per unit of economic production (I/Y).

The IPAT equation was suggested in a period when environmental concerns focused on the ability of the environment to absorb pollutants that are by-products of modern technology (e.g., pesticides, asbestos, radioactive waste, petrochemicals, household waste) (Pebley 1998; Ruttan 1993). In the early 1990s, environmental concerns shifted toward changes occurring on a global scale, such as climate change. In this new context, the IPAT conceptual framework has strongly influenced research carried out by demographers on the impact of demographic factors on greenhouse gas emissions (Pebley 1998).

Dietz and Rosa (1994) made the IPAT equation operational for statistical analysis. Their formulation, known as STIRPAT (Stochastic Impacts by Regression on Population, Affluence and Technology), has been extensively used to evaluate the role of demographic factors in the explanation of CO₂ emissions. Population size has been the main demographic variable under analysis. Dietz and colleagues estimated a unitary elasticity of CO₂ emissions with respect to population size, using a cross-national data sample (Dietz and Rosa 1997; Rosa et al. 2004; York et al. 2003). They thus empirically supported the underlying assumption of the IPAT equation of unitary elasticity of I with respect to P. On the other hand, Shi (2003) obtained a higher estimate. Based on a panel data set for 93 countries for the period 1975–1996, Shi estimated that a 1% increase in population size raises emissions on average by 1.4%.

The role of several demographic variables on CO₂ emissions has been evaluated within the context of IPAT-based models. For instance, York et al. (2003) showed that urbanization is positively correlated with CO₂ emissions. Most importantly for the purposes of this study, the IPAT framework has stimulated some investigation of the effect of changing age structure on CO₂ emissions. Dietz and Rosa (1994) suggested that countries with a higher proportion of working-age population consume more energy and resources and thus produce more emissions. MacKellar et al. (1995) used households, instead of individuals, as the unit of analysis for their IPAT-based model and showed that population aging may have a large, positive impact on CO₂ emissions. As a matter of fact, population aging is partly responsible for the observed increase in number of households in the more developed regions of the world over the last several decades. The growth in household numbers in more developed regions of the world is projected to be substantially larger than population growth, leading to higher levels of CO₂ emissions than accounted for by models that do not consider changes in age structure and behavioral determinants of household formation and dissolution (Mackellar et al. 1995). Shi (2003) found a positive association between percentage of population in working age and CO₂ emissions. Fan et al. (2006) concluded that the proportion of the population between ages 15 and 64 has a negative impact on CO₂ emissions for countries with a high income level, whereas it has a positive impact for countries at other income levels. The effects of age structure are mediated by the labor force’s productions and individual behaviors. O’Neill and Chen (2002) discussed the limitations of IPAT decompositions and provided a standardization exercise for the United States, showing that the increase in the fraction of the population living with a householder older than 65 years will increase residential energy use and decrease transportation energy use, with consequences for CO₂ emissions.

In the IPAT literature, there has been some discussion about the differential impact on CO₂ emissions of population dynamics associated with different economic structures. For instance, Shi (2003) showed that the elasticity of CO₂ emissions with respect to population size depends on the level of income of the country. The lowest elasticity is estimated for high-income countries (0.83%) and the highest is estimated for lower-middle-income countries (1.97%). This result is consistent with the observation that the structure of the economy is important for the explanation of levels of emissions (York et al. 2003) and that the impact of population is different at different levels of development (Fan et al. 2006). In IPAT-based models, it has thus been suggested to consider the relative importance of manufacture production versus services, to capture the difference in the economic structure of each country (Shi 2003).

More detailed analyses of the role of the economic structure in the explanation of environmental outcomes have been done using input-output economic models, which date back to the pioneering work of Leontief (e.g. 1936, 1953, 1970, 1986). In the context of demographic analysis of environmental impact, relevant contributions appeared in the 1970s, when the U.S. Commission on Population Growth and the American Future asked Resources for the Future, a research organization, to undertake a project to identify the principal resource and environmental consequences of future population growth in the United States. The project was an important attempt to assess the environmental consequences of demographic, economic, and technological dynamics using input-output economic tables (Herzog and Ridker 1972; Ridker 1972).

The application of input-output economic analysis to environmental studies has grown with the goal of providing information about the environmental impacts of industrial production processes. This has typically been done by analyzing resource use and flows of industrial products, consumer products, and wastes. Duchin has worked extensively on the theory and methods that relate changes in technology, lifestyles, and the environment (e.g., Duchin 1998; Duchin and Lange 1994). Among other work, she has discussed the challenge of describing concrete technological and lifestyle alternatives that work best to tackle environmental problems. She suggested classifying household types in different societies according to common patterns of work, leisure, consumption, attitudes, and values, and to evaluate how activities are carried out in different societies, their outcomes, and the best alternatives to obtain a specific result (Duchin 1996).

The past two decades have seen increased attention to the role played by consumers and their lifestyles on environmental outcomes (Bin and Dowlatabadi 2005). Schipper and colleagues linked energy use to consumers’ activities, time use, and demographic variables. They estimated that about half of total energy use is influenced by personal transportation, personal services, and home energy use (Schipper 1996; Schipper et al. 1989). Reinders et al. (2003) extended studies of energy requirements of households in the Netherlands (e.g., Vringer and Blok 1995) to several European countries. They used household budget data to evaluate the relationship between household expenditures and energy use, and they found that the share of direct energy in the total energy requirement ranges from 34% to 64% in the countries considered. Lenzen (1998) used an input-output approach to evaluate energy use in Australia. He concluded that most greenhouse gas emissions are ultimately attributable to household purchases of goods and services and that the increase in emissions is strongly correlated with income growth. Pachauri and Spreng (2002) proposed a study of household energy requirements in India based on input-output tables and found that the main drivers of energy requirements are per-capita expenditures, population trends, and energy intensity in the food and agricultural sectors. Hertwich (2005) reviewed the environmental impact of household consumption in the context of integrated input-output models and life cycle analysis of products. He showed that in more-developed countries, household consumption is the most important final demand category in terms of energy use and CO₂ emissions. In developing countries, exports are more important if there are a lot of heavily export-oriented industries. Peters and Hertwich (2008) discussed the advantages of a consumption-based approach versus a production-based approach in constructing greenhouse gas inventories that account for international trade. Based on a detailed study for Norway, they also showed that the environmental impacts of consumers may be underestimated if emissions embodied in imports are not taken into account (Peters and Hertwich 2006). Tukker and Jansen (2006) provided a review of studies of environmental impact of products. The main idea behind these studies is that consumption of households and governments drives the environmental effects of economic activities, both directly and indirectly, through the impacts of production, use, and waste management of economic goods. Across all studies considered for European countries, expenditures on housing (including heating and electricity use), transportation, and food account for most emissions of CO₂. In the case of the United States, Bin and Dowlatabadi (2005) estimated that CO₂ emissions related to direct influences (emissions that occur while the product or service is in use, e.g., personal travel) are about 70% of those related to indirect influences (emissions that occur during the production and delivery of a product or service, e.g., transportation operation, food). Their results are partly based on the use of the Environmental Input-Output Life Cycle Analysis (EIO-LCA) model developed at Carnegie Mellon University (Hendrickson et al. 2006). The main implication of these studies is that both direct and indirect energy use have to be considered in the evaluation of the role played by consumers’ lifestyles on CO₂ emissions.

The literature that relies on economic input-output tables to analyze the impact of consumption on energy use and CO₂ emissions is extensive. However, little attention has been given to the role of specific demographic factors, such as population age structure. Dalton et al. (2008) offer a notable exception. They incorporated household age structure into a dynamic energy-economic growth model and estimated that population aging may reduce long-term CO₂ emissions in the United States.

In this article, I integrate the approaches developed in the two areas of IPAT-based modeling and environmental input-output analysis to evaluate the effect of changing population-age structure on CO₂ emissions in the United States. Methodologically, I first present a generalization of the IPAT equation to a multisector economy with an age-structured population, and I discuss the insights obtained in the context of stable population theory (e.g., Keyfitz and Caswell 2005). Second, I propose a statistical framework to calibrate the theoretical model. In particular, I suggest a model of household consumption as a function of household size and age structure. The model is used to evaluate the extent of economies of scale in consumption of energy-intensive goods and to estimate age-specific consumption profiles.

I look at age profiles of consumption from an individual, rather than a household, perspective. There are advantages and disadvantages to using either households or individuals as the unit of analysis. For instance, some household characteristics have been identified as key determinants of residential energy demand (e.g., O’Neill and Chen 2002; Schipper 1996; Schipper et al. 1989). In addition, household size may have important consequences on per-capita energy use because of the existence of economies of scale at the household level (e.g., Vringer and Blok 1995). On the other hand, within the framework that I propose, the choice of the individual makes it simpler to evaluate the effects of changes in age structure. It also potentially makes it easier to incorporate the work that I propose into the economic demography literature that explores the macroeconomic consequences of population aging, and whose unit of analysis is the individual (e.g., Lee 1994, 2000; Lee et al. 2006).

Empirically, I offer an illustration of the methodologies that I propose using data for the United States. I estimate the extent of economies of scale in consumption from cohabitation, for a set of energy-intensive goods, and I derive age-specific consumption profiles for the same goods. These results are then used to estimate an age-specific profile of emissions. They are also used as inputs for the theoretical model in order to evaluate expected variations in CO₂ emissions associated with changes in population growth and age structure.

The Theoretical Model

This section is dedicated to the formal discussion of the conceptual scheme that I propose to use to analyze the impact of demographic dynamics on CO₂ emissions.

First, I offer a generalization of the IPAT equation to a multisector economy with an age-structured population. The model is intended to capture the environmental consequences of changes in population age structure, mediated by levels of per-capita consumption, existing technology, and interrelationships between sectors of the economy.

Second, I formally analyze the effect of changes in mortality and fertility rates on the growth rate and age structure of a stable population, and the related consequences on CO₂ emissions. I show the analogies between the classical IPAT approach and its generalization, and I discuss the additional insights that can be gleaned from the latter.

A Generalization of the IPAT Equation

I propose a theoretical model that can be interpreted as a generalization of the IPAT equation to a multisector economy with an age-structured population. First, I provide a formal description of an input-output model for environmental analysis, using the notation of Hendrickson et al. (2006). Then, I introduce a demographic component (e.g., population age structure) to the model, and I discuss its role with reference to IPAT-based modeling.

Consider an economy with m sectors, indexed by i. The total monetary output for sector i, y _i , is written as

$$ {y_i} = {z_i}_1 + {z_i}_2 + ...{ } + {z_{im}} + {d_i}, $$

(2)

where z _ij is the monetary flow of goods from sector i to sector j, and d _i is the final demand for the good i. The model is typically rewritten to represent the flows between sectors as a percentage of sectoral output. Thus, if I write

$$ {q_{ij}} = \frac{{{z_{ij}}}}{{{y_j}}}, $$

the model is expressed as

$$ {y_i} = {q_{i1}}{y_1}+{q_{i2}}{y_2} + \ldots + {q_{im}}{y_m} + {d_i} $$

(3)

or, equivalently,

$$ - {q_{i1}}{y_1} - {q_i}_2{y_2} - \cdots + (1 - {q_{ii}}){y_i} - \cdots - {q_{im}}{y_m} = {d_i}. $$

(4)

By letting Q be the m × m matrix containing all the coefficients q _j , Y be the m × 1 vector containing all the output y _i terms, and D be the m × 1 vector of final demands d _i , the model is written in a more compact form as follows:

$$ {\left[ {{\mathbf{I}} - {\mathbf{Q}}} \right]}{\mathbf{Y}} = {\mathbf{D}}. $$

(5)

This way, given the vector of final demands and the matrix of coefficients Q, the vector of outputs by sector is obtained as

$$ {\mathbf{Y}} = {\left[ {{\mathbf{I}} - {\mathbf{Q}}} \right]}^{{ - 1}} {\mathbf{D}}. $$

(6)

Hendrickson et al. (2006) used this model to evaluate human environmental impact. In particular, they provided estimates for a set of coefficients that transform monetary economic output of each sector into environmental burdens. They used the phrase environmental burden to indicate a wide range of factors that affect the environment, such as toxic emissions, air pollution, and greenhouse gas emissions. Here, I use the expression environmental burden as a synonym for CO₂ emissions.

Let R be an m × m matrix with diagonal elements representing the impact per dollar of output for each stage of production, and let B be the m × 1 vector of environmental burdens for each production sector. Then,

$$ {\mathbf{B}} = {\mathbf{RY}} = {\mathbf{R}}{\left[ {{\mathbf{I}} - {\mathbf{Q}}} \right]}^{{ - 1}} {\mathbf{D}}. $$

(7)

I analyze the role of demographic factors within the conceptual framework described in Eq. 7. In particular, I represent the vector of final demands as the product of age-specific average consumption profiles and population size by age groups,

$$ {\mathbf{D}} = {\mathbf{CK}}, $$

(8)

where C is an m × s matrix whose row i represents the profile of average consumption by age group for the output produced in sector i. K is an s × 1 vector of population sizes for the s age groups considered.

By plugging Eq. 8 into Eq. 7, I obtain

$$ {\mathbf{B}} = {\mathbf{R}}{\left[ {{\mathbf{I}} - {\mathbf{Q}}} \right]}^{{ - 1}} {\mathbf{CK}}. $$

(9)

Equation 9 represents the model that I suggest to analyze the impact of demographic changes on environmental burdens. It is the core of my analysis, and it can be interpreted as a generalization of the IPAT equation, which states that environmental impact (I) is the product of population size (P), affluence (A), and technology (T):

$$ {\underbrace {\mathbf{B}}_{I}} = {\underbrace {{\mathbf{R}}{\left[ {{\mathbf{I}} - {\mathbf{Q}}} \right]}^{{ - 1}} }_{T}}{\underbrace {\mathbf{C}}_{A}}{\underbrace {\mathbf{K}}_{P}} $$

(10)

In the conceptual framework that I suggest, the vector B of environmental burdens corresponds to the scalar I in the IPAT equation. K has the role of P, the demographic factor. C represents the level of age-specific per-capita consumption and can be interpreted as the level of affluence, or A in the IPAT terminology. Finally, ${\mathbf{R}}{\left[ {{\mathbf{I}} - {\mathbf{Q}}} \right]}^{{ - 1}}$ is a product of terms that is intended to give a synthetic representation of the technology in use, the structure of the economy, the level of energy efficiency, the carbon intensity of the energy supply (i.e., types of fuels used in production or consumption), and so on. It has a role analogous to the one of the T term in the IPAT equation because it translates monetary value into units of environmental impact (e.g., metric tons of CO₂ emissions).

The model that I propose is a generalization of the IPAT equation to a multisector economy with an age-structured population. When we consider an economy with only one sector and ignore population age structure, the model reduces to the one depicted by the IPAT equation. In addition, the model differentiates consumption according to the sectors of the economy to which we can impute the production of final goods and thus generalizes the study of Waggoner and Ausubel (2002), who reconceptualized the IPAT identity in order to separate the leverage of “workers” from the one of “consumers.”

This article focuses on the role of population age structure, but the model represented in Eq. 10 is very general and can account for other types of demographic heterogeneity, such as urban-rural differences. This could be done by having the K column vector represent age-specific population sizes by urban and rural residency, one after the other. Then the component C will be a block matrix with age-specific profiles of consumption by residency. The term CK will give a vector of age-specific final demand for consumption goods by residency. This vector, when multiplied by an appropriate matrix of indicator variables, will generate a vector of overall demands of consumption goods.

The Leverage of a Change in Mortality and Fertility

In order to obtain insights on the effect of changes in mortality and fertility rates on CO₂ emissions, I consider the generalization of the IPAT equation within the framework of stable population theory (e.g., Keyfitz and Caswell 2005) and the Solow model of economic growth (Solow 1956). First, I discuss the insights that can be uncovered in the context of a traditional IPAT-based approach. Then, I extend the analysis to the generalization that I propose, and I discuss the additional insights.

The IPAT approach was originally introduced with the intention of refusing the notion that demography is only a minor contributor to environmental crises and with the goal of showing that population size and growth are relevant quantities in the explanation of environmental outcomes (Ehrlich and Holdren 1971). One of the major points in the IPAT literature is that population size (P) has a multiplicative role on environmental impacts (I). Several representations of the original IPAT identity have been suggested in the literature in order to make the approach operative for statistical analysis (e.g., Chertow 2001; Dietz and Rosa 1994, 1997). One way to look at IPAT-based models is to rearrange the terms in order to express the growth rate of CO₂ emissions in terms of population and income growth rates (e.g., Preston 1996; Zagheni and Billari 2007):

$$ \frac{{\mathop {I}\limits^\bullet }}{I} = \phi \frac{{\mathop {P}\limits^\bullet }}{P} + \varphi \frac{{\mathop {Y}\limits^\bullet }}{Y}, $$

(11)

where $\mathop {I}\limits^\bullet$, $\mathop {P}\limits^\bullet$, and $\mathop {Y}\limits^\bullet$ are, respectively, the first derivatives of CO₂ emissions, population size, and income with respect to time. ϕ and φ are parameters.

Assuming that the economy can be represented with a neoclassic model of economic growth, such as the Solow model, then in steady-state, the output growth rate ${\left( {{\mathop Y\limits^ \bullet }_{t} /Y_{t} } \right)}$ is determined by the rate of technological progress (g), the growth rate of the labor force (r), and a factor controlling for the extent of diminishing marginal returns to capital (α):

$$ \frac{{\mathop {Y}\limits^\bullet }}{Y} = \frac{g}{{1 - \alpha}} + r. $$

(12)

By plugging Eq. 12 into Eq. 11 and considering the case of a stable population, I obtain

$$ \frac{{\mathop {I}\limits^\bullet }}{I} = (\phi + \varphi )r + \varphi \frac{g}{{1 - \alpha}}. $$

(13)

Since I am considering a population with stable age structure, the population and labor force growth rate, r, can be linearly approximated to

$$ r \approx \frac{{\ln (NRR)}}{{{\alpha f}}}, $$

(14)

where NRR is the net reproduction ratio and a _f is the mean age at childbearing.

By plugging Eq. 14 into Eq. 13, and expressing the NRR in terms of its components, the growth rate of CO₂ emissions becomes

$$ \frac{{\mathop {I}\limits^\bullet }}{I} \approx (\phi + \varphi )\frac{{\ln (p({a_f}) \times F \times {f_{fab}})}}{{{a_f}}} + \varphi \frac{g}{{1 - a}}, $$

(15)

where F is the total fertility rate, f _fab is the fraction of females at birth, and p(a _f ) is the proportion of female births surviving to the mean age at childbearing.

Equation 15 explicitly links demographic factors—such as survivorship, fertility, and mean age at childbearing—to the growth rate of CO₂ emissions (or any other environmental burden considered). Thus, the leverage of each demographic factor on the growth rate of CO₂ emissions is isolated.

The formal discussion of the effect of changes of fertility and mortality schedules on the growth rate of a stable population is based on a long history of mathematical thought. Keyfitz and Caswell (2005) and Lee (1994) gave a very good summary of the main results in this context and discussed the study of the formal demography of aging. The approach described in Lee (1994) can be applied to this case to evaluate the effect of a change in mortality, indexed by i, on the growth rate of CO₂ emissions:

$$ \frac{{\partial ^{{{\mathop I\limits^ \bullet }}}_{{\overline{I} }} }}{{\partial {i} }} \approx {\left( {\phi + \varphi } \right)}\frac{{{\partial {p} {\left( {a_{f} } \right)}} \mathord{\left/ {\vphantom {{\partial _{p} {\left( {a_{f} } \right)}} {\partial {i} }}} \right. } {\partial _{i} }}}{{p{\left( {a_{f} } \right)} \times a_{f} }}. $$

(16)

Analogously, the effect of changes in fertility on the CO₂ growth rate can be isolated:

$$ \frac{{\partial \frac{{{\mathop I\limits^ \bullet }}} {I}}} {{\partial F}} \approx \frac{{{\left( {\phi + \varphi } \right)}}} {{F \times a_{f} }}. $$

(17)

Within the IPAT framework, the relevant demographic quantity for the explanation of CO₂ emissions growth rate is population growth rate. Improvements in mortality conditions tend to increase the growth rate of the population and CO₂ emissions. Increments in life expectancy of one year tend to have a smaller and smaller positive effect on population and CO₂ growth rates, the higher the initial level of life expectancy. Analogously, increases in fertility have a positive effect on population and CO₂ emission growth rates. The positive effect of a unit increase in the total fertility rate gets smaller and smaller the higher the starting level of the total fertility rate.

With the generalization of the IPAT equation that I propose, analogous analytical results can be obtained, based on the same set of assumptions and within the context of stable population theory and a neoclassical model of economic growth. In addition to that, with the model based on an age-structured population, one can evaluate the effect of changes in population age structure on environmental outcomes that are invisible to the classic analytical framework of the IPAT equation.

Population age structure plays an important role in the model of environmental burdens that I suggest. Given an age profile of average consumption for energy-intensive goods, population age structure determines the level of final demand for the consumption goods and, consequently, CO₂ emissions.

In a stable population, the effect of changes in fertility on population age structure is clear: higher fertility is associated with increasing size of more recently born cohorts, relative to older ones, and it thus makes the population younger. Conversely, the effect of mortality decline on population age structure is ambiguous. On the one hand, better survival probabilities tend to make the population older through individual aging. On the other hand, more women survive through childbearing age as a result of improved mortality conditions. This translates into more births and thus tends to make the population younger (see, e.g., Lee 1994). Depending on the initial level of life expectancy, improvements in mortality can make the population either younger or older.

Given a specific population growth rate and the associated age structure, the environmental outcome is strongly dependent on the age profile of consumption of energy-intensive goods and the amount of CO₂ emissions embedded in each of the consumption goods. The role of age structure and age-specific consumption profiles is not directly addressed in the classic IPAT formulation. In this article, I discuss the effect of changes in population age structure on CO₂ emissions, and I evaluate their importance.

Age-Specific Consumption of Energy-Intensive Goods

The effect of changing population age structure on CO₂ emissions has been discussed from a theoretical point of view so far. The model presented in Eq. 9 can also be calibrated to a specific context or country, such as the United States. Several data sources are necessary to estimate key input quantities, such as consumption profiles, input-output tables, and CO₂ coefficients for production sectors and consumption goods. Most of these quantities have been estimated for the United States and are already available in the literature (e.g., Bin and Dowlatabadi 2005; EIO-LCA 2009; EIA 2009a; Hendrickson et al. 2006). The main component that is missing is a set of age-specific consumption profiles for energy-intensive goods. In this section, I discuss the empirical strategy that I propose, I show some estimates of consumption profiles, and I discuss their relevance.

Data

The empirical analysis focuses on the United States and is based on data from the Consumer Expenditure Survey (CES) 2003, provided by the Bureau of Labor Statistics of the U.S. Department of Labor. CES is a nationally representative survey that provides data on household expenditures for several consumption goods and services in the United States. Demographic and economic data for household units are also gathered. The data are collected in independent quarterly interviews and weekly diary surveys of approximately 7,000 sample households. Each survey has its own independent sample and collects data on household income and socioeconomic characteristics. The interview survey includes monthly out-of-pocket expenditures such as housing, apparel, transportation, health care, insurance, and entertainment. The diary survey includes weekly expenditures of frequently purchased items such as food and beverages, tobacco, personal care products, and nonprescription drugs and supplies. The two data sources are then integrated into one data set.

Empirical Strategy to Estimate Consumption Profiles by Age

Given data on household expenditures on several consumption goods, a first goal is to assign to each member of the household his or her own share of consumption (in monetary terms). I also would like to estimate the extent of economies of scale and to separate the income effects from purely demographic effects.

In the literature, Mankiw and Weil (1989) faced a similar problem in the context of modeling demand for housing: they suggested modeling household consumption of goods and services as an additive function of the consumption of its members. In what follows, I first discuss the Mankiw and Weil approach applied to this case. Then I propose a new method, based on the use of an equivalence scale, to quantitatively evaluate the extent of economies of scale in consumption from cohabitation.

Let c _ij be the consumption of good i by household j, in monetary terms. Then,

$$ {c_{ij}} = \sum\limits_{k = 1}^M {{c_{ijk}},} $$

(18)

where c _ijk is the demand of the kth member, and M is the total number of people in the household.

The consumption of the good i for each individual is a function of age: each age has its own consumption parameter, so that an individual demand is given by

$$ {c_{ijk}} = {\beta_0}Ind{(0)_k} + {\beta_1}Ind{(1)_k} + \cdots + {\beta_{80}}Ind{(80)_k}, $$

(19)

where

$$ Ind{(h)_k} = \left\{ {\begin{array}{*{20}{c}} {1\,{\hbox{if}}\,{\hbox{age}}\,{\hbox{of}}\,{\hbox{member}}\,{{k}}\,{\hbox{is}}\,{\hbox{equal}}\,{\hbox{to}}\,h} \\{0\,{\hbox{otherwise}}} \\\end{array} .} \right. $$

The parameter β _h is the demand for consumption by a person of age h. Combining Eq. 18 with Eq. 19, the equation for consumption of good i by household j becomes

$$ {c_{ij}} = \beta \sum\limits_k {Ind{{(0)}_k} + {\beta_1}\sum\limits_k {Ind{{(1)}_k}} + \cdots + {\beta_{80}}\sum\limits_k {Ind{{(80)}_k}.} } $$

(20)

The parameters of Eq. 20 are estimated by using the least squares technique. After appropriately smoothing (see, e.g., Friedman 1984) the sequence of estimated parameters over age, an age profile of demand for consumption of good i is calculated. This age-specific schedule of consumption can be interpreted as the impact of an additional person of a particular age on expenditure on a specific good. To separate the effect of age from the one of income, one can apply the same method to fraction of household expenditures instead of overall consumption.

To the extent that there are not economies of scale in household consumption (or they are negligible) and to the extent that household formation is fairly constant, this approach is fairly accurate (Mankiw and Weil 1989). However, economies of scale may be relevant in the current case, and I want to be able to evaluate them with a statistical model and to estimate consumption profiles by age accordingly.

I address the problem of evaluating the importance of economies of scale by suggesting a parametric equivalence scale that takes into account that children consume less than adults and that living arrangements with more than one person may be more efficient. In what follows, I present the model that I suggest and the strategy that I propose to estimate the parameters and the consumption profiles.

Let n _cj , n _aj , and n _ej be, respectively, the number of children, adults, and elderly who live in household j, where children are defined as those people 14 years old and younger, adults are those between 15 and 64 years, and the elderly are those 65 and older. Let S _ia and S _ie be, respectively, the average consumption of good i by adults and elderly who live alone. An equivalence scale, then, could be written as

$$ {c_{ij}} = {({n_{cj}}{\gamma_i}{S_{ia}} + {n_{aj}}{S_{ia}} + {n_{ej}}{S_{ie}})^{{\theta_i}}} + {\varepsilon_j}, $$

(21)

where γ _i is a parameter that represents the relative consumption of children, with respect to adults, within households. γ _i = 0 means that only adults are considered responsible for the consumption of good i; γ _i = 1 means that no distinction is made between adults and children in terms of consumption of good i. θ _i is a parameter that represents the extent of economies of scale from cohabitation for good i. θ _i < 1 means that cohabitation generates economies of scale; θ _i > 1 means that cohabitation generates diseconomies of scale. ε _j is an error term.

The equivalence scale in Eq. 21 is a nonlinear model. I estimate the parameters γ _i and θ _i for the different consumption goods by using the least squares technique. Given the estimated values for S _ia and S _ie , I choose the pair (${\hat \gamma_i}$, ${\hat \theta_i}$) such that

$$ ({\hat \gamma_i},{\hat \theta_i}) = {\hbox{argmi}}{{\hbox{n}}_{{{\hat \gamma }_i},\hat \theta_{i} }}\sum\limits_j {{{({c_{ij}} - {{({n_{cj}}{\gamma_i}{S_{ia}} + {n_{aj}}{S_{ia}} + {n_{ej}}{S_{ie}})}^{{\theta_i}}})}^2}} . $$

(22)

Once estimates for the couple of parameters (${\widehat \gamma_i}$, ${\hat \theta_i}$) have been produced, a consumption profile by age based on the equivalence scale needs to be reconstructed. In what follows, I explain the strategy that I suggest. An extra parameter ψ _i needs to be estimated, representing the relative consumption of good i by the elderly, with respect to adults, within household j. This parameter is estimated as the mean relative consumption for the good i in the population of single-person households, that is, ${\hat \psi_i} = \frac{{{S_{ie}}}}{{{S_{ia}}}}$. Then the equivalence scale becomes

$$ {c_{ij}} = {({n_{cj}}{\hat \gamma_i}con{s_{ij}} + {n_{aj}}con{s_{ij}} + {n_{ej}}{\hat \psi_i}con{s_{ij}})^{{{\hat \theta }_i}}}, $$

(23)

where cons _ij is the average consumption of good i by an adult in household j. It can be retrieved as

$$ cons_{{ij}} = \frac{{c^{{{\left( {1/\widehat{\theta }_{i} } \right)}}}_{{ij}} }} {{n_{{cj}} \widehat{\gamma }_{i} + n_{{aj}} + n_{{ej}} \widehat{{\psi _{i} }}}}. $$

(24)

For household j, the average consumption of a child will be $con{s_{ij}}{\hat \gamma_i}$, and the average consumption of an elderly person will be $con{s_{ij}}{\hat \psi_i}$. These two quantities represent the shares of consumption for the good i of children and elderly, respectively.

By applying the same procedures to all households in the data set, consumption by age for the goods considered can be estimated. The average consumption profile by age is then obtained by taking the mean of these values by age and appropriately smoothing them by age (e.g., Friedman 1984).

Age-Specific Consumption Profiles

Following the presentation of the methods to estimate individual consumption profiles by age, I present some estimates for a selected group of energy-intensive goods in the United States. The estimated profiles show the role of a crucial demographic variable, age, on consumption of a set of goods that have a relevant impact on CO₂ emissions.

I analyze consumption patterns for a set of goods for which data are available through the CES and for which embedded CO₂ emissions are among the highest (see, e.g., Bin and Dowlatabadi 2005). The empirical analysis is not intended to provide an exhaustive account of all consumption categories in the economy and the associated CO₂ emissions. It should be thought of as an illustration of the methodology that I presented in the previous sections on a specific set of consumption goods. However, such goods, although not representative of the whole economy, have been chosen according to their importance in terms of CO₂ emissions and provide a general picture of the overall trend in CO₂ emissions for the United States.

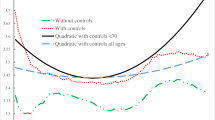
Figure 1 shows estimates of age-specific demand for electricity, natural gas, gasoline, air flights, tobacco products, clothes, food, cars (including maintenance), and furniture. These estimates are obtained by using the method suggested by Mankiw and Weil (1989), and they give the impact on demand of a specific good associated to the presence of an additional person, by age. Estimated values can be negative in some circumstances, meaning that the presence of a person of a particular age tends to reduce the household demand for the good. For instance, the presence of children in a household may have a negative impact on the number of cigarettes smoked by adults or the amount of money spent on air flights.

Fig. 1

U.S. profiles of age-specific demand for consumption of a selected group of energy-intensive goods. Estimates are based on the approach suggested by Mankiw and Weil (1989). Data are from the Consumer Expenditure Survey, 2003

As Fig. 1 shows, demand for the selected group of consumption goods tends to increase with age until the person reaches the adult life stage. For some goods, such as electricity and natural gas, demand increases with age also for the elderly. For other goods, such as gasoline, air flights, tobacco, clothes, cars, and furniture, demand declines with age after the adult life stage. Finally, expenditure on food tends to be fairly constant in the adult and old-age stages of life. The observed life cycle consumption patterns may be related to specific preferences and characteristics that vary over the life course. For instance, the ability and willingness to drive is strongly associated with age and may mediate the relationship between age and demand for gasoline. In addition, cohort effects may play a role in shaping the demand by age. For instance, the decrease in demand for gasoline and vehicles at older ages may be partially related to the specific circumstances experienced by older generations.

Some of the trends in age-specific demand for consumption goods may be driven by levels of income by age. To separate the income effect from the demographic effect on demand for consumption goods, I apply Mankiw and Weil’s (1989) method on fractions of household expenditures. Figure 2 shows the estimated age-specific profiles of demand for the selected good, net of the income effect. Several changes in the age-specific profiles of consumption can be observed when the income effect is controlled. The profiles of fraction of expenditure on electricity, natural gas, and food at old ages are steeper than the respective profiles of absolute consumption. The opposite is true for gasoline, clothes, cars, and furniture, for which the profiles of fraction of expenditure at old ages are rather flat compared with the estimated profiles of absolute consumption, which tend to decline fairly rapidly at old ages. The profiles of consumption and fraction of expenditures are rather similar for goods such as air flights and tobacco. These observations are potentially relevant for understanding implications of changing levels of wealth for the elderly on their consumption of energy-intensive goods.

Fig. 2

U.S. profiles of age-specific demand for consumption of a selected group of energy-intensive goods, net of the income effect. Estimates are based on the approach suggested by Mankiw and Weil (1989) applied to fractions of household expenditures. Data are from the Consumer Expenditure Survey, 2003

Figure 3 shows estimates of age-specific consumption profiles obtained using the equivalence scale approach that I suggest. These estimated profiles are qualitatively consistent with the ones obtained using the Mankiw and Weil (1989) approach. They are also consistent with the results obtained by O’Neill and Chen (2002) using a different set of data and methods. As a matter of fact, O’Neill and Chen estimated that residential energy use rises with the age of the householder, whereas transportation energy use rises to a peak, when the householder is in his early 50s, and then falls to low levels at the oldest ages. In O’Neill and Chen (2002), the unit of analysis is the household. Here, I complement their work by estimating profiles for individuals and by quantitatively evaluating the extent of economies of scale in consumption that arise from cohabitation.

Fig. 3

U.S. annual average expenditure by age for a selected group of energy-intensive goods. Estimates are obtained using the equivalence scale approach. Data are from the Consumer Expenditure Survey, 2003

Table 1 gives the estimated average consumption of the selected goods for adults living alone, S _a , and for elderly living alone, S _e . Among the consumption goods considered, expenditures on food and cars are the most relevant ones, in monetary terms, for the household budget. Table 2 gives the least-squares estimates for the parameters of the equivalence scales for the selected consumption goods, together with the 95% bootstrap confidence intervals (Efron and Tibshirani 1993; Huet et al. 2003; Seber and Wild 1989). The estimated parameters show that economies of scale are noticeable for most of the selected consumption goods. The extent of economies of scale is largest for consumption of natural gas. There are slight diseconomies of scale for expenditures on gasoline, cars, and furniture. The presence of children in the household does not have a sizable impact on consumption of gasoline, air flights, tobacco, cars, or furniture. Conversely, children have a noticeable impact on household expenditures on electricity, natural gas, food, and clothes.

Table 1 Average expenditure on selected energy-intensive consumption goods for adults living alone, S _a , and for elderly living alone, S _e , in the United States

Table 2 Estimates of the parameters of the equivalence scale for a selected group of energy-intensive consumption goods

Comparative Statics of Changing Population Age Structure

In this section, I evaluate the effect of changes in population age structure on overall levels of consumption of energy-intensive goods and the related CO₂ emissions. This analysis is an empirical application of the theoretical model expressed in Eq. 9 and focuses on past and future demographic trends in the United States. In summary, CO₂ emissions are expressed as a product of distinct components. The demographic component is represented as a vector of population size by age group. By multiplying the population vector by a matrix containing age-specific profiles of per-capita consumption for different goods, I obtain the final demand for the consumption goods considered. A set of coefficients then transform monetary demand for goods into CO₂ emissions. The coefficients account for both the direct and indirect influences of consumer activities on CO₂ emissions. Changes in population age structure affect the overall level of consumption and, therefore, CO₂ emissions.

Age-Specific Profile of CO₂ Emissions

I estimated and discussed monetary age-specific profiles of consumption for a set of relevant goods in a previous section. In order to carry out a comparative statics analysis of the effect of changes in population age structure on CO₂ emissions, I need a set of coefficients that transforms final demand of goods into CO₂ emissions. For this purpose, I follow the approach of Bin and Dowlatabadi (2005). In particular, I use the Environmental Input-Output Life Cycle Analysis model (EIO-LCA 2009; Hendrickson et al. 2006) to estimate the indirect consequences of consumption (i.e., CO₂ emissions that occur during the production and delivery of a product or service, and before its use). As for direct consequences of consumption (i.e., CO₂ emissions that occur while the product or service is in use), I use the coefficients reported by the Energy Information Administration (EIA 2009a). Such coefficients are necessary to account for emissions associated with the use phase of gasoline and natural gas, since the EIO-LCA model accounts only for emissions embedded in the production of consumption goods but not for emissions associated with the burning of such fuels when in use. Figure 4 shows estimated CO₂ intensity for the set of consumption goods under consideration. The estimates, obtained by combining information from EIO-LCA (2009) and EIA (2009a), account for both direct and indirect consequences of consumption. Consistent with the work of Bin and Dowlatabadi (2005), I observe that the most CO₂-intensive consumer activities are related to consumption of utilities and personal travel. It is also interesting to note the very high CO₂ intensity of electricity consumption, which is related to the fact that most fossil energy used to produce electricity is lost in production, transmission, and distribution.

Fig. 4

Estimated CO₂ intensity for the set of consumption goods considered in the empirical analysis. Estimates account for both direct and indirect consequences of consumption. Data are from the EIO-LCA (2009) and EIA (2009a)

CO₂ intensities can be thought of as weights that apply to the consumption goods considered. Profiles of consumption for single goods can thus be aggregated to estimate a profile of per-capita CO₂ emissions by age. Figure 5 shows the estimated age-specific profile of per-capita CO₂ emissions. Observe that, for the set of goods considered, average emissions increase with age until the person is in his or her late 60s; then, per-capita emissions decrease with age.

Fig. 5

Estimated profile of per-capita CO₂ emissions by age, based on the set of goods considered in the analysis

The estimation of an age-specific profile of CO₂ emissions is a relevant and novel empirical result of this article. Such a profile differs from the typical age patterns of overall consumption and production. The shape of the CO₂ emissions profile depends on demographic factors as well as the technology in use and the structure of the economy. It is an informative result for the analysis of the individual life cycle of CO₂ emissions and for the effect of macro-demographic changes on emissions.

The Leverage of Changing Population Age Structure on CO₂ Emissions

Given an age-specific profile of CO₂ emissions, changes in population age structure potentially have relevant implications on overall levels of emissions. I first look at historical demographic trends in the United States to evaluate the effect of improvements in mortality on population age structure and CO₂ emissions. I then look at population forecasts to assess the leverage of expected changes in population size and age structure on future CO₂ emissions.

To gain insights on the effect of improvements in mortality on CO₂ emissions, I propose a comparative statics analysis for populations in a stable state. I consider two stable populations with the same age-specific fertility rates but different age-specific mortality rates. By constructing the Leslie matrices for the two populations and by projecting the two populations over a long period of time, I obtain the stable age structures associated to the two sets of vital rates. I can thus evaluate how the stable age distribution will change when mortality levels change.

For instance, one may want to know how the stable age distribution for the United States would change if the current levels of mortality were identical to those of the 1930s. I consider the population of the United States in 2001 and in 1933: I use the female life tables provided by the Human Mortality Database and the fertility rates provided by the U.S. Census Bureau to construct a Leslie matrix based on the vital rates of 2001 and a Leslie matrix based on fertility rates of 2001 and mortality rates of 1933. The two Leslie matrices lead to the stable age structures shown in Fig. 6: the two profiles show the impact of an increase in life expectancy at birth of 16.7 years, from a starting value of 63.02 years to a value of 79.68, given the U.S. age-specific fertility rates of 2001.

Fig. 6

Stable age structures resulting from the projection over the long run of populations with the fertility rates of the United States in 2001, and the mortality rates of the United States in 1933 and 2001. Data are from the Human Mortality Database and U.S. Census Bureau

Figure 6 shows the net effect of an improvement in mortality on the age structure, independent of its growth rate effect. Given the estimates of consumption profiles based on the equivalence scale, I can use comparative statistics. Table 3 shows the estimated effect of increasing life expectancy by one year on percentage change of consumption for the goods considered and the associated absolute change in CO₂ emissions, given a fixed population size of 300 million people. I observe that an increase in life expectancy, from about 63 years to about 80 years, is associated with positive changes in consumption of electricity, natural gas, air flights, and food, whereas the change in consumption is negative for gasoline, tobacco, clothes, cars, and furniture. This is consistent with the results of O’Neill and Chen (2002), who estimated that a 1% increase in the fraction of the population living with householders aged 65 or older generates a 0.03% increase in residential energy use and a 0.06% decrease in transportation energy use. Except for gasoline, whose consumption is expected to slightly decline with increases in life expectancy, consumption for the most CO₂-intensive goods increases with improvements in life expectancy. If we consider a population of 300 million people (i.e., of the magnitude of the population of the United States), the overall increase in CO₂ emissions associated with a year of gained life expectancy is estimated to be about 4.5 million metric tons. Such amount, although fairly large in absolute terms, is small in relative terms, since over the period 1990–2008, CO₂ emissions in the United States have increased at a pace of about 240 million metric tons per year of gained life expectancy (EIA 2009b and Human Mortality Database 2010). However, since the year 2000, the level of CO₂ emissions in the United States has been fairly stable, with an estimated value of 5,844 million metric tons in 2000, a peak of 5,972 in 2005, and a decline to 5,802 million metric tons in 2008 (EIA 2009b).

Table 3 Estimated effect of increasing life expectancy by one year on percentage change in consumption for the goods considered, and associated absolute change in CO₂ emissions (in metric tons), given a fixed population size of 300 million people

Population forecasts for the United States allow the calculation of some comparative statics to evaluate the effect on CO₂ emissions of expected changes in population size and age structure over the next decades, all other factors held constant. I use population forecasts for the United States, provided by the U.S. Census Bureau, for the period 2007–2050. Table 4 shows the estimated annual percentage change in the consumption of goods, and the associated level of CO₂ emissions, for that period. The composite effect of changes in population size and age structure, as well as the effect of changes only in population age structure, are evaluated. Considering the joint effect of population size and age structure, the consumption of all goods is expected to increase. The average annual percentage change for the goods considered is in the range of 0.76% to 1.02%. Given the differences in CO₂ intensity of the consumption goods, electricity, gasoline, natural gas, and food account for most of the expected average annual change in CO₂ emissions, which is estimated to be about 32 million metric tons. When I consider only the effect of population age structure, I observe that the overall average annual percentage change in consumption is slightly negative. However, increases are expected in consumption for the most CO₂-intensive goods except for gasoline. Electricity and natural gas consumption are expected to increase by about 0.1% per year, whereas consumption of gasoline is expected to decrease by 0.05% per year due to changes in age structure. This is consistent with the results of O’Neill and Chen (2002), who projected an age-driven percentage change in residential energy consumption of between +2% and +5% for the period 2000–2050. They also projected an age-driven percentage change in transportation energy consumption of between –1% and 0% for the same period. The expected increase in consumption of the most CO₂-intensive goods, due to changes in population age structure, leads to an average annual estimated increase in CO₂ emissions of about 1 million metric tons.

Table 4 Estimated average annual percentage change in consumption of the goods considered, and the associated absolute change in CO₂ emissions (in metric tons), for the period 2007–2050

The comparative statics exercise gives a general idea of the importance of a demographic factor, such as age distribution, in the explanation of energy requirements and CO₂ emissions of an economy like the United States’. The impact of changing age distribution is fairly small in relative terms, considering that, in the United States, the estimated annual CO₂ emissions are in the order of 5,800 million metric tons and that large gains in terms of life expectancy may occur over a rather long period of time. However, the impact of changing age distribution is relevant in absolute terms, and particularly noticeable, considering that the level of emissions in the United States has been fairly stable over the past few years.

Discussion

In this article, I discuss the effect of changing population age structure on CO₂ emissions. Methodologically, I first proposed a generalization of the well-known IPAT equation to account for the role of population age structure and interrelationships between sectors of the economy. Second, I developed a statistical model to estimate the extent of economies of scale in consumption that arise from cohabitation. Third, I suggested a technique to estimate age-specific consumption profiles from data on household expenditure and household composition. Empirically, I offered an application of the methods, based on a set of CO₂-intensive goods for the United States. I found that per-capita CO₂ emissions increase with age until the individual is in his or her 60s. Then, per-capita CO₂ emissions tend to decline. Improvements in life expectancy and low levels of fertility shift the distribution of person-years lived toward old ages. An exercise of comparative statics shows that this process has a positive, although rather small, effect on CO₂ emissions in the next few decades. In the longer term, when the proportion of person-years lived at very old ages increases, the effect may become negative, given the estimated age-specific profile of CO₂ emissions.

The empirical analysis performed in the paper mainly serves as an illustration of the methodological contribution and does not represent a comprehensive account of all consumption goods in the economy. However, the goods have been chosen based on their relevance in terms of CO₂ emissions and account for a large part of CO₂ emissions in the United States, making the results fairly general. The proposed model and empirical analysis provide a systematization of previous IPAT-based studies that evaluate the effect of population age composition and economic structure on CO₂ emissions (e.g., Dietz and Rosa 1994; Fan et al. 2006; Mackellar et al. 1995; Shi 2003). The previous IPAT-based literature on the topic relied on simple measures of age composition and economic structure and did not come to conclusive evidence on their effect on CO₂ emissions. This study provides a more articulated framework to interpret previous IPAT-based literature and to further develop analytic tools and empirical strategies to evaluate the relationships between demographic dynamics and CO₂ emissions. The empirical results seem to confirm the recent findings of Fan et al. (2006) that the effect of population age composition is related to the economic structure of the economy, and that, in high-income countries, aging has a positive effect on CO₂ emissions, at least in the relatively short term.

The estimated age-specific consumption profiles show a pattern of residential energy use consistent with the one estimated by O’Neill and Chen (2002) for the life cycle of households. The effect of changing population age structure on CO₂ emissions has also been evaluated in literature that relies on energy-economic growth models. The benchmark study in this area of research is given by Dalton et al. (2008). They used a general equilibrium model with multiple dynasties of heterogeneous households, calibrated with input-output data, to evaluate the effect of aging on CO₂ emissions in the United States. The model that they proposed can be thought of, to a certain extent, as a dynamic version of the static model that I suggest in this article. They found that population aging reduces long-term emissions. The effect of aging on per-capita emissions is not apparent until after 2050 because of population momentum. In the Dalton et al. model, the most relevant impacts of aging are caused by differentials in labor income across age groups, which generate complex dynamics for consumption and savings. Their results are driven mainly by the crucial assumption that per-capita labor force participation is fixed over time. Population aging and the scarcity of young workers then cause a downward trend in per-capita labor income for dynasties, with relevant consequences on per-capita consumption and CO₂ emissions. The assumption is fairly strong, since it is likely that people in the older age groups will increase their labor force participation, both because of improved health conditions at older ages and because of pressures on the pension system that will translate into increases in the age at retirement or in the number of hours worked. In this article, I implicitly assume that estimated consumption profiles are sustainable and that the economy will adjust to population aging through changes in labor force participation or the number of hours worked. Relaxing the assumption of fixed labor force participation in Dalton et al. (2008) would likely reduce the difference between their projections for the relatively short term and the results that I present. In the long term, the reduction in CO₂ emissions due to aging, suggested by Dalton et al. (2008), is consistent with the age-specific profile of CO₂ emissions that I estimate and that implies a decrease in CO₂ emissions at very old ages. There are indications that consumption of energy-intensive goods keeps decreasing at very old ages, although estimates of consumption profiles past age 80 may be highly stochastic due to reduced sample sizes. If that is the case, in a scenario of rapid population aging, changing population age structure may have a substantial negative effect on CO₂ emissions, as Dalton et al. (2008) have suggested.

There are several different ways societies can finance consumption by the elderly, with important consequences on macroeconomic quantities and CO₂ emissions (see, e.g., O’Neill et al. 2001). In an aging society, current workers may reduce their consumption or work longer to transfer resources to the elderly, either through familial transfers or a PAYGO system. Alternatively, current workers may save in order to finance their retirement (e.g., through a pre-funded pension system). Different choices have different consequences on macroeconomic quantities, such as saving rates, and ultimately affect the growth rate of economic output. Research on these issues is central to the field of economic demography, and results from this discipline are relevant for our purposes. A significant set of studies focuses on the relationships between economy and demography in golden rule steady states, under several different assumptions (e.g., Cutler et al. 1990; Diamond 1965; Lee 1994; Willis 1988). Population aging may generate lower aggregate saving rates but, at the same time, may cause increased capital per worker and higher consumption (Cutler et al. 1990), which would translate into higher levels of emissions. Lee (1994) has shown that population aging may increase or decrease levels of life cycle consumption across golden rule steady states, depending on whether transfers to children or to the elderly dominate.

It is beyond the scope of this article to discuss in detail the literature on the economic consequences of population aging. However, I would like to make an important observation about the unit of analysis. A large body of literature in the field of economic demography relies on representations of the individual economic life cycle. Although constructing consumption profiles that vary with the age of the household head is simpler, given that data are usually collected at the household level, it is not straightforward to translate changes in population age structure into changes in the age structure of household heads and household memberships. Moreover, an accounting based on households would not reveal transfers within households, which represent an important share of societal redistribution of resources (Lee et al. 2006). The approach that I suggest in this article relies on the estimation of consumption profiles for individuals. It complements previous works that use households as the unit of analysis and opens possibilities to bridge the gap between the literatures on the demographic determinants of CO₂ emissions and the economic consequences of population aging and intergenerational transfers.

The interpretation of the empirical results that I present is quite focused. The idea is to evaluate the effect of changes in population age structure on CO₂ emissions, holding all other things constant. This demographic exercise provides important insights on the life cycle profile of CO₂ emissions. However, it is important to be aware that several demographic and economic variables are directly or indirectly affected by changes in population age structure. The estimated consumption profiles are not fixed over time. Instead, they evolve for several reasons, including changes in age structure. Population aging is associated with a fairly large increase in the number of households and a reduction in the average household size, which potentially influence age-specific consumption profiles.

Population aging also affects productivity. For instance, old workers may be more experienced and productive than younger ones. Conversely, it is possible that young workers are more dynamic and productive. Depending on which effect is stronger, productivity may increase or decrease with age, with consequences on economic growth and consumption patterns. My estimates of consumption profiles are based on cross-sectional data and are influenced by the pace of economic growth. Rapid economic growth raises the income of young people, relative to the elderly, and makes longitudinal profiles of consumption steeper than the ones estimated from cross-sectional data.

Technology is an important variable in the explanation of CO₂ emissions. The approach used in this article is based on a static representation of technology (e.g., the input-output model). However, technical change may play a key role in the future. For instance, reducing the CO₂ intensity of electricity may counteract the effect of increasing consumption due to population aging. On the other hand, international trade may shift the production of certain goods to countries where the technology in use is more energy-intensive, thus leading to an overall increase in CO₂ emissions which is not captured by input-output tables that do not account for trade.

In this article, I focus on the United States and formalize the intuition that observed patterns of energy use in developed countries imply that population aging may have a positive impact on CO₂ emissions (e.g., Haq et al. 2007). I also offer insights for a country like China, one of the main contributors to global CO₂ emissions. In China, the process of population aging is extremely fast and is likely to have a significant impact on CO₂ emissions. In particular, population aging comes together with rapid economic growth, which will likely increase the overall level of consumption and will make the age-specific profiles increase more steeply with age. Changes in age structure potentially have large consequences in developing countries and, more generally, on global CO₂ emissions. In the context of a developing country, however, it is important to consider the process of aging and reduction in household size together with urbanization. As a matter of fact, the processes of economic development and urbanization is expected to drive CO₂ emissions in countries like China and India (Dalton et al. 2007) and need further consideration for estimation and prediction of global CO₂ emissions.

Further research must be pursued in order to inform official forecasts for CO₂ emissions with an improved understanding of the role of demographic dynamics. In particular, I think that interdisciplinary work to bring together different areas of expertise will be central to improving our understanding of the impact of population dynamics on CO₂ emissions in both developed and developing countries.