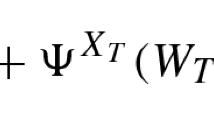Abstract
We present a model of discrete-time mean-field game with compact state and action spaces and average reward. Under some strong ergodicity assumption, we show it possesses a stationary mean-field equilibrium. We present an example showing that in general an equilibrium for this game may not be a good approximation of Nash equilibria of the n-person stochastic game counterparts of the mean-field game for large n. Finally, we identify two cases when the approximation is good.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mean-field game theory has been developed independently by Lasry and Lions [39] and by Huang et al. [37] to study non-cooperative differential games with a large number of identical players. The main idea behind their models was that by approximating the game with a limit where the number of players is infinite, we can reduce the game problem, which for a large finite number of players becomes untractable, to a much simpler single-agent decision problem. The idea has been largely accepted by the differential game community, which resulted in a huge number of publications on the topic over the last decade. The reader interested in differential-type mean-field game models discussed so far is referred to the books [8, 21] or the survey [32].
Our focus in this paper is, however, on similar discrete-time models, which, surprisingly, appeared in the game-theoretic literature long before the pioneering works on mean-field games. In the seminal paper by Jovanovic and Rosenthal [38], each player controls an individual discrete-time Markov chain, while the global state of the game, defined as the probability distribution over individual states of all the players, becomes deterministic. While the tools used there were significantly different from those considered in differential mean-field game literature, the general principle, which was to simplify the original large game problem by considering an approximation with one-agent optimization models, stayed the same. Some generalizations of model of Jovanovic and Rosenthal were given in [2, 9, 10, 22, 27, 45]. All of these papers considered games with discounted rewards (costs). Discounted discrete-time mean-field games were also studied in a number of economic applications, see references in [2].
Our paper deals with a different reward criterion—long-run average reward (sometimes also called ergodic reward), often used in Markov decision process and dynamic game problems, yet hardly present in the discrete-time mean-field game literature. To the best of our knowledge, there are only three papers dealing with this kind of problems in a discrete-time setting, discussed in more detail below. The literature on differential-type mean-field games with this payoff criterion is a lot more extensive. In [28, 39], results about relation between games with a large finite number of players and mean-field games of this type are proved. [18,19,20] discuss the relation between the solutions of ergodic mean-field games and mean-field games with large fixed time horizon. Existence and uniqueness of solutions to average-reward mean-field games are addressed in many articles including [5,6,7, 23,24,25, 30, 31, 39, 40, 42] and a number of preprints. Finally, [1, 4, 15] provide some numerical methods for solving this type of games. The first model of discrete-time mean-field game with average reward has been introduced in [48], where the existence of a stationary mean-field equilibrium has been proved under some ergodicity assumption in case when state and action spaces of the players are finite. Under the additional assumption that the individual transitions of the players do not depend on the empirical distribution of states or actions of all the players, it also shows that the mean-field model approximates well the n-person models for n large enough. Similar assumption has also been made in [12], where average-reward games with \(\sigma \)-compact Polish individual state spaces were studied. The problem is that apart from this assumption, the results in [12] used some strong regularity conditions stated in terms of a specific metric topology on the state of stationary policies, which seem to be too strong to be satisfied under any reasonable assumptions. In the last paper, we need to mention here [16] average-reward discrete-time mean-field games were used to study a dynamic routing model. The main contribution of the paper was presenting a linear-programming formulation of the problem of finding a stationary equilibrium in games of this type.
In our paper, we do not consider such a general setting as that in [12], limiting ourselves to the games with compact state and action spaces. In return, within this framework we make assumptions that are satisfied by a large class of models. Moreover, we state them in terms of basic primitives of the model, making them rather easy to verify. Finally, in general we do not require the independence of the individual transitions from the empirical distribution of states and actions of the players. In our article, we give the results of two types. First, under the assumptions given in Sect. 3, we show that the mean-field game has a stationary equilibrium. Then, we provide several results, both positive and negative, linking equilibria in the model with a continuum of players with \(\varepsilon \)-equilibria in its n-person stochastic counterparts when n is large.
The organization of the paper is as follows: In Sect. 2, we present the general framework we are going to work with and define what kind of solutions we will be looking for. In Sect. 3, we present our assumptions. Sections 4 and 5 provide our main results—in Sect. 4 we prove the existence of the stationary equilibrium in the mean-field game model, while in Sect. 5 we give results linking equilibria in the mean-field game with approximate equilibria in games with large finite number of players. We end the paper with conclusions in Sect. 6.
2 The Model
2.1 Discrete-Time Mean-Field Games
A discrete-time mean-field game is described by the following objects:
We assume that the game is played in discrete time, that is, \(t\in \{ 1,2,\ldots \}\).
The game is played by an infinite number (continuum) of players. Each player has a private state\(s\in S\), changing over time. We assume that the set of individual states S is the same for each player and that it is a non-empty compact metric space. Private state of player i at time t is denoted by \(s^i_t\). If we refer to an arbitrary player, we skip the superscript i.
A probability distribution \(\mu \) over Borel setsFootnote 1 of S is called a global state of the game. It describes the proportion of the population which is in each of the individual states. Global state at time t will be denoted by \(\mu _t\). We assume that at every stage of the game, each player knows both his private state and the global state, and that his knowledge about individual states of his opponents is limited to the global state.
The set of actions available to any player in state \((s,\mu )\) is given by \(A(s,\mu )\), with \(A:=\bigcup _{(s,\mu )\in S\times \Delta (S)}A(s,\mu )\)—a compact metric space. \(A(\cdot ,\cdot )\) is a non-empty valued correspondence.
The global distribution of the state–action pairs is denoted by \(\tau \in \Delta (S\times A)\). If we refer to the global state–action distribution at a specific time t, we write \(\tau ^t\).
Individual’s immediate reward is given by a bounded measurable function \(r:S\times A\times \Delta (S\times A)\rightarrow \mathbb {R}\). \(r(s,a,\tau )\) gives the reward of a player at any stage of the game when his private state is s, his action is a and the distribution of state–action pairs among the entire player population is \(\tau \).
Transitions are defined for each individual separately with a transition kernel \(Q:S\times A\times \Delta (S\times A)\rightarrow \Delta (S)\). \(Q(B|\cdot ,\cdot ,\tau )\) is product measurable for any \(B\in \mathcal {B}(S)\) and any \(\tau \in \Delta (S\times A)\).
Global state at time \(t+1\) is given by the aggregation of individual transitions of the players,
$$\begin{aligned} \Phi \big (\cdot |\tau ^t\big )=\int _{S\times A}Q\big (\cdot |s,a,\tau ^t\big )\tau ^t\big (\mathrm{{d}}s\times \mathrm{{d}}a\big ), \end{aligned}$$As it can be clearly seen from the above formula, the transition of the global state is deterministic.
A function \(f:S\times \Delta (S)\rightarrow \Delta (A)\), such that \(f(B|\cdot ,\mu )\) is measurable for any \(B\in \mathcal {B}(A)\) and any \(\mu \in \Delta (S)\), satisfying \(f(A(s,\mu )|s,\mu )=1\) for every \(s\in S\) and \(\mu \in \Delta (S)\) is called a stationary strategy. The set of all stationary strategies is denoted by \(\mathcal {F}\). In the paper, we never consider general (history-dependent) strategies. When we talk about mean-field games, we also use stationary strategies depending only on the individual state of the player. Since in general the set of feasible actions is also a function of the global state, we define \(\mathcal {F}(\mu )\) as the set of functions \(f:S\rightarrow \Delta (A)\) such that \(f(B|\cdot )\) is measurable for any \(B\in \mathcal {B}(A)\), satisfying \(f(A(s,\mu )|s)=1\) for every \(s\in S\). We can identify any \(f\in \mathcal {F}(\mu )\) with the class of all stationary strategies \(\widetilde{f}\in \mathcal {F}\) satisfying \(f(\cdot |s)=\widetilde{f}(\cdot |s,\mu )\) for any \(s\in S\).
Next, let \(\Pi (f,\mu )\) denote the state–action distribution of the players in the mean-field game corresponding to a global state \(\mu \) and a stationary strategy \(f\in \mathcal {F}(\mu )\), that isFootnote 2
Given the evolution of the global state, which depends on the strategies of the players in a deterministic manner, we can define the individual history of a player i as the sequence of his consecutive individual states and actions \(h=(s^i_0,a^i_0,s^i_1,a^i_1,\ldots )\). By the Ionescu-Tulcea theorem (see Chap. 7 in [11]), for any stationary strategies f of player i and g of other players and any initial individual state distribution \(\mu _0\), there exists a unique probability measure \(\mathbb {P}^{\mu _0,Q,f,g}\) on the set of all infinite histories of the game \(H=(S\times A)^\infty \) endowed with Borel \(\sigma \)-algebra, such that for any \(B\in \mathcal {B}(S)\), \(D\in \mathcal {B}(A)\) and any partial history \(h^i_t=(s^i_0,a^i_0,\ldots ,s^i_{t-1},a^i_{t-1},s^i_t)\in (S\times A)^t\times S=:H_t\), \(t\in \mathbb {N}\),
with state–action distributions defined recursively by \(\tau ^0=\Pi (g,\mu _0)\), \(\tau ^{t+1}=\Pi (g,\Phi (\cdot |\tau ^t))\) for \(t=1,2,\ldots \). We can define the long-time average reward of a player using policy \(f\in \mathcal {F}\) when all the other players use policy \(g\in \mathcal {F}\) and the initial state distribution (both of the player and his opponents) is \(\mu _0\), to beFootnote 3
where \(\tau ^0=\Pi (g,\mu _0)\) and \(\tau ^{t+1}=\Pi (g,\Phi (\cdot |\tau ^t))\) for \(t=1,2,\ldots \).
Next, we define the solution we will be looking for:
Definition 1
A stationary strategy f and a measure \(\mu \in \Delta (S)\) form a stationary mean-field equilibrium in the long-time average reward game if \(f\in \mathcal {F}(\mu )\), for every other stationary strategy \(g\in \mathcal {F}(\mu )\)
and \(\mu =\Phi (\cdot |\Pi (f,\mu ))\) (i.e. if \(\mu _0=\mu \) then \(\mu _t=\mu \) for every \(t\ge 1\)).
2.2 n-Person Stochastic Games
The main reason to consider mean-field games is that usually under some fairly mild assumptions they can approximate well some n-person dynamic games defined with the same data when n is large enough. It is similar in our case. The n-person games that will be approximated by our model are discrete-time n-person stochastic games as defined in [34]. In our case, we consider n-person stochastic counterparts of the mean-field game defined by the following objects:
The state space is \(S^n\) and the action space for each player is A. Similarly as in the case of the mean-field game, the set of actions available to player i in state \(\overline{s}=(s_1,\ldots ,s_n)\) is given by \(A^i_n(\overline{s}):=A\left( s_i,\frac{1}{n}\sum _{j=1}^n\delta _{s_j}\right) \).
Individual immediate reward of player i, \(r^i_n:S^n\times A^n\rightarrow \mathbb {R}\), \(i=1,\ldots ,n\) is defined for any profile of players’ states \(\overline{s}=(s_1,\ldots ,s_n)\) and any profile of players’ actions \(\overline{a}=(a_1,\ldots ,a_n)\) by
$$\begin{aligned} r^i_n(\overline{s},\overline{a}):=r\left( s_i,a_i,\frac{1}{n}\sum _{j=1}^n\delta _{(s_j,a_j)}\right) . \end{aligned}$$The transition probability \(Q_n:S^n\times A^n\rightarrow \Delta (S^n)\) can be defined for any \(\overline{s}\in S^n\) and \(\overline{a}\in A^n\) by the formula (for the clarity of exposition we write it only for Borel rectangles, which obviously defines the product measure):
$$\begin{aligned}&Q_n(B_1\times \ldots \times B_n|\overline{s},\overline{a})\\&\quad :=Q\left( B_1|s_1,a_1,\frac{1}{n}\sum _{j=1}^n\delta _{(s_j,a_j)}\right) \ldots Q\left( B_n|s_n,a_n,\frac{1}{n}\sum _{j=1}^n\delta _{(s_j,a_j)}\right) . \end{aligned}$$In n-person game, we consider stationary strategies \(f:S^n\rightarrow \Delta (A)\) (satisfying, for each player i, two standard conditions: \(f(B|\cdot )\) is measurable for any \(B\in \mathcal {B}(A)\) and \(f(A^i_n(\overline{s})|\overline{s})=1\) for every \(\overline{s}\in S^n\)). The set of all stationary strategies for player i is denoted by \(\mathcal {F}_n^i\).
The functional maximized by each player is his average reward defined for any initial state \(\overline{s_0}\in S^n\) and any profile of stationary strategies \(\overline{f}=(f_1,\ldots ,f_n)\) by the formula
$$\begin{aligned} J_n^i\big (\overline{s_0},\overline{f}\big ):=\liminf _{T\rightarrow \infty } \frac{1}{T+1}\mathbb {E}^{\overline{s_0},Q_n,\overline{f}} \sum _{t=0}^Tr^i_n(\overline{s_t},\overline{a_t}) \end{aligned}$$with \(\mathbb {P}^{\overline{s_0},Q_n,\overline{f}}\) denoting the measure on the set of all infinite histories of the game corresponding to \(\overline{s_0}\), \(Q_n\) and \(\overline{f}\) defined with the help of the Ionescu-Tulcea theorem similarly as in case of the mean-field game.
Finally, the solution we will be looking for in n-person counterparts of the stochastic game is that of Nash equilibrium, which is the standard solution concept considered in the stochastic game literature:
Definition 2
A profile of strategies \(\overline{f}\in \mathcal {F}_n^1\times \ldots \times \mathcal {F}_n^n\) is a Nash equilibrium in the n-person stochastic game if
for any \(\overline{s}\), any \(g\in \mathcal {F}_n^i\), and \(i\in \{ 1,\ldots , n\}\).
The notation \([\overline{f}_{-i},g]\) denotes here and in the sequel the profile of strategies \(\overline{f}\) with its ith component replaced by g. If we only show that the above inequality is only true for strategies g from some subclasses \(\mathcal {F}_n^i(0)\subset \mathcal {F}_n^i\), we say that \(\overline{f}\) is a Nash equilibrium in the class \(\mathcal {F}_n^1(0)\times \ldots \times \mathcal {F}_n^1(0)\). If (3) is true up to some \(\varepsilon >0\), we say that \(\overline{f}\in \mathcal {F}_n^1\times \ldots \times \mathcal {F}_n^n\) is an \(\varepsilon \)-Nash equilibrium.
Remark 1
Note that for any n and any \(i\in \{ 1,\ldots ,n\}\), \(\mathcal {F}\) can be viewed as a subset of \(\mathcal {F}_n^i\). Moreover, it can be easily seen that in case all the players except some player i in an n-person counterpart of the mean-field game use strategies from \(\mathcal {F}\), the best response of i is also to use a strategy from \(\mathcal {F}\). This immediately implies that a Nash equilibrium in the class \((\mathcal {F})^n\) is in fact a Nash equilibrium in \(\mathcal {F}_n^1\times \ldots \times \mathcal {F}_n^n\). For that reason, in the sequel we will no longer use general strategies from \(\mathcal {F}_n^i\) when we talk about n-person games, concentrating on strategies from \(\mathcal {F}\) or from some subsets of this set.
2.3 Notation
As we have written, we assume that state and action spaces S and A are compact metric. The metric on S will be denoted by \(d_S\) while that on A by \(d_A\). Whenever we relate to a metric on a product space, we mean the sum of the metrics on its coordinates.
The convergence of probability measures defined on one of these spaces may be of three types. The one that we will use most often is the weak convergence. To denote the weak convergence of measures, we will always use the symbol \(\Rightarrow \). It is known that for a compact metric set X, \(\Delta (X)\) endowed with weak convergence topology is compact and metrizable (see e.g. Prop. 7.22 in [11]). There are several metrics consistent with weak convergence topology. In all of our considerations, whenever we use a metric on \(\Delta (X)\) defining the weak convergence, we use the metric (see Theorem 11.3.3 in [26])
where \(\mu _1,\mu _2\in \Delta (X)\) and \(\Vert \cdot \Vert _{BL}\) is the metric on the set of bounded Lipschitz continuous functions from X to \(\mathbb {R}\) defined by the formula
To make a distinction between metrics defining weak convergence on different sets, we will also use subscripts S, A etc.
The second type of convergence used in the paper is the convergence in the complete variation norm \(\Vert \cdot \Vert _v\) (usually simply called ‘norm convergence’) defined for any finite signed measure \(\mu \) on \((X,\mathcal {B}(X))\) as follows:
When writing about this type of convergence, we will directly relate to the norm.
The last type of convergence we will be using is the strong (or setwise) convergence denoted by \(\rightarrow \) and defined as follows:
It is weaker than norm convergence, but the topology defined by it is neither metrizable nor sequential, which makes it much less useful in practice.
Finally, in some proofs, we will also make use of the 1-Wasserstein distance defined for measures on \((X,\mathcal {B}(X))\) with finite 1st moment. If we assume that X is compact, each probability measure has a finite 1st moment; hence, the 1-Wasserstein distance can be used for any \(\mu _1,\mu _2\in \Delta (X)\). One of equivalent definitions of the 1-Wasserstein distance \(W_1\) is then as follows (see p. 234 in [13]):
It is clear from the definitions of \(\rho \), \(\Vert \cdot \Vert _v\) and \(W_1\) that for any \(\mu _1,\mu _2\in \Delta (S)\) we have
We will make use of these inequalities several times in our proofs.
Whenever we speak about continuity of correspondences, we refer to the following definitions:
Let X and Y be two metric spaces and \(F:X\rightarrow Y\), a correspondence. Let \(F^{-1}(G)=\{ x\in X: F(x)\cap G\ne \emptyset \}\). We say that F is upper semicontinuous iff \(F^{-1}(G)\) is closed for any closed \(G\subset Y\). F is lower semicontinuous iff \(F^{-1}(G)\) is open for any open \(G\subset Y\). F is said to be continuous iff it is both upper and lower semicontinuous. For more on (semi)continuity of correspondences, see [35], “Appendix D” or [3], Chapter 17.2.
Further, we define k-step transitions in mean-field and n-person models. For any stationary strategy \(f\in \mathcal {F}\) and any constant state–action distribution \(\tau \in \Delta (S\times A)\), we can define k-step individual transition probability corresponding to Q when player uses strategy f against state–action distribution of the others \(\tau \) as followsFootnote 4:
Here, \(Q^1(\cdot |s,f,\tau )=Q(\cdot |s,f,\tau )\).
Next, let us define k-step transition probability in n-person counterpart of the mean-field game corresponding to \(Q_n\) and the profile of stationary strategies \(\overline{f}=(f_1,\ldots ,f_n)\in \mathcal {F}^n\) when the initial states of the players are \(s_1,\ldots ,s_n\) (for the clarity of exposition again we write it only for Borel rectangles):
As before, we use the convention that \(Q_n^1(\cdot |(s_1,\ldots ,s_n),\overline{f}) =Q_n(\cdot |(s_1,\ldots ,s_n),\overline{f})\).
3 Assumptions
In the following section, we present our main assumptions which will be used in case of both mean-field games and their stochastic counterparts. Unlike in [12], all the assumptions are directly related to the primitives of the model.
- (A1):
Function r is continuous on \(S\times A\times \Delta (S\times A)\).
- (A2):
For any sequence \(\{ s_n,a_n,\tau _n\}\subset S\times A\times \Delta (S\times A)\) such that \(s_n\rightarrow s^*\), \(a_n\rightarrow a^*\) and \(\tau _n\Rightarrow \tau ^*\), \(Q(\cdot |s_n,a_n,\tau _n)\Rightarrow Q(\cdot |s^*,a^*,\tau ^*)\). Moreover, for any fixed s and any sequence \(\{ a_n,\tau _n\}\subset A\times \Delta (S\times A)\) such that \(a_n\rightarrow a^*\) and \(\tau _n\Rightarrow \tau ^*\), \(Q(\cdot |s,a_n,\tau _n)\rightarrow Q(\cdot |s,a^*,\tau ^*)\).
- (A3):
(minorization property) There exist a constant \(\gamma >0\) and a probability measure \(P\in \Delta (S)\) such that
$$\begin{aligned} Q(D|s,a,\tau )\ge \gamma P(D) \end{aligned}$$for every \(s\in S\), \(a\in A\), \(\tau \in \Delta (S\times A)\) and any Borel set \(D\subset S\).
- (A4):
The correspondence A is continuous.Footnote 5
A weaker version of assumption (A2) will be used in several places:
- (A2’):
For any sequence \(\{ s_n,a_n,\tau _n\}\subset S\times A\times \Delta (S\times A)\) such that \(s_n\rightarrow s^*\), \(a_n\rightarrow a^*\) and \(\tau _n\Rightarrow \tau ^*\), \(Q(\cdot |s_n,a_n,\tau _n)\Rightarrow Q(\cdot |s^*,a^*,\tau ^*)\).
Remark 2
While assumptions (A1) and (A4) are both quite easy to check and satisfied for a wide variety of models, for many readers it may not be obvious, what kind of stochastic kernels satisfy assumptions (A2–A3). In the following, we try to answer this question. The most natural type of stochastic kernels that satisfy (A2) is defined by the formula
where \(q:S\times S\times A\times S\times A\rightarrow \mathbb {R}^+\cup \{ 0\}\) is a measurable probability density function continuous with respect to \((s,a,s',a')\) for every fixed \(z\in S\), and \(\mu \) is any fixed \(\sigma \)-finite measure on S. This gives already quite a large class of transition probabilities satisfying (A2), including as a particular case any kernel concentrated on a fixed discrete subset of S. It can be further extended by considering stochastic kernels being convex combinations with continuous weight functions \(\lambda _i:S\times A\times \Delta (S\times A)\rightarrow [0,1]\) of several kernels of form (4) (probably defined with the help of different measures \(\mu _i\)) and those of two following forms (in both cases the transition does not depend on a or \(\tau \)):
where \(h:S\rightarrow S\) is continuous;
where Y is some Borel space, \(F:S\times Y\rightarrow S\) is a measurable function such that \(F(\cdot ,y)\) is continuous on S for every fixed \(y\in Y\) and \(\nu \) is a probability distribution on Y. If we assume that for some \(i_0\), \(Q(B|s,a,\tau )\equiv \mu _{i_0}\) for some probability measure \(\mu _{i_0}\) [this is obviously a specific case of kernel of type (4)] and \(\lambda _{i_0}>0\), the transition probability obtained automatically satisfies the minorization property (A3) with \(P=\mu _{i_0}\) and \(\gamma =\min _{(s,a,\tau )\in S\times A\times \Delta (S\times A)}\lambda _{i_0}(s,a,\tau )\).
A stochastic kernel satisfying (A2’) and (A3) can be constructed in a similar manner, but here we should consider convex combinations of kernels of types (4), (5) with kernels defined by
with \(h:S\times A\times \Delta (S\times A)\rightarrow S\) continuous.
It is a standard result in dynamic programming [43] that the minorization property is for a time-invariant Markov decision process equivalent to another property of uniform geometric ergodicity. In the following, we present a lemma that adapts this result to our case, linking the constants appearing in both assumptions. It also summarizes some other useful properties implied by (A3).
Lemma 1
Suppose the transition probability Q satisfies assumption (A3). Then:
- (a)
for any \(f\in \mathcal {F}\) and any fixed state–action distribution of other players \(\tau \in \Delta (S\times A)\) there exists a unique measure \(p_{f,\tau }\in \Delta (S)\) such that
$$\begin{aligned} \left\| Q^k(\cdot |s,f,\tau )-p_{f,\tau }\right\| _v\le 2\left( 1-\frac{\gamma }{2}\right) ^{k} \quad \text{ for } k\ge 1,s\in S. \end{aligned}$$(6) - (b)
for any \(n\in \mathbb {N}\) and \(f_1,\ldots ,f_n\in \mathcal {F}\) there exists a unique measure \(p^n_{f_1,\ldots ,f_n}\in \Delta (S^n)\) such that
$$\begin{aligned} \left\| Q_n^k(\cdot |\overline{s},f_1,\ldots ,f_n)-p^n_{f_1,\ldots ,f_n}\right\| _v \le 2\left( 1-\frac{\gamma ^n}{2}\right) ^{k} \quad \text{ for } k\ge 1,\overline{s}\in S^n. \end{aligned}$$(7)withFootnote 6\(p^n_{\overline{f}}=p^{(n)}_{f_1,\overline{f}}\ldots p^{(n)}_{f_n,\overline{f}}\), where \(p^{(n)}_{f_i,\overline{f}}\in \Delta (S)\), \(i=1,\ldots ,n\) depend only on individual strategy of the player and the profile \(\overline{f}\); in particular, they are equal for any two players using the same strategy.
The proof of this lemma is given in “Appendix”.
Remark 3
Note that using (6) we can show that for any \(B\in \mathcal {B}(S)\), \(\tau \in \Delta (S\times A)\), \(f\in \mathcal {F}\) and \(k\in \mathbb {N}\)
which implies that
As the Markov chain of individual states of a player using f against \(\tau \) is by Lemma 1 geometrically ergodic, it is known that for any strategy \(f\in \mathcal {F}\), any distribution of initial individual state \(\mu _0\) and any \(\tau \in \Delta (S\times A)\) fixed over time,
with expectation on the LHS taken with respect to the unique probability measure \(\mathbb {P}^{\mu _0,Q(\cdot |\cdot ,\cdot ,\tau ),f}\) on H satisfying for any \(B\in \mathcal {B}(S)\), \(D\in \mathcal {B}(A)\) and \(h^i_t=(s^i_0,a^i_0,\ldots ,s^i_{t-1},a^i_{t-1},s^i_t)\in H_t\), \(t\in \mathbb {N}\), (1–2) (with superscript \({\mu _0,Q,f,g}\) replaced by \({\mu _0,Q(\cdot |\cdot ,\cdot ,\tau ),f}\)) and
defined with the help of the Ionescu-Tulcea theorem.
Similarly, we can show that (7) implies for any \(\overline{s_0}\in S^n\) and \(\overline{f}\in \mathcal {F}^n\)
and
These are important properties that we will repeatedly use to compute average rewards corresponding to strategies in both the mean-field game and its n-person stochastic counterparts.
Example 1
It is important to note that the thesis of part (a) of Lemma 1 cannot be strengthened by showing that the limit measure \(p_{f,\tau }\) does not depend on the initial global state \(\mu _0=\tau _S\)—-only on strategies used by the players. Suppose \(S=\{ 0,1\}\) and the transition kernel Q depends only on the global state of the game (thus, whatever the strategy, it does not affect the transitions) in the following way:
It is easy to check that for any \(\alpha \in (0,1)\), Q satisfies all the assumptions of our model; in particular, assumption (A3) is satisfied for \(\gamma =\alpha \) and \(P=\delta _0\). Clearly, however, for \(\mu =\delta _0\) the individual state of the player moves after one step to 0 and stays there forever, while for \(\mu =\alpha \delta _0+(1-\alpha )\delta _1\), \(Q^k(\cdot |\mu )\equiv \alpha \delta _0+(1-\alpha )\delta _1\).
The fact that, unlike in n-person games considered in case (b) of the lemma, the limit distribution of individual states of a player may depend on the initial global state of the mean-field game suggests that in general the stationary behaviour of the mean-field game will not approximate well the limit behaviour of its n-person counterparts for large n.
4 The Existence of a Stationary Mean-Field Equilibrium
In this section, we address the problem of the existence of an equilibrium of discrete-time mean-field games with long-run average payoff. Its main result is given as follows.
Theorem 1
Any discrete-time mean-field game with long-run average payoff satisfying assumptions (A1–A4) has a stationary mean-field equilibrium.
Remark 4
Some ergodicity assumption is necessary for the existence of an equilibrium in discrete-time average-payoff mean-field game. See Example 3.1 in [48]. It is a matter of discussion though if we can assume less than (A3).
We precede the proof of the theorem with three lemmas.
Lemma 2
Suppose assumption (A4) holds. Then for any \(\mu \in \Delta (S)\) and \(\varepsilon >0\) there exist \(K_\varepsilon ^\mu \in \mathbb {N}\) and Borel-measurable functions \(\alpha _i^\mu :S\rightarrow A\), \(i=1,\ldots ,K_\varepsilon ^\mu \) such that for any \(a\in A(s,\mu )\), \(\min _{i\le K_\varepsilon ^\mu } d_A(a,\alpha _i^\mu (s))<\varepsilon \).
Proof
Let us fix \(\mu \in \Delta (S)\) and \(\varepsilon >0\). A is compact, which implies it has a finite \(\frac{\varepsilon }{2}\)-net \(\{ a_1,\ldots ,a_{K_\varepsilon ^\mu }\}\). Then for \(i=1,\ldots ,K_\varepsilon ^\mu \) we define correspondences \(A_i:S\rightarrow A\), \(i=1,\ldots ,K_\varepsilon ^\mu \), as follows:
The map \(A(s,\mu )\) is continuous with non-empty compact values, and the functions \(a\mapsto d_A(a, a_i)\) are continuous. Hence, by Theorem 18.19 in [3] each \(A_i^\mu \) admits a Borel-measurable selection. Let \(\alpha _i^\mu \) be the measurable selector from \(A_i^\mu \). Then by the definition of \(\frac{\varepsilon }{2}\)-net for any \(s\in S\) and any \(a\in A(s,\mu )\) there exists an i such that \(d_A(a,a_i)<\frac{\varepsilon }{2}\). But for such an i,
as by the definition of \(A_i^\mu \), \(d_A(\hat{a},a_i)<\frac{\varepsilon }{2}\) for any \(\hat{a}\in A_i^\mu (s)\). \(\square \)
In the previous lemma, we have proved the existence of a finite set of measurable functions \(\alpha _i^\mu \) such that for any \(s\in S\) and \(\mu \in \Delta (S)\) the set of values of these functions at s is an \(\varepsilon \)-net of \(A(s,\mu )\). In the next one, for any sequence of state–action distributions \(\eta _n\Rightarrow \eta \) and any strategy \(f\in \mathcal {F}(\eta _S)\), we construct strategies \(f_n\in \mathcal {F}((\eta _n)_S)\) using at any point \((s,\mu )\) only actions from the set \(\{\alpha ^\mu _i(s), i=1,\ldots , K^\mu _{\frac{1}{n}}\}\), which approximate well in some sense the strategy f. This will be used to prove that the graph of the best response correspondence is closed in weak convergence topology.
Lemma 3
Suppose (A1–A4) are satisfied and \(\eta ,\eta _n\in \Delta (S\times A)\), \(n=1,2,\ldots \) are such that \(\eta _n\Rightarrow \eta \). Let \(f\in \mathcal {F}(\eta _S)\) and define for \(n=1,2,\ldots \), \(i=1,\ldots ,K_{\frac{1}{n}}^{(\eta _n)_S}\)
(where \(\alpha _i^{(\eta _n)_S}\) are the functions defined in Lemma 2 with \(\varepsilon =\frac{1}{n}\)). Then \(f_n\in \mathcal {F}((\eta _n)_S)\) and \(\Pi (f_n,p_{f_n,\eta _n})\Rightarrow \Pi (f,p_{f,\eta })\).
Proof
It is clear that \(\bigcup _{i=1}^{K_{\frac{1}{n}}^{(\eta _n)_S}} \mathcal {A}_i^n(s)=A(s,\eta )\), which implies
for any \(s\in S\). Thus, proving that \(f_n\in \mathcal {F}((\eta _n)_S)\) requires only showing that for any fixed \(B\in \mathcal {B}(A)\), \(f_n(B|s)\) is a measurable function of s. First note that
thus to prove the measurability of \(f_n(B|\cdot )\) we only need to show that for every n and i, function \(f(\mathcal {A}_i^n(\cdot )|\cdot )\) is measurable. Clearly,
Since f is a Borel-measurable stochastic kernel, according to Proposition 7.29 in [11], to prove that \(f(\mathcal {A}_i^n(\cdot )|\cdot )\) is measurable we need to show that \(\xi _i^n:S\times A\rightarrow \mathbb {R}\) defined by
is Borel-measurable. Clearly, for any \(E\subset \mathbb {R}\), \((\xi _i^n)^{-1}(E)=\{ (s,a)\in S\times A: a\in \mathcal {A}_i^n(s)\}=:\mathcal {C}_i^n\), its complement or the empty set. Thus, what we only need to show is that for any n and i the set \(\mathcal {C}_i^n\in \mathcal {B}(S\times A)\). To this end, first note that
The first set is the graph of \(A(\cdot ,\eta _S)\), which is closed by (A4). To show that each of the \(K_{\frac{1}{n}}^{(\eta _n)_S}-1\) other sets is Borel, we only need to note that for any two functions \(g: A\times A\rightarrow \mathbb {R}\) and \(h:S\rightarrow A\) such that g is continuous and h Borel-measurable, the set \(\{ (s,a)\in S\times A: g(h(s),a)<0\}\) is Borel, as \((s,a)\mapsto g(h(s),a)\) is a composition of Borel functions and hence also a Borel function. This leads us to the conclusion that each \(\mathcal {C}_i^n\) is also Borel as a finite intersection of Borel sets, which proves that functions \(f_n(B|\cdot )\) are measurable.
Next, let us define
We will show that \(\varepsilon _n\rightarrow _{n\rightarrow \infty }0\). Suppose it is not the case, which means that there exists a subsequence of \(\{\varepsilon _n\}\) converging to some \(\beta >0\). Without loss of generality, we may assume that it is the entire sequence \(\{\varepsilon _n\}\) that converges to \(\beta \). This implies that for n big enough there exist \(s_n\in S\) and \(a_n\in A(s_n,\eta _S)\) such that
Since A and S are compact, there exists a subsequence of \(\{ s_n,a_n\}\), \(\{ s_{n_k},a_{n_k}\}\), converging to some \((s^*,a^*)\). The values of A are closed, so \(a^*\in A(s^*,\eta _S)\). Next, since by assumption (A4) A is continuous, there exists another sequence \(\{ \widehat{a}_{n_k}\}\) such that \(\widehat{a}_{n_k}\in A(s_{n_k},(\eta _{n_k})_S)\) for each k and \(\lim _{k\rightarrow \infty }\widehat{a}_{n_k}=a^*\). From the definition of functions \(\alpha _{i}^{(\eta _n)_S}\), we know that for each k there exists an \(i_k\) such that
Then
However, this, together with (13), and the fact that \(\{ a_{n_k}\}\) and \(\{\widehat{a}_{n_k}\}\) have the same limit imply that
so for k large enough
which contradicts (12).
Now, using the above fact about the sequence of \(\varepsilon _n\) we prove that \(\Pi (f_n,p_{f_n,\eta _n})\Rightarrow \Pi (f,p_{f,\eta })\). We do it in three steps. In step 1, we prove by induction that for any fixed values of \(k\in \mathbb {N}\) and \(s\in S\), \(Q^k(\cdot |s,f_n,\eta _n)\rightarrow Q^k(\cdot |s,f,\eta )\).
Let us take any \(\varepsilon >0\). For \(k=1\) and any \(B\in \mathcal {B}(S)\), we have
The function \(Q(B|s,\cdot ,\cdot )\) is by (A2) continuous on a compact domain \(A\times \Delta (S\times A)\), hence uniformly continuous. Then there exists a \(\zeta >0\) such that for any \(a_1,a_2\in A\) such that \(d_A(a_1,a_2)<\zeta \) and \(\tau _1,\tau _2\in \Delta (S\times A)\) such that \(\rho _{S\times A}(\tau _1,\tau _2)<\zeta \), \(|Q(B|s,a_1,\tau _1)-Q(B|s,a_2,\tau _2)|<\varepsilon \). If we now take an \(n_0\) such that for \(n\ge n_0\), \(\rho _{S\times A}(\eta _n,\eta )<\zeta \) and \(\varepsilon _n<\zeta \), we obtain
which proves that \(Q^1(\cdot |s,f_n,\eta _n)\rightarrow Q^1(\cdot |s,f,\eta )\).
Now suppose that for any fixed s, \(Q^k(\cdot |s,f_n,\eta _n)\rightarrow Q^k(\cdot |s,f,\eta )\). We will prove the same is true for \(k+1\). As before, we fix \(B\in \mathcal {B}(S)\).
but, as \(Q^{k+1}(\cdot |s,f_n,\eta _n)\rightarrow Q^{k+1}(\cdot |s,f,\eta )\) by the induction assumption and \(Q(B|\widehat{s},f_n,\eta _n)\rightarrow Q(B|\widehat{s},f,\eta )\) for any \(\widehat{s}\) by the first step of the induction, Prop. C.12 in [35] (see also [44] p. 232) implies that (14) goes to zero as n goes to infinity, proving that for any \(k\in \mathbb {N}\) and \(s\in S\), \(Q^k(\cdot |s,f_n,\eta _n)\rightarrow Q^k(\cdot |s,f,\eta )\).
The next step of the proof is showing that \(p_{f_n,\eta _n}\rightarrow p_{f,\eta }\). Take an \(\varepsilon >0\) and fix any \(B\in \mathcal {B}(S)\) and \(s_0\in S\). By Lemma 1,
and
for k big enough, say \(k\ge k_0\). From what we have already shown, we can also find an \(n_0\in \mathbb {N}\), such that for \(n\ge n_0\),
If we add (15–17) side by side, we obtain
The value of \(\varepsilon \) was arbitrary, so this proves that \(p_{f_n,\eta _n}\rightarrow p_{f,\eta }\). To end the proof of the lemma, we only need to show that \(\Pi (f_n,p_{f_n,\eta _n}) \Rightarrow \Pi (f,p_{f,\eta })\).
Take any bounded continuous function \(w:S\times A\rightarrow \mathbb {R}\).
The first term goes to zero as n goes to infinity, as \(\int _Aw(s,a)f(\mathrm{{d}}a|s)\) is a bounded measurable function and, as we have just shown, \(p_{f_n,\eta _n}\rightarrow p_{f,\eta }\). To prove that the second term also converges to zero as \(n\rightarrow \infty \), take any \(\varepsilon >0\)
w is a continuous function defined on a compact domain, hence uniformly continuous. Let thus \(\zeta >0\) be such that for \(a_1,a_2\in A\) and \(s\in A\), \(|w(s,a_1)-w(s,a_2)|<\varepsilon \) if \(d_A(a_1,a_2)<\zeta \) and let \(n_0\) be such that \(\varepsilon _n<\zeta \) for \(n\ge n_0\). Then (19) is smaller than \(\varepsilon \). As \(\varepsilon \) was taken arbitrary, this proves that the second term in (18) goes to zero as n goes to infinity, ending the proof that \(\Pi (f_n,p_{f_n,\eta _n}) \Rightarrow \Pi (f,p_{f,\eta })\). \(\square \)
In the next lemma, we show that any state–action distribution satisfying certain invariance property can be disintegrated into a stationary strategy and an invariant measure [as introduced in part (a) of Lemma 1] corresponding to this strategy. This will allow us to construct the best response correspondence used in the proof of Theorem 1 as a correspondence on the set of state–action measures rather than on a set of strategies.
Lemma 4
Let \(\tau \in \Delta (S\times A)\) and suppose \(\eta \in \Delta (S\times A)\) satisfies
and
Then there exists a stationary strategy \(f\in \mathcal {F}(\tau _S)\) such that
Moreover, for any initial distribution of the private state \(\mu _0\in \Delta (S)\)
Proof
It is known from e.g. [36] p. 89, that \(\eta \) satisfying (21) can be disintegrated into a stochastic kernel \(f\in \mathcal {F}(\tau _S)\) and its marginal on S, \(\eta _S\), that is, satisfying for any \(D\in \mathcal {B}(S\times A)\)
If we input this into (20), we obtain
Iterating this equation k times, we obtain
Now take any \(B\in \mathcal {B}(S)\). By (23) and part (a) of Lemma 1, we have
Passing to the limit as \(k\rightarrow \infty \), we obtain that \(\eta _S=p_{f,\tau }\). Now, (22) follows from (9). \(\square \)
Proof of Theorem 1
Let us consider the correspondences defined on \(\Delta (S\times A)\):
We will show that \(\Psi \) has a fixed point and then that this fixed point corresponds to a stationary mean-field equilibrium in the game.
First note that for any \(\tau \in \Delta (S\times A)\), and any stationary strategy \(f\in \mathcal {F}(\tau _S)\), \(\eta =\Pi (f,p_{f,\tau })\in \Theta (\tau )\), as for any \(B\in \mathcal {B}(S)\),
where the first equality and the last equality follow from the definition of \(\Pi (\cdot ,\cdot )\), the second and penultimate ones follow from Lemma 1, the third from the definition of the \(k+1\)-step transition probability, while the fourth one from the fact that \(Q(B|\cdot ,f,\tau )\) is a measurable function bounded by 1.
Next we show that the graph of \(\Theta \) is closed in weak convergence topology. To prove that, first note that for any bounded continuous function \(w:S\rightarrow \mathbb {R}\), \(\int _Sw(s)Q(\mathrm{{d}}s|\cdot ,\cdot ,\cdot )\) is, by the weak continuity of Q, a continuous function. This then implies that for any sequences \(\eta _n,\tau _n\in \Delta (S\times A)\) such that \(\eta _n\in \Theta (\tau _n)\) with \(\eta _n\Rightarrow \eta \) and \(\tau _n\Rightarrow \tau \), \(\int _Sw(s)Q(\mathrm{{d}}s|\cdot ,\cdot ,\tau _n)\) converges continuously to \(\int _Sw(s)Q(\mathrm{{d}}s|\cdot ,\cdot ,\tau )\); hence, by Theorem 3.3 in [46] we have
which means that \(\int _{S\times A}Q(\cdot |s,a,\tau _n)\eta _n(\mathrm{{d}}s\times \mathrm{{d}}a)\Rightarrow \int _{S\times A}Q(\cdot |s,a,\tau )\eta (\mathrm{{d}}s\times \mathrm{{d}}a)\). From the uniqueness of the limit this implies that \(\eta =\int _{S\times A}Q(\cdot |s,a,\tau )\eta (\mathrm{{d}}s\times \mathrm{{d}}a)\), hence \(\eta \in \Theta (\tau )\), which implies that the graph of \(\Theta \) is closed.
Since \(u^\tau (\eta ):=\int _{S\times A}r(s,a,\tau )\eta (\mathrm{{d}}s\times \mathrm{{d}}a)\) is clearly a continuous function as by (A1) r is continuous, it assumes a maximum on \(\Theta (\tau )\), which implies that for any \(\tau \in \Delta (S\times A)\), \(\Psi (\tau )\ne \emptyset \). From the linearity of integral, it is also clear that for each \(\tau \in \Delta (S\times A)\), \(\Psi (\tau )\) is convex.
Next we show that the graph of \(\Psi \) is closed. Suppose it is not. Then there exist sequences \(\tau _n,\eta _n\in \Delta (S\times A)\) such that \(\eta _n\in \Psi (\tau _n)\) with \(\eta _n\Rightarrow \eta \) and \(\tau _n\Rightarrow \tau \) satisfying \(\eta \not \in \Psi (\tau )\). Since the graph of \(\Theta \) is closed, this implies that there exists a \(\sigma \in \Theta (\tau )\) such that
for some \(\varepsilon >0\). By Lemma 4, there exists a stationary strategy \(f_\sigma \in \mathcal {F}(\tau _S)\) such that
Then by Lemma 3 there exist stationary strategies \(f_\sigma ^n\in \mathcal {F}((\tau _n)_S)\) such that \(\Pi (f_\sigma ^n,p_{f_\sigma ^n,\tau _n})\Rightarrow \Pi (f_\sigma ,p_{f_\sigma ,\tau })=\sigma \). By (A1), r is a continuous function; hence, for n large enough, say \(n\ge n_0\),
and
On the other hand, we can easily show that for each n, \(\Pi (f_\sigma ^n,p_{f_\sigma ^n,\tau _n})\in \Theta (\tau _n)\). Suppose it is not the case. Then there exists a \(B\in \mathcal {B}(S)\) and a \(\zeta >0\) such that
However, by the definition of \(p_{f_\sigma ^n,\tau _n}\) and the fact that \(Q(B|\cdot ,f_\sigma ^n,\tau _n)\) is a bounded measurable function, this can be rewritten for some \(\widehat{s}\in S\) as
which is an obvious contradiction. As \(\eta _n\in \Psi (\tau _n)\), \(\Pi (f_\sigma ^n,p_{f_\sigma ^n,\tau _n})\in \Theta (\tau _n)\) implies that
which contradicts (24), ending the proof that the graph of \(\Psi \) is closed.
The existence of a fixed point of \(\Psi \) follows now from Glickberg’s fixed point theorem [29].
Suppose \(\tau ^*\) is this fixed point. By Lemma 4, there exists a stationary strategy \(f^*\in \mathcal {F}(\tau ^*_S)\) such that
with \(p_{f^*,\tau ^*}=\tau ^*_S\). We will show that \((f^*,p_{f^*,\tau ^*})\) is a stationary mean-field equilibrium in our game. Clearly, as \(\tau ^*\in \Theta (\tau ^*)\), \(\mu _0=p_{f^*,\tau ^*}\) implies \(\mu _t=p_{f^*,\tau ^*}\) for any \(t\in \mathbb {N}\). Next, take any \(g\in \mathcal {F}(\tau ^*_S)\). Using exactly the same arguments as in the proof that \(\Pi (f_\sigma ^n,p_{f_\sigma ^n,\tau _n})\in \Theta (\tau _n)\) we can show that \(\Pi (g,p_{g,\tau ^*})\in \Theta (\tau ^*)\), which, as \(\tau ^*\in \Psi (\tau ^*)\), implies that
However, by Lemma 4 this can be rewritten as
where both sides of the inequality are independent of the initial state distribution \(\mu _0\), which implies that \(J(p_{f^*,\tau ^*},f^*,f^*)\ge J(p_{f^*,\tau ^*},g,f^*)\). \(\square \)
Remark 5
Note that the strong continuity part of assumption (A2) was only used in the proof of Lemma 3, which, in turn, was used to prove that the graph of \(\Psi \) is closed. If we assume that the feasible action correspondence \(A(s,\mu )\) does not depend on \(\mu \), then we do not need Lemma 3 for that (\(f_\sigma ^n=f_\sigma \in \mathcal {F}((\tau _n)_S)\) for any n, as \(\mathcal {F}(\mu )\equiv \mathcal {F}\) in that case). Hence, in that case the thesis of Theorem 1 is true under assumptions (A1), (A2’), (A3) and (A4).
5 Approximate Equilibria of n-Person Stochastic Games
In this section, we present two results showing that under some additional assumptions stationary equilibria of mean-field games considered in the previous section well approximate stationary strategy Nash equilibria of their n-person stochastic counterparts when n is large enough. The main problem with making such an approximation is that stationary mean-field equilibria only specify the behaviour of the players for one value of the global state of the game. It may be enough for the mean-field game, as there we can guarantee that this initial global state does not change over the course of the game, but certainly is not enough in case of its n-person counterparts. What we can do there whenever the game is in a global state different than the one specified by the mean-field equilibrium is to approximate it in some sense using the values of the equilibrium strategy specified for the mean-field equilibrium stationary global state. It turns out, in general, this is not enough to obtain a good approximation of equilibrium for n-person stochastic counterparts of the mean-field game, as shown by the following example. It is worth mentioning here that we know of only one other result of this kind appearing in the mean-field game literature [17]. In that paper, however, failure of the usual n-player game approximation by its mean-field counterpart is a result of absorbing states in the model, whereas in the present paper this phenomenon seems to come from the ergodic cost structure.
Example 2
Consider an average-reward mean-field game with \(S=\{ 0,1\}=A\) defined with the individual transition kernel Q and the reward function r depending only on the state and the action of the individual and the global state of the game \(\mu \) rather than the state–action distribution \(\tau \) in the following way:
Q and r clearly satisfy (A1–A4). We will show that \(f^*\in \mathcal {F}\) prescribing always to take action 0 and stationary distribution \(\mu ^*=\frac{1}{3}\delta _0+\frac{2}{3}\delta _1\) is a stationary mean-field equilibrium in this game. \(\mu ^*\) is clearly a stationary distribution corresponding to \(f^*\); hence, if the game starts in global state \(\mu ^*\) and all the players use strategy \(f^*\), the global state does not change. Suppose that a player uses stationary strategy \(g\in \mathcal {F}(\mu ^*)\) defined with the formula \(g(\cdot |s)=\alpha _s\delta _0+(1-\alpha _s)\delta _1\) where \(\alpha _0,\alpha _1\in [0,1]\) against constant global state \(\mu ^*\). It is easy to see that
which gives unique stationary distribution \(\left( \frac{5-2\alpha _1}{9+2\alpha _0-2\alpha _1}, \frac{4+2\alpha _0}{9+2\alpha _0-2\alpha _1}\right) \). Thus, the average reward corresponding to strategy g and global state \(\mu ^*\) equals
It is tedious but elementary to show that it attains maximum over \([0,1]^2\) for \(\alpha _0=\alpha _1=1\) which corresponds to strategy \(f^*\), which shows that indeed \((f^*,\mu ^*)\) is a stationary mean-field equilibrium in our game.
Now suppose all the players in n-person counterpart of this game use strategy \(f^*\). Note that the situation when all the individual states are zeros is clearly an absorbing state of the Markov chain of states of the n-person game. Also, regardless of the initial state of the game, the probability of not reaching it after t stages of the game is no more than \(\left( 1-\frac{1}{3^n}\right) ^t\), which goes to zero as t goes to infinity. This clearly implies that after a finite number of stages all private states become zeros with probability 1. Hence, the average reward corresponding to the profile consisting of strategies \(f^*\) in the n-person counterpart of the mean-field game is 0. Now suppose that one of the players changes his strategy to \(g(\cdot |s,\mu )=\delta _1(\cdot )\). Then the game is still absorbed at all private states equal to 0, but the ergodic reward of the player using strategy g is 1, so the profile of \(f^*\) is not an \(\varepsilon \)- stationary Nash equilibrium in the n-person game for any \(\varepsilon < 1\).
In the following, we present two results showing that under some additional assumption the mean-field approximation of n-person anonymous stochastic games is good. In the first one, we consider the case where the individual transitions are independent from the global state of the game. This kind of assumption often appears in the mean-field game literature. Notably, it is considered in both existing papers on discrete-time mean-field games with average rewards [12, 48].
Theorem 2
Suppose that \((f^*,\mu ^*)\) is a mean-field equilibrium in a discrete-time mean-field game with long-run average payoff satisfying assumptions (A1), (A2’), (A3) and (A4). Assume further that the individual transitions of the players \(Q(\cdot |s,a,\tau )=\widetilde{Q}(\cdot |s,a)\) for any \(s\in S\), \(a\in A\) and \(\tau \in \Delta (S\times A)\) and that the feasible action correspondence \(A(s,\mu )\) does not depend on \(\mu \). Then for any \(\varepsilon >0\) there exists an \(n_0\) such that for any \(n\ge n_0\) the profile of strategies where each player uses strategy \(f(\cdot |s,\mu )\equiv f^*(\cdot |s)\) is an \(\varepsilon \)-Nash equilibrium in n-person counterpart of the mean-field game.
The proof of this theorem is preceded by a lemma.
Lemma 5
Suppose that \(Q(\cdot |s,a,\tau )=\widetilde{Q}(\cdot |s,a)\) for any \(s\in S\), \(a\in A\) and \(\tau \in \Delta (S\times A)\) and that the feasible action correspondence \(A(s,\mu )\) does not depend on \(\mu \). Then for any strategies \(f_1,\ldots ,f_n\in \mathcal {F}\) such that \(f_i(\cdot |s,\mu )=\widetilde{f}_i(\cdot |s)\) for any \(s\in S\), \(\mu \in \Delta (S)\) and \(i=1,\ldots ,n\),
for any \(B_1,\ldots ,B_n\in \mathcal {B}(S)\), \(\tau \in \Delta (S\times A)\) and \(k\in \mathbb {N}\).
Proof
We prove the result by induction. First note that for any \(B_1,\ldots ,B_n\in \mathcal {B}(S)\) and any \(\tau \in \Delta (S\times A)\)
Next assume that the statement of lemma is true for k and consider \(k+1\).
which by the induction principle shows that \(Q_n^{k}(B_1\times \ldots \times B_n|(s_1,\ldots ,s_n)\overline{f})=Q^k(B_1|s_1,f_1,\tau )\cdot \ldots \cdot Q^k(B_n|s_n,f_n,\tau )\) for any k. \(\square \)
Proof of Theorem 2
Before we start the actual proof note that since the individual transitions do not depend on the global state–action distribution \(\tau \), neither does \(p_{f^*,\tau }\) (the same is true for any other strategy). Moreover, since by (8) \(p_{f^*,\tau }\) must be the invariant distribution of the Markov chain of individual states of the player corresponding to strategy f and \(\mu ^*\) is one by the definition of stationary mean-field equilibrium,
On the other hand, if we combine the results of Lemmas 1 and 5, we immediately see that for any \(g\in \mathcal {F}\),
Now, let us take an \(\varepsilon >0\). By (9), (28) and the fact that \(p_{g,\tau }\) does not depend on \(\tau \), for any \(g\in \mathcal {F}\) we have
Let us denote here and in the sequel by \(\Pi _m(\overline{f^*},\mu ^*)\), \(m\in \mathbb {N}\) the random measure describing the empirical distribution of state–action pairs when m players employ global-state-independent strategy \(f^*\) when their states are drawn according to \(\mu ^*\). Then (31) can be written as
We can now write using (30) and (32) that for any \(g\in \mathcal {F}\),
We will now show that the first term on the RHS of (33) is smaller than \(\frac{\varepsilon }{6}\) for n large enough and that the second one is at most twice bigger.
To show it for the first term, note that for any bounded continuous \(w:S\times A:\rightarrow \mathbb {R}\) and any measure \(\widetilde{\tau }\in \Delta (S\times A)\)
If we now take \(n_1\) such that for every \(s\in S\), \(a\in A\) and \(\tau ^1,\tau ^2\in \Delta (S\times A)\) such that \(\rho _{S\times A}(\tau ^1,\tau ^2)<\frac{2}{n_1}\), \(|r(s,a,\tau ^1)-r(s,a,\tau ^2)|<\frac{\varepsilon }{6}\), we immediately obtain that the first term on the RHS of (33) is smaller than \(\frac{\varepsilon }{6}\).
To show the inequality for the second term note that by Corollary 2.5 in [14], there exist positive constants \(C^1\) and \(C^2\) such that
If we take \(n_2\ge n_1\) such that \(C^1\mathrm{{e}}^{-C^2n_2}<\frac{\varepsilon }{12\Vert r\Vert _\infty }\), we can rewrite the second term on the RHS of (33) as
for \(n\ge n_2\), where the inequality follows from the definition of \(n_2\) and the fact that \(W_1\) majorizes \(\rho \). This shows that for \(n\ge n_2\),
for any \(g\in \mathcal {F}\) and \(\overline{s}\in S^n\).
By the definition of stationary mean-field equilibrium, for any \(g\in \mathcal {F}\),
If we combine it with (34) applied to strategies g and \(f^*\), we obtain
for \(n\ge n_2\), which shows that for such an n the profile of \(f^*\) strategies is an \(\varepsilon \)-Nash equilibrium in the n-person stochastic counterpart of the mean-field game. \(\square \)
It turns out that when we assume that the transitions of the players depend on the global state–action distribution, obtaining a result linking equilibria in the mean-field game with \(\varepsilon \)-equilibria in its n-person counterparts requires some very strong assumptions both about the transition kernel Q and about the mean-field game equilibrium strategy, which can imply the independence from \(\tau \) of the invariant measure of the Markov chain governed by the transition probability \(Q(\cdot |s,g,\tau )\) for any given strategy g. This kind of conditions is used in the next theorem. What is worse though is that in that case we can no longer show that the profile of mean-field equilibrium strategies is an \(\varepsilon \)-equilibrium in n-person counterpart of the mean-field game for n large enough in the class of all stationary strategies of the players \(\mathcal {F}\), but we need to limit ourselves to the class defined as follows.
Theorem 3
Suppose that \((f^*,\mu ^*)\) is a mean-field equilibrium in a discrete-time mean-field game with long-run average payoff satisfying assumptions (A1–A4). Assume further that:
- (a)
The stationary strategy f defined with the formula \(f(\cdot |s,\mu )=f^*(\cdot |s)\) for any \(s\in S\) and \(\mu \in \Delta (S)\) is an element of \(\mathcal {F}\). Moreover, it is weakly Lipschitz continuous with constant \(\beta _f\) as a function of s.
- (b)
The transition kernel Q satisfies for any \(s\in S\), \(a_1,a_2\in A\) and \(\tau _1,\tau _2\in \Delta (S\times A)\)
$$\begin{aligned} \Vert Q(\cdot |s,a_1,\tau _1)-Q(\cdot |s,a_2,\tau _2)\}\Vert _v\le \beta _Q(\max \{ d_A(a_1,a_2),\rho _{S\times A}(\tau _1,\tau _2)\}). \end{aligned}$$(35) - (c)
The constants \(\beta _f,\beta _Q\) satisfy \(\beta _Q(1+\beta _f)<\frac{\gamma }{2}\).
Then for any \(\varepsilon >0\) and \(L>0\) there exists an \(n_0\) such that for any \(n\ge n_0\) the profile of strategies where each player uses strategy f is an \(\varepsilon \)-Nash equilibrium in the class \((\mathcal {F}_L)^n\) in the n-person counterpart of the mean-field game.
The proof of the theorem is preceded by three lemmas. In the first one, we prove that under the assumptions of Theorem 3 the invariant measures of the process of individual states of any given player in the mean-field game are uniquely determined given a strategy of this player and that of his opponents, which, as shown in Example 1, is not true in general.
Lemma 6
Suppose that all the assumptions of Theorem 3 are satisfied. Then for any \(g\in \mathcal {F}\) there exists exactly one \(\mu _{gf}\in \Delta (S)\) such that for any \(B\in \mathcal {B}(S)\),
Moreover, \(\mu _{gf}=p_{g,\Pi (f,\mu _{ff})}\).
Proof
We start by defining the operator \(M_f:\Delta (S)\rightarrow \Delta (S)\) as follows:
In what follows, we will show that \(M_f\) is a contraction mapping. Let \(w:S\times A\rightarrow \mathbb {R}\) be a function with \(\Vert w\Vert _{BL}\le 1\) and let \(\mu \) be an arbitrary element of \(\Delta (S)\). We define
For any \(s_1,s_2\in S\), we have
where the last inequality follows from the Lipschitz continuity of f and w. This proves that \(w_f^{\mu }\) is a \((1+\beta _f)\)-Lipschitz continuous function. Next let \(\mu _1,\mu _2\in \Delta (S)\). We will show that \(\Pi (f,\cdot )\) is Lipschitz continuous with the same constant.
where the second equality is true because f does not depend on the global state while the penultimate inequality makes use of the Lipschitz continuity of \(w_f^{\mu _2}\). Obviously, this implies that
and further that
where the last inequality follows from (37) and (35).
Next, (38), (52) and Corollary 2 in [41] imply that
where \(\beta :=\frac{2\beta _Q(1+\beta _f)}{\gamma }<1\). Since \(\rho _S(M_f(\mu _1),M_f(\mu _2))\le \Vert M_f(\mu _1)-M_f(\mu _2)\Vert _v\), this implies that \(M_f\) is a contraction mapping from \(\Delta (S)\) into itself. As \(\Delta (S)\) is compact metric and hence complete, Banach fixed point theorem [33] implies that it has a unique fixed point, say \(\mu _{ff}\). Note, however, that by (8) \(\mu _{ff}=p_{f,\Pi (f,\mu _{ff})}\) implies (36). Moreover, if some \(\widetilde{\mu }\ne \mu _{ff}\) satisfies (36), it is an invariant distribution of the Markov chain of individual states of a player corresponding to f and \(\widetilde{\mu }\) and hence (by the uniqueness of the invariant measure for a geometrically ergodic Markov chain) it must be equal to \(p_{f,\Pi (f,\widetilde{\mu })}\). Then (8) implies it is a fixed point of \(M_f\) which contradicts the uniqueness of such a fixed point. This establishes the first part of the lemma for \(g=f\).
To prove the lemma for \(g\ne f\), note that by (8), \(p_{g,\Pi (f,\mu _{ff})}\) is an invariant measure corresponding to the Markov chain of individual states of a player when the behaviour of other players is distributed according to the distribution \(\Pi (f,\mu _{ff})\), so \(\mu _{gf}=p_{g,\Pi (f,\mu _{ff})}\) satisfies (36). As by Lemma 1, the chain is geometrically ergodic, the invariant measure is unique, so \(\mu _{gf}=p_{g,\Pi (f,\mu _{ff})}\). \(\square \)
The next lemma provides a strong technical result which will be repeatedly used to prove the convergence of the utilities in n-person counterparts of the mean-field game to those in the mean-field game as n goes to infinity.
Lemma 7
-
(a)
Suppose f is as given in Theorem 3 and let \(g_1,h_1,g_2,h_2\ldots \in \mathcal {F}_L\). Let further \(\mu ^n_f,\mu _g^n,\mu _h^n\in \Delta (S)\), \(n=1,2,\ldots \) and \(\tau ^n_g=\Pi (g_n(\cdot |\cdot ,\mu ^n_f),\mu ^n_g)\), \(\tau ^n_h=\Pi (h_n(\cdot |\cdot ,\mu ^n_f),\mu ^n_h)\) and \(\tau ^n_f=\Pi (f(\cdot |\cdot ,\mu ^n_f),\mu ^n_f)\). If there exists a sequence \(\{ n_m\}\) such that \(\tau ^{n_m}_g\Rightarrow _{m\rightarrow \infty }\tau ^*_g\), \(\tau ^{n_m}_h\Rightarrow _{m\rightarrow \infty }\tau ^*_h\) and \(\tau ^{n_m}_f\Rightarrow _{m\rightarrow \infty }\tau ^*_f\) for some \(\tau ^*_g,\tau ^*_h,\tau ^*_f\in \Delta (S\times A)\), then for any continuous function \(u:S\times A\times \Delta (S\times A)\rightarrow \mathbb {R}\) the following is true:
$$\begin{aligned}&\int _{S^{n_m}}\int _{A^{n_m}}u\left( s_i,a_i,\frac{1}{n_m}\sum _{k=1}^{n_m}\delta _{(s_k,a_k)}\right) g\left( \mathrm{{d}}a_i|s_i,\frac{1}{n_m}\sum _{k=1}^{n_m}\delta _{s_k}\right) \nonumber \\&\quad \times \, h\left( \mathrm{{d}}a_l|s_l,\frac{1}{n_m}\sum _{k=1}^{n_m}\delta _{s_k}\right) \Pi _{j\ne i,l}f\left( \mathrm{{d}}a_j|s_j,\frac{1}{n_m}\sum _{k=1}^{n_m}\delta _{s_k}\right) \nonumber \\&\quad \times \, \mu _g^{n_m}(\mathrm{{d}}s_i)\mu _h^{n_m}(\mathrm{{d}}s_l)\Pi _{j\ne i,l}\mu _f^{n_m}(\mathrm{{d}}s_j)\rightarrow _{m\rightarrow \infty }\int _S \int _Au(s_i,a_i,\tau ^*_f)\tau ^*_g(\mathrm{{d}}s_i\times \mathrm{{d}}a_i)\qquad \quad \end{aligned}$$(39) -
(b)
If for each n, \(g_n=g\), then the RHS of (39) can be written as
$$\begin{aligned} \int _S\int _Au\big (s_i,a_i,\tau ^*_f\big )g(\mathrm{{d}}a_i|s_i,\big (\tau ^*_f\big )_S)\big (\tau ^*_g\big )_S(\mathrm{{d}}s_i). \end{aligned}$$
Proof
First note that the function \(\Gamma :(\Delta (S\times A))^2\rightarrow \mathbb {R}\) defined by
is clearly continuous as for \(\tau _n\Rightarrow \tau \) and \(\eta _n\Rightarrow \eta \) we have
by Theorem 3.3 in [46].
To complete the proof of the lemma let us introduce some additional notation. Let \(\left[ \tau ^n_f\right] ^k\) be a random measure describing empirical distribution when k players’ behaviour is consistent with the distribution \(\tau ^n_f\), that is,
Note that
can be written using random measures \(\left[ \tau ^n_f\right] ^k\) as
We next take any \(\varepsilon >0\). At the beginning of the proof, we have shown that the function \(\Gamma \) is continuous. As its domain \((\Delta (S\times A))^2\) is compact, the continuity is uniform. Let \(\zeta >0\) be such that
By Corollary 2.4 in [14], there exist positive constants \(C_1\) and \(C_2\) such that for anyFootnote 7n and k,
Let \(m_0\) be such that \(C_1\mathrm{{e}}^{-C_2n_{m_0}}<\frac{\varepsilon }{3\Vert u\Vert _\infty }\), \(\rho _{S\times A}(\tau ^{n_{m}}_g,\tau ^*_g)<\zeta \) for \(m\ge m_0\), \(\rho _{S\times A}(\tau ^{n_{m}}_f,\tau ^*_f)<\zeta \) for \(m\ge m_0\) and \(\frac{4L}{n_{m_0}}<\zeta \). Then for \(m\ge m_0\), any \(w:S\times A\rightarrow \mathbb {R}\) with \(\Vert w\Vert _{BL}\le 1\) and any fixed \(s_i,s_l\in S\), \(a_i,a_l\in A\):
whence
with probability 1. This implies
with probability 1.
Then we can write as follows:
where the last inequality makes use of (41), (42) and the fact that \(W_1\) dominates \(\rho \). As \(\varepsilon \) was arbitrary, this ends the proof of part (a) of the lemma.
To prove part (b), first note that clearly \(\tau _g^{n_m}\Rightarrow _{m\rightarrow \infty }\tau ^*_g\) implies \(\mu _g^{n_m}=(\tau _g^{n_m})_S\Rightarrow _{m\rightarrow \infty }(\tau ^*_g)_S\). Then, note that if we replace the last term on the LHS of (43) withFootnote 8
and show that it is still smaller than \(\frac{\varepsilon }{3}\) for m big enough, we obtain the thesis of part (b) of the lemma. Note, however, that for any sequence of elements of S, \(s_i^n\rightarrow _{n\rightarrow \infty }s_i\),
goes to zero as \(n\rightarrow \infty \) by Theorem 3.3 in [46]. Then we can use the same theorem once more to obtain (44). We can now take \(m_1\ge m_0\) such that the quantity in (44) is smaller than \(\frac{\varepsilon }{3}\) for \(m\ge m_1\) to obtain the thesis of part (b) of the lemma. \(\square \)
In the last lemma, we prove the convergence of the unique invariant measures of the process of individual states of a player corresponding to given strategies of the player and his opponents in n-person counterparts of the mean-field game to those in the mean-field game.
Lemma 8
Suppose that all the assumptions of Theorem 3 are satisfied. Then for any \(g\in \mathcal {F}_c\),
Proof
To start the proof, first note that for any bounded continuous \(v:S\rightarrow \mathbb {R}\),
where the first equality follows from part (b) of Lemma 1, while the second from (10).
Let now \(\tau ^n_g:=\Pi (g,p^{(n)}_{g,[\overline{f}_{-i},g]})\) and \(\tau ^n_f:=\Pi (f,p^{(n)}_{f,[\overline{f}_{-i},g]})\). As \(\Delta (S\times A)\) is compact metric, every sequence \(\{(\tau ^{n_m}_g,\tau ^{n_m}_f)\}\) must contain a convergent subsequence. Let \(\tau ^*_g=\lim _{l\rightarrow \infty } \tau ^{n_{m_l}}_g\) and \(\tau ^*_f=\lim _{l\rightarrow \infty }\tau ^{n_{m_l}}_f\).
We can now use Lemma 7 for sequences \(\mu ^{n_m}_g=p^{(n_m)}_{g,[\overline{f}_{-i},g]}\) and \(\mu ^{n_m}_f=\mu ^{n_m}_h=p^{(n_m)}_{f,[\overline{f}_{-i},g]}\) (with \(\tau ^n_h=\tau ^n_f\)) and the function \(u(s_i,a_i,\tau )=\int _Sv (\widehat{s}_i)Q(\mathrm{{d}}\widehat{s}_i|s_i,a_i,\tau )\), obtaining
which, in view of (45) and part (b) of Lemma 1 implies that
and consequently
Using the same reasoning, but this time taking \(\tau ^n_g:=\tau ^n_f\), \(\tau ^n_h:=\tau ^n_g\), \(\mu ^{n_m}_g=\mu ^{n_m}_f :=p^{(n_m)}_{f,[\overline{f}_{-i},g]}\), \(\mu ^{n_m}_h:=p^{(n_m)}_{g,[\overline{f}_{-i},g]}\) in Lemma 7, we obtain
By Lemma 6, \(\mu _{ff}\) is the only probability measure satisfying this equation; hence, \(\tau ^*_f=\mu _{ff}\). Then, if we input \(\tau ^*_f=\mu _{ff}\) into (46), we obtain
which, again by Lemma 6, implies that \(\tau ^*_g=\mu _{gf}\).
So far we have shown that \((\tau ^{n_m}_g)_S=p^{(n_m)}_{g,[\overline{f}_{-i},g]}\) has a subsequence converging to \(\mu _{gf}\). However, as the subsequence \(\tau ^{n_m}_g\) was arbitrary, this proves that the entire sequence \((\tau ^n_g)_S=p^{(n)}_{g,[\overline{f}_{-i},g]}\) converges to \(\mu _{gf}\). \(\square \)
Proof of Theorem 3
Take any \(g\in \mathcal {F}_L\). We start by computing the rewards corresponding to one player using strategy g against f used by everyone else in the mean-field game and in its n-person counterpart. Note that by the definition of the mean-field equilibrium and Lemma 6, \(\mu ^*=\mu _{ff}=p_{g,\Pi (f,\mu _{ff})}\), hence by (9)
Then by (11), for any \(\overline{s}\in S^n\)
As r is continuous, by Lemma 7 the RHS of (48) converges to the RHS of (47) as n goes no infinity. Thus, the mean-field equilibrium inequality (note that for \(\mu =\mu ^*\ f(\cdot |s,\mu )=f^*(\cdot ,s,\mu )\) for any \(s\in S\))
implies that for any \(\varepsilon >0\) there exists an \(N_g\in \mathbb {N}\) such that
for any \(\overline{s}\in S^n\) and \(n\ge N_g\). Thus, to prove the thesis of the theorem we only need to show that \(N_g\) does not depend on the choice of g.
Suppose the contrary, that is, for some \(\varepsilon >0\) there exist a sequence \(\{g_n\}\) of elements of \(\mathcal {F}_L\) and an increasing sequence of integers \(\{N^n\}\) satisfying \(N^n\ge N_{g_n}\) for \(n=1,2,\ldots \) such that
Then, let us take \(\mu ^n_h=\mu ^n_f=p^{(n)}_{f,[\overline{f}_{-i},g_n]}\), \(\mu ^n_g=p^{(n)}_{g_n,[\overline{f}_{-i},g_n]}\), \(\tau ^n_h=\tau ^n_f=\Pi (f(\cdot |\cdot ,\mu ^n_f),\mu ^n_f)\) and \(\tau ^n_g=\Pi (g(\cdot |\cdot ,\mu ^n_f),\mu ^n_g)\). As \(\Delta (S\times A)\) is compact, the sequence \(\{\tau ^n_f,\tau ^n_g\}\) has a convergent subsequence, say \(\tau ^{n_m}_f\rightarrow _{m\rightarrow \infty }\tau ^*_f\) and \(\tau ^{n_m}_g\rightarrow _{m\rightarrow \infty }\tau ^*_g\). Then we can use part (a) of Lemma 7 to the RHS of
obtaining
If we disintegrate \(\tau ^*_g\), we obtain a \(g\in \mathcal {F}((\tau ^*_f)_S)\) (note that for each m the measure \(\tau ^{n_m}_g\) was concentrated on the graph of \(A(\cdot ,(\tau ^{n_m}_f)_S)\); hence, by the continuity of A the limit measure \(\tau ^*_g\) is concentrated on the graph of \(A(\cdot ,(\tau ^*_f)_S)\)) and the marginal of \(\tau ^*_g\) on S satisfying for any \(D\in \mathcal {B}(S\times A)\),
We can also show (using some straightforward computations) that \(\tau ^*_f\) can be disintegrated into f and \((\tau ^*_f)_S\). Now we can mimic the proof of Lemma 8 (we only need to replace g in the definitions of \(\tau ^n_g\), \(\tau ^n_f\), \(\mu ^n_g\) and \(\mu ^n_f\) with \(g_n\) there—the rest of the proof is identical) to show that \((\tau ^*_f)_S=\mu _{ff}\) and \((\tau ^*_g)_S=\mu _{gf}\). Inputting this into (50), we obtain
Thus, we can pass to the limit in (49), getting
which is a contradiction, as \((\mu ^*,f)\) was a stationary mean-field equilibrium in the mean-field game. \(\square \)
Remark 6
If in addition to all the assumptions of Theorem 3 we assume that the reward function r is Lipschitz continuous, we may prove (only slightly complicating the proofs of Lemmas 6 and 7) that the thesis of the theorem is true under weaker assumptions on stationary strategy f of the form: There exists a stationary strategy \(f\in \mathcal {F}\) such that \(f(\cdot |s,\mu )=f^*(\cdot |s)\) for any \(s\in S\) and satisfying
Then the constants \(\beta _f,\beta ^*_f,\beta _Q\) need to satisfy \(\beta _Q(1+2\beta _f+\beta ^*_f)<\frac{\gamma }{2}\). This kind of assumption is still very strong but more likely to be satisfied for a stationary strategy in a mean-field game when the correspondence A depends on the global state of the game.
6 Concluding Remarks
In the paper, we have presented a model of discrete-time mean-field game with compact state and action spaces and average reward. Under some strong ergodicity assumption, we have shown that it possesses a stationary mean-field equilibrium. Next, we have presented an example showing that in case of average-reward criterion usual approximation of n-person games with its mean-field counterpart may fail. Finally, we have identified some cases when stationary equilibria of the mean-field game can approximate well the Nash equilibria of its n-person stochastic game counterparts. As we have seen, some strong additional assumptions were required to obtain this kind of results. A natural question arises whether there are other conditions that can give a good approximation of n-person models by their counterpart with a continuum of players. One of the directions that we can follow in answering this question is limiting ourselves to games played on subsets of the real line. In that case, considering some assumptions of ordinal type rather than general topological properties may give a good result. Other natural questions are, whether the results from this article can be extended to games played on general, non-compact state and action sets and whether considering Markov strategies instead of stationary ones can result in a larger class of models where mean-field limit approximates well its n-person counterparts when n is large. All these questions seem both interesting and highly nontrivial.
Notes
Here and in the sequel, the Borel \(\sigma \)-algebra on a given set X is denoted by \(\mathcal {B}(X)\), while the set of probability distributions on \((X,\mathcal {B}(X))\) is denoted by \(\Delta (X)\).
We shall use similar notation also in case of general stationary strategies from \(\mathcal {F}\). In that case, \(\Pi (f(\cdot |\cdot ,\mu _1),\mu _2)(D)\) will denote \(\int _D f(\mathrm{{d}}a|s,\mu _1)\mu _2(\mathrm{{d}}s)\).
Here we omit the superscript i used to define the measure \(\mathbb {P}^{\mu _0,Q,f}\), as the situation is symmetric.
Here and in the sequel, for any \(\tau \in \Delta (S\times A)\), \(\tau _S\) denotes the S-marginal of the measure \(\tau \).
With the source space \(\Delta (S)\) endowed with the weak convergence topology.
The notation \(P=P_1\cdots P_n\) stands here and in the sequel for the product measure \(P\in \Delta (S^n)\) defined by the formula
$$\begin{aligned} P(B)=\int _BP_1(\mathrm{{d}}s_1)\cdot \ldots \cdot P_n(\mathrm{{d}}s_n)\quad \text{ for } B\in \mathcal {B}(S^n). \end{aligned}$$See also Theorems A.6 and 2.3 in [14], defining the constants appearing in Corollary 2.4. The fact that the constants \(C_1\) and \(C_2\) can be taken independently from n follows from compactness of \(S\times A\)—then K in Theorem 2.3 can be taken equal to \(S\times A\) and a in Theorem A.6 may be arbitrary.
We make use here of the assumption that \(g_{n}=g\) for each n.
References
Achdou Y, Capuzzo Dolcetta I (2010) Mean field games: numerical methods. SIAM J Numer Anal 48–3:1136–1162
Adlakha S, Johari R (2013) Mean field equilibrium in dynamic games with strategic complementarities. Oper Res 61(4):971–989
Aliprantis CD, Border KC (1999) Infinite dimensional analysis. A Hitchhiker’s guide. Springer, Berlin
Almulla N, Ferreira R, Gomes DA (2017) Two numerical approaches to stationary mean-field games. Dyn Games Appl 7(4):657–682
Arapostathis A, Biswas A, Carroll J (2017) On solutions of mean field games with ergodic cost. J Math Pures Appl 107(2):205–251
Bardi M, Feleqi E (2016) Nonlinear elliptic systems and mean-field games. NoDEA Nonlinear Differ Equ Appl 23(4):44
Bardi M, Priuli FS (2014) Linear-quadratic \(N\)-person and mean-field games with ergodic cost. SIAM J Control Optim 52(5):3022–3052
Bensoussan A, Frehse J, Yam P (2013) Mean field games and mean field type control theory. Springer, New York
Bergin J, Bernhardt D (1992) Anonymous sequential games with aggregate uncertainty. J Math Econ 21:543–562
Bergin J, Bernhardt D (1995) Anonymous sequential games: existence and characterization of equilibria. Econ Theory 5(3):461–89
Bertsekas DP, Shreve SE (1978) Stochastic optimal control: the discrete time case. Academic Press, New York
Biswas A (2015) Mean field games with ergodic cost for discrete time Markov processes. arXiv:1510.08968
Bogachev VI (2007) Measure theory, vol II. Springer, Berlin
Boissard E (2011) Simple bounds for convergence of empirical and occupation measures in 1-Wasserstein distance. Electron J Probab 16:2296–2333
Briceno-Arias L, Kalise D, Silva FJ (2018) Proximal methods for stationary mean field games with local couplings. SIAM J Control Optim 56(2):801–836
Calderone D, Sastry SS (2017) Infinite-horizon average-cost Markov decision process routing games. In: IEEE 20th international conference on intelligent transportation systems (ITSC), Yokohama, pp 16–19
Campi L, Fischer M (2018) \(N\)-player games and mean-field games with absorption. Ann Appl Probab 28(4):2188–2242
Cardaliaguet P (2013) Long time average of first order mean field games and weak KAM theory. Dyn Games Appl 3(4):473–488
Cardaliaguet P, Lasry JM, Lions PL, Porretta A (2012) Long time average of mean field games. Netw Heterog Media 7(2):279–301
Cardaliaguet P, Lasry JM, Lions PL, Porretta A (2013) Long time average of mean field games with a nonlocal coupling. SIAM J Control Optim 51(5):3558–3591
Carmona R, Delarue F (2018) Probabilistic theory of mean field games with applications. Springer, Berlin
Chakrabarti SK (2003) Pure strategy Markov equilibrium in stochastic games with a continuum of players. J Math Econ 39(7):693–724
Cirant M (2015) Multi-population mean field games systems with Neumann boundary conditions. J Math Pures Appl 103(5):1294–1315
Cirant M (2016) Stationary focusing mean-field games. Commun Partial Differ Equ 41(8):1324–1346
Dragoni F, Feleqi E (2018) Ergodic mean field games with Hörmander diffusions. Calc Var Partial Differ Equ 57:116. https://doi.org/10.1007/s00526-018-1391-1
Dudley RM (2004) Real analysis and probability. Cambridge University Press, Cambridge
Elliot R, Li X, Ni Y (2013) Discrete time mean-field stochastic linear-quadratic optimal control problems. Automatica 49:3222–3233
Feleqi E (2013) The derivation of ergodic mean field game equations for several populations of players. Dyn Games Appl 3(4):523–536
Glicksberg IL (1952) A further generalization of the Kakutani fixed point theorem with application to Nash equilibrium points. Proc Am Math Soc 3:170–174
Gomes DA, Mitake H (2015) Existence for stationary mean-field games with congestion and quadratic Hamiltonians. NoDEA Nonlinear Differ Equ Appl 22(6):1897–1910
Gomes DA, Patrizi S, Voskanyan V (2014) On the existence of classical solutions for stationary extended mean field games. Nonlinear Anal 99:49–79
Gomes DA, Saúde J (2014) Mean field games models—a brief survey. Dyn Games Appl 4(2):110–154
Granas A, Dugundji J (2003) Fixed point theory. Springer, New York
Haurie A, Krawczyk JB, Zaccour G (2012) Games and dynamic games. World Scientific, Singapore
Hernández-Lerma O, Lasserre JB (1996) Discrete-time Markov control processes: basic optimality criteria. Springer, Berlin
Hinderer K (1970) Foundations of non-stationary dynamic programming with discrete-time parameter, vol 33. Lecture notes in operations research and mathematical systems. Springer, Berlin
Huang M, Malhamé RP, Caines PE (2006) Large population stochastic dynamic games: closed-loop McKean–Vlasov systems and the Nash certainty equivalence principle. Commun Inf Syst 6:221–252
Jovanovic B, Rosenthal RW (1988) Anonymous sequential games. J Math Econ 17:77–87
Lasry J-M, Lions P-L (2007) Mean field games. Jpn J Math 2(1):229–260
Mészáros AR, Silva FJ (2017) On the variational formulation of some stationary second-order mean field games systems. SIAM J Math Anal 50(1):1255–1277
Nowak A (1998) A generalization of Ueno’s inequality for \(n\)-step transition probabilities. Appl Math 25(4):295–299
Pimentel EA, Voskanyan V (2017) Regularity for second order stationary mean-field games. Indiana Univ Math J 66:1–22
Rieder U (1979) On non-discounted dynamic programming with arbitrary state space. University of Ulm, Ulm
Royden HL (1968) Real analysis. Macmillan, London
Saldi N, Başar T, Raginsky M (2016) Markov-Nash equilibria in mean-field games with discounted cost. arXiv:1612.07878
Serfozo R (1982) Convergence of Lebesgue integrals with varying measures. Sankhya: Indian J Stat, Ser A 44(3):380–402
Ueno T (1957) Some limit theorems for temporally discrete Markov process. J Fac Sci Univ Tokyo 7:449–462
Więcek P, Altman E (2015) Stationary anonymous sequential games with undiscounted rewards. J Optim Theory Appl 166(2):686–710
Acknowledgements
The author would like to thank two anonymous referees for their constructive remarks which helped to significantly improve the presentation of the results. He is also greatly indebted to professor Andrzej S. Nowak for his help during the writing of this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is supported by the NCN Grant No. 2016/23/B/ST1/00425.
Appendix
Appendix
The proof of Lemma 1
To prove part (a), we first show that for any fixed \(\tau \in \Delta (S\times A)\) and any \(f\in \mathcal {F}\)
Suppose this inequality is not true. Then there exist \(s,s'\in S\) such that
This implies that either \(Q(B|s,f,\tau )>1-\frac{\gamma }{2}\) and \(Q(B|s',f,\tau )<\frac{\gamma }{2}\) or \(Q(B|s',f,\tau )>1-\frac{\gamma }{2}\) and \(Q(B|s,f,\tau )<\frac{\gamma }{2}\). Without loss of generality, we may assume the former, which implies that \(Q(B^C|s,f,\tau )<\frac{\gamma }{2}\) and \(Q(B|s',f,\tau )<\frac{\gamma }{2}\). Hence, as by definition
(A3) implies that \(P(B^C)<\frac{1}{2}\) and \(P(B)<\frac{1}{2}\), which is impossible, as P is a probability measure.
By Ueno’s inequality [47], (51) implies for any k
or equivalently
for any \(B\in \mathcal {B}(S)\). If we integrate it side by side with respect to the measure \(Q^m(\mathrm{{d}}s'|s,\mu ,f,g)\), we obtain
which means that \(Q^k(\cdot |s,f,\tau )\) is a Cauchy sequence, whence, as the space of probability measures with total variation norm is complete, there exists a probability measure \(p^s_{f,\tau }\) such that \(\Vert Q^k(\cdot |s,f,\tau )-p^s_{f,\tau }\Vert _v \rightarrow _{k\rightarrow \infty }0\). The rate of convergence follows directly from (53) when m goes to infinity. What remains is to show that \(p^s_{f,\tau }\) does not depend on s. Suppose it is not true, that is, there exist \(s,s'\in S\) such that \(\Vert p^s_{f,\tau }-p^{s'}_{f,\tau }\Vert _v>\beta >0\). But, clearly there exists an m such that
for \(k\ge m\) and, by (52) there exists a \(k_0\) such that
for \(k\ge k_0\). Combining these inequalities for \(k=\max \{ m,k_0\}\) we obtain
which is a contradiction.
To prove part (b) first note that for any \(\overline{s}\in S^n\), \(\mu \in \Delta (S)\) and \(B\in \mathcal {B}(S^n)\),
where \(P^n\) denotes the product measure on \((S^n,\mathcal {B}(S^n))\) induced by measure P. The rest of the proof looks exactly the same as the proof of the main part of (a).
To see that \(p^n_{\overline{f}}\) is a product measure note that by definition for any \(k\ Q_n^k(\cdot |\overline{s},\mu ,\overline{f})\) is a product measure. The norm-limit of product measures must also be a product measure. To see that \(p^n_{f_i,\overline{f}} =p^n_{f_j,\overline{f}}\) if \(f_i=f_j\), note that the Markov chain of states of the game when strategy profile \(\overline{f}\) is applied is symmetric in the sense that the transitions of individual states of i and j are the same if their initial individual states are the same, which results in the same ergodic behaviour in this case. However, in view of the independence of \(p^n_{\overline{f}}\) from the initial state \(\overline{s}\), \(p^n_{f_i,\overline{f}} =p^n_{f_j,\overline{f}}\) for any initial state of the chain. \(\square \)
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Więcek, P. Discrete-Time Ergodic Mean-Field Games with Average Reward on Compact Spaces. Dyn Games Appl 10, 222–256 (2020). https://doi.org/10.1007/s13235-019-00296-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-019-00296-1