Normal Forms and Unfoldings of Singular Strategy Functions

Abstract

We study adaptive dynamics strategy functions by defining a form of equivalence that preserves key properties of these functions near singular points (such as whether or not a singularity is an evolutionary or a convergent stable strategy). Specifically, we compute and classify normal forms and low codimension universal unfoldings of these functions. These calculations lead to a classification of local pairwise invasibility plots that can be expected in systems with two parameters. This problem is complicated because the allowable coordinate changes at such points are restricted by the specific nature of strategy functions; hence the needed singularity theory is not the standard one. We also show how to use the singularity theory results to help study a specific adaptive game: a generalized hawk—dove game studied previously by Dieckmann and Metz.

1 Introduction and Overview of Results

The adaptive dynamics approach for studying evolution of phenotypic traits has been explored by various authors such as Dieckmann and Law [4], Dercole and Rinaldi [6], Geritz et al. [8], McGill and Brown [15], and Waxman and Gavrilets [20]. We describe some of the previous work and introduce preliminary concepts before describing our results.

1.1 Evolutionary Game Theory

Adaptive dynamics uses a game theoretic approach to study the evolution of phenotypes or heritable traits, such as the beak lengths of birds belonging to the same species. For a given fixed trait, the values of the trait are referred to as strategies. A fixed strategy value $x$ represents all individuals or groups whose trait has value $x$. Generally strategies can be represented as vectors in $\mathbf {R}^n$, where $n$ can be thought of as the number of traits (though there are other interpretations); our discussion is restricted to one trait, that is $n=1$, as in [1, 8, 20].

The evolution of strategies is modeled using evolutionary interactions coming from a two-player game. A game is defined using a real-valued function $f(x,y)$ representing the advantage for strategy $y$ when playing against strategy $x$. We use the word advantage generally, with the only restriction being that if $f(x,y)$ is positive (resp. negative, zero), then $y$ has an advantage (has a disadvantage, is unaffected) through the interaction. For a fixed strategy $x$, adaptive dynamics assumes that there is no advantage for $x$ in an interaction with $x$. In other words, $f(x,x)=0$ for all $x$.

Definition 1.1

The smooth function $f:\mathbf {R}\times \mathbf {R}\rightarrow \mathbf {R}$ is a strategy function if $f(x,x)=0$ for all $x$.

There are many names used to describe strategy functions in the literature including invasion fitness, invasion exponent, initial growth rate, and fitness [8, 15, 20].

In this paper, we classify the low codimension singularities of strategy functions and their universal unfoldings. Singularity theory has been used in many contexts, but none of the standard theories (such as catastrophe theory [10, 16, 17, 21], zeros of mappings [12], or bifurcation theory [11]) are appropriate for the study of strategy functions. There are two reasons: the types of singularities of strategy functions in adaptive dynamics are different from those in other theories and the changes of coordinates that preserve the singularities of strategy functions are also different from the changes of coordinates in these other theories. Since singularity theory proceeds by classifying singularities up to allowable changes of coordinates, it follows that we must develop a new singularity theory to study strategy functions. Having said this, Damon [2] developed a general unfolding theory for contexts in which singularity theory is feasible and the new notion of strategy equivalence that we define (see Definition 1.7) falls into the class that Damon considered. As a result, we will not need to re-prove the main theorems in this new context. Note that in order to use singularity theory, we assume that strategy functions $f$ are $\fancyscript{C}^\infty$ smooth.

Next we describe the two types of singularities (ESS and CvSS) that occur in adaptive dynamics.

Evolutionarily stable strategies (ESS) Maynard-Smith and Price [13, 14] used game theoretic techniques to model problems in animal conflict. They were interested in optimal (or winning) strategies $s$ defined as follows: the greatest advantage to $y$ while playing against $s$ is obtained by playing $s$. Such a strategy $s$ was called an evolutionarily stable strategy (ESS). Their definition of ESS formed the basis of much future work. We note that the models used by Maynard-Smith and Price were defined on a discrete set of trait values; we focus on continuous trait models. In recent theory, the definition of an ESS point $s$ is given as a nondegenerate local maximum of $f(s,\cdot )$.

Definition 1.2

A strategy $s$ for the strategy function $f$ is a singular strategy if $f_y(s,s)=0$. A singular strategy $s$ is an ESS if $f_{yy}(s,s)<0$.

Since locally other strategies have a disadvantage when playing against an ESS, there was an understanding in early work that an ESS would emerge as the winner of the evolutionary process. Note that Definition 1.2 does not specify the sign of $f(x,s)$, that is, the advantage that an ESS strategy $s$ has against other strategies.

The concept of ESS has been generalized in many ways. Vincent and Brown [18] extend Definition 1.2 to strategy functions on $(\mathbf {R}^n)^m$ for $m$ strategies and $n$ traits, but we restrict our attention to two players ($m=2$) and a single trait ($n=1$).

Convergence stable strategies (CvSS) Adaptive dynamics is a technique that uses strategy functions to describe strategy evolution for a given trait $r$. The underlying idea is that an environment contains players playing all possible strategies, and that $r$ evolves in time $t$ according to the advantage or disadvantage obtained by playing $r$ against nearby strategies or mutations. Indeed, adaptive dynamics assumes that $r$ moves towards mutations $y$ when $f(r,y)>0$ and moves away from $y$ when $f(r,y)<0$. Note that up to first order, the sign of $f(r,y)$ is given by the sign of the selective fitness gradient $f_y(x,y)$ when $x=y=r$; that is,

$$\begin{aligned} \frac{{\text {d}}r}{{\text {d}}t}=\beta f_y(r,r), \end{aligned}$$

(1.1)

where $\beta >0$ is a constant.

Definition 1.2 implies that ESS is an equilibrium of (1.1). A second kind of singular strategy follows from the assumption of adaptive dynamics.

Definition 1.3

A singular strategy $s$ is a convergence stable strategy (CvSS) if $s$ is a linearly stable equilibrium for (1.1).

Note that an equilibrium of (1.1) at $s$ may or may not be be stable. Thus, a fixed strategy can move closer to or farther away from a singular strategy $s$.

In addition, certain derivatives of a strategy function $f$ vanish along the diagonal $(x,x)$. For example,

$$\begin{aligned} \begin{array}{rcl} f_{x}+f_{y} &{}&{} = 0 \\ f_{xx}+2f_{xy}+f_{yy} &{}&{} = 0 \\ f_{xxx}+3f_{xxy}+3f_{xyy}+f_{yyy} &{}&{} = 0\\ \end{array} \end{aligned}$$

(1.2)

at $(x,x)$ for all $x$. It follows that $s$ is a singular strategy if and only if $\nabla f=0$ at $(s,s)$.

Lemma 1.4

A singular strategy is a CvSS if and only if $f_{yy}-f_{xx}<0$ at $(s,s)$.

Proof

An equilibrium $s$ of (1.1) is linearly stable if and only if the derivative of $f_y(r,r)$ with respect to $r$ at $s$ is negative; that is, if

$$\begin{aligned} \frac{\partial }{\partial r}f_y(r,r)=f_{xy}(r,r)+f_{yy}(r,r)<0 \end{aligned}$$

at $r=s$. By (1.2) $f_{xy}=-\frac{1}{2}(f_{xx}+f_{yy})$ at $(s,s)$ and hence

$$\begin{aligned} 0> f_{xy}+f_{yy} = \frac{1}{2}(f_{yy}-f_{xx}) \end{aligned}$$

at $(s,s)$. $\square$

Remark 1.5

Definitions 1.2 of ESS and 1.3 of CvSS do not imply one another. It is easy to check that the two derivatives $f_{yy}$ and $f_{yy}-f_{xx}$ are independent at $(s,s)$. Thus, a given singular strategy may be either ESS or not and either CvSS or not. For example, at the origin, $f(x,y)=(x-y)y$ is CvSS but not ESS.

We note that Dieckmann and Law [4] and Geritz et al. [8] have codified the canonical equation of adaptive dynamics as

$$\begin{aligned} \frac{{\text {d}}r}{{\text {d}}t}=\frac{1}{2} \alpha (r) \hat{N}(r) \sigma ^2(r) f_y(r,r), \end{aligned}$$

(1.3)

where $\alpha$ is the probability per birth event, $\hat{N}$ is the equilibrium population size, and $\sigma ^2$ is the variance of phenotypic effect. See [3] for a discussion of the canonical equation. The important point for us is that a singular strategy $s$ is linearly stable for (1.1) if and only if it is linearly stable for the more general adaptive dynamics equation (1.3).

1.2 Adaptive Dynamics Singular Strategy Types

Suppose $f$ is a strategy function with a singular strategy at $s$. We label the type of the singular strategy in the following way. A singular strategy $s$ is

$$\begin{aligned} \begin{array} {lcrcl} \mathrm {CvSS}_+&{} \quad \text {if}\quad &{} f_{yy}(s,s)-f_{xx}(s,s) &{} <&{} 0 \\ \mathrm {CvSS}_-&{} \quad \text {if}\quad &{} f_{yy}(s,s)-f_{xx}(s,s)&{} >&{} 0 \\ \mathrm {CvSS}_0&{} \quad \text {if}\quad &{} f_{yy}(s,s)-f_{xx}(s,s)&{} =&{} 0 \\ \mathrm {ESS}_+&{} \quad \text {if}\quad &{} f_{yy}(s,s)&{} <&{} 0 \\ \mathrm {ESS}_-&{}\quad \text {if}\quad &{} f_{yy}(s,s)&{} >&{} 0 \\ \mathrm {ESS}_0&{} \quad \text {if}\quad &{} f_{yy}(s,s) &{} = &{} 0. \\ \end{array} \end{aligned}$$

(1.4)

The type of a given singular strategy is given by its CvSS label and its ESS label. For example, a singular strategy is labeled $\mathrm {CvSS}_+\mathrm {ESS}_+$ if it is CvSS and ESS. In some of the literature, a singularity that is both $\mathrm {ESS}_+$ and $\mathrm {CvSS}_+$ is called a continuously stable strategy or CSS [7, 15]. Singularity theory studies properties of singularities of functions that are invariant under changes of coordinates. In our study, we define changes of coordinates that preserve ESS and CvSS singularity types.

We refer to singular strategies of type $\mathrm {ESS}_0$ or $\mathrm {CvSS}_0$ as degenerate singular strategies. McGill and Brown [15] studied the nondegenerate singular strategies. Dieckmann and Metz [5] observed the simplest (codimension one) example of a $\mathrm {ESS}_0$ degenerate singularity. Geritz et al. [9] observed the simplest (codimension one) example of a $\mathrm {CvSS}_0$ degenerate singularity as well as a more degenerate (codimension two) $\mathrm {CvSS}_0$ singularity. In this paper, we provide a theory that enables us to classify nondegenerate and degenerate singular strategies of strategy functions and their perturbations, and we carry out this complete classification through (topological) codimension two. See Table 1.

Table 1 Solution to the recognition problem for singularities of low codimension for strategy functions $f$ with a singular strategy at $(0,0)$. $E_1,E_2, E_3$ are defined in (1.9) and $\delta = \pm 1, \varepsilon =\pm 1$

In Geritz et al. [8], the authors introduce a classification scheme based on CvSS and ESS along with two additional singularity types, as follows. If $f_{xx}(s,s)<0$, the singular strategy $s$ wins against all mutant strategies. If $f_{xx}(s,s)+f_{yy}(s,s)>0$, then there exist open regions of pairs $x,y$ near $r$ where $x$ has an advantage against $y$ and $y$ has an advantage against $x$. Such pairs are called dimorphisms. This classification leads to eight different types of singular strategies. See Vutha [19, Chap. 6] for a description of the singularity theory that corresponds to the scheme in [8]. In this paper, we restrict our attention to the theory that preserves only the ESS and CvSS types of a singular strategy.

1.3 Equivalence of Strategy Functions

We define a notion of equivalence between two strategy functions $f$ and $\hat{f}$ that preserves ESS and CvSS type singularities.

In singularity theory, two functions $f,\hat{f}:\mathbf {R}^2 \rightarrow \mathbf {R}$ are contact equivalent if

$$\begin{aligned} \hat{f}(x,y)=S(x,y)f(\Phi (x,y)), \end{aligned}$$

(1.5)

where $S:\mathbf {R}^2 \rightarrow \mathbf {R}$ is a smooth map and $\Phi :\mathbf {R}^2\rightarrow \mathbf {R}^2$ is a diffeomorphism such that

• (a) $S(x,y)>0$

• (b) $\det (d\Phi )_{x,y} > 0$

Remark 1.6

Contact equivalence gives the most general coordinate changes that preserve singularities of functions. Suppose $f=f_x=f_y=0$ at $(x_0,y_0)$. If $\hat{f}$ is contact equivalent to $f$, then $\hat{f}=\hat{f}_x=\hat{f}_y=0$ at $\Phi ^{-1}(x_0,y_0)$.

In this paper, we modify contact equivalence so that the structure of strategy functions and the types of their singularities are also preserved. That is, if $f$ is a strategy function, then so is $\hat{f}$. In particular, $\hat{f}$ must vanish on the diagonal for every strategy function $f$. Hence, $\Phi$ must map the diagonal into itself and there must exist $\phi :\mathbf {R}\rightarrow \mathbf {R}$ such that

• (c) $\Phi (x,x)=(\phi (x),\phi (x))$ for every $x$

In Proposition 1.8, we show that contact equivalences for which the diagonal condition [(c)] holds also preserve the CvSS type at a singular point $(x_0,x_0)$. Note that if $\Phi \equiv (\Phi _1,\Phi _2)$ for $\Phi _i:\mathbf {R}^2\rightarrow \mathbf {R}$, the diagonal condition (c) implies

$$\begin{aligned} \Phi _{1x}+\Phi _{1y}=\Phi _{2x}+\Phi _{2y} \end{aligned}$$

at $(x,x)$ for all $x$.

We also require that the equivalence preserves ESS type at a singular strategy. We show in Proposition 1.8 and Lemma 1.10 that ESS type is preserved if and only if

• (d) $\Phi _{1y}(x,x)=0$ for every $x$

Definition 1.7

A pair $(S,\Phi )$ is a strategy equivalence if the pair satisfy (1.5) (a)–(d). The strategy functions $\hat{f}=Sf(\Phi )$ and $f$ are called strategy equivalent and denoted as $\hat{f} \simeq f$.

Note that the set of strategy equivalences is a group. In particular, $(S,\Phi )^{-1}=\left( \frac{1}{S},\Phi ^{-1} \right)$.

Proposition 1.8

Let $f$ and $\hat{f}=Sf(\Phi )$ be strategy equivalent. Suppose $f$ has a singular strategy at $(x_0,x_0)$. Then, $\hat{f}$ has a singular strategy at $\Phi ^{-1}(x_0,x_0)$. Moreover, the singularity of $\hat{f}$ at $\Phi ^{-1}(x_0,x_0)$ has the same CvSS and ESS type as the singularity of $f$ at $(x_0,x_0)$ has.

Proof

Remark 1.6 notes that $\hat{f}=\hat{f}_y=\hat{f}_x=0$ at $(\phi ^{-1}(x_0),\phi ^{-1}(x_0))$ whenever $f=f_x=f_y=0$ at $(x_0,x_0)$. Therefore, $\hat{f}$ has a singular strategy at $(\phi ^{-1}(x_0),\phi ^{-1}(x_0))$ whenever $f$ has a singular strategy at $x_0$. We prove the proposition for left changes of coordinates described by $S$ and for right changes of coordinates described by $\Phi$ separately.

Suppose

$$\begin{aligned} \hat{f}(x,y)=S(x,y)f(x,y), \end{aligned}$$

where $S(x,y)>0$. Then a calculation shows

$$\begin{aligned} \hat{f}_{xx}=Sf_{xx} \qquad \hat{f}_{yy}=Sf_{yy} \end{aligned}$$

at $(x,y)=(x_0,x_0)$. Since $S(x_0,x_0)>0$, we have

$$\begin{aligned} \mathrm {sgn}(\hat{f}_{yy}-\hat{f}_{xx})&=\mathrm {sgn}(f_{yy}-f_{xx}) \\ \mathrm {sgn}(\hat{f}_{yy})&=\mathrm {sgn}(f_{yy}) \end{aligned}$$

at $(x_0,x_0)$. Therefore, the singularity $(x_0,x_0)$ of $f$ has the same ESS type and the same CvSS type as the singular strategy $(x_0,x_0)$ of $\hat{f}$.

Next, suppose

$$\begin{aligned} \hat{f}(x,y)=f(\Phi (x,y)), \end{aligned}$$

where $\Phi (x,y)$ satisfies (1.5) (b)–(d). Write

$$\begin{aligned} \Phi (x,y) = \left( \begin{array}{rrrrrrrrrrrrrrrrrr} a&{}\quad 0 \\ c &{}\quad d \end{array}\right) \left( \begin{array}{rrrrrrrrrrrrrrrrrr} x\\ y \end{array}\right) + \cdots \end{aligned}$$

Since $\Phi$ preserves the diagonal, it follows that $a=c+d$. A calculation shows

$$\begin{aligned} \hat{f}_{xx}&= a^2 f_{xx}(\Phi ) +2ac f_{xy}(\Phi ) + c^2 f_{yy}(\Phi ) \\ \hat{f}_{yy}&= d^2 f_{yy}(\Phi ) \end{aligned}$$

at $(\phi ^{-1}(x_0),\phi ^{-1}(x_0))$. In particular,

$$\begin{aligned} \mathrm {sgn}(\hat{f}_{yy}(\phi ^{-1}(x_0),\phi ^{-1}(x_0)))=\mathrm {sgn}(f_{yy}(x_0,x_0)) \end{aligned}$$

Therefore, $(x_0,x_0)$ for $f$ has the same ESS type as $(\phi ^{-1}(x_0),\phi ^{-1}(x_0))$ for $\hat{f}$. We show that the CvSS type is also preserved. Since $f(\Phi )$ vanishes on the diagonal $x=y$, it follows from (1.2) that

$$\begin{aligned} 2f_{xy}(\Phi ) = -(f_{xx}(\Phi )+f_{yy}(\Phi )) \end{aligned}$$

at $(\phi ^{-1}(x_0),\phi ^{-1}(x_0))$. Therefore,

$$\begin{aligned} \hat{f}_{xx} = (a-c)(a f_{xx}(\Phi ) - c f_{yy}(\Phi )) = d(a f_{xx}(\Phi ) - c f_{yy}(\Phi )) \end{aligned}$$

at $(\phi ^{-1}(x_0),\phi ^{-1}(x_0))$. This implies

$$\begin{aligned} \hat{f}_{yy}-\hat{f}_{xx} = ad(f_{yy}-f_{xx}) \end{aligned}$$

at $(\phi ^{-1}(x_0),\phi ^{-1}(x_0))$. Since $\det (d\Phi )_{x_0,x_0}=ad>0$, Therefore, under left changes, the singular strategy $(\phi ^{-1}(x_0),\phi ^{-1}(x_0))$ has the same CvSS type for $\hat{f}$ as the singular strategy $(x_0,x_0)$ has for $f$. $\square$

Remark 1.9

Suppose $f$ and $\hat{f}=Sf(\Phi )$ are contact equivalent. The proof of Proposition 1.8 shows that CvSS singularities are preserved whenever (1.5)(c) holds, whereas the proof of this proposition shows that ESS singularities are preserved whenever both (1.5)(c) and (1.5)(d) hold.

Lemma 1.10

Suppose the ESS type of a singular strategy is preserved by the contact equivalence $\hat{f}=f(\Phi )$ for every strategy function $f$ with a singular strategy at $(x_0,x_0)$. Then, (1.5) (d) is satisfied at all points on the diagonal.

Proof

Suppose ESS type is preserved for every strategy function $f$. Writing,

$$\begin{aligned} \Phi (x,y) = (ax+by,cx+dy)+\cdots \end{aligned}$$

we find

$$\begin{aligned} \hat{f}_{yy}=b^2 f_{xx}(\Phi ) +2bd f_{xy}(\Phi ) + d^2 f_{yy}(\Phi ) \\ \end{aligned}$$

at $\Phi ^{-1}(x_0,x_0)$. Choose $f_{yy}(\Phi )=0$ and $f_{xx}(\Phi )=1$. Remark 1.2 implies $f_{xy}(\Phi )=-\frac{1}{2}$. Substituting, we find

$$\begin{aligned} \hat{f}_{yy}=b^2-bd \end{aligned}$$

at $\Phi ^{-1}(x_0,x_0)$. Since ESS type is preserved and $\hat{f}_{yy}=0$ at $\Phi ^{1}(x_0,x_0)$, we must have

$$\begin{aligned} 0=b^2-bd \end{aligned}$$

In other words, $b=0$ or $b=d$. But $(d\Phi )_{x,x}>0$ and (1.5)(d) imply $b \ne d$, which imply $b=0$. Since we can choose the singular point anywhere on the diagonal, (1.5)(d) is satisfied at all points on the diagonal. $\square$

1.4 Singularity theory

As discussed in Golubitsky and Schaeffer [11], there are four major types of result in local singularity theory: determinacy; classification; unfoldings and codimension; and determinacy for universal unfoldings. We discuss these types of result in the context of strategy equivalence.

1.4.1 Determinacy Theory for Strategy Functions

Consider a strategy function $f:\mathbf {R}^2 \rightarrow \mathbf {R}$ defined on a neighborhood of a singular point. Determinacy theory solves the problem of when a strategy function $f$ is strategy equivalent to given normal form $h$. The solution has two features: defining conditions and nondegeneracy conditions, which are given in terms of the derivatives of $f$ at the singularity. More precisely, defining conditions are equalities and nondegeneracy conditions are inequalities among the derivatives of $f$ at the singularity. For example, we prove in Theorem 5.5(b),

Theorem 1.11

A strategy function $f$ is strategy equivalent to the normal form

$$\begin{aligned} h(x,y) = \varepsilon (y-x)x, \end{aligned}$$

(1.6)

on a neighborhood of the origin if and only if the defining conditions

$$\begin{aligned} f=f_y=f_{yy}=0 \end{aligned}$$

(1.7)

are satisfied at (0,0) and the nondegeneracy condition

$$\begin{aligned} f_{xx} \ne 0 \end{aligned}$$

(1.8)

is satisfied at (0,0), where $\varepsilon = -\mathrm {sgn}(f_{xx}(0,0))$.

In other words, the defining conditions (1.7) and the nondegeneracy condition (1.8) solve the recognition problem for the normal form $h$ in (1.6). In Sect. 4, we present methods that lead to a solution of the recognition problem for a given strategy function $h$. This information is useful in applications, since in principle one can test whether a strategy function $f$ is strategy equivalent to a (presumably) simpler normal form strategy function $h$.

1.4.2 Classification for Strategy Functions

The answer to the question of obtaining an appropriate normal form for a given strategy function is still complicated, because one does not know in advance which recognition problem needs to be solved. One way around this difficulty is to classify the normal forms with a fixed number of defining conditions. This classification gives a flow chart of possible singularities. One then tests in order the defining and nondegeneracy conditions of the classified singularities until one finds which singularity is present in $f$ and what the normal form of $f$ is. In Table 1, we present the classification of normal forms with five or fewer defining conditions. These conditions involve the derivatives

$$\begin{aligned} E_1&=f_{xxy}+2f_{xyy}+f_{yyy} \nonumber \\ E_2&=f_{xxxy}+3f_{xxyy}+3f_{xyyy}+f_{yyyy}\nonumber \\ E_3&=-\frac{1}{36}(4f_{xxx}f_{yyy}+3(f_{xyy}+f_{yyy})^2) \end{aligned}$$

(1.9)

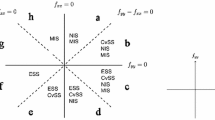
at the singular point, and are given by the Classification Theorem 5.5. The information in Table 1 is most easily understood using the flow chart in Fig. 1.

Fig. 1

Flowchart for recognition of low codimension singularities of Table 1

1.4.3 Unfolding Theory and Codimension for Strategy Functions

Unfolding theory is the deepest part of singularity theory; universal unfoldings classify up to equivalence all small perturbations of a given $f$. Unfoldings are parametrized families of strategy functions and universal unfoldings are parametrized families that contain all nearby singularities up to strategy equivalence. The number of parameters in a universal unfolding of $f$ is the codimension of $f$, denoted $\mathrm {codim}f$.

The classification mentioned previously is a classification by codimension. Once a degenerate singularity is identified, unfolding theory allows us to classify all possible nondegenerate games that can be obtained from small perturbations of $f$. For example, in Theorem 5.5(b), we prove that the universal unfolding of $h$ in (1.6) has codimension $1$ and is

$$\begin{aligned} H(x,y,a)= \varepsilon (y-x)(x+a(y-x)) \end{aligned}$$

(1.10)

for $a$ near $0$. The parameter value $a=0$ separates region $a>0$ from region $a<0$ where the unfolding leads to inequivalent games. The universal unfoldings of the normal forms in Table 1 are given in Table 2.

Table 2 Universal unfoldings $H$ of normal forms $h$ in Table 1 and recognition of universal unfoldings $F$ of $f$ when $f \simeq h$

1.4.4 Determinacy Theory for Universal Unfoldings

Suppose that $F(x,y,\alpha )$ is a $k$-parameter unfolding of $f(x,y)=F(x,y,0)$ where $f$ has a codimension $k$ singular strategy at the origin. Suppose also that $f(x,y)$ is strategy equivalent to a normal form $h(x,y)$. That is, we know that $f$ satisfies the defining and nondegeneracy conditions of $h$. We then ask when is the given $F$ a universal unfolding of $f$? This question is discussed in Sect. 6 where the answer can be given by showing that a certain matrix has a nonzero determinant. The answer for the normal forms in Table 1 is also given in Table 2. These results are used in Sect. 3 when we analyze the Dieckmann–Metz example.

1.5 Structure of the Paper

Having introduced the singularity theory classification and unfolding results in this opening section, we present the corresponding pairwise invasibility plots in Sect. 2. In Sect. 3, we apply our results to a highly nonlinear hawk-dove game studied by Dieckmann and Metz [5]. We show that the singularity studied in [5] is one of the two codimension one singularities in our classification (Table 1). We also show that the elliptic topological codimension two singularity appears at certain parameter values in the Dieckmann–Metz model. Further discussion is needed to understand the importance of the existence of specific higher order singularities in applications.

Sections 4 and 5 answer the question: When are two singularities of strategy functions equivalent? We present the needed singularity theory results in Sect. 4 and show how this theory can be used to classify the singularities that might be expected in two parameter systems in Sect. 5. Note that the strategy function assumption $f(x,x)\equiv 0$ implies that

$$\begin{aligned} f(x,y) = (y-x)g(x,y). \end{aligned}$$

We call $g$ a payoff function. The singularity theory calculations are best done using payoff functions rather than strategy functions and in coordinates $u=x, v=y-x$ whose axes are the vertical line and the diagonal. These results are then translated back to the results in $xy$ coordinates listed in this section.

The final section (Sect. 6) discusses the theory behind universal unfoldings (which classify all small perturbations of a given singularity up to strategy equivalence) and how to compute universal unfoldings of a given singularity. The discussion in Sects. 4–6 show how subspaces and ideals in the space of functions that are defined locally near a singularity (germs) can be used to prove the existence of normal forms and universal unfoldings and how to relate the abstract classification results to tools that help analyze specific applications.

We end this introduction by noting that the singularity theory results are all based on the specific kinds of strategy equivalences we chose. In this case, we have chosen the most general changes of coordinates that preserve ESS and CvSS singularities in single trait models. If additional singularity types are preserved, then the allowable changes of coordinates will change, as will the classification results. See Vutha [19]. One of the most interesting questions for future work is to consider the singularity theory setting for dimorphisms, where the game theoretic singularities of $f(x,y)$ and $f(y,x)$ are simultaneously preserved.

2 Geometry of Unfolding Space

In a given universal unfolding, the classification of small perturbations proceeds by determining parameter values where singularity types change. See [11, Chap. III, §5]. In the parameter space of a universal unfolding of a strategy function, there are three varieties where such changes occur; these varieties are based on degeneracies ($\mathrm {CvSS}_0$, $\mathrm {ESS}_0$) and bifurcations. Bifurcation points in parameter space occur at points in phase space where the zero set of $F$ is singular. Specifically, suppose $F(x,y,\alpha )$, where $\alpha \in \mathbf {R}^k$, is a universal unfolding of $f(x,y)$. Then we define

$$\begin{aligned} \fancyscript{C}&= \{\alpha \in \mathbf {R}^k : \exists \; x \;\hbox {such that}\; F_x= F_{yy} - F_{xx} = 0\; \hbox {at} \; (x,x,\alpha )\} \nonumber \\ \fancyscript{E}&= \{\alpha \in \mathbf {R}^k : \exists \; x \;\hbox {such that}\; F_x= F_{yy}=0\; \hbox {at} \; (x,x,\alpha ) \} \nonumber \\ \fancyscript{B}&= \{\alpha \in \mathbf {R}^k : \exists \; x,y \;\hbox {such that}\; F = F_x = F_y = 0\; \hbox {at} \; (x,y,\alpha )\} \end{aligned}$$

(2.1)

The transition variety is the union of the degenerate CvSS variety $\fancyscript{C}$, the degenerate ESS variety $\fancyscript{E}$, and the bifurcation variety $\fancyscript{B}$; that is,

$$\begin{aligned} \fancyscript{T}= \fancyscript{C}\cup \fancyscript{E}\cup \fancyscript{B}\end{aligned}$$

The transition variety is a codimension 1 real algebraic variety in parameter space whose complement consists of connected components. The main geometric result about universal unfoldings states that strategy functions associated to two sets of parameters in the same connected component of the complement of the transition variety $\fancyscript{T}$ in parameter space are strategy equivalent. More specifically, each connected component of the complement corresponds to a unique pairwise invasibility plot (up to equivalence). See Sect. 2.2.

2.1 Transition Varieties

We can simplify the calculation of the transition varieties in two ways. First, since universal unfoldings vanish on the diagonal, they can be written as

$$\begin{aligned} F(x,y,\alpha ) = (y-x)G(x,y,\alpha ). \end{aligned}$$

Second, in the theoretical calculations, it is simpler to work in the coordinates $u=x$ and $v = y-x$. That is, we define

$$\begin{aligned} G'(u,v) = G(u,u+v) = G(x,y) \end{aligned}$$

We begin by rewriting (2.1) in terms of $\tilde{G}$ and obtain

$$\begin{aligned} \fancyscript{C}&= \{\alpha \in \mathbf {R}^k : \exists \; x \;\hbox {such that}\; G = G_x + G_y = 0\; \hbox {at} \; (x,x,\alpha )\} \nonumber \\ \fancyscript{E}&= \{\alpha \in \mathbf {R}^k : \exists \; x \;\hbox {such that}\; G = G_y=0\; \hbox {at} \; (x,x,\alpha ) \} \nonumber \\ \fancyscript{B}&= \{\alpha \in \mathbf {R}^k : \exists \; x,y \;\hbox {such that}\; G = G_x = G_y = 0\; \hbox {at} \; (x,y,\alpha )\} \end{aligned}$$

(2.2)

Next, we rewrite (2.2) using $uv$ coordinates and $G$ to obtain

$$\begin{aligned} \fancyscript{C}&= \{\alpha \in \mathbf {R}^k: \exists \; u \;\text {such that}\; G'=G'_u=0 \text { at } (u,0,\alpha ) \} \nonumber \\ \fancyscript{E}&= \{\alpha \in \mathbf {R}^k: \exists \; u \;\text {such that}\; G'=G'_v=0 \text { at } (u,0,\alpha ) \} \nonumber \\ \fancyscript{B}&= \{\alpha \in \mathbf {R}^k: \exists \; u,v \;\text {such that}\; G'=G'_u=G'_v=0 \text { at } (u,v,\alpha ) \} \end{aligned}$$

(2.3)

Using (2.3), we compute the transition varieties for the low codimension singularities displayed in Table 2 and list the results in Table 3.

Table 3 Transition varieties for universal unfoldings of normal forms of topological codimension $\le 2$. Normal forms are written in $u,v$ coordinates. Note that $\varepsilon =\pm 1$ and $\delta =\pm 1$

2.2 Persistent Pairwise Invasibility Plots

We classify persistent perturbations (those perturbations corresponding to the connected components of the complement of the transition variety) of the universal unfolding of each singularity of low codimension. Persistent perturbations $h(x,y)$ are displayed using pairwise invasibility plots. These are plots of the zero set of $h$ in the $xy$ plane; regions where $h(x,y)$ is positive (advantage to mutant) are indicated by $+$ and regions where $h(x,y)$ is negative (disadvantage to mutant) are indicated by $-$. In addition, the types of singularities in $h$ are also indicated.

We describe the type of a given singular point using the CvSS and ESS labels in (1.4). Recall that a singular point is $\mathrm {CvSS}_+$ if it is a linearly stable equilibrium for the canonical equation (1.1), whereas a singular point is $\mathrm {ESS}_+$ if all mutant strategies experience a disadvantage against the singular strategy. Near a degenerate $\mathrm {CvSS}_0$ or $\mathrm {ESS}_0$ singular point, a small change in parameters can change the number and CvSS and ESS type of the singular point and it can change the number of signed regions (often by introducing new bounded signed regions). The formation or loss of these regions occurs independently of changes in the number of nondegenerate singularities and their type. Therefore, the singularity theory approach to classification of strategy functions provides an extra level of detail in adaptive dynamics, and this detail corresponds to a phenomenon that is away from the diagonal and captured by the bifurcation variety $\fancyscript{B}$. Indeed, one of the benefits of unfolding theory is that it can rigorously capture quasi-global information using local techniques.

The pairwise invasibility plots of persistent perturbations that we draw all indicate the singularity type according to the following scheme. The ESS singularity type is given by color and the CvSS singularity type is given by shape. Specifically, red indicates $\mathrm {ESS}_+$ and green indicates $\mathrm {ESS}_-$; circle indicates $\mathrm {CvSS}_+$ and square indicates $\mathrm {CvSS}_-$. Therefore, a red square indicates an $\mathrm {CvSS}_-\mathrm {ESS}_+$ singularity, etc. In addition, degenerate singularity types are specified as follows: yellow indicates $\mathrm {ESS}_0$ and diamond indicates $\mathrm {CvSS}_0$. See Table 4.

Table 4 Markers for different singularity types on the pairwise invasibility plots (Color table online)

In the following, we show pairwise invasibility plots associated to universal unfoldings (see Table 2) of normal forms with topological codimension 0, 1, and 2 (see Table 1). The captions in the figures for codimensions 0 and 1 give game theoretic interpretations. The unfoldings of higher codimension singular strategies contain combinations of the lower codimension cases. In particular, the multiplicity of singular strategies and the regions of advantage and disadvantage are quite complicated to explain in words; the figures adequately enumerate the possibilities.

Codimension zero In Fig. 2, we show the pairwise invasibility plots of codimension $0$ normal forms (see Theorem 5.5 (a)) given by $f(x,y)=\varepsilon (y-x)(x+\delta (y-x))$ for $\varepsilon =\pm 1, \delta =\pm 1$. Since these normal forms have codimension $0$, the ESS and CSS type of a singular point for these normal forms is preserved under all perturbations of the strategy function. The four representative normal forms recover the classification of strategy functions discussed in McGill and Brown [15].

Fig. 2

Codimension zero normal forms $\varepsilon (y-x)(x+\delta (y-x))$. These singularities are distinguished as follows: when $\delta =-1$ the best that player B can do against player A is to to play the same strategy as player A. The singular strategy is stable on an evolutionary time scale when $\varepsilon =-1$ and unstable when $\varepsilon =+1$. An analogous description holds when $\delta =+1$

Codimension one For codimension one singularities with unfolding parameter $a$, the transition variety is the origin and it divides parameter space into two connected components $a<0$ and $a>0$.

There are two pairs of codimension one singularities. The first pair is given by the normal form (1.6) and universal unfolding (1.10); it consists of singularities that are degenerate ESS and nondegenerate CvSS. Strategy functions corresponding to one connected component have a nondegenerate $\mathrm {ESS}_+$ singular point, whereas those corresponding to the other connected component have a nondegenerate $\mathrm {ESS}_-$ singular point. See Fig. 3.

Fig. 3

Codimension one unfolding of degenerate $\mathrm {ESS}_0$: $\varepsilon (y-x)(x+a(y-x))$. When $\varepsilon =-1$, the singular strategy is stable on an evolutionary time scale and there is a transition from unstable ESS for $a<0$ to stable ESS for $a>0$. When $\varepsilon =+1$, the singular strategy is unstable on an evolutionary time scale and there is a similar transition in ESS type

The second pair is given by the normal form $f(x,y) =\varepsilon (y-x)(y-x+x^2)$ with universal unfolding $F(x,y,a) = \varepsilon (y-x)(y-x+x^2+a)$; it consists of singularities that are degenerate CvSS with nondegenerate ESS. Strategy functions with $a<0$ have no singular points whereas they have a $\mathrm {CvSS}_+$–$\mathrm {CvSS}_-$ pair of nondegenerate singular points for $a>0$. See Fig. 4.

Fig. 4

Codimension one unfolding of degenerate $\mathrm {CvSS}_0$: $\varepsilon (y-x)(y-x+x^2+a)$. Two singular strategies, one of which is stable on an evolutionary time scale and the other unstable, coalesce and disappear as $a$ increases through $0$. The type of ESS depends on the the sign of $\varepsilon$. In addition, there is a transition in the regions of advantage and disadvantage

Codimension two In Fig. 5, we show invasibility plots for the codimension two normal form $f(x,y)=\varepsilon (y-x)(y-x+\delta x^3)$ (Theorem 5.5 (c) when $k=2$). This normal form is a higher codimension example of a strategy function with a $\mathrm {CvSS}_0$ singularity. The universal unfolding of $f(x,y)$ is

$$\begin{aligned} F(x,y,a,b)=\varepsilon (y-x)(y-x+\delta x^3+a+bx) \end{aligned}$$

$F(\cdot ,a,b)$ has a singular strategy for all values of $a,b$ given by the intersection of the zero set of the cubic payoff function $g(x,y)=y-x+\delta x^3+a+bx$ and the diagonal $x=y$. The transition variety consists of $\fancyscript{C}=\{a^2=\frac{4}{27} \delta b^3\}$ and is a cusp in the $ab$ plane. The complement of this transition variety consists of two disconnected components. In one component, $F(\cdot ,a,b)$ has a single nondegenerate singular strategy. In the other component, $F(\cdot ,a,b)$ has three nondegenerate singular strategies. See Fig. 5. The precise types of these singularities depend on $\varepsilon$ and $\delta$ as shown in that figure.

Fig. 5

Codimension two unfoldings of the four degenerate $\mathrm {CvSS}_0$ singularities given by $\varepsilon =\pm 1; \delta =\pm 1$; $H(x,y,a,b) = \varepsilon (y-x)(y-x+\delta x^3+a+bx)$

The transition from one to three singular points is a higher codimension analog of the CvSS transition in codimension one. In fact, the two newly formed singular points are necessarily a $\mathrm {CvSS}_+$,$\mathrm {CvSS}_-$ pair of nondegenerate singular points which preserve the ESS type of the degenerate point. Note that two bounded signed regions form during this transition.

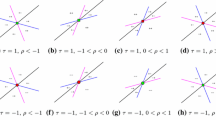
Codimension three; topological codimension two In Figs. 6, 7, 8 and 9, we show transition varieties and pairwise invasibility plots for the topological codimension two normal form

$$\begin{aligned} f(x,y)=(y-x)((x+\sigma (y-x))^2+\delta y^2) \end{aligned}$$

These normal forms have codimension three and are the simplest examples of strategy functions that have a $\mathrm {CvSS}_0\mathrm {ESS}_0$ singularity. The parameter $\sigma$ is a modal parameter (see [11, Chap V]; that is, strategy functions for different $\sigma$ are strategy inequivalent, but they all have the same codimension (in this case three). The universal unfolding of $f(x,y)$ is

$$\begin{aligned} F(x,y,a,b,\tau )=(y-x)((x+(\sigma +\tau )(y-x))^2+\delta y^2+a+b(y-x)), \end{aligned}$$

where $a,b,\tau$ are near $0$. The parameters $a,b$ are unfolding parameters (of the entire codimension three one-parameter family $f$ that depends on $\sigma$). Therefore, $f$ is said to have $C^{\infty }$ codimension three and topological codimension two.

Fig. 6

Transition variety $\fancyscript{T}$ in $ab$ plane for the topological codimension two normal form $h(x,y)=(y-x)((x+\sigma (y-x))^2+(y-x)^2)$. See Fig. 7 for associated pairwise invasibility plots

Fig. 7

Pairwise invasibility plots for the topological codimension two universal unfolding $H(x,y)=(y-x)((x+\sigma (y-x))^2+(y-x)^2+a+b(y-x))$ for regions given in Fig. 6

Fig. 8

Transition variety $\fancyscript{T}$ in $ab$ plane for the topological codimension two normal form $h(x,y)=(y-x)((x+\sigma (y-x))^2-(y-x)^2$. See Fig. 9 for the associated pairwise invasibility plots

Fig. 9

Pairwise invasibility plots for the topological codimension two universal unfolding $H(x,y)=(y-x)((x+\sigma (y-x))^2-(y-x)^2+a+b(y-x))$ for regions given in Fig. 8

Different types of pairwise invasibility plots corresponding to parameters $a,b$ (for fixed $\sigma$) are enumerated by connected components of the complement of the transition variety, where

$$\begin{aligned} \fancyscript{C}=\{a=0\} \quad \fancyscript{E}=\{b^2=-4a\sigma ^2\} \quad \fancyscript{B}=\{b^2=4a\delta \}. \end{aligned}$$

For a fixed value of $\sigma$, these varieties are given as a line and two parabolas in the $ab$ plane.

Persistent invasibility plots consist of the diagonal $x=y$ and either an ellipse ($\delta =+1$) or an hyperbola ($\delta =1$). The possible intersections of the conic with the diagonal depend on $\sigma$ in certain ranges: $\sigma <0$ or $\sigma >0$ in the elliptical case or $\sigma <-1, -1<\sigma <0,0<\sigma <1,1<\sigma$ in the hyperbolic case. See the transition varieties and their complements in Figs. 6 and 8.

3 The Dieckmann–Metz Example

Dieckmann and Metz [5] consider generalizations of the classical hawk-dove game that lead to strategy functions. The hawk-dove game has two players $A$ and $B$ who can play either a hawk strategy or a dove strategy with payoffs given in Table 5. Here $V > 0$ is a reward and $C \ge 0$ is a cost. The entries in the matrix give the payoff that player A receives when different combinations of strategies are pursued. Specifically, when both players play hawk, the players share equally the reward $V$ and the cost $C$. When both players play the dove strategy, the reward $V$ is shared equally by both players. Finally, when one player plays hawk and the other plays dove, the player playing hawk gets the reward $V$. Hence, the payoff matrix for player A is the one in Table 5.

Table 5 The hawk-dove game

In fact, [5] considers a game where $A$ plays hawk with probability $x$ (and therefore dove with probability $1-x$) and $B$ plays hawk with probability $y$. Dieckmann and Metz then show that the advantage for $B$ in this game is given by the strategy function

$$\begin{aligned} f(x,y)=(y-x)(V-Cx) \end{aligned}$$

(3.1)

Note that for $x^*= V/C$, $f(x^*,y)=0$ for all $y$. Therefore, $B$ has no advantage or disadvantage against $A$ when $A$ plays $x^*$. Direct calculation shows that $f=f_y=f_{yy}=0$ and $f_{xx}>0$ at $(x^*,x^*)$. Hence, $f$ has a codimension one $\mathrm {ESS}_0$ singularity at $(x^*,x^*)$ whose universal unfolding is

$$\begin{aligned} F(x,y,a)=f(x,y) + a(y-x)(y-x^*), \end{aligned}$$

where $a$ near $0$. The universal unfolding $F$ has two different outcomes based on the sign of $a$. If $a>0$ then $B$ has an advantage for all strategies, whereas if $a<0$, then $B$ has a disadvantage for all strategies. In other words, the ESS type at the singular strategies changes under small perturbations. Dieckmann and Metz refer to $f$ as a degenerate game.

Dieckmann and Metz consider variations of (3.1) that lead to parametrized families of strategy functions, which are based on various ecological assumptions [5]. Their most complicated game has the form

$$\begin{aligned} f(x,y)=\ln \left( \frac{1+Q(x,y)}{1+Q(x,x)}\right) , \end{aligned}$$

(3.2)

where

$$\begin{aligned} Q(x,y)&= A(x,y)B(x,y)/R \\ A(x,y)&= \frac{1}{2}\sqrt{P(x)P(y)} \\ P(x)&= r_0+r_1(x-x_0)+r_2(x-x_0)^2\\ B(x,y)&= V(1-x+y)-Cxy. \end{aligned}$$

The strategy function (3.2) has parameters $V,C,R,r_0>0$ and $x_0,r_1,r_2$ which are fixed. We will choose $f$ so that it has a singularity at $(x_0,x_0)$. Therefore, we need $f(x_0,x_0)$ to be defined, that is, we require $1+Q(x_0,x_0)>0$, which follows from assuming

$$\begin{aligned} x_0^2 < \frac{r_0V+2R}{r_0C}. \end{aligned}$$

(3.3)

In [5], Dieckmann and Metz claim that the strategy function (3.2) has the same $\mathrm {ESS}_0$ degeneracy as in (3.1) for certain parameter values. In Theorem 3.2 (a), we verify the existence of this codimension one singularity using the techniques in this paper. We also note that our classification theorem gives us a way to calculate degenerate singularities in a given model. (Such degeneracies were called an organizing centers by Thom [17] and Zeeman [21].) We can do this by checking certain derivatives and following the logic in the flow chart in Fig.1. Indeed, by using these techniques, we extend the analytic results of Dieckmann and Metz on the hawk-dove system [5] in Theorem 3.2 (b,c). In our calculations, we show that singularities of (3.2) and their respective types can be given in terms of $Q$ and its derivatives.

Lemma 3.1

The strategy function (3.2) has a singular strategy at $(x_0,x_0)$ if and only if $Q_y(x_0,x_0)=0$. Moreover, at a singular strategy

$$\begin{aligned} \mathrm {sgn}(f_{xx})&= -\mathrm {sgn}(2Q_{xy}+Q_{yy})\nonumber \\ \mathrm {sgn}(f_{yy})&= \mathrm {sgn}(Q_{yy})\nonumber \\ \mathrm {sgn}(f_{yy}-f_{xx})&= \mathrm {sgn}(Q_{xy}+Q_{yy}). \end{aligned}$$

(3.4)

Proof

Observe that

$$\begin{aligned} f_x(x,y)&=\frac{Q_x(x,y)}{1+Q(x,y)}-\frac{Q_x(x,x)+Q_y(x,x)}{1+Q(x,x)} \nonumber \\ f_y(x,y)&=\frac{Q_y(x,y)}{1+Q(x,y)} \end{aligned}$$

(3.5)

Therefore, since $1+Q(x_0,x_0)$ is assumed positive, $f$ has a singular strategy at $(x_0,x_0)$ if and only if $Q_y(x_0,x_0)=0$. If $(x_0,x_0)$ is a singular strategy of (3.2), then a calculation using (3.5) shows that at $(x_0,x_0)$.

$$\begin{aligned} f_{xx}&=-\frac{2Q_{xy}+Q_{yy}}{1+Q}\\ f_{yy}&=\frac{Q_{yy}}{1+Q}\\ f_{yy}-f_{xx}&= 2\frac{Q_{xy}+Q_{yy}}{1+Q} \end{aligned}$$

from which (3.4) follows. $\square$

Theorem 3.2

The following singularities and their universal unfoldings may be found in (3.2).

• (a) Fix

  $$\begin{aligned} V \ne C, r_1=r_2=0, \quad and \quad x_0=V/C. \end{aligned}$$

  (3.6)

  Assume

  $$\begin{aligned} r_0V\left( 1-\frac{V}{C}\right) >-2 \end{aligned}$$

  (3.7)

  Then the strategy function $f(x,y)$ near $(x_0,x_0)$ is strategy equivalent to

  $$\begin{aligned} h=-(y-x)x. \end{aligned}$$

  Let $F(x,y,r_2)$ be the unfolding of $f$ obtained by letting $r_2$ vary near $0$. Then $F$ is a universal unfolding of $f$.

• (b) Fix

  $$\begin{aligned} x_0=0,r_0=1, r_1=-2, r_2=0, 3V=C \end{aligned}$$

  (3.8)

  Then the strategy function $f(x,y)$ near $(0,0)$ is strategy equivalent to

  $$\begin{aligned} h=(y-x)(y-x+x^2). \end{aligned}$$

  Let $F(x,y,r_1)$ be the unfolding of $f$ obtained by letting $r_1$ vary near $-2$. Then $F$ is a universal unfolding of $f$.

• (c) Fix

  $$\begin{aligned} x_0=-3, r_0=2,r_1=2,r_2=1, V=C=\frac{1}{9} \end{aligned}$$

  (3.9)

  Then the strategy function $f(x,y)$ near $(-3,-3)$ is strategy equivalent to

  $$\begin{aligned} h=(y-x)((x+\frac{21}{\sqrt{13}}(y-x))^2+(y-x)^2). \end{aligned}$$

  Let $F(x,y,r_1,r_2)$ be the unfolding of $f$ obtained by letting $(r_1,r_2)$ vary near $(2,1)$. Then $F$ is a universal unfolding of $f$.

Remark 3.3

In their pictures, Dieckmann and Metz [5] assume

$$\begin{aligned} V = \frac{1}{2} \quad C=1 \quad R=2 \quad r_0=1 \end{aligned}$$

which satisfies (3.7). The pairwise invasibility plots for Theorem 3.2 (a) are given in Fig. 3, which are identical to those in [5]. The plots for Theorem 3.2 (b) are given in Fig. 4. Note that the degenerate singularity in (a) is the simplest form of a degenerate $\mathrm {ESS}_0$, the degenerate singularity in (b) is the simplest form of a degenerate $\mathrm {CvSS}_0$, and the singularity in (c) is one of the simplest degeneracies of both $\mathrm {ESS}_0$ and $\mathrm {CvSS}_0$ type. In particular, the hawk-dove model contains the pairwise invasibility plots associated with Fig. 4 ($\varepsilon =-1$) in case (b) and with Fig. 7 ($\sigma >0$) in case (c). Note that in diagram (2), there is a surprising region of advantage for player B that is surrounded by a region of disadvantage.

Lemma 3.4

Calculations yield

$$\begin{aligned} Q_y&= \frac{r_1(V-Cx_0^2)+2r_0(V-Cx_0)}{4R}\nonumber \\ Q_{yy}&= \frac{(4r_0r_2-r_1^2)(V-Cx_0^2)+ 2r_0r_1(V-Cx_0)}{4r_0R}\nonumber \\ Q_{xy}&= \frac{r_1(V-Cx_0^2)- 2r_0C(r_0+x_0r_1)}{4r_0R} \end{aligned}$$

(3.10)

Proof

These calculations are done directly from the definition of $Q$. $\square$

Remark 3.5

Suppose $F(x,y,\alpha )$ for $\alpha$ near $0$ is an unfolding of $f$. Then a calculation shows

$$\begin{aligned} F_{\alpha y}&=\frac{Q_{y\alpha }}{1+Q}-\frac{Q_{\alpha }Q_{y}}{(1+Q)^2} \\ F_{\alpha yy}&=\frac{Q_{yy\alpha }}{1+Q}-\frac{Q_{\alpha }Q_{yy}}{(1+Q)^2} \\ F_{\alpha xx}&=\frac{-2Q_{xy\alpha }+Q_{yy\alpha }}{1+Q}-\frac{Q_{\alpha }(-2Q_{xy}+Q_{yy})}{(1+Q)^2} \end{aligned}$$

at $(x_0,x_0,0)$.

Proof of Theorem 3.2: (a) From Table 1, we need to show that $f_x=f_y=f_{yy}=0$ and that $f_{yy}-f_{xx} <0$ at $(x_0,x_0)$. Note that $f_y=0$ and $f_{yy}=0$ if and only if $Q_y=0$ and $Q_{yy}=0$, which follow from (3.10) and (3.6). Since $f_x=-f_y$ for all strategy functions, $f_x=0$. Remark 3.4 shows that $\varepsilon =\mathrm {sgn}(f_{yy}-f_{xx}) = \mathrm {sgn}(Q_{xy})$, since $Q_{yy}=0$. It follows from (3.10) that $Q_{xy}<0$ and $\varepsilon =-1$. By Theorem (b), $f(x,y)$ is strategy equivalent to the normal form

$$\begin{aligned} h=-(y-x)x \end{aligned}$$

We show that $F(x,y,r_2)$ is a $1$-parameter universal unfolding. Using Table 2, we need

$$\begin{aligned} \det \begin{pmatrix} f_{yy}-f_{xx} &{}\quad f_{xyy}+f_{yyy} \\ 2F_{r_2y} &{}\quad F_{r_2 yy} \end{pmatrix} \ne 0 \end{aligned}$$

at $(x_0,x_0,0)$. Using the fact that $Q_{y}=0$ at $(x_0,x_0)$ and Remark 3.5, we note that

$$\begin{aligned} F_{r_2y}=\frac{Q_{r_2y}}{1+Q}=0 \end{aligned}$$

We also showed earlier that $\mathrm {sgn}(f_{yy}-f_{xx})=\mathrm {sgn}(Q_{xy})=-1$. Therefore, $F$ is a $1$-parameter universal unfolding of $f$ if and only if

$$\begin{aligned} F_{r_2yy}\ne 0 \end{aligned}$$

at $(x_0,x_0,0)$. We calculate using the fact that $Q_{yy}=0$ and Remark 3.5 to find that

$$\begin{aligned} F_{r_2yy}=\frac{Q_{r_2yy}}{1+Q}=\frac{V}{R}\left( 1-\frac{V}{C}\right) \ne 0 \end{aligned}$$

which holds by (3.6). Condition (3.7) follows from (3.3).

(b) From Table 1, we need to show that $f=f_x=f_y=f_{yy}-f_{xx}=0$ and

$$\begin{aligned} E_1=f_{xxy}+2f_{xyy}+f_{yyy} \ne 0 \end{aligned}$$

at $(x_0,x_0)$. Note that $f_x=f_y=0$ and $f_{yy}-f_{xx}=0$ if and only if $Q_y=0$ and $Q_{xy}+Q_{yy}=0$, which follows from (3.10) and (3.8). Remark 3.4 shows that $\varepsilon =\mathrm {sgn}(f_{yy})=\mathrm {sgn}(Q_{yy})$. It follows from (3.10) that $Q_{yy}<0$ and $\varepsilon )=-1$. By Table 1, $f(x,y)$ is strategy equivalent to the normal form

$$\begin{aligned} h=-(y-x)(y-x+x^2) \end{aligned}$$

if and only if

$$\begin{aligned} E_1=-\frac{31V}{3R} \ne 0 \end{aligned}$$

which holds for (3.2).

We show that $F(x,y,r_1)$ is a universal unfolding near $r_1=-2$. Using Table 2, $F(x,y,r_1)$ is a $1$-parameter universal unfolding if and only if

$$\begin{aligned} F_{r_1y}\ne 0 \end{aligned}$$

at $(0,0,-2)$. By direct calculation, we find that $\displaystyle F_{r_1y}=\frac{2}{3R} \ne 0$; hence the result holds.

(c) Using Table 1, we need to show that the defining conditions $f_x=f_y=f_{xx}=f_{yy}=0$ and the nondegeneracy conditions

$$\begin{aligned} \begin{array}{l} E_1= f_{xxy}+2f_{xyy}+f_{yyy} \ne 0 \\ E_3=-(4f_{xxx}f_{yyy}+3(f_{xyy}+f_{yyy})^2)/36 \ne 0 \end{array} \end{aligned}$$

are satisfied at $(x_0,x_0)$. Note that (3.10) implies that the defining conditions are equivalent to $Q_y=Q_{xy}=Q_{yy}=0$, which holds for (3.9). By direct calculation

$$\begin{aligned} E_1=\frac{4}{R}>0 \qquad E_3=\frac{13}{144R^2}>0 \end{aligned}$$

at $(0,0,2,1)$. In particular, $\delta =\mathrm {sgn}(E_3)=1$. Therefore, by Table 1, $f(x,y)$ is strategy equivalent to the normal form

$$\begin{aligned} h=(y-x)((x+\sigma (y-x))^2+(y-x)^2). \end{aligned}$$

Note that in this normal form, we do not actually have to know the value of $\sigma$, though it is $21\sqrt{13}$. Using Table 2, we see that $F(x,y,r_1,r_2)$ is a $2$-parameter universal unfolding of $f$ if and only if

$$\begin{aligned} \det \begin{pmatrix} 0 &{}\quad f_{xxx}+f_{xxy} &{}\quad f_{xyy}+f_{yyy} \\ F_{r_1y} &{}\quad F_{r_1xx} &{}\quad F_{r_1yy} \\ F_{r_2y} &{}\quad F_{r_2xx} &{}\quad F_{r_2yy} \end{pmatrix} \ne 0 \end{aligned}$$

(3.11)

Since $Q_{y}$ is independent of $r_2$ by (3.10), Remark 3.5 implies $F_{r_2y}=0$. Note also that $Q_{xy}$ is independent of $r_2$ by (3.10). Remark 3.5 implies $F_{r_2xx}=F_{r_2yy}=-\frac{8}{9R} \ne 0$ at $(0,0,2,1)$. It is easy to check that $F_{r_1y}=-\frac{2}{9R} \ne 0$. In particular, (3.11) holds whenever

$$\begin{aligned} f_{xxx}+f_{xxy}-f_{xyy}-f_{yyy} \ne 0 \end{aligned}$$

(3.12)

Using Remark 3.5, we find that the expression in (3.12) equals $-\frac{8}{R}$ and hence the conclusion holds. $\square$

4 The Restricted Tangent Space

Let $f=(y-x)g$ and $\hat{f}=(y-x)\hat{g}$ be strategy functions with corresponding payoff functions $g$ and $\hat{g}$. We begin this section by proving that $\hat{f}$ is strategy equivalent to $f$ more or less if and only if $\hat{g}$ is strategy equivalent to $g$. See Proposition 4.2. The remainder of the section develops the techniques, particularly that of the restricted tangent space, needed to answer the question: When is $g+p$ strategy equivalent to $g$? Theorem 4.7 and Corollary 4.10 are important steps in answering this question.

4.1 Strategy Equivalence of Payoff Functions

The nondiagonal zero contour of the strategy function $f=(y-x)g$ is the set $g=0$. The following lemma relates singular points of $f$ on the diagonal to intersections of $g=0$ with the diagonal.

Lemma 4.1

A strategy function $f=(y-x)g$ has a singular strategy at $s$ if and only if $g(s,s)=0$. In addition,

• (a) $s$ is an ESS if and only if $g_y(s,s)<0$.

• (b) $s$ is a CvSS if and only if $g_x(s,s)+g_y(s,s)<0$.

Proof

Direct calculation shows that

$$\begin{aligned} f_y(s,s)&= g(s,s) \\ f_{yy}(s,s)&=2g_y(s,s) \\ f_{yy}(s,s)-f_{xx}(s,s)&= 2(g_x(s,s)+g_y(s,s)) \end{aligned}$$

Parts (a) and (b) follow from Definitions 1.2 and 1.3 of ESS and CvSS. $\square$

We now show that strategy equivalences lead to similar changes of coordinates on the corresponding payoff functions.

Proposition 4.2

$\hat{f}=(y-x)\hat{g}$ is strategy equivalent to $f=(y-x)g$ if and only if $\hat{g}(x,y)$ is strategy equivalent to either $g(x,y)$ or $-g(-x,-y)$.

Proof

Begin by observing that $f(x,y)$ is strategy equivalent to $f(-x,-y)= -(y-x)g(-x,-y)$.

We prove the proposition for left changes of coordinates described by $S$ and right changes of coordinates described by $\Phi$ separately. Note that for $S(x,y)>0$,

$$\begin{aligned} \hat{f}(x,y)=S(x,y) f(x,y) \quad \text { if and only if } \quad \hat{g}(x,y)=S(x,y)g(x,y) \end{aligned}$$

Hence, the proposition holds for left changes of coordinates.

Next, suppose

$$\begin{aligned} \hat{f}(x,y)=f(\Phi (x,y)) \end{aligned}$$

where $\Phi \equiv (\Phi _1,\Phi _2)$ satisfies Definition 1.7 (b)–(d). By Definition 1.7 (c),

$$\begin{aligned} \Phi _1(x,x)=\Phi _2(x,x) \end{aligned}$$

for all $x$. Therefore, there exists $\Omega :\mathbf {R}^2\rightarrow \mathbf {R}$ such that

$$\begin{aligned} \Phi _2(x,y)-\Phi _1(x,y)=(y-x)\Omega (x,y) \end{aligned}$$

Next, observe that

$$\begin{aligned} (y-x)\hat{g}(x,y)&=\hat{f}(x,y)\\&=f(\Phi (x,y))\\&=(\Phi _{2}(x,y)-\Phi _{1}(x,y))g(\Phi (x,y)) \\&=(y-x)\Omega (x,y)g(\Phi (x,y)) \end{aligned}$$

Therefore,

$$\begin{aligned} \hat{f}(x,y)=f(\Phi (x,y)) \quad \text { if and only if }\quad \hat{g}(x,y)=\Omega (x,y)g(\Phi (x,y)) \end{aligned}$$

By defintion $\Omega (x,x)=\Phi _{2y}(x,x)$, which is nonzero by Definition 1.7 (b). Therefore,

$$\begin{aligned} \Omega (x,y)g(\Phi (x,y)) \simeq g(\Phi (x,y)) \end{aligned}$$

If $\Omega (x,y)>0$, then $\hat{g}$ and $g$ are strategy equivalent. If $\Omega (x,y)<0$, then $\hat{g}(x,y)$ is strategy equivalent to $-g(-x,-y)$. Hence, the statement also holds for right changes of coordinates. $\square$

4.2 Restricted Tangent Space of a Payoff Function

Let $\mathcal {E}$ be the space of all payoff functions $g:\mathbf {R}^2 \rightarrow \mathbf {R}$ that are $C^{\infty }$ on some neighborhood of the origin. Suppose $g \in \mathcal {E}$ with $g(0,0)=0$. Singularity theory helps answer the recognition problem: When is the payoff function $\hat{g}$ strategy equivalent to the payoff function $g$? An important step to answering this question is

Question For which perturbations $p$ are $g+tp$ strategy equivalent to $g$ for all small $t$?

We answer the question by adapting the discussion in [11]. In particular, we first use differentiation with respect to $t$ to find a necessary condition on $p$. Suppose that $p\in \mathcal {E}$ satisfies $p(0,0)=0$. Suppose also that $g+tp$ is strongly strategy equivalent to $g$ for all small $t$. That is, suppose there exists a smooth $t$-dependent strategy equivalence such that

$$\begin{aligned} g(x,y)+tp(x,y)=S(x,y,t) g(\Phi (x,y,t)), \end{aligned}$$

(4.1)

where

$$\begin{aligned} \Phi (0,0,t) = (0,0) \quad \Phi _{1,y}(x,x,t)=0 \quad S(x,y,0)=1 \quad \Phi (x,y,0)=(x,y). \end{aligned}$$

(4.2)

Differentiating both sides of (4.1) with respect to $t$ and evaluating at $t=0$ gives

$$\begin{aligned} p(x,y) = \dot{S}(x,y,0) g(x,y) + \dot{\Phi }_1 (x,y,0) g_x(x,y) + \dot{\Phi }_2(x,y,0)g_y(x,y), \end{aligned}$$

(4.3)

where the dot indicates differentiation with respect to $t$. Note that $\dot{S}(x,y,0)$ can be chosen arbitrarily in (4.3), whereas $\dot{\Phi }(x,y,0)$ is restricted by conditions (4.2). Specifically,

$$\begin{aligned} \dot{\Phi }(x,x,0)= (0,0) \quad \text {and}\quad \dot{\Phi }_{1y}(x,x,0)=0 \end{aligned}$$

It follows that $p$ must satisfy

$$\begin{aligned} p(x,y)=a(x,y)g(x,y)+b(x,y) g_x(x,y)+c(x,y) g_y(x,y), \end{aligned}$$

(4.4)

where the function $a$ is arbitrary and the functions $b$ and $c$ satisfy

$$\begin{aligned} b(x,x)=c(x,x) \quad b(0,0)=0 \quad b_y(x,x)=0 \end{aligned}$$

(4.5)

Definition 4.3

The restricted tangent space of $g$, denoted $\mathrm {RT}(g)$, consists of all $p\in \mathcal {E}$ that satisfy (4.4) and (4.5)

The goal of this subsection is to explicitly determine $\mathrm {RT}(g)$ (see Proposition 4.6). To do this, we will use the fact that $\mathcal {E}$ is a commutative algebra (addition and multiplication of functions in $\mathcal {E}$ stay in $\mathcal {E}$) and some facts about ideals in $\mathcal {E}$ of finite codimension.

4.2.1 Maximal Ideals and Finite Codimension

An ideal $\mathcal {J}$ is finitely generated if there exist $q_1,\ldots ,q_k\in \mathcal {J}$ such that every element in $\mathcal {J}$ has the form $a_1q_1+\cdots +a_kq_k$ where $a_j\in \mathcal {E}$. In this case, we denote $\mathcal {J}$ by $\langle q_1,\ldots ,q_k\rangle$.

A vector subspace $W\subset \mathcal {E}$ has finite codimension if there is a finite-dimensional subspace $V\subset \mathcal {E}$ such that $\mathcal {E}=W+V$. If no such subspace exists, we say that $W$ has infinite codimension.

The maximal ideal in $\mathcal {E}$ is

$$\begin{aligned} \mathcal {M}=\{a \in \mathcal {E}: a(0,0)=(0,0)\}. \end{aligned}$$

Taylor’s Theorem implies that $\mathcal {M}=\langle x,y\rangle$. The product ideal $\mathcal {M}^k=\langle x^k,x^{k-1}y,\ldots , y^k \rangle$ consists of all functions whose Taylor expansion at the origin vanishes through order $k-1$.

A standard theorem from commutative algebra states (cf. [11, Proposition II, 5.7]):

Proposition 4.4

Let $\mathcal {I}\subset \mathcal {E}$ be an ideal. There is an integer $k$ such that $\mathcal {M}^k \subset \mathcal {I}$ if and only if $\mathcal {I}$ has finite codimension.

Nakayama’s Lemma helps determine when ideals have finite codimension. In its simplest form, Nakayama’s Lemma states

$$\begin{aligned} \mathcal {M}^k\subset \mathcal {J}\quad \text {if and only if}\quad \mathcal {M}^k\subset \mathcal {J}+\mathcal {M}^{k+1} \end{aligned}$$

More generally (see [11, Lemma II, 5.3]):

Lemma 4.5

(Nakayama’s Lemma) Let $\mathcal {I}$ is a finitely generated ideal. Then

$$\begin{aligned} \mathcal {I}\subset \mathcal {J}\quad \text {if and only if}\quad \mathcal {I}\subset \mathcal {J}+\mathcal {M}\mathcal {I}\end{aligned}$$

4.2.2 Computation of the Restricted Tangent Space $\mathrm {RT}(g)$

With this background, we can compute the restricted tangent space of a payoff function $g$. Define

$$\begin{aligned} \mathcal {I}(g)= \langle g,(y-x)g_y, (y-x)^2g_x \rangle \end{aligned}$$

(4.6)

We say that $g$ has finite codimension if $\mathcal {I}(g)$ has finite codimension.

Proposition 4.6

Let $g$ be a payoff function with finite codimension. Then

$$\begin{aligned} \mathrm {RT}(g) = \mathcal {I}(g) + \mathbf {R}\{x(g_x+g_y), \ldots , x^s(g_x+g_y)\} \end{aligned}$$

(4.7)

for some $s$.

Proof

Suppose $p\in \mathrm {RT}(g)$. By Definition 4.3, there exist functions $a(x,y), b(x,y), c(x,y)$ satisfying (4.5) such that $p$ satisfies (4.4). We claim that $b,c$ satisfy (4.5) if and only if there exist functions $\ell (x,y), n(x,y), q(x)$ such that

$$\begin{aligned} b(x,y)&= xq(x)+(y-x)^2m(x,y)\nonumber \\ c(x,y)&= xq(x)+(y-x)n(x,y) \end{aligned}$$

(4.8)

To verify (4.8), first let $d(x)=b(x,x)=c(x,x)$ and note that $d(0)=0$. Hence $d(x)=xq(x)$. Next, note that there exist functions $\ell (x,y),n(x,y)$ such that

$$\begin{aligned} b(x,y)&= xq(x)+(y-x)\ell (x,y)\nonumber \\ c(x,y)&= xq(x)+(y-x)n(x,y) \end{aligned}$$

(4.9)

Finally, since $b_y(x,x)=\ell (x,x)$, it follows that $\ell (x,x)=0$. Hence there exists $m(x,y)$ such that $\ell (x,y)=(y-x)m(x,y)$, thus verifying the claim.

The claim along with (4.4) shows that

$$\begin{aligned} p&= ag+n(y-x)g_y+m(y-x)^2g_x+q(x)x(g_x+g_y) \\&\in \mathcal {I}(g) + \mathbf {R}\{x(g_x+g_y),\ldots ,x^s(g_x+g_y),\ldots \}. \end{aligned}$$

Since $\mathcal {I}(g)$ has finite codimension, it follows from Proposition 4.4 that $\mathcal {M}^{s+1}\subset \mathcal {I}(g)$ for some $s$. Since $x^{s+1}(g_x+g_y)\in \mathcal {M}^{s+1}$, it follows that all terms after $x^s(g_x+g_y)$ are in $\mathcal {I}(g)$. $\square$

4.3 Modified Tangent Space Constant Theorem

The definition of $\mathrm {RT}(g)$ implies that if $g+tp$ is strategy equivalent to $g$ for all small $t$, then $p \in \mathrm {RT}(g)$. In the converse direction, we have the following theorem.

Theorem 4.7

(Modified Tangent Space Constant Theorem) Let $g$ be a payoff function. If

$$\begin{aligned} \mathcal {I}(g+tp)=\mathcal {I}(g) \text { for all } t \in [0,1], \end{aligned}$$

(4.10)

Then $g+tp$ is strategy equivalent to $g$ for all $t\in [0,1]$.

Remark 4.8

The proof of this theorem is a straightforward modification of the proof of an analogous theorem in bifurcation theory (see [11, Chapter II Theorem 2.2]). The details of the proof, which are standard in singularity theory, are in Vutha [19].

Definition 4.9

A payoff function $g(x,y)$ is $k$-determined if $g+h \simeq g$ for all $h\in \mathcal {M}^{k+1}$.

Corollary 4.10

If $\mathcal {M}^k\subset \mathcal {I}(g)$, then $g$ is $k$-determined.

Proof

Let $h\in \mathcal {M}^{k+1}$. We claim that $\mathcal {I}(g+th)$ is independent of $h$. Since

$$\begin{aligned} h, (x-y)^2h_x, (x-y)h_y\in \mathcal {M}^{k+1}\subset \mathcal {I}(g), \end{aligned}$$

it follows that

$$\begin{aligned} \mathcal {I}(g+th) = \langle g+th, (x-y)^2(g_x+th_x), (x-y)(g_y+th_y)\rangle \subset \mathcal {I}(g) + \mathcal {M}^{k+1}\subset \mathcal {I}(g) \end{aligned}$$

Conversely,

$$\begin{aligned} \mathcal {I}(g+th) \subset \mathcal {I}(g) + \mathcal {M}^{k+1}\subset \mathcal {I}(g)+\mathcal {M}\mathcal {I}(g). \end{aligned}$$

Nakayama’s Lemma 4.5 implies that $\mathcal {I}(g+th) = \mathcal {I}(g)$ for all $t$. By Theorem 4.7, $g+h \simeq g$. $\square$

5 Recognition of Low Codimension Singularities

In this section, we use Theorem 4.7 and Corollary 4.10 to solve the recognition problem for payoff function singularities of low codimension appearing. The results are summarized in Table 1. We found that the calculations are more easily done in the coordinates

$$\begin{aligned} u = x \quad v = y-x \qquad x = u \quad y = u + v. \end{aligned}$$

We translate the singularity theory methods to $uv$ coordinates in Sect. 5.1 and we perform the actual calculations in Sect. 5.2.

5.1 A Change of Coordinates

Given a payoff function $g(x,y)$ write $g(x,y)$ as $g'(u,v)$ in $uv$ coordinates. That is,

$$\begin{aligned} g(x,y) = g(u,u+v) \equiv g'(u,v) \end{aligned}$$

Observe that

$$\begin{aligned} \begin{array}{l} g'_u(u,v) = g_x(u,u+v)x_u + g_y(u,u+v)y_u = g_x(x,y) + g_y(x,y) \\ g'_v(u,v) = g_x(u,u+v)x_v + g_y(u,u+v)y_v = g_y(x,y) \end{array} \end{aligned}$$

Hence

$$\begin{aligned} g_x(x,y) = g'_u(u,v)-g'_v(u,v) \qquad g_y(x,y) = g'_v(u,v) \end{aligned}$$

and

$$\begin{aligned} \mathcal {I}(g) = \langle g, (y-x)g_y, (y-x)^2g_x \rangle = \langle g', vg'_v, v^2(g'_u-g'_v)\rangle = \langle g', vg'_v, v^2g'_u\rangle \end{aligned}$$

(5.1)

Remark 5.1

We will calculate the normal forms for payoff functions $g(x,y)$ written in $uv$ coordinates. We continue to call the payoff functions $g(u,v)$ rather than $g'(u,v)$.

Proposition 5.2

In $uv$ coordinates, we have

• (a) $\mathcal {M}=\{g:g(0,0)=0\}=\langle u,v \rangle$

• (b) $\mathcal {I}(g)=\langle g, vg_v, v^2 g_u \rangle$

• (c) $\mathrm {RT}(g)=\mathcal {I}(g)+\mathbf {R}\{ug_u, u^2g_u, \ldots \}$

Proof

(a) follows directly from the definition of $\mathcal {M}$ and Taylor’s theorem in $uv$ coordinates. (b) follows from (5.1) on dropping the primes. Recall from (4.7) that

$$\begin{aligned} \mathrm {RT}(g) = \mathcal {I}(g) + \mathbf {R}\{x(g_x+g_y), \ldots , x^s(g_x+g_y)\}. \end{aligned}$$

Hence (c) follows from the fact that $x=u$ and $g_x+g_y=g_u$. $\square$

We can also write the change of coordinates in terms of the map

$$\begin{aligned} \psi (u,v) \equiv (u,u+v) =\left( \begin{array}{rrrrrrrrrrrrrrrrrr} 1 &{}\quad 0\\ 1 &{}\quad 1 \end{array}\right) \left( \begin{array}{rrrrrrrrrrrrrrrrrr} u\\ v \end{array}\right) \end{aligned}$$

When we do so we write $g' = g\circ \psi$. Next we describe the form that strategy equivalences take in $uv$ coordinates.

Proposition 5.3

Suppose that the payoff functions $g,\hat{g}$ are strategy equivalent. That is $\hat{g} = Sg\circ \Phi$ where $S$ and $\Phi$ satisfy Definition 1.7. Let $g'=g\circ \psi$ and $\hat{g}' = \hat{g}\circ \psi$. Then $g'$ and $\hat{g}'$ are contact equivalent; that is

$$\begin{aligned} \hat{g}' = S'g'\circ \Phi ', \end{aligned}$$

where $S' = S\circ \psi$ and $\Phi ' = \psi ^{-1}\circ \Phi \circ \psi$. Moreover

$$\begin{aligned} \Phi '_2(u,0) = 0 \quad \text{ and } \quad \Phi '_{1,v}(u,0) = 0. \end{aligned}$$

(5.2)

Proof

We compute

$$\begin{aligned} \hat{g}' =\hat{g}\circ \psi&= (Sg\circ \Phi )\circ \psi \\&= (S\circ \psi )(g\circ \psi \circ \psi ^{-1}\circ \Phi \circ \psi ) \\&= S'(g\circ \psi \circ \Phi ') \\&= S'g'\circ \Phi ', \end{aligned}$$

as desired. Note that the diagonal $y=x$ is $v=0$ in the $uv$ coordinates. Therefore,

$$\begin{aligned} \Phi '(u,0) = (\Phi '_1(u,0),\Phi '_2(u,0)) \end{aligned}$$

implies that $\Phi '_2(u,0)=0$. Moreover, the derivative with respect to $y$ corresponds to the derivative with respect to $v$. So, $\Phi _{1,y}(x,x)=0$ implies that $\Phi '_{1,v}(u,0)=0$. $\square$

Remark 5.4

It follows from (5.2) that $S'(u,v)$ satisfies $S(u,v)>0$ and $\Phi '(u,v)$ is a diffeomorphism that satisfies $\Phi '(u,0)= (\phi (u),0)$ and that

$$\begin{aligned} (d\Phi ')_{u,0} = \begin{pmatrix} a &{}\quad 0\\ 0 &{}\quad b \end{pmatrix}. \end{aligned}$$

5.2 Recognition of Low Codimension Singularities

We now present normal form theorems for singularities of low codimension. In this subsection, all derivatives are computed at the origin unless otherwise indicated. Also, we denote the $i$th derivative of $g$ with respect to $u$ at the origin by $g_u^{(i)}$.

Theorem 5.5

Suppose $g=0$ at $(0,0)$.

• (a) Then $g \simeq \varepsilon u+\delta v$ where $\varepsilon =\mathrm {sgn}(g_u)$ and $\delta = \mathrm {sgn}(g_v)$ if and only if $g_v \ne 0$ and $g_u \ne 0$.

• (b) Suppose $g_v=0$ and $\varepsilon =\mathrm {sgn}(g_u)$. Then $g \simeq \varepsilon u$ if and only if $g_u\ne 0$.

• (c) Suppose $g_u=\cdots =g^{(k-1)}_u=0$, $\varepsilon =\mathrm {sgn}(g_{v})$, and $\delta =\varepsilon \mathrm {sgn}(g^{(k)}_{u})$. Then $g \simeq \varepsilon (v+\delta u^k)$ if and only if $g_v \ne 0$ and $g^{(k)}_{u} \ne 0$. Moreover, when $k$ is even we may take $\delta =+1$.

• (d) Suppose $g_u=g_v=0$, $g_{uu}\ne 0$, $E\equiv g_{uu}g_{vv}-g_{uv}^2\ne 0$ and $\sigma \equiv g_{uv}/\sqrt{E}$. Then

  $$\begin{aligned} g(u,v) \simeq (u+\sigma v)^2 + \delta v^2, \end{aligned}$$

  where $\delta =\mathrm {sgn}(E)$. Moreover, $\sigma$ is a modal parameter.

Proof

(a) Since $g(0,0)=0$, use Taylor’s theorem to write $g(u,v) = g_u u+g_v v + \cdots$. Note that $g\circ \Phi$ where $\Phi (u,v) = (u/|g_u|,v/|g_v|)$ yields $g \simeq \varepsilon u+ \delta v + \cdots$. Next calculate $\mathcal {I}(\varepsilon u+\delta v)=\mathcal {M}$. It follows from Corollary 4.10 that $\varepsilon u+\delta v$ is 1-determined and $g$ has the desired normal form. The converse is straightforward.

(b) Since $g=g_v=0$, use Taylor’s Theorem to write $g = g_u u+p$ where $p \in \mathcal {M}^2$. Divide by $|g_u|$ to obtain $g \simeq \varepsilon (u+p)$ for $\varepsilon =\mathrm {sgn}(g_v)$ and a modified $p \in \mathcal {M}^2$. WLOG we can assume $\varepsilon =+1$. Dividing $u+p$ by $1+\frac{1}{2}p_{uu}u^2+p_{uv}uv$ shows that $u+p$ is strategy equivalent to $u+av^2+q$ where $a\in \mathbf {R}$ and $q\in \mathcal {M}^3$. It follows that

$$\begin{aligned} \mathcal {I}(u+av^2+q)&\equiv \langle u+av^2+q, v^2(1+q_u(u,v)), 2av^2+ vq_v(u,v) \rangle \\&= \langle u+av^2+q, v^2, 2av^2+ vq_v(u,v) \rangle \\&= \langle u+q, v^2, vq_v(u,v) \rangle \\&= \langle u,v^2\rangle \end{aligned}$$

for all $a\in \mathbf {R}$ and $q\in \mathcal {M}^3$. Then use Theorem 4.7 to conclude that $g$ has the desired normal form. The converse is straightforward.

(c) Assume $g=g_u=\cdots =g^{(k-1)}_{u}=0$ and $g_v \ne 0\ne g^{(k)}_{u}$. By Taylor’s theorem

$$\begin{aligned} g(u,v)=(g_v + p_1(u,v))v + u^kp_2(u,v), \end{aligned}$$

where $p_1 \in \mathcal {M}$ and $p_2(0,0)\ne 0$. Dividing by $\varepsilon (g_v+p_1(u,v))$ yields $g \simeq \varepsilon (v+\delta u^k p)$ where $p(0,0)> 0$. Now compute

$$\begin{aligned} \mathcal {I}(v+\delta u^kp) = \langle v+\delta u^kp, v(1+u^kp_v(u,v)), v^2u^{k-1}(p_u(u,v)+up)\rangle = \langle u^kp, v \rangle = \langle u^k,v\rangle \end{aligned}$$

Therefore, by Theorem 4.7, $g \simeq \varepsilon (v+\delta u^k)$. Note that when $k$ is even, the equivalence of $g$ with $-g(-u,-v)$ allows us to set $\delta =1$.

(d) Since $g=g_u=g_v=0$ at $(0,0)$, use Taylor’s theorem and multiply by $2$ to obtain

$$\begin{aligned} g(u,v) \simeq g_{uu} u^2+2g_{uv}uv+ g_{vv} v^2 + p, \end{aligned}$$

where $p \in \mathcal {M}^3$. Using the transformation $g\mapsto -g(-u,-v)$ if needed, we can assume $\mathrm {sgn}(g_{uu})=1$. Dividing by $g_{uu}$, we get

$$\begin{aligned} g \simeq u^2+Buv+Cv^2+p, \end{aligned}$$

where $p\in \mathcal {M}^3$ and

$$\begin{aligned} B=2\frac{g_{uv}}{g_{uu}} \quad \text{ and } \quad C=\frac{g_{vv}}{g_{uu}}. \end{aligned}$$

Complete the square and rewrite $g$ as

$$\begin{aligned} g = (u+\sigma _1 v)^2+\rho _1 v^2+p, \end{aligned}$$

where $\sigma _1=\frac{g_{uv}}{g_{uu}}$ and $\rho _1=\frac{E}{g_{uu}^2}$. Rescaling $v$ leads to

$$\begin{aligned} g \simeq (u+\sigma v)^2+\delta v^2+p. \end{aligned}$$

Let $h = (u+\sigma v)^2+\delta v^2$. We claim $\mathcal {M}^3 \subset \mathcal {I}(h)$. It follows from Corollary 4.10 that $h$ is $2$-determined, thus proving the assertion. Compute

$$\begin{aligned} \mathcal {I}(h) = \langle (h, v^2 (u+\sigma v), v(\sigma (u+\sigma v)+\delta v) \rangle \end{aligned}$$

Note that $\mathcal {M}^3=\langle (u+\sigma v)^3,(u+\sigma v)^2v,(u+\sigma v)v^2,v^3 \rangle$. Since the determinant of the $4\times 4$ matrix in Table 6 is $-\delta \ne 0$, it follows that $\mathcal {M}^3\subset \mathcal {I}(h)$ as desired. Note that the normal forms for different $\sigma$ are all payoff inequivalent. Parameters that lead to continuous families of inequivalent functions are called modal parameters; so $\sigma$ is a modal parameter. $\square$

Table 6 Calculation of elements of $\mathcal {I}(p)$ in $\mathcal {M}^3$

5.3 Translation of Results from Payoff to Strategy Functions

Tables 7 and 8 summarize the calculations needed to translate results from payoff functions $g(u,v)$ to strategy functions $f(x,y)$. For example, consider the defining and nondegeneracy conditions

$$\begin{aligned} g=g_v=0 \quad g_u \ne 0 \end{aligned}$$

(5.3)

in Theorem 5.5(b). Since

$$\begin{aligned} g_v(u,0)=g_y(x,x) \quad g_u(u,0)=g_x(x,x)+g_y(x,x), \end{aligned}$$

(5.3) can be rewritten as

$$\begin{aligned} g=g_y=0 \quad g_x \ne 0. \end{aligned}$$

Moreover, in terms of the corresponding strategy function $f=(y-x)g$

$$\begin{aligned} \begin{array}{lclclcl} f &{} = &{} (y-x)g &{}&{}&{}&{}\\ f_x &{} = &{} (y-x)g_x-g &{} \qquad &{} f_{y} &{} = &{} (y-x)g_x+g \\ f_{xx} &{} = &{} (y-x)g_x-2g_x &{} \qquad &{} f_{yy} &{} = &{} (y-x)g_y+2g_y \end{array} \end{aligned}$$

(5.4)

In particular, (5.3) holds at $(x,x)$ whenever

$$\begin{aligned} f=f_x=f_y=f_{yy}=0 \quad f_{xx} \ne 0 \end{aligned}$$

Tables 7 and 8 show calculations for payoff functions and their derivatives up to third order. See Tables 1 and 2 for the translated results.

Table 7 Translation of derivatives at $(u,0)$ in $uv$ coordinates to $(x,x)$ in $xy$ coordinates

Table 8 Translation of derivatives from payoff functions $g$ to strategy functions $f$ at $(x,x)$

6 The Universal Unfolding Theorem

Unfolding theory could be described in terms of either strategy or payoff functions and in either $xy$ or $uv$ coordinates. In this section, we discuss unfolding theory of payoff functions in $uv$ coordinates.

Definition 6.1

Let $g \in \mathcal {E}$. The function $G: \mathbf {R}^2 \times \mathbf {R}^k$ is a k-parameter unfolding of $g$ if

$$\begin{aligned} G(u,v,0)=g(u,v) \end{aligned}$$

Suppose $G(u,v,\alpha )$, $\alpha \in \mathbf {R}^k$, and $H(u,v,\beta )$, $\beta \in \mathbf {R}^\ell$ are unfoldings of $g$. We say that the perturbations in the $H$ unfolding are contained in the $G$ unfolding if for every $\beta \in \mathbf {R}^l$, there exists $A(\beta ) \in \mathbf {R}^k$ such that $G(\cdot , \cdot ,A(\beta ))$ is strategy equivalent to $H(\cdot , \cdot , \beta )$. We formalize this in the following definition.

Definition 6.2

Let $G(u,v,\alpha )$ be a $k$-parameter unfolding of $g \in \mathcal {E}$ and let $H(u,v,\beta )$ be an $\ell$-parameter unfolding of $g$. We say that H factors through G if there exist maps $S:\mathbf {R}^2\times \mathbf {R}^\ell \rightarrow \mathbf {R}$, $\Phi :\mathbf {R}^2\times \mathbf {R}^\ell$, and $A:\mathbf {R}^\ell \rightarrow \mathbf {R}^k$ such that

$$\begin{aligned} H(u,v,\beta )=S(u,v,\beta )G(\Phi (u,v,\beta ), A(\beta )), \end{aligned}$$

where

• (a) $S(u,v,0)=1$

• (b) $\Phi (u,v,0)=(u,v)$

• (c) $\Phi _1(0,0,\beta )=\Phi _2(u,0,\beta )$

• (d) $\Phi _{1y}(u,0,\beta )=0$

• (e) $A(0)=0$

Remark 6.3

We do not require that $\Phi (0,0,\beta )=(0,0)$; that is, when $\beta$ is nonzero, the equivalence does not always preserve the origin.

There exist special unfoldings $G$ which contain all perturbations of $g$, up to strategy equivalence. These unfoldings are characterized as follows.

Definition 6.4

An unfolding $G$ of $g$ is versal if every unfolding of $g$ factors through $G$. A versal unfolding depending on the minimum number of parameters is called universal. That minimum number is called the ($C^\infty$) codimension of $g$ and denoted $\mathrm {codim}(g)$.

Suppose $G(u,v,\alpha )$, $\alpha \in \mathbf {R}^k$ is a universal unfolding of a payoff function $g$. This implies, in particular, that all one-parameter unfoldings of $g$ can be factored through $G$. For any perturbation $q$, consider the one-parameter unfolding

$$\begin{aligned} H(u,v,t)=g(u,v)+t q(u,v) \end{aligned}$$

Since $H$ factors through $G$, we write

$$\begin{aligned} H(u,v,t)=S(u,v,t) g(\Phi (u,v,t)), \end{aligned}$$

(6.1)

where $S,\Phi ,A$ satisfy Definition 6.2.

On differentiating (6.1) with respect to $t$ and evaluating at $t=0$, we find

$$\begin{aligned} q(u,v)=\left. \frac{d}{{\text {d}}t}[S(u,v,t) g(\Phi (u,v,t)]\right| _{t=0} +\sum _{i=1}^k\dot{A}_i(0) G_{\alpha _i}(u,v,0), \end{aligned}$$

(6.2)

where $A(t)=(A_1(t),\ldots ,A_k(t))$ in coordinates and $\dot{}$ is differentiation with respect to $t$.

6.1 Tangent Spaces and Unfolding Theorems

Definition 6.5

The tangent space of a payoff function $g$, denoted by $T(g)$, is the set of all $p$ of the form given in the first term on the RHS of (6.2).

Remark 6.6

The only difference between the definition of $T(g)$ and $RT(g)$ is the fact noted in Remark 6.3 that $\Phi (\cdot ,\cdot ,t)$ need fix the origin. Given a payoff function $g$, a simple calculation shows

$$\begin{aligned} T(g)=RT(g)+\mathbf R \{g_v\} \end{aligned}$$

Therefore, $RT(g)$ has finite codimension if and only if $T(g)$ has finite codimension.

The calculation in (6.2) leads to a necessary condition for $G$ to be a universal unfolding of $g$. Specifically, if an unfolding $G$ is versal, then

$$\begin{aligned} \mathcal {E}=T(g)+ \mathbf {R}\left\{ G_{\alpha _1}(u,v,0), \ldots , G_{\alpha _k}(u,v,0) \right\} . \end{aligned}$$

(6.3)

One of the most important results in singularity theory states that (6.3) is also a necessary condition for $G$ to be a versal unfolding. See [2] §$9$.

Theorem 6.7

(versal unfolding theorem) Let $g \in \mathcal {E}$ and let $G$ be a $k$-parameter unfolding of $g$. Then $G$ is a versal unfolding of $g$ if and only if (6.3) is satisfied.

Corollary 6.8

An unfolding $G$ of $g \in \mathcal {E}$ is universal if and only if the sum in (6.3) is a direct sum. The number of parameters in $G$ equals the codimension of $T(g)$. In particular, if $g$ has codimension $k$ and $p_1,\ldots ,p_k \in \mathcal {E}$ are chosen so that

$$\begin{aligned} \mathcal {E}=T(g) \oplus \mathbf {R}\{p_1, \ldots , p_k \}, \end{aligned}$$

then

$$\begin{aligned} G(u,v,\alpha )=g(u,v)+ \alpha _1 p_1(u,v) + \cdots + \alpha _k p_k(u,v) \end{aligned}$$

is a universal unfolding of $g$.

6.2 Universal Unfoldings of Low Codimension Singularities

Let $h$ be a normal form payoff function. It is straightforward to compute $\mathrm {T}(h)$ from $\mathcal {I}(h)$. Specifically,

$$\begin{aligned} \mathrm {T}(h)=\mathcal {I}(h)+\mathbf {R}\{h_u,uh_u,\ldots \} \end{aligned}$$

We can then use Corollary 6.8 to explicitly determine a universal unfolding of $h$ by computing a complementary subspace $V_h$ to $\mathrm {T}(h)$ in $\mathcal {E}$. Note that the codimension of $h$ is just $\dim (V_h)$.

The data needed to compute universal unfoldings of the low codimension normal forms that we have studied in this paper are summarized in Table 9.

Table 9 Algebraic data for low codimension singularities in Theorem 5.5

6.3 Recognition Problem for Universal Unfoldings

We consider the following situation which commonly arises in applications: Let $G(x,y,\alpha )$ be an unfolding of a payoff function $g(u,v)$, where $g$ is a strategy equivalent to a normal form $h$. When is $G$ a universal unfolding of $g$? We use the approach in [11, Chap. III, Sect. 4] to answer this question for low codimension normal forms.

Let $\gamma = (S,\Phi )$ be a strategy equivalence. That is, $S$ and $\Phi$ satisfy conditions Definition 1.7 (a)–(d) and $\gamma (h)=S h \circ \Phi$.

Lemma 6.9

Suppose $g=\gamma (h)$. Then

$$\begin{aligned} \mathrm {T}(g)=\gamma (\mathrm {T}(h)) \end{aligned}$$

Proof

Define a smooth curve of strategy equivalences $\delta _t$ at $h$ as

$$\begin{aligned} \delta _t(h)=S(u,v,t)h(\Phi (u,v,t)), \end{aligned}$$

where $S,\Phi$ vary smoothly in $t$. Assume further that $S(u,v,0)=1$ and $\Phi (u,v,0)=(u,v)$. Then $p=\left. \frac{\mathrm {d}}{\mathrm {d}t}\delta _t(h) \right| _{t=0}$ is a typical member of $\mathrm {T}(h)$. Let $\hat{\delta }_t=\gamma \delta _t \gamma ^{-1}$ and calculate

$$\begin{aligned} \gamma (p)&=\gamma \left. \frac{\mathrm {d}}{\mathrm {d}t}\delta _t(h) \right| _{t=0}\nonumber \\&=\left. \frac{\mathrm {d}}{\mathrm {d}t} \gamma \delta _t\gamma ^{-1} \gamma (h) \right| _{t=0}\nonumber \\&=\left. \frac{\mathrm {d}}{\mathrm {d}t} \hat{\delta }_t(g) \right| _{t=0}. \end{aligned}$$

(6.4)

Since $\hat{\delta }_t$ is a smooth curve of strategy equivalences and $\hat{\delta }_0$ is the identity map we see that $\gamma (p) \in \mathrm {T}(g)$. Hence $\gamma (\mathrm {T}(h))\subset \mathrm {T}(g)$; interchanging the roles of $g$ and $h$ shows that $\mathrm {T}(g)=\gamma (\mathrm {T}(h))$, as claimed. $\square$

Define the pullback mapping $\Phi ^*:\mathcal {E}\rightarrow \mathcal {E}$ as $\Phi ^*(g)(u,v)=g(\Phi (u,v))$.

Lemma 6.10

Let $\mathcal {I}=\langle p_1,\ldots ,p_k \rangle$. Then $\Phi ^*(\mathcal {I})$ is the ideal $\langle \Phi ^*(p_1), \cdots , \Phi ^*(p_k)\rangle$.

Proof

Follows directly from $\Phi ^*(g+h)=\Phi ^*(g)+\Phi ^*(h) \qquad \Phi ^*(g\cdot h)=\Phi ^*(g) \cdot \Phi ^*(h)$. $\square$

Lemma 6.11

If $\mathcal {I}$, $\mathcal {J}$ are ideals, then Lemma 6.10 implies that

$$\begin{aligned} \Phi ^*(\mathcal {I}+\mathcal {J})=\Phi ^*(\mathcal {I})+\Phi ^*(\mathcal {J}) \quad \Phi ^*(\mathcal {I}\cdot \mathcal {J})=\Phi ^*(\mathcal {I}) \cdot \Phi ^*(\mathcal {J}) \end{aligned}$$

(6.5)

When solving recognition problems for low codimension normal forms, we often write $\mathrm {T}(g)$ using powers of the maximal ideal $\mathcal {M}$ and the ideal $\langle y-x \rangle$. We show that these ideals are invariant under pullback maps coming from strategy equivalences that fix the origin.

Definition 6.12

An ideal $\mathcal {I}$ is intrinsic if for every strategy equivalence $\gamma =(S,\Phi )$ such that $\Phi (0)=0$, we have $\gamma (\mathcal {I})=\mathcal {I}$

Proposition 6.13

The ideal

$$\begin{aligned} \mathcal {J}=\mathcal {M}^{k}+ \mathcal {M}^{k_1} \langle v^{l_1} \rangle +\cdots +\mathcal {M}^{k_s} \langle v^{l_s}\rangle \end{aligned}$$

is intrinsic for any finite set of nonnegative integers $k_i,l_i$.

Proof

The ideals $\langle v \rangle$ and $\mathcal {M}$ are intrinsic since $\mathcal {M}$ consists of maps that vanish at the origin and $\langle v \rangle$ consists of maps that vanish on the diagonal and strategy equivalences preserve the origin and the diagonal. The proof now follows from Lemma 6.11. $\square$

Let $h$ be a normal form with codimension $k$. We now calculate necessary and sufficient conditions for the $k$ parameter unfolding $G$ to be a universal unfolding of $g$ when $g=\gamma (h)$ is strategy equivalent to $h$. We do this as follows:

• (a) Write $\mathrm {T}(h)=\mathcal {J}\oplus W_h$ where $\mathcal {J}$ is intrinsic.

• (b) Using Lemma 6.9 and the fact that $\mathcal {J}$ is intrinsic, we can write $\mathrm {T}(g)=\mathcal {J}\oplus W_g$.

• (c) By Theorem 6.7, $G$ is a universal unfolding of $g$ if and only if

  $$\begin{aligned} \mathcal {E}=\mathcal {J}\oplus W_g\oplus \mathbf {R}\{G_{\alpha _1},\ldots , G_{\alpha _k}\} \end{aligned}$$

  (6.6)

• (d) A complementary space to $\mathcal {J}$ in $u,v$ coordinates always consisted of $\dim W_g + k$ monomials. We can choose a basis for $W_g$ in terms of $g$ and its derivatives. Then we solve the problem by writing the Taylor coefficients of this basis and the $G_{\alpha _j}$ in the monomials that are not in $\mathcal {J}$. It follows that $G$ is a universal unfolding if and only if this matrix has a nonzero determinant.

The results for the low codimension singularities are given in Table 10; these results can be translated using the derivatives in Tables 7, 8 to obtain the results listed in Table 2.

Table 10 Recognition problem for universal unfoldings of singularities in Theorem 5.5