Analysis of activation energy and its impact on hybrid nanofluid in the presence of Hall and ion slip currents

Abstract

Chemical reaction is considered with entropy generation in mixed convection magnetohydrodynamic (MHD) hybrid nanoliquid flow across a porous medium containing Hall and ion slip currents. The main focus of this research is the entropy production, SWCNT-MWCNT/water hybrid nanofluids and Hall effect. The complex coupled system of differential equations is transformed into a non-dimensional form through an acceptable similarity transformation. To measure the rate of heat transfer the volume fraction of MWCNT is taken fixed 3% and for SWCNT changes 1–5%. The influence of different flow field parameters on axial velocity, temperature distribution, concentration field, entropy generation, and Bejan number is expressed graphically. The comparison of nanofluid and hybrid nanofluid is shown graphically. The enhances value of variable viscosity parameter, porous parameter, and coefficient of inertia decreases the velocity distribution. Further the solid volume fraction enhances the velocity and temperature distribution.

Introduction

In recent years, the use of advanced nanofluids coupled with specific nanoparticles to boost the thermo-physical properties of common fluids has been given growing attention. Several scientists have addressed this class of nanofluids, called hybrid nanofluids. In certain works, the combination of metal-oxide and metallic nanoparticles has been used in the base fluid to suspend nanoparticles. For instance, hybrid nanofluid thermo-physical properties such as ${\text{Cu}} - {\text{TiO}}_{{2}} {\text{/water}}$ (Madhesh et al. 2014; Suresh et al. 2012), and ${\text{Ag}} - {\text{MgO/water}}$ (Esfe et al. 2015) were reported. Some scientists attached them to metal-oxide nanoparticles because of the special thermal properties of carbon nanotubes (CNTs). In such manner, Munkhbayar et al. (2013) investigated significant improvements in ${\text{Ag}} - {\text{MWCNTs/water}}$ thermal conductivity. They demonstrated that a fluid containing “0.05 wt% MWCNTs–3 wt% Ag” composite gained the maximum thermal conductivity enhancement. Soltanimehr and Afrand (Soltanimehr and Afrand 2016) showed an increase in COOH-functional MWCNTs/ethylene glycol–water nanofluid thermal conductivity. The thermal conductivity of ${\text{MWCNTs}} - {\text{Fe}}_{{3}} {\text{O}}_{{4}} {\text{/water}}$ hybrid nanofluids was investigated by Sundar et al. (2014) for solid volume fractions of 0.1% and 0.3% at temperatures ranging from 30 to 60 °C. Their experimental data showed a 40% maximum increase in thermal conductivity. Nadeem et al. (2019) debated the feature of heat transfer in ${\text{SWCNT}} - {\text{MWCNT/water}}$ hybrid nanofluid flow with heat generation. They found that hybrid nanofluid gives more rate of heat transfer than simple nanofluid. Ahmad and Nadeem (2019) investigated the new concept of Thomson and Troian slip condition in the ${\text{SWCNT}} - {\text{MWCNT/water}}$ hybrid nanofluid with variable viscosity and activation energy. Recently many researchers explored the importance of nanofluid flow (Alamri et al. 2019; Akbar et al. 2016; Ahmad et al. 2020; Sarafraz et al. 2020).

The second thermodynamics law (Feroz et al. 2019) gives the result of entropy generation, which specifies that when the system is in a steady state or undergoes reversible procedures, at that point the measure of total entropy persists consistently and, in irreversible (opposite) processes, the total entropy constantly boosts. Irreversible processes include fluid flow by flow resistance, friction within a system between viscid liquid and solid surface, diffusion, thermal resistance, Joule fluid heating, and chemical reaction. Clausius (2006) is the founder of the entropy theory. Initially Bejan (1980) explored the rate of entropy generation and developed a thermodynamic optimization method. Entropy generation of carbon nanotubes 3D flow through porous media on a nonlinear inclined stretching plate was explained by Jain and Gupta (2019). He found the numerical solution using the Runge–Kutta fourth-order method. Alshaheen et al. (2019) explored the impacts of using carbon-based nanofillers/water nanofluids as a coolant fluid in a photovoltaic thermal system are portrayed experimentally from both energy and exergy points of view. The results show that the use of GNP/water, MWCNT/water, and SWCNT/water increases the overall total energy efficiency by 19.3%, 9.46%, and 15.24% compared to pure water. Rehman et al. (2017) spoke about thermal slip entropy of radioactive nanofluid flow. Ellahi et al. (2019) investigated to develop an innovative mathematical model for electro-osmotic flow of Couette–Poiseuille nanofluids with entropy generation. Further the application of entropy generation is discussed in Ellahi et al. (2016,2018) and Lu et al. (2018).

In the involvement of applied magnetic field, the partially ionized liquid encounters force of more than one kind. Because of applied magnetic field these forces contain magnetic forces, Hall force produced due to collision of electron and ion slip force due to the collision of ions. It is verified experimentally that due to the magnetic field implementation, the Hall and ion slip forces are contrary to the force. Utilizing generalized Ohm’s law (Nazarov 1995) forces because of ion slip and Hall effect is computed along with laws counting momentum, mass conservation, a set of Maxwell equations, and energy equation; a few investigations on magneto-hydrodynamic (MHD) flow of partially ionized fluid using the laws referred to in Nawaz et al. (2018) were debated. Nawaz and Uzair (2019) explored the performance of partially ionized Carreau liquid fluid in the presence of hybrid nanoliquid. Khan et al. (2017) designed the role of chemical reactions in the transportation dynamics of non-Darcian porous fluid species and solved highly complex problems using the Runge–Kutta method to evaluate the effect of porous media on speed and species concentration. By taking into account homogeneous–heterogeneous chemical reactions, the studies listed in Motsa and Shateyi (2012), Nawaz and Zubair (2017), Abdelsalam and Bhatti (2018) and Odelu and Kumar (2018) and the references explained different effects on partially ionized liquids.

To the best of our knowledge, entropy analysis with activation energy, variable viscosity, joule heating, and nonlinear thermal radiation were not studied in partially ionized hybrid nanofluid flow. Bvp4c form Matlab solves the complicated mathematical models. Results for horizontal and vertical velocity profiles, temperature distribution, concentration field, entropy optimization rate and Bejan number are graphically displayed.

Physical structure

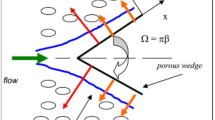
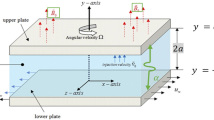
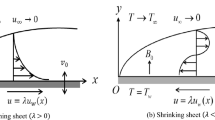
Consider the mixed convection three-dimensional radiative hybrid nanofluid flow over a nonlinear stretching sheet with Hall and ion slip effects. Darcy-Forchheimer law is utilized to measure the flow analysis. Further the nonlinear source/sink, activation energy, and variable viscosity effect are examined.

In the current research, hybrid nanofluid is acquired in consideration of the mixture of SWCNT into MWCNT/Water. Next, MWCNT nanoparticles are dissolved into water to form a MWCNT/Water nanofluid, and then SWCNT nanoparticles of changed fractions ($\phi_{2}$) are applied to the nanofluid mixture to produce a homogeneous mixture of SWCNT-MWCNT/Water hybrid nanofluid.

Variable viscosity is mathematically defined by Farooq et al. (2018)

$$\mu_{{\text{f}}} (\hat{T}) = \frac{1}{{\mu_{\infty }^{ - 1} \left\{ {1 + (\hat{T} - \hat{T}_{\infty } )\delta } \right\}}}.$$

(1)

Imposing a boundary layer approximation, the equations which governs the flow phenomena are presented as,

$$\frac{{\partial \hat{v}}}{\partial y} + \frac{{\partial \hat{u}}}{\partial x} + \frac{{\partial \hat{w}}}{\partial z} = 0,$$

(2)

$$\begin{aligned} \hat{v}\frac{{\partial \hat{u}}}{\partial y} & + \hat{u}\frac{{\partial \hat{u}}}{\partial x} + \hat{w}\frac{{\partial \hat{u}}}{\partial z} = \frac{1}{{\rho_{{{\text{hnf}}}} }}\frac{\partial }{\partial y}\left( {\mu_{{{\text{hnf}}}} (\hat{T})\,\frac{{\partial \hat{u}}}{\partial z}} \right) - \frac{{\sigma_{{\text{f}}} B_{0}^{2} (x + y)^{m - 1} }}{{\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} + \beta_{{\text{e}}}^{{2}} } \right]}}\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )\hat{u} - \beta_{{\text{e}}} \hat{v}} \right] \\ & - \frac{{\mu_{{{\text{hnf}}}} (\hat{T})}}{{\rho_{{{\text{hnf}}}} K^{**} }}\hat{u} - F^{**} \hat{u}^{2} { + }\left( {\rho_{{{\text{f}}\infty }} g(1 - C_{\infty } )\beta_{{\text{T}}} \frac{m + 1}{2}} \right)(\hat{T} - \hat{T}_{\infty } ) - \left( {g\left( {\rho_{{\text{p}}} - \rho_{f\infty } } \right)\frac{m + 1}{2}} \right)\left( {\hat{C} - \hat{C}_{\infty } } \right), \\ \end{aligned}$$

(3)

$$\begin{aligned} \hat{v}\frac{{\partial \hat{v}}}{\partial y} + \hat{u}\frac{{\partial \hat{u}}}{\partial x} + \hat{w}\frac{{\partial \hat{v}}}{\partial z} & = \frac{1}{{\rho_{{{\text{hnf}}}} }}\frac{\partial }{\partial y}\left( {\mu_{{{\text{hnf}}}} (\hat{T})\,\frac{{\partial \hat{v}}}{\partial z}} \right) \\ & \,\,\, - \frac{{\sigma_{{\text{f}}} B_{0}^{2} }}{{\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} + \beta_{{\text{e}}}^{2} } \right]}}\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )\hat{v} + \beta_{{\text{e}}} \hat{u}} \right] - F^{**} \hat{v}^{2} - \frac{{\mu_{{{\text{hnf}}}} (\hat{T})}}{{\rho_{{{\text{hnf}}}} K^{**} }}\hat{v}, \\ \end{aligned}$$

(4)

$$\begin{aligned} \hat{v}\frac{{\partial \hat{T}}}{\partial y} + \hat{u}\frac{{\partial \hat{T}}}{\partial x} + \hat{w}\frac{{\partial \hat{T}}}{\partial z} & = \frac{\partial }{\partial y}\left( {\left( {\alpha_{{{\text{hnf}}}} + \frac{{16\sigma^{*} \hat{T}^{3} }}{{3k^{*} (\rho C_{{\text{p}}} )_{{{\text{hnf}}}} }}} \right)\frac{{\partial \hat{T}}}{\partial z}} \right) + \frac{{Q^{\prime\prime\prime}}}{{(\rho C_{p} )_{{{\text{hnf}}}} }} \\ & \;\; + \frac{{\sigma_{{\text{f}}} B_{0}^{2} (\hat{u}^{2} + \hat{v}^{2} )}}{{(\rho C_{{\text{p}}} )_{{{\text{hnf}}}} \left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} + \beta_{{\text{e}}}^{2} } \right]}}, \\ \end{aligned}$$

(5)

$$\hat{v}\frac{{\partial \hat{C}}}{\partial y} + \hat{u}\frac{{\partial \hat{C}}}{\partial x} + \hat{w}\frac{{\partial \hat{C}}}{\partial z} = \frac{{D_{f} }}{{(1 - \phi_{1} )^{ - 2.5} (1 - \phi_{2} )^{ - 2.5} }}\frac{{\partial^{2} \hat{C}}}{{\partial z^{2} }} - k_{{\text{r}}}^{{2}} \left( {\frac{{\hat{T}}}{{\hat{T}_{\infty } }}} \right)^{n} \exp \left( {\frac{{ - E_{{\text{a}}} }}{{k\hat{T}}}} \right)(\hat{C} - \hat{C}_{\infty } ).$$

(6)

The appropriate boundary conditions are specified by:

$$\left. u \right|_{z = 0} = c(x + y)^{m} ,\, \, \left. v \right|_{z = 0} = d(x + y)^{m} , \, \left. w \right|_{z = 0} = 0, \, \left. T \right|_{z = 0} = T_{w} ,\left. C \right|_{z = 0} = C_{w} ,$$

(7a)

$$\left. u \right|_{{z \to \infty }} \to 0,\;\left. v \right|_{{z \to \infty }} \to 0,{\text{ }}\left. T \right|_{{z \to \infty }} \to T_{\infty } ,\,\left. C \right|_{{z \to \infty }} \to C_{\infty } .$$

(7b)

The values of $\alpha_{{{\text{nf}}}}$, $\mu_{{{\text{nf}}}}$, and $\rho_{{{\text{nf}}}}$ for SWCNT/Water nanofluid are specified as,

$$\alpha_{{{\text{nf}}}} = \frac{{k_{{{\text{nf}}}} }}{{(\rho C_{{\text{p}}} )_{{{\text{nf}}}} }}, \, \frac{{\mu_{{{\text{nf}}}} }}{{\mu_{{\text{f}}} }} = \frac{1}{{(1 - \phi )^{2.5} }},k_{{{\text{nf}}}} = k_{{\text{f}}} \frac{{(1 - \phi ) + 2\phi \left( {\tfrac{{k_{{{\text{SWCNT}}}} }}{{k_{{{\text{SWCNT}}}} - k_{{\text{f}}} }}} \right)\ln \left( {\tfrac{{k_{{{\text{SWCNT}}}} + k_{{\text{f}}} }}{{k_{{\text{f}}} }}} \right)}}{{(1 - \phi ) + 2\phi \left( {\tfrac{{k_{{\text{f}}} }}{{k_{{{\text{SWCNT}}}} - k_{{\text{f}}} }}} \right)\ln \left( {\tfrac{{k_{{{\text{SWCNT}}}} + k_{{\text{f}}} }}{{k_{{\text{f}}} }}} \right)}},$$

(8)

$$\frac{{(\rho C_{{\text{p}}} )_{{{\text{nf}}}} }}{{(\rho C_{{\text{p}}} )_{{\text{f}}} }} = \phi \frac{{(\rho C_{{\text{p}}} )_{{{\text{SWCNT}}}} }}{{(\rho C_{{\text{p}}} )_{{\text{f}}} }} + (1 - \phi ),\frac{{\rho_{{{\text{nf}}}} }}{{\rho_{{\text{f}}} }} = \phi \frac{{\rho_{{{\text{SWCNT}}}} }}{{\rho_{{\text{f}}} }} + 1 - \phi .$$

(9)

The values of $\alpha_{{{\text{hnf}}}}$, $\mu_{{{\text{hnf}}}}$, and $\rho_{{{\text{hnf}}}}$, for SWCNT-MWCNT/Water hybrid nanofluid are characterized as,

$$\begin{aligned} \rho_{{{\text{hnf}}}} & = \phi_{2} \rho_{{{\text{SWCNT}}}} + (1 - \phi_{2} )\left\{ {(1 - \phi_{1} )\rho_{f} + \phi_{1} \rho_{{{\text{MWCNT}}}} } \right\}, \\ (\rho C_{{\text{p}}} )_{{{\text{hnf}}}} & = \phi_{2} (\rho C_{{\text{p}}} )_{{{\text{SWCNT}}}} + (1 - \phi_{2} )\left\{ {(1 - \phi_{1} )(\rho C_{{\text{p}}} )_{{\text{f}}} + \phi_{1} (\rho C_{{\text{p}}} )_{{{\text{MWCNT}}}} } \right\}, \\ \end{aligned}$$

(10)

$$\begin{gathered} \frac{{k_{{{\text{hnf}}}} }}{{k_{{{\text{bf}}}} }} = \frac{{(1 - \phi_{2} ) + 2\phi_{2} \left( {\tfrac{{k_{{{\text{SWCNT}}}} }}{{k_{{{\text{SWCNT}}}} - k_{{{\text{bf}}}} }}} \right)\ln \left( {\tfrac{{k_{{{\text{SWCNT}}}} + k_{{{\text{bf}}}} }}{{k_{{{\text{bf}}}} }}} \right)}}{{(1 - \phi_{2} ) + 2\phi_{2} \left( {\tfrac{{k_{{{\text{bf}}}} }}{{k_{{{\text{SWCNT}}}} - k_{{{\text{bf}}}} }}} \right)\ln \left( {\tfrac{{k_{{{\text{SWCNT}}}} + k_{{{\text{bf}}}} }}{{k_{{{\text{bf}}}} }}} \right)}}, \hfill \\ \frac{{k_{{{\text{bf}}}} }}{{k_{{\text{f}}} }} = \frac{{(1 - \phi_{1} ) + 2\phi_{1} \left( {\tfrac{{k_{{{\text{MWCNT}}}} }}{{k_{{{\text{MWCNT}}}} - k_{{\text{f}}} }}} \right)\ln \left( {\tfrac{{k_{{{\text{MWCNT}}}} + k_{{\text{f}}} }}{{k_{{\text{f}}} }}} \right)}}{{(1 - \phi_{1} ) + 2\phi_{1} \left( {\tfrac{{k_{{\text{f}}} }}{{k_{{{\text{MWCNT}}}} - k_{{\text{f}}} }}} \right)\ln \left( {\tfrac{{k_{{{\text{MWCNT}}}} + k_{{\text{f}}} }}{{k_{{\text{f}}} }}} \right)}}. \hfill \\ \end{gathered}$$

(11)

where $\phi_{1} , \, \phi_{2}$ are the solid volume fraction of MWCNT and SWCNT respectively, is volume fraction of nanoliquid, $k_{{\text{f}}}$ are the thermal conductivity of regular liquid, and specific heat is $C_{{\text{p}}} \;$.

Similarity transformation

Using the following non-dimensional transformation to modify the above-mentioned non-linear differential equation, i.e.

$$\left. \begin{gathered} \eta = z\sqrt {\tfrac{m + 1}{2}\tfrac{{c(x + y)^{m - 1} }}{{\upsilon_{f} }}} ,\,\hat{u} = f^{\prime}(\eta )c(x + y)^{m} ,\hat{v} = g^{\prime}(\eta )c(x + y)^{m} ,\hat{T} = \hat{T}_{\infty } + \left( {\hat{T}_{w} - \hat{T}_{\infty } } \right)\theta (\eta ), \hfill \\ \hat{w} = - \sqrt {\tfrac{m + 1}{2}\upsilon_{f} c(x + y)^{m - 1} } \left[ {(f + g) + \left( {\tfrac{m - 1}{{m + 1}}} \right)\eta (g^{\prime} + f^{\prime})} \right],\hat{C} = \hat{C}_{\infty } + \left( {\hat{C}_{w} - \hat{C}_{\infty } } \right)h(\eta ). \hfill \\ \end{gathered} \right\}$$

(12)

Continuity equation are automatically fulfilled, and Eqs. (3–6) change into,

$$\begin{gathered} D_{1} = (1 - \phi_{2} )^{2.5} (1 - \phi_{1} )^{2.5} ,D_{2} = \left( {\phi_{2} \tfrac{{\rho_{SWCNT} }}{{\rho_{f} }} + \left\{ {(1 - \phi_{1} ) + \phi_{1} \tfrac{{\rho_{MWCNT} }}{{\rho_{f} }}} \right\}(1 - \phi_{2} )} \right), \hfill \\ D_{4} = \left( {\phi_{2} \tfrac{{(\rho C_{p} )_{SWCNT} }}{{(\rho C_{p} )_{f} }} + \left\{ {(1 - \phi_{1} ) + \phi_{1} \tfrac{{(\rho C_{p} )_{MWCNT} }}{{(\rho C_{p} )_{f} }}} \right\}(1 - \phi_{2} )} \right). \hfill \\ \end{gathered}$$

$$\begin{aligned} \frac{{f^{\prime\prime\prime}}}{{1 + \theta_{{\text{r}}} \theta }}\, & + D_{1} D_{2} \left\{ { - \frac{2m}{{m + 1}}(f^{\prime} + g^{\prime})f^{\prime} + \lambda_{{\text{b}}} \theta - R_{{\text{b}}} h + (f + g)f^{\prime\prime} - \frac{{2F_{{\text{r}}} }}{m + 1}f^{\prime 2} } \right\} - \frac{{\theta_{{\text{r}}} \theta^{\prime}f^{\prime\prime}}}{{\left( {1 + \theta_{{\text{r}}} \theta } \right)^{2} }} \\ & \;\; - \frac{{2P_{{\text{m}}} f^{\prime}}}{{(m + 1)(1 + \theta_{{\text{r}}} \theta )}} - \left( {\frac{2}{m + 1}} \right)\frac{{D_{1} {\text{Ha}}((1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )f^{\prime} - \beta_{{\text{e}}} g^{\prime})}}{{\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} + \beta_{{\text{e}}}^{2} } \right]}} = 0, \\ \end{aligned}$$

(13)

$$\begin{aligned} \frac{{g^{\prime\prime\prime}}}{{1 + \theta_{{\text{r}}} \theta }} & + D_{1} D_{2} \left\{ {(g + f)g^{\prime\prime} - \frac{{2F_{{\text{r}}} }}{m + 1}g^{{\prime}{2}} - \frac{2m}{{m + 1}}(g^{\prime} + f^{\prime})g} \right\} - \frac{{2P_{{\text{m}}} g^{\prime}}}{(m + 1)} - \frac{{\theta_{{\text{r}}} \theta^{\prime}g^{\prime\prime}}}{{\left( {1 + \theta_{r} \theta } \right)^{2} }} \\ & \;\; - \frac{{2D_{1} {\text{Ha}}((1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )g^{\prime} + \beta_{{\text{e}}} f^{\prime})}}{{(m + 1)\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} + \beta_{{\text{e}}}^{2} } \right]}} = 0, \\ \end{aligned}$$

(14)

$$\begin{aligned} \left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }} + \left( {1 + \theta (\theta _{{\text{w}}} - 1)} \right)^{3} R_{{\text{d}}} } \right)\theta ^{\prime\prime} & + 3R_{{\text{d}}} \left( {1 + \theta (\theta _{{\text{w}}} - 1)} \right)^{2} (\theta _{w} - 1)\theta ^{{\prime 2}} + \left( {\frac{{{\text{Ha}}\Pr E_{{\text{c}}} \left[ {f^{{\prime 2}} + g^{{\prime 2}} } \right]}}{{\left[ {(1 + \beta _{{\text{e}}} \beta _{{\text{i}}} )^{2} + \beta _{{\text{e}}} ^{2} } \right]}}} \right) \\ & \;\; + \left( {\frac{2}{{m + 1}}} \right)\left[ {I_{1} f^{\prime} + I_{2} \theta } \right] + \Pr D_{4} (f + g)\theta ^{\prime} = 0, \\ \end{aligned}$$

(15)

$$\left( {\frac{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} }}{{S_{{\text{c}}} }}} \right)h^{\prime\prime} + (f + g)h^{\prime} - \frac{2}{m + 1}R_{{\text{c}}} (1 + \alpha_{1} \theta )^{n} h\exp \left( {\frac{ - E}{{1 + \alpha_{1} \theta }}} \right) = 0,\,$$

(16)

and the boundary condition (7a) and (7b) gives the form below.

$$f(0) = 0,\,f^{\prime}(0) = 1,\,\theta (0) = 1,g(0) = 0,g^{\prime}(0) = \alpha , \, h(0) = 1,$$

(17a)

$$f^{\prime}(\eta ) = 0,\, \, \theta (\eta ) = 0, \, g^{\prime}(\eta ) = 0,h(\eta ) = 0,{\text{ at }}\eta \to \infty .$$

(17b)

The involved nonsimilar parameters are

$$\begin{aligned} {\text{Ha}} & = \frac{{\sigma_{{\text{f}}} B^{2}_{0} }}{{c\rho_{{\text{f}}} }}, \, \theta_{{\text{w}}} = \frac{{T_{{\text{w}}} }}{{T_{\infty } }}, \, F_{{\text{r}}} = \frac{{C_{{\text{b}}} }}{{\rho_{{\text{f}}} \sqrt {K^{**} } }},E = \frac{{E_{{\text{a}}} }}{{kT_{\infty } }}, \, \\ P_{{\text{m}}} &= \frac{{\nu_{{\text{f}}} }}{{cK^{**} }}, \, S_{{\text{c}}} = \frac{{\nu_{{\text{f}}} }}{{D_{{\text{f}}} }}, \theta_{{\text{r}}} = \delta^{*} \left( {T_{{\text{w}}} - T_{\infty } } \right),\alpha_{1} = \frac{{T_{{\text{w}}} - T_{\infty } }}{{T_{\infty } }},\\ {\Pr}& = \frac{{\nu_{{\text{f}}} }}{{\alpha_{{\text{f}}} }},R_{{\text{d}}} = \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k_{f} k^{*} }},\alpha = \frac{d}{c},R_{{\text{c}}} = \frac{{k_{{\text{r}}}^{{2}} }}{c}. \\ \end{aligned}$$

(18)

Physical quantities

The dimensional form of the skin friction coefficient, local Nusselt number, and Sherwood number are classified as,

$$\begin{aligned} C_{{\text{f}}}& = \frac{{\tau_{{{\text{w1}}}} }}{{u_{{\text{w}}}^{2} \rho_{{\text{f}}} }},{\text{Sh}} = \frac{{q_{{\text{m}}} }}{{D_{{{\text{hnf}}}} (\hat{C}_{{\text{w}}} - \hat{C}_{\infty } )}},C_{{\text{g}}} = \frac{{\tau_{{{\text{w2}}}} }}{{u_{{\text{w}}}^{2} \rho_{{\text{f}}} }}, \\ {\text{Nu}} &= \frac{{\left( {\left( {\frac{\partial T}{{\partial z}}} \right)_{z = o} + (q_{r} )_{z = 0} } \right)(x + y)}}{{(T_{{\text{w}}} - T_{\infty } )}}.\end{aligned}$$

(19)

Now surface shear stress ($\tau_{{\text{w}}}$) and mass flux are accepted by

$$\begin{aligned} \tau_{{{\text{w2}}}} &= \mu_{{{\text{hnf}}}} (T)\left( {\frac{{\partial \hat{v}}}{\partial z} + \frac{{\partial \hat{w}}}{\partial y}} \right)_{z = o} ,\tau_{{{\text{w1}}}} = \mu_{{{\text{hnf}}}} (T)\left( {\frac{{\partial \hat{u}}}{\partial z} + \frac{{\partial \hat{w}}}{\partial x}} \right)_{z = o} ,\\ q_{{\text{m}}} & = - \;D_{{{\text{hnf}}}} \left. {\tfrac{{\partial \hat{C}}}{\partial y}} \right|_{z = 0} . \end{aligned}$$

(20)

Consuming Eqs. (12) and (20), in Eq. (19) we obtain

$$\begin{aligned} C_{{\text{g}}} Re^{1/2} & = g^{\prime\prime}(0)\left( {\frac{{\left( {1 + \theta (0)\theta_{{\text{r}}} } \right)^{ - 1} }}{{\left( {(1 - \phi_{2} )(1 - \phi_{1} )} \right)^{2.5} }}} \right),C_{{\text{f}}} Re^{1/2} = f^{\prime\prime}(0)\left( {\frac{{\left( {1 + \theta (0)\theta_{{\text{r}}} } \right)^{ - 1} }}{{\left( {(1 - \phi_{2} )(1 - \phi_{1} )} \right)^{2.5} }}} \right), \\ {\text{Re}}^{ - 1/2} {\text{Nu}} & = - \left\{ {\frac{m + 1}{2}} \right\}\theta^{\prime}(0)\left[ {(1 + R_{{\text{d}}} (1 + \theta (0)(\theta_{{\text{w}}} - 1))^{3} } \right],{\text{Re}}^{ - 1/2} {\text{Sh}} = - h^{\prime}(0). \\ \end{aligned}$$

(21)

In which ${\text{Re}} = \frac{{c(x + y)^{2} }}{{\nu_{f} }}$ is the local Reynold number.

Entropy analysis

The volumetric and local entropy rate of viscous fluid is described as (Bejan 1980; Jain and Gupta 2019)

$$\begin{aligned} S_{{\text{G}}} & = \frac{{k_{{\text{f}}} }}{{\hat{T}_{\infty }^{2} }}\left[ {\frac{{16\sigma^{*} \hat{T}_{\infty }^{3} }}{{3k^{*} k_{{\text{f}}} }} + \frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }}} \right]\left( {\frac{{\partial \hat{T}}}{\partial z}} \right)^{2} + \left( {\frac{{\mu_{{{\text{hnf}}}} (\hat{T})}}{{\hat{T}_{\infty } }}} \right)\left\{ {\left( {\frac{{\partial \hat{u}}}{\partial z}} \right)^{2} + \left( {\frac{{\partial \hat{v}}}{\partial z}} \right)^{2} } \right\} \\ & \;\;\;{ + }\frac{{\sigma_{{\text{f}}} B_{0}^{2} (\hat{v}^{2} + \hat{u}^{2} )}}{{\hat{T}_{\infty } \left[ {\beta_{{\text{e}}}^{2} + (1 + \beta_{{\text{i}}} \beta_{{\text{e}}} )^{2} } \right]}} + \frac{{{\text{RD}}}}{{\hat{C}_{\infty } }}\left( {\frac{{\partial \hat{C}}}{\partial z}} \right)^{2} + \frac{{{\text{RD}}}}{{\hat{T}_{\infty } }}\left( {\frac{{\partial \hat{C}}}{\partial z}\frac{{\partial \hat{T}}}{\partial z}} \right). \\ \end{aligned}$$

(22)

The related relationship can structure the dimensionless entropy generation

$$N_{{\text{s}}} = \frac{{T_{\infty } (z/\eta )^{2} }}{{k_{{\text{f}}} (T_{{\text{w}}} - T_{\infty } )}}S_{{\text{G}}} .$$

(23)

After using the transformation (12), the dimensionless form of entropy generation becomes

$$\begin{aligned} N_{{\text{s}}} (\eta ) & = \left( {R_{{\text{d}}} \left( {1 + (\theta_{{\text{w}}} - 1)\theta } \right)^{3} + \frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }}} \right)\left( {\frac{m + 1}{2}} \right)\alpha_{1} \theta^{{\prime}{2}} \\ & \quad + \frac{{{\text{Br}}\left( {1 + \theta_{{\text{r}}} \theta } \right)^{ - 1} }}{{\left( {(1 - \phi_{1} )(1 - \phi_{2} )} \right)^{2.5} }}\left( {\frac{m + 1}{2}} \right)\left( {f^{{\prime\prime}{2}} + g^{{\prime\prime}{2}} } \right) \\ & \quad +\left( {\frac{{{\text{HaBr}}\left[ {f^{{\prime}{2}} + g^{{\prime}{2}} } \right]}}{{\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} + \beta_{{\text{e}}}^{2} } \right]}}} \right) + Lh^{\prime}\theta^{\prime} + L\frac{{\alpha_{2} }}{{\alpha_{1} }}h^{{\prime}{2}} . \\ \end{aligned}$$

(24)

Parameter used in above equation are define as,

$$\alpha_{1} = \frac{\Delta T}{{T_{\infty } }},\alpha_{2} = \frac{\Delta C}{{C_{\infty } }},{\text{Br}} = \frac{{\mu_{{\text{f}}} u_{{\text{e}}}^{2} }}{{k_{{\text{f}}} \Delta T}},L = \frac{{{\text{RD}}(C_{{\text{w}}} - C_{\infty } )}}{{k_{{\text{f}}} }}.$$

Bejan number is illustrate as the proportional of the entropy minimization by thermal irreversibility to the total entropy optimization, i.e.,

$${\text{Be}} = \frac{{\text{Entropy production by thermal irreversibility}}}{{\text{Total entropy generation}}}.$$

(25)

It stated in mathematical terms as,

$${\text{Be}} = \frac{{\left( {R_{{\text{d}}} (1 + \theta (\theta_{{\text{w}}} - 1))^{3} + \frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }}} \right)\alpha_{1} \left( {\frac{m + 1}{2}} \right)\theta^{{\prime}{2}} }}{{\left\{ \begin{gathered} \left( {R_{{\text{d}}} (1 + \theta (\theta_{{\text{w}}} - 1))^{3} + \frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }}} \right)\alpha_{1} \left( {\frac{m + 1}{2}} \right)\theta^{{\prime}{2}} + \frac{{{\text{Br}}\left( {1 + \theta_{{\text{r}}} \theta } \right)^{ - 1} }}{{\left( {(1 - \phi_{1} )(1 - \phi_{2} )} \right)^{2.5} }}\left( {\frac{m + 1}{2}} \right)\left( {f^{{\prime\prime}{2}} + g^{{\prime\prime}{2}} } \right) \hfill \\ \, + Lh^{\prime}\theta^{\prime}{ + }\left( {\frac{{Ha\left[ {f^{{\prime}{2}} + g^{{\prime}{2}} } \right]{\text{Br}}}}{{\beta_{e}^{2} \left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} } \right]}}} \right) + L\frac{{\alpha_{2} }}{{\alpha_{1} }}h^{{\prime}{2}} \hfill \\ \end{gathered} \right\}}}.$$

(26)

Bejan number requirement lie between $0 < {\text{Be}} < 1$, there is no entropy generation when ${\text{Be}} = 0$ because of heat transfer. Similarly, when ${\text{Be}} < 0.5$ the entropy minimization is less by heat transfer.

Result and discussion

Numerical method and validation

The numerical solution of Eqs. (13–16) equivalent to boundary condition (17a) and (17b) are clarified by means of MATLAB built-in function bvp4c. For this reason, firstly we changed the third and second order differential equation to the classification of a first-order ordinary differential equation by giving new parameters such that:

$$f = y(1),f^{\prime} = y(2),\,f^{\prime\prime} = y(3),$$

(27)

$$\begin{aligned} yy1 & = \left( {1 + \theta_{r} y(7)} \right)D_{1} D_{2} \left\{ {\frac{2m}{{m + 1}}\left( {y(2) + y(5)} \right)y(2) - \lambda_{{\text{b}}} \theta + R_{{\text{b}}} h - (f + g)y(3) + \frac{{2F_{{\text{r}}} }}{m + 1}y(2)^{2} } \right\} \\ \, & \;\;\; + \frac{{\theta_{{\text{r}}} y(8)y(3)}}{{\left( {1 + \theta_{{\text{r}}} y(7)} \right)}}{ + }\frac{{2P_{{\text{m}}} y(2)}}{(m + 1)} + \left( {\frac{2}{m + 1}} \right)\frac{{(1 + \theta_{{\text{r}}} \theta )D_{1} {\text{Ha}}((1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )y(2) - \beta_{{\text{e}}} y(5))}}{{\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} + \beta_{{\text{e}}}^{2} } \right]}}, \\ \end{aligned}$$

(28)

$$g = y(4),g^{\prime} = y(5),\,g^{\prime\prime} = y(6),$$

(29)

$$\begin{aligned} yy2 & = \frac{{D_{1} D_{2} }}{{\left( {1 + \theta_{{\text{r}}} \theta } \right)^{ - 1} }}\left\{ {\frac{{2F_{{\text{r}}} }}{m + 1}y(5)^{2} - (g + f)y(6) + \frac{2m}{{m + 1}}\left( {y(2) + y(5)} \right)y(5)} \right\} + \frac{{2P_{{\text{m}}} y(5)}}{{\left( {1 + \theta_{{\text{r}}} \theta } \right)^{ - 1} (m + 1)}} \\ \, & \;\;\; + \frac{{\theta_{{\text{r}}} y(8)y(6)}}{{\left( {1 + \theta_{{\text{r}}} \theta } \right)}}{ + }\frac{{2\left( {1 + \theta_{{\text{r}}} \theta } \right)D_{1} {\text{Ha}}((1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )y(5) + \beta_{{\text{e}}} y(2))}}{{(m + 1)\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} + \beta_{{\text{e}}}^{2} } \right]}}, \\ \end{aligned}$$

(30)

$$\theta = y(7),\,\theta ^{\prime} = y(8),$$

(31)

$$yy3 = \frac{ - 1}{{\left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }} + \left( {1 + \theta (\theta_{w} - 1)} \right)^{3} R_{{\text{d}}} } \right)}}\left\{ \begin{gathered} 3R_{{\text{d}}} \left( {1 + \theta (\theta_{{\text{w}}} - 1)} \right)^{2} (\theta_{{\text{w}}} - 1)y(8)^{2} { + }\left( {\frac{2}{m + 1}} \right)\left[ {I_{1} y(2) + I_{2} \theta } \right] \hfill \\ + \left( {\frac{{{\text{Ha}}\Pr E_{{\text{c}}} \left[ {y(2)^{2} + y(5)^{2} } \right]}}{{\left[ {(1 + \beta_{{\text{e}}} \beta_{{\text{i}}} )^{2} + \beta_{{\text{e}}}^{2} } \right]}}} \right) + \Pr D_{4} (f + g)y(8) \hfill \\ \end{gathered} \right\}\,,$$

(32)

$$h = y(9),\,h^{\prime} = y(10),$$

(33)

$$yy4 = \left( {\frac{{S_{{\text{c}}} }}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} }}} \right)\left\{ {\frac{2}{m + 1}R_{{\text{c}}} \left( {1 + \alpha_{1} \theta } \right)^{n} h\exp \left( {\frac{ - E}{{1 + \alpha_{1} \theta }}} \right) - \left( {f + g} \right)y(10)} \right\},\,$$

(34)

with conditions

$$\begin{aligned} y_{0} (1) & = 0,\,y_{0} (2) - 1 = 0,\,y_{0} (7) - 1 = 0,y_{0} (4) = 0,y_{0} (5) - \alpha = 0, \, y_{0} (9) - 1 = 0, \\ y_{\inf } (2) & = 0,\, \, y_{\inf } (7) = 0, \, y_{\inf } (5) = 0,y_{\inf } (9) = 0. \\ \end{aligned}$$

(35)

The built-in function bvp4c necessities an initial guess for the clarification and the tolerance for the existing problem is occupied as $10^{ - 6}$. The initial guess we take must satisfy the boundary condition asymptotically and retain the manner of the solution. We used suitable finite values of $\eta \to \infty$, that is $\eta = \eta_{\infty } = 6$, depending on the values of the parameters involved. The thermophysical properties of the nanofluid are given in Table 1. In the absence of variable viscosity, magnetic field, hybrid nanofluid and mixed convection, the comparison is made among the published article Khan et al. (2014) and our present result which is depict in Table 2.

Table 1 Thermo-physical characteristics (Ahmad et al. 2020) of the base and nanofluid

Table 2 Comparison of $f^{\prime\prime}(0)$ and $g^{\prime\prime}(0)$ for dissimilar values of $\alpha$ when $n = 1,{\text{Ha}} = F_{r} = \theta_{{\text{r}}} = 0 = R_{{\text{b}}} = \lambda_{{\text{b}}}$

Parametric study

The results of solid volume fraction of SWCNT $\phi_{2}$ on the axial velocity along x and y axis, temperature field, and concentration profile are confirmed in Figs. 1, 2, 3, and 4. It is seen that the both component of velocity profile and their corresponding momentum boundary layer thickness enhances with enlarge the $\phi_{2}$. Which is given in Figs. 1 and 2. The thermal boundary layer thickness is higher for hybrid nanofluid than nanofluid with larger the $\phi_{2}$ (see in Fig. 3). In Fig. 4 decreasing behavior occur for concentration profile with increasing value of SWCNT solid volume fraction. Figures 5 and 6 explains that the horizontal velocity diminishes and tangential velocity increases by the high estimations of the inertial parameter $F_{{\text{r}}}$. The reduction of velocity component along x and y-direction is perceived from Figs. 7 and 8 for enhancing porosity parameter. Figures 9 and 10 show that both the velocity component ($f^{\prime}(\eta ){\text{ and }}g^{\prime}(\eta )$) slow down with the escalating magnetic field parameter $\rm{Ha}$ values. It is because the magnetic field exerts a force that suppresses the velocity, known as the Lorentz effect. And as a result, temperature distribution enhances (see Fig. 11). Figures 12, 13, 14 exemplify the x and y-component of velocity and temperature distribution against Hall parameter $\beta_{{\text{e}}}$ in the presence of hybrid nanofluid and nanofluid. From Figs. 12 and 14, when the Hall parameter $\beta_{{\text{e}}}$ takes the maximum range, it is observed that the x direction of velocity component and temperature field increases. While the y-direction of velocity field diminishes (see Fig. 12). A prominent growth in y-component of velocity is detected when $\alpha$ is amplified (see Fig. 15). Figures 16 and 17 portrays the effects of parameters $\lambda_{{\text{b}}}$ (thermal Rayleigh number) and $R_{{\text{b}}}$ (concentration Rayleigh number) on the axial velocity in the flow of hybrid nanofluid. It is seen that the velocity distribution enhances with enhancing the thermal Rayleigh number. Which is demonstrated in Fig. 16. The $R_{{\text{b}}}$ enhancement characterizes the destabilizing effect, resulting in a reduction in axial velocity as shown in Fig. 17. Figures 18, 19, and 20 explore the variation in the horizontal and vertical velocity field ($f^{\prime}(\eta ){\text{ and }}g^{\prime}(\eta )$) and temperature field when variable viscosity $\theta_{{\text{r}}}$ varies. Here the horizontal and vertical velocity field declines for the dominant variable viscosity parameter. The fluid temperature improves because of an improvement in $\theta_{{\text{r}}}$. Actually, growing the $\theta_{{\text{r}}}$ (variable viscosity parameter), the cohesive forces among the fluid’s particles decrease due to a decline in viscosity while momentum transfer in fluid particles is high which intensifies the temperature field (see in Fig. 19). The performance of temperature field under non-uniform heat generation/absorption coefficient ($I_{1} {\text{ and }}I_{2}$) is explained in Figs. 21 and 22. Non-uniform heat generation/absorption outcomes a significant improvement in temperature of ionized liquid. Physically, generated heat provides to the partially ionized liquid and as a result of this generation of heat, fluid temperature improves. Figures 23 and 24 highlight the behavior of temperature difference $\theta_{{\text{w}}}$ and radiation parameter $R_{{\text{d}}}$ on the temperature distribution. Temperature difference parameter $\theta_{{\text{w}}}$ enhance the temperature distribution ($\theta (\eta )$) because with enhancing the $\theta_{{\text{w}}}$ the surface temprature enhances which provide more heat to nanofluid (see Fig. 23). It is found from Fig. 24 that the ditribution of temperature boosts with boosting radiation parameter. Figure 25 recognizes the concentration field for changing values of Schmidt number ($S_{{\text{c}}}$). As we know, Schmidt's number is inversely related to the mass diffusivity. This is why the distribution of concentrations and the related thickness of the boundary layer decreases the Schmidt number from gradually rising values. The impact of activation energy on concentration field is explored in Fig. 26. It is demonstrated that activation energy enhances the concentration distribution $h(\eta )$. Figures 27, 28, 29 exemplify the effect of temperature and concentration ($\alpha_{1} ,\alpha_{2}$) difference and solid volume fraction $\phi_{2}$ on entropy optimization. The parameter $\alpha_{1} , \, \alpha_{2}$ reduce the entropy number while $\phi_{2}$ enhance the entropy optimization. The effect of $\beta_{{\text{e}}}$, $\phi_{2}$, and $\theta_{{\text{w}}}$ on Bejan number is shown in Figs. 30, 31, and 32. Bejan number diminishe with ion slip parameter, while it increases with $\phi_{2}$, and $\theta_{{\text{w}}}$. Tables 3, 4, and 5 gives the numerical values of skin friction along x and y direction, Nusselt number, and Sherwood number for both hybrid nanofluid and nanofluid. It is found that the skin friction along x and y direction enhances for enhancing value of $\alpha$ (velocity ratio parameter), $\phi_{2}$ (SWCNT volume fraction), ${\text{Ha}}$ (Hartmann number), and $\theta_{{\text{r}}}$ (variable viscosity) while it diminishes for $\beta_{i}$ (ion slip parameter). Table 4 demonstrates that the numerical value of Nusselt number decreases for $\phi_{2}$, ${\text{Ha}}$, $\theta_{{\text{r}}}$, and $I_{1}$ while it reduces for radiation parameter. In Table 5 the numerical value of Sherwood number ehances for all values of $\phi_{2}$, $S_{{\text{c}}}$, $R_{{\text{c}}}$, and $\alpha_{1}$.

Fig. 1

Impact of $\phi_{2}$ on velocity profile

Fig. 2

Impact of $\phi_{2}$ on $g^{\prime}(\eta )$

Fig. 3

Impact of $\phi_{2}$ on temperature field

Fig. 4

Effect of $\phi_{2}$ on concentration profile

Fig. 5

Impact of $F_{{\text{r}}}$ on velocity profile

Fig. 6

Influence of $F_{{\text{r}}}$ on $g^{\prime}(\eta )$

Fig. 7

Impact of $P_{{\text{m}}}$ on $f^{\prime}(\eta )$

Fig. 8

Effect of $P_{{\text{m}}}$ on $g^{\prime}(\eta )$

Fig. 9

Influence of ${\text{Ha}}$ on $f^{\prime}(\eta )$

Fig. 10

Action of ${\text{Ha}}$ on $g^{\prime}(\eta )$

Fig. 11

Upshot of ${\text{Ha}}$ on $\theta (\eta )$

Fig. 12

Influence of $\beta_{{\text{e}}}$ on $f^{\prime}(\eta )$

Fig. 13

Impact of $\beta_{{\text{e}}}$ on $g^{\prime}(\eta )$

Fig. 14

Impact of $\beta_{{\text{e}}}$ on $\theta (\eta )$

Fig. 15

Upshot of $\alpha$ on $g^{\prime}(\eta )$

Fig. 16

Upshot of $\lambda_{{\text{b}}}$ on $f^{\prime}(\eta )$

Fig. 17

Upshot of $R_{{\text{b}}}$ on $f^{\prime}(\eta )$

Fig. 18

Result of $\theta_{{\text{r}}}$ on $f^{\prime}(\eta )$

Fig. 19

Outcome of $\theta_{{\text{r}}}$ on $\theta (\eta )$

Fig. 20

Upshot of $\theta_{{\text{r}}}$ on $g^{\prime}(\eta )$

Fig. 21

Effect of $I_{1}$ on $\theta (\eta )$

Fig. 22

Influence of $I_{2}$ on $\theta (\eta )$

Fig. 23

Impression of $\theta_{{\text{w}}}$ on $\theta (\eta )$

Fig. 24

Effect of $R_{{\text{d}}}$ on $\theta (\eta )$

Fig. 25

Outcome of $S_{{\text{c}}}$ on $h(\eta )$

Fig. 26

Influence of $E$ on $h(\eta )$

Fig. 27

Impact of $\alpha_{1}$ on $N_{{\text{s}}} (\eta )$

Fig. 28

Action of $\alpha_{2}$ on $N_{{\text{s}}} (\eta )$

Fig. 29

Action of $\phi_{2}$ on $N_{{\text{s}}} (\eta )$

Fig. 30

Impact of $\beta_{{\text{e}}}$ on ${\text{Be}}$

Fig. 31

Effect of $\phi_{2}$ on ${\text{Be}}$

Fig. 32

Impact of $\theta_{{\text{w}}}$ on ${\text{Be}}$

Table 3 Numerical value of skin friction for various parameters when $\phi_{1} = 0.03,P_{{\text{m}}} = 0.1 = F_{{\text{r}}} = \lambda_{{\text{b}}} ,\beta_{{\text{e}}} = 0.5,R_{{\text{b}}} = 0.01$

Table 4 Numerical value of Nusselt number for numerous parameters when $\phi_{1} = 0.03,\Pr = 6.2,I_{2} = 0.1,\beta_{{\text{e}}} = 0.5,E_{{\text{c}}} = 0.1$

Table 5 Numerical value of Sherwood number for various parameters when $\phi_{1} = 0.03,\Pr = 6.2$

Concluding remarks

Simultaneous influences of nano-sized particle dispersion, nonlinear thermal radiation, activation energy, joule heating, Hall and ion slip currents, entropy generation, mixed convection, heat generation and Darcy-Forchheimer in partially ionized fluid are examined numerically in the presence of variable viscosity. In order to consider the behavior of flow fields, detailed numerical experiments are performed. The following are the main observations:

• 1. Higher coefficient of inertia, variable factor of viscosity, and porous parameter decreases the distribution of velocity.

• 2. SWCNT volume fraction boosts the horizontal and tangential velocity, temperature distribution, entropy optimization and Bejan number, while reduce the concentration distribution.

• 3. The ion slip effect enhances the horizontal velocity and temperature profile while reduce the vertical velocity.

• 4. Escalation the $\alpha_{1}$, $R_{{\text{c}}} ,{\text{ and }}S_{{\text{c}}}$ concentration distribution decreases.

• 5. Temperature profile is an increasing function of $I_{1}$, $I_{2}$, $\theta_{w}$, and $R_{d}$.

• 6. Hartmann number enhance the skin friction and reduce the Nusselt number.