Abstract
Polyvinyl alcohol (PVA) is an important industrial chemical, which is used in numerous chemical engineering applications. It is important to study and predict the flow behavior of PVA solutions and the role of nanoparticles in heat transfer applications to be used in chemical processes on industrial scale. Therefore, the present study deals with the PVA solution-based non-Newtonian Al2O3-nanofluid flow along with heat transfer over wedge. The power-law model is used for this non-Newtonian nanofluid which exhibited shear-thinning behavior. The influences of PVA and nanoparticles concentrations on the characteristics of velocity and temperature profiles are examined graphically. The impacts of these parameters on wall shear stress and convective heat transfer coefficient are also studied through tabular form. During the numerical computations, the impacts of these parameters on flow index and consistency index along with other physical properties of nanofluid are also considered. In this study, we found an improvement in heat transfer and temperature profile of fluid by distribution of Al2O3 nanoparticles. It is also noticed that resistance between adjacent layers of moving fluid is enhanced due to these nanoparticles which leads to decline in velocity profile and increases in shear stress at wall.
Similar content being viewed by others
Introduction
Polyvinyl alcohol (PVA) is a synthetic polymer with number of applications in chemical industries. It is commonly used in paper production, textile industry (Chinn et al. 2003), food packaging industries and medical applications (Salabat and Mehrdad 2010). However, it has to be noted that at room temperature polyvinyl alcohol is white powder (melting point 200 °C). Hence, it is very important to study its behavior in solutions especially if it has to be used in heat transfer applications in industry (Baker et al. 2012). For instance, due to its high corrosion resistance against common day solvents and aqueous solutions, it is used as a coating material in paint and paper industry (Creighton 1915; Zhou et al. 2017). In this particular coating application, a shear thin fluid is required to uniformly make the coating film. Hence, it is imperative to study the velocity and temperature distribution during flow of polyvinyl alcohol solutions (DeMerlis and Schoneker 2003). In addition, it has been previously reported that nanoparticles of aluminum oxide (Al2O3) have significant effect on heat flux of water in pool boiling heat transfer. The results showed that nanoparticles of Al2O3 enhanced the critical heat flux (CHF) in pool boiling. Ellahi et al. (2015a) studied the behavior of copper nanoparticles on mixed convection flow of shear thinning fluid over stretching sheet and found that temperature and heat flux of shear thinning fluid enlarged due to the increment in concentrations of small size particles. Shakouri et al. (2015) analyzed the effect of titanium dioxide (TiO2) nanoparticles on rheological behavior of polyvinyl alcohol solutions. However, they did not report any temperature or velocity distribution data, which is essential for applications in chemical industry. In addition, titanium dioxide nanoparticles are expensive as compared to aluminum oxide (Al2O3) especially if these particles are used in chemical industry in bulk quantity.
On the other hand, during the recent decades, nanofluids grabbed the attention of various researchers due to its substantial applications in the enhancement of thermal conductivity and heat transfer rate in traditional heat transfer liquids (Chamkha et al. 2012; Chamkha and Rashad 2012; RamReddy et al. 2013). Nanofluids contain very small particles (nanometer sized particles) approx. 1–100 nm. In most of the nanofluids are dilute suspension of nanoparticles in fluids and consist of few nanoparticles, less than 1 percent (by volume). Because nanoparticles are small in size, continuous suspension of these small nanoparticles would dramatically and indefinitely diminish the clogging and erosion as compared to the suspension of large nanoparticles. According to the results of recent experimental investigations, it is determined that stable suspension of nanoparticles in the conventional fluids significantly enhances the thermal conductivity of the base fluids. It is also noticed that stable nanofluids have significant properties such as higher thermal conductivity rate with small amount of nanoparticle concentrations (Eastman et al. 2001; Ellahi et al. 2016), the relation is nonlinear between particle concentration and thermal conductivity (Murshed et al. 2005; Hong et al. 2005; Choi et al. 2001), a powerful size- and temperature-dependent viscosity (Chon et al. 2005; Das et al. 2003), and an increment in threefold critical heat flux in pool boiling as compared to base liquids (You et al. 2003; Vassallo et al. 2004). Moreover, it is also found that nanofluids significantly increased the heat transfer coefficient up to 100 percent as compared to water (Faulkner et al. 2004; Ding et al. 2006; Li et al. 2003). Further, nanofluids very helpful in the following manner, i.e., decrease the friction coefficient, reduced the pumping power needs, lighter and smaller cooling systems, higher cooling rates, enhanced wear resistance and decreased the inventory of heat transfer fluids.
Some more novel applications of nanofluids involve diagnostics and sensors that immediately recognize the chemical warfare agents in the water- or food-born contaminations. Further biomedical applications involve cancer treatment, cooling of the medical devices, recognize the unhealthy materials in blood, and drug delivery systems. In view of these applications, different authors determine the nanofluid flow problem in different geometrical situations under various assumptions and conditions. For instance, Gorla et al. mass and heat transfer characteristics of free convection flow of non-Newtonian nanofluid (Gorla and Chamkha 2013). Sheikholeslami et al. (2014) considered the heat transfer on nanofluid flow through permeable stretching walls in a porous medium. Chamkha et al. (2014) described the non-similar solutions of non-Newtonian nanofluid flow over wedge. A mathematical and theoretical study of Prandtl nanofluid propagating in a peristaltic rectangular duct was explored by Ellahi et al. (2014). Bhatti et al. (2016) explained the numerical behavior of nanofluid flow using Carreau fluid model in the presence of magnetic over a shrinking sheet. Few more studies on the present topic are available in refs. and several therein (Bhatti and Rashidi 2016; Domairry et al. 2011; Chamkha et al. 2015; Ellahi et al. 2015b).
In this study, effect of aluminum oxide nanoparticles on flow of polyvinyl alcohol solutions over a wedge is investigated. To design a process for chemical industry, it is very important to know the parameters like temperature distribution, velocity distribution, Nusselt number and skin fraction. Further, in different chemical industrial process, fluid propagates through different equipment having different shapes and conditions. For example, a chemical reactor can easily be a replica of wedge shape on which fluid flows. Hence, it is important not only to study these parameters but also to familiarize the flow behavior when it propagates over a particular shape. To achieve this goal, the present work is organized in the following way. In mathematical formulation section, fundamental hydrodynamic equations and correlation models that support effective physical properties are formulated. These highly non-linear equations are solved through Homotopy analysis method (HAM) consisting of BVPh 2.0 package in solution of the problem section. The impact of pertinent flow quantities on velocity and temperature profiles as well as on wall shear stress and local Nusselt number is demonstrated and discussed in results and discussion section. In last section, achievements of study are concluded.
Mathematical modeling of the problem
Flow modeling
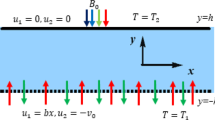
Consider an incompressible, steady state, Power-law nanofluid flow propagating over a wedge. We have considered the Cartesian coordinate system in which x-axis is measured along the direction of propagation of the fluid and y-axis is taken along normal to it as shown in Fig. 1.
The shear stress of power law model is characterized as
where μ is a consistency index, \( \dot{\gamma } \) is a shear rate and n is a flow behavior index. The case n = 1 corresponds to a Newtonian fluid. The case 0 < n < 1 is the power law relation proposed as being descriptive of shear-thinning fluid and n > 1 describe the shear-thickening fluid in nature. For the present flow, shear-thinning polymer solution of polyvinyl alcohol (PVA) is taken as a base fluid and aluminum oxide is taken as nanomaterial. Under the boundary layer assumptions, the governing equations for power law model are defined as
with boundary conditions
In above, u and v are the velocity components in x and y directions. The temperature on the surface of a wedge and away from the surface is maintained with constant temperatures T w and T∞ (T w > T∞). The potential flow velocity u e can be written as
where c is an arbitrary constant. The relation between the Falkner–Skan power-law parameter and wedge angle Ω = βπ is given as
It should be pointed out that u e increases along the wedge surface when β > 0 and decrease when β < 0.
The pressure can be calculated from the Bernoulli in the outer inviscid flow
The stream function ψ(x, y) which satisfied the equation of continuity by expression \( u = \frac{\partial \psi }{\partial y} \) and \( v = - \frac{\partial \psi }{\partial x} \), similarity variable η and dimensionless temperature function θ are defined as (Kim 2000)
Substituting Eq. (10) into Eqs. (2, 3, 4, 5), we get the following differential Eqs. (11) and (12) in non-dimensional form as
and boundaries equations are
Here \( \Pr = \frac{{\nu_{f} }}{{\alpha_{f} }}\frac{{U^{n - 1} }}{{\left( {T_{w} - T_{\infty } } \right)^{n - 1} }} \) is a modified Prandtl number (Zheng et al. 2006, 2012).
Physical properties of nanofluid
In Eqs. (11) and (12), the effective density (ρ nf ) and heat capacitance (C p ) nf of the nanofluid are described by
Further the effective viscosity is
where the consistency index (μ) and flow behavior index (n) are functions of particles and PVA concentrations as given in Table 1.
The flow behavior index for fluid has been obtained using intercepts and slopes of the fitted lines (Shakouri et al. 2015; Tian et al. 2016) as displayed in Fig. 2 and the consistency index is calculated by Brinkman equation (Brinkman 1952) as shown in Fig. 3. In these Figs., it can be viewed that the consistency index of nanofluid is enhanced whereas its flow behavior index is reduced to less than 1 which shows the shear-thinning behavior when concentration of nanoparticle is increased.
The behavior of temperature distribution in a thermal boundary layer reveals the convective heat transfer between the solid surface and the propagation of fluid over it. Simultaneously, both thermal and velocity boundary layer occurs on heated/cooled surface during the propagation of the fluid. It is noticed here that the velocity of a fluid will have greater impact on a temperature profile; the production of a velocity boundary layer associated with the thermal boundary layer will have a greater influence on the heat transfer convection process. So, assumed that thermal conductivity is act as viscosity in non-Newtonian fluid and given as (Zheng et al. 2006, 2012)
where k is function of particle concentrations. The thermal conductivities at different concentrations of PVA are given in Table 2.
Physical interest parameters
To understand the convection boundary layers, it is compulsory to understand convective heat transfer between a surface and a propagation of fluid over it. The convective heat transfer can be calculated as
where A is area of wedge’s surface and h is the convection heat transfer coefficient of the flow. The heat transfer at the surface by conduction is
These two terms have to be equal; thus,
The heat transfer coefficient in terms of Nusselt number is defined as
where \( N = \frac{{\left( {T_{w} - T_{\infty } } \right)^{n - 1} \text{Re}^{{\frac{n}{n + 1}}} }}{{x^{n - 1} }} \) is similarity number (Zheng et al. 2006, 2012).
The fluid layer in-touch with a surface will take an attempt to drag along via friction forces. Likewise, a faster fluid layer will take an attempt to drag the adjacent slower fluid layer by exerting a friction force due to the friction among two layers. Friction force per unit area is called shear stress. The shear stress at wall, for a non-Newtonian nano-fluid is defined as
The wall shear stress can be expressed in terms of skin friction coefficient is given by
Solution methodology
In this part, we will show the analytic and uniformly valid solutions using BVPh 2 Package (Ellahi et al. 2017). The formulation for BVPh 2.0 requires the governing equations along with associated boundary conditions, initial guess and auxiliary linear operators. Thus, taken the auxiliary linear operators corresponding to the Eqs. (11) and (12) as
By taking the boundary conditions in Eq. (13), we, respectively, selected the following initial guess as
Taking the linear auxiliary operators in Eq. (24) and the initial guess in Eq. (25), the coupled nonlinear Eqs. (11) and (12) subject to the Eq. (13) can be solved directly by package BVPh 2.0. Finally, the solutions of stream function and temperature profile can be exposed explicitly by means of an infinite series of the following form (Ellahi et al. 2017; Zheng et al. 2013; Marin and Baleanu 2016; Marin 1997, 2010)
where fi,m(η) and θi,m(η) are governed by high-order deformation equations. The results for the stream function, the temperature distribution, Sink friction coefficient and Nusselt numbers for different non-dimensional numbers are obtained up to 20th iterations of package.
To check the accuracy of this method, we compare values of f̋″(0) and − θ′(0) with the results from the existing literature and found an excellent agreement with these results as shown in Tables 3 and 4 (Kuo 2005; White 1991; Yacob et al. 2011).
Results and discussion
The effects of governing parameters include in the expressions of velocity and temperature distribution for shear-thinning based nanofluid that contains aluminum oxide nanoparticles are examined through Figs. 4, 5, 6 and 7. To see the impacts of different particle volume fractions and concentration of PVA on velocity and temperature profiles, values of emerging parameters like modified Prandtl number Pr, Reynolds number Re and similarity number N at different situation are calculated in Table 5.
The impact of particle volume friction on the velocity and temperature profiles is displayed in Figs. 4 and 5, respectively. It is perceived that several velocity lines have been exposed in resultant of different nanoparticles concentrations in Fig. 4. This is due to divergent collisions among neighboring particles in fluid flow that produce diverse velocity lines. It is also noticed that when the nanoparticle concentration is enhanced, the resistance between adjacent layers of moving fluid is enhanced that leads to a fall down in velocity profile. On the other hand, in Fig. 5, the temperature profile of nanofluid is increased by raising the particle volume friction. This fluid, aside from having high thermal conductivity values, has high thermal capacity and low melting point. It is remained at higher temperature than conventional fluid’s temperature. In these Figs, it is noted that the thermal boundary layer is much thinner than the momentum boundary layer which means that heat diffuses very slowly relative to momentum, but heat diffusivity is improved by distribution of nanoparticles.
The Figs. 6 and 7 demonstrate the behavior of different concentrations of PVA on the velocity and temperature profiles of nanofluid. In Fig. 6, it is examined that velocity of nanofluid is decreased when the concentration of PVA is enhanced. It is because of the reason that nanofluid becomes thinner when the concentration of PVA is increased that produces a frictional force between layers that slows down the flow of fluid. On other side, the temperature profile is decreased when PVA concentration is increased. These figures also illustrate that the thermal boundary layer becomes further thinner than momentum boundary layer when concentration of PVC powder is increased. It means that heat diffuses very slowly in case of high concentration of PVC.
The second set of solutions is represented in tabular form to describe parameters of physical interest with influence of embedding parameters. Table 6 shows the results for shear stress and convective heat transfer coefficient at wall against nanoparticle concentrations. When fluid layer is contacted with the surface of wedge, it tries to exert a frictional force on it. This frictional force is further increased in presence of nanoparticle concentrations improvement. The convective heat transfer rate over the surface is directly associated to the temperature gradient and it is increased when nanoparticle concentration is enhanced. It is seen that Nusselt number is multiple of similarity number and temperature gradient. The similarity number is decline by particle concentration enhancement. This Nusselt number decreases by decreasing similarity number. Table 7 illustrates the results of shear stress and heat transfer coefficient at wall when base fluid is modified by PVA concentrations. It is observed that base fluid becomes denser when PVA concentration is increased. So, in this consequence, friction force at wall is more increased. On the other hand, thermal diffusion is decreased when the concentration of PVA powder is increased in solution. The impact of geometry on shear stress and convective heat transfer coefficient at wall is shown in Table 8. It is seen that when angle of wedge is increased, the shear stress at wall is enhanced and whereas the values of convective heat transfer coefficient are decreased.
Conclusions
In this study, PVA-water base Al2O3-non-Newtonian nanofluid flow along with heat transfer is theoretically investigated over wedge. Based on the obtained results, this fluid reveals shear-thinning behavior that obeys the power law model. PVA and Al2O3 nanoparticle concentrations generate an impact on flow index, consistency index and other physical properties. In this consequence, velocity and temperature profiles are affected. The velocity profile is decreased due to increasing of effective viscosity by concentrations of PVA and Al2O3. The temperature profile rises by rising of particle concentrations and decreases by increasing of PVA concentrations. Furthermore, shear stress at wall is enhanced by Al2O3 and PVA concentrations, but it goes to maximum by PVA concentrations. The temperature gradient is increased because of rising of thermal diffusion by Al2O3 and decreased due to low thermal diffusion by PVA concentration. Thus, these results can help design a chemical process, e.g., coating application where behavior of fluid dictates the efficiency of the process. By these results, chemical engineers can predict the behavior of fluid in terms of heat transfer, temperature and velocity profiles to design a more efficient and environmental friendly process.
References
Baker MI, Walsh SP, Schwartz Z, Boyan BD (2012) A review of polyvinyl alcohol and its uses in cartilage and orthopedic applications. J Biomed Mater Res B Appl Biomater 100(5):1451–1457
Bhatti M, Rashidi M (2016) Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J Mol Liq 221:567–573
Bhatti MM, Abbas T, Rashidi MM, Ali ME (2016) Numerical simulation of entropy generation with thermal radiation on MHD Carreau nanofluid towards a shrinking sheet. Entropy 18(6):200
Brinkman H (1952) The viscosity of concentrated suspensions and solutions. J Chem Phys 20(4):571
Chamkha A, Rashad A (2012) Natural convection from a vertical permeable cone in a nanofluid saturated porous media for uniform heat and nanoparticles volume fraction fluxes. Int J Numer Meth Heat Fluid Flow 22(8):1073–1085
Chamkha J, Modather A, EL-Kabeir MM, Rashad A (2012) Radiative effects on boundary-layer flow of a nanofluid on a continuously moving or fixed permeable surface. Recent Pat Mech Eng 5(3):176–183
Chamkha J, Rashad AM, Subba Reddy Gorla R (2014) Non-similar solutions for mixed convection along a wedge embedded in a porous medium saturated by a non-newtonian nanofluid: natural convection dominated regime. Int J Numer Meth Heat Fluid Flow 24(7):1471–1486
Chamkha A, Abbasbandy S, Rashad A (2015) Non-darcy natural convection flow for non-Newtonian nanofluid over cone saturated in porous medium with uniform heat and volume fraction fluxes. Int J Numer Meth Heat Fluid Flow 25(2):422–437
Chinn H, Inoguchi Y, Loechner U (2003) SRI Consulting CEH Report Polyvinyl Alcohol, 2007, Menlo Park, California, (c) E. Chiellini, A. Corti, S. D’Antone, R. Solaro. Prog Polym Sci 28:963
Choi S, Zhang Z, Yu W, Lockwood F, Grulke E (2001) Anomalous thermal conductivity enhancement in nanotube suspensions. Appl Phys Lett 79(14):2252–2254
Chon CH, Kihm KD, Lee SP, Choi SU (2005) Empirical correlation finding the role of temperature and particle size for nanofluid (Al2O3) thermal conductivity enhancement. Appl Phys Lett 87(15):153107
Creighton HJM (1915) A relation concerning the distribution of an electrolyte between water and some second solvent and its dissociation constant in aqueous solution. J Franklin Inst 180(1):63–87
Das SK, Putra N, Thiesen P, Roetzel W (2003) Temperature dependence of thermal conductivity enhancement for nanofluids. J Heat Transf 125(4):567–574
DeMerlis C, Schoneker D (2003) Review of the oral toxicity of polyvinyl alcohol (PVA). Food Chem Toxicol 41(3):319–326
Ding Y, Alias H, Wen D, Williams RA (2006) Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids). Int J Heat Mass Transf 49(1):240–250
Domairry D, Sheikholeslami M, Ashorynejad HR, Gorla RSR, Khani M (2011) Natural convection flow of a non-Newtonian nanofluid between two vertical flat plates. Proc Inst Mech Eng Part N 225(3):115–122
Eastman JA, Choi S, Li S, Yu W, Thompson L (2001) Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl Phys Lett 78(6):718–720
Ellahi R, Riaz A, Nadeem S (2014) A theoretical study of Prandtl nanofluid in a rectangular duct through peristaltic transport. Appl Nanosci 4(6):753–760
Ellahi R, Hassan M, Zeeshan A (2015a) A study of heat transfer in power law nanofluid. Therm Sci 00:129
Ellahi R, Hassan M, Zeeshan A (2015b) Study of natural convection MHD nanofluid by means of single and multi-walled carbon nanotubes suspended in a salt-water solution. IEEE Trans Nanotechnol 14(4):726–734
Ellahi R, Hassan M, Zeeshan A, Khan AA (2016) The shape effects of nanoparticles suspended in HFE-7100 over wedge with entropy generation and mixed convection. Appl Nanosci 6(5):641–651
Ellahi R, Tariq M, Hassan M, Vafai K (2017) On boundary layer nano-ferroliquid flow under the influence of low oscillating stretchable rotating disk. J Mol Liq 229:339–345
Faulkner DJ, Rector DR, Davidson JJ, Shekarriz R (2004) Enhanced heat transfer through the use of nanofluids in forced convection. In: ASME 2004 international mechanical engineering congress and exposition. American Society of Mechanical Engineers, pp 219–224
Gorla RSR, Chamkha A (2013) Free convection past a vertical plate embedded in a porous medium saturated with a non-Newtonian nanofluid. J Nanofluids 2(4):297–302
Hong T, Yang H, Choi C (2005) Study of the enhanced thermal conductivity of Fe nanofluids. J Appl Phys 97(6):064311
Kim YJ (2000) Convection heat transfer of power-law fluids past a wedge embedded in a porous medium. WIT Trans Eng Sci 27:290–298
Kuo B (2005) Heat transfer analysis for the Falkner-Skan wedge flow by the differential transformation method. Int J Heat Mass Transf 48(23):5036–5046
Li Q, Xuan Y, Wang J (2003) Investigation on convective heat transfer and flow features of nanofluids. J Heat Transf 125(2003):151–155
Marin M (1997) On weak solutions in elasticity of dipolar bodies with voids. J Comput Appl Math 82(1–2):291–297
Marin M (2010) Harmonic vibrations in thermoelasticity of microstretch materials. J Vib Acoust 132(4):044501
Marin M, Baleanu D (2016) On vibrations in thermoelasticity without energy dissipation for micropolar bodies. Bound Value Probl 1:1–19
Murshed S, Leong K, Yang C (2005) Enhanced thermal conductivity of TiO2—water based nanofluids. Int J Therm Sci 44(4):367–373
RamReddy C, Murthy P, Chamkha AJ, Rashad A (2013) Soret effect on mixed convection flow in a nanofluid under convective boundary condition. Int J Heat Mass Transf 64:384–392
Salabat A, Mehrdad A (2010) Viscometric and volumetric study of dilute aqueous solutions of binary and ternary poly (ethylene glycol)/poly (vinyl alcohol) systems at different temperatures. J Mol Liq 157(1):57–60
Shakouri A, Ahmari H, Hojjat M, Zeinali Heris S (2015) Effect of TiO2 nanoparticle on rheological behavior of poly (vinyl alcohol) solution. J Vinyl Addit Technol 23(3):234–240
Sheikholeslami M, Ellahi R, Ashorynejad H, Domairry G, Hayat T (2014) Effects of heat transfer in flow of nanofluids over a permeable stretching wall in a porous medium. J Comput Theor Nanosci 11(2):486–496
Tian J, He Z, Xu T, Fang X, Zhang Z (2016) Rheological property and thermal conductivity of multi-walled carbon nano-tubes-dispersed non-Newtonian nano-fluids based on an aqueous solution of carboxymethyl cellulose. Exp Heat Transf 29(3):378–391
Vassallo P, Kumar R, D’Amico S (2004) Pool boiling heat transfer experiments in silica–water nano-fluids. Int J Heat Mass Transf 47(2):407–411
White F (1991) Viscous fluid flow. McGraw-Hill, New York
Yacob NA, Ishak A, Pop I (2011) Falkner–Skan problem for a static or moving wedge in nanofluids. Int J Therm Sci 50(2):133–139
You S, Kim J, Kim K (2003) Effect of nanoparticles on critical heat flux of water in pool boiling heat transfer. Appl Phys Lett 83(16):3374–3376
Zheng L, Zhang X, Lu C (2006) Heat transfer for power law non-Newtonian fluids. Chin Phys Lett 23(12):3301–3304
Zheng L, Lin Y, Zhang X (2012) Marangoni convection of power law fluids driven by power-law temperature gradient. J Franklin Inst 349(8):2585–2597
Zheng L, Zhang C, Zhang X, Zhang J (2013) Flow and radiation heat transfer of a nanofluid over a stretching sheet with velocity slip and temperature jump in porous medium. J Franklin Inst 350(5):990–1007
Zhou M, Cheng K, Jia G (2017) Molecular dynamics simulation studies of dopamine aqueous solution. J Mol Liq 230:137–142
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hassan, M., Faisal, A. & Bhatti, M.M. Interaction of aluminum oxide nanoparticles with flow of polyvinyl alcohol solutions base nanofluids over a wedge. Appl Nanosci 8, 53–60 (2018). https://doi.org/10.1007/s13204-018-0651-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13204-018-0651-x