1 Introduction

Commonly used net present value analyses tend to undervalue information technology investment projects (ITIPs) such as investments in standard software (e.g., Angelou and Economides 2008; Taudes et al. 2000; Wu et al. 2009), individual software (e.g., Bardhan et al. 2004; Diepold et al. 2011; Schwartz and Zozaya-Gorostiza 2003), or new technologies (e.g., Benaroch and Kauffman 2000; Ji 2010),Footnote 1 mainly because they neglect managerial flexibilities that can be exploited by project managers (cf., Benaroch et al. 2006, 2010; Taudes 1998). In this context, real option analysis (ROA) for the valuation of managerial flexibilities in ITIPs has increasingly caught the attention of practitioners and researchers (cf., Benaroch et al. 2006, 2010). A real option is a right – but not an obligation – to act on an underlying non-financial asset (e.g., an ITIP) either by deferring (postponing an ITIP), by changing capacities, by abandoning (to stop an ITIP if it turns out to be economically inefficient), or by expanding (scaling up an ITIP) at predetermined costs and after a predetermined period of time (Copeland and Antikarov 2003).Footnote 2 To value such real options, most papers featuring in the IS literature use standard financial option pricing models such as the Black–Scholes model (BSM; e.g., Benaroch et al. 2006; Heinrich et al. 2011; Taudes 1998), its discrete counterpart the Binomial model (e.g., Kambil et al. 1991; Khan et al. 2013), or the Margrabe model (e.g., Bardhan et al. 2004; Dos Santos 1991). These models, however, were not developed for complex real investments such as ITIPs and usually simplify the complexities of ROA. Consequently, managers feel that financial option pricing models overvalue real investments because there is a hiatus in the underlying assumptions (cf., Copeland and Tufano 2004; Van Putten and MacMillan 2004). In this context, researchers should not only increase the understanding of “option thinking” (Taudes et al. 2000) but also develop approaches by which the value of real options in ITIPs can be judged as accurately as possible.

Accordingly, we develop a ROA approach based on relaxed assumptions as suggested by Tallon et al. (2002), thus paving the way for a more accurate valuation of real options in ITIPs.

By relaxing the BSM assumptionsFootnote 3 in our approach (i.e., by taking the discounted cash-flows and the runtime to be uncertain as well as the market to be incomplete), the resulting option value contains idiosyncratic risk that has to be taken into account in ITIP decision making. For the realistic case of a risk averse decision maker, even a low degree of risk aversion usually leads to a lower risk adjusted option value compared to the option value calculated by means of the BSM. Consequently, the use of the BSM overvalues the option value for risk averse decision makers. This confirms the above-mentioned feedback given by managers who feel that financial option pricing models frequently overvalue ITIPs and hence induce flawed decision-making on ITIPs.

The research presented in this paper is based on the Design Science Research (DSR) paradigm (cf., Gregor and Hevner 2013; Hevner et al. 2004; Peffers et al. 2008). After introducing the particular research problem to be addressed, we discuss the related literature. Therein, we present arguments for a relaxation of the BSM assumptions to better represent the characteristics of ITIPs (descriptive knowledge). Subsequently, we discuss existing ROA approaches regarding their compliance with our relaxed assumptions (prescriptive knowledge) and state the remaining research gap. In a next step, we build and evaluate our design artifact as a rigorous formal simulation model. Here, as a first step, we duplicate the BSM representing the benchmark for modifying the BSM assumptions in four design steps. These modified assumptions (M1)–(M4) represent instantiations of the relaxed assumptions (A1′)–(A4′). In the last step, we present our final simulation model capable of simultaneously considering the four modified assumptions (M1)–(M4). For the purpose of demonstration, we instantiate our simulation model (instantiated artifact) in terms of a prototypical implementation and demonstrate that the artifact can be given a material existence (Gregor and Hevner 2013) in the shape of an operative (decision support) system. To evaluate the results of our ROA approach, we apply the instantiated artifact for each design step to the example introduced by Taudes (1998), compare the resulting option values with the option values from the BSM (competing artifacts), and finally illustrate possible consequences for ITIP decision-making. To further evaluate the compliance of our approach with ITIPs, we conducted several expert interviews with IT executives who confirm that our relaxed assumptions better represent the general characteristics of ITIPs compared to the BSM assumptions. Finally, we discuss limitations, directions for future research, and managerial implications before concluding with a summary of our key findings.

2 Related Literature

For our literature search we followed the guidelines given by Webster and Watson (2002), taking into account related literature from IS, Finance, and Economics. We included IS journals from the basket of eight of the AIS,Footnote 4 Finance and Economics journals that are ranked B or higher according to the German Academic Association for Business Research,Footnote 5 and additionally, all relevant Finance and Economics journals from the Financial Times Ranking.Footnote 6 After eliminating duplicates, we conducted a keyword search within the resulting journals, searching for “Real Option” solely as well as in combination with the terms “Assumption”, “Black–Scholes”, “Brownian Motion”, “Stochastic Process”, “Complete Market”, “Valuation”, “Option Runtime”, and the corresponding plural forms. Next we closely examined the references of the articles identified so far in order to determine previous key contributions (going back in time). Finally, going forward, we used Google Scholar to track down the contributions which cited the previously identified articles. Next we conducted a title analysis which resulted in the identification of 183 articles for further consideration. From this set of articles we extracted the descriptive knowledge (cf., Gregor and Hevner 2013) which criticized the assumptions of financial option pricing models. Based on the resulting 25 articles we investigate how the assumptions of standard financial option pricing models need to be relaxed to better represent the characteristics of ITIPs (cf., Table 1). Further, we extracted the prescriptive knowledge (cf., Gregor and Hevner 2013) where ROA approaches are presented that are based on at least one modification of the BSM assumption. These 43 articles are presented in Table 2. All articles used for the discussion of the related literature are summarized in an Online Appendix (available via http://link.springer.com).

Table 1 Relaxations of the BSM assumptions
Full size table
Table 2 Contributions treating the relaxed assumptions (A1′)–(A4′)
Full size table

2.1 Descriptive Knowledge

In the IS literature, the core assumptions of the BSM are (implicitly) transferred to the valuation of real options in ITIPs (cf., Benaroch and Kauffman 1999; Heinrich et al. 2011; Taudes et al. 2000) as follows:

  • Assumption (A1): the discounted cash-inflows (DCIF) of ITIPs are uncertain and follow a geometric Brownian motion (GBM).

  • Assumption (A2): the market is complete.

  • Assumption (A3): the discounted cash-outflows (DCOF) of ITIPs are certain and known.

  • Assumption (A4): the option runtime is certain and known.

In the next four subsections we discuss the compatibility of the four core assumptions, taking into account the actual characteristics of ITIPs.

2.1.1 Discounted Cash-Inflows

In several articles of the IS field, DCIF of ITIPs are modelled to follow GBM (e.g., Benaroch et al. 2006; Heinrich et al. 2011; Su et al. 2009; Taudes 1998). The probability distribution of GBM at any one point in time is lognormal with linearly increasing mean and variance in time (given a strictly positive drift parameter; cf., Hull 2009, p. 278). This implies that GBM is unbounded above (Metcalf and Hassett 1995) and its mean and variance go to infinity as time progresses (Brandimarte 2006, p. 101).Footnote 7 While this seems to be an appropriate assumption to make in the speculative setting of a stock market (Ewald and Yang 2008), it rarely applies to ITIPs.Footnote 8 Software or technology investment projects are usually subject to life cycles (Bollen 1999; Mahajan et al. 1990) implying that the mean of DCIF will only increase up to a certain point in time and decrease thereafter. Moreover, DCIF of ITIPs often result from cost savings that are always bounded. This contradicts a linear increase of mean and variance. Another criticism of GBM in the context of ITIPs concerns its infinitesimally small increments, which cannot account for sudden impacts (jumps) such as the launch of a new technology or the entrance of a competitor into a narrow market (Kauffman and Kumar 2008). Hence, assumption (A1) is relaxed as follows:

Assumption (A1′): DCIF of ITIPs follow an arbitrary non-negative stochastic process Footnote 9 depending on the characteristics of the underlying ITIP.

2.1.2 Completeness of the Market

A complete market implies that the underlying ITIP is continuously traded in any amount and thus, a perfect hedge can be built to eliminate its risk. Through the elimination of the risk, the resulting option value is deterministic and independent of the decision maker’s risk preference (cf., Black and Scholes 1973; Hull 2009, p. 289).

Continuously traded ITIPs are very rare (e.g., Diepold et al. 2011; Kambil et al. 1991; Schwartz and Zozaya-Gorostiza 2003). Many authors agree on this point of criticism and argue that it is sufficient to identify a “twin security” (Sick and Gamba 2010; Smith and Nau 1995; Taudes et al. 2000) that perfectly correlates with the underlying ITIP’s DCIF. However, as the majority of ITIP risk factors are unique, a perfect hedge of an ITIP’s risk by means of a twin security is unrealistic (Benaroch and Kauffman 2000) and the identification of a twin security that correlates highly but not perfectly is insufficient for obtaining an accurate option value (Hubalek and Schachermayer 2001).

Hence, without the possibility of perfectly hedging the risk of ITIPs, the resulting option value is uncertain and a decision maker has to consider her individual risk preference (cf., Diepold et al. 2011). Accordingly, assumption (A2) is relaxed as follows:

Assumption (A2′): the market is incomplete.

Consequently, the risk of ITIP’s DCIF is either unhedgeable or can only be partially hedged.

2.1.3 Discounted Cash-Outflows

As DCOF of ITIPs are usually subject to different risk factors (e.g., unforeseen changing requirements or labor costs), assumption (A3) is also criticized by several authors (e.g., Angelou and Economides 2008; Bardhan et al. 2004; Benaroch and Kauffman 1999; Kauffman and Kumar 2008; Ji 2010; Schwartz and Zozaya-Gorostiza 2003), who take DCOF to be uncertain. This raises the question of how DCOF are distributed. Several authors suggest that, similar to DCIF, DCOF should follow GBM (e.g., Bardhan et al. 2004; Dos Santos 1991; Kumar 1996, 2002; Taudes 1998). However, GBM does not seem to be reasonable for all types of ITIPs especially if DCOF mainly result from the following two sources: cash-outflows for IT infrastructure (e.g., hardware costs) and labor costs (e.g., of software developers). Costs of obtaining a specified hardware infrastructure usually decrease over time and changes in labor costs usually occur as a result of specific events such as changes in labor agreements or staffing. In this case DCOF do not seem to linearly increase over time contrary to what GBM implies. Accordingly, assumption (A3) is relaxed as follows:

Assumption (A3′): DCOF of ITIPs follow an arbitrary non-negative stochastic Footnote 10 process depending on the characteristics of the underlying ITIP.

2.1.4 Option Runtime

A very common real option in the context of ITIPs is the strategic growth option (e.g., Benaroch et al. 2006; Diepold et al. 2011; Dos Santos 1991; Heinrich et al. 2011; Taudes 1998; Taudes et al. 2000). Strategic growth options spawn new investment opportunities. One example is an infrastructure investment project that enables the pursuance of further follow-up ITIPs. In this case, the option runtime equals the runtime of the infrastructure investment project. Within this infrastructure investment project unforeseeable events such as staffing problems or collaboration problems might come up and influence the runtime. To take these uncertainties into account when valuing real options, Brach (2003) suggests to use an uncertain option runtime. Consequently, assumption (A4) is relaxed as follows:

Assumption (A4′): the option runtime is uncertain and represented by a non-negative random variable depending on the characteristics of the underlying ITIP.

All relaxed assumptions are summarized in Table 1.

2.2 Prescriptive Knowledge

To discuss the suitability of existing ROA approaches for the valuation of ITIPs, we analyzed whether these approaches are based on modifications of the BSM assumptions that coincidentally represent instantiations of the relaxed assumptions (A1′)–(A4′) (cf., Table 2).Footnote 11

We identified several ROA approaches that are based on the standard assumptions of the BSM (cf., Row 1 of Table 2). We even found approaches where single BSM assumptions are modified. Some approaches assume an incomplete market (cf., Row 5 of Table 2) in compliance with the relaxed assumption (A2′), or DCOF to be uncertain following GBM (cf., Row 3 of Table 2) representing an instantiation of the relaxed assumption (A3′), or DCIF to follow geometric mean reversion (GMR) (cf., Row 7 of Table 2) representing an instantiation of the relaxed assumption (A1′). We further identified two articles where more than one BSM assumption is modified: Jaimungal et al. (2013) assume DCIF and DCOF to follow GMR (cf., Row 9 of Table 2), and Ewald and Yang (2008) assume DCIF to follow GMR and an incomplete market (cf., Row 11 of Table 2).

To sum up, single assumptions of the BSM are modified in several articles. However, to the best of our knowledge there is no ROA approach where more than two assumptions are simultaneously modified, coincidentally representing instantiations of the relaxed assumptions (A1′)–(A4′).

3 Real Option Analysis Approach Based on Relaxed Assumptions

In the next subsections we develop and prototypically implement a simulation model which enables us to consider the relaxed assumptions (A1′)–(A4′) for valuing ITIPs. Before we present the simulation model, we introduce a running example that we use to demonstrate and evaluate our approach.

3.1 Running Example

To illustrate the effects of different modifications of the BSM assumptions that represent instantiations of the relaxed assumptions (A1′)–(A4′) on the option value, we use the example of Taudes (1998) and Taudes et al. (2000) of a company manufacturing auto parts and arms. Their example illustrates a case where the company decides whether to upgrade and continue using SAP R/2 or to switch to the client/server version of SAP R/3. The migration to SAP R/3 enables the adoption of further IS functions such as electronic data interchange (EDI; e.g., EDI-based purchasing and invoicing), workflow management for sales, document retrieval and archiving, or an e-commerce system. Thus, the company holds several strategic growth options (i.e., call options) by having the right but not the obligation to invest in the additional IS functions that are enabled by the migration to SAP R/3. The value of such a software platform, in this case SAP R/3, depends highly on the further IS functions that can be implemented in the future as it usually does not generate positive value on its own. Taudes (1998) and Taudes et al. (2000) focus on the distinct valuation of the option to invest in the EDI technology. The value of this additional IS function results from DCIF (S 0; cf., Table 3) of the EDI technology, which depend mostly on savings in inventory holding costs (e.g., decreasing buffer stocks, write-offs of obsolete inventory), transportation cost (e.g., increased accuracy enables efficient use of transportation capacities), premium freight (e.g., reduction in emergency deliveries), and document handling costs (e.g., savings on a number of tasks such as data entry or document filing). By contrast, its DCOF (X T ; cf., Table 3) result from the implementation costs of the EDI technology.

Table 3 Input parameters and initial values of the running example
Full size table

In the next section we use the input parameters of the example from Taudes (1998) who provides multiple input parameter combinations to reveal their consequences on the option value. These parameters and their initial values are summarized in Table 3.

Taudes (1998) uses the BSM to value the growth option. The calculated option values (in percent of S 0) are summarized in Table 4 for the different input parameter combinations.

Table 4 Initial option values of the BSM calculated using the running example
Full size table

These results are used in the next subsections to illustrate the consequences of modifications of the BSM assumptions (A1)–(A4) that represent instantiations of the relaxed assumptions (A1′)–(A4′) on the growth option value.

3.2 Simulation Model

Our simulation model is capable of considering various modifications of the BSM assumptions that coincidentally represent instantiations of the relaxed assumptions (A1′)–(A4′). These modified assumptions can be considered in isolation and in combination. Specifically, the artifact can duplicate the BSM and is further capable of dealing with uncertain DCOF, different stochastic processes (e.g., GBM (including jumps), GMR (including jumps)) for DCIF and DCOF, the integrated consideration of hedgeable and unhedgeable risks, and an uncertain option runtime. To the best of our knowledge, this is the first artifact which is capable of simultaneously considering all relaxed assumptions (A1′)–(A4′).

3.2.1 Base Model

To have a benchmark for our following modifications, we first duplicate the BSM. According to assumption (A1), we take DCIF S t to follow GBM, which is defined by Eq. (1) (cf., Hull 2009, p. 266):

$$\frac{{dS_{t}}}{{S_{t}}} = \mu_{S} dt + \sigma_{S} dW_{t}$$
(1)

W t represents the Wiener process driving DCIF over time (cf., Hull 2009, p. 261).

As GBM results in a lognormally distributed random variable S T at the certain and known end of the option’s runtime [cf., assumption (A4)], we use Eq. (2) to calculate a realization S T,i of DCIF (cf., Brigo et al. 2007):

$$S_{T,i} = S_{0} \cdot exp\left\{{\left({r - \frac{1}{2}\sigma_{S}^{2}} \right)T + \sigma_{S} \sqrt T \varepsilon_{i}} \right\}$$
(2)

Here, ɛ i is a realization of a standard normally distributed random variable.

To approximate the option value C [cf., Eq. (3)] of the BSM, we independently draw n random realizations ɛ i (i = 1, …, n), calculate the resulting realizations ST,i using Eq. (2), discount the differences between the realizations ST,i and the certain and known X T [cf., assumption (A3)], take the maximum of the result and zero (this is equivalent to exercising an option if and only if its value is positive), and finally take the average of the n resulting values.Footnote 12

$$C = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} max\left({e^{- rT} \left({S_{T,i} - X_{T}^{{}}} \right);0} \right)$$
(3)

We conduct n = 100,000 simulation runs for each input parameter combination of the running example and calculate their respective option values. As we receive the same results as calculated by means of the BSM (cf., Table 4), we show that our base model works correctly (“evaluation of correctness”; cf., Hevner et al. 2004).

Based upon Eq. (3), we iteratively develop our simulation model and analyze the consequences of our relaxed assumptions on the real option value in the following subsections. Here, we implement multiple modified assumptions [i.e., (M1)–(M4)] as feasible instantiations of the relaxed assumptions (A1′)–(A4′) that better represent the characteristics of ITIPs. Finally, we instantiate our artifact (i.e., a ROA approach) which considers the modified assumptions (M1)–(M4) simultaneously (cf., Sect. 3.2.6).

3.2.2 Modification of (A1) according to (A1′)

As argued in Sect. 2.1.1, GBM does not offer an adequate representation of DCIF of ITIPs. One possible stochastic process for DCIF that may better represent the characteristics of ITIPs is GMR, which is also suggested by, for example, Ewald and Yang (2008) and Sarkar (2003). GMR has the characteristics that the ITIP’s DCIF revert to a certain mean and have a diminishing growth of variance (cf., Ewald and Yang 2008; Singh et al. 2004). Specifically, in the example of Taudes (1998) the EDI’s DCIF result from savings that can be categorized into decreasing inventory holding costs, transportation costs, premium freight, document handling cost, and obsolete inventory costs. As cost savings are bounded, a process such as GMR seems to be more reasonable compared to GBM because mean and variance of GMR are bounded in contrast to GBM. Thus, our first modified assumption is (M1):

(M1) DCIF (S t ) are uncertain and follow a GMR.

Taking this modified assumption into account, we substitute Eq. (1) with Eq. (4) (cf., Ewald and Yang 2008):

$$\frac{{dS_{t}}}{{S_{t}}} = \alpha \left({\theta - S_{t}} \right)dt + \sigma_{S} dW_{t}$$
(4)

In Eq. (4), α represents the speed of mean reversion, and thus the velocity of S t being dragged back over time to its long-term mean \(\mathop S\limits^{ - }\) resulting from θ.

As we cannot calculate the realizations S T,i of a GMR in closed form (c.f., Eq. (2) for the case of GBM), we approximate GMR by a process with similar characteristics called exponential mean reversion (EMR). EMR is frequently used in the literature for exactly this purpose (e.g., Brigo et al. 2007). Thus, we substitute Eq. (4) with Eq. (5):

$$\frac{{dS_{t}}}{{S_{t}}} = \alpha \left({\theta - ln\left({S_{t}} \right)} \right)dt + \sigma_{S} dW_{t}$$
(5)

As the resulting distribution of S T is lognormal, we can use Eq. (6) to calculate a realization S T,i of DCIF (cf., Brigo et al. 2007):

$$S_{T,i} = exp\left\{{ln\left({S_{0}} \right)e^{- \alpha T} + \left({\theta - \frac{{\sigma_{S}^{2}}}{4\alpha}} \right)\left({1 - e^{- \alpha T}} \right) + \sqrt {\left({1 - e^{- 2\alpha T}} \right)\frac{{\sigma_{S}^{2}}}{2\alpha}} \varepsilon_{i}} \right\}$$
(6)

To calculate the resulting option values in the running example, we set the expected long-term mean \(\mathop S\limits^{ - }\) equal to the expected value of GBMFootnote 13 with the runtime T: \(\mathop S\limits^{ - } = exp\left( {\theta - \frac{{\sigma_{S}^{2} }}{4\alpha }} \right) = S_{0} e^{rT}\). We additionally take the mean reversion speed α to be equal to 0.4.Footnote 14 Conducting n = 100,000 simulation runs for each input parameter combination of the running example, we calculate the option values depicted in Table 5 by means of Eq. (3).

Table 5 Option values given that DCIF follow GMR (M1)
Full size table

In relation to the option values of the BSM in Table 4, we find significantly lower option values due to the lower overall variance of GMR/EMR. This stems from DCIF being bounded because they mainly result from cost savings. The deviation from the option value calculated by means of the BSM increases in time, as the impact of GMR/EMR on the overall variance of the process increases in T. Additionally, the option value decreases in mean-reversion speed due to a decreasing variance. These results are in accordance with the ROA literature (cf., Ewald and Yang 2008; Metcalf and Hassett 1995). Consequently, ITIPs which are subject to a life cycle or where DCIF are mainly realized through cost savings are overestimated by the BSM (all other factors being constant).

We additionally included jumps to GMR/EMR and found higher option values depending on jump frequency and jump size compared to the values in Table 5.Footnote 15

3.2.3 Modification of (A2) according to (A2′)

As argued in Sect. 2.1.2, it is unrealistic to assume that all ITIPs risks can be hedged and thus, to assume the market for DCIF of ITIPs to be complete. In the example of Taudes (1998), decreasing premium freight over time is due to an unexpected reduction of emergency deliveries. As it seems to be hard to find a twin security to hedge such a risk, DCIF include unhedgeable risks. Consequently, this leads to the modified assumption (M2):

(M2) The market is incomplete.

To observe the consequences of unhedgeable risk in our simulation model, we split DCIF \(\tilde{S}_{T}\) into one hedgeable part H S T and another unhedgeable part \({}_{U}^{{}} \tilde{S}_{T}\) Footnote 16:

$$\mathop {\tilde{S}}\nolimits_{T} = {}_{H}^{{}} S_{T} + {}_{U}^{{}} \mathop {\tilde{S}}\nolimits_{T}$$
(7)

We assume the unhedgeable part \({}_{U}^{{}} \tilde{S}_{T}\) to have an expected value of zero.Footnote 17 , Footnote 18 Accordingly, we have to substitute Eq. (3) with Eq. (8) to calculate the expected option value \(E[ {\mathop {\tilde{C}}} ]\):

$$E[ {\mathop {\tilde{C}} } ] = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} max\left( {e^{ - rT} \left( {{}_{H}^{{}} S_{T,i} + {}_{U}^{{}} \mathop {\tilde{S}}\nolimits_{T,i} - X_{T}^{{}} } \right);0} \right).$$
(8)

Here, \(\mathop {\tilde{C}}\) represents the uncertain option value with expected value \(E[ {\mathop {\tilde{C}} } ]\) and standard deviation \(\sigma [ {\mathop {\tilde{C}} } ]\).

Due to space restrictions we only treat the instantaneous variance \( \sigma_{S}^{2} \) = 0.2, and vary the proportion of unhedgeable risk according to the vector ϑ = (0, 0.25, 0.5, 0.75, 1).Footnote 19 Conducting n = 100,000 simulation runs for each input parameter combination of the running example, we obtain the results shown in Table 6.

Table 6 Expected option values and standard deviations given that the hedgeable part of DCIF varies (M2)
Full size table

The different values of ϑ yield the corresponding idiosyncratic risk of the option value represented through its standard deviation \(\sigma[ {\mathop {\tilde{C}} } ]\), which is depicted in brackets below the associated expected option value \(E[ {\mathop {\tilde{C}} } ]\). The expected option value is constant in ϑ and equal to the associated option values in the BSM (Table 4). However, the idiosyncratic risk of the option value is increasing in ϑ, starting from ϑ = 0, where the overall risk of DCIF is hedgeable (i.e., the BSM case), to the point where the overall risk is assumed to be unhedgeable (ϑ = 1). This holds for increasing time horizons T, as well as for increasing levels of the instantaneous variance of overall DCIF \( \sigma_{S}^{2} \).

We found several approaches in the ROA literature that assume the entire risk of the underlying asset to be unhedgeable (cf., Diepold et al. 2011; Hilhorst et al. 2006; Guthrie 2007). To the best of our knowledge, the ROA approach presented here is the first able to vary the proportion of hedgeable and unhedgeable risk and reveals the implications on the value and risk of a real option embedded in an ITIP.

3.2.4 Modification of (A3) according to (A3′)

In Sect. 2.1.3, we argued for uncertain DCOF mainly resulting from labor and infrastructure costs (cf., Sect. 2.1.3) which also holds for the running example to implement EDI, presented by Taudes (1998). Moreover, around half of all large ITIPs – defined as those with initial price tags exceeding $15 million – massively blow their budget (Bloch et al. 2012). This indicates that DCOF can be unbounded and consequently be assumed to follow a GBM. Accordingly, we present the following modified assumption (M3) for DCOF:

(M3) DCOF (\(\mathop {\tilde{X}}\nolimits_{t}\)) are uncertain, follow a GBM and the associated risk is unhedgeable.

Thus, we calculate realizations of DCOF \(\mathop {\tilde{X}}\nolimits_{t}\) using Eq. (2). To calculate the expected option value based on n simulation runs, we substitute Eq. (3) with Eq. (9):

$$E[ {\mathop {\tilde{C}} } ] = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} max\left( {e^{ - rT} \left( {S_{T,i} - \mathop {\tilde{X}}\nolimits_{{T,i}} } \right);0} \right).$$
(9)

We take the instantaneous variance of DCOF \( \sigma_{X}^{2} \) to be equal to the instantaneous variance of DCIF \( \sigma_{X}^{2} \) = \( \sigma_{S}^{2} \).Footnote 20 Conducting n = 100,000 simulation runs for each input parameter combination of the running example, we obtain the results shown in Table 7.

Table 7 Expected option values and standard deviations given that DCOF follow GBM and are unhedgeable (M3)
Full size table

Taking DCOF to follow a GBM results in higher expected option values in relation to the BSM values. This stems from the considered uncertainty associated with labor and infrastructure costs. Since we take this risk to be unhedgeable, the resulting option values contain idiosyncratic risk. The effect of taking DCOF to be uncertain on the expected option value is extensively discussed in the literature (e.g., Bardhan et al. 2004; Dos Santos 1991). However, the consequences of unhedgeable DCOF on the option value’s risk has not been considered in existing ROA approaches so far.

In further modifications of (A3) we included jumps (cf., footnote 15), for example, or modelled DCOF to follow GMR (cf., Sect. 3.2.2). In all cases, we found the expected option value, as well as its risk, to be higher in comparison to the BSM values (cf., Table 4).

3.2.5 Modification of (A4) according to (A4′)

In Sect. 2.1.4 we argued that especially for strategic growth options, the option runtime often deviates from the initially planned runtime. In the running example of Taudes (1998) it can hardly be assumed that the time when the migration to the client/server version of SAP R/3 is finished (i.e., option runtime) is known with certainty ex-ante. Accordingly, we present the following modified assumption (M4):

(M4) The option runtime (\(\mathop {\tilde{T}}\)) is represented by a Poisson distributed random variable Footnote 21 and the associated risk is unhedgeable.

To calculate the expected option value based on the modified assumption (M4) we replace Eq. (3) with Eq. (10):

$$E[ {\mathop {\tilde{C}} } ] = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} max\left( {e^{{ - r\mathop {\tilde{T}}\nolimits_{i} }} \left( {S_{{\mathop {\tilde{T}}\nolimits_{i} ,i}} - X_{T}^{{}} } \right);0} \right).$$
(10)

We take the expected value of the option runtime \(E\left[ {\mathop {\tilde{T}} } \right]\) to be equal to the initial option runtime T of Taudes (1998) (cf., Table 3) and its minimum option runtime to be exactly half the initial option runtime \(\frac{T}{2}\). Since there is almost no evidence that ITIPs are finished earlier than initially planned, we set all realizations of the option runtime \(\mathop {\tilde{T}}\) that are lower than T to be equal to T. Based on n = 100,000 simulation runs for each input parameter combination of the running example, we obtain the results reproduced in Table 8.

Table 8 Expected option values and standard deviations given that the option runtime is represented by a Poisson distributed random variable (M4)
Full size table

By taking the option runtime to be uncertain, the expected option values are slightly higher than in the BSM and the option value is associated with a non-negligible amount of risk. This results from the fact that the implementation of EDI depends on the initial migration project which can take longer than initially planned. To the best of our knowledge, an uncertain option runtime has not yet been considered in existing ROA approaches.

3.2.6 Modification of (A1), (A2), (A3), and (A4) according to (A1′), (A2′), (A3′), and (A4′)

In this subsection we demonstrate that multiple assumptions of the BSM can be modified simultaneously according to the relaxed assumptions by means of our simulation model.

We combine (M1) DCIF (S t ) are uncertain and follow a GMR including jumps,Footnote 22 (M2) the market is incomplete, (M3) DCOF (\(\mathop {\tilde{X}}\nolimits_{t}\)) are uncertain, follow a GBM and the associated risk is unhedgeable, and (M4) the option runtime (\({\tilde{T}}\)) is represented by a Poisson distributed random variable and the associated risk is unhedgeable.

Considering the modified assumptions (M1)–(M4), we modify and expand Eq. (3) to calculate the expected option value:

$$E[ {\mathop {\tilde{C}} } ] = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} max\left( {e^{{ - r\mathop {\tilde{T}}\nolimits_{i} }} \left( {S_{\mathop {\tilde{T}}\nolimits_{i} ,i} - {{\mathop {\tilde{X}}}_{\mathop{\tilde{T}}\nolimits_{i} ,i}}} \right);0} \right).$$
(11)

We set all parameter values according to the parameter values in the modified assumptions (M1)–(M4). Additionally, we take jumps in DCIF to occur approximately once every 3 years (λ = 0.3) and their instantaneous variance is assumed to be \( \sigma_{J}^{2} \) = 0.3.

We finally conduct n = 100,000 simulation runs for each input parameter combination of the running example. The results are shown in Table 9.

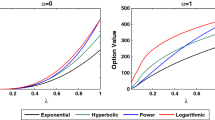
Table 9 Expected option values and standard deviations given a combination of our different modified assumptions (M1)–(M4)
Full size table

In comparison to the results in Table 4 we observe the additional risk induced by jumps of DCIF, uncertain DCOF, as well as the uncertain option runtime to overall increase the expected option value. As all sources of risk are assumed to be unhedgeable, the option value contains idiosyncratic risk. In a comparative analysis for the case T = 2, X 0 = 100 %, \( \sigma_{S}^{2} \) = 10 % we illustrate the difference between the expected option value of our approach from Table 9 and the option value of the BSM from Table 4 depending on varying sets of different input parameter values (see Fig. 1, Panel A). Accordingly, we illustrate the difference between the standard deviation of our approach from Table 9 and the standard deviation of the BSM, which equals zero due to the assumed non-existence of unhedgeable risks (see Fig. 1, Panel B).

Fig. 1
figure 1

Comparative analysis

Full size image

We see that the difference in the (expected) option value is positive and increases in instantaneous variance of DCOF (Var DCOF \( \sigma_{X}^{2} \) ∊ [0.1; 0.5]) and in jump parameters (Jump Freq. λ and Size \( \sigma_{J}^{2} \) ∊ [0.3; 0.5]). It further decreases in instantaneous variance of DCIF (Var DCIF \( \sigma_{S}^{2} \) ∊ [0.1; 0.5]) and in option runtime (Time T ∊ [2; 10]). We additionally see that the difference in the standard deviation is positive and increases in all mentioned input parameters.

3.3 Decision Making

Since the option values calculated by means of our ROA approach contain a significant amount of idiosyncratic risk, a decision maker has to take this risk into consideration in addition to the expected option value in ITIPs decision making. To make rational and theoretically well founded decisions based on the expected value and the risk of a random variable (in our case, the option value), preference functions that are compatible with the Bernoulli principle (cf., Bernoulli 1954) can be used. The choice of an appropriate preference function mainly depends on (1) the chosen risk measure, (2) the risk preference of the decision maker, and (3) the distribution of the considered random variable.

  1. 1.

    Preference functions are usually defined for a specific risk measure. As risks can be deemed to deviate from an expected or target value either negatively, or both negatively and positively, a corresponding risk measure has to be selected. This consequently restricts the choice of a preference function.

  2. 2.

    Most preference functions are contingent on the decision maker’s risk preference. Thus, before a preference function can be chosen, it has to be determined whether the decision maker is risk seeking, risk neutral, or risk averse.

  3. 3.

    Some preference functions can only be used for random variables with specific probability distributions such as normally distributed random variables.

Since (1) most companies consider risk of ITIPs as a negative deviation from a target value (Otim et al. 2012), (2) managerial decision makers are usually risk averse (cf., Parnell et al. 2013, p. 56; Ross 2014; Sandmo 1971), and (3) the probability distribution for the resulting option value cannot be determined in general, we choose the following preference function that complies with the above mentioned realizations of the criteria (1)–(3):

$$\varPhi = E[ {\mathop {\tilde{C}} } ] - \xi LPM_{1} .$$
(12)

The parameter ξ > 0 represents the decision maker’s degree of risk aversion and LPM 1 is the first lower partial moment representing the expected loss. The expected loss is calculated as \(LPM_{1} \left( {z; {\tilde{C}}_{i} } \right) = \frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} \left( {z - {\tilde{C}}_{i} } \right)f\left( { {\tilde{C}}_{i} } \right)\) (cf., Unser 2000). Thereby, z represents a target value (in our case we set \(z = E[ {\mathop {\tilde{C}} } ]\)), \({\tilde{C}}_{i}\) is a realization of the uncertain option value, and \(f\left( { {\tilde{C}}_{i} } \right) = 1\) for \({\tilde{C}}_{i} < z\) and \(f\left( { {\tilde{C}}_{i} } \right) = 0\) for \({\tilde{C}}_{i} \ge z\).

Table 10 lists the risk aversion parameters ξ that lead to the same risk adjusted option value compared to the option value calculated by means of the BSM (i.e., the break-even value) for all input parameter value combinations of our running example.Footnote 23

Table 10 Risk aversion parameters that lead to the same risk-adjusted option value as the BSM
Full size table

Thus, for a decision maker’s degree of risk aversion that is greater than the break-even values in Table 10 (e.g., ξ = 0.19 in case of T = 2, X 0 = 100 % and \( \sigma_{S}^{2} \) = 10 %), the risk adjusted option value is lower compared to the option value calculated by means of the BSM (and vice versa). Since the risk aversion parameter ξ is strictly positive and can take arbitrary high values,Footnote 24 we conclude that even for a low degree of risk aversion the BSM usually overvalues the real option. Thus, using the BSM to value ITIPs may lead to flawed investment decisions where in fact unprofitable investments are undertaken.Footnote 25

4 Expert Evaluation of the Relaxed Assumptions

So far, we have already evaluated our simulation model in terms of correctness by applying it to the running example of Taudes (1998) based on the BSM assumptions and receiving the same option values as calculated by means of the BSM (cf., Sect. 3.2.1). Consequently, the deviations from the BSM option values in the Sects. 3.2.2–3.2.6 solely result from the modified assumptions (M1)–(M4) which were stated in accordance with our relaxed assumptions (A1′)–(A4′). In order to verify whether these relaxed assumptions better represent the characteristics of ITIPs, we conducted five semi-structured interviews with decision makers in industry. This included an associate of an IT consulting company, a senior ERP architect of a multinational engineering and electronics company, a freelancer who works for different clients in various ITIPs, a consultant of a business consulting company, and the Financial Manager of IT Strategies and Corporate IT of a global IT services provider. As the interviewees work in different ITIPs, functions and companies, their contributions provide a “triangulation of subjects” (cf., Rubin and Rubin 2011). Each of the interviews took about an hour. We structured the interview questions according to the four topics given by the relaxed assumptions: (1) DCIF, (2) market completeness, (3) DCOF, and (4) option runtime. The interview guidelines were sent out to the interviewees prior to the interviews. All interviews were audio-taped, transcribed, notes were taken during the interviews and written summaries produced immediately after the interviews were completed. We subsequently performed a qualitative content analysis (cf., Patton 2002) of the interview transcripts and summaries, resulting in insights from practice concerning the relaxed assumptions for ITIPs. In the following we briefly present the results.

  1. 1.

    DCIF: All interviewees commented that according to their experience DCIF are uncertain, cannot reach arbitrarily high values, and that changes in DCIF often result from specific unforeseeable events (e.g., a new competitive product in the market, or unforeseen changes in government regulations). Moreover, all interviewees stated that if the runtime of an underlying ITIP increases, the DCIF are more likely to remain constant or even decrease, rather than increase. An example was mentioned by one interviewee who said that “the longer we take to roll out an ITIP, the lower the market potentials usually will be” (i.e., time-to-market effects). Another interviewee mentioned that “delaying an ITIP, in our case a SAP HANA project, usually leads to later operational cost savings that are intended by the project”. Two interviewees mentioned that the DCIF may increase in time if the underlying technology is still in an early developmental stage. The specific example mentioned was that “if the technology we roll out is in an early development stage and we increase the runtime, the new functionalities have more time to mature and consequently DCIF are likely to increase”. On the other hand, they also stated that for mature technologies the DCIF may decrease over time. This supports the argument that GBM provides an inadequate representation of DCIF for ITIPs that are subject to a technology life cycle. This also supports our modified assumption (M1) that DCIF follow GMR.

  2. 2.

    Market completeness: All interviewees agreed that it is not possible to completely hedge the risk of ITIPs with a twin security on the financial market and that the majority of the risk cannot be hedged at all. Examples for risk factors that cannot be hedged are a shortage of resource availability (e.g., programming experts are needed by another project), changing requirements, or external risk factors such as changing government regulations. The interviewees also argued that hedgeable risks are very rare and only make up the minority of risks of ITIPs. An example was given by one interviewee who said that “we only hedge currency risks associated with the overall (world-wide) ITIP portfolio of our company”. This supports our modified assumption (M2) that risks associated with ITIPs cannot be hedged at all, or at best partially.

  3. 3.

    DCOF: All interviewees stated that, in their experience, DCOF of ITIPs are uncertain. Examples the interviewees mentioned for uncertain DCOF were that “resources can fail and need to be replaced immediately by a more expensive one”. Consequently, this undermines the plausibility of the BSM assumption of certain and known DCOF for ITIPs and supports our relaxed assumption that DCOF follow an arbitrary non-negative stochastic process. Moreover, the interviewees mentioned that an unexpected increase in the option runtime leads to increasing, rather than decreasing, DCOF. In this context, one interviewee stated that “we often only identify new requirements during the runtime of an ITIP, which leads to an extended scope of the ITIP that again extends the runtime and increases DCOF”. This therefore supports our modified assumption (M3) that DCOF are uncertain and follow a GBM.

  4. 4.

    Option runtime: All five interviewees considered the runtime of ITIPs to be uncertain. They further mentioned that it is unrealistic for ITIPs to be completed ahead of schedule. An explanation for this phenomenon was given by one interviewee who said “ITIPs are never completed earlier because people make use of the estimated time, even if they could have come to an end earlier”. By contrast, the majority of ITIPs take longer to complete than planned. This supports our relaxed assumption (A4′) that the option runtime is uncertain, at least for real options where the completion of an ITIP is the precondition for their execution (e.g., strategic growth options which, according to our interviewees, are one of the most frequently occurring option types in practice). This also supports the implementation of the uncertain option runtime within our ROA approach, where we do not allow for realizations of the option runtime to be any shorter than the initially scheduled option runtime.

These results verify our central claim that our relaxed assumptions offer a better representation of ITIP characteristics and thus support our modified assumptions. This is a strong indication that our ROA approach leads to a more accurate valuation of ITIPs compared to ROA approaches that were presented in the literature so far.

5 Discussion

Although we rigorously designed and evaluated our ROA approach, we recognize some limitations. In the following subsections we present possible directions on how to address these limitations in future research and discuss potential consequences of the implementation of our approach in practice.

5.1 Implications for Future Research

We implicitly assume the correlation between DCIF and DCOF to be approximately zero. However, cases may exist where DCIF and DCOF may be correlated. This means that decision makers have to be aware that the option value of an ITIP will be affected if DCIF and DCOF are correlated (cf., Dos Santos 1991; Kumar 1996). As stated by Dos Santos (1991) and Taudes (1998), a positive correlation between DCIF and DCOF reduces the option value since the probability of a high difference between DCIF and DCOF will be lower. We aim to incorporate such correlations into our simulation model in future research.

Our simulation results are based on specific input parameter value combinations. We further conducted multiple simulations for a large set of reasonable input parameter value combinations and found that for all these combinations the findings stay the same. This indicates that our results hold in general.

As is the case with economic models in general, the more we relax restrictive assumptions, the more parameters have to be estimated (cf., the additionally required input parameters estimated for a combination of the modified assumptions (M1)–(M4)). Hence, decision makers have to be aware of the trade-off between the additional value of a more precise approach and the additional effort and uncertainty concerning the estimation of more input parameters in comparison to a closed form solution such as the BSM. To reduce this effort and uncertainty, we aim to empirically analyze already completed ITIPs to find the best fitting non-negative stochastic processes and parameterizations for DCIF and DCOF, especially. The results of this study can be used as default parameterizations of our approach for different types of ITIPs.

5.2 Managerial Implications

ROA approaches are considered to be highly relevant for enabling the improved planning and selection of ITIPs, but they are currently rarely applied by companies for two main reasons: first, managers are not satisfied with the results of current ROA approaches, given that investment projects are far more complex than financial options, and it would not be appropriate to try to make the investment project fit into a financial option pricing approach which considerably reduces its complexity (cf., Copeland and Tufano 2004; Van Putten and Macmillan 2004). Second, ROA approaches are too difficult to apply in practice (cf., Copeland and Tufano 2004). With the ROA approach presented here, we specifically address the first issue by adequately considering the higher complexity within the relaxed assumptions and by providing an ROA approach that paves the way for an accurate valuation of managerial flexibilities in ITIPs. To address the second issue and to simplify the application of ROA in practice, we aim to further develop our prototypical implementation to arrive at a user friendly decision support system for ITIP selection decisions. For that purpose, we aim to add a user-friendly interface and generate default parameterizations based on historical data of different types of ITIPs (cf., Sect. 5.1). This allows decision makers to use our ROA approach without knowing the mathematical details. We also plan to visualize the results via graphics to make them more accessible. Thus, we believe that our ROA approach and its implementation will help to close the gap between research and practice and to increase the acceptance of ROA in practice.

6 Conclusion

“A major challenge for IS research lies in making models and theories that were developed in other academic disciplines usable in IS research and practice” (Benaroch and Kauffman 1999). Against this backdrop, we developed an ROA approach based on relaxed assumptions which paves the way for an accurate valuation of managerial flexibilities in ITIPs. This research is based on the Design Science Research paradigm (cf., Gregor and Hevner 2013; Hevner et al. 2004; Peffers et al. 2008). We started by arguing that, due to their restrictive assumptions, standard financial option pricing models such as the BSM are not generally applicable. Based on the IS, Finance, and Economics literature we relaxed these assumptions to better represent the characteristics of ITIPs. We then developed a simulation model that enables the valuation of real options on ITIPs based on different modifications of the BSM assumptions that represent instantiations of the relaxed assumptions (A1′)–(A4′). To the best of our knowledge, this is the first ROA approach capable of simultaneously considering arbitrary modifications of the BSM assumptions (A1)–(A4).

By relaxing the BSM assumptions (i.e., taking the discounted cash-flows and the runtime to be uncertain as well as the market to be incomplete), the option value resulting from our ROA approach contains idiosyncratic risk that has to be taken into account in ITIP decision making. For the realistic case of a risk averse decision maker, even a low level of risk aversion usually results in a lower risk-adjusted option value compared to the option value calculated by means of the BSM. In other words, the use of the BSM overvalues the option value for risk averse decision makers. This confirms the perception by managers that ITIPs tend to be overvalued by financial option pricing models and can lead to flawed ITIP selection decisions.

We would like to conclude by outlining the generalizability and the breadth of the results of our approach. We deduced the modifications of the BSM’s restrictive assumptions from existing discussions in the ROA literature and the key characteristics of ITIPs. These modifications do not seem to be restricted to ITIPs alone but rather to be general enough to apply to other real investments such as natural resource investments, investments in supply chains, etc. Hence, our simulation model seems to be capable of valuing a more general class of real options and the findings of this paper are likely to have a broader relevance beyond ITIPs.