Abstract
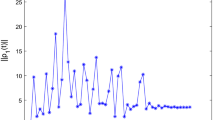
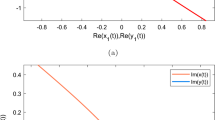
This paper deals with the synchronization issue of fractional-order complex-valued Hopfield neural networks with time delay. In this paper, by means of properties of the fractional-order inequality, such as Hölder inequality and Gronwall inequality, sufficient conditions are presented to guarantee the finite-time synchronization of the fractional-order complex-valued delayed neural networks when 1/2 ≤ γ < 1 and 0 < γ < 1/2. Finally, two numerical simulations are provided to show the effectiveness of the obtained results.
Similar content being viewed by others
References
D. Zeng, R. Zhang, Y. Liu, and S. Zhong, “Sampleddata synchronization of chaotic Lur’e systems via inputdelay–dependent–free–matrix zero equality approach,” Applied Mathematics and Computation, vol. 315, pp. 34–46, December 2017.
R. Zhang, X. Liu, D. Zeng, S. Zhong, and K. Shi, “A novel approach to stability and stabilization of fuzzy sampleddata Markovian chaotic systems,” Fuzzy Sets and Systems, vol. 344, pp. 108–128, 2017.
I. Podlubny. Fractional Differential Equations, Academic, New York, NY, USA, 1999.
D. Cafagna, “Fractional calculus: A mathematical tool from the past for present engineers [Past and present],” Industrial Electronics Magazine IEEE, vol. 1, no. 2, pp. 35–40, July 2007.
A. A. Kilbas, H. M. Srivastava, and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Elesvier, New York, NY, USA, 2006.
X. Wu, J. Li, and G. Chen, “Chaos in the fractional order unified system and its synchronization,” Journal of the Franklin Institute, vol. 345, no. 4, pp. 392–401, July 2008.
Y. Li, Y. Q. Chen, and I. Podlubny, “Technical communique: Mittag–Leffler stability of fractional order nonlinear dynamic systems,” Automatica, vol. 45, no. 8, pp. 1965–1969, August 2009.
X. Wu, H. Lu, and S. Shen, “Synchronization of a new fractional–order hyperchaotic system,” Physics Letters A, vol. 373, no. 27, pp. 2329–2337, June 2009.
M. J. Seow, V. K. Asari, and A. Livingston, “Learning as a nonlinear line of attraction in a recurrent neural network,” Neural Computing and Applications, vol. 19, no. 2, pp. 337–342, March 2010.
J. Cao and M. Xiao, “Stability and Hopf bifurcation in a simplified BAM neural network with two time delays,” IEEE Transactions on Neural Networks, vol. 18, no. 2, pp. 416–430, March 2007.
W. Yu, J. Cao, and G. Chen, “Stability and Hopf bifurcation of a general delayed recurrent neural network,” IEEE Trans Neural Networks, vol. 19, no. 5, pp. 845–854, May 2008.
Q. Zhu and J. Cao, “Stability analysis of Markovian jump stochastic BAM neural networks with impulse control and mixed time delays,” IEEE Transactions on Neural Networks Learning Systems, vol. 23, no. 3, pp. 467–479, March 2012.
R. Zhang, D. Zeng, S. Zhong, and Y. Yu, “Event–triggered sampling control for stability and stabilization of memristive neural networks with communication delays,” Applied Mathematics and Computation, vol. 310, pp. 57–74, October 2017.
P. Arena, R. Caponetto, L. Fortuna, and D. Porto, “Bifurcation and chaos in noninteger order cellular neural networks,” International Journal of Bifurcation and Chaos, vol. 8, no. 7, pp. 1527–1539, July 1998.
I. Petras, “A note on the fractional–order cellular neural networks,” Proc. of IEEE International Joint Conference on Neural Networks, pp. 1021–1024, July 2006.
A. Boroomand and M. B. Menhaj, “Fractional–order Hopfield neural networks,” Proceedings of the 15th international conference on Advances in neuro–information processing. pp. 883–890, 2008.
H. Huang, T. Huang, and X. Chen, “A mode–dependent approach to state estimation of recurrent neural networks with Markovian jumping parameters and mixed delays,” Neural Networks, vol. 46, no. 10, pp. 50–61, October 2013.
H. Bao, J. Cao, and J. Kurths, “State estimation of fractional–order delayed memristive neural networks,” Nonlinear Dynamics, vol. 94, no. 2, pp. 1215–1225, 2018.
H. Wu, X. Zhang, S. Xue, L. Wang, and Y. Wang, “LMI conditions to global Mittag–Leffler stability of fractionalorder neural networks with impulses,” Neurocomputing, vol. 193, pp. 148–154, June 2016.
J. Yu, C. Hu, and H. Jiang, “a–stability and a–synchronization for fractional–order neural networks,” Neural Networks, vol. 35, pp. 82–87, August 2012.
L. Chen, Y. Chai, R. Wu, “Letters: dynamic analysis of a class of fractional–order neural networks with delay,” Neurocomputing, vol. 111, no. 6, pp. 190–194, July 2013.
F. Wang, Y. Yang, and M. Hu, “Asymptotic stability of delay fractioanal–order neural networks with impulsive effects,” Neurocomputing, vol. 154, pp. 239–244, April 2015.
H. Wu, X. Zhang, S. Xue, and P. Niu, “Quasi–uniform stability of Caputo–type fractional–order neural networks with mixed delay,” International Journal of Machine Learning and Cybernetics, vol. 8, no. 5, pp. 1501–1511, October 2017.
E. Kaslik and S. Sivasundaram, “Nonlinear dynamics and chaos in fractional–order neural networks,” Neural Networks the Official Journal of the International Neural Network Society, vol. 32, no. 1, pp. 245–256, February 2012.
H. Bao, J. H. Park, and J. Cao, “Adaptive synchronization of fractional–order memristor–based neural networks with time delay,” Nonlinear Dynamics, vol. 82, no. 3, pp. 1343–1354, November 2015.
H. Bao, J. H. Park, and J. Cao, “Synchronization of fractional–order delayed neural networks with hybrid coupling,” Complexity, vol. 21, pp. 106–112, 2016.
S. Zhou, X. Lin, L. Zhang, and Y. Li, “Chaotic synchronization of a fractional neurons network system with two neurons,” Proc. of International Conference on Communications, Circuits and Systems, pp. 773–776, 2010.
M. Bohner, V. S. H. Rao, and S. Sanyal, “Global stability of complex–valued neural networks on time scales,” Differential Equations and Dynamical Systems, vol. 19, no. 1–2, pp. 3–11, January 2011.
J. Hu and J. Wang, “Global stability of complex–valued recurrent neural networks with time–delays,” IEEE Transactions on Neural Networks and Learning Systems, vol. 23, no. 6, pp. 853–865, May 2012.
R. Rakkiyappan, J. Cao, and G. Velmurugan, “Existence and uniform stability analysis of fractional–order complexvalued neural networks with time delays,” IEEE Transactions on Neural Networks and Learning Systems, vol. 26, no. 1, pp. 84–97, January 2015.
S. Tyagi, S. Abbas, and M. Hafayed, “Global Mittag–Leffler stability of complex valued fractional–order neural network with discrete and distributed delays,” Rendiconti del Circolo Matematico di Palermo Series 2, vol. 65, no. 3, pp. 485–505, December 2016.
R. Zhang, D. Zeng, J. Park, Y. Liu, and S. Zhong, “Nonfragile Sampled–Data Synchronization for Delayed Complex Dynamical NetworksWith Randomly Occurring Controller Gain Fluctuations,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 48, no. 12, pp. 2271–2281, Dec. 2017.
H. Bao, H. P. Ju, and J. Cao, “Synchronization of fractional–order complex–valued neural networks with time delay,” Neural Networks, vol. 681, pp. 16–28, May 2016.
D. S. Mitrinovic, Analytic Inequalities, Springer, New York, 1970.
M. Kuczma, An Introduction to the Theory of Functional Equations and Inequalities: Cauchy’s Equation and Jensen’s Inequality. Birkhauser, Switzerlang, 2009.
C. Corduneanu, Principle of Differential and Intergral Equations, Allyn and Bacon, USA, 1971.
Author information
Authors and Affiliations
Corresponding author
Additional information
Recommended by Editor Jessie (Ju H.) Park. This work was jointly supported by the National Natural Science Foundation of China (61573306), the National Natural Science Foundation of China (61403331) and the Natural Science Foundation of Hebei Province of China (F2016203427). The authors are extremely grateful to anonymous reviewers for their careful reading of the manuscript and insightful comments, which help to enrich the content of the paper. We would also like to acknowledge the valuable comments and suggestions from the editors, which vastly contributed to improve the presentation of the paper.
Xinxin Zhang is working on her Ph.D. degree in the School of Electrical Engineering, Yanshan University, Qinhuangdao, China. She received the B.S. degree from Hebei Normal University of Science and Technology, Qinhuangdao, China, in 2013. She received the master’s degree from Yanshan University, Qinhuangdao, China, in 2016. Her current research interests include fractional-order neural networks.
Peifeng Niu received his Ph.D. degree from Dongbei University in 1997. He is currently working in the School of Electrical Engineering, Yanshan University, Qinhuangdao, China. His research interests include thermal process automation, metallurgical automation, artificial intelligence control, machine learning and neural network.
Nan Liu has received her College degree, and she is currently working in the Yanshan University, Qinhuangdao, China. Her research interest includes computer technology.
Guoqiang Li received his Ph.D. degree form Yanshan Univer- sity, Qinhuangdao, China. He is currently working in the School of Electrical Engineering, Yanshan University, Qinhuangdao, China. His research interests include artificial intelligent, machine learning and the modeling and control of complex industrial systems.
Rights and permissions
About this article
Cite this article
Zhang, X., Niu, P., Liu, N. et al. Global Synchronization in Finite-time of Fractional-order Complexvalued Delayed Hopfield Neural Networks. Int. J. Control Autom. Syst. 17, 521–535 (2019). https://doi.org/10.1007/s12555-018-0167-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12555-018-0167-x