Skip to main content
SpringerLink
Log in

Command shaping for flexible systems: A review of the first 50 years

  • Published:
International Journal of Precision Engineering and Manufacturing Aims and scope Submit manuscript

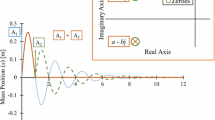
Abstract

The control of flexible systems is a large and important field of study. Unwanted transient deflection and residual vibration are detrimental to many systems ranging from nano-positioning devices to large industrial cranes. Thousands of researchers have worked diligently for decades to provide solutions to the challenging problems posed by flexible dynamic systems. The work can roughly be broken into three categories:1) Hardware design, 2) Feedback control, and 3) Command shaping. This paper provides a review of command-shaping research since it was first proposed in the late 1950’s. The important milestones of the research advancements, as well as application examples, are used to illustrate the developments in this important research field.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Khalid, A., Huey, J., Singhose, W., Lawrence, J. and Frakes, D., “Human Operator Performance Testing Using an Input-Shaped Bridge Crane,” ASME J. of Dynamic Systems, Measurement, and Control, Vol. 128, No. 4, pp. 835–841, 2006.

    Google Scholar 

  2. Kim, D. and Singhose, W., “Studies of Human Operators Manipulating Double-Pendulum Cranes,” Proc. European Control Conference, pp. WeC10.1, 2007.

  3. Manning, R., Kim, D. and Singhose, W., “Reduction of Distributed Payload Bridge Crane Oscillations,” Proc. WSEAS International Conference on Automatic Control, Modeling, and Simulation, pp. 133–139, 2008.

  4. Smith, O. J. M., “Posicast Control of Damped Oscillatory Systems,” Proc. the IRE, Vol. 45, No. 9, pp. 1249–1255, 1957.

    Google Scholar 

  5. Smith, O. J. M., “Feedback Control Systems,” McGraw-Hill Book Co., Inc., 1958.

  6. Tallman, G. H. and Smith, O. J. M., “Analog Study of Dead-Beat Posicast Control,” IRE Transactions on Automatic Control, Vol. 4, No. 1, pp. 14–21, 1958.

    Google Scholar 

  7. Tesar, D. and Mathew, G. K., “The Dynamic Synthesis, Analysis, and Design of Modeling Cam Systems,” Lexington Books, 1935.

  8. Rothbart, H., “Cams: Design, Dynamics, and Accuracy,” John Wiley & Sins, Inc., 1956.

  9. Kwakernaak, H. and Smith, J., “Minimum Vibration Cam Profiles,” J. of Mechanical Engineering Science, Vol. 10, pp. 219–227, 1968.

    Google Scholar 

  10. Wiederrich, J. L. and Roth, B., “Design of Low Vibration Cam Profiles,” Proc. Conference on Cams and Cam Mechanisms, 1974.

  11. Gimpel, D. J. and Calvert, J. F., “Signal Component Control,” AIEE Transactions, pp. 339–343, 1952.

    Google Scholar 

  12. Calvert, J. F. and Gimpel, D. J., “Method and Apparatus for Control of System Output Response to System Input,” U.S. Patent No. 2801351, 1957.

  13. Aspinwall, D. M., “Acceleration Profiles for Minimizing Residual Response,” ASME Journal of Dynamic Systems, Measurement, and Control, Vol. 102, No. 3, pp. 3–6, 1980.

    Google Scholar 

  14. Swigert, C. J., “Shaped Torque Techniques,” Journal of Guidance and Control, Vol. 3, No. 5, pp. 460–467, 1980.

    Google Scholar 

  15. Turner, J. D. and Junkins, J. L., “Optimal Large-Angle Single-Axis Rotational Maneuvers of Flexible Spacecraft,” Journal of Guidance and Control, Vol. 3, pp. 578–585, 1980.

    MATH  Google Scholar 

  16. Meckl, P. H. and Seering, W. P., “Minimizing Residual Vibration for Point-to-Point Motion,” Journal of Vibration, Acoustics, Stress and Reliability in Design, Vol. 107, No. 3, pp. 378–382, 1985.

    Google Scholar 

  17. Meckl, P. H. and Seering, W. P., “Experimental Evaluation of Shaped Inputs to Reduce Vibration for a Cartesian Robot,” J. of Dynamic Systems, Measurement, and Control, Vol. 112, No. 2, pp. 159–165, 1990.

    Google Scholar 

  18. Singer, N. C. and Seering, W. P., “Preshaping Command Inputs to Reduce System Vibration,” Journal of Dynamic Systems, Measurement, & Control, Vol. 112, No. 1, pp. 76–82, 1990.

    Google Scholar 

  19. Ogata, K., “Modern Control Engineering,” Prentice-Hall, Inc., p. 282, 1970.

  20. Cook, G., “An Application of Half-Cycle Posicast,” IEEE Trans. on Automatic Control, Vol. 11, No. 3, pp. 556–559, 1966.

    Google Scholar 

  21. Shields, V. C. and Cook, G., “Application of an Approximate Time Delay to a Posicast Control System,” International Journal of Control, Vol. 14, No. 4, pp. 649–657, 1971.

    Google Scholar 

  22. Mee, D. H., “A Feedback Implementation of Posicast Control Using Sampling Circuits,” Proc. of the Institute of Radio and Electronics Engineering, pp. 11–15, 1974.

  23. Singer, N. C. and Seering, W. P., “Using Acausal Shaping Techniques to Reduce Robot Vibration,” Proc. of the IEEE International Conference on Robotics and Automation, Vol. 3, pp. 1434–1439, 1988.

    Google Scholar 

  24. Singer, N. and Seering, W. P., “Experimental Verification of Command Shaping Methods for Controlling Residual Vibration in Flexible Robots,” Proc. of the American Control Conference, 1989.

  25. Singer, N. C., “Residual Vibration Reduction in Computer Controlled Machines,” Mechanical Engineering, Ph. D. thesis, Massachusetts Institute of Technology, 1989.

  26. Yurkovich, S., Tzes, A. P. and Hillsley, K. L., “Controlling Coupled Flexible Links Rotating in the Horizontal Plane,” Proc. of the American Control Conference, pp. 362–368, 1990.

  27. Bhat, S. P. and Miu, D. K., “Precise Point-to-Point Positioning Control of Flexible Structures,” ASME Winter Annual Meeting, 1989.

  28. Tzes, A. P., Englehart, M. J. and Yurkovich, S., “Input Preshaping With Frequency Domain Information For Flexible-Link Manipulator Control,” Proc. of the AIAA Guidance, Navigation and Control Conference, pp. 1167–1175, 1989.

  29. Tzes, A. P. and Yurkovich, S., “Adaptive Precompensators for Flexible-Link Manipulator Control,” 28th IEEE Conference on Decision and Control, Vol. 3, pp. 2083–2088, 1989.

    Google Scholar 

  30. Bhat, S. P. and Miu, D. K., “Precise Point-to-Point Positioning Control of Flexible Structures,” ASME Journal of Dynamic Systems, Measurement, and Control, Vol. 112, No. 4, pp. 667–674, 1990.

    Google Scholar 

  31. Bhat, S. P. and Miu, D. K., “Solutions to Point-to-Point Control Problems using Laplace Transform Technique,” Proc. American Control Conf., 1990.

  32. Singh, T. and Vadali, S. R., “Robust Time-Delay Control,” ASME Journal of Dynamic Systems, Measurement, and Control, Vol. 115, pp. 303–306, 1993.

    MATH  Google Scholar 

  33. Pao, L. Y. and Singhose, W. E., “Robust Minimum Time Control of Flexible Structures,” Automatica, Vol. 34, pp. 229–236, 1998.

    MathSciNet  MATH  Google Scholar 

  34. Singhose, W. E., Seering, W. P. and Singer, N. C., “Shaping Inputs to Reduce Vibration: A Vector Diagram Approach,” Proc. IEEE Int. Conf. on Robotics and Automation, pp. 922–927, 1990.

  35. Singhose, W., Seering, W. and Singer, N., “Residual Vibration Reduction Using Vector Diagrams to Generate Shaped Inputs,” J. of Mechanical Design, Vol. 116, pp. 654–659, 1994.

    Google Scholar 

  36. Park, U. H., Lee, J. W., Lim, B. D. and Sung, Y. G., “Design and Sensitivity Analysis of an Input Shaping Filter in the Z-Plane,” J. of Sound and Vibration, Vol. 243, pp. 157–171, 2001.

    Google Scholar 

  37. Singhose, W. E., Porter, L. J., Tuttle, T. D. and Singer, N. C., “Vibration Reduction Using Multi-Hump Input Shapers,” J. of Dynamic Systems, Measurement, and Control, Vol. 119, pp. 320–326, 1997.

    MATH  Google Scholar 

  38. Singer, N. C. and Seering, W. P., “An Extension of Command Shaping Methods for Controlling Residual Vibration Using Frequency Sampling,” Proc. IEEE International Conference on Robotics and Automation, pp. 800–805, 1992.

  39. Singhose, W., Seering, W. and Singer, N., “Input Shaping for Vibration Reduction with Specified Insensitivity to Modeling Errors,” Proc. Japan-USA Sym. on Flexible Automation, pp. 307–313, 1996.

  40. Singhose, W., Kim, D. and Kenison, M., “Input Shaping Control of Double-Pendulum Bridge Crane Oscillations,” ASME J. Dynamic Systems, Measurement, and Control, Vol. 130, p. 034504, 2008.

    Google Scholar 

  41. Pao, L. Y., Chang, T. N. and Hou, E., “Input Shaper Designs for Minimizing the Expected Level of Residual Vibration in Flexible Structures,” Proc. American Control Conf., pp. 3542–3546, 1997.

  42. Pao, L. and Lau, M., “Robust Input Shaper Control Design for Parameter Variations in Flexible Structures,” J. of Dynamic Systems, Measurement, and Control, Vol. 122, pp. 63–70, 2000.

    Google Scholar 

  43. Tzes, A. and Yurkovich, S., “An Adaptive Input Shaping Control Scheme for Vibration Suppression in Slewing Flexible Structures,” IEEE Transactions on Control Systems Technology, Vol. 1, pp. 114–121, 1993.

    Google Scholar 

  44. Khorrami, F., Jain, S. and Tzes, A., “Experiments of Rigid-Body Based Controllers with Input Preshaping for a Two-Link Flexible Manipulator,” Proc. American Control Conf., pp. 2957–2961, 1992.

  45. Khorrami, F., Jain, S. and Tzes, A., “Experimental results on adaptive nonlinear control and input preshaping for multi-link flexible manipulators,” Automatica, Vol. 31, pp. 83–97, 1995.

    MathSciNet  MATH  Google Scholar 

  46. Khorrami, F., Jain, S. and Tzes, A., “Adaptive Nonlinear Control and Input Preshaping for Flexible-Link Manipulators,” Proc. American Control Conf., pp. 2705–2709, 1993.

  47. Kojima, H. and Singhose, W., “Adaptive Deflection Limiting Control for Slewing Flexible Space Structures,” AIAA J. of Guidance, Control, and Dynamics, Vol. 30, pp. 61–67, 2007.

    Google Scholar 

  48. Bodson, M., “An Adaptive Algorithm for the Tuning of Two Input Shaping Methods,” Automatica, Vol. 34, pp. 771–776, 1998.

    MATH  Google Scholar 

  49. Park, J. and Chang, P. H., “Learning Input Shaping Technique for Not-LTI Systems,” Proc. American Control Conference, 1998.

  50. Rhim, S. and Book, W., “Adaptive Time-delay Command Shaping Filter for Flexible Manipulator Control,” IEEE/ASME Trans. on Mechatronics, Vol. 9, pp. 619–626, 2004.

    Google Scholar 

  51. Park, J. and Rhim, S., “Extraction of Optimal Time-delay in Adaptive Command Shaping Filter for Flexible Manipulator Control,” J. of Inst. of Control, Robotics and System, Vol. 14, pp. 564–572, 2008.

    Google Scholar 

  52. Rhim, S. and Book, W., “Adaptive Command Shaping Using Adaptive Filter Approach in Time Domain,” Proc. American Control Conference, pp. 81–85, 1999.

  53. Bodson, M., “Experimental Comparison of Two Input Shaping Methods for the Control of Resonant Systems,” Proc. IFAC World Congress, 1996.

  54. Magee, D. P. and Book, W. J., “Implementing Modified Command Filtering to Eliminate Multiple Modes of Vibration,” Proc. American Controls Conference, pp. 2700–2704, 1993.

  55. Magee, D. P. and Book, W. J., “Experimental Verification of Modified Command Shaping Using a Flexible Manipulator,” Proc. of the 1st International Conference on Motion and Vibration Control, 1992.

  56. Rhim, S. and Book, W., “Noise Effect on Time-domain Adaptive Command Shaping Methods for Flexible Manipulator Control,” IEEE Trans. of Control Systems Technology, Vol. 9, pp. 84–92, 2001.

    Google Scholar 

  57. Cook, G., “Control of Flexible Structures Via Posicast,” Proc. Eighteenth Southeastern Symp. on System Theory, pp. 31–35, 1986.

  58. Hyde, J. M. and Seering, W. P., “Inhibiting Multiple Mode Vibration in Controlled Flexible Systems,” Proc. American Control Conf., 1991.

  59. Hyde, J. M. and Seering, W. P., “Using Input Command Pre Shaping to Suppress Multiple Mode Vibration,” Proc. IEEE Int. Conf. on Robotics and Automation, pp. 2604–2609, 1991.

  60. Singhose, W. E., Crain, E. A. and Seering, W. P., “Convolved and Simultaneous Two-Mode Input Shapers,” IEE Control Theory and Applications, Vol. 144, pp. 515–520, 1997.

    MATH  Google Scholar 

  61. Sung, Y.-G. and Singhose, W., “Robustness Analysis of Input Shaping Commands for Two-mode Flexible Systems,” IET Control Theory and Applications, Vol. 3, pp. 722–730, 2009.

    MathSciNet  Google Scholar 

  62. Hillsley, K. L. and Yurkovich, S., “Vibration Control of a Two-Link Flexible Robot Arm,” Proc. IEEE Int. Conf. on Robotics and Automation, pp. 2121–2126, 1991.

  63. Magee, D. P. and Book, W. J., “Filtering Schilling Manipulator Commands to Prevent Flexible Structure Vibration,” Proc. American Control Conf., pp. 2538–2542, 1994.

  64. Magee, D. P. and Book, W. J., “Filtering Micro-Manipulator Wrist Commands to Prevent Flexible Base Motion,” Proc. American Control Conf., pp. 924–928, 1995.

  65. Magee, D. P. and Book, W. J., “Eliminating Multiple Modes of Vibration in a Flexible Manipulator,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 474–479, 1993.

  66. Hillsley, K. L. and Yurkovich, S., “Vibration Control of a Two-Link Flexible Robot Arm,” J. of Dynamics and Control, Vol. 3, pp. 261–280, 1993.

    MathSciNet  MATH  Google Scholar 

  67. Banerjee, A. K., “Dynamics and Control of the WISP Shuttle-Antennae System,” J. of Astronautical Sciences, Vol. 41, pp. 73–90, 1993.

    Google Scholar 

  68. Banerjee, A. K. and Singhose, W. E., “Command Shaping in Tracking Control of a Two-Link Flexible Robot,” J. of Guidance, Control, and Dynamics, Vol. 21, pp. 1012–1015, 1998.

    Google Scholar 

  69. Singh, T. and Vadali, S. R., “Input-Shaped Control of Three-Dimensional Maneuvers of Flexible Spacecraft,” J. of Guidance, Control, and Dynamics, Vol. 16, pp. 1061–1068, 1993.

    Google Scholar 

  70. Sung, Y. G. and Wander, J. P., “Applications of Vibration Reduction of Flexible Space Structure Using Input Shaping Technique,” Proc. Southeastern IEEE Conference, pp. 333–336, 1993.

  71. Tuttle, T. D. and Seering, W. P., “Vibration Reduction in 0-g Using Input Shaping on the MIT Middeck Active Control Experiment,” Proc. American Control Conf., pp. 919–923, 1995.

  72. Tuttle, T. D. and Seering, W. P., “Vibration Reduction in Flexible Space Structures Using Input Shaping on MACE: Mission Results,” Proc. IFAC World Congress, pp. 55–60, 1996.

  73. Banerjee, A., Pedreiro, N. and Singhose, W., “Vibration Reduction for Flexible Spacecraft Following Momentum Dumping with/without Slewing,” AIAA J. of Guidance, Control, and Dynamics, Vol. 24, pp. 417–428, 2001.

    Google Scholar 

  74. Robertson, M., Timm, A. and Singhose, W., “Evaluation of Command Generation Techniques for Tethered Satellite Retrieval,” Proc. AAS/AIAA Space Flight Mechanics Conference, 2005.

  75. Hu, Q., “Input shaping and variable structure control for simultaneous precision positioning and vibration reduction of flexible spacecraft with saturation compensation,” Journal of Sound and Vibration, Vol. 318, pp. 18–35, 2008.

    Google Scholar 

  76. Kim, D. and Singhose, W., “Human Operator Learning On Double-Pendulum Bridge Cranes,” ASME IMECE, 2007.

  77. Sorensen, K. L., Danielson, J. and Singhose, W. E., “Anti-Sway and Positioning Control For An Industrial Bridge Crane With Multi-Mode Dynamics,” Proc. ASME International Symposium on Flexible Automation, 2008.

  78. Hong, K.-T. and Hong, K.-S., “Input Shaping and VSC of Container Cranes,” Proc. IEEE International Conference on Control Applications, pp. 1570–1575, 2004.

  79. Singh, T. and Heppler, G. R., “Shaped Input Control of a System with Multiple Modes,” ASME Journal of Dynamic Systems, Measurement, and Control, Vol. 115, pp. 341–347, 1993.

    MATH  Google Scholar 

  80. Lim, S. and How, J., “Input Command Shaping Techniques for Robust, High-Performance Control of Flexible Structures,” Proc. AIAA Guidance, Navigation, and Control Conf., 1996.

  81. Lim, S., Stevens, H. D. and How, J. P., “Input Shaping Design for Multi-input Flexible Systems,” J. of Dynamic Systems, Measurement and Control, Vol. 121, pp. 443–447, 1999.

    Google Scholar 

  82. Cutforth, C. F. and Pao, L. Y., “A Modified Method for Multiple Actuator Input Shaping,” Proc. American Control Conf., pp. 66–70, 1999.

  83. Pao, L. Y., “Multi-Input Shaping Design for Vibration Reduction,” Automatica, Vol. 35, pp. 81–89, 1999.

    MATH  Google Scholar 

  84. Vaughan, J. and Singhose, W., “Reducing Vibration and Providing Robustness with Multi-Input Shapers,” Proc. American Control Conference, 2009.

  85. Kenison, M. and Singhose, W., “Concurrent Design of Input Shaping and Proportional Plus Derivative Feedback Control,” ASME J. of Dynamic Systems, Measurement, and Control, Vol. 124, pp. 398–405, 2002.

    Google Scholar 

  86. Muenchhof, M. and Singh, T., “Concurrent Feedforward/Feedback Controller Design Using Time-Delay Filters,” Proc. AIAA Guidance, Navigation and Control Conference, 2002.

  87. Fortgang, J. and Singhose, W., “Concurrent Design of Vibration Absorbers and Input Shapers,” Journal of Dynamic Systems, Measurement, and Controls, Vol. 127, pp. 329–335, 2005.

    Google Scholar 

  88. Magee, D. P., Cannon, D. W. and Book, W. J., “Combined Command Shaping and Inertial Damping for Flexure Control,” Proc. American Control Conf., Vol. 3, pp. 1330–1334, 1997.

    Google Scholar 

  89. Pontryagin, L. S., Boltyanskii, V. G., Gamkrelidze, R. V. and Mishchenko, E. F., “The Mathematical Theory of Optimal Processes,” John Wiley & Sons, 1962.

  90. Athens, M. and Falb, P. L., “Optimal Control,” McGraw-Hill, 1966.

  91. Hermes, H. and Lasalle, J. P., “Functional Analysis and Time Optimal Control,” Academic Press, 1969.

  92. Bryson, A. and Ho, Y.-C., “Applied Optimal Control,” Hemisphere Publishing, 1975.

  93. Ben-Asher, J., Burns, J. A. and Cliff, E. M., “Time-Optimal Slewing of Flexible Spacecraft,” J. of Guidance, Control, and Dynamics, Vol. 15, pp. 360–367, 1992.

    MATH  Google Scholar 

  94. Vander Velde, W. and He, J., “Design of Space Structure Control Systems Using On-Off Thrusters,” Journal Guidance, Control and Dynamics, Vol. 6, No. 1, pp. 53–60, 1983.

    MATH  Google Scholar 

  95. Liu, Q. and Wie, B., “Robust Time-Optimal Control of Uncertain Flexible Spacecraft,” Journal of Guidance, Control, and Dynamics, Vol. 15, pp. 597–604, 1992.

    MATH  Google Scholar 

  96. Wie, B. and Liu, Q., “Comparison Between Robustified Feedforward and Feedback for Achieving Parameter Robustness,” Journal of Guidance, Control, and Dynamics, Vol. 15, pp. 935–943, 1992.

    MATH  Google Scholar 

  97. Wie, B., Sinha, R. and Liu, Q., “Robust Time-Optimal Control of Uncertain Structural Dynamic Systems,” J. of Guidance, Control, and Dynamics, Vol. 15, pp. 980–983, 1993.

    Google Scholar 

  98. Singh, T. and Vadali, S. R., “Robust Time-Optimal Control: A Frequency Domain Approach,” Journal of Guidance, Control and Dynamics, Vol. 17, pp. 346–353, 1994.

    MATH  Google Scholar 

  99. Singhose, W., Derezinski, S. and Singer, N., “Extra-Insensitive Input Shapers for Controlling Flexible Spacecraft,” J. of Guidance, Control, and Dynamics, Vol. 19, pp. 385–391, 1996.

    Google Scholar 

  100. Singhose, W., Bohlke, K. and Seering, W. “Fuel-Efficient Pulse Command Profiles for Flexible Spacecraft,” J. of Guidance, Control, and Dynamics, Vol. 19, pp. 954–960, 1996.

    MATH  Google Scholar 

  101. Wie, B., Sinha, R., Sunkel, J. and Cox, K., “Robust Fuel- and Time-Optimal Control of Uncertain Flexible Space Structures,” Proc. Guidance, Navigation, and Control Conference, pp. 939–948, 1993.

  102. Singh, T., “Fuel/Time Optimal Control of the Benchmark Problem,” J. of Guidance, Control, and Dynamics, Vol. 18, pp. 1225–1231, 1995.

    MATH  Google Scholar 

  103. Meyer, J. L. and Silverberg, L., “Fuel Optimal Propulsive Maneuver of an Experimental Structure Exhibiting Spacelike Dynamics,” Journal of Guidance, Control, and Dynamics, Vol. 19, pp. 141–149, 1996.

    MATH  Google Scholar 

  104. Driessen, B. J., “On-off minimum-time control with limited fuel usage: Near global optima via linear programming,” Optimal Control Applications & Methods, Vol. 27, pp. 161–168, 2006.

    MathSciNet  Google Scholar 

  105. Singhose, W., Singh, T. and Seering, W., “On-Off Control with Specified Fuel Usage,” Journal Dynamic Systems, Measurement, and Control, Vol. 121, pp. 206–212, 1999.

    Google Scholar 

  106. Singhose, W., Banerjee, A. and Seering, W., “Slewing Flexible Spacecraft with Deflection-Limiting Input Shaping,” J. of Guidance, Control, and Dynamics, Vol. 20, pp. 291–298, 1997.

    MATH  Google Scholar 

  107. Singhose, W., Mills, B. and Seering, W., “Closed-Form Methods for Generating On-Off Commands for Undamped Flexible Structures,” J. of Guidance, Control, and Dynamics, Vol. 22, pp. 378–382, 1999.

    Google Scholar 

  108. Dhanda, A. and Franklin, G., “Vibration Control via Preloading,” Proc. American Control Conference, pp. 3574–3579, 2005.

  109. Singhose, W., Biediger, E., Okada, H. and Matunaga, S., “Closed-Form Specified-Fuel Commands for On-Off Thrusters,” AIAA J. of Guidance, Control, and Dynamics, Vol. 29, pp. 606–611, 2006.

    Google Scholar 

  110. Sung, Y.-G. and Singhose, W., “Closed-Form Specified-Fuel Commands for Two Flexible Modes,” AIAA Journal of Guidance, Control, and Dynamics, Vol. 30, pp. 1590–1596, 2007.

    Google Scholar 

  111. Robertson, M. J. and Singhose, W. E., “Specified-Deflection Command Shapers for Second-Order Position Input Systems,” ASME Journal of Dynamic Systems, Measurement and Control, Vol. 129, pp. 856–859, 2007.

    Google Scholar 

  112. Sung, Y.-G. and Singhose, W., “Deflection-Limiting Commands for Systems with Velocity Limits,” AIAA J. Guidance, Control, and Dynamics, Vol. 31, pp. 472–478, 2008.

    Google Scholar 

  113. Singhose, W., “Shaping Inputs to Reduce Vibration: A Vector Diagram Approach,” MIT Artificial Intelligence Lab, Memo No. 1223, 1990.

  114. Rogers, K. and Seering, W. P., “Input Shaping for Limiting Loads and Vibration in Systems with On-Off Actuators,” Proc. AIAA Guidance, Navigation, and Control Conference, 1996.

  115. Song, G., Buck, N. and Agrawal, B., “Spacecraft Vibration Reduction Using Pulse-Width Pulse-Frequency Modulated Input Shaper,” J. of Guidance, Control & Dynamics, Vol. 22, pp. 433–440, 1999.

    Google Scholar 

  116. Buffinton, K. W., Hoffman, K. L., Hekman, K. A. and Berg, M. C., “Optimal pulse-width control of flexible dynamic systems,” Proc. IASTED International Conference on Robotics and Applications, 2007.

  117. Vaughan, J., Singhose, W., Debenest, P., Fukushima, E. and Hirose, S., “Initial Experiments on the Control of a Mobile Tower Crane,” ASME IMECE, 2007.

  118. Danielson, J., Vaughan, J., Singhose, W., Widler, L. and Glauser, U., “Design of a Mobile Boom Crane for Research and Educational Applications,” Proc. International Conference on Motion and Vibration Control, 2008.

  119. Parker, G. G., Groom, K., Hurtado, J. E., Feddema, J., Robinett, R. D. and Leban, F., “Experimental Verification of a Command Shaping Boom Crane Control System,” Proc. American Control Conference, pp. 86–90, 1999.

  120. Masoud, Z. N. and Daqaq, M. F., “A Graphical Approach to Input-Shaping Control Design for Container Cranes with Hoist,” IEEE Transactions on Control Systems Technology, Vol. 14, No. 6, pp. 1070–1077, 2006.

    Google Scholar 

  121. Zrnić, N., Petković, Z. and Bošnjak, S., “Automation of Ship-To-Shore Container Cranes: A Review of State-of-the-Art,” FME Transactions, Vol. 33, pp. 111–121, 2005.

    Google Scholar 

  122. Park, B. J., Hong, K.-S. and Huh, C. D., “Time-Efficient Input Shaping Control of Container Cranes,” Proc. International Conference on Control Applications, pp. 80–85, 2000.

  123. Daqaq, M. F. and Masoud, Z. N., “Nonlinear Input-Shaping Controller for Quay-Side Container Cranes,” Nonlinear Dynamics, Vol. 45, No. 1–2, pp. 149–170, 2006.

    MathSciNet  MATH  Google Scholar 

  124. Yoon, J., Singhose, W., Kim, M. D., Ramirez, G. and Tawde, S. K., “Dynamics and Control of Bouncing and Tilting Crane Payloads,” ASME IDETC, 2009.

  125. Jones, S. and Ulsoy, A. G., “An Approach to Control Input Shaping with Application to Coordinate Measuring Machines,” J. of Dynamics, Measurement, and Control, Vol. 121, pp. 242–247, 1999.

    Google Scholar 

  126. Seth, N., Rattan, K. and Brandstetter, R., “Vibration Control of a Coordinate Measuring Machine,” Proc. IEEE Conf. on Control Apps., pp. 368–373, 1993.

  127. Singhose, W., Singer, N. and Seering, W., “Improving Repeatability of Coordinate Measuring Machines with Shaped Command Signals,” Precision Engineering, Vol. 18, pp. 138–146, 1996.

    Google Scholar 

  128. Fortgang, J., Singhose, W. and Márquez, J. d. J., “Command Shaping for Micro-Mills and CNC Controllers,” Proc. American Control Conference, 2005.

  129. Singhose, W. and Singer, N., “Effects of Input Shaping on Two-Dimensional Trajectory Following,” IEEE Trans. on Robotics and Automation, Vol. 12, pp. 881–887, 1996.

    Google Scholar 

  130. deRoover, D., “Motion Control of a Wafer Stage,” Delft University Press, 1997.

  131. Park, S.-W., Hong, S.-W., Choi, H.-S. and Singhose, W., “Discretization Effects of Real-Time Input Shaping in Residual Vibration Reduction for Precise XY Stage,” Trans. of the Korean Society of Machine Tool Engineers, Vol. 16, pp. 71–78, 2007.

    Google Scholar 

  132. Vaughan, J., Yano, A. and Singhose, W., “Comparison of Robust Input Shapers,” Journal of Sound and Vibration, Vol. 315, pp. 797–815, 2008.

    Google Scholar 

  133. Vaughan, J., Yano, A. and Singhose, W., “Robust Negative Input Shapers for Vibration Suppression,” ASME J. Dynamic Systems, Measurement, and Control, Vol. 131, pp. 031014-1–9, 2009.

    Google Scholar 

  134. Starr, G. P., “Swing-Free Transport of Suspended Objects with a Path-Controlled Robot Manipulator,” J. of Dynamic Systems, Measurement and Control, Vol. 107, pp. 97–100, 1985.

    Google Scholar 

  135. Murphy, B. R. and Watanabe, I., “Digital Shaping Filters for Reducing Machine Vibration,” IEEE Transactions on Robotics and Automation, Vol. 8, pp. 285–289, 1992.

    Google Scholar 

  136. Feddema, J. T., “Digital Filter Control of Remotely Operated Flexible Robotic Structures,” Proc. American Control Conf., pp. 2710–2715, 1993.

  137. Yano, K. and Terashima, K., “Sloshing suppression control of liquid transfer systems considering a 3-D transfer path,” IEEE-ASME Transactions on Mechatronics, Vol. 10, pp. 8–16, 2005.

    Google Scholar 

  138. Feddema, J., Dohrmann, C., Parker, G., Robinett, R., Romero, V. and Schmitt, D., “Control for Slosh-Free Motion of an Open Container,” IEEE Control Systems, Vol. 17, pp. 29–36, 1997.

    Google Scholar 

  139. Zou, K., Drapeau, V. and Wang, D., “Closed Loop Shaped-Input Strategies for Flexible Robots,” Int. J. of Robotics Research, Vol. 14, pp. 510–529, 1995.

    Google Scholar 

  140. Rappole, B. W., Singer, N. C. and Seering, W. P., “Multiple-Mode Impulse Shaping Sequences for Reducing Residual Vibrations,” Proc. 23rd Biennial Mechanisms Conference, pp. 11–16, 1994.

  141. Kwon, D.-S., Hwang, D.-H., Babcock, S. M. and Burks, B. L., “Input Shaping Filter Methods for the Control of Structurally Flexible, Long-Reach Manipulators,” Proc. IEEE Conf. on Robotics and Automation, pp. 3259–3264, 1994.

  142. Chang, T., Godbole, K. and Hou, E., “Optimal input shaper design for high-speed robotic workcells,” Journal of Vibration and Control, Vol. 9, pp. 1359–1376, 2003.

    MATH  Google Scholar 

  143. Grosser, K. and Singhose, W., “Command Generation for Reducing Perceived Lag in Flexible Telerobotic Arms,” JSME International Journal, Vol. 43, pp. 755–761, 2000.

    Google Scholar 

  144. Wilson, D. G., Stokes, D., Starr, G. and Robinett, R. D., “Optimized Input Shaping for a Single Flexible Robot Link,” SPACE 96: 5th International Conf. and Expo. on Engineering, Construction, and Operations in Space, 1996.

  145. Singhose, W., “Trajectory Planning for Flexible Robots: CRC Robotics and Automation Handbook, T. Kurfess, Ed.,” CRC Press, 2004.

  146. Mohamed, Z. and Tokhi, M. O., “Command Shaping Techniques for Vibration Control of a Flexible Robot Manipulator,” Mechatronics, Vol. 14, pp. 69–90, 2004.

    Google Scholar 

  147. Alici, G. U., Kapucu, S. and Baysec, S., “A Robust Motion Design Technique for Flexible-Jointed Manipulation Systems,” Robotica, Vol. 24, pp. 95–103, 2006.

    Google Scholar 

  148. Chang, T., Jaroonsiriphan, P., Bernhardt, M. and Ludden, P., “Web-based command shaping of cobra 600 robot with a swinging load,” IEEE Transactions on Industrial Informatics, Vol. 2, pp. 59–69, 2006.

    Google Scholar 

  149. Freese, M., Fukushima, E., Hirose, S. and Singhose, W., “Endpoint Vibration Control of a Mobile Mine-Detecting Robotic Manipulator,” Proc. American Control Conference, 2007.

  150. Gurleyuk, S. S., “Optimal unity-magnitude input shaper duration analysis,” Archive of Applied Mechanics, Vol. 77, pp. 63–71, 2007.

    MATH  Google Scholar 

  151. Huey, J. R., Sorensen, K. L. and Singhose, W. E., “Useful Applications of Closed-Loop Signal Shaping Controllers,” Control Engineering Practice, Vol. 16, pp. 836–846, 2008.

    Google Scholar 

  152. Kinceler, R. and Meckl, P. H., “Corrective Input Shaping for a Flexible-joint Manipulator,” Proc. American Control Conference, pp. 1335–1339, 1997.

  153. Kozak, K., Singhose, W. and Ebert-Uphoff, I., “Performance Measures For Input Shaping and Command Generation,” ASME J. Dynamic Systems, Meas., & Control, Vol. 128, pp. 731–736, 2006.

    Google Scholar 

  154. Parker, G. G., Eisler, G. R., Phelan, J. and Robinett, R. D., “Input Shaping for Vibration-Damped Slewing of a Flexible Beam Using a Heavy-Lift Hydraulic Robot,” Proc. American Control Conf., 1994.

  155. Tokhi, M. O. and Mohamed, Z., “Combined Input Shaping and Feedback Control of a Flexible Manipulator,” 10th International Congress on Sound and Vibration, pp. 299–306, 2003.

  156. Sung, Y.-G. and Lee, K.-T., “An Adaptive Tracking Controller for Vibration Reduction of Flexible Manipulator,” IJPEM, Vol. 7, No. 3, pp. 51–55, 2006.

    Google Scholar 

  157. Jung, J.-K., Youm, W.-S. and Park, K.-H., “Vibration Reduction Control of a Voice Coil Motor (VCM) Nano Scanner,” IJPEM, Vol. 10, No. 3, pp. 167–170, 2009.

    Google Scholar 

  158. Rathbun, D. B., Berg, M. C. and Buffinton, K. W., “Pulse width control for precise positioning of structurally flexible systems subject to stiction and coulomb friction,” J. of Dynamic Systems, Measurement and Control, Vol. 126, pp. 131–138, 2004.

    Google Scholar 

  159. Lawrence, J., Singhose, W. and Hekman, K., “Friction-Compensating Input Shaping for Vibration Reduction,” ASME J. of Vibration and Acoustics, Vol. 127, pp. 307–314, 2005.

    Google Scholar 

  160. Robertson, M. J. and Erwin, R., “Command Shapers for Systems with Actuator Saturation,” Proc. American Control Conference, pp. 760–765, 2007.

  161. Andersch, P., Sorensen, K. and Singhose, W., “Effects of Rate Limiting on Common Input Shaping Filters,” Recent Advances in Systems Engineering and Applied Mathematics, pp. 33–38, 2008.

  162. Meckl, P. H., Arestides, P. B. and Woods, M. C., “Optimized S-Curve Motion Profiles for Minimum Residual Vibration,” Proc. American Control Conference, pp. 2627–2631, 1998.

  163. Singh, T., “Jerk Limited Input Shapers,” J. of Dynamic Systems, Measurement, and Controls, Vol. 126, pp. 215–219, 2004.

    Google Scholar 

  164. Danielson, J., Lawrence, J. and Singhose, W., “Command Shaping for Flexible Systems Subject to Constant Acceleration Limits,” ASME J. of Dynamic Systems, Meas., and Control, Vol. 130, pp. 0510111–0510118, 2008.

    Google Scholar 

  165. Pao, L. Y. and La-Orpacharapan, C., “Shaped Time-Optimal Feedback Controllers for Flexible Structures,” J. Dynamic Systems, Measurement, and Control, Vol. 126, pp. 173–186, 2004.

    Google Scholar 

  166. Banerjee, A., Singhose, W. and Blackburn, D., “Orbit Boosting of an Electrodynamic Tethered Satellite with Input-Shaped Current,” Proc. AAS/AIAA Astrodynamics Specialist Conference, 2005.

  167. Parman, S. and Koguchi, H., “Controlling the attitude maneuvers of flexible spacecraft by using time-optimal/fuelefficient shaped inputs,” Journal of Sound and Vibration, Vol. 221, pp. 545–565, 1999.

    Google Scholar 

  168. Gorinevsky, D. and Vukovich, G., “Nonlinear Input Shaping Control of Flexible Spacecraft Reorientation Maneuver,” J. of Guidance, Control, and Dynamics, Vol. 21, pp. 264–270, 1998.

    Google Scholar 

  169. Biediger, E., Singhose, W., Okada, H. and Matunaga, S., “Trajectory Planning for Coordinating Satellites using Command Generation,” Proc. 10th International Space Conference of Pacific-basin Societies, 2003.

  170. Singhose, W., Biediger, E., Okada, H. and Matunaga, S., “Experimental Verification of Real-Time Control for Flexible Systems with On-Off Actuators,” ASME J. of Dynamic Systems, Measurement, and Controls, Vol. 128, pp. 287–296, 2006.

    Google Scholar 

  171. Ninneman, R. and Denoyer, K., “Middeck Active Control Experiment Reflight (MACE II): Lessons learned and reflight status,” Proc. of SPIE — The International Society for Optical Engineering, pp. 131–137, 2000.

  172. Tuttle, T. and Seering, W., “Experimental Verification of Vibration Reduction in Flexible Spacecraft Using Input Shaping,” J. of Guidance, Control, and Dynamics, Vol. 20, pp. 658–664, 1997.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, Georgia, 30332, USA

    William Singhose

Authors
  1. William Singhose
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to William Singhose.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Singhose, W. Command shaping for flexible systems: A review of the first 50 years. Int. J. Precis. Eng. Manuf. 10, 153–168 (2009). https://doi.org/10.1007/s12541-009-0084-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12541-009-0084-2

Keywords

Search

Navigation