Abstract
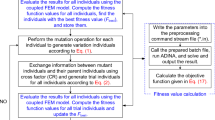
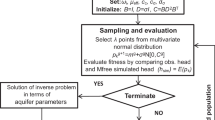
In this research, a simulation-optimization model is utilized to determine the optimum location of wells on two unconfined aquifers (steady condition and transient state) with different boundary conditions. Meshless local Petrov-Galerkin (MLPG) and particle swarm optimization (PSO) are employed for the simulation model and optimization algorithm, respectively. MLPG model is first verified by comparing results with analytical and finite difference solutions. The obtained results from MLPG show more accuracy than FDM. In PSO, the objective function is defined as the summation of the absolute difference between water table before and after extraction in each node. In the first aquifer, results show that the content of objective function before using simulation-optimization model is 61 m; however, it reaches 17 m when the optimal location is selected. The value of objective function after using simulation-optimization model has 27% reduction in value. The second aquifer has ten extraction wells and investigated in two cases with different boundary conditions. In both cases, the value of objective function is decreased significantly after applying SO model.












Similar content being viewed by others
References
Akbari A, Bagri RA, Bordas SPA, Rabczuk T (2010) Analysis of ThermoelasticWaves in a two-dimensional functionally graded materials domain by the Meshless local Petrov-Galerkin (MLPG) method. Comput Model Eng Sci 65(1):27–74
Al-Naeem A (2014) Effect of excess pumping on groundwater salinity and water level in hail region of Saudi Arabia. Res J Environ Toxicol 8(3):124–135
Atluri SN, Zhu TA (1998) A new MEshless method (MLPG) approach in computational mechanics. Comput Mech 22(2):117–127
Atluri SN, Zhu TL (2000) The meshless local Petrov-Galerkin (MLPG) approach for solving problems in elasto-statics. Comput Mech 25:169–179
Ayvaz MT (2009) Application of harmony search algorithm to the solution of groundwater. Adv Water Resour 32:916–924
Ayvaz MT, Karahan H (2008) Simulation/optimization model for the identification of unknown groundwater well locations and pumping rates. J Hydrol 257:76–92
Bartolino J, Cunningham WL (2003) Ground-water depletion across the nation, USGS
Bear J (1979) Hydraulics of groundwater, the University of Michigan. McGraw-Hill International Book Co
Belytschko T, Lu YY, Gu L (1994) Elements free Galerkin methods. Int J Numer Methods Eng 30(2):229–256
Blaszyk T, Gorski J (1981) Ground-water quality changes during exploitation. Groundwater 19:28–33
Boddula Swathi, T.I. Eldho, (2014) Groundwater flow simulation in unconfined aquifers using meshless local Petrov–Galerkin method. Engineering Analysis with Boundary Elements 48:43-52
Cyriac R, Rastogi AK (2016) Optimization of pumping policy using coupled finite element-particle swarm optimization modelling. ISH J Hydraul Eng 22(1):88–99
Duouit J (1863) Estudes Theoriques et Pratiques sur le Mouvement desEaux. Dunod, Paris
El-Ghandour HA, Elsaid A (2013) Groundwater management using a new coupled model of flow analytical solution and particle swarm optimization. Int J Water Resour Environ Eng 5(1):1–11
Elsheikh WHY, Shigidi AMT (2018) OPTIMIZATION OF PUMPING FROM AL-SIDIR WELLFIELD, BARA AQUIFER, 2nd conference of civil engineering, Sudan
Ganji Khorramdel N, Mohammadi K, Monem MJ (2008) Optimization of observation well network for the estimation of groundwater balance using double water table fluctuation method. J Water Soil 22(2):359–370
Gaur S, Chahar BR, Graillot D (2011) Analytic elements method and particle swarm optimization based simulation–optimization model for groundwater management. J Hydrol 402:217–227
Ghaseminijad A, Shourian M (2019) A simulation–optimization approach for optimal design of groundwater withdrawal wells’ location and pumping rateconsidering desalination constraints. Environ Earth Sci 78:270–281
Gill MK, Kaheil YH, Khalil A, McKee M, Bastidas L (2006) Multiobjective particle swarm optimization for parameter estimation in hydrology. Water Resour Res 42(7)
Gou X, Hu T, Wu C, Zhang T, Lv Y (2013) Multi-objective optimization of the proposed multi-reservoir operating policy using improved NSPSO. Water Resour Manag 27:2137–2153
Hamraz BS, Akbarpour A, Pourreza Bilondi M, Sadeghi Tabas S (2015) On the assessment of ground water parameter uncertainty over an arid aquifer. Arab J Geosci 8(12):10759–10773
Izady A, Abdalla O, Joodavi A, Chen M (2017) Groundwater Modeling and Sustainability of a Transboundary Hardrock–Alluvium Aquifer in North Oman Mountains. Water 9(3):161
Izquierdo J, Montalvo I, Pérez R, Tavera M (2008) Optimization in water systems: a PSO approach, in Proceedings of the 2008 Spring simulation multiconference
Joodavi A, Zare M, Mahootchi M (2015) Development and application of a stochastic optimization model for groundwater management: crop pattern and conjuctive use consideration. Stoch Environ Res Risk Assesss 29(6):1637–1648
Kennedy J, Eberhart R (1995) Particle swarm optimization, in Proceeding of IEEE Intenational Conference on neural networks
Ketabchi H, Ataie-Ashtiani B (2015) Assessment of a parallel evolutionary optimization approach for efficient management of coastal aquifers. Environ Model Softw 74:21–38
Kulkarni NH (2015) Numerical simulation of groundwater recharge from an injection well. Int J Water Resour Environ Eng 7(5):75–83
Kumar N, Reddy J (2007) Multipurpose reservoir operation using particle swarm optimization. J Water Resour Plan Manag 133:192–201
Liu G (2002) Mesh free methods: moving beyond the finite element method. CRC press, Boca Raton
Liu GR, Gu YT (2005) An introduction to Meshfree methods and their programming. Springer, Singapore
Mategaonkar Meenal, T. I. Eldho, (2011a) MESHLESS POINT COLLOCATION METHOD FOR 1D AND 2D GROUNDWATER FLOW SIMULATION. ISH Journal of Hydraulic Engineering 17 (1):71-87
Mategaonkar Meenal, T.I. Eldho, (2011b) Simulation of groundwater flow in unconfined aquifer using meshfree point collocation method. Engineering Analysis with Boundary Elements 35 (4):700-707
McKinney D, Lin M (1994) Genetic algorithm solution of groundwater management models. Water Resour Manag 30:1897–1906
Mohtashami A, Akbarpour A, Mollazadeh M (2017a) Development of two dimensional groundwater flow simulation model using meshless method based on MLS approximation function in unconfined aquifer in transient state. J Hydroinf 19(5):640–652
Mohtashami A, Akbarpour A, Mollazadeh M (2017b) Modeling of groundwater flow in unconfined aquifer in steady state with meshless local Petrov-Galerkin. Modares Mech Eng 17(2):393–403
Mohtashami A, Hashemi Monfared SA, Azizyan G, Akbarpour A (2019) Determination the capture zone of wells by using meshless local Petrov-Galerkin numerical model in confined aquifer in unsteady state( case study: Birjand aquifer). Iranian J Ecohydrol 6(1):239–255
Mollazadeh M, Barani G A, Rasouli A (2008) Optimiztion the shape of gravity dams using particle swarm optimization, in 6th of Iranian hydraulic conference, Shahrekord
Saadatpour M, Afshar A (2013) Multi objective simulation-optimization approach in pollution spill response management model in reservoirs. Water Resour Manag 27:1851–1865
Sadeghi Tabas S, Akbarpour A, Pourreza Bilondi M, Samadi SZ (2015) Application of cuckoo optimization algorithm in automatic calibration of aquifer hydrodynamic parameters using mathematical model. Iranian J Irrig Drain 9(2):345–356
Sadeghi Tabas S, Samadi SZ, Akbarpour A, Pourreza Bilondi M (2016) Sustainable groundwater modeling using single-and multi-objective optimization algorithm. J Hydroinf 18(5):1–18
Saeedpanah I, Samsami-Khodadad H (2015) Numerical simulation of groundwaters flow by using analytical particle, in 8th National Congress of civil engineering, Babol
Stacey A, Jancic M, Grundy I (2003) Particle swarm optimization with mutation, in Congress on Evolutionary Computation
Tissa HI, Doll P (1989) A discrete kernel method of Charactristic model of solute transport in water table Aqufers. Water Resour Manag 25(5):857–867
Vrugt JA, Robinson BA (2007) Improved evolutionary optimization from genetically adaptive multimethod search. PNAS Proc Natl Acad Sci U S A 104(3):708–711
Zambrano-Bigiarini M, Rojas R (2006) A model-independent particle swarm optimisation software for model calibration. Environ Model Softw 43:5–25
Zhang Z, Jiang Y, Zhang S, Geng S, Wang H, Sang G (2014) An adaptive particle swarm optimization algorithm for reservoir operation optimization. Appl Soft Comput 18:167–177
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Zeynal Abiddin Erguler
Rights and permissions
About this article
Cite this article
Mohtashami, A., Monfared, S.A.H., Azizyan, G. et al. Determination of the optimal location of wells in aquifers with an accurate simulation-optimization model based on the meshless local Petrov-Galerkin. Arab J Geosci 13, 26 (2020). https://doi.org/10.1007/s12517-019-5039-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12517-019-5039-z