Abstract
Nutrient mass balance analyses are a way of obtaining ‘whole system’ viewpoints on coastal biogeochemical functions and their forcing. Seasonal mass balances are presented for four large bay systems in New Zealand (NZ), with the aim of showing how they can inform coastal management. Freshwater volumes, and surface and groundwater, wastewater and atmospheric inorganic and organic nitrogen (N) and phosphorus (P) were balanced with levels of salinity, N and P from ocean surveys, used to determine non-conservative N and P fluxes and, via stoichiometry, carbon (C) fluxes. For Golden and Tasman Bays and Hauraki Gulf, exchange with adjacent shelf waters usually dominated total N supply (80–85%). In contrast, for the Firth of Thames, 51% of total N and 85% of dissolved inorganic N supply originated from its agricultural catchment. Net ecosystem metabolism (NEM; balance of autotrophy and heterotrophy) of Golden and Tasman Bays and Hauraki Gulf was usually nearly balanced. In contrast, Firth NEM was highly seasonally variable, often exhibiting strong heterotrophy coincident with expression of respiration-related stressors (low O2 and high DIC/low pH). Denitrification accounted for about 51% of total N export across the four systems, signifying its importance as a eutrophication-regulating ecosystem service. Budgets made 12 years apart in the Firth showed decreased denitrification efficiency, coincident with large increases in system N and phytoplankton. The findings for land-ocean nutrient balance, NEM and denitrification showed how mass balance budgeting can inform coastal management, including inventories of nutrient inputs, balances of oceanic and terrestrial nutrient loading, and potential for risk associated with biogeochemical responses.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The ecosystem services of coastal waters are underpinned by nutrient supply from offshore and land, and the accompanying biogeochemical cycles driving organic production, respiration and elemental losses (Boynton and Kemp 2008). These features have important implications for coastal resource management (Swaney and Giordani 2011). For example, if systems are found to sustain periods of high respiration, the twin ecosystem stressors of eutrophication-driven anoxia and acidification may be indicated (Provoost et al. 2010; Wallace et al. 2014). If these effects are tied to catchment-derived nutrient enrichment that imposes eutrophication stress, managers may consider it important to engage countermeasures through nutrient limits, land-use policy setting or point source remediation. On the other hand, if oceanic loads dominate, it is important for managers to understand that ecosystem responses are more strongly driven by ocean dynamics and that acquiring capability for forecasting those dynamics is a priority.
To gain information on relative strengths of ocean and catchment influence and accompanying biogeochemical responses, it is useful to consider a ‘whole-system’ viewpoint that incorporates the riverine, oceanic, atmospheric and biogeochemical sources and sinks of nutrients and carbon. Ways of doing this include accumulating and synthesising data from field data and experiments (e.g. studies of benthic fluxes, primary production, physical water exchanges derived from current meters) or using fully dynamic ecosystem modelling which parameterises and links processes to create data on the system. A third approach is ‘inverse’ modelling, which is essentially a model driven by data, and represents a middle ground between the first two approaches (Swaney 2011). Here, we use the third approach, biogeochemical mass balance inverse modelling, to evaluate important ecosystem parameters of four large coastal systems in New Zealand (NZ). Our objective is to demonstrate how the mass balances evaluate the ocean-catchment balance and its accompanying biogeochemical properties and show how these are useful for coastal management.
Biogeochemical mass balance calculations are essentially budgets of water, salt and nutrients which must balance for the model to be realistic (Gordon et al. 1996; Smith et al. 2005; Swaney 2011). From these calculations, whole-system descriptions can be made by positing that differences between predicted and observed nutrient quantities represent estimates of system-wide net biogeochemical fluxes. The budgets also provide information on ‘where the systems stand’, including inventories of catchment-derived nutrients (riverine, atmospheric, groundwater, wastewater), water residence times and proportions of catchment vs oceanic nutrients supplied to the systems. They provide frameworks for organising survey data so that the relative importance of various nutrient sources and sinks can be assessed.
From their calculations of fluxes, sources and sinks, the budgets can evaluate the net balance of production and respiration, or net ecosystem metabolism (NEM):
This describes the uptake of CO2 and inorganic nutrients in primary production of organic matter and O2 (autotrophy), and the back-reaction that consumes O2 to respire organic matter to inorganic nutrients and CO2 (heterotrophy) (Caffrey 2004; Gordon et al. 1996). The budgets therefore provide information on potential for attendant fluxes of dissolved inorganic carbon (DIC) and decreased O2, to drive ecosystem stressors of decreased pH and deoxygenation (Cai et al. 2017; Kemp et al. 2005; Sunda and Cai 2012; Waldbusser and Salisbury 2014; Wallace et al. 2014).
Budgeting can also yield information on balance of nitrogen (N) fixation and loss (denitrification) with respect to the system. Fluxes of N are particularly important, because it is typically the limiting nutrient in coastal waters (Howarth and Marino 2006; NRC 2000; Vitousek and Howarth 1991) and when in excess can cause eutrophication (Boynton and Kemp 2008; NRC 2000). Large fractions of N loss in coastal systems can be attributed to denitrification (Cornwell et al. 2014; Fennel et al. 2009; Seitzinger 1988), making it a valuable ecosystem service for the maintenance of coastal water quality. However, its rates can be deleteriously affected by eutrophication (Boynton and Kemp 2008; Eyre and Ferguson 2009; Hale et al. 2016; Kemp et al. 1990; Sloth et al. 1995), indicating a need for assessing its rates with respect to N loading and N inventories in coastal waters (Sutula 2011).
Resource managers can thus improve their ability to set coastal management priorities by considering the results of physical exchanges, nutrient sources and sinks, and fundamental relationships involved in NEM and denitrification. We demonstrate this with biogeochemical budgets for Golden and Tasman Bays in central NZ and Hauraki Gulf and adjacent Firth of Thames in northern NZ (Fig. 1a). The budgets combine marine data collected using oceanographic surveys of the four systems with data from NZ national archives on freshwater inputs and nutrient water quality monitoring. When possible, the budgets are resolved seasonally, which reflects the fact that coastal biogeochemical function changes seasonally (Kemp et al. 1997) and, in general, is driven by seasonally variable physical dynamics, nutrient supply and productivity. The biogeochemistry and biological oceanography responsible for the fluxes and transports driving the origin and fate of nutrients are described.
a Locations of Golden and Tasman Bays and Hauraki Gulf/Firth of Thames in New Zealand. b Sampling stations used in mass balance budgets for Golden Bay (green) and Tasman Bay (blue), separated from Greater Cook Strait shelf stations by solid lines marking system boundaries. c Sampling stations (green) used in mass balance budgets for Firth of Thames, Hauraki Gulf and the Northeast Shelf, separated by solid lines marking system boundaries. The orange circle marks the location of the long-term (1998–present) NIWA monitoring site in Firth of Thames. In b and c, open circles and dashed lines denote sampling stations and transects used for property plots (“Results”). Also labelled are promontories used for designating system boundaries, major river mouths draining to each bay and cities of Nelson and Auckland. Data were plotted using 'Ocean Data View' (Schlitzer, R., Ocean Data View, http://odv.awi.de, 2015)
Preparing biogeochemical mass balance budgets is a useful exercise within a single system to determine dominant nutrient drivers, sources and sinks, and is also usefully applied to more than one system to contrast functioning between systems. Here, we compare functioning among the four systems. Also, because we budgeted the Hauraki Gulf/Firth of Thames system twice, in 2000–2001 and 2012–2013, we compare their functioning at two times separated by more than a decade. Finally, we compare the four systems with a global metadata set of budgeted systems (Smith et al. 2010), and other literature values, to place their functionality in broader context.
In NZ, mass balance budgeting has advised marine resource management in several publicly available reports for NZ government and industry (reviewed in Swaney 2011). We conclude by describing how biogeochemical mass balance budgeting informed this advice.
Methods
Environmental Settings
Golden and Tasman Bays (Fig. 1b) are 790 and 1300 km2 in area and 16 and 23 m average depth, respectively. Their provisioning ecosystem services include scallop and fin-fisheries, a large mussel farming industry and the marine-based Abel Tasman National Park and Farewell Spit Wildlife Sanctuary. The subtropical shelf waters (Greater Cook Strait) offshore are periodically influenced by upwelling (Chiswell et al. 2016), representing a potentially strong source of nutrients for the bays. Each bay has contributions from two main rivers: the Aorere and Takaka rivers into Golden Bay and the Motueka and Wairoa rivers into Tasman Bay (Fig. 1b). Their lower catchments support horticulture, while their hinterlands are in introduced species forestry, native forest or scrub. There is also groundwater exposure to the sea in both bays.
The Hauraki Gulf (Fig. 1c) is a large (2800 km2, 30 m mean depth) embayment on the north-eastern North Island, lying adjacent to NZ’s largest city, Auckland. The Gulf supports many commercial, recreational and cultural resources throughout its many bays, islands and waterways (Peart 2016), placing high priority on its marine resource management (Kelly et al. 2017). At its outer boundary, the Hauraki Gulf exchanges with northeast shelf waters which are periodically affected by upwelling (Zeldis et al. 2004) and increased nutrient levels (Zeldis 2004).
Inshore, the Gulf is bounded by the Firth of Thames, a large (1100 km2, 15 m mean depth) sub-bay (Fig. 1c). The Firth has primary production rates at least twice that of the seaward Gulf (Gall and Zeldis 2011; Zeldis and Willis 2015) and supports the largest spawning and nursery grounds for NZ’s most valuable inshore fin-fishery (for snapper: Zeldis and Francis 1998) and some of NZ’s largest marine farms (for mussels and oysters). The rivers entering the Firth drain the Hauraki Plains (4200 km2) in the Waikato region, the most intensively farmed region in NZ (LIC 2016), with about 65% of its area in pasture (mainly dairy) and about 20% in native land cover (Vant 2011). The rivers draining to the Firth deliver high nutrient loads on NZ standards (Snelder et al. 2017) and ca. 78% of that load is anthropogenic (Vant 2013). Resource managers have thus placed a high priority on understanding effects of nutrient loading on the Firth’s receiving environment (Kelly et al. 2017).
Mass Balance Budgeting Overview
The method uses ‘stoichiometrically linked water-salt-nutrient budgets’(Gordon et al. 1996; Swaney 2011), developed within the ‘Land Oceans Interactions in the Coastal Zone’ (LOICZ) programme of the International Geosphere-Biosphere Programme (IGBP). The budgets for Golden and Tasman Bays each use a single-bay compartment adjacent to its offshore compartment (Greater Cook Strait: Fig. 2), whereas the budgets for Hauraki Gulf/Firth of Thames use a three-compartment model in series, with the Firth inshore of the Gulf which in turn is inshore of the northeast shelf. For each bay system, the method derives water, salt and nutrient budgets which are solved in the order described below (based on Gordon et al. 1996).
Water Budgets
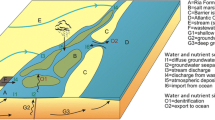
A budget is established of freshwater flows into and out of each system (Fig. 2). Assuming (approximate) average steady-state conditions, there must be compensating outflow to the adjacent system, to balance the net freshwater volume flowing into the system. This is the ‘residual’ flow of water VR, calculated as:
where subscripts R, Q, O, G, P and E identify volumes of total residual flow, river runoff, wastewater, groundwater, precipitation and evaporation, respectively. Note that the VE term is negative. Because residual flow is out of each system, VR is negative.
Salt Budgets
Salt must be conserved in the system when its volume and salinity are at steady state. Therefore, salt removed from the system by the residual flow to the seaward compartment must be replaced by exchange between the seaward compartment and the system, to sustain the salinity difference observed between them (Fig. 2). The water and salt budgets thus calculate the exchange of water between the system and its seaward compartment due to the processes of advection and mixing. The resulting steady-state balance of salt can be defined by:
where the salinity of the residual flow (SR) is the average of salinities of system (S1) and seaward compartment (S2) and represents the salinity composition at the mouth of the system. Rearrangement of this expression allows calculation of VX, the exchange between system and its seaward compartment, required to balance the residual flows of salt:
Implementing the Gulf/Firth budget as a three-compartment model in series meant that residual flow from the Gulf to the shelf was calculated as the sum of the absolute value of the residual flow between the Firth and the Gulf and the freshwater terms affecting the Gulf (Swaney 2011). Also, the exchanges of nutrients with respect to the Gulf compartment were estimated as the sum of the nutrient residual and exchange terms between the Firth and the Gulf and the Gulf and the shelf.
The mean residence time, τ, of water in each system was calculated as:
where V is the volume of water in the system. In the Gulf/Firth three-compartment case, the residence time of the Hauraki Gulf was calculated using the summed residual flows as calculated above and the summed exchange terms between the Firth and Gulf and the Gulf and the shelf (Swaney 2011).
A limiting factor in the calculation of the exchange term Vx is that there be a suitably strong salinity difference between adjacent system compartments (Swaney 2011) in order to obtain reasonable Vx estimates. In cases where this was not achieved (generally where salinity differences between adjacent compartments were ≤ 0.1), budgets produced residence time estimates that were not realistic for the bays concerned (“Discussion”) and their biogeochemical flux estimates were not used.
Nutrient Budgets
Nutrient (N and P) inputs are from river, groundwater, wastewater and atmospheric sources. Nutrients also will exchange between the systems and adjacent compartments according to the conservative residual and mixing flows described above (Fig. 2), but their concentrations (Y) will deviate from predictions based on conservative transport due to net non-conservative reactions in the systems.
At steady state, the flux of these reactive materials thus includes an additional term, ΔY, to account for the net non-conservative fluxes (release–uptake) within the systems (Fig. 2):
The ΔY values are therefore calculated from the sums of freshwater, residual (VRYR) and exchange (VxYx), where YR = the average of nutrient concentrations in adjacent compartments and Yx = their difference.
Net Ecosystem Metabolism and Denitrification
Net ecosystem metabolism (NEM) is the balance between net primary production and decomposition of organic matter by the system. Carbon fluxes involved in NEM have both aqueous and gas phases, namely aqueous dissolved inorganic and organic C (DIC, DOC) and CO2 gas which exchanges across the air-sea interface. This means that NEM cannot be determined by C measurements in the budgeting method, which measures fluxes of materials between dissolved and particulate phases only (Gordon et al. 1996). However, because there is no gas phase for P flux, it may be used as a proxy for NEM, by using the Redfield relationship between C and P. That is, the non-conservative net flux of dissolved inorganic P (ΔDIP) can be considered an approximation of net inorganic C metabolism, at the scale of the ecosystem.
Thus, by using ΔDIP, we may estimate the net rate at which DIC is either produced or consumed by the system (ΔDIC) and thereby its NEM balance. The difference between production and respiration (p − r) in terms of net DIC flux is evaluated using the Redfield molar stoichiometry between C and P, here taken to be 106:1, such that (p − r) = − ΔDIP × 106.
Nitrogen also has a major flux pathway involving a gas phase related to the balance between denitrification (which evolves N2 gas from DIN) and biological N fixation which fixes N2 gas. Again, this means that denitrification cannot be determined in the budgeting method by N measurements alone, because the budgeting does not measure gas phases. However, the expected flux of DIN may be predicted from DIP flux (which has no gas phase), by using the Redfield molar stoichiometry between N and P, here taken to be 16:1. The deviation of the observed (i.e. budgeted) non-conservative fluxes of DIN from that expected (based on net non-conservative DIP flux) provides an estimate of net rate at which the system is either fixing or denitrifying N with respect to the atmosphere, such that (nfix − denit) = (16 × ΔDIP) − ΔDIN. Following Smith et al. (1991), we include dissolved organic N and P fluxes in this calculation by adding (nfix − denit) calculated using DOP and DON to (nfix − denit) calculated DIP and DIN.
Application to Golden/Tasman Bays and Hauraki Gulf/Firth of Thames
The following sections describe the application of the budgeting procedure to the four systems.
System Definitions and Volumes
For Golden and Tasman Bays, the system boundaries (Fig. 1) divide the bays from shelf waters offshore, using the promontories of Farewell Spit, Separation Point, Abel Head and Cape Soucis. For Hauraki Gulf/Firth of Thames, the system boundaries separate the Firth from the Gulf using lines from Coromandel to Waiheke Is. to Ruakura Pt. and the Gulf from the northeast shelf using the promontories of Takatu Point and Cape Colville. Golden and Tasman Bays have respective volumes of 13 and 31 km3 and the Hauraki Gulf and Firth of Thames have respective volumes of 82 and 16 km3.
Marine Salinity and Nutrients
For Golden and Tasman Bays and Hauraki Gulf/Firth systems, the marine components of the mass balance budgets used quarterly salinity and nutrient samples collected in voyages in spring (September), summer (December), autumn (March) and winter (July). Salinity and nutrient profiles were collected using a SeaBird 911 CTD-rosette system. Nutrient samples (250 ml) were filtered (GFF), frozen on board and assayed in the laboratory using flow injection analysis for seawater (NO3−, NH4+, DIP: Astoria methods, and total dissolved N and P (TDN, TDP): Lachat methods). Detection limits on these assays were 0.07 μmol for NO3− and NH4+, 0.7 μmol for TDN and 0.03 μmol for DIP and TDP. Dissolved organic N (DON) was determined by differencing TDN with sum of NO3− and NH4+ (DIN), and DOP by differencing TDP with DIP. Seasonal mean salinity and nutrient levels were calculated using arithmetic averaging of data from all depths and stations in each system and its adjacent compartments.
The Golden and Tasman Bays’ surveys were conducted in 2001–2002. For Golden Bay, totals of 60 and 75 samples were taken in system and shelf station sets (Fig. 1), respectively, and for Tasman Bay, totals of 75 and 77 samples were taken in its respective system and shelf sets. Full station sets were available for the autumn, winter and spring voyages but for the summer voyage, very rough sea conditions caused numerous stations to be missed, including three of four bay stations in Golden Bay and four of five shelf stations in Tasman Bay. To judge whether these summer budgets were reliable, we considered whether their respective calculated residence times and biogeochemical flux estimates were reasonable with respect to previous estimates of residence time from other studies (see “Discussion”). On this basis, the Golden Bay budget, with residence time 1 day, was rejected, whereas the Tasman Bay budget, with residence time 20 days, was accepted.
The two Hauraki Gulf/Firth surveys were in 2000–2001 and 2012–2013 and were conducted using nearly identical station sets (Fig. 1). The 2000–2001 survey collected totals of 52, 108 and 96 salinity and nutrient samples in Firth, Gulf and shelf waters, respectively. The 2012–2013 survey collected 55, 113 and 96 respective samples. In both surveys, the samples were divided nearly equally among their four seasonal voyages. Salinity differences between Gulf/Firth compartments for 3 of its 16 seasonal budgets were too small to enable reliable Vx estimates (≤ 0.1). This occurred between the Firth and Gulf in winter 2001, and between the Gulf and the shelf in autumn of both 2001 and 2013. Because flux estimates for the Gulf in the three-compartment model depended on exchanges both with the shelf and the Firth (see above), the Gulf fluxes in winter 2001 budget also could not be estimated.
In common with typical LOICZ budgetary procedures, particulate organic nitrogen (PON) was not sampled in the bay systems (Gordon et al. 1996). Instead, we estimated PON flux as the difference between the sum of catchment loads, residual and exchange fluxes of DIN and DON, and (nfix − denit), as per Smith et al. (1989). Because this calculation relied on valid estimates of (nfix − denit), PON could not be estimated for seasonal cases where (nfix − denit) could not be estimated.
Freshwater Fluxes and Freshwater and Atmospheric Nutrient Loadings
Supplementary Material S1 details the procedures used to extract all freshwater fluxes and freshwater and atmospheric nutrient loadings for the four systems. These procedures are outlined briefly below.
Surface freshwater flows and nutrient loadings at coastal terminal reaches of all rivers and streams entering the four systems were determined by combining model estimates for unmonitored river reaches and available data for monitored reaches from NZ National Institute of Water and Atmosphere (NIWA) and NZ regional council hydrometric databases. Seasonalised estimates were made using gauged daily flows for the 30 days preceding the completion date of each ocean survey, and averaged. Seasonal nutrient concentrations were estimated from monthly mean nutrient concentrations for the gauged rivers. These data did not allow separation of organic dissolved and particulate N and P, so their values are given as their sums.
Submarine groundwater discharge (SGD) of water and nutrients to Golden/Tasman Bays was estimated using recharge rate (water balance) and environmental tracer methods, and NZ Geological and Nuclear Sciences data. For Golden/Tasman Bays, it was assumed that SGD flux was constant through the year. It was assumed that SGD was a negligible contributor to inflow to the Hauraki Gulf/Firth coastal region because the land is composed largely of impermeable sandstones.
Wastewater and wastewater nutrient fluxes for Tasman Bay and Golden Bays were compiled using sewage treatment plant (STP) data from the bays. For the Hauraki Gulf/Firth, discharges of treated sewage effluent to the Gulf, mainly from Auckland but also other smaller discharges further up the Gulf west coast, were obtained. Urban wastewater inputs to the Firth were neglected as its catchment has little urban development. For all four systems, STP fluxes of water and nutrients were not determined seasonally and were held constant for all seasonal budgets.
For Golden and Tasman Bays, coastal rainfall and evaporation data were gathered from a NIWA hydrological catchment model (TOPNET) (Bandaragoda et al. 2004). For the Hauraki Gulf and Firth, rainfall and evaporation were evaluated using annual averages of data collected between 1986 and 1996 at four NIWA hydrometric coastal sites around the region. Over-water evaporation was assumed to be 0.7 times the terrestrial evaporation (M. Duncan, NIWA, pers. comm., November 1998). For all systems, rainfall and evaporation were estimated seasonally, using data averaged for the 30-day period preceding the completion date of each ocean survey.
Estimates of atmospheric wet and dry deposition (AD) of inorganic and organic N and P were made using published compilations of NZ studies made from 1976 to 2005 (Verburg et al. 2016; P. Verburg, NIWA, pers. comm., December 2017). AD was not determined seasonally and was held constant for all seasonal budgets.
Results
Inventories of Freshwater Inflows and Non-marine Nutrient Loads
Seasonal freshwater river inflows to Golden and Tasman Bays (Fig. 3) were greatest in summer and winter and for Hauraki Gulf/Firth, inflows were greatest in spring and winter. Annually averaged inflows (not shown) were greatest in Golden and Tasman Bays, followed by the Firth and Hauraki Gulf. Mean annual rainfall-minus-evaporation (not shown) was 19 and 22% of river inputs for Golden and Tasman Bays. For the Gulf and Firth, these percentages were very similar in the 2000–2001 and 2012–2013 surveys, averaging 20 and 4% respectively. The average SGD inflows to Golden and Tasman Bays were 1 and 2 m3 s−1, respectively, which were very small proportions of their surface flows (Table 1).
Across the nutrient species, nutrient loading to Golden and Tasman Bays was usually greater in summer and winter than spring and autumn (Fig. 3). Loading to the Gulf and Firth was more strongly seasonal, with considerably greater nutrient loads in spring and winter than summer and autumn. Irrespective of its lower river inflows, DIP and DIN loads to the Firth greatly exceeded those of Golden and Tasman Bays (Fig. 3; Table 1) because of the poor water quality of Firth main rivers (Waihou and Piako Rivers: Fig. 1). Gulf loads were least among the four systems, reflecting its relatively low river inflows. Organic P and N loads followed similar patterns to inorganic nutrients among the four systems (Fig. 3) and again were much larger into the Firth than either Golden and Tasman Bays or the Gulf (Table 1).
For Golden and Tasman Bays, inventories of annually averaged nutrient loads (Table 1) from rivers, AD, SGD and wastewater (WW) showed that river loads were the dominant catchment inputs. For the Firth, river loads of inorganic and organic nutrients dominated those from AD, SGD and WW. In Hauraki Gulf, however, loads of inorganic nutrients from rivers, AD and WW were similar and, for organic N, dominated by AD.
Marine Salinity and Nutrients
Hydrographic transects running from inner Golden and Tasman Bays to Greater Cook Strait waters (Fig. 4; see Fig. 1 for transect locations) showed lower salinity in bay waters than shelf waters across the seasonal surveys. Inshore salinities were least when river flows were greatest (Fig. 3). There was usually less DIP and DIN in system than shelf waters, with large pools of DIP and DIN in deeper shelf waters, reaching maxima adjacent to Greater Cook Strait. Nutrient stocks in the upper water columns were depleted in spring, summer and autumn and restored in winter.
Vertical sections of salinity and nutrients (mmol m−3) on transects (Fig. 1) from inner Golden and Tasman Bays to Greater Cook Strait. Salinity was sampled at 1-m intervals and nutrients were sampled at 5- or 10-m intervals (lines and dots on respective panels). Arrowheads indicate central stations on transects used for bay and shelf budgeting compartments (green and blue symbols in Fig. 1b)
Hydrographic transects from inner Firth of Thames through Hauraki Gulf to the northeast shelf (Fig. 5) showed lower salinity in Firth waters than in the Gulf and shelf, reflecting the major freshwater inputs from Firth rivers. In contrast to Golden and Tasman Bays (Fig. 4), in the Firth, there were often higher concentrations of DIP in the inshore (system) waters than in offshore (Hauraki Gulf or shelf) waters (Fig. 5). DIN was usually depleted in the Firth and showed a pool in deeper offshore waters, albeit at considerably lower concentration than the deep DIN pools in the Golden and Tasman Bays’ shelf waters. An exception was occurrence of high DIN in the Firth in winter 2013. DIN was more abundant in 2012–2013 than in 2000–2001 in the Firth, for the stations occupied in both surveys (Fig. 5).
Vertical sections of salinity and nutrients (mmol m−3) on transects (shown in Fig. 1) from inner Firth of Thames through Hauraki Gulf to northeast shelf for surveys in 2000–2001 and 2012–2013. Salinity was sampled at 1-m intervals and nutrients were sampled at 5- or 10-m intervals (lines and dots on respective panels). Note that the inner three transect stations in the Firth were not occupied in 2000–2001. Arrowheads indicate central stations on transects used for bay and shelf budgeting compartments (green symbols in Fig. 1c)
System Residence Times
Golden Bay water residence times (τ) were substantially shorter than for Tasman Bay (Table 2), caused by its smaller volume (13 vs 31 km3) and its greater river flows, precipitation/evaporation balance and groundwater flows (Fig. 3, Table 1). As noted in “Methods”, the summer budgets for Golden and Tasman Bays were less reliable than other seasons because of missing stations. In addition, the summer budget for Golden Bay had very little salinity contrast (≤ 0.1) between bay and shelf compartments, further compromising its reliability and resulting in very short residence time (1 day). The summer budget for Tasman Bay, while missing stations, had an acceptable salinity contrast and a reasonable residence time (20 days: see “Discussion”). The winter residence times for both bays were also short, driven by high winter river inputs (Fig. 3).
Hauraki Gulf residence times were similar between 2000–2001 and 2012–2013 budgets (Table 2), except for long residence time in summer 2000 when river flows were low into the Firth and Gulf (Fig. 3). Unrealistic Hauraki Gulf residence times were estimated for autumn 2001 and 2012 (Table 2) because of weak salinity contrasts between the Gulf and the northeast shelf compartments. This also occurred for the Gulf budget for winter 2001, when contrast between the Firth and Gulf was weak. Residence times tended to track seasonality in river flow for the Gulf and the Firth (Fig. 3) and were longer in summer than other seasons, when river flows were low. A similar response to river flows was found for Tasman Bay, although in that case, summer had short residence time (along with high river flows), as did winter. Firth of Thames residence times were similar between 2000–2001 and 2012–2013 budgets (annual means of 24 and 21 days, respectively: Table 2) reflecting relatively stable river inputs and residual and exchange flows. As mentioned above, lack of salinity contrast between the Firth and the Gulf in winter 2001 precluded a valid Firth budget at that time.
Balances of N Loading to the Bays
For each of the four systems, the seasonal summed catchment fluxes of DIN and TN (DIN + DON + PON) from rivers, the atmosphere, groundwater and wastewater were compared with the net inward DIN and TN fluxes across their marine system boundaries as catchment flux/(catchment flux + inward marine flux). For Golden and Tasman Bays, the proportions of DIN and TN loads from catchments were generally low across the seasons (< 20%: Fig. 6), showing that flux from the shelf dominated N loading to those bays. On occasion, elevated catchment proportions occurred, notably for Golden Bay in winter when catchment loading was high (Fig. 3) and Tasman Bay in autumn when residence time was long (Table 2).
For the Hauraki Gulf, the proportions of N load from its catchment were usually low (Fig. 6). An exception was in summer 2000, when shelf fluxes were lower, indicated by relatively weak shelf exchange and long Gulf residence time (Table 2). As noted, in this three-compartment budget, exchange also occurred between the Gulf and Firth. The high boundary flux to the Gulf in winter 2013 (and, conversely, its low catchment flux: Fig. 6) was in fact almost entirely across its boundary with the Firth (97%: not shown). This meant that the Firth, and by extension, its catchment, could at times have a strong influence on Gulf dissolved N climate.
For the Firth, as expected from its high DIN and DON river loads (Fig. 3), dissolved N loading was dominated by catchment runoff (Fig. 6a), with input from the Gulf minor. In fact, in three Firth budgets (spring 2000, autumn and winter 2013), the DIN exchanges with the Gulf were outward (i.e. zero net inward flux from the Gulf). When PON was included in the fluxes, the proportions of catchment N decreased, indicating PON introduction from the Gulf (Fig. 6b).
Nutrient Fluxes, Net Ecosystem Metabolism and Denitrification
The non-conservative fluxes of DIP and ΔDIP (Table 2) were evaluated as the sums of riverine, groundwater, wastewater, residual and exchange DIP fluxes. The often negative values of ΔDIP for Golden and Tasman Bays across the seasons indicated that these systems were usually sinks for DIP, with internal system reactions consuming DIP and producing dissolved and particulate organic matter, i.e. they were often net C fixing, autotrophic systems. Therefore, the differences between production and respiration (p − r) for Golden and Tasman Bays were usually positive (Fig. 7), or nearly balanced, with (p − r) ≅ 0. The uptakes of DIP were largest in Golden Bay in autumn and in Tasman Bay in spring and summer. In winter, Golden Bay functioned as a source of DIP (net heterotrophic).
For Hauraki Gulf, uniformly negative or near-zero ΔDIP values (Table 2) signified that like Golden and Tasman Bays, it was net autotrophic or approximately balanced between net autotrophy and heterotrophy (Fig. 7). For Firth of Thames, in contrast to the other systems, ΔDIP was often strongly positive (Table 2), indicating a strong non-conservative DIP source and net heterotrophic metabolism, with internal system reactions consuming organic matter and regenerating DIP. This occurred in all budgets for 2000–2001 with autumn most heterotrophic (Fig. 7: recalling that the 2001 winter budget could not be calculated). In 2012–2013, (p − r) was more seasonal, with spring and summer nearly balanced, and autumn and winter net heterotrophic.
The contrasting (p − r) conditions between the systems (Fig. 7) corresponded with the presence of DIP maxima in offshore waters in Golden and Tasman Bays (Fig. 4), whereas in the Gulf/Firth system, DIP maxima were usually inshore, in the Firth (Fig. 5). These patterns indicated the contrasts between the system net non-conservative DIP sources, measured by ΔDIP.
In contrast to the variable ΔDIP values among the systems and seasons, the nearly uniformly negative values of ΔDIN (Table 2) indicated that the four systems were nearly always net sinks for DIN. DON fluxes were either weakly negative or often positive, indicating that the systems were often net sources of dissolved organic matter.
The deviations of the observed DIN and DON fluxes (Table 2) from their expected values, predicted via stoichiometry based on their respective DIP and DOP fluxes, were used to calculate (nfix − denit) for the systems. This showed that the systems were almost always net denitrifying (i.e. negative (nfix − denit): Table 2). The exception was in winter in Golden and Tasman Bays when positive (nfix − denit) values were calculated. A potential cause for this anomalous result is considered in “Discussion”.
The efficiency of denitrification as an N sink for the four systems was shown by the ratios of (nfix − denit) to TN exports. For Golden and Tasman Bays, these values were 0.65 and 0.63, respectively, averaged across their seasonal budgets. For Hauraki Gulf in 2000–2001 and 2012–2013 surveys, the respective mean ratios were 0.11 and 0.56. For the Firth, the two surveys had mean efficiencies of 0.71 and 0.37, respectively. Across all systems, this metric averaged 0.51.
Discussion
Here we compare the four systems’ budget results for residence time, balance of catchment and oceanic nutrient loading, NEM and net denitrification. The NEM and net denitrification results are discussed in context of a global dataset of LOICZ mass balance budget values and other literature. We discuss the implications of contrasting catchment loading across the systems and seasons for ecosystem stressors associated with NEM state (including lowered O2, pH) and denitrification (eutrophication) and conclude by considering the utility of the budgeting results for coastal management.
Residence Times
Tasman Bay had annual mean residence time of 44 days (range: 13–77 days) which was consistent with Harris (1990) who used a method based on salinity and river flow, for an estimate of 2 months. There are no published residence times for Golden Bay. For the Firth, the methods of Plew et al. (2018), based on the modified tidal prism modelling of Luketina (1998), were used to estimate residence time, yielding a time of 12 days. This is a shorter time than we estimated (annual averages of 24 day in 2000–2001 and 21 days in 2012–2013). The shorter time was explicable, however, in that the Firth water body definition used by Plew et al. (2018) placed the Firth boundary considerably inshore of our boundary and yielded a considerably smaller estuary volume (5 km3) than in our study (16 km3). There are no published residence time values for the Hauraki Gulf. Our residence times determined by mass balance were thus consistent with available published values obtained using other methods. Furthermore, the published values confirmed the validity of our selection of cases to exclude from further analysis, based on their unrealistically short calculated residence times.
The Balance of Catchment and Oceanic Nutrient Loading to the Systems
River DIN loadings to Golden and Tasman Bays were much less than to the Firth, while offshore loading of DIN to Golden and Tasman Bays was much greater than to the Firth. The latter was a function of the greater DIN levels in the Cook Strait source waters for the bays (~ 2.6 μmol) than for the marine source waters for the Firth (i.e. the Hauraki Gulf: ~ 0.6 μmol). Averaged exchange rates (Vx) for Golden and Tasman Bays with their shelf waters were also greater than between the Firth and the Gulf (about 1.9-fold) (Table 2). Thus, Cook Strait shelf waters seaward of Golden and Tasman Bays dominated supply of N to the bays, in setting their nutrient stock levels. Similar strong shelf exchanges were found for Hauraki Gulf, although on occasion (winter 2013) the Firth exported large proportions of loading to the Gulf (Table 2). This probably arose because of winter light limitation of N uptake by Firth primary producers (see below), combined with high river loading (Figs. 3 and 5). Golden and Tasman Bays and Hauraki Gulf were found to export DON on average, consistent with their often autotrophic metabolism.
For the Firth, the 2000–2001 and 2012–2013 budgets showed averages of ~ 85% of its DIN contributions were catchment-derived (all sources), with remainders arising from mixing with the adjacent Hauraki Gulf. The Firth consumed PON on a net basis, to balance its denitrification sink. When PON was included in the Firth N fluxes, the average N contributions to Firth system fluxes from the Firth catchment were ~ 51%.
In the following sections, we consider the consequences of these contrasting nutrient source balances for the key biogeochemical functions of NEM and denitrification.
NEM, Seasonality and Land Use History
Golden and Tasman Bays usually had positive or near neutral (p − r), indicating net autotrophy or near-balanced NEM. The seasonal (p − r) values for the two bays were similar and were near the modal value of (p − r) estimates derived from ~ 150 budgets in the global LOICZ budget database (Fig. 8a) compiled from data in Smith et al. (2010). The (p − r) values for Hauraki Gulf also lay near the modal value.
Histograms of a 150 values of (p − r) and b 155 values of (nfix − denit) from a meta-dataset of LOICZ budgets compiled from Smith et al. (2010). The values for seasonal budgets of these parameters for Golden/Tasman Bays and Hauraki Gulf/Firth of Thames are overlaid. The LOICZ datasets had upper and lower 5th percentiles removed
The approximately balanced metabolisms of Golden/Tasman Bays and Hauraki Gulf contrasted with the Firth (Fig. 8a), which was often net heterotrophic. Unlike Golden and Tasman Bays and Hauraki Gulf, DIN loading to the Firth was dominated by catchment input (Table 2). Catchment DON loading to the Firth was also much greater (3- to 5-fold) than from Golden/Tasman Bays and Hauraki Gulf catchments. In addition, it apparently received substantial input of PON from the Gulf, contributing to its heterotrophy.
In addition to the oxidation of imported organic material, the loading of substantial DIN to the Firth suggests that this was also involved in the net heterotrophy observed. The mechanism by which this occurs was indicated by the seasonality of NEM in the Firth (Fig. 7) and consideration of the primary production cycle in the Hauraki Gulf/Firth system. Net primary production (NPP) measured at the NIWA outer Firth monitoring site (Fig. 1) increases in spring and is maximal in summer (Chang et al. 2003; Zeldis and Willis 2015), but with onset of summer water column stratification (see Fig. 9c) and decreased river loads (Fig. 3), nutrients are reduced at rates faster than their re-supply. By autumn and early winter, nutrient limitation becomes intense, slowing production in the upper water column. Thus, while production and respiration are continuous processes the year around, their seasonal balance changes, becoming increasingly net heterotrophic later in the production season.
Oxygen and physical properties from quarterly ship sampling using CTD at the NIWA Firth of Thames monitoring site (Fig. 1), plotted by depth and time, from 1998 to 2013. Shown are a O2 (% surface saturation), b temperature (°C) and c water column vertical stratification (Brunt Väisälä frequency: higher values mean more strongly stratified). Vertical lines of dots show 1-m depth intervals and times of profiles. Ticks on x-axes are 1 January of each year
Zeldis et al. (2015) presented moored chl-a fluorometry data from the upper and lower water columns at the NIWA Firth monitoring site (Fig. 1) that showed deepening of the phytoplankton distribution in autumn, as the cells senesce and sink under nutrient stress. Zeldis et al. (2015) also showed that the inner Firth supports the highest chl-a and dissolved organic matter concentrations, and the most intense seasonal DIC production (in autumn) of the whole Firth system. This area also has a higher residence time than the outer Firth, which is exposed to the Hauraki Gulf (Ferreira et al. 2005). Consequently, as well as having high exposure to riverine DIN and organic N loading, the inner Firth supports the greatest potential for retention of the resulting phytoplankton and the respiration of its breakdown products.
That succession of net production and net respiration that occurs in the Firth is shown by time series of O2 data (Fig. 9a) at the long-term NIWA monitoring site (Fig. 1). This 15-year, three-monthly time series showed that the whole water column was generally well-oxygenated (> 90% saturation) in winter and spring but that starting in late summer and autumn (when temperature was maximal: Fig. 9b), there was usually DO depression in the lower 20 m of the water column (often between 70 and 60% saturation although with extreme events as low as < 40%). The water column tended to be density-stratified at these low DO times (Fig. 9c). The changing seasonal balance between production and respiration described above therefore coincides with cycles in O2 (Fig. 9) and DIC (Table 2) concentration, as also described by Sunda and Cai (2012) and Wallace et al. (2014).
The seasonal O2 and stratification patterns (Fig. 9) resemble those seen in a number of eastern USA estuaries including Chesapeake Bay (Kemp et al. 2005; Kemp et al. 1992; Scully 2016) and Narragansett Bay (Wallace et al. 2014) where seasonal stratification is a necessary (but not sufficient) driver of low O2. The onset of seasonal hypoxia in Chesapeake Bay is set by the timing of seasonal physical stratification, but the severity and extent of hypoxia are more closely related to the variability in the production cycle including eutrophication effects (Hagy et al. 2004). Although oxygen depression is more severe in these very heavily loaded estuaries than in the Firth, the systems share this sensitivity to stratification and the primary production cycle.
It was notable that while the winter 2012–2013 budget showed strong heterotrophy in the Firth, there was typically little expression of O2 depletion in winter in the long-term time series (Fig. 9a). This is explicable in that in winter, the Firth water column is actively physically mixed (Fig. 9c), equilibrating its O2 with the atmosphere. This was similar to dynamics described by Wallace et al. (2014) and Ianson et al. (2016) who described stoichiometric de-coupling between DIC concentration (which we index using P in the budgeting) and O2 saturation, driven by physical mixing.
The history of the Firth’s catchment agricultural development helps explain its accentuated late season heterotrophy. For the developed catchments of the Firth (the Hauraki Plains: Fig. 1), point and diffuse (agricultural) human sources now contribute about 8 and 70%, respectively, of TN load to its major rivers, with ‘natural’ sources the remainder (Vant 2013). Thus, while the Firth is now heavily catchment N loaded (Fig. 6), prior to its land use intensification, ocean-side loading was likely to have contributed a larger percentage to a much lower overall nutrient load. This is consistent with other works showing dominant effects of agricultural intensification on nutrient export from NZ landscapes (Cooper and Thomsen 1988; Quinn and Stroud 2002; Snelder et al. 2017). Although land use intensification has continued in the Hauraki Plains in the last 20 years, its development was largely complete by the 1990s (Kelly et al. 2017). Intensification has increased nutrient leaching rates to the major Hauraki Plains’ rivers (Waihou and Piako Rivers), making them among the most heavily N-loaded rivers in NZ (Snelder et al. 2017). The findings that ca. 78% of Hauraki Plains’ loading is anthropogenic, combined with the heavy catchment-side N loading shown by our budgeting (51% for TN, 85% for DIN), lead to the conclusion that historical land use intensification has substantially increased the N loads to the Firth (by 42 and 66%, for TN and DIN, respectively). Snelder et al. (2017) reported anthropogenic increases of Waikato region river TN yields of 82% over natural levels. Given that about half the total Firth TN load is from its catchment, our estimate of 42% is consistent with this.
The catchments of Golden and Tasman Bays, on the other hand, have experienced much less historical increase in TN load (38%) in their rivers, starting from a lower natural level (2.3 vs 14.9 Gg year−1 for Firth rivers) (Snelder et al. 2017). The lack of large catchment inputs for Golden and Tasman Bays probably allows the relatively neutral (p −r ) they exhibit, which is instead fuelled by mixing of externally mineralised inorganic nutrients into the bays from offshore. The Hauraki Gulf is similar, with relatively neutral (p − r) and ocean-side nutrient supply usually dominant. This conclusion is consistent with the observation by Wallace et al. (2014) that the intensity of DIC elevation across systems was a function of their catchment loading rates.
Physical water exchange appears to have a role in conditioning susceptibility to strong (p − r) effects across the systems. Golden and Tasman Bays and Hauraki Gulf all had higher physical exchange rates (Vx: m3 year−1) than Firth of Thames (Table 2). This suggests that the fact that the Firth is a relatively enclosed water body rather than a more open system further accentuates its potential for trophic impact (Ferreira et al. 2005), especially toward the head of the estuary. However, in some seasonal cases, the differences in physical exchange between the more open systems and the Firth were not large (e.g. for Tasman Bay, and for Hauraki Gulf in 2000–2001—order of 25%). This suggests that other factors, including the absolute size of the load and its inorganic/organic makeup, are also influential (Caffrey 2004). The Firth has been substantially enriched with increased catchment loading, and its present day expression of low O2 and elevated DIC is consistent with the responses of estuaries elsewhere that have undergone cultural eutrophication, as described by Provoost et al. (2010) for European estuaries and Wallace et al. (2014) in eastern USA.
Denitrification and Trends in Water Quality
In general, the systems all exhibited net denitrification (Table 2), with areal (m−2) rates consistent with near modal values in the LOICZ meta-analysis literature (Fig. 8b). Our estimated rates (0.1 to 1.5, mean 0.7 mmol N2 m−2 day−1) were also within the ranges for San Francisco Bay (0.6–1.0 mmol N2 m−2 d−1) and 20 other coastal systems listed by Cornwell et al. (2014), which were largely between 0 and 4 mmol N2 m−2 day−1.
Our measures of denitrification as a proportion of total N exports for the four coastal systems ranged from ~ 0.1 to 0.7, with mean of 0.51, indicating the critical importance of this regulating ecosystem service (MacDiarmid et al. 2013) in terms of ameliorating eutrophication. A mean estimate of 39% of denitrified proportions was reported by Seitzinger (1988) across 10 coastal systems.
An exception to the findings of uniform net denitrification was in winter in Golden and Tasman Bays (Table 2), which showed strong net N fixation. We consider this an unreliable result for the following reasons. It was driven by strong net export of DON in winter, accompanied by weak fluxes of DOP (Table 2). This imbalance may be explained by research showing that organic P is more readily mineralised to its inorganic form than is organic N (Álvarez-Salgado et al. 1997; Garber 1984; Hopkinson et al. 2002; Lønborg et al. 2009). When residence times are short, this can result greater hydrographic export of DON relative to DOP (Álvarez-Salgado et al. 1997). In our study, the short winter water residence times in both Golden and Tasman Bays (Table 2) were consistent with this explanation. Strong N fixation was further discounted by findings from phytoplankton samples taken during our surveys that showed no N fixing species (e.g. Trichodesmium spp.) present in either bay (J. Zeldis, unpubl. data). Seagrass beds can fix N (Welsh 2000), and Golden Bay supports seagrass (Zostera muelleri) beds at Farewell Spit (Fig. 1). However, their areal extent is only 1.6% of the area of Golden Bay (Battley et al. (2005) and only 0.02% of Tasman Bay (Robertson and Stevens 2012). Mean areal N fixation rate of temperate Zostera species (Welsh 2000) was 77 mmol m−2 year−1, which is less than the denitrification values we budgeted for the bays in the other seasons (over much larger areas: Table 2). These results showed that bay-wide net N fixation was not occurring in winter in Golden and Tasman Bays.
For the Firth, denitrification averaged over 2012–2013 was only 42% of the average rate in 2000–2001 (Table 2). All seasonal budgets in common to the two surveys (spring, summer and autumn) showed lower values in 2012–2013 than in 2001–2002. These decreased rates coincided with a period of significant increases in N and phytoplankton concentration in the Firth (Fig. 10). Nutrient and phytoplankton concentrations sampled at the NIWA monitoring site in the 15-year, three-monthly time series showed DIN increased by 5% per year (p < 0.01) from 1998 to 2013 (seasonal Kendall trend tests (Jowett 2014)). DON increased by 2% per year (p < 0.02) and micro-phytoplankton cell numbers increased by 7% per year (p < 0.00). DIP, on the other hand, had no trend (not shown).
Nutrient and phytoplankton concentrations from CTD water samples at the NIWA Firth of Thames monitoring site (Fig. 1), plotted by depth and time, three-monthly from 1998 to 2013. Shown are a dissolved inorganic N (μmol), b dissolved organic N (μmol) and c micro-phytoplankton (cells L−1). Depths of water samples are shown by black dots and ticks on the x-axes correspond to 1 January of each year
Zeldis et al. (2015) examined whether this enrichment arose from changed offshore oceanographic circulation patterns. Trend analysis of salinity and temperatures recorded during the three-monthly surveys showed no evidence of higher salinity and cooler water (with respect to freshened and warmer coastal water), which would indicate increased upwelled supply of N from offshore, nor did satellite sea-surface temperature for the adjacent shelf exhibit a long-term cooling trend. Southern Oscillation Index (SOI) state is related to wind directions and upwelling frequency in the NE North Island (MacDiarmid et al. 2013). SOI varied between negative and positive states over frequencies considerably higher than the long-term increasing trend observed in the DIN time series, including negative (upwelling favourable) phases when DIN concentrations were low and positive phases when they were high. It therefore did not predict the nutrient trends.
Freshwater flows from Firth rivers also showed no time trends, indicating that rate of estuarine circulation would not have changed. This was confirmed with current meter data from the NIWA monitoring site showing no trends in rates of exchange of outer Firth waters with the seaward Hauraki Gulf. Firth river water quality changes also were not a strong driver of the trends in enrichment. Published water quality trends between 1993 and 2012 (Vant 2013) showed, for TN, improvements in the Piako River and deteriorations in the Waihou River (Fig. 1). The Waihou River (which contributed approximately 60% of the TN loadings to the Firth in the mass balances) showed increasing TN slopes of 0.5, 1.0 and 1.7% per year at its gauging sites. These rates of change were considerably less than the trends in DIN in the marine record (Fig. 10). Thus, there was little evidence of either ocean- or catchment-side change that would explain the decadal enrichment observed in the Firth.
The key role of denitrification in loss of N from the Firth system described above means that decreases in denitrification efficiency could have important effects on water quality. Studies in the USA and Australian coastal systems have shown that denitrification efficiency drops with degree of organic enrichment in sediments (Cook et al. 2004; Eyre and Ferguson 2009; Hale et al. 2016; Harris et al. 1996; Kemp et al. 2005; Kemp et al. 1990). In the Firth, the mass balance analyses showed reduced denitrification rates (by 58%) between 2000–2001 and 2012–2013, consistent with the observed Firth water-column enrichment over the 15-year period (Fig. 10).
Shipboard studies of Firth benthic nutrient, oxygen and carbon fluxes showed sediment oxygen consumption (SOC) in 2003 (Giles et al. 2007) and 2012 (Zeldis et al. 2015) increased by 1.5–1.7-fold between the dates (although this comparison was compromised by differences in sampling seasons (summer vs autumn)). Published relationships between denitrification efficiency and CO2 efflux rates indicate that efflux rates > 1000 μmol CO2 m−2 h−1 correspond with lowered denitrification efficiency (Cook et al. 2004; Eyre and Ferguson 2009). In 2012, measured SOC (assumed equal and opposite to CO2 efflux) in the inner Firth averaged 1800 μmol O2 m−2 h−1, where efficiency was predicted to drop to around 50% (ibid.).
These findings were consistent with the hypothesis that water quality in the Firth has declined over the last decade because of reduced denitrification efficiency. The accelerated availability of nutrients to primary producers would be a positive feedback on eutrophication and organic enrichment, as indicated by the coincident increase in phytoplankton abundance (Fig. 10c). Although the trends of increasing nutrient and phytoplankton concentrations do not appear to be a consequence of contemporaneous increases in inflowing nutrients, we hypothesise that they may be a consequence of cumulative effects of its historically high nutrient loading.
Reliability of Mass Balance Budget Approach
It is important to examine reliability of our mass balance approach with respect to assumptions implicit in the mass balance methodology and with respect to the size of effects in NEM and denitrification across the systems.
Potential errors in the LOICZ mass balance approach were described by Webster et al. (2000). They identified errors introduced by neglecting seasonality in modelling the system. We included seasonality, so minimising this error. They identified the importance of setting the locations of marine sampling down-estuary of major nutrient and freshwater inputs, which we also achieved. Finally, they signified the importance of vertical structure in modelling of highly stratified estuaries, noting that two-box representations (in the vertical) would be most appropriate in highly stratified systems (in their case, with salinity varying 3-fold between upper and lower strata). They concluded that single-layer representations were most appropriate in weakly stratified systems, such as the systems we modelled.
Phosphorus demand (or supply), related to P adsorption/desorption processes, can be significant in highly turbid or anoxic systems, potentially biasing estimates of its non-conservative behaviour (Swaney 2011). However, these conditions do not apply to the systems investigated here, which have relatively clear water columns (Gall and Zeldis 2011; MacKenzie and Gillespie 1986) and oxic conditions near the sea bed (Fig. 9) and within the surficial sediments (Giles et al. 2006), (C. Depree, NIWA pers. comm., 2015).
To further assess the reliability of the conclusions regarding NEM (p − r) and denitrification (nfix − denit) made from mass balance, in Supplementary S2, we considered the sensitivity of those estimates to variability in their components. Those results suggest that cumulative error involved in the (p − r) calculation for its most sensitive parameters (river flow, marine DIP concentrations, Redfield estimates) is on the order of 15%. This is considerably less than the observed contrasts in (p − r) between, for example, the Firth and Golden Bay (Fig. 7). The cumulative errors involved in the (nfix − denit) calculation (Supplementary S2) for its most sensitive parameters (river flow, marine DIN concentrations, Redfield estimates) suggest that (nfix − denit) error could be on the order of 25–30%. Given this scale of error, we consider that the Firth budgetary estimates made between the 2000–2001 and 2012–2013 showing a 58% decrease in denitrification support the hypothesis that ongoing, high nutrient enrichment has decreased denitrification efficiency. This is supported by the findings over the same period of increased water column DIN, DON and micro-plankton biomass (Fig. 10), and results of SCOC experiments described above.
Our conclusions could be further tested using independent approaches toward ‘whole-system’ description (field survey and experiment-based, spatially and temporally resolved dynamic modelling, mass balance) and checking whether their conclusions converge, similar to the cross-comparison of methods by Gazeau et al. (2005). Toward this, we are presently undertaking dynamic biogeochemical modelling of the Hauraki Gulf/Firth of Thames system. Also, our NEM results will be compared with field data on Hauraki Gulf/Firth carbonate system dynamics (pCO2, DIC, alkalinity, pH) that were sampled coincidentally with the 2012–2013 mass balance budgets (Zeldis et al. 2015).
Implications for Resource Management of the Systems
We believe our budget findings are useful for resource management of Golden and Tasman Bays, Hauraki Gulf and Firth of Thames. First, the nutrient budgets of the systems provide inventories and comparisons among their catchment nutrient loading terms (Table 1). For Golden and Tasman Bays, submarine groundwater discharges were small relative to surface water (river) inputs in terms of system loading (13–14% for NO3−), even though the aquifers have concentrated nutrients. Wastewater was a minor nutrient contributor relative to rivers (1% for NO3−) in Golden Bay but a larger contributor (10%) in the more urbanised Tasman Bay adjacent to Nelson city. There are many reasons to manage nutrient levels in groundwater and wastewater at local scales, but it is useful for managers to know that these sources are not important at bay-wide scales in Golden and Tasman Bays relative to river inputs. In contrast, for the Hauraki Gulf adjacent to NZ’s largest city, Auckland, wastewater inputs were comparable to inputs from its catchments (Table 1). Also, direct atmospheric inputs were found to exceed those from both wastewater and catchment sources. This was the first evaluation of atmospheric deposition for NZ coastal waters, and this finding, along with uncertainties surrounding its estimation (Supplementary S1), indicates that it should receive further research.
Irrespective of their catchment inputs, oceanic mixing usually dominated the nutrient budgets of Golden and Tasman Bays and the Hauraki Gulf. On occasion, however, mixing with the inshore waters of the Firth and by extension, its agricultural catchment, can affect the Gulf’s nutrient climate. The influences of agricultural nutrient inputs on the Firth and the wider Hauraki Gulf are a key concern for its regional managers (Kelly et al. 2017). The results therefore signify to managers that understanding both offshore and onshore circulation dynamics is critical for predicting the provisioning and regulating ecosystem services of the four systems (MacDiarmid et al. 2013).
We found that NEM of Golden and Tasman Bays and the Hauraki Gulf was approximately balanced between net autotrophy and net heterotrophy. This suggests that these bays may not exhibit significant levels of stressors associated with strong heterotrophy (high DIC, reduced O2 and pH: Wallace et al. 2014). To date, there has been no direct sampling of the carbonate systems of Golden and Tasman Bays (e.g. surveys of pCO2/DIC/alkalinity) and relatively little study of their O2 climates. These would further inform the implications of their relatively neutral NEM for DIC and O2-associated stressors. As noted, surveys of carbonate dynamics of the Hauraki Gulf/Firth system have been carried out and will be reported in a future publication (see also Law et al. 2017).
The mean percentages of denitrification-to-total N export were high across the four systems, showing that denitrification was an important term in their N budgets. Clearly, maintaining this regulating ecosystem service is critical in terms of preventing N enrichment. Results presented here, that evidence of declining denitrification efficiency is coincident with N enrichment of the Firth, is a concern of managers of Hauraki Gulf/Firth of Thames regional marine resources (Kelly et al. 2017). Negative feedbacks between eutrophication and denitrification show that from this standpoint alone, eutrophication should be avoided. This should include management of fine sediment loading (mud), because of the known association of increased sediment muddiness and enrichment by solid and aqueous phase nutrients (%OM, %N) (Engelsen et al. 2008). Morrison et al. (2009) showed that fine sediment accumulation rate (SAR) in NZ estuaries has accelerated often by an order of magnitude with agricultural and forestry intensification. This includes the Firth, which now sustains high SAR values (7 mm year−1 in the inner Firth: Pritchard et al. 2015).
Calculations using these mass balance budgets have been used to place anthropogenic N sources arising from fish farms and sinks arising from mussel farms in ecological context (Zeldis et al. 2011; Zeldis 2005; reviewed in Swaney et al. 2011). Example findings were that under scenarios of maximal mussel farm development in the Firth, phytoplankton depletion by the farms in terms of N and C were very small with respect to system-wide fluxes, while proposed fish farm N loadings to the system were significant proportions of bay-wide denitrification (~ 25%). Other reports (Kelly et al. 2017; Zeldis 2008) to central and regional NZ government have used the mass balance information to advise on risks associated with biogeochemical stressors.
The present day loadings received by Golden and Tasman Bays and Hauraki Gulf represent much less of an ‘anthropogenic legacy’ than those entering the Firth, in terms of effects of catchment nutrient loading on trophic state. The findings for land-ocean nutrient balance, NEM and denitrification signal that understanding ocean-coastal interactions of Golden and Tasman Bays and Hauraki Gulf is essential for predicting their ecosystem services, whereas managing water quality of catchment inputs will be most effective in sustaining Firth of Thames ecosystem health. Thus, mass balance budgeting has provided inventories of important state variables including catchment loading, the balance of land and ocean nutrient loading and important biogeochemical responses, relevant to coastal management.
References
Álvarez-Salgado, X.A., C.G. Castro, F.F. Perez, and F. Fraga. 1997. Nutrient mineralization patterns in shelf waters of the Western Iberian upwelling. Continental Shelf Research 17 (10): 1247–1270.
Bandaragoda, C., D. Tarboton, and R. Woods. 2004. Application of TOPNET in the distributed model intercomparison project. Journal of Hydrology (New Zealand) 298 (1-4): 178–201.
Battley, P.F., D.S. Melville, R. Schuckard, and P.F. Ballance. 2005. Quantitative survey of the intertidal benthos of Farewell Spit Golden Bay. Marine Biodiversity Biosecurity Report 7: 119. New Zealand Ministry of Fisheries.
Boynton, W., and W. Kemp. 2008. Estuaries. In Nitrogen in the marine environment, ed. D. Capone, D. Bronk, M. Mulholland, and E. Carpenter, 809–856. Burlington, Massachusetts: Elsevier.
Caffrey, J. 2004. Factors controlling net ecosystem metabolism in U.S. estuaries. Estuaries 27 (1): 90–101.
Cai, W.-J., W.-J. Huang, G.W. Luther, D. Pierrot, M. Li, J. Testa, M. Xue, A. Joesoef, R. Mann, J. Brodeur, Y.-Y. Xu, B. Chen, N. Hussain, G.G. Waldbusser, J. Cornwell, and W.M. Kemp. 2017. Redox reactions and weak buffering capacity lead to acidification in the Chesapeake Bay. Nature Communications 8 (1): 369.
Chang, F.H., J. Zeldis, M. Gall, and J. Hall. 2003. Seasonal and spatial variation of phytoplankton functional groups on the northeastern New Zealand continental shelf and in Hauraki Gulf. Journal of Plankton Research 25 (7): 737–758.
Chiswell, S.M., J.R. Zeldis, M.G. Hadfield, and M.H. Pinkerton. 2016. Wind-driven upwelling and surface chlorophyll blooms in Greater Cook Strait. New Zealand Journal of Marine and Freshwater Research: 1–25.
Cook, P.L.M., B.D. Eyre, R. Leeming, and E.C.V. Butler. 2004. Benthic fluxes of nitrogen in the tidal reaches of a turbid, high-nitrate sub-tropical river. Estuarine, Coastal and Shelf Science 59 (4): 675–685.
Cooper, A., and C. Thomsen. 1988. Nitrogen and phosphorus in streamwaters from adjacent pasture, pine, and native forest catchments. New Zealand Journal of Marine and Freshwater Research 22 (2): 279–291.
Cornwell, J., P. Glibert, and M. Owens. 2014. Nutrient fluxes from sediments in the San Francisco Bay Delta. Estuaries and Coasts 37 (5): 1120–1133.
Engelsen, A., S. Hulth, L. Pihl, and K. Sundbäck. 2008. Benthic trophic status and nutrient fluxes in shallow-water sediments. Estuarine, Coastal and Shelf Science 78 (4): 783–795.
Eyre, B., and A.P. Ferguson. 2009. Denitrification efficiency for defining critical loads of carbon in shallow coastal ecosystems. Hydrobiologia 629 (1): 137–146.
Fennel, K., D. Brady, D. DiToro, R.W. Fulweiler, W.S. Gardner, A. Giblin, M.J. McCarthy, A. Rao, S. Seitzinger, M. Thouvenot-Korppoo, and C. Tobias. 2009. Modeling denitrification in aquatic sediments. Biogeochemistry 93 (1-2): 159–178.
Ferreira, J.G., W.J. Wolff, T.C. Simas, and S.B. Bricker. 2005. Does biodiversity of estuarine phytoplankton depend on hydrology? Ecological Modelling 187 (4): 513–523.
Gall, M., and J. Zeldis. 2011. Phytoplankton biomass and primary production responses to physico-chemical forcing across the northeastern New Zealand continental shelf. Continental Shelf Research 31 (17): 1799–1810.
Garber, J.H. 1984. Laboratory study of nitrogen and phosphorus remineralization during the decomposition of coastal plankton and seston. Estuarine, Coastal and Shelf Science 18 (6): 685–702.
Gazeau, F., A.V. Borges, C. Barron, C.M. Duarte, N. Iversen, J.J. Middelburg, B. Delille, M.-D. Pizay, M. Frankignoulle, and J.P. Gattuso. 2005. Net ecosystem metabolism in a micro-tidal estuary (Randers Fjord, Denmark): evaluation of methods. Marine Ecology Progress Series 301: 23–41.
Giles, H., C.A. Pilditch, and D.G. Bell. 2006. Sedimentation from mussel (Perna canaliculus) culture in the Firth of Thames, New Zealand: impacts on sediment oxygen and nutrient fluxes. Aquaculture 261 (1): 125–140.
Giles, H., C. Pilditch, S. Nodder, J. Zeldis, and K. Currie. 2007. Benthic oxygen fluxes and sediment properties on the northeastern New Zealand continental shelf. Continental Shelf Research 27 (18): 2373–2388.
Gordon, D.J., P. Boudreau, K. Mann, J.-E. Ong, W. Silver, S. Smith, G. Wattayakorn, F. Wulff, and T. Yanagi. 1996. LOICZ biogeochemical modelling guidelines LOICZ/RandS/95-5: 96. Texel.
Hagy, J., W. Boynton, C. Keefe, and K. Wood. 2004. Hypoxia in Chesapeake Bay, 1950–2001: Long-term change in relation to nutrient loading and river flow. Estuaries 27: 634–658.
Hale, S.S., G. Cicchetti, and C.F. Deacutis. 2016. Eutrophication and hypoxia diminish ecosystem functions of benthic communities in a New England estuary. Frontiers in Marine Science 3.
Harris, T.F.W. 1990. Greater Cook Strait: form and flow. Wellington: DSIR Marine and Freshwater.
Harris, G., G. Batley, D. Fox, D. Hall, P. Jernakoff, R. Molloy, A. Murray, J. Newell, G. Parslow, G. Skyring, and S. Walker. 1996. Port Phillip Bay environmental study final report, 239. Australia: CSIRO, Canberra.
Hopkinson, C.S., J.J. Vallino, and A. Nolin. 2002. Decomposition of dissolved organic matter from the continental margin. Deep Sea Research Part II: Topical Studies in Oceanography 49 (20): 4461–4478.
Howarth, R.W., and R. Marino. 2006. Nitrogen as the limiting nutrient for eutrophication in coastal marine ecosystems: evolving views over three decades. Limnology and Oceanography 51 (1part2): 364–376.
Ianson, D., S.E. Allen, B.L. Moore-Maley, S.C. Johannessen, and W.R. Macdonald. 2016. Vulnerability of a semienclosed estuarine sea to ocean acidification in contrast with hypoxia. Geophysical Research Letters 43: 5793–5801.
Jowett, I. 2014. Time Trends Software. http://www.jowettconsulting.co.nz/home/time-1.
Kelly, S., C. Sim-Smith, J. Bartley, B. Cowie, and C. Murray. 2017. State of our Gulf 2017: Hauraki Gulf/Tīkapa Moana/Te Moana-nui-a-Toi. State of Environment Report: 195. Auckland: Hauraki Gulf Forum.
Kemp, W., P. Sampou, J. Cafrey, M. Mayer, K. Henriksen, and W. Boynton. 1990. Ammonium recycling versus denitrification in Chesapeake Bay sediments. Limnology and Oceanography 35 (7): 1545–1563.
Kemp, W., P. Sampou, J. Garber, J. Tuttle, and W. Boynton. 1992. Seasonal depletion of oxygen from bottom waters of Chesapeake Bay: roles of benthic and planktonic respiration and physical exchange processes. Marine Ecology Progress Series 85: 137–152.
Kemp, W., E. Smith, M. Marvin-DiPasquale, and W. Boynton. 1997. Organic carbon balance and net ecosystem metabolism in Chesapeake Bay. Marine Ecology Progress Series 150: 229–248.
Kemp, W., W.R. Boynton, J.E. Adolfi, D.F. Boesch, W.C. Boicourt, G. Brush, J.C. Cornwell, T.R. Fisher, P.M. Glibert, J.D. Hagy, L.W. Harding, E.D. Houde, D.G. Kimmel, W.D. Miller, R.I.E. Newell, M.R. Roman, E.M. Smith, and J.C. Stevenson. 2005. Eutrophication of Chesapeake Bay: historical trends and ecological interactions. Marine Ecology Progress Series 303: 1–29.
Law, C.S., J.J. Bell, H.C. Bostock, C.E. Cornwall, V.J. Cummings, K. Currie, S.K. Davy, M. Gammon, C.D. Hepburn, C.L. Hurd, M. Lamare, S.E. Mikaloff-Fletcher, W.A. Nelson, D.M. Parsons, N.L.C. Ragg, M.A. Sewell, A.M. Smith, and D.M. Tracey. 2017. Ocean acidification in New Zealand waters: trends and impacts. New Zealand Journal of Marine and Freshwater Research 52(2):155–195.
LIC. 2016. New Zealand dairy statistics 2015–16: 55 pp. Hamilton. https://www.dairynz.co.nz/media/5416078/nz-dairy-statistics-2015-16.pdf
Lønborg, C., X.A. Álvarez-Salgado, K. Davidson, and A.E.J. Miller. 2009. Production of bioavailable and refractory dissolved organic matter by coastal heterotrophic microbial populations. Estuarine, Coastal and Shelf Science 82 (4): 682–688.
Luketina, D. 1998. Simple tidal prism models revisited. Estuarine, Coastal and Shelf Science 46 (1): 77–84.
MacDiarmid, A., C. Law, M. Pinkerton, and J. Zeldis. 2013. New Zealand marine ecosystem services. Lincoln: Manaaki Whenua Press.
MacKenzie, A.L., and P.A. Gillespie. 1986. Plankton ecology and productivity, nutrient chemistry and hydrography of Tasman Bay, New Zealand, 1982-1984, N. New Zealand Journal of Marine and Freshwater Research 20 (3): 365–395.
Morrison, M., M. Lowe, D. Parsons, N. Usmar, and I. McLeod. 2009. A review of land-based effects on coastal fisheries and supporting biodiversity in New Zealand. New Zealand Aquatic Environment and Biodiversity Report 37: 100. Wellington. https://www.researchgate.net/publication/236673074_A_review_of_land-based_effects_on_coastal_fisheries_and_supporting_biodiversity_in_New_Zealand
NRC. 2000. Clean coastal waters understanding and reducing the effects of nutrient pollution. Washington DC: National Academy Press.
Peart, R. 2016. The Hauraki Gulf: discovery, transformation, restoration: David Bateman Ltd.
Plew, D., J. Zeldis, U. Shankar, and S. Elliot. 2018. Using simple dilution models to predict New Zealand estuarine water quality Estuaries and Coasts.
Pritchard, M., A. Swales, and M. Green. 2015. Influence of buoyancy- and wind-coupling on sediment dispersal and deposition in the Firth of Thames, New Zealand. In Australasian coasts & ports conference 2015. Auckland, New Zealand.
Provoost, P., S. van Heuven, K. Soetaert, R.W.P.M. Laane, and J.J. Middelburg. 2010. Seasonal and long-term changes in pH in the Dutch coastal zone. Biogeosciences 7 (11): 3869–3878.
Quinn, J.M., and M.J. Stroud. 2002. Water quality and sediment and nutrient export from New Zealand hill-land catchments of contrasting land use. New Zealand Journal of Marine and Freshwater Research 36 (2): 409–429.
Robertson, B., and L. Stevens. 2012. Tasman Coast Waimea Inlet to Kahurangi Point: 167.
Scully, M.E. 2016. The contribution of physical processes to inter-annual variations of hypoxia in Chesapeake Bay: a 30-yr modeling study. Limnology and Oceanography 61 (6): 2243–2260.
Seitzinger, S. 1988. Denitrification in freshwater and coastal marine ecosystems: ecological and geochemical significance. Limnology and Oceanography 33: 702–724.
Sloth, N.P., H. Blackburn, L. Stenvang Hansen, N. Nisgaard-Petersen, and B.A. Lomstein. 1995. Nitrogen cycling in sediments with different organic loading. Marine Ecology Progress Series 116: 163–170.
Smith, S.V., J.T. Hollibaugh, S.J. Dollar, and S. Vink. 1989. Tomales Bay, California: a case for carbon-controlled nitrogen cycling. Limnology and Oceanography 34 (1): 37–52.
Smith, S., J. Hollibaugh, S. Dollar, and S. Vink. 1991. Tomales Bay metabolism: C-N-P stoichiometry and ecosystem heterotrophy at the land-sea interface. Estuarine, Coastal and Shelf Science 33 (3): 223–257.
Smith, S.V., R.W. Buddemeier, F. Wulff, D.P. Swaney, V.F. Camacho-Ibar, L.T. David, V.C. Dupra, J.A. Kleypas, C. McLaughlin, and P. Sandhei. 2005. C, N, P fluxes in the coastal zone. Berlin Heidelberg: Springer.
Smith, S.V., D.P. Swaney, and L. Talaue-McManus. 2010. Carbon–nitrogen–phosphorus fluxes in the coastal zone: the LOICZ approach to global assessment. In In Carbon and nutrient fluxes in continental margins: a global synthesis, ed. K.K. Liu, L. Atkinson, R. Quiñones, and L. Talaue-McManus, 575–586. Berlin Heidelberg: Springer-Verlag.
Snelder, T.H., S.T. Larned, and R.W. McDowell. 2017. Anthropogenic increases of catchment nitrogen and phosphorus loads in New Zealand. New Zealand Journal of Marine and Freshwater Research: 1–26.
Sunda, W., and W.-J. Cai. 2012. Eutrophication induced CO2-acidification of subsurface coastal waters: interactive effects of temperature, salinity and atmospheric pCO2. Environmental Science and Technology 46 (19): 10651–10659.
Sutula, M. 2011. Review of indicators for development of nutrient numeric endpoints in California estuaries. Southern California Coastal Water Research Project Technical Report: 269.
Swaney, D. 2011. Biogeochemical budgeting in estuaries. In Treatise on estuarine and coastal science, ed. E. Wolanski and D. McLusky, 343–362. Waltham: Academic Press.
Swaney, D., and G. Giordani. 2011. Proceedings of the LOICZ Workshop on biogeochemical budget methodology and applications, Providence, Rhode Island, November 9–10, 2007 LOICZ Research and Studies Helmholtz-Zentrum Geesthacht 37: 195. http://www.loicz.org/imperia/md/content/loicz/print/rsreports/biogeochemical_budget_methodology_and_applications.pdf
Swaney, D.P., S.V. Smith, and F. Wulff. 2011. 9.08—the LOICZ biogeochemical modeling protocol and its application to estuarine ecosystems. In Treatise on estuarine and coastal science, 135–159. Waltham: Academic Press.
Vant, B. 2011. Water quality of the Hauraki rivers and southern Firth of Thames, 2000–09. Waikato Regional Council Technical Report: 32.
Vant, B. 2013. Trends in river water quality in the Waikato region, 1993-2012. Waikato Regional Council Technical Report 2013 (/20): 50.
Verburg, P., S. Elliott, M. Schallenberg, and C. McBride. 2016. Nutrient budgets in lakes In Lake restoration handbook, ed. D. Hamilton, K. Collier, C. Howard-Williams and J. Quinn: Springer.
Vitousek, P., and R. Howarth. 1991. Nitrogen limitation on land and in the sea: how can it occur? Biogeochemistry 13: 87–115.
Waldbusser, G.G., and J.E. Salisbury. 2014. Ocean acidification in the coastal zone from an organism’s perspective: multiple system parameters, frequency domains, and habitats. Annual Review of Marine Science 6 (1): 221–247.
Wallace, R.B., H. Baumann, J.S. Grear, R.C. Aller, and C.J. Gobler. 2014. Coastal ocean acidification: the other eutrophication problem. Estuarine, Coastal and Shelf Science 148: 1–13.
Webster, I.T., S.V. Smith, and J.S. Parslow. 2000. Implications of spatial and temporal variation for biogeochemical budgets of estuaries. Estuaries 23 (3): 341–350.
Welsh, D.T. 2000. Nitrogen fixation in seagrass meadows: regulation, plant–bacteria interactions and significance to primary productivity. Ecology Letters 3 (1): 58–71.
Zeldis, J.R. 2004. New and remineralised nutrient supply and ecosystem metabolism on the northeastern New Zealand continental shelf. Continental Shelf Research 24 (4-5): 563–581.
Zeldis, J.R. 2005. Magnitudes of natural and mussel farm-derived fluxes of carbon and nitrogen in the Firth of Thames. NIWA Client Report 35. https://www.waikatoregion.govt.nz/services/publications/technical-reports/tr/tr200530
Zeldis, J.R. 2008. Origin and processing of nutrients in Golden and Tasman Bays. NIWA Client Report CHC2008-052: 23. May 2008. http://www.tasman.govt.nz/environment/coastal-marine/coastal-marine-management/oceanography-and-marine-water-quality-in-the-nelson-bays/
Zeldis, J.R., and R.I.C.C. Francis. 1998. A daily egg production method estimate of snapper biomass in Hauraki Gulf, New Zealand. ICES Journal of Marine Science: Journal du Conseil 55 (3): 522–534.
Zeldis, J., and K. Willis. 2015. Biogeographic and trophic drivers of mesozooplankton distribution on the NE continental shelf and in Hauraki Gulf, New Zealand. New Zealand Journal Marine and Freshwater Research 49 (1): 69–86.
Zeldis, J.R., R.A. Walters, M.J.N. Greig, and K. Image. 2004. Circulation over the northeastern New Zealand continental slope, shelf and adjacent Hauraki Gulf, from spring to summer. Continental Shelf Research 24 (4-5): 543–561.
Zeldis, J., D. Morrisey, N. Broekhuizen, and J. Stenton-Dozey. 2011. Tasman aquaculture: guidance on farming additive species—stage 2. NIWA Client Report CHC2011-029: 69. http://www.tasman.govt.nz/environment/coastal-marine/coastal-marine-management/aquaculture-and-fisheries-within-nelson-bays/
Zeldis, J., A. Swales, K. Currie, K. Safi, S. Nodder, C. Depree, F. Elliott, M. Pritchard, M. Gall, J. O’Callaghan, D. Pratt, S. Chiswell, M. Pinkerton, D. Lohrer, and S. Bentley. 2015. Firth of Thames water quality and ecosystem health—data report. NIWA Client Report CHC2014–123: 177 pp. http://www.waikatoregion.govt.nz/tr201523/
Acknowledgements
We thank Tasman District Council for permission to use SWQMP hydrometric data and for valuable advice from Joseph Thomas and Trevor James. Thanks to Roddy Henderson, Maurice Duncan, Ude Shankar and Kathy Walter (NIWA), for hydrometric and GIS contributions. Mark Gall, Malcolm Grieg, Fiona Elliott and other scientific staff, as well as ship’s crew of NIWA R.V. Kaharoa and NIWA Chemistry Laboratory, enabled the ocean-going data. We are grateful to Steve Smith within the LOICZ programme who reviewed an earlier version of this report and budget calculations, and constructive comments of two other reviewers.
Funding
Project support was from the New Zealand Ministry of Business, Innovation and Employment (MBIE)-funded ‘Coasts and Oceans’ Outcome-Based Investment contract C01X0501, NIWA Strategic Science Investment Fund project ‘Ocean Flows and Productivity’, ‘Sustainable Seas’ National Science Challenge contract 4.4.2. and ‘Coastal Acidification-Rates, Impacts and Management’ contract C01X1510.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Isaac Santos
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zeldis, J.R., Swaney, D.P. Balance of Catchment and Offshore Nutrient Loading and Biogeochemical Response in Four New Zealand Coastal Systems: Implications for Resource Management. Estuaries and Coasts 41, 2240–2259 (2018). https://doi.org/10.1007/s12237-018-0432-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12237-018-0432-5