Abstract
An unsteady two-fluid model of blood flow through a tapered arterial stenosis with variable viscosity in the presence of variable magnetic field has been analysed in the present paper. In this article, blood in the core region is assumed to obey the law of Jeffrey fluid and plasma in the peripheral layer is assumed to be Newtonian. The values for velocity, wall shear stress, flow rate and flow resistance are numerically computed by employing finite-difference method in solving the governing equations. A comparison study between the velocity profiles obtained by the present study and the experimental data represented graphically shows that that the rheology of blood obeys the law of Jeffrey fluid rather than that of Newtonian fluid. The effects of parameters such as taper angle, radially variable viscosity, hematocrit, Jeffrey parameter, magnetic field and plasma layer thickness on physiologically important parameters such as wall shear stress distribution and flow resistance have been investigated. The results in the case of radially variable magnetic field and constant magnetic field are compared to observe the effect of magnetic field in driving the blood flow. It is observed that increase in hematocrit increases the wall shear stress. The values of wall shear stress and flow resistance are obtained at various time instances and compared. It is pertinent to note that the magnitudes of flow resistance are higher in the case of converging tapered than non-tapered and diverging tapered artery.












Similar content being viewed by others
Abbreviations
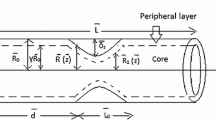
- \(\bar{z}\) :
-
axial distance
- \(\bar{r}\) :
-
radial distance
- \(\bar{t}\) :
-
time
- \(\bar{R}_1(\bar{z})\) :
-
radius of the central core region
- \(\bar{R}(\bar{z})\) :
-
radius of the artery in the stenotic region
- \(\bar{u}_c\) :
-
axial velocity of the core fluid
- \(\bar{v}_c\) :
-
radial velocity of the core fluid
- \(\bar{u}_p\) :
-
axial velocity of plasma
- \(\bar{v}_p\) :
-
radial velocity of plasma
- \(\bar{p}\) :
-
pressure
- \(\bar{B}_0^2(\bar{r})\) :
-
variable magnetic field
- \(\bar{\mu }(\bar{r})\) :
-
consistency function
- \(\bar{\mu }_c(\bar{r})\) :
-
variable viscosity of the central core fluid
- \(\bar{\mu }_p\) :
-
viscosity of the plasma
- \(\bar{\rho }_c\) :
-
density of the central core fluid
- \(\bar{\rho }_p\) :
-
density of plasma
- \(\bar{\sigma }\) :
-
electrical conductivity of the fluid
- \(\bar{\lambda }_2\) :
-
retardation time
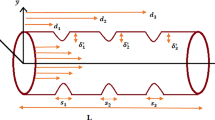
- \(\delta _s\) :
-
maximum stenotic height
- d :
-
location of the stenosis
- \(n_1\) :
-
shape of stenosis
- \(\psi \) :
-
taper angle
- \(\lambda _1\) :
-
ratio of relaxation to retardation times
- \(A_0\) :
-
amplitude of steady pressure gradient
- \(A_1\) :
-
amplitude of pulsatile pressure gradient
- \(\beta \) :
-
constant in variable core viscosity
- \(h_m\) :
-
hematocrit
- \(Q_c\) :
-
flow rate in the core region
- \(Q_p\) :
-
flow rate in the peripheral plasma region
- Q :
-
total flow rate
- M :
-
magnitude of magnetic field strength
- \(\alpha _1\) :
-
constant in variable magnetic field
- \(S_{rz}\) :
-
shear stress
- \(\tau _w\) :
-
wall shear stress
- \(\delta \) :
-
plasma layer thickness
- \(\lambda \) :
-
flow resistance
References
Young D F 1968 Effects of a time-dependent stenosis on flow through a tube. Trans. ASME J. Eng. Ind. 90: 248–254
Young D F and Tsai F Y 1973 Flow characteristic in models of arterial stenosis-I: steady flow. J. Biomech. 6: 395–410
Chaturani P and Ponnalagarsamy R 1986 Pulsatile flow of Casson’s fluid through stenosed arteries with applications to blood flow. Biorheology 23: 499–511
Ponalagusamy R 1986 Blood flow through stenosed tube. Ph.D Thesis. Bombay, India: IIT
Young D F 1979 Fluid mechanics of arterial stenosis. Trans. ASME J. Biomech. Eng. 101: 157–175
Caro C G 1981 Arterial fluid mechanics and atherogenesis. Recent Adv. Cardiovas. Dis. 2(Suppl.): 6–11
Ku D N 1997 Blood flow in arteries. Annu. Rev. Fluid Mech. 29: 399
Kumar S and Kumar D 2009 Research note: Oscillatory MHD flow of blood through an artery with mild stenosis. IJE Trans. A: Bas. 22: 125–130
Chaturani P and Ponnalagarsamy R 1983 Blood flow through stenosed arteries. In: Proceedings of the First International Conference on Physiological Fluid Dynamics, pp. 63–67
Mekheimer K S and EI Kot M A 2008 The micropolar fluid model for blood flow through a tapered artery with a stenosis. Acta Mech. Sin. 24: 637–644
Bloch E H 1962 A quantitative study of the hemodynamics in the living microvascular system. Am. J. Anat. 110: 125–153
Jeffords J V and Knisley M H 1956 Concerning the geometric shapes of arteries and arteriols. Angiology 7: 105–136
El-Shahed M 2003 Pulsatile flow of blood through a stenosed porous medium under periodic body acceleration. Appl. Math. Comput. 138: 479–488
El-Shehawey E F, Eibarbary E M E, Afifi N A S and El-Shahed M 2000 Pulsatile flow of blood through a porous medium under periodic body acceleration. Int. J. Theoret. Phys. 39: 183–188
Sharma M K, Bansal K and Bansal S 2012 Pulsatile unsteady flow of blood through porous medium in a stenotic artery under the influence of transverse magnetic field. Korea-Australia Rheol. J. 24: 181–189
Chaturani P and Ponnalagarsamy R 1984 Analysis of pulsatile blood flow through stenosed arteries and its applications to cardiovascular diseases-I. In: Proceedings of the 13th National Conference on Fluid Mechanics and Fluid Power, pp. 463–468
El-Shehawey E F, Eibarbary E M E, Afifi N A S and El-Shahed M 2000 MHD flow of an elastic-viscous fluid under periodic body acceleration. J. Math. Sci. 23: 795–799
Ramachandra Rao A and Deshikachar K S 1988 Physiological type flow in a circular pipe in the presence of a transverse magnetic field. J. Indian Inst. Sci. 68: 247–260
Haldar K and Ghosh S N 1994 Effect of a magnetic field on blood flow through an indented tube in the presence of erythrocytes. Indian J. Pure Appl. Math. 25: 345–352
Voltairas P A, Fotiadis D I and Michalis L K 2002 Hydrodynamics of magnetic drug targeting. J. Biomech. 35: 813–821
Vardanian V A 1973 Effect of magnetic field on blood flow. Biofizika 18: 491–496
Bhargava R, Rawat S, Takhar H S and Beg O A 2007 Pulsatile magneto-biofluid flow and mass transfer in a non-Darcian porous medium channel. Meccanica 42: 247–262
Ponalagusamy R and Tamil Selvi R 2015 Influence of magnetic field and heat transfer on two-phase fluid model for oscillatory blood flow in an arterial stenosis. Meccanica 50: 927–943
Mathur P and Jain S 2011 Pulsatile flow of blood through a stenosed tube: effect of periodic body acceleration and a magnetic field. J. Biorheol. 25: 71–77
Motta M, Haik Y, Gandhari A and Chen C J 1998 High magnetic field effects on human deoxygenated hemoglobin light absorption. Bioelectrochem. Bioenerg. 47: 297–300
Midya C, Layek G C, Gupta A S and Roy Mahapatra T 2003 Magnetohydrodynamic viscous flow separation in a channel with constrictions. ASME. J. Fluid Eng. 125: 952–962
Nadeem S and Ijaz S 2015 Theoretical analysis of metallic nanoparticles on blood flow through stenosed artery with permeable walls. Phys. Lett. A 379: 542–554
Bugliarello B and Sevilla J 1970 Velocity distribution and other characteristics of steady and pulsatile blood flow in fine glass tubes. Biorheology 7: 85–107
Cokelet G R 1972 The rheology of human blood. In: Biomechanics N.J.: Prentice-Hall, Englewood Cliffs
Ponalagusamy R 2007 Blood flow through an artery with mild stenosis, a two-layered model, different shapes of stenoses and slip velocity at the wall. J Appl Sci. 7: 1071–1077
Chaturani P and Ponnalagarsamy R 1982 A two layered model for blood flow through stenosed arteries. In: Proceedings of the 11th National Conference on Fluid Mechanics and Fluid Power, pp. 16–22
Ponalagusamy R and Tamil Selvi R 2011 A study on two-layered model (Casson-Newtonian) for blood flow through an arterial stenosis: axially variable slip velocity at the wall. J. Franklin Inst. 348: 2308–2321
Sankar D S and Lee U 2010 Two-fluid Casson model for pulsatile blood flow through stenosed arteries: a theoretical model. Commun. Nonlin. Sci. Numer. Simul. 15: 2086–2097
Srivastava V P 1996 Two phase model of blood flow through stenosed tubes in the presence of a peripheral layer: applications. J Biomech. 29: 1377–1382
Chaturani P and Ponnalagarsamy R 1986 Dilatancy effects of blood on flow through arterial stenosis. In: Proceedings of the 28th Congress of ISTAM, India, pp. 87–96
Ikbal M A, Chakravarty S, Wong K K L, Mazumdar J and Mandal P K 2009 Unsteady response of non-Newtonian blood flow through a stenosed artery in magnetic field. J. Comput. Appl. Math. 23: 243–259
Mustapha N, Amin N, Chakravarty S and Mandal P K 2009 Unsteady magnetohydrodynamic blood flow through irregular multi-stenosed arteries. Comput. Biol. Med. 39: 896–906
Eldesoky I M, Kamel M H, Hussien R M and Abumanndour R M 2013 Numerical study of unsteady MHD pulsatile flow through porous medium in an artery using generalized differential quadrature method (GDQM). Int. J. Mater. Mech. Manuf. 1(2): 200–206
Akbar N S, Nadeem S, Hayat T and Hendi A A 2012 Effects of heat and chemical reaction on Jeffrey fluid model with stenosis. Appl. Anal. 91(9): 1631–1647
Nallapu S and Radhakrishnamacharya G 2014 Jeffrey fluid flow through porous medium in the presence of magnetic field in narrow tubes. Int. J. Eng. Math. 2014: 713–831
Jyothi K L, Devaki P and Sreenadh S 2013 Pulsatile flow of a Jeffrey fluid in a circular tube having internal porous lining. Int. J. Math. Arch. 4: 75–82
Akbar N S, Nadeem S and Lee C 2013 Characteristics of Jeffrey fluid model for peristaltic flow of chime. Results Phys. 3: 152–160
Srinivasa Rao K and Koteswara Rao P 2012 Effect of heat transfer on MHD oscillatory flow of Jeffrey fluid through a porous medium in a tube. Int. J. Math. Arch. 3(11): 4692–4699
Akbar N S and Nadeem S 2012 Simulation of variable viscosity and Jeffrey fluid model for blood flow through a tapered artery with a stenosis. Commun. Theor. Phys. 57(1): 133–140
Ellahi R, Rahman S U and Nadeem S 2014 Blood flow of Jeffrey fluid in a catheterized tapered artery with the suspension of nanoparticles. Phys. Lett. A 378: 2973–2980
Ponnalagarsamy R and Kawahara M 1989 A finite element analysis of laminar unsteady flows of viscoelastic fluids through channels with non-uniform cross-sections. Int. J. Numer. Methods Fluids 9: 1487–1501
Haynes R H 1960 Physical basis of the dependence of blood viscosity on tube radius. Am. J. Physiol. 198: 1193–1200
Ponalagusamy R 2012 Mathematical analysis on effect of non-Newtonian behaviour of blood on optimal geometry of microvascular bifurcation system. J. Franklin Inst. 349: 2861–2874
Nichols W W and O’Rourke M F 1990 McDonald’s blood flow in arteries. Sevenoaks, Kent: Edward Arnold
Fung Y C 1984 Biodynamics: circulation. New York: Springer-Verlag
Ponalagusamy R and Gopalan N P 1993 Numerical study on steady state, three dimensional atmospheric diffusion of sulphur dioxide and sulphate dispersion with non-linear kinetics. Int. J. Comput. Fluid Dyn. 1: 339–349
Gopalan N P and Ponnalagarsamy R 1992 Investigation on laminar flow of a suspension in corrugated straight tubes. Int. J. Eng. Sci. 30: 631–644
Shaw S, Murthy P V S N and Pradhan S C 2010 The effect of body acceleration on two dimensional flow of Casson fluid through an artery with asymmetric stenosis. Open Transport Phenom. J. 2: 55–68
Bhatti M M and Ali Abbas M 2016 Simultaneous effects of slip and MHD on peristaltic blood flow of Jeffrey fluid model through a porous medium. Alexandria Eng. J. 55: 1017–1023
Pontrelli G 1998 Pulsatile blood flow in a pipe. Comput. Fluids 27(3): 367–380
Hayat T, Ali N, Asghar S and Siddiqui A M 2006 Exact peristaltic flow in tubes with an endoscope. Appl. Math. Comput. 182: 359–368
Vajravelu K, Sreenadh S and Lakshminarayana 2011 The influence of heat transfer on peristaltic transport of a Jeffrey fluid in a vertical porous stratum. Commun. Nonlin. Sci. Numer. Simul. 16: 3107–3125
Acknowledgements
One of the authors (S Priyadharshini) is thankful to the Ministry of Human Resource Development, the Government of India, for the grant of fellowship. The authors thank the editor and reviewers for their valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
The continuity and momentum equations governing the pulsatile flow of Jeffrey fluid in the presence of magnetic field are given by (Eqs. (2)–(4)) in section 2)
where the stress components are expressed as follows:
Using non-dimensionalization as in Eq. (9), the governing equations in dimensionless form are given as follows:
where
and \(f_1(r) = 1+\beta _1h_m(R_1^{m_2}-r^{m_2})\). The non-dimensional retardation time may be defined as \(\lambda _2 = \frac{\bar{\lambda }_2\bar{u}_0}{\bar{L}_0}\).
In the initial stage of mild stenosis, \(\delta _s = \frac{\bar{\delta }_s}{\bar{R}_0}<< 1\); in this case, from Eq. (A-8), \(\frac{\partial u_c}{\partial z}<< 1\). Using the assumptions in [1, 4, 10] subject to the conditions
(i) \(\frac{Re \bar{\delta }_s n_1^{\frac{1}{n_1-1}}}{\bar{L}_0}<< 1\) and (ii) \(\epsilon n_1^{\frac{1}{n_1-1}}\sim {\mathrm{O(1)}} \, (\epsilon = \frac{\bar{R}_0}{\bar{L}_0})\),
the lumen radius is very small compared to the wavelength of pressure wave, equation of motion in radial direction (A-10) will reduce to \(\frac{\partial p}{\partial r} = 0\) [53] and low-Reynolds-number approximation [54, 55], and the momentum equations become
Similarly, the governing equation for Newtonian fluid in peripheral plasma region can be obtained by performing an order of magnitude analysis as done here. For further details regarding the order of magnitude analysis, see references [56, 57].
Rights and permissions
About this article
Cite this article
PRIYADHARSHINI, S., PONALAGUSAMY, R. Computational model on pulsatile flow of blood through a tapered arterial stenosis with radially variable viscosity and magnetic field. Sādhanā 42, 1901–1913 (2017). https://doi.org/10.1007/s12046-017-0734-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12046-017-0734-5