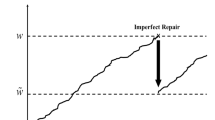
Abstract
Most often, perfect repair is conventionally understood as a replacement of the failed item by the new one. However, contrary to the common perception, new does not mean automatically that the distribution to the next failure is identical to that on the previous cycle. First, it can be different due to dynamic environment and, secondly, due to heterogeneity of items for replacement. Both of these causes that affect the failure mechanism of items are studied. Environment is modeled by the non-homogeneous Poisson shock process. Two models for the failure mechanism defined by the extreme shock model and the cumulative shock model are considered. Examples illustrating our findings are presented.




Similar content being viewed by others
References
Atwood CL (1992) Parametric estimation of time-dependent failure rates for probabilistic risk assessment. Reliab Eng Syst Saf 37:181–194
Aven T, Jensen U (1999) Stochastic models in reliability. Springer, New York
Aven T, Jensen U (2000) A general minimal repair model. J Appl Probab 37:187–197
Badía FG, Berrade MD, Campos CA (2001) On the behavior of aging characteristics in mixed populations. Probab Eng Inf Sci 15:83–94
Badía FG, Berrade MD, Campos CA (2002) Aging properties of the additive and proportional hazard mixing models. Reliab Eng Syst Saf 78:165–172
Barlow RE, Hunter L (1960) Optimum preventive maintenance policies. Oper Res 8:90–100
Block HW, Borges WS, Savits TH (1985) Age-dependent minimal repair. J Appl Probab 22:370–385
Cha JH, Finkelstein M (2016) New shock models based on the generalized Polya process. Eur J Oper Res 251:135–141
Cha JH, Mi J (2007) Study of a stochastic failure model in a random environment. J Appl Probab 44:151–163
Cocozza-Thivent C (1997) Processus Stochastigues et Fiabilite’ des Systkmes. Springer, Berlin
Crowder MJ, Kimber AC, Smith RL, Sweeting TJ (1991) Statistical analysis of reliability data. Chapman and Hall, London
Finkelstein M (1992) Some notes on two types of minimal repair. Adv Appl Probab 24:226–228
Finkelstein M (2008) Failure rate modelling for reliability and risk. Springer, London
Jiang R, Kim MJ, Makis V (2013) Availability maximization under partial observations. OR Spectr 35:691–710
Miziuła P, Navarro J (2017) Sharp bounds for the reliability of systems and mixtures with ordered components. Nav Res Logist 64:108–116
Miziuła P, Navarro J (2018) Bounds for the reliability functions of coherent systems with heterogeneous components. Appl Stoch Models Bus Ind 34:158–174
Navarro J (2016) Stochastic comparisons of generalized mixtures and coherent systems. Test 25:150–169
Navarro J, del Águila Y (2017) Stochastic comparisons of distorted distributions, coherent systems and mixtures with ordered components. Metrika 80:627–648
Papadakis IS, Kleindorfer PR (2005) Optimizing infrastructure network maintenance when benefits are interdependent. OR Spectr 27:63–84
Vesely WE (1977) Estimating common cause failure probabilities in reliability and risk analysis: Marshall–Olkin specializations. In: Fussell JB, Burdick GR (eds) Nuclear systems reliability engineering and risk assessment. SIAM, Philadelphia, pp 314–341
Zhu Q, Peng H, van Houtum GJ (2015) A condition-based maintenance policy for multi-component systems with a high maintenance setup cost. OR Spectr 37:1007–1035
Acknowledgements
The authors thank the referees for valuable comments and constructive suggestions. The work of the first author was supported by the National Research Foundation of Korea (NRF) Grant funded by the Korea government (MSIP) (No. 2016R1A2B2014211). The work of the second author was supported by the NRF (National Research Foundation of South Africa) Grant IFR2011040500026.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Cha, J.H., Finkelstein, M. Is perfect repair always perfect?. TEST 29, 90–104 (2020). https://doi.org/10.1007/s11749-019-00645-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11749-019-00645-7