Introduction

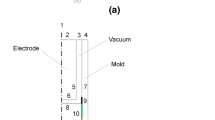
The vacuum arc remelting (VAR) process is a method of refining a consumable metal electrode to produce various alloys such as stainless steel, Nickel-based, and Titanium-based alloys. A DC arc supplies thermal energy to melt the tip of electrode (impure alloy), resulting in the formation of droplets under vacuum condition. The droplets drip through the vacuum to reach the melt pool, solidifying in a water-cooled mold to build the high-grade ultraclean alloy ingot. Low-density oxide inclusions are transferred to the solidification rim (more precisely, the surface of ingot) near the mold. Unfavorable elements with high vapor pressure such as Pb, Sn, Bi, Te, As, and Cu are evaporated under vacuum condition. The VAR process is schematically shown in Figure 1(a). An axisymmetric cross-section of the process is also illustrated in Figure 1(b) to indicate different regions and boundaries of the computational domain.

Fig. 1
figure 1

(a) Schematic representation of the VAR process; (b) an axisymmetric cross-section of the VAR process is shown to mark different regions and corresponding interfaces/boundaries. A 2D axisymmetric swirl calculation is performed

Full size image

Diverse phenomena exist in VAR, including cathode spots at the tip of electrode,[1,2] the vacuum plasma,[3,4,5] the thermal radiation in the vacuum,[6] melting of the electrode,[7,8] solidification of the ingot,[9,10,11] and the interplay between the electromagnetic field and the flow as known as magnetohydrodynamics (MHD) in the melt pool.[12,13,14]

The electric current flowing through the entire system produces a self-induced magnetic field dominantly in the azimuthal direction. An external axial magnetic field (AMF) is often deliberately introduced to stabilize the arc.[1,2,15,16,17,18] The axial magnetic field impacts various aspects of the process, including the behavior of the arc, the movement of cathode spots,[1,19] MHD in the melt pool,[20,21] and consequently the solidification (macrosegregation and grain structure) of the ingot.[11,22,23,24,25,26]

In the absence of an axial magnetic field, a significant amount of electric current (~ 30 to 70 pct) is transferred directly between the electrode and mold through the arc as known as “side-arcing.”[5,6,27] Side-arcing conveys a large amount of energy to the mold, and it is a safety-critical parameter since the involving materials of ingot and mold are highly reactive. In the presence of an axial magnetic field, the arc is confined below the shadow of electrode, and, as a result, the amount of side-arcing is reduced.[28]

The thermal field and consequently solidification of the ingot is governed by the flow field in the melt pool that in turn is driven by thermosolutal buoyancy and Lorentz force. The latter arises from the interaction between the electric current density and both self-induced, axial magnetic fields. The early analysis revealed that notable changes in the amount of imposed electric current or slight variation in the axial magnetic field could vigorously alter the flow pattern in the melt pool.[20]

In the present study, we perform a comprehensive investigation on the impact of an axial magnetic field on transport phenomena in a VAR process of a titanium-based (Ti–6Al–4V) alloy. Both static and time-varying axial magnetic fields are studied. The electromagnetic and thermal fields are computed in the entire system, including the electrode, vacuum plasma, ingot, and mold. Calculations of thermal radiation in the vacuum region and solidification of the ingot are carried out. Experimental results considering the marked melt pool profile are used to validate the modeling results.[29] A detailed analysis of the flow field in the melt pool considering the amount of side-arcing and the amount of (static/time-varying) axial magnetic field is presented. The main goal is to obtain a fundamental understanding of the VAR through numerical modeling to help engineers optimize the design and operational parameters of the process.

Modeling

The transport phenomena, including flow, electromagnetic, and thermal/solidification fields, are calculated using the well-established Finite Volume Method (FVM) to discretize the governing equations. Numerous User-defined functions (UDF) are implemented in the commercial CFD software, ANSYS FLUENT v.14.5, to consider special boundary conditions and modeling equations related to the arc, solidification, etc.[30] A 2D axisymmetric cross-section of the VAR process is shown in Figure 1(b), where different regions and boundaries are described.

The following assumptions are made for all simulation trials:

  1. (i)

    A one-way coupling is considered in which the thermal, plasma, and flow fields do not influence the electromagnetic field in the entire domain except the ingot. The interplay between the electromagnetic field and the flow field in the melt pool of the ingot is taken into account.

  2. (ii)

    A pre-defined length for the contact zone (20 mm) at the top edge of the VAR ingot among the as-solidified shell and mold is assumed. Below that region, the as-solidified shell shrinks away from the mold to form an air gap. The effect of the metal crown formation (~ 20 mm) at the top edge of the ingot on the electromagnetic field is considered.[14]

  3. (iii)

    The top surface of ingot (vacuum–ingot interface) is assumed to be stationary and flat.

  4. (iv)

    The formation of droplets at the tip of electrode and the dripping of droplets in the vacuum are not modeled. Thus, the global electromagnetic field is calculated ignoring the droplets. However, droplets carry momentum, energy, and mass into the melt pool, which is implicitly modeled as source terms in the corresponding conservation equations. Those source terms are extensively described in Reference 31.

  5. (v)

    The arc is implicitly modeled considering a Gaussian distribution of electric current density as a function of radial position on the tip of the electrode and the top of the ingot.[14,32,33,34]

Governing Equations

The 2D axisymmetric swirl model is used to compute the poloidal components, including radial (\( u_{\rm r} \)) and axial (\( u_{x} \)) velocities as well as the toroidal component (\( u_{\theta } \)) of the velocity field (\( \vec{u} = \left( {u_{\rm r} ,u_{\theta } ,u_{x} } \right). \)). The fluid (liquid metal) in the ingot zone is regarded as Newtonian and incompressible. Furthermore, a condition of no gradients exists in the toroidal direction for the flow,

$$ \frac{1}{r}\frac{{\partial \left( {ru_{\rm r} } \right)}}{\partial r} + \frac{{\partial u_{x} }}{\partial x} = 0. $$
(1)
$$ \frac{{\partial \left( {\rho u_{x} } \right)}}{\partial t} + \frac{1}{r}\frac{\partial }{\partial x}\left( {r\rho u_{x} u_{x} } \right) + \frac{1}{r}\frac{\partial }{\partial r}\left( {r\rho u_{x} u_{\rm r} } \right) = - \frac{\partial P}{\partial x} + \frac{1}{r}\frac{\partial }{\partial r}\left[ {r\mu \left( {\frac{{\partial u_{x} }}{\partial r} + \frac{{\partial u_{\rm r} }}{\partial x}} \right)} \right] + \frac{1}{r}\frac{\partial }{\partial x}\left[ {r\mu \left( {2\frac{{\partial u_{x} }}{\partial x} - \frac{2}{3}\left( {\frac{1}{r}\frac{{\partial \left( {ru_{\rm r} } \right)}}{\partial r} + \frac{{\partial u_{x} }}{\partial x}} \right)} \right)} \right] + \rho_{0} g\beta \left( {T - T_{0} } \right) - \frac{\mu }{K}\left( {u_{x} - u_{\rm s} } \right) + F_{x}. $$
(2)
$$ \frac{{\partial \left( {\rho u_{\rm r} } \right)}}{\partial t} + \frac{1}{r}\frac{\partial }{\partial x}\left( {r\rho u_{x} u_{\rm r} } \right) + \frac{1}{r}\frac{\partial }{\partial r}\left( {r\rho u_{\rm r} u_{\rm r} } \right) = - \frac{\partial P}{\partial r} + \frac{1}{r}\frac{\partial }{\partial x}\left[ {r\mu \left( {\frac{{\partial u_{x} }}{\partial r} + \frac{{\partial u_{\rm r} }}{\partial x}} \right)} \right] - \frac{{2\mu u_{\rm r} }}{{r^{2} }} + \frac{{\rho u_{\theta }^{2} }}{r} + \frac{1}{r}\frac{\partial }{\partial x}\left[ {r\mu \left( {2\frac{{\partial u_{\rm r} }}{\partial r} - \frac{2}{3}\left( {\frac{1}{r}\frac{{\partial \left( {ru_{\rm r} } \right)}}{\partial r} + \frac{{\partial u_{x} }}{\partial x}} \right)} \right)} \right] + \frac{2\mu }{3r}\left( {\frac{1}{r}\frac{{\partial \left( {ru_{\rm r} } \right)}}{\partial r} + \frac{{\partial u_{x} }}{\partial x}} \right) - \frac{\mu }{K}u_{\rm r} + F_{\rm r}. $$
(3)
$$ \frac{{\partial \left( {\rho u_{\theta } } \right)}}{\partial t} + \frac{1}{r}\frac{\partial }{\partial x}\left( {r\rho u_{x} u_{\theta } } \right) + \frac{1}{r}\frac{\partial }{\partial r}\left( {r\rho u_{\rm r} u_{\theta } } \right) = \frac{1}{r}\frac{\partial }{\partial x}\left[ {r\mu \frac{{\partial u_{\theta } }}{\partial x}} \right] + \frac{1}{{r^{2} }}\frac{\partial }{\partial r}\left[ {r^{3} \mu \frac{\partial }{\partial r}\left( {\frac{{u_{\theta } }}{r}} \right)} \right] - \rho \frac{{u_{\rm r} u_{\theta } }}{r} - \frac{\mu }{K}u_{\theta } + F_{\theta },$$
(4)

where ρ is density, P is pressure, µ denotes effective viscosity including the effect of turbulence, T is temperature, g is gravity constant (−9.81 m s−2), β is the thermal expansion coefficient considering Boussinesq approximation, and ρ0 and T0 are reference density and reference temperature, respectively. Darcy’s law[35] is applied to account for interdendritic flow inside the ingot considering the drag resistance force in the mushy zone that involves casting speed (us) and permeability (K).[14] For that purpose, the isotropic model of Kozeny–Carman is utilized.[14,36] Computations of the components of Lorentz force (\( \vec{F} = \left( {F_{\rm r}, F_{\theta }, F_{x} } \right) \)) are described after introducing the governing equations of the electromagnetic field.

The turbulence is calculated according to the Scale-Adaptive Simulation (SAS) model[37,38] that is insensitive to the grid spacing of the near wall cells.[37] SAS is computationally cost-effective, and the accuracy of the obtained results is comparable to that of the LES model. Details of the model are described in Reference 37 and 38.

No-slip boundary condition is applied at all boundaries enclosing the ingot except the top surface of ingot where a free-slip condition is applied. The casting speed (\( u_{\rm s} \)) is specified at the ingot bottom.[14]

Conventionally, \( A{-}\varphi \) method[14,39] or induction method (\( B_{\theta } \)) were applied to compute the electromagnetic field in VAR process, where \( \varphi \) is electric potential; \( \vec{A} = \left( {A_{\rm r}, A_{\theta }, A_{x} } \right) \) denotes the magnetic vector potential; \( B_{\theta } \) is the magnetic flux density. To accurately calculate the electromagnetic field considering the static/time-varying axial magnetic field, the following model known as \( A_{\theta } - B_{\theta } \) method is utilized,

$$ \frac{{\partial B_{\theta } }}{\partial t} + \frac{{\partial \left( {u_{x} B_{\theta } } \right)}}{\partial x} + \frac{{\partial \left( {u_{\rm r} B_{\theta } } \right)}}{\partial r} = \frac{\partial }{\partial r}\left( {\frac{1}{{r\sigma\mu_{0} }}\frac{{\partial \left( {rB_{\theta } } \right)}}{\partial r}} \right) + \frac{\partial }{\partial x}\left( {\frac{1}{{\sigma\mu_{0} }}\frac{{\partial B_{\theta } }}{\partial x}} \right) - \frac{{u_{\rm r} B_{\theta } }}{r} - \frac{{B_{\theta } }}{{\sigma \mu_{0} r^{2} }} - \frac{{\partial \left( {u_{\theta } B_{x} } \right)}}{\partial x} - \frac{{\partial \left( {u_{\theta } B_{\rm r} } \right)}}{\partial r}, $$
(5)
$$ \sigma \frac{{\partial A_{\theta } }}{\partial t} + \sigma u_{x} \frac{{\partial A_{\theta } }}{\partial x} + \sigma u_{\rm r} \frac{{\partial A_{\theta } }}{\partial r} = \frac{\partial }{\partial r}\left( {\frac{1}{{r\mu_{0} }}\frac{{\partial \left( {rA_{\theta } } \right)}}{\partial r}} \right) + \frac{\partial }{\partial x}\left( {\frac{1}{{\mu_{0} }}\frac{{\partial A_{\theta } }}{\partial x}} \right) - \frac{{\sigma u_{\rm r} A_{\theta } }}{r} - \frac{{A_{\theta } }}{{\mu_{0} r^{2} }}, $$
(6)

where \( \sigma \) and \( \mu_{0} \)are electrical conductivity and magnetic permeability, respectively.

Other components of the magnetic field are easily calculated considering (\( \vec{B} = \nabla \times \vec{A} \)) as follows:

$$ B_{\rm r} = - \frac{{\partial A_{\theta } }}{\partial x} $$
(7)
$$ B_{x} = \frac{1}{r}\frac{{\partial \left( {rA_{\theta } } \right)}}{\partial r} $$
(8)

Afterward, all components of electric current density are calculated considering Ampere’s law (\( \vec{j} = \frac{1}{{\mu_{0} }} \nabla \times \vec{B} \)) as follows:

$$ j_{\rm r} = - \frac{1}{{\mu_{0} }}\frac{{\partial B_{\theta } }}{\partial x} $$
(9)
$$ j_{\theta } = - \sigma \left( {\frac{{\partial A_{\theta } }}{\partial t} + u_{x} \frac{{\partial A_{\theta } }}{\partial x} + \frac{{u_{\rm r} }}{r}\frac{{\partial \left( {rA_{\theta } } \right)}}{\partial r}} \right) $$
(10)
$$ j_{x} = \frac{1}{{r\mu_{0} }}\frac{{\partial \left( {rB_{\theta } } \right)}}{\partial r}. $$
(11)

As boundary conditions, the electric current density at all boundaries enclosing the vacuum region are specified. The electric current density at crown (\( j_{\rm crown} = \frac{{I_{0} f_{\rm side-arc} }}{{A_{\rm crown} }} \)) is dependent on the amount of side-arcing.[14] \( A_{\rm crown} \) denotes the area of crown, and \( f_{\rm side-arc} \) denotes the fraction of the total imposed current (\( I_{0} \)) which flows through the crown. Customarily, a Gaussian distribution of electric current density as a function of radial position (r) is specified at electrode tip (\( \vec{j}_{\rm tip} \)) and ingot-top surface (\( \vec{j}_{\rm ingot-top} \)) as follows[14,32,33,34]:

$$ j_{\rm tip} = \frac{{I_{0} \exp \left( { - \frac{{r^{2} }}{{R_{\rm a}^{2} }}} \right)}}{{\mathop \smallint \nolimits_{0}^{{R_{\rm e} }} 2\pi r\exp \left( { - \frac{{r^{2} }}{{R_{\rm a}^{2} }}} \right) \text{d}r}} $$
(12)
$$ j_{\text{ingot-top}} = \frac{{I_{0} \left( {1 - f_{\text{side-arc}} } \right)\exp \left( { - \frac{{r^{2} }}{{R_{\rm a}^{2} }}} \right)}}{{\mathop \int \nolimits_{0}^{{R_{i} }} 2\pi r\exp \left( { - \frac{{r^{2} }}{{R_{\rm a}^{2} }}} \right) {\text{d}}r}}. $$
(13)

In Eqs. [12] and [13], Re denotes electrode radius, and Ri is the radius of the ingot. The radius of arc (Ra) is considered as a fraction (fR) of ingot radius,

$$ R_{\rm a} = f_{\rm R} R_{\rm i}. $$
(14)

The electric current density at the top of electrode (\( \vec{j}_{\rm electrode-top} \)) is specified considering the magnitude of imposed electric current and the cross-sectional area (\( A_{\rm electrode} \)) of electrode,

$$ \vec{j}_{\rm electrode-top} = - \frac{{I_{0} }}{{A_{\rm electrode} }}. $$
(15)

As described in Eqs. [7] to [8], the axial (\( B_{x} = \frac{{\partial A_{\theta } }}{\partial r} + \frac{{A_{\theta } }}{r}. \)) and radial (\( B_{\rm r} = - \frac{{\partial A_{\theta } }}{\partial x} \)) magnetic fields are dependent on \( A_{\theta } \). A condition of (\( A_{\theta } = \pm \frac{{rB_{\rm AMF} }}{2} \)) is assigned for Eq. [6] at mold–water interface, where \( B_{\rm AMF} \) denotes the static/time-varying axial magnetic field. Of note, the positive or negative sign indicates the direction of the axial magnetic field.

Eventually, all Lorentz force components inside the ingot zone are computed, and they are added as momentum source terms to Eqs. [2] through (4),

$$ F_{\rm r} = j_{\theta } B_{x} - j_{x} B_{\theta}.$$
(16)
$$ F_{\theta } = j_{x} B_{\rm r} - j_{\rm r} B_{x}.$$
(17)
$$ F_{x} = j_{\rm r} B_{\theta } - j_{\theta } B_{\rm r}.$$
(18)

To avoid making this paper long winded, the governing equations and corresponding boundary conditions related to heat transfer in the entire system, the radiation in vacuum region, and solidification (solid–liquid phase change) of the ingot are not presented. They are elaborated in details elsewhere.[14] The interested readers are highly encouraged to consult Reference 14.

Other Settings

Hosamani[29] conducted numerous experiments to study the influence of an imposed axial magnetic field (AMF) on the solidification behavior (pool profile) of the VAR ingot of a Titanium-based (Ti–6Al–4V) alloy. Herein, the numerical model is configured according to his experimental setup.[29] The operating conditions are listed in Table I. The material properties of the alloy, such as specific heat capacity and thermal conductivity, are temperature-dependent. All material properties are extracted from References 40,41,42,43. A summary of the material properties (Ti–6Al–4V) is available in Reference 14.

Table I Operating Conditions of the Process Used in Our Calculations
Full size table

Results and Discussions

Impact of Static Magnetic Field on Transport Phenomena

As previously mentioned, the distribution of arc on the surface of ingot, as known as arc radius, and the amount of side-arcing significantly impact the electromagnetic field in the VAR process. Herein, those parameters are kept constant in all simulation trials to study the influence of AMF on magnetohydrodynamics (MHD) in the melt pool. Of note, the impact of AMF is not limited to MHD in the melt pool. The expansion of plasma in the vacuum zone as well as the movement of cathode spots and, consequently, the melting behavior of the tip of electrode are also sensitive to the applied AMF.[1] With the increase of the magnitude of AMF, the melt rate of electrode decreases, as reported in Table I. Nevertheless, the magnitude of arc radius is assumed to be 70 pct. of the ingot radius. Additionally, 30 pct. of the total imposed current is considered to be the amount of side-arcing. The sensitivity of our modeling results to the aforementioned parameters, i.e., side-arcing and arc radius, are further elucidated in C. Model verification.

As shown in Figure 2(a), the magnetic field and electric current density are strong under the tip of electrode where the arc plasma is emitted from the cathode spots. Magnitudes of those parameters reduce as the plasma expands in the vacuum zone. A non-uniform distribution of electric current density and magnetic field exists in the melt pool as a consequence of mold current at ingot–mold interface and side-arcing. A notable amount of electric current density flows near the contact area between ingot and mold at the top of melt pool. The strength of Lorentz force in the melt pool is determined by the interaction between the electric current density and the magnetic fields (both the induced one and AMF) considering Eqs. [16] through [18]. As shown in Figure 2(b), an intense Lorentz force exists in the poloidal direction (\( F_{\rm LP} = \sqrt {F_{\rm r}^{2} + F_{x}^{2} } \)) under the shadow of electrode where both magnetic field and electric current density are strong. Lorentz force is generally directed toward the center of ingot in the poloidal plane. However, the force bends downward adjacent to the contact area between the ingot and mold. The interplay between AMF and the radial component of electric current density gives rise to the toroidal part of Lorentz force (\( F_{\theta } = F_{L\theta } \)). As anticipated, the peak value is observed under the shadow of electrode. The influence of AMF on the thermal/solidification field is illustrated in Figure 2(c). Following References 12,13,14, 20,21,22,23,24,25,26, 33,34,35, a linear relationship among the liquid volume fraction and temperature, \( f = min\left\{ {1,max\left\{ {0,\frac{{T - T_{\rm s} }}{{T_{\rm L} - T_{\rm s} }}} \right\}} \right\} \), is used to estimate the solidification behavior of the ingot. Here, f denotes liquid volume fraction, \( T_{\rm s} \) is solidus temperature, and \( T_{\rm L} \) is liquidus temperature of the alloy. To scrutinize the impact of AMF on transport phenomena in VAR, three different cases are examined: (i) ignoring AMF, (ii) earth magnetic field equivalent to 0.5 G, (iii) an imposed static AMF equivalent to 45 G. As shown in Figure 2(c), the thermal field and solidification pool profile of the ingot are greatly influenced by AMF. The temperature field is relatively uniform within the melt pool due to rigorous mixing.

Fig. 2
figure 2

Calculated field structures of VAR considering different values for static AMF, i.e., 0, 0.5, and 45 G are shown: (a) contour of the electromagnetic field including magnetic flux density (left half) and electric current density (right half); (b) distribution of Lorentz force in the ingot in poloidal plane (left half) and toroidal plane considering \( B_{\rm AMF} = 45\,\text{G}\) (right half); (c) distribution of thermal field in the entire system as well as plots of isolines of liquidus temperature and solidus temperature in the ingot zone (left half), and contour of the liquid fraction to demonstrate solidification of ingot (right half). Each contour is labeled according to the applied AMF

Full size image

The observed variations of the solidification profiles of the ingot as a consequence of AMF are originated in the velocity field in the melt pool. The poloidal velocity (\( u_{\rm P} = \sqrt {u_{\rm r}^{2} + u_{x}^{2} } \)) and toroidal velocity (\( u_{\theta } \)) fields are illustrated in Figure 3. Three different patterns for the velocity field were developed. Ignoring AMF (\( B_{\rm AMF} = 0 \)) leads to the development of an intense electro-vortex flow in the poloidal plane, whereas no flow (\( u_{\theta } = 0 \)) exists in the toroidal direction. In this case, the vortical flow rotates in a clockwise direction. Surprisingly, the presence of a weak axial magnetic field such as the one from earth (\( B_{\rm AMF} = 0.5\,\text{G}\)) can dramatically alter the flow pattern in the melt pool. A toroidal flow develops in the melt pool where the peak value is observed near the ingot center (~ 0.1 m s−1). Additionally, a vortical flow composed of two counter-rotating vortexes develops in the poloidal plane. The imposition of AMF (\( B_{\rm AMF} = 45\,\text{G}\)) in the third case results in the so-called “Ekman pumping” in which the flow is dominantly driven by centrifugal force. Consequently, the flow is promoted in the toroidal direction where the peak value is in the vicinity of the mold. Additionally, the vortical flow in the poloidal direction rotates in the counter-clockwise direction.

Fig. 3
figure 3

Distributions of the velocity field in the melt pool, including poloidal velocity (left half) and toroidal velocity (right half) considering different values for static AMF, i.e., 0, 0.5, and 45 G, are shown. Each contour is labeled according to the applied AMF. (a) \( B_{\rm AMF} = 0 \), (b) \( B_{\rm AMF} = 0.5\,\text{G}\), (c) \( B_{\rm AMF} = 45\,\text{G}\). Note that there exists no toroidal velocity for \( B_{\rm AMF} = 0 \)

Full size image

Impact of Time-Varying Magnetic Field on Transport Phenomena

A time-varying AMF considering ten seconds for the reversal time of the direction of magnetic field as reported for the operating condition in the experiment (Reference 29) is studied. Figure 4 indicates the variation of both poloidal and toroidal velocity fields sometime (t0) in the middle of the process in the melt pool. During one full cycle (20 s), the direction of the axial magnetic field (AMF) changes twice. The direction is upward in the first 10 seconds, whereas the direction is downward in the next 10 seconds according to the specified reversal time as the operating condition of the process. Firstly, an intense electro-vortex flow develops in the poloidal plane along with a strong toroidal flow with the peak value situated away from the center of ingot. Secondly, the “Ekman pumping” pattern develops in the poloidal plane after altering the direction of AMF. Meanwhile, the flow in toroidal direction slows down to change its direction. Once again, the peak value in the toroidal plane is located away from the center of ingot. Of note, the positive value means that the velocity vector points inward, whereas the negative value means that the velocity vector points outward in the toroidal plane. It is not possible to effectively demonstrate transport phenomena such as flow field using images. Thus, the transient results are shown through animation in supplemental materials. Readers are encouraged to observe “TimeVaryingAMF_VAR.avi” file.

Fig. 4
figure 4

Snapshots at different times of both poloidal (left half) and toroidal (right half) velocity fields in the melt pool starting sometime in the middle of the process (t0) are shown. Snapshots are taken during one full cycle (20 s). Each contour is labeled considering the evolution of time in seconds, including t0, t0+4, t0+8, t0+12, t0+16, t0+20

Full size image

Despite the transient nature of poloidal and toroidal velocity fields, the pool profile is firmly steady, and the system reaches a quasi-steady state. The chaotic flow in the melt pool is spatially disordered. A statistical analysis of the flow is performed in order to quantitatively characterize the transient behavior of both poloidal and toroidal velocity fields. The instantaneous velocity components are decomposed to mean and fluctuating values. Distributions of fluctuations in velocity components are analyzed considering poloidal variance (\( s_{\rm p}^{2} \)) and toroidal variance (\( s_{\theta }^{2} \)). Variances are calculated over a long period of time (~ 30 min) until the achievement of statistical invariance as follows:

$$ s_{i}^{2} = \frac{1}{N}\mathop \sum \limits_{n = 1}^{N} (u_{i} - \bar{u}_{i} )^{2},\quad i = p,\theta,$$
(19)

where\( N \)denotes the total number of samples (~ 20,000). The results of the analysis are illustrated in Figure 5. In contrast to developing an “Ekman pumping” flow pattern for static AMF, the mean velocity pattern follows an electro-vortex flow. The peak values are observed in regions under the shadow of electrode and adjacent to the axis where small fluctuations also exist in the poloidal plane. Furthermore, the flow remains statistically invariant deep into the melt pool and near the mold wall in the poloidal plane. The peak value for mean and fluctuation components of toroidal velocity is observed near the mold wall. The mean toroidal velocity remains minimal (nearly zero), whereas the fluctuation in the toroidal direction (\( s_{\theta }^{2} \)) is significant. Of note, the mean toroidal velocity must become zero after a long period of calculations considering Eq. [4], as the mean Lorentz force in θ direction is zero. This implies that applying a time-varying AMF can significantly influence the transient toroidal velocity in the melt pool. In other words, the direction of toroidal velocity changes as the direction of AMF alters, as also illustrated in the animation “TimeVaryingAMF_VAR.avi.”

Fig. 5
figure 5

Calculated characteristics of the velocity field in the melt pool, including mean velocity and variance considering time-varying AMF (\( B_{\rm AMF} = 45\,\text{G}\)) with reversal time of ten seconds are shown: (a) poloidal mean velocity (left half) and toroidal mean velocity (right half); (b) poloidal variance (left half) and toroidal variance (right half)

Full size image

Model Verification

The pool profile of the ingot is sensitive to several operational parameters, such as the magnitude of AMF and the reversal time of AMF. The parameters related to arc, such as the amount of side-arcing and the arc radius, are also influenced to a great extent by AMF. It is essential to study the sensitivity of modeling results to those parameters, although they are chosen/determined with our best knowledge within the range of the reported values in the literature. For that purpose, an extensive series of simulations considering the static AMF was performed. A summary of results related to the predicted pool profile of the ingot is shown in Figure 6(a). Expectedly, the pool depth increases as the radius of arc decreases. The large radius of arc indicates a diffusive mode, whereas the arc conforms to a constricted mode as the radius decreases. Interestingly, the depth remains relatively insensitive to the amount of side-arcing. The experimental results of the pool profile reported by Hosamani[29] are used to validate our modeling results, as shown in Figures 6(b) through (c). In the experiments, Nickel particles were used to mark the pool profile.[29] As shown in Figure 6(b), a V-shaped pool profile of ingot is predicted ignoring AMF (\( B_{\rm AMF} = 0 \)). Thus, the model fails to predict the shape of melt pool. However, the modeling result fairly agrees with the experimental result once the AMF through the earth magnetic field (\( B_{\rm AMF} = 0.5\,\text{G}\)) is taken into account. In this case, a U-shaped pool profile is developed. Of note, the experimental pool profile is not entirely axisymmetric so that a full 3D model is required to predict the pool profile precisely. The experimental pool profile complies with an axisymmetric one for the time-varying AMF (\( B_{\rm AMF} = 45{\text{G}} \)) as shown in Figure 6(c) in which a good agreement is observed among the modeling result and the experiment.

Fig. 6
figure 6

(a) Calculated pool profile (f = 0.98) using the model considering various arc radius and amount of side-arcing; (b) considering the static earth magnetic field (\( B_{\rm AMF} = 0.5\,\text{G}\)), a comparison is made between the calculated pool profile (f = 0.98) using the model and the marked pool profile that is extracted from Ref. [29]; (c) considering the time-varying magnetic field (\( B_{\rm AMF} = 45\,\text{G}\)) with a reversal time of ten seconds, a comparison is made between the calculated pool profile (f = 0.98) using the model and the marked pool profile extracted from Ref. [29]. Reference [29] is available under Creative Commons By Attribution 4.0 in: https://creativecommons.org/licenses/by/4.0/

Full size image

Summary

Vacuum arc remelting (VAR) process is extensively used to produce ultraclean alloys such as Titanium-based alloy. The process comprises a wide range of physical phenomena such as formation and movement of cathode spots on the electrode surface, the vacuum arc plasma, the thermal radiation in the vacuum region, magnetohydrodynamics (MHD) in the melt pool, melting of the electrode, and the solidification of the ingot. Conventionally, an axial magnetic field (AMF) is introduced to the process through an external coil to stabilize the arc plasma. Meanwhile, the imposition of AMF remarkably influences the magnetohydrodynamics (MHD) in the melt pool that in turn impacts the final quality of the VAR ingot. Herein, we put forward a comprehensive model to study the effect of both static and time-varying AMF on transport phenomena in a VAR process of a titanium-based (Ti–6Al–4V) alloy. The electromagnetic and thermal fields are calculated in the entire system involving the electrode, vacuum plasma, ingot, and mold. Computations of thermal radiation in the vacuum region and solidification of the ingot are also performed. A detailed analysis of the predicted flow field in the melt pool by the model considering the static/time-varying AMF is presented.

Furthermore, a statistical analysis of the flow considering time-varying AMF is carried out to characterize the transient behavior of the velocity field quantitatively. The presence of a weak AMF such as the one from the earth can drastically alter the flow pattern in the melt pool. The following flow patterns are predicted: “Electro-vortex flow” is obtained in the absence of AMF or in the presence of a time-varying AMF; “Ekman pumping” is predicted in the presence of a static AMF. It is found that the amount of side-arcing becomes no longer a significant parameter to influence the depth of melt pool in the presence of AMF. Contrastingly, the arc radius continues to be a decisive parameter in the absence/presence of AMF to determine the pool profile of the ingot. Our modeling results regarding the melt pool profiles are validated against experimental results.