Multigrain and Multiphase Mathematical Model for Equiaxed Solidification

Abstract

A deterministic multigrain and multiphase model of equiaxed solidification of binary alloys is proposed, implemented, and analyzed. An important feature of the present model is the creation of classes of dendritic and globulitic grains according to their instantaneous sizes during solidification. Globulitic and dendritic grain growth, coarsening of secondary dendrite arms, distribution of nucleation undercoolings, and equiaxed eutectic growth are consistently included in the model equations. Important model assumptions are uniform temperature, negligible liquid convection, and negligible grain movement. Calculated cooling curves, solid fraction evolution, average grain sizes, and eutectic fractions agree well with predictions of previous models for dendritic and globulitic equiaxed grains. Predicted grain sizes decrease with an increase in cooling rate for an Al-2.12 pct Cu alloy and with an increase in Si concentration up to 3 pct for Al-Si alloys, agreeing quantitatively with experimental results. Simulations for an Al-7 pct Si alloy predict that an increase in grain size correlates with an increase in the magnitude of the recalescence observed in cooling curves. These calculations agree well with experimental results when the transition from a globulitic to a dendritic morphology occurs in the model before the minimum temperature of recalescence is reached.

Appendix

1.1 Macroscopic Conservation Equations

The general transport theorem[19] applied to the volume V _k of constituent k within a REV of constant volume V ₀ can be written as

$$ \frac{\text{d}}{{{\text{d}}t}}\left( {\varepsilon_{k} \frac{1}{{V_{k} }}\int\limits_{{V_{k} }} {\psi_{k} {\text{d}}V} } \right) = \frac{1}{{V_{0} }}\int\limits_{{V_{k} }} {\frac{{\partial \psi_{k} }}{\partial t}} {\text{d}}V + \frac{1}{{V_{0} }}\oint\limits_{{A_{kj} + A_{kb} }} {\psi_{k} \vec{w}_{k} \cdot \vec{n}_{k} {\text{d}}A}, $$

(A1)

where ψ _k is a field variable defined in constituent k; A _kj is the total interfacial area between constituent k and all adjacent constituents within V ₀; A _kb is the boundary area formed by the REV boundary cutting through constituent k; $\vec{w}_{k}$ is the velocity of all interfaces and boundaries of k, being zero for its boundaries coinciding with the REV boundary (A _kb ), which is motionless; $\vec{n}_{k}$ is a normal unit vector at the interfaces of k and pointing out of V _k .

For ψ _k  = ρ, which is the mass density and is assumed constant and equal for all constituents, Eq. [A1] gives

$$ \frac{{{\text{d}}\varepsilon_{k} }}{{{\text{d}}t}} = \frac{1}{{V_{0} }}\int\limits_{{A_{kj} }} {\vec{w}_{k} \cdot \vec{n}_{k} {\text{d}}A} $$

(A2)

For $\psi_{k} = \rho {\kern 1pt} C_{k},$where C _k is the mass fraction of solute in constituent k, the species conservation equation in differential form, namely $\partial \left( {\rho C_{k} } \right)/\partial t = - \vec{\nabla } \cdot \vec{j}_{k}$ (where $\vec{j}_{k}$ is the diffusive flux of solute), can be substituted on the right-hand side of Eq. [A1]. After application of Gauss theorem and consideration that no solute flows through the REV boundary, the equation becomes

$$ \rho \frac{{{\text{d}}\left( {\varepsilon_{k} \left\langle {C_{k} } \right\rangle^{k} } \right)}}{{{\text{d}}t}} = \frac{1}{{V_{0} }}\int\limits_{{A_{kj} }} {\left( {\rho C_{k} \vec{w}_{k} - \vec{j}_{k} } \right) \cdot \vec{n}_{k} } {\text{d}}A $$

(A3)

Some of the surface integrals in these equations can be simplified by the following two approximations[43–45]

$$ \frac{1}{{V_{0} }}\int\limits_{{A_{kj} }} {\vec{w}_{k} \cdot \vec{n}_{k} {\text{d}}A} = S_{kj} \bar{w}_{kj} $$

(A4)

$$ - \frac{1}{{V_{0} }}\int\limits_{{A_{kj} }} {\vec{j}_{k} \cdot \vec{n}_{k} {\text{d}}A} = \rho D_{k} \frac{{S_{kj} }}{{\delta_{k} }}\left( {\bar{C}_{k} - \left\langle {C_{K} } \right\rangle^{k} } \right), $$

(A5)

where $\bar{w}_{kj}$ is the average normal interface velocity; S _kj  = A _kj /V ₀ is an interfacial area concentration; $\bar{C}_{k}$ and δ _k are, respectively, the surface average solute concentration and the effective diffusion length in constituent k at the interface between constituents k and j; and D _k is the diffusion coefficient of solute in k. In the absence of convection, the following two integrated jump condition can be used[19]

$$ \int\limits_{{A_{kj} }} {\vec{w}_{k} \cdot \vec{n}_{k} {\text{d}}A} = - \int\limits_{{A_{kj} }} {\vec{w}_{j} \cdot \vec{n}_{j} {\text{d}}A} $$

(A6)

$$ \int\limits_{{A_{kj} }} {\left( {\rho C_{k} \vec{w}_{k} - \vec{j}_{k} } \right) \cdot \vec{n}_{k} } {\text{d}}A = - \int\limits_{{A_{kj} }} {\left( {\rho C_{j} \vec{w}_{j} - \vec{j}_{j} } \right) \cdot \vec{n}_{j} } {\text{d}}A $$

(A7)

1.2 Development of the Main Equations

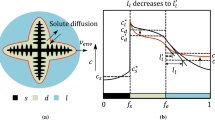
The general equations developed in the previous section were applied to the primary solid (si) and interdendritic liquid (di) of all grains belonging to an arbitrary class i and also to the eutectic (e) and external liquid (l), shown in Figure 1. Since the constituents si and di are defined for each of the N classes, there can be at most 2N + 2 different constituents in the model. As shown in Figure 1, the possible interfacial areas between each pair of constituents are A _le , A _sdi , A _ldi , A _lsi , A _die , and A _sie , where subscripts indicate the interface between constituents.

1.2.1 Mass Conservation

Equation [A2] could be applied to the eutectic (k = e), although there are dividing surfaces of discontinuities (interfaces between the solid phases) inside it, because ρ is constant. When $A_{kj} = A_{le} + \sum\nolimits_{i = 1}^{N} {\left( {A_{sie} + A_{die} } \right)}$, $\vec{w}_{e} = 0$ on A _sie , and Eq. [A4] is substituted, Eq. [A2] becomes

$$ \frac{{{\text{d}}\varepsilon_{e} }}{{{\text{d}}t}} = \frac{1}{{V_{0} }}\int\limits_{{A_{le} + \sum\nolimits_{i = 1}^{N} {A_{die} } }} {\vec{w}_{{e{\kern 1pt} }} \cdot \vec{n}_{e} {\text{d}}A} = \left( {S_{le} + \sum\limits_{i = 1}^{N} {S_{die} } } \right)\bar{w}_{e} $$

(A8)

where S _die  = A _die /V ₀ and S _le  = A _le /V ₀. The volume fraction of the external eutectic (ɛ _ee ), i.e., the eutectic formed in the external liquid is calculated from

$$ \frac{{{\text{d}}\varepsilon_{ee} }}{{{\text{d}}t}} = \frac{1}{{V_{0} }}\int\limits_{{A_{le} }} {\vec{w}_{e} \cdot \vec{n}_{e} {\text{d}}A} = S_{le} \bar{w}_{e}. $$

(A9)

Application of Eq. [A2] to the primary solid (k = si) implies $A_{kj} = A_{sdi} + A_{lsi}$ and gives the following important equation

$$ \frac{{{\text{d}}\varepsilon_{si} }}{{{\text{d}}t}} = \frac{1}{{V_{0} }}\int\limits_{{A_{lsi} }} {\vec{w}_{si} \cdot \vec{n}_{si} {\text{d}}A} + \frac{1}{{V_{0} }}\int\limits_{{A_{sdi} }} {\vec{w}_{si} \cdot \vec{n}_{si} {\text{d}}A} $$

(A10)

Equation [A2] was applied to the interdendritic liquid ($k = d{\kern 1pt} i$) using $A_{kj} = A_{sdi} + A_{ldi}$ and added to Eq. [A10], canceling the integral over A _sdi owing to Eq. [A6]. The simplification given by Eq. [A4] is also used giving

$$ \frac{{{\text{d}}\varepsilon_{gi} }}{{{\text{d}}t}} = \frac{1}{{V_{0} }}\int\limits_{{A_{ldi} }} {\vec{w}_{di} \cdot \vec{n}_{di} {\text{d}}A} + \frac{1}{{V_{0} }}\int\limits_{{A_{lsi} }} {\vec{w}_{si} \cdot \vec{n}_{si} {\text{d}}A} = S_{ldi} \bar{w}_{ldi} + S_{lsi} \bar{w}_{lsi}, $$

(A11)

where ɛ _gi  = ɛ _di  + ɛ _si , which is the volume fraction of all grains in class i, before the eutectic reaction occurs; S _ldi  = A _ldi /V ₀; and S _lsi  = A _lsi /V ₀.

For the external liquid (l), the following constitutive relation is valid

$$ \varepsilon_{l} = 1 - \varepsilon_{ee} - \sum\limits_{i = 1}^{N} {\varepsilon_{gi} } $$

(A12)

1.3 Species Conservation

Local thermodynamic equilibrium is assumed at the solid–liquid interface, implying that C _si  = KC _di at A _sdi (dendritic grains) and that C _si  = KC _l at A _lsi (globulitic grains), where K is the solute partition coefficient. Also C _di or C _l adjacent to solid–liquid interfaces can be related to T using the liquidus line, indicated for dendritic grains as C _di  = C _liq(T) and for globulitic grains as C _l  = C _liq,gi (T, R ^ext _i ), where R ^ext _i is the radius of curvature of the globulitic grains in class i (Section II–C–2). Equation [A3] was applied to the primary solid (k = si) adopting $A_{kj} = A_{sdi} + A_{lsi}$, giving

$$ \rho \frac{{{\text{d}}\left( {\varepsilon_{si} \left\langle {C_{si} } \right\rangle^{si} } \right)}}{{{\text{d}}t}} = \frac{1}{{V_{0} }}\int\limits_{{A_{sdi} }} {\left( {\rho KC_{\text{liq}} \vec{w}_{si} - \vec{j}_{si} } \right) \cdot \vec{n}_{si} } {\text{d}}A + \frac{1}{{V_{0} }}\int\limits_{{A_{lsi} }} {\left( {\rho KC_{{{\text{liq}},gi}} \vec{w}_{si} - \vec{j}_{si} } \right) \cdot \vec{n}_{si} } {\text{d}}A $$

(A13)

Substituting Eq. [A5], considering the local thermodynamic equilibrium and noting that C _liq and C _liq,gi are uniform within the REV give

$$ \begin{aligned} \rho \frac{{{\text{d}}\left( {\varepsilon_{si} \left\langle {C_{si} } \right\rangle^{si} } \right)}}{{{\text{d}}t}} & = \rho KC_{liq} \left( {\frac{1}{{V_{0} }}\int\limits_{{A_{sdi} }} {\vec{w}_{si} \cdot \vec{n}_{si} } {\text{d}}A} \right) + \rho KC_{liq,gi} \left( {\frac{1}{{V_{0} }}\int\limits_{{A_{lsi} }} {\vec{w}_{si} \cdot \vec{n}_{si} } {\text{d}}A} \right) + \\ & \quad + \rho D_{s} \frac{{S_{sdi} }}{{\delta_{sdi} }}\left( {KC_{\text{liq}} - \left\langle {C_{si} } \right\rangle^{si} } \right) + \rho D_{s} \frac{{S_{lsi} }}{{\delta_{lsi} }}\left( {KC_{{{\text{liq}},gi}} - \left\langle {C_{si} } \right\rangle^{si} } \right) \\ \end{aligned}. $$

(A14)

The integral over A _sdi is replaced with Eq. [A10] and all integrals over A _lsi are simplified using Eq. [A4] to give

$$ \begin{aligned} \frac{{{\text{d}}\left( {\varepsilon_{si} \left\langle {C_{si} } \right\rangle^{si} } \right)}}{{{\text{d}}t}} & = KC_{\text{liq}} \left( {\frac{{d\varepsilon_{si} }}{dt} - S_{lsi} \bar{w}_{lsi} } \right) + KC_{{{\text{liq}},gi}} S_{lsi} \bar{w}_{lsi} + \\ & \quad + D_{s} \frac{{S_{sdi} }}{{\delta_{sdi} }}\left( {KC_{\text{liq}} - \left\langle {C_{si} } \right\rangle^{si} } \right) + D_{s} \frac{{S_{lsi} }}{{\delta_{lsi} }}\left( {KC_{{{\text{liq}},gi}} - \left\langle {C_{si} } \right\rangle^{si} } \right) \\ \end{aligned} $$

(A15)

Equation [A3] is applied to the interdendritic liquid ($k = d{\kern 1pt} i$), considering $A_{kj} = A_{sdi} + A_{ldi}$ and substituting Eq. [A7]. Owing to local equilibrium and uniformity of the interdendritic liquid composition, $C_{l} = C_{\text{liq}}$ at A _ldi , the equation becomes

$$ \rho \frac{\text{d}}{{{\text{d}}t}}\left( {\varepsilon_{{d{\kern 1pt} i}} \left\langle {C_{di} } \right\rangle^{{d{\kern 1pt} i}} } \right) = - \frac{1}{{V_{0} }}\int\limits_{{A_{sdi} }} {\left( {\rho KC_{\text{liq}} \vec{w}_{si} - \vec{j}_{si} } \right) \cdot \vec{n}_{si} } {\text{d}}A - \frac{1}{{V_{0} }}\int\limits_{{A_{ldi} }} {\left( {\rho C_{\text{liq}} \vec{w}_{l} - \vec{j}_{l} } \right) \cdot \vec{n}_{l} } {\text{d}}A. $$

(A16)

Substituting again Eq. [A5] and noting that C _liq is uniform in A _sdi and A _ldi gives

$$ \begin{aligned} \frac{\text{d}}{{{\text{d}}t}}\left( {\varepsilon_{{d{\kern 1pt} i}} \left\langle {C_{{d{\kern 1pt} i}} } \right\rangle^{{d{\kern 1pt} i}} } \right) & = - KC_{\text{liq}} \left( {\frac{1}{{V_{0} }}\int\limits_{{A_{sdi} }} {\vec{w}_{si} \cdot \vec{n}_{si} } {\text{d}}A} \right) - C_{\text{liq}} \left( {\frac{1}{{V_{0} }}\int\limits_{{A_{ldi} }} {\vec{w}_{l} \cdot \vec{n}_{l} } {\text{d}}A} \right) \\ & \quad - D_{s} \frac{{S_{sdi} }}{{\delta_{sdi} }}\left( {KC_{\text{liq}} - \left\langle {C_{si} } \right\rangle^{si} } \right) - D_{l} \frac{{S_{ldi} }}{{\delta_{li} }}\left( {C_{\text{liq}} - \left\langle {C_{l} } \right\rangle^{l} } \right) \\ \end{aligned} $$

(A17)

In the integral over A _ldi , $\vec{n}_{l} = - \vec{n}_{di}$, $\vec{w}_{l} = \vec{w}_{di}$, and Eq. [A11] is substituted. The integral over A _sdi is again replaced with Eq. [A10], forcing the integral on A _lsi to appear, which is finally approximated by Eq. [A4], resulting in

$$ \begin{aligned} \left\langle {C_{{d{\kern 1pt} i}} } \right\rangle^{di} \frac{{{\text{d}}\varepsilon_{di} }}{{{\text{d}}t}} & = - \varepsilon_{{d{\kern 1pt} i}} \frac{{{\text{d}}\left\langle {C_{{d{\kern 1pt} i}} } \right\rangle^{{d{\kern 1pt} i}} }}{{{\text{d}}t}} - K{\kern 1pt} C_{\text{liq}} \left( {\frac{{{\text{d}}\varepsilon_{si} }}{{{\text{d}}t}} - S_{lsi} \bar{w}_{lsi} } \right) + C_{\text{liq}} \left( {\frac{{{\text{d}}\varepsilon_{gi} }}{{{\text{d}}t}} - S_{lsi} \bar{w}_{lsi} } \right) \\ & \quad - D_{s} \frac{{S_{sdi} }}{{\delta_{sdi} }}\left( {KC_{\text{liq}} - \left\langle {C_{si} } \right\rangle^{si} } \right) - D_{l} \frac{{S_{ldi} }}{{\delta_{li} }}\left( {C_{\text{liq}} - \left\langle {C_{l} } \right\rangle^{l} } \right) \\ \end{aligned}. $$

(A18)

Considering $\varepsilon_{{d{\kern 1pt} i}} = \varepsilon_{gi} - \varepsilon_{si}$ and 〈C _di 〉^di = C _liq, after some arrangement the final equation is

$$ \begin{aligned} \left( {1 - K} \right)C_{\text{liq}} \frac{{{\text{d}}\varepsilon_{si} }}{{{\text{d}}t}} & = \left( {\varepsilon_{{g{\kern 1pt} i}} - \varepsilon_{{s{\kern 1pt} i}} } \right)\frac{{{\text{d}}C_{\text{liq}} }}{{{\text{d}}t}} + \left( {1 - K} \right)C_{\text{liq}} S_{lsi} \bar{w}_{lsi} \\ & \quad + D_{s} \frac{{S_{sdi} }}{{\delta_{sdi} }}\left( {KC_{\text{liq}} - \left\langle {C_{si} } \right\rangle^{si} } \right) + D_{l} \frac{{S_{ldi} }}{{\delta_{li} }}\left( {C_{\text{liq}} - \left\langle {C_{l} } \right\rangle^{l} } \right) \\ \end{aligned}. $$

(A19)

Equation [A3] is applied to the external liquid (l), implying that the surface integrals are done over A _ldi and A _lsi of all N grain classes. Also C _l  = C _liq at A _ldi , and C _l  = C _liq,gi at A _lsi , giving

$$ \rho \frac{{{\text{d}}\left( {\varepsilon_{l} \left\langle {C_{l} } \right\rangle^{l} } \right)}}{{{\text{d}}t}} = \sum\limits_{i = 1}^{N} {\left[ {\frac{1}{{V_{0} }}\int\limits_{{A_{ldi} }} {\left( {\rho C_{\text{liq}} \vec{w}_{l} - \vec{j}_{l} } \right) \cdot \vec{n}_{l} } {\text{d}}A + \frac{1}{{V_{0} }}\int\limits_{{A_{lsi} }} {\left( {\rho C_{{{\text{liq}},gi}} \vec{w}_{l} - \vec{j}_{l} } \right) \cdot \vec{n}_{l} } {\text{d}}A} \right]}. $$

(A20)

As before, C _liq and C _liq,gi are taken out of the integral sign, $\vec{w}_{l} = \vec{w}_{di}$ and $\vec{n}_{l} = - \vec{n}_{di}$ are substituted in the integral over A _ldi , while $\vec{w}_{l} = \vec{w}_{si}$ and $\vec{n}_{l} = - \vec{n}_{si}$ are substituted in the integral over A _lsi . Also, substituting Eq. [A5] gives

$$ \begin{aligned} \frac{{{\text{d}}\left( {\varepsilon_{l} \left\langle {C_{l} } \right\rangle^{l} } \right)}}{{{\text{d}}t}} & = - \sum\limits_{i = 1}^{N} {\left[ {C_{\text{liq}} \left( {\frac{1}{{V_{0} }}\int\limits_{{A_{ldi} }} {\vec{w}_{di} \cdot \vec{n}_{di} } {\text{d}}A} \right) + C_{{{\text{liq}},gi}} \left( {\frac{1}{{V_{0} }}\int\limits_{{A_{lsi} }} {\vec{w}_{si} \cdot \vec{n}_{si} } {\text{d}}A} \right) } \right.} \\ & \quad \left. { - D_{l} \frac{{S_{ldi} }}{{\delta_{li} }}\left( {C_{\text{liq}} - \left\langle {C_{l} } \right\rangle^{l} } \right) - D_{l} \frac{{S_{lsi} }}{{\delta_{li} }}\left( {C_{{{\text{liq}},gi}} - \left\langle {C_{l} } \right\rangle^{l} } \right)} \right] \\ \end{aligned}. $$

(A21)

The integrals over A _ldi and A _lsi are approximated by Eqs. [A11] and [A4], and $\sum\nolimits_{i = 1}^{N} {{\text{d}}\varepsilon_{gi} /{\text{d}}t = - {\text{d}}\varepsilon_{l} /{\text{d}}t}$ (valid before the eutectic) is used, giving the final equation

$$ \begin{aligned} \frac{{{\text{d}}\left( {\varepsilon_{l} \left\langle {C_{l} } \right\rangle^{l} } \right)}}{{{\text{d}}t}} & = C_{\text{liq}} \frac{{{\text{d}}\varepsilon_{l} }}{{{\text{d}}t}} + \sum\limits_{i = 1}^{N} {\left[ {\left( {C_{\text{liq}} - C_{{{\text{liq}},gi}} } \right)S_{lsi} \bar{w}_{lsi} } \right]} + D_{l} \left( {\sum\limits_{i = 1}^{N} {\frac{{S_{ldi} }}{{\delta_{li} }}} } \right)\left( {C_{\text{liq}} - \left\langle {C_{l} } \right\rangle^{l} } \right) \\ & \quad + D_{l} \sum\limits_{i = 1}^{N} {\left[ {\frac{{S_{lsi} }}{{\delta_{li} }}\left( {C_{{{\text{liq}},gi}} - \left\langle {C_{l} } \right\rangle^{l} } \right)} \right]} \\ \end{aligned} $$

(A22)