Application of GPR and seismic methods for noninvasive examination of glacial and postglacial sediments in the Psia Trawka glade: the Tatra Mts., Poland

Abstract

Presented study gives an insight into general proportions of the actual geomorphology, subglacial morphology and thickness of the drift (quaternary sediments) particularly well-pronounced glacial morphology in the Tatras and, on the other hand, the general scarcity of the data in this field. Objectives of the geophysical survey in this study were imaging of the morphology of bedrock surface under the drift (glacial and postglacial) sediments and determination of thickness of the drift and its composition. Two methods were applied: Ground Penetrating Radar (GPR) and seismic refraction profiling. GPR was used to examine drift sediments due to its high resolution and low depth of penetration. Seismic method with lower resolution but higher penetration depth gave an image of boundary between bedrock and drift. In addition, the results of seismic tomography allowed the velocity field imaging which shows changes inside the postglacial deposits. The results of the two methods used in this research suggest that points of depression exist in the subglacial morphology with a depth of about c.a. 40 below the present-day terrain surface and c.a. 25 m below surrounding subglacial surface. This trough has also been estimated to be about 150 m wide. Its considerable depth and steep slopes show that its origin can be related to erosion of subglacial water during the decay of the last (Würm) glaciation of the Sucha Woda and Panszczyca valleys.

Introduction

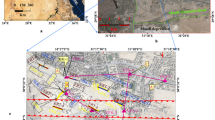
The geophysical studies were conducted in the Psia Trawka glade (Fig. 1), which is located in the central part of the Tatra Mountains (the Carpathian Mountains, Poland).

Fig. 1

a Location of the investigation site (marked by read square; Backdrop: Google Maps); b View of the Psia Trawka glade

The first objective of the noninvasive geophysical surveys was imaging the morphology of bedrock roof under the drift (glacial and postglacial) sediments. The second objective was determination of thickness of deposits and analysis of their composition.

For this purposes, seismic and geoelectrical survey methods are most commonly used (Magiera et al. 2019; Żogała et al. 2010; Ohioma et al. 2017). In this case, the geophysical measurements were taken with the application of two methods, i.e., Ground Penetrating Radar (GPR) method and seismic one. Due to its high resolution and unfortunately low-depth penetration, GPR method was applied for examination of the drift sediments. Seismic method, which characterizes itself by lower resolution but higher penetration depth, was applied for imaging of boundary between bedrock and drift. Proposed methods were chosen on the basis of former experience of authors gained during application of different geophysical methods in mountainous conditions (Tomecka-Suchon and Golebiowski 2010, 2011; Sobotka and Farbisz-Michałek 2016; Tomecka-Suchoń et al. 2017; Baumgart-Kotarba et al. 2003, 2008).

Geology and geomorphology

Psia Trawka glade actually is a small remnant of a clearing of c.a. 200 m long and 80 m wide, located on a flat floor of the Sucha Woda Valley, in the area where smaller Panszczyca Valley joins. The Sucha Woda Valley is one of the general Tatra Valleys that cut N slopes of the mountains from the main ridge to their northern margin. The two valleys are not only the landforms that actually considerably shape this fragment of the Tatras, but they played important role in its preglacial and glacial history. Therefore, actual image of the glacial and fluvioglacial sediments and landforms in that area is quite impressive and are considered as one of the most interesting in the Polish Tatras (Fig. 2a).

Fig. 2

Geology of the study area (marked by red rectangle): a (left)—drift, b (right)—solid. Fragments of the Detailed Geological Map of the Tatra Mts. 1:10,000 (Piotrowska 2007). Explanations in the text

It is obvious that history of both valleys begins well before Pleistocene and is controlled to a large extent by lithology and tectonics of the solid bedrock (Klimaszewski 1960; Zasadni and Klapyta 2016). The glade is located within the Križne (Fatric) nappe (Subtatric nappes group). Silty shales and limestones of the Gresten Formation (Kopieniec layers, Lower Jurassic) form vast NNW–SSE trending zone of rather moderately differentiated geomorphology of the high mountains forehills (Fig. 2b—formation described with abbreviation: lmcwF1Jh). Relatively, soft shales allowed for development of valleys, while more resistant limestones built hills. The valley floors in the study area are at the height of c.a. 1170–1190 m a.s.l, while surrounding hills peak up to c.a. 1300 m a.s.l. It seems that general (inferred) fault that runs from the granite core in SSE to the Tatras margin in NNE could have considerable controlled development of the Sucha Woda Valley (Fig. 2b). Middle Triassic Dolomites (abbreviation: dolF2Ta) occur further NW and SW of the study area.

Actually Psia Trawka glade and its vicinity represent typical postglacial geomorphology (Baumgart-Kotarba and Kotarba 2001). The end moraines of the Tatras last glaciations (Wűrm; Fig. 1a—abbreviation: ^g_głruQ^kw_p3) form “classical” lobes with terminal depressions and small dead-ice lakes or their remnants (abbreviation: _tnQ_h). Fluvioglacial terraces and fans (abbreviation: ^fg_głżpQ^tIII_p4) occur in lower parts of the valley slopes. Valley floors are narrow and are covered with postglacial alluvium (abbreviation: ^f_głżpQ^t2_h). The glade itself is located on a fragment of narrow fluvioglacial terrace, formed of boulders, gravels, sands and silts.

Thickness of the soft sediments in the study area is unknown. Solid bedrock does not show on the surface in the valley. It can be expected; however, that it can be considerable big, up to tens of meters or even more than 100 m, as it is located within a zone of a past confluence of two large and active glaciers.

Theoretical background of geophysical surveys

Theoretical background of GPR method

The GPR method uses many different measurement techniques, and because the studies conducted in the Psia Trawka glade were of a reconnaissance nature, therefore the standard measurement technique was applied, that is the short-offset reflection profiling (SORP) technique. In the SORP surveys, the transmitter (Tx) and receiver (Rx) antennae move along the profile with constant and short offset (Fig. 3a), where the transmitter antenna emits electromagnetic signals at every specified distance interval (Δx). The signal propagates in the form of an electromagnetic (em) wave within the geological formation, reflecting from underground objects (e.g., from rock debris located in postglacial deposit) and geological boundaries (Fig. 3a). The reflected waves are recorded by the receiver antenna and displayed on the computer screen during the measurement in the form of a radargram. The horizontal axis on the radargram is recorded on the length scale, whereas the vertical axis is recorded on the time scale; during the processing of measurement data, the time axis is converted into the depth axis, taking into consideration the information on the velocity of the em wave within the studied formation.

Fig. 3

a SORP surveys; b WARR profiling technique

For evaluation of em velocity, WARR (wide-angle reflection and refraction) profiling was carried out (Fig. 3b); in this technique, transmitter antenna (Tx) is put at defined position and receiver antenna (Rx) moves along profile and records different waves (Fig. 3b). During WARR surveys, a hodograph is recorded and adequate analysis of recorded waves allows to determine velocities of several waves in the examined formation.

The em wave propagation is dependent on the electromagnetic properties, i.e., the relative electrical permittivity ε_r [−] and the electrical conductivity σ [mS/m] of the geological formation (Table 1). The contrast of values ε_r between rock debris (made mainly of limestone) and the surrounding postglacial deposits (i.e., mixture of gravel, sand and clay) decides upon the value of the reflection coefficient R [−], according to the formula (1), and in consequence upon the amplitude of the reflections recorded on the radargram. The value of the relative electrical permittivity determines also the velocity of em wave, according to the simplified formula (2).

Table 1 Electromagnetic and elastic properties of examined geological media (Annan 2001; Wu and Liu 2012)

Taking into account information presented in Table 1, module of reflection coefficient R between rock debris and postglacial deposits is as follows: (a) |R| = 0.05 (for dry deposits) and (b) |R| = 0.44 (for water-saturated deposits); only in situation when postglacial deposits are in wet condition or are fully water saturated, the value of R is sufficient for recognizing of accumulations of rock debris and detection of limestone boulders.

The value of the electrical conductivity σ decides upon the attenuation α [dB/m] of the em wave, according to the simplified formula (3). In GPR method, there is assumed that conductivity of examined medium greater than 10 mS/m makes it impossible to record a readable radargram. Taking into account this assumption and information presented Table 1, it might be expected that interpretation of radargrams will be possible only when examined deposits are in dry or wet condition.

$$R = \frac{{\sqrt {\varepsilon_{{{\text{r}}_{\text{deposits}} }} } - \sqrt {\varepsilon_{{{\text{r}}_{\text{limestone}} }} } }}{{\sqrt {\varepsilon_{{{\text{r}}_{\text{deposits}} }} } + \sqrt {\varepsilon_{{{\text{r}}_{\text{limestone}} }} } }}$$

(1)

$$v = \frac{30}{{\sqrt {\varepsilon_{\text{r}} } }}$$

(2)

$$\alpha \approx \frac{2\sigma }{{\sqrt {\varepsilon_{\text{r}} } }} \left[ {10^{3} {\text{dB/m}}} \right]$$

(3)

GPR method due to its versatility founds its usefulness for agriculture, building and road engineering, mining, environmental protection, criminology, glaciology, sedimentology, archaeology, etc. (Annan 2001; Akinsunmade et al. 2019; Gołębiowski et al. 2019; Marcak et al. 2005, 2018; Tomecka-Suchoń 2012; Tomecka-Suchoń and Marcak 2015).

Theoretical background of seismic method

Seismic refraction maps the contrasts of seismic velocities—the velocities of seismic wave propagation through soil, deeper layers and bedrock. Velocity usually well correlates with rock hardness and density, which in turn tends to correlate with changes in lithology, degree of fracturing, water content and weathering (Dec 2004; Jarzyna  et al. 2012; Harba and Pilecki 2017; Pilecki et al. 2017). That is why very often in seismic investigations of bedrock quality, this morphology and quaternary cover thickness, the seismic refraction surveys are applied.

There are two basic approaches to the analysis of refraction data: classic, based on layered model and newer one—tomographic imaging of the geological model.

It is not always the case that in the near-surface seismic velocities divide this zone into high-contrast discrete layers and velocities inside layers are constant horizontally. In this case, if clear layering is not apparent in the raw data, the tomographic approach is generally more appropriate.

In classic interpretation for layer-cake model often the generalized reciprocal method (GRM) can be used (Fig. 4), especially in the case of large and rapid changes of the refractor morphology (Palmer 1981). In GRM method, two functions are defined:

Fig. 4

Refraction ray paths along seismic profile on the AB distance (by Lankston 1986). A, B—shot points, X, Y—receiver points, G-point of depth and velocity determining, h_G—depth, i_c—critical angle, v₁, v₂—P wave velocities

$$T_{\text{G}} = \frac{{T_{AY} + T_{BX} - T_{AB} - (XY/V)}}{2}$$

(4)

$$T_{\text{V}} = \frac{{T_{AY} - T_{BX} + T_{AB} }}{2}$$

(5)

where, T_G—time–depth function and T_V—velocity analysis function.

For a pair of points (X, Y), both functions are calculated. Values of these functions are related to point G. The TV curves are calculated as a function of offset AG for a variety of XY distances. The optimal XY is when TV curve is the smoothest. Refractor velocity V is the reciprocal of the slope of TV curve. In this way, for different G points we can determine velocity value along the profile. Similarly, TG function is calculated (for optimal XY, TG curve is the roughest). Next, the average velocity from surface to refractor is determined. Using TG values and the average velocity, the depth is calculated.

Refraction tomography has been used since the 1980s. A general overview was provided by White (1989). The different inversion methods and resolution analysis were discussed by Zhang et al. (1998), and practical aspects of tomography are included in paper Lanz et al. (1998). Tomographic method was based on the iteration solution. In this method, a velocity model is created for which we get the best fit of the theoretical and the measured times. In each iteration for current model, velocity values are corrected, and ray tracing is made for new model. The first breaks are computed. Iterations stop when differences between calculated and measured first breaks reach minimum.

Project of terrain measurements

In the investigation site, two GPR profiles (namely, G-1 and G-2) were designed for two-dimensional, SORP, 50-MHz surveys (Fig. 5a). In the central part of the Psia Trawka glade, 12 parallel GPR profiles were designed for 3D, SORP, 100-MHz surveys (Fig. 5b). In the beginning and ending parts of profile G-1 and in the ending part of profile G-2, WARR surveys were carried out with the use of 50-MHz and 100-MHz antennae.

Fig. 5

a Profiles designed for 2D seismic and GPR surveys with the use of 50-MHz antennae. b Parallel profiles designed for 3D GPR surveys with the use of 100 MHz antennae

GPR measurements were taken with the ProEx georadar system of the Swedish company MALA GeoScience. Terrain surveys were performed with the use of antennae with the frequency of 50 MHz and 100 MHz, the parameters of which are presented in Table 2. During the field measurements, the following distance intervals between traces were assumed: Δx = 0.2 m (for 50 MHz) and Δx = 0.1 m (for 100 MHz).

Table 2 Main parameters of the MALA GeoScience antennae (Mala 2003)

Also, in place of investigations the seismic refraction measurements were taken. The refraction profile S-1 was located along Sucha Woda Valley (Fig. 5a). During field works was used 48 channels seismometer Terraloc Mk-6 of the Swedish company ABEM and as receivers the high-frequency geophones L–40a 100 Hz (Mark Products, USA) were applied. Profile length was 235 m and geophones distance 5 m. Along the profile refraction sounding was performed (Fig. 6).

Fig. 6

Scheme of seismic measurement line

Shot point interval equals c.a. 30 m and shots were located in points at coordinates: − 40, 0, 30, 60, 90, 120, 150, 180, 210, 235 and 275 m along profile.

Owing to specific environment protection conditions in the Tatra National Park, the location of seismic soundings according to the method requirements was impossible, and thus, the limitations imposed made the task even more difficult. Due to the above constrains, the seismic sources may not be located off-roads and off-tourists trails (Baumgart-Kotarba et al. 2008). In this case, as a source was applied weight drops 250 kg (ESS 500, GISCO USA—Fig. 7). This is the environmental-friendly very mobile source, which is characterized by a high repeatability of sourcing signal. If the terrain surface is loose, source signal is weak, and a noise level is high, this device allows to improve data quality by vertical stacking.

Fig. 7

Seismic source ESS 500 (GISCO)

The shot conditions were variable along the profile. Stones and boulders made it difficult to locate the source and to obtain correct plate—ground contact. Additionally, with the use of 100 Hz geophones, much high-frequency noise can be registered, especially when the conditions for a shot are poor (mud, uneven surface, etc.). To overcome this problem, vertical stacking was performed. Five or more stacks were sufficient to obtain low-noise field recording. In Fig. 8, example of seismic record at shot position 0 m was shown.

Fig. 8

Seismic record for shot 0 m. Red dots—first breaks

Results of geophysical surveys

Seismic interpretation

In interpretation with the application of GRM method, the off-end records were used. As a result of the interpretation, the depth and velocity model were obtained. Interpreted model is a three-layer model (Fig. 9). Estimated P wave velocity in the first layer is about 930 m/s and horizontal changes of this values are small. It is a typical value for loose quaternary deposits. The thickness of this layer changes in the range 10–15 m. The second layer (postglacial material) is a mixture of boulders, sand and clay. Estimated P wave velocity in this layer is about 2100 m/s. The third layer, basement, is a high-velocity layer—the velocity value is 3750 m/s and this value is related to hard limestone.

Fig. 9

Result of interpretation (GRM)—depth section

In interpretation with the application of refraction tomography, all shot records were used. The model with the velocity gradient was adopted as the starting model. Gradient value equals 50 m/s/m and in the first iteration, depth of the second refractor was stabilized. Generally, in final solution (Fig. 10) horizontal changes of velocity inside layers (L1 and L2) are small. In the vertical direction, the velocity increases. This indicates that the degree of quaternary material compaction increases with depth.

Fig. 10

Final tomographic solution—depth section. L1—noncompacted postglacial deposits, L2—postglacial deposits (thickly clastic, compacted), L3—limestone, solid lines—GRM results

In the basement (limestone), we observe the horizontal changes of velocity. Directly below the refractor, the velocity value is smaller than for the GRM solution. Maybe the top of the bedrock is some meters deeper than determined from the GRM method, or upper part of the limestone is fractured. Deeper, velocity value corresponds to the value obtained in the GRM method (3750 m/s). Visible in some places in the third layer, increase in the velocity value (up to 4300 m/s) can be related to more compacted, hard rock.

GPR interpretation

At the first stage of GPR surveys, WARR measurements were taken (Fig. 11) in order to determine velocity of em wave for proper time–depth conversion of radargrams. In Fig. 11a, example hodograph with all em waves (described in Fig. 3b) was shown. Unfortunately, in the investigation site only three types of em waves were recorded, i.e., Direct Air Wave (DAW), Direct Ground Wave (DGW) and Reflected Wave (RW)—Figs. 11b–f.

Fig. 11

a Example hodograph (Bohidar and Hermance 2002); WARR recorded with the use of 50-MHz antennae in the ending part of profile G-1 (b) and profile G-2 (c); WARR recorded with the use of 100-MHz antennae in the beginning part of profile G-1 (d), in the ending part of profile G-1 (e) and in the ending part of profile G-2 (f)

Adequate analysis of velocities of em waves was carried out on the basis of recorded hodographs (Figs. 11b–f) allowed to estimate the velocities in the shallow part of the postglacial deposits; the velocities of the DGW changed from 0.093 to 0.098 m/ns, so the mean value equals 0.096 m/ns. From the formula (2), the relative electrical permittivity in near-surface zone equals c.a. 9.7 which depicts that it is slightly wet formation. In deeper part of the postglacial deposits, velocity of the RW changed from 0.083 to 0.09 m/ns, so mean value equals 0.086 m/ns. Using the formula (2), we have estimated the value of ε_r as equals c.a. 12 which depicted that it is wet formation. As it was discussed in the section “Theoretical Background of GPR Method” in wet postglacial deposits, attenuation of em wave α is low and sufficient value of reflection coefficient R appears between deposits and rock debris (or limestone boulders), so SORP surveys should deliver the satisfied results. For time–depth conversion of radargrams, mean constant velocity which equals 0.09 m/ns was assumed.

The radargrams presented in the paper were subjected to standard digital signal processing in the ReflexW software of the German company SandmeierGeo. Radargrams were presented either in the form of the distribution of the amplitudes of reflections (Fig. 12) or in the form of the distribution of envelops (Figs. 13 and 14), calculated on the basis of the Hilbert transform. Amplitudes and envelopes were normalized to the max. amplitude of the DAW. The detailed description of the applied processing procedures can be found, among others, in the works of Annan (1999), ReflexW (2016).

Fig. 12

Results of GPR surveys (50-MHz antennae) along profiles G-1 (a) and G-2 (b)

Fig. 13

Results of 3D GPR surveys (100-MHz antennae) along profiles from GPR-1 to GPR-8

Fig. 14

Results of 3D GPR surveys (100-MHz antennae) along profiles from GPR-8 to GPR-10 (a) and from GPR-10 to GPR-12 (b)

In Fig. 12 radargrams recorded along profiles G-1 and G-2 with the use of 50-MHz antennae were shown. In Fig. 12, positions of WARR profiles and the beginning of profile G-2 were inserted. In Fig. 12a, high-amplitude reflections were recorded over the seismic boundary (Fig. 10) to the depths c.a. 10÷15 m; as it was mentioned before, resolution of 50-MHz antenna is c.a. 0.5 m, so several, stochastically distributed reflections depict to the small limestone boulders; connected, linear reflections originate rather from accumulation of rock debris or gravel. Several high-amplitude reflections below the seismic boundary originate from fractures in the bedrock.

In Fig. 12b similar anomalies (i.e., high-amplitude reflections) to those presented in Fig. 12a may be distinguished. Accumulation of rock debris and gravel occurs in the near-surface zone, and roof of this formation is located at depths c.a. 2÷3 m. Small limestone boulders are located at greater depths in the postglacial deposits between distances along profile from 10 to 30 m as well as in the ending part of the profile G-2. There is no possibility to depict the boundary between deposits and bedrock neither in Fig. 12a nor in Fig. 12b; it was perhaps caused by scattering attenuation of em wave in postglacial deposits and may be insufficient contrast of values of ε_r between deposits and fractured bedrock (where fractures were colmatated by deposits) occurred.

The results of three-dimensional GPR surveys with the use of 100-MHz antennae are presented in Figs. 13 and 14. Spatial distribution of envelops in relatively small area (i.e., central part of the Psia Trawka glade) delivered information that rock debris and accumulations of gravel in the examined area are distributed very heterogeneously.

For instance, we observe a large amount of rock debris and/or gravel between positions y = 22 m and y = 38 m (Fig. 14a) and few meters from this anomaly, i.e., between y = 10 m and y = 22 m, a thickness of accumulation zone is reduced twice (Fig. 14a). Similar situations are observed in Figs. 14c and 15a where reduction in accumulation of rock debris and/or gravel is even triple. On the contrary, in Figs. 13b and 14b accumulation of rock debris and/or gravel has more less the same thickness equals c.a. 10 m.

Fig. 15

Reconstruction of possible orientation of a subglacial trough in the area of the Psia Trawka glade. Backdrop: Google Maps

Geological interpretation

Strong contrast of the reflected wave velocity clearly visible in the seismic model (Figs. 9 and 10) points to a depression existing in the subglacial morphology. The depth of the depression is up to c.a. 40 m below the present-day terrain surface and c.a. 25 m below surrounding subglacial surface. The depression is c.a. 150 m wide. Single seismic profile does not allow us to interpret 3D shape of the depression; however, it seems very likely that the depression visible in the seismic model is a section of a trough of unknown orientation. Next, again, it is very likely that the trough is related to general trend (N–S) of the actual and glacial morphology. Its considerable depth and steep slopes show that its origin can be related to erosion of subglacial water during the decay of the last (Würm) glaciation in the area. However, it is apparent that the trough is not parallel to the present-day valley axis, as its seismic profile oriented N–S has concave shape (Figs. 9 and 10). Its course must be oblique to the valley, therefore. Further on, it is more likely that its course is rather parallel to the axis of the Panszczyca Valley, i.e., runs SE–NW than transverse to it. Thus, the reconstruction of the course of the trough (Fig. 15) does not seem only an unjustified speculation. The trough can be a result of erosion of subglacial streams of the Panszczyca Valley (or meandering Sucha Woda Valley).

General scarcity of the data on the thickness of glacial, fluvioglacial and postglacial sediments in the Tatras makes the result of the present study an important contribution to the study in this field. It gives an insight into general proportions of the present-day geomorphology, subglacial morphology and thickness of the drift (Fig. 16) in the area of particularly well-pronounced glacial morphology in the Tatras.

Fig. 16

Morphologic section across the Sucha Woda Valley (Psia Trawka glade). Hypothetical subglacial through is marked

Conclusions

The research carried out contributes much to the knowledge resources about the considered area, whose geological structure has so far been interpreted only on the basis of geological exposures.

Taking into account the very difficult acquisition conditions associated with large denivelation of the area, dense foliage, occurrence of rocky soil and very difficult accessibility of the area, it should be noted that the applied geophysical methods have provided the satisfactory results in the diagnosis of the geological structure and physical features of rocks occurring in the area of the Psia Trawka glade in the Sucha Woda Valley.

The seismic method allowed the separation of three layers with different elastic properties, which were interpreted as noncompacted postglacial deposit, compacted postglacial deposit and limestone.

The GPR method supported by the analysis of signal attributes allows to determine the distribution of loosening to a depth of about 20 m.

Present study gives an insight into general proportions of the actual geomorphology, subglacial morphology and thickness of the drift (quaternary sediments) in the area of, on the one hand, particularly well-pronounced glacial morphology in the Tatras and, on the other hand, of general scarcity of the data in this field.