Abstract
We present SUSPECT, an open source toolkit that symbolically analyzes mixed-integer nonlinear optimization problems formulated using the Python algebraic modeling library Pyomo. We present the data structures and algorithms used to implement SUSPECT. SUSPECT works on a directed acyclic graph representation of the optimization problem to perform: bounds tightening, bound propagation, monotonicity detection, and convexity detection. We show how the tree-walking rules in SUSPECT balance the need for lightweight computation with effective special structure detection. SUSPECT can be used as a standalone tool or as a Python library to be integrated in other tools or solvers. We highlight the easy extensibility of SUSPECT with several recent convexity detection tricks from the literature. We also report experimental results on the MINLPLib 2 dataset.
Similar content being viewed by others
1 Introduction
Mixed-integer nonlinear optimization problems (MINLP) arise in many engineering applications [5, 8, 25, 26]. Existing solvers that globally optimize MINLP include: ANTIGONE [38, 40], Baron [49], Couenne [6, 34], LINDOGlobal [19], Minotaur [35],and SCIP [54]. The special structure of an optimization problem may expedite its solution, e.g. convexity may be exploited to generate polyhedral cutting planes [41, 49] or only relax the nonconvexities [1, 46]. MINLP have the form [15]:
Simplifying, we write \(f_m({\varvec{x}}): \mathbb {S}^N \mapsto \mathbb {R}\) instead of \(f_m({\varvec{y}}, {\varvec{w}}, {\varvec{z}})\) and denote \(\mathbb {S}\) as the domain of \({\varvec{x}}\). Table 1 contains this manuscript’s notation.
Contributions This paper presents data structures and algorithms used to implement SUSPECT. The primary contribution of SUSPECT is its easy extensibility to detect the convexity of complex expressions. Custom MINLP solvers can leverage SUSPECT during preprocessing to make informed decisions about how to best customize the solution process. For example, a solver could use SUSPECT to identify which problem variables appear in nonconvex expressions, thereby reducing the space over which it must apply spatial branch and bound. SUSPECT’s extensibility allows domain experts to add new convexity detectors, thereby expanding the range of expressions that SUSPECT can correctly classify. Finally, SUSPECT may also be used to provide special structure detection and bounds tightening when developing new global optimization tools. This paper is published alongside the source code [10], licensed under the Apache License, version 2. All global solvers have some convexity detection facilities, but SUSPECT is the first open source code to explicitly detect convexity as a stand-alone utility.
The rest of the paper is organized as follows. Section 2 introduces convexity detection, the Python library Pyomo and data structures to represent nonlinear optimization problems. Bound tightening and propagation algorithms are described in Sect. 3, while Sect. 4 gives an overview of the monotonicity and convexity propagation rules used in SUSPECT. In Sect. 5 we describe the data structures and algorithms implemented in SUSPECT and in Sect. 6 we introduce the plugin-based architecture used to extend SUSPECT. The test suite and results are presented in Sect. 7. We conclude in Sect. 8.
2 Background
Different methods exist for proving or disproving convexity of an expression (or an optimization problem). Tree-walking approaches [17, 18] are suited for preprocessing given their low computational complexity. More computationally expensive methods (i) use automatic differentiation techniques to compute the interval Hessian [42, 44], (ii) reduce convexity questions to real quantifier elimination problems [45], or (iii) sample to verify convexity [12]. Some solvers, e.g. CVX [22, 23], CVXPY [14] and Convex.jl [51], impose a set of conventions when constructing problems and thereby obtain a convex optimization problem [24].
The bound tightening techniques described in this paper are similar to those used in interval arithmetic and constraint programming [37, 47]. Other bound tightening techniques use pair of inequalities [3], tightening with a linear optimization problem (LP) [4], or solving two LPs for each variable [20].
2.1 Pyomo expression trees
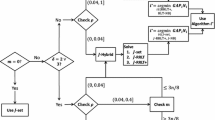
SUSPECT works with optimization models formulated using Pyomo [27, 28], a Python-based Algebraic Modeling Language (AML). Pyomo supports most features common to AMLs, e.g. (i) separating the model definition from the instance data and solution method, (ii) supporting linear and nonlinear expressions, and (iii) structuring modeling using indexing sets and multi-dimensional variables, parameters, and constraints. Pyomo focuses on an open, extensible object model. As with most AMLs, Fig. 1 shows that Pyomo represents objectives and constraints using expression trees,Footnote 1 with internal nodes representing operators and leaf nodes representing operands. Operands may be variable objects, literal constants (integer or floating point numbers, or strings), or placeholders for literal constants (“mutable parameters”). Internal nodes come in three fundamental categories: Unary operators (negation, absolute value, and trigonometric functions), binary operators (subtraction, multiplication, division, exponentiation, and comparison), and n-ary operators (addition, linear expressions).
2.2 Directed acyclic graphs
SUSPECT represents problems using a Directed Acyclic Graph (DAG) to group common subexpressions in a single node [47, 55]. Variables and constants in the problem are sources, while the functions \(f_0\) and \(f_m\), \(m \in \{1, \dots , M\}\) are sinks. SUSPECT represents an MINLP instance as a DAG G, \(G = (V, E)\), where V is the set of vertices and E the set of directed edges \(E \subseteq V \times V\). Each vertex v represents an operation \(\otimes _v\), the children of v are its operands, while the parents of v are the expressions of which v is an operand. More formally, define the children of v as \(c(v) = \{w \in V : (w, v) \in E\}\) and the parents of v as \(p(v) = \{w \in V : (v, w) \in E\}\). Note that sources have \(c(v) = \emptyset \) since they don’t have any operand, and sinks have \(p(v) = \emptyset \) since they are top level operations. The vertex vdepth is:
The SUSPECT instance graph G is similar to combining all Pyomo expression trees for that instance except that Pyomo explicitly avoids shared subexpressions and restricts each operator vertex to have at most one parent. Therefore, any two Pyomo expressions share no common internal nodes. In contrast, SUSPECT actively identifies and combines common vertices across expressions [54]. Figure 2 represents Optimization Problem (1) and shows the DAG vertices grouped by depth d(v).
Pictorial representation of Optimization Problem (1), with vertices grouped by depth d(v)
3 Bound tightening and propagation
Feasibility-based bounds tightening propagates bounds from sources to sinks and from sinks to sources. To propagate bounds from sources to sinks, SUSPECT computes the new bounds \(B'_v\) of each node v with existing bound \(B_v\) and bounds on its children nodes \(B_u\) as:
For each operator \(\otimes _v\), SUSPECT computes the bound using the interval arithmetic rules in Appendix A [32, 43]. For functions \(g({\varvec{x}})\), \({\varvec{x}} \in X\), \(X \subseteq {{\,\mathrm{\mathbf {dom}}\,}}g\), the expression bound \(g({\varvec{x}})\) is the image of \(g(X) := \{ g({\varvec{x}}) | {\varvec{x}} \in X\}\). If \(X \nsubseteq {{\,\mathrm{\mathbf {dom}}\,}}g\) for some DAG vertex, SUSPECT throws an exception. In normal operation, SUSPECT has \(X \subseteq {{\,\mathrm{\mathbf {dom}}\,}}g\), but this feature helps researchers extend SUSPECT.
Example 1
Consider the function \(g(x_1) := \sqrt{x_1}\), SUSPECT will compute the bound of g as [0, 2] if \(x_1 \in [0, 4]\), but will throw an exception for \(x_1 \in [-1, 1]\).
The reverse step of feasibility-based bound tightening propagates bounds from sinks to sources. A DAG vertex v with unary function \(\otimes _v\) and bound \(B_v\) implies a child u with bound \(B_u\) that is equal to or tighter than \(\otimes _v^{-1}(B_v)\), where \(\otimes _v^{-1}\) is the inverse of the function \(\otimes _v\) if it exists, otherwise it is a function that maps all arguments to \([-\infty , \infty ]\). The absolute value and square functions are the only exceptions in the current implementation: they are not invertible, but we update the bound of \(B_u\) using \(\otimes _v^{-1}(B_v) = B_v \cup (-B_v)\) and \(\otimes _v^{-1}(B_v) = \sqrt{B_v} \cup \left( - \sqrt{B_v} \right) \), respectively. Equation (2) gives the bound tightening step SUSPECT performs for each vertex v that represents an unary function:
Example 2
Consider the function \(k(x_1) := \sqrt{x_1}\), with \(k(x_1) \in [0, 2]\), then the bound of \(x_1\) will be [0, 4]. If the expression is \(k(x_1) := |x_1|\), with \(k(x_1) \in [1, 2]\), then \(x_1 \in [-2, 2]\). SUSPECT does not support disjoint intervals because their support is uncommon in most solvers, so the bound is not \([-2, -1] \cup [1, 2]\).
Appendix B shows that SUSPECT also tightens the bounds of the children of linear expressions, but not of other non-unary functions, e.g. product and division.
4 Special structure detection
SUSPECT detects monotonicity and convexity recursively. The rules assume an expression has only unary or binary vertices, but SUSPECT deduces properties of n-ary vertices \(k = g_0 \circ g_1 \circ \cdots \circ g_l\) by applying the rules as \((((g_0 \circ g_1) \circ g_2) \circ \cdots \circ g_l)\), where \(g_i: Z \rightarrow Y\), \(Z \subseteq \mathbb {R}^l\), \(Y \subseteq \mathbb {R}\). This section introduces rules computing the monotonicity and convexity properties of the composition \(k = g \circ h: X \rightarrow Y\) of the functions \(g: Z \rightarrow Y\) and \(h: X \rightarrow Z\), where \(X \subseteq \mathbb {R}^n\), \(Y \subseteq \mathbb {R}\), \(Z \subseteq \mathbb {R}^l\), and \({{\,\mathrm{\mathbf {dom}}\,}}{k} = \{{\varvec{x}} \in {{\,\mathrm{\mathbf {dom}}\,}}h | h({\varvec{x}}) \in {{\,\mathrm{\mathbf {dom}}\,}}{g} \}\) [9]. A function \(k({\varvec{x}})\) is nondecreasing (nonincreasing) if its gradient \(\nabla k({\varvec{x}}) \ge 0\) (\(\nabla k({\varvec{x}}) \le 0\)) \(\forall \, {\varvec{x}} \in X\). Applying the chain rule and computing the gradient of k, the monotonicity of k depends on the signs of \(\nabla g(h({\varvec{x}}))\) and \(\nabla h({\varvec{x}})\):
A function \(k({\varvec{x}})\) is convex (concave) if its Hessian \(\nabla ^2 k({\varvec{x}}) \ge 0\) (\(\nabla ^2 k({\varvec{x}}) \le 0\)) for all \({\varvec{x}} \in X\):
If any of g or h are not differentiable, then the monotonicity and convexity of k are considered unknown. SUSPECT has special routines for the absolute value function: if the domain of |x| specifies \(x \ge 0\) (\(x \le 0\)) then we compute first and second derivatives as if \(|x| = x\) (\(|x| = -x\)). We assume nothing if \(x = 0\) is in the interior of the domain. For a more detailed list of monotonicity and convexity rules refer to Appendix C of the supplementary material.
5 Implementation details
SUSPECT is implemented in Python and is compatible with Python version 3.5 and later. The source code is freely available on GitHub.Footnote 2 SUSPECT can be used as a standalone command line application or included in other applications as a library.
5.1 Data structures
SUSPECT implements a problem DAG by storing all vertices in a list, sorted by ascending depth. This sorting ensures that if SUSPECT traverses the list forward (backward), it visits a vertex after having visited all its children (parents). Each vertex stores a reference to its children and parents. Other approaches to representing the DAG are possible, e.g. using adjacency lists [13]. The SUSPECT class hierarchy for vertices, which is diagrammed in Fig. 3, is similar to Pyomo, but SUSPECT has a class for each available unary function because we often need to dispatch based on a vertex type. Having a type for each unary function enables leveraging the same functions used by the other vertex types. Figure 4 represents Optimization Problem (1): the DAG also contains dictionaries to map variables, constraints, and objectives names to their respective vertex.
SUSPECT expression hierarchy. Different from the Pyomo classes shown in Fig. 1, each unary function has its own class, and constraints and objectives are a special type of expression
5.2 Converting Pyomo models to SUSPECT
SUSPECT represents an optimization problem as a DAG, but Pyomo represents problems using separate expression trees for each constraint and objective. SUSPECT uses a hashmap-like data structure to correctly map a Pyomo expression to an existing SUSPECT expression if present, or otherwise create a new expression. The heuristic approach of hashing Pyomo expressions may not converge to the DAG with the fewest vertices, but it should obtain an acceptable DAG. The DAG structure depends on the model building style since no simplifications are performed.
Implementation of the DAG for Optimization Problem (1). The DAG is a list of vertices sorted by \(d(\textit{v})\), together with dictionaries to map variables, constraints, and objectives names to the relative object
The hash function needs: (i) to compute the same value for equivalent expressions but different values for different expressions, and (ii) to limit collisions with a uniform distribution. Computing the hash is recursive: SUSPECT starts from the expression tree leaves and moves to the root. The hash of a variable is its ID. SUSPECT implements two possible strategies for the hash of a constant coefficient:
Each unique number gets an increasing ID [SUSPECT default] This is best when there are few distinct floating point numbers, e.g. many coefficients are 1. SUSPECT stores floating point numbers in a binary tree with their associated ID.
Rounded number is the hash value This is best when there are many unique floating point numbers.
Hashes of non-leaf nodes combine the hashes of their children expressions, together with the node. Equation (3) shows how the hash function of a vertex v is computed [30], where h is the hash function and \(c_0, \dots , c_n\) are the children of the vertex v.
Figure 5 represents the expression hash map. SUSPECT inserts an expression by hashing the expression into a bucket index and then iterating through the bucket to check for the expression, otherwise SUSPECT appends it to the list. The Python built-in hash map manages the buckets. For lookups, SUSPECT hashes the expression for the bucket and then searches linearly through the bucket. This method matches some equivalent expressions, e.g. reordering a summation \(x_0 + x_1\) to \(x_1 + x_0\). Since SUSPECT represents linear expressions as a summation of variables with the associated coefficients, the expressions \(x_0 + x_1\) and \(x_0 + x_2 + x_3\) would be represented by different linear expression vertices. SUSPECT could be improved by matching polynomials, e.g. \((x - 2)^2 = \left( x^2 - 4x + 4 \right) \).
ExpressionDict implementation. Floating point coefficients make building a dictionary of expressions and values (in this case Bound objects) challenging. SUSPECT uses a hash function that ignores coefficients to insert similar expressions in the same bucket, then compares each expression for equality
SUSPECT builds the DAG by: (i) associating Pyomo expressions to SUSPECT expressions, (ii) adding all problem variables, and (iii) visiting all Pyomo constraint and objective trees. For each Pyomo tree, SUSPECT walks from the leaves (variables and constants) to the root (functions) and modifies the DAG when it finds new subexpressions. This process terminates with a DAG equivalent to the Pyomo model.
5.3 Tree-walking rules: forward and backward visitors
The rules detecting monotonicity and convexity are naturally expressed recursively. The SUSPECT implementation avoids recursion because it can lead to stack overflows. To overcome this challenge, we devise a strategy to compute recursive rules without recursion. A node’s vertex depth is greater than the depth of its children, so visiting nodes in ascending order: (i) visits a node after visiting its children and (ii) visits a node at most once. The problem DAG methods that visit vertices take two parameters: a visitor object (a subclass of ForwardVisitor or BackwardVisitor) and a context. The visitor is called on a node while the context shares information between visitors. SUSPECT uses this context to store information, e.g. bounds, polynomiality, monotonicity, and convexity.
The visitor classes implement the register_handlers and handle_result methods. The first method returns a dictionary associating expression types to a callback. SUSPECT calls the second after each vertex visit to update special structure information. The callbacks registered in the visitor are called with two parameters: the current expression and the context object. Callbacks can use the context to lookup information about other vertices, e.g. children in forward mode and parents in backward mode. To reduce computation time in forward (backward) mode, SUSPECT only visits nodes if any of its children (parents) changed in the previous iteration. To use this feature, implementations return a Boolean from the handle_result method to indicate if the vertex value was updated or not. If the vertex value changes, then SUSPECT adds the node parents (children) to the list of nodes to visit.
5.4 Bound tightening and propagation
DAGs are commonly used for bound propagation and tightening [47, 55]. SUSPECT implements the bound propagation rules defined in Sect. 3 using the Sect. 5.3 tree-walking rules. Since convergence time of the bound tightening step can be infinite [31], SUSPECT incorporates a maximum iteration parameter (default 10).
Floating point operations are subject to rounding errors [21] that are propagated in bounds tightening. To mitigate errors, SUSPECT algorithms work with the generic Bound interface. SUSPECT provides an implementation of this interface using arbitrary precision arithmetic [36], but users can supply their own implementation, e.g. using interval arithmetic [7]. Appendix D discusses the Bound interface.
6 Extending SUSPECT
SUSPECT may be extended to include other convexity structures detectors. SUSPECT already incorporates convexity detection for four important convex expressions:
- 1.
Quadratic expression \(g({\varvec{x}}) = {\varvec{x}}^T Q {\varvec{x}}\) is convex if matrix Q is positive semidefinite and concave if Q is negative semidefinite.
- 2.
Second-Order Cone, i.e. the Euclidean norm \(||{\varvec{x}}||_2 := \sqrt{\sum _{x \in {\varvec{x}}} x^2}\) is convex [33].
- 3.
Perspective Functions with \(x_2 \ge 0\) and \(0 \le x_1 \le 1\) are defined:
$$\begin{aligned} g(x_1, x_2) := {\left\{ \begin{array}{ll} x_1 h(x_2 / x_1) &{} x_1 > 0, \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$If the function \(h({\varvec{x}})\) is convex (concave), then \(g({\varvec{x}})\) is convex (concave) [29, 48].
- 4.
Fractional Expressions where \(x, a_1, a_2, b_1, b_2 \in \mathbb {R}\) have the form:
$$\begin{aligned} g(x) := \frac{a_1 x + b_1}{a_2 x + b_2} \end{aligned}$$The second derivative \(g''(x)\) derives rules for concavity and convexity [40].
SUSPECT adopts a plugin-based architecture to enable third parties to extend its convexity detection capabilities without having to change SUSPECT itself. SUSPECT is distributed with the aforementioned convexity extensions. SUSPECT uses the numpy library, which provides Python wrappers around LAPACK dsyevd routines, to compute the Q matrix eigenvalues. Since dsyevd uses double precision floating point arithmetic, it may obtain incorrect results because of numerical issues. An alternative approach to determine whether Q is positive (negative) semidefinite is to perform two Cholesky decompositions with pivoting, this could also result in a more stable algorithm. As numpy does not currently implement Choelesky decomposition with pivoting, this method has not yet been implemented in SUSPECT.
Writing a new convexity detector requires the user to implement the detector as a class extending ConvexityDetector, and register it with SUSPECT. A convexity detector visitor is similar to the Sect. 5.3 visitors, but each callback returns a Convexity object. When SUSPECT visits a vertex and the built-in convexity detector is inconclusive, it will iterate over the registered detectors that can handle the expression and assign the convexity as the first conclusive result encountered.
SUSPECT uses Python’s setuptools entry points to handle extensions registration. Entry points are a mechanism for the SUSPECT package to advertise extension points in its source. SUSPECT looks for extensions registered under the suspect.convexity_detection and suspect.monotonicity_detection groups for convexity and monotonicity detectors. Users extending SUSPECT need to package their extensions using setuptools and provide a setup.py file.
Example 3
Optimizing heat exchanger network design uses the reciprocal of log mean temperature difference (\(\text {RecLMTD}^\beta \)) with the limits defined:
with variables \(x, y \in \mathbb {R}_{+}\), and constant parameter \(\beta \ge -1\). \(\text {RecLMTD}^\beta \) is concave if \(\beta = -1\), strictly concave if \(-1< \beta < 0\), linear if \(\beta = 0\), and convex if \(\beta > 0\) [41].
Listings 1–3 in Appendix E contain the detector source code. The register_handlers method returns a callback for the expression with PowerExpression as root (case \(x \ne y\)) and one for the expression with DivisionExpression as root (case \(x = y\)). Both callbacks check whether the expression they are given matches the subgraph representing the \(\text {RecLMTD}^\beta \) expression.
Listing 4 contains the setup.py source code necessary to register the new convexity detector with SUSPECT.
7 Numerical results
We consider the MINLPLib 2 dataset [53] which, when we accessed it on 13th December 2017, contained 1527 problems. We conducted the tests as a batch job on a cluster of Amazon AWS C5 instances. Each problem was assigned a single instance to run and each instance is equivalent to 2 cores of a 3.0 GHz Intel Xeon processor with 4 GB memory. To increase reproducibility, the SUSPECT command line tool was packaged as a Docker image running Python 3.5. The results shown in this manuscript were generated using the version of SUSPECT with Git tag v7, dated 18th of May 2018. Together with SUSPECT, we used Pyomo version 5.2. The problems are expected to be in the OSiL [16] format and we use the binary tree strategy for hashing floating point constants.
Figure 6 shows the time (in CPU seconds) needed to run the special feature detection algorithms. The horizontal line marks the percentage of instances SUSPECT can read and start processing. Recall that SUSPECT can manage the Fig. 4 functions. SUSPECT fails at reading 135 (9%) of the 1527 instances because of unsupported nonlinear functions, e.g. the error function, or because the problem size is too big and SUSPECT time outs after more than 5 min converting from Pyomo to SUSPECT. SUSPECT processes 1003 (72%) of the remaining 1392 instances instances in under 2 s. This low computational overhead is due to the strength of tree-walking algorithms. Using the MINLPLib structure information as an oracle and considering the 1392 instances SUSPECT processes, our results matched the expected results in 1275 cases (91.6%). In 35 cases (2%), SUSPECT times out or encounters an exception while performing special structure detection. Table 15 of Appendix F lists the instances where SUSPECT did not detect the convexity properties.
SUSPECT does not have false positives on the test set, this gives confidence in the implementation and makes it possible to use it for solver selection. The johnall problem is labeled as having nonlinear objective function by MINLPLib but SUSPECT detects it as having polynomial objective type. The lip objective function is detected as concave because it is a convex maximization problem. Of the remaining 82 problems not recognized as convex (or concave), 53 fail because of numerical errors when computing the eigenvalues of the quadratic expressions. These problems are marked with a dagger\(^\dagger \) in Table 15. The trim loss minimization problems (tls{2, 4, 5, 6, 7, 12}) are convex but SUSPECT fails at detecting it because they contain the square root of the product of two nonnegative variables. The problem st_e17 contains the constraint \(x_1 - (0.2458 x_1^2)/x_2 \ge 6\) that SUSPECT fails to recognize as convex.
8 Conclusions and future work
This manuscript presents SUSPECT, a tool detecting and reporting special structure in optimization problems formulated using the Pyomo algebraic modeling library. The project can be developed further in different directions. On the convexity detection side, we can add an additional step of convexity disproving if the convexity detection is inconclusive. We can add the ability to detect nonconvex objective functions, e.g. the difference of two convex expressions [2, 50] to take advantage of new algorithms [52] specialized in solving this class of problems or to recognize pooling problem structure [11]. We can improve the bound tightening step using Optimization Based Bound Tightening, for example using one of the recent implementations [20] that started to emerge. It would be easy to extend SUSPECT to work with other algebraic modeling languages since the special structure detection algorithms work on SUSPECT’s own DAG or to extend the family of expression forms known [39]. SUSPECT could be integrated with existing nonlinear solvers to detect the problem type and choose the best optimization algorithm for it.
Notes
Pyomo supports several systems for representing expression trees. SUSPECT targets “Pyomo4” expression trees, and as such the discussion here focuses on that expression system.
References
Adjiman, C.S., Androulakis, I.P., Floudas, C.A.: Global optimization of mixed-integer nonlinear problems. AIChE J. 46(9), 1769–1797 (2000)
An, L.T.H.: D.C. Programming for solving a class of global optimization problems via reformulation by exact penalty. In: Global Optimization and Constraint Satisfaction, pp. 87–101. Springer, Berlin, Heidelberg (2003)
Belotti, P.: Bound reduction using pairs of linear inequalities. J. Glob. Optim. 56(3), 787–819 (2013)
Belotti, P., Cafieri, S., Lee, J., Liberti, L.: Feasibility-based bounds tightening via fixed points. In: Combinatorial Optimization and Applications, pp. 65–76. Springer, Berlin, Heidelberg (2010)
Belotti, P., Kirches, C., Leyffer, S., Linderoth, J., Luedtke, J., Mahajan, A.: Mixed-integer nonlinear optimization. Acta Numer. 22, 1–131 (2013)
Belotti, P., Lee, J., Liberti, L., Margot, F., Wächter, A.: Branching and bounds tightening techniques for non-convex MINLP. Optim. Met. Softw. 24(4–5), 597–634 (2009)
Benhamou, F., Older, W.J.: Applying interval arithmetic to real, integer, and boolean constraints. J. Log. Program. 32(1), 1–24 (1997)
Boukouvala, F., Misener, R., Floudas, C.A.: Global optimization advances in mixed-integer nonlinear programming, MINLP, and constrained derivative-free optimization, CDFO. Eur. J. Oper. Res. 252(3), 701–727 (2016)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Ceccon, F.: SUSPECT: https://doi.org/10.5281/zenodo.1216808 (2018)
Ceccon, F., Kouyialis, G., Misener, R.: Using functional programming to recognize named structure in an optimization problem: application to pooling. AIChE J. 62(9), 3085–3095 (2016)
Chinneck, J.W.: Analyzing mathematical programs using MProbe. Ann. Oper. Res. 104(1–4), 33–48 (2001)
Cormen, T.H.: Introduction to Algorithms. MIT Press, New York (2009)
Diamond, S., Boyd, S.: Cvxpy: a python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 17(1), 2909–2913 (2016)
Floudas, C.A.: Nonlinear and Mixed-Integer Optimization: Fundamentals and Applications. Oxford University Press, Oxford (1995)
Fourer, R., Ma, J., Martin, K.: OSiL: an instance language for optimization. Comput. Optim. Appl. 45(1), 181–203 (2010)
Fourer, R., Maheshwari, C., Neumaier, A., Orban, D., Schichl, H.: Convexity and concavity detection in computational graphs: tree walks for convexity assessment. INFORMS J. Comput. 22(1), 26–43 (2010)
Fourer, R., Orban, D.: DrAmpl: a meta solver for optimization problem analysis. Comput. Manag. Sci. 7(4), 437–463 (2010)
Gau, C.Y., Schrage, L.E.: Implementation and Testing of a Branch-and-Bound Based Method for Deterministic Global Optimization: Operations Research Applications, pp. 145–164. Springer, Boston (2004)
Gleixner, A.M., Berthold, T., Müller, B., Weltge, S.: Three enhancements for optimization-based bound tightening. J. Glob. Optim. 67(4), 731–757 (2017)
Goldberg, D.: What every computer scientist should know about floating-point arithmetic. ACM Comput. Surv. 23(1), 5–48 (1991)
Grant, M., Boyd, S.: Graph implementations for nonsmooth convex programs. In: Recent Advances in Learning and Control, pp. 95–110. Springer (2008)
Grant, M., Boyd, S.: CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx (2014)
Grant, M.C.: Disciplined convex programming. Ph.D. thesis, Stanford University (2004). Accessed May 2018
Grossmann, I.E.: Global Optimization in Engineering Design. Springer, New York (1996)
Grossmann, I.E., Kravanja, Z.: Mixed-integer nonlinear programming: a survey of algorithms and applications. In: Large-scale optimization with applications, pp. 73–100. Springer, New York, NY (1997)
Hart, W.E., Laird, C.D., Watson, J.P., Woodruff, D.L., Hackebeil, G.A., Nicholson, B.L., Siirola, J.D.: Pyomo-Optimization Modeling in Python, 2nd edn. Springer, Berlin (2017)
Hart, W.E., Watson, J.P., Woodruff, D.L.: Pyomo: modeling and solving mathematical programs in Python. Math. Program. Comput. 3(3), 219–260 (2011)
Hiriart-Urruty, J.B., Lemaréchal, C.: Convex Analysis and Minimization Algorithms I, Grundlehren der mathematischen Wissenschaften, vol. 305. Springer Berlin Heidelberg, Berlin, Heidelberg (1993)
Hoad, T.C., Zobel, J.: Methods for identifying versioned and plagiarised documents. J. Assoc. Inf. Sci. Technol. 54(3), 203–215 (2003)
Hooker, J.N.: Integrated Methods for Optimization, International Series in Operations Research & Management Science, vol. 170. Springer, Boston (2012)
Kulisch, U.W.: Complete interval arithmetic and its implementation on the computer. In: Numerical Validation in Current Hardware Architectures, pp. 7–26. Springer Berlin Heidelberg (2009)
Lobo, M.S., Vandenberghe, L., Boyd, S., Lebret, H.: Applications of second-order cone programming. Linear Algebra Appl. 284(1–3), 193–228 (1998)
Lougee-Heimer, R.: The common optimization INterface for operations research: promoting open-source software in the operations research community. IBM J. Res. Dev. 47(1), 57–66 (2003)
Mahajan, A., Leyffer, S., Linderoth, J., Luedtke, J., Munson, T.: Minotaur: A Mixed-Integer Nonlinear Optimization Toolkit (2017)
Millman, K.J., Aivazis, M.: Python for scientists and engineers. Comput. Sci. Eng. 13(2), 9–12 (2011)
Misener, R., Floudas, C.A.: Global optimization of mixed-integer quadratically-constrained quadratic programs (MIQCQP) through piecewise-linear and edge-concave relaxations. Math. Program. 136(1), 155–182 (2012)
Misener, R., Floudas, C.A.: GloMIQO: global mixed-integer quadratic optimizer. J. Glob. Optim. 57(1), 3–50 (2013)
Misener, R., Floudas, C.A.: A framework for globally optimizing mixed-integer signomial programs. J. Optim. Theory Appl. 161(3), 905–932 (2014)
Misener, R., Floudas, C.A.: ANTIGONE: Algorithms for coNTinuous/Integer Global Optimization of Nonlinear Equations. J. Glob. Optim. 59(2–3), 503–526 (2014)
Mistry, M., Misener, R.: Optimising heat exchanger network synthesis using convexity properties of the logarithmic mean temperature difference. Comput. Chem. Eng. 94, 1–17 (2016)
Mönnigmann, M.: Efficient calculation of bounds on spectra of Hessian matrices. SIAM J. Sci. Comput. 30(5), 2340–2357 (2008)
Moore, R.E., Kearfott, R.B., Cloud, M.J.: Introduction to Interval Analysis. Society for Industrial and Applied Mathematics, Philadelphia (2009)
Nenov, I.P., Fylstra, D.H., Kolev, L.: Convexity determination in the Microsoft Excel Solver using automatic differentiation techniques. In: Fourth International Workshop on Automatic Differentiation (2004)
Neun, W., Sturm, T., Vigerske, S.: Supporting global numerical optimization of rational functions by generic symbolic convexity tests. In: Computer Algebra in Scientific Computing, pp. 205–219. Springer, Berlin, Heidelberg (2010)
Nowak, I., Vigerske, S.: LaGO: a (heuristic) Branch and Cut algorithm for nonconvex MINLPs. Central Eur. J. Oper. Res. 16(2), 127–138 (2008)
Schichl, H., Neumaier, A.: Interval analysis on directed acyclic graphs for global optimization. J. Glob. Optim. 33(4), 541–562 (2005)
Stubbs, R.A., Mehrotra, S.: A branch-and-cut method for 0–1 mixed convex programming. Math. Program. 86(3), 515–532 (1999)
Tawarmalani, M., Sahinidis, N.V.: A polyhedral branch-and-cut approach to global optimization. Math. Program. 103(2), 225–249 (2005)
Tuy, H.: A General Deterministic Approach to Global Optimization VIA D.C. Programming, vol. 129, pp. 273–303. North-Holland Mathematics Studies, Amsterdam (1986)
Udell, M., Mohan, K., Zeng, D., Hong, J., Diamond, S., Boyd, S.: Convex optimization in Julia. In: Proceedings of the 1st First Workshop for High Performance Technical Computing in Dynamic Languages, pp. 18–28. IEEE Press (2014)
Van Voorhis, T., Al-Khayyal, F.A.: Difference of convex solution of quadratically constrained optimization problems. Eur. J. Oper. Res. 148(2), 349–362 (2003)
Vigerske, S.: (MI)NLPLib 2. Tech. Rep. July (2015)
Vigerske, S., Heinz, S., Gleixner, A., Berthold, T.: Analyzing the computational impact of MIQCP solver components. Numer. Algebra Control Optim. 2(4), 739–748 (2012)
Vu, X.H., Schichl, H., Sam-Haroud, D.: Interval propagation and search on directed acyclic graphs for numerical constraint solving. J. Glob. Optim. 45(4), 499–531 (2009)
Acknowledgements
This work was funded by an Engineering & Physical Sciences Research Council Research Fellowship to RM [Grant Number EP/P016871/1]. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia LLC, a wholly owned subsidiary of Honeywell International Inc. for the U.S. Department of Energys National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ceccon, F., Siirola, J.D. & Misener, R. SUSPECT: MINLP special structure detector for Pyomo. Optim Lett 14, 801–814 (2020). https://doi.org/10.1007/s11590-019-01396-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-019-01396-y