Model-Based Phenotypic Signatures Governing the Dynamics of the Stem and Semi-differentiated Cell Populations in Dysplastic Colonic Crypts

Abstract

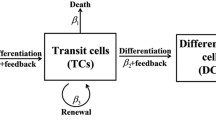
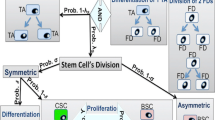
Mathematical modeling of cell differentiated in colonic crypts can contribute to a better understanding of basic mechanisms underlying colonic tissue organization, but also its deregulation during carcinogenesis and tumor progression. Here, we combined bifurcation analysis to assess the effect that time delay has in the complex interplay of stem cells and semi-differentiated cells at the niche of colonic crypts, and systematic model perturbation and simulation to find model-based phenotypes linked to cancer progression. The models suggest that stem cell and semi-differentiated cell population dynamics in colonic crypts can display chaotic behavior. In addition, we found that clinical profiling of colorectal cancer correlates with the in silico phenotypes proposed by the mathematical model. Further, potential therapeutic targets for chemotherapy resistant phenotypes are proposed, which in any case will require experimental validation.

Appendix

1.1 Andronov–Hopf Bifurcation for Second Fixed Points $\bar{{N}}_0 \ne 0 ,\bar{{N}}_1 \ne 0.$

The case $\tau _1 >0,\;\tau _2 =0.$

According to Nikolov et al. (2013), we assume that the finite time delay $\tau _1$ is longer than$\tau _2$. Setting $\tau _2 =0$ in (14), the characteristic equation becomes

$$\begin{aligned} \chi ^{2}+K_{13} \chi +K_{22} =\ell ^{-\chi \tau _1 }\left( {\psi _2 \chi +T_{13} } \right) , \end{aligned}$$

(A.1)

where $K_{13} =K_1 -\psi _0 ,\quad K_{22} =K_2 -T_2$ and $T_{13} =T_1 -T_3$.

It is well known that that the stability of the equilibrium state $\bar{E}^{1}$ depends on the sign of the real parts of the roots of (A.1). We recall that a steady state is locally asymptotically stable if and only if all roots of (A.1) have negative real parts, and its stability can only be lost if these roots cross the vertical axis, that is if purely imaginary roots appear. Generally speaking, the transcendental equation (A.1) (for nonzero delay) cannot be solved analytically and has an indefinite number of roots. In essence, we have two main tools besides direct numerical integration: firstly, the linear stability analysis in the case of a small time delay, and secondly, the Hopf bifurcation theorem. From biological point of view it is known that time delay, $\tau _1$, is bigger than one (Nikolov et al. 2013) here we use Hopf bifurcation theorem. Thus, we let$\chi =m+in \quad \left( {m,\;n\in R} \right)$ and rewrite (A.1) in terms of its real and imaginary parts as

$$\begin{aligned} \left| {\begin{array}{l} m^{2}-n^{2}+K_{13} m+K_{22} =\ell ^{-m\tau _1 }\left[ {\left( {m\psi _2 +T_{13} } \right) \cos n\tau _1 +\psi _2 n\sin n\tau _1 } \right] , \\ 2mn+K_{13} n=\ell ^{-m\tau _1 }\left[ {\psi _2 n\cos n\tau _1 -\left( {m\psi _2 +T_{13} } \right) \sin n\tau _1 } \right] . \\ \end{array}} \right. \end{aligned}$$

(A.2)

To find the first bifurcation point, we look for purely imaginary roots$\chi =\pm in$, $n\in R$ of (A.1), i.e., we set $m=0.$ Then the above two equations are reduced to

$$\begin{aligned} \left| {\begin{array}{l} -n^{2}+K_{22} =T_{13} \cos n\tau _1 +\psi _2 n\sin n\tau _1 , \\ K_{13} n=\psi _2 n\cos n\tau _1 -T_{13} \sin n\tau _1 , \\ \end{array}} \right. \end{aligned}$$

(A.3)

or another one

$$\begin{aligned} \cos n\tau _1= & {} \frac{K_{13} \psi _2 n^{2}+T_{13} \left( {-n^{2}+K_{22} } \right) }{T_{13}^2 +\psi _2^2 n^{2}}, \nonumber \\ \sin n\tau _1= & {} \frac{n\left[ {\left( {-n^{2}+K_{22} } \right) \psi _2 -T_{13} K_{13} } \right] }{T_{13}^2 +\psi _2^2 n^{2}}. \end{aligned}$$

(A.4)

It is clear that if the first bifurcation point is $\left( {n_b^0 ,\;\tau _b^0 } \right)$, then the other bifurcation points $\left( {n_b ,\;\tau _b } \right)$ satisfy $n_b \tau _b =n_b^0 \tau _b^0 +2\nu \pi , \quad \nu =1,\;2,\;\ldots ,\;\infty$.

One can notice that if n is a solution of (A.3) (or (A.4)), then so is $-n$. Hence, in the following we only investigate for positive solutions n of (A.3) or (A.4), respectively. By squaring the two equations into system (A.2) and then adding them, it follows that:

$$\begin{aligned} n^{4}-\left( {2K_{22} -K_{13}^2 +\psi _2^2 } \right) n^{2}+K_{22}^2 -T_{13}^2 =0. \end{aligned}$$

(A.5)

As $\bar{{E}^{1}}$ is locally asymptotically stable at $\tau _1 =0$, it satisfies the Routh–Hurwitz conditions for stability for a square polynomial. Equation (A.5) is a square in $n^{2}$, and the left-hand side is positive for very large values of $n^{2}$ and negative for $n=0$ if and only if $T_{13}^2 >K_{22}^2$, i.e., when Eq. (A.5) has at least one positive real root. Moreover, to apply the Hopf bifurcation theorem, according to Khan and Greenhalgh (1999), the following theorem in this situation applies:

Theorem 1

Suppose that $n_b$ is the least positive simple root of (A.5). Then, $in\left( {\tau _b } \right) =in_b$ is a simple root of (A.1) and $m\left( {\tau _1 } \right) +in\left( {\tau _1 } \right)$ is differentiable with respect to $\tau _1$ in a neighborhood of$\tau _1 =\tau _b$.

To establish an Andronov–Hopf bifurcation at$\tau _1 =\tau _b$, we need to show that a pair of complex eigenvalues crosses the imaginary axis with nonzero speed, i.e., the following transversally condition $\left. {\frac{\hbox {d}\left( {Re\chi } \right) }{\hbox {d}t}} \right| _{\tau =\tau _b } \ne 0$ is satisfied.

From (A.3) we know that $\tau _{b_k }$corresponding to $n_b$ is

$$\begin{aligned} \tau _{b_k }= & {} \frac{1}{n_b }\arccos \left[ {{\left( {\left( {K_{13} \psi _2 -T_{13} } \right) n_b^2 +T_{13} K_{22} } \right) }\bigg /{\left( {T_{13}^2 +\psi _2^2 n_b^2 } \right) }} \right] \nonumber \\&+\frac{2k\pi }{n_b },\quad \;k=0, 1, 2, \ldots \end{aligned}$$

(A.6)

Because for $\tau _1 =0$, equilibrium $\bar{E}^{1}$ is stable, by Butler’s lemma (Freedman and Rao 1983), equilibrium remains stable for $\tau _1 <\tau _{b_k }$, where $\tau _b =\tau _{b_k }$ as $k=0.$ We have now to show that $\left. {\frac{\hbox {d}\left( {Re\chi } \right) }{\hbox {d}t}} \right| _{\tau =\tau _b } \ne 0$.

Hence, if denote

$$\begin{aligned} H\left( {\chi ,\;\tau _1 } \right) =\chi ^{2}+K_{13} \chi +K_{22} -\ell ^{-\chi \tau _1 }\left( {\psi _2 \chi +T_{13} } \right) , \end{aligned}$$

(A.7)

then

$$\begin{aligned} \frac{\hbox {d}\chi }{\hbox {d}\tau _1 }=-{\frac{\partial H}{\partial \tau _1 }}\bigg /{\frac{\partial H}{\partial \chi }}=\frac{\chi \ell ^{-\chi \tau _1 }\left( {\psi _2 \chi +T_{13} } \right) }{2\chi +K_{13} +\tau _1 \ell ^{-\chi \tau _1 }\left( {\psi _2 \chi +T_{13} } \right) -\ell ^{-\chi \tau _1 }\psi _2 }.\quad \quad \end{aligned}$$

(A.8)

Evaluating the real part of this equation at $\tau _1 =\tau _b$ and setting $\chi =in_b$ yield

$$\begin{aligned} \left. {\frac{\hbox {d}m}{\hbox {d}\tau _1 }} \right| _{\tau _1 =\tau _b } =\left. {\frac{\hbox {d}\left( {Re\chi } \right) }{\hbox {d}t}} \right| _{\tau _1 =\tau _b } =-\frac{n_b^2 \left( {2n_b^2 -2K_{22} +K_{13}^2 -\psi _2^2 } \right) }{L^{2}+I^{2}} \end{aligned}$$

(A.9)

where

$$\begin{aligned} L=K_{13} +\tau _b \left( {-n_b^2 +K_{22} } \right) -\psi _2 \cos n_b \tau _b ,\quad I=2n_b \tau _b n_b K_{13} +\psi _2 \sin n_b \tau _b .\nonumber \\ \end{aligned}$$

(A.10)

Let $\theta =n_b^2$, then, (A.5) reduces to

$$\begin{aligned} g\left( \theta \right) =\theta ^{2}-\left( {2K_{22} -K_{13}^2 +\psi _2^2 } \right) \theta +K_{22}^4 -T_{13}^2 . \end{aligned}$$

(A.11)

Then, for ${g}'\left( \theta \right)$ we have

$$\begin{aligned} {g}'\left( \theta \right) =2\theta -2K_{22} +K_{13}^2 -\psi _2^2 . \end{aligned}$$

(A.12)

If $n_b$ is the least positive simple root of (A.5), then

$$\begin{aligned} \left. {\frac{dg}{d\tau _1 }} \right| _{\theta =n_b^2 } >0. \end{aligned}$$

(A.13)

Hence,

$$\begin{aligned} \left. {\frac{\hbox {d}m}{\hbox {d}\tau _1 }} \right| _{\tau _1 =\tau _b } =\left. {\frac{\hbox {d}\left( {Re\chi } \right) }{\hbox {d}t}} \right| _{\tau _1 =\tau _b } =-\frac{n_b^2 {g}'\left( {n_b^2 } \right) }{L^{2}+I^{2}}<0. \end{aligned}$$

(A.14)

According to the Hopf bifurcation theorem (Marsden and McCracken 1976), we define Theorem 2:

Theorem 2

If $n_b$ is the least positive root of (A.5), then an Andronov–Hopf bifurcation occurs as $\tau _1$ passes through$\tau _b$.

The case $\tau _1>0,\;\tau _2 >0.$

We return to the study of (14) with $\tau _1 ,\;\tau _2 >0.$ In order to investigate the local stability of the equilibrium state $\bar{{E}}^{1}$ of system (1), we first prove a result regarding the sign of the real parts of the characteristic roots of (14) in the next theorem:

Theorem 3

If all roots of (A.1) are with negative real parts for$\tau _1 >0$ , then there exists a $\tau _2^{bif} \left( {\tau _1 } \right) >0$ such that all roots of the characteristic equation (14) have negative real parts at$\tau _2 <\tau _2^{bif} \left( {\tau _1 } \right)$ , i.e., when$\tau _2 \in \left[ {0,\;\left. {\tau _2^{bif} \left( {\tau _1 } \right) } \right) } \right.$.

Here we omit the proof of Theorem 3 because it is similar to those in Adimy et al. (2006), Nikolov (2013).