Abstract
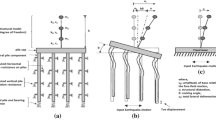
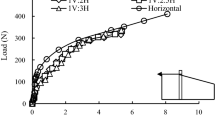
Dynamic experimental studies on the active lengths of a fixed-head floating pile under static and dynamic loading conditions are reported, focusing on the effects of local nonlinearity and resonant behavior of soil. Results obtained from the laterally loaded model soil-pile system subjected to low-to-high amplitude pile head loading suggest a strong influence of local nonlinearity on the active lengths of the pile. Such obtained experimental results are further compared with the available approximate equations for estimating the active lengths. The comparisons reveal the closeness in values for very low amplitude of loadings, but for intermediate-to-high amplitude of loadings, the experimental values are smaller than predicted by the approximate equations. Moreover, both the static and dynamic active lengths of the pile converge to an approximately identical value of six times the diameter of the pile for intermediate-to-high amplitude of loadings. This suggests that the active lengths of the pile are, in fact, the same for both the static and dynamic loadings, under nonlinear conditions. Additionally, results also suggest that the passive-type failures of soil induced by the applied lateral loadings in front of the pile govern the active lengths. Furthermore, the dynamic active lengths of the pile do not show any significant dependency on the resonance in the soil.















Similar content being viewed by others
Abbreviations
- \( C_{\text{u}} \) :
-
Coefficient of uniformity
- \( d \) :
-
Diameter of pile
- \( D_{60,30,10} \) :
-
Particle size parameters for soil
- \( e_{\hbox{max} ,\hbox{min} } \) :
-
Maximum/minimum void ratio
- \( E_{\text{p}} \) :
-
Young’s modulus of pile
- \( {{E_{\text{p}} } \mathord{\left/ {\vphantom {{E_{\text{p}} } {E_{{{\text{s}} - {\text{eq}}}} }}} \right. \kern-0pt} {E_{{{\text{s}} - {\text{eq}}}} }} \) :
-
Elasticity contrast
- \( E_{\text{s}} \) :
-
Young’s modulus of soil at a depth equal to the diameter of pile
- \( E_{{{\text{s}} - {\text{eq}}}} \) :
-
Equivalent Young’s modulus of soil
- \( E_{\text{s}}^{{{\text{low}} - {\text{strain}}}} \) :
-
Low-strain modulus of elasticity of soil at a depth equal to the diameter of pile
- \( f_{\text{n}} \) :
-
Natural frequency
- \( G \) :
-
Shear modulus of soil
- \( G_{0} \) :
-
Initial shear modulus of soil
- \( G_{\text{m}} \) :
-
Shear modulus of model
- \( G_{\text{p}} \) :
-
Shear modulus of prototype
- \( G_{\text{s}} \) :
-
Specific gravity of soil
- \( H \) :
-
Height of soil layer
- \( L \) :
-
Length of pile
- \( L/d \) :
-
Slenderness ratio of pile
- \( l_{\text{d}} \) :
-
Dynamic active length of pile
- \( l_{\text{s}} \) :
-
Static active length of pile
- \( q \) :
-
Applied acceleration amplitude in m/s2
- \( s \) :
-
Shape factor
- \( u \) :
-
Displacement applied at pile head
- \( V_{\text{s}} \) :
-
Shear wave velocity in soil
- \( \lambda \) :
-
Geometric scaling ratio of the model to prototype
- \( \eta \) :
-
Density scaling ratio of the model to prototype
- \( \omega_{\text{m}} \) :
-
Circular frequency of model
- \( \omega_{\text{p}} \) :
-
Circular frequency of prototype
- \( \gamma_{\text{m}} \) :
-
Dynamic strain in model
- \( \gamma_{\text{p}} \) :
-
Dynamic strain in prototype
- \( \rho_{\text{s}} \) :
-
Density of soil
- \( \rho_{\text{p}} \) :
-
Density of pile
- \( \varphi \) :
-
Friction angle of soil
References
Matlock H, Reese LC (1960) Generalized solutions for laterally loaded piles. J Soil Mech Found Div ASCE 86(SM5):63–94
Matlock H (1970) Correlations for design of laterally loaded piles in soft clay. In: Proceedings of the 2nd annual offshore technology conference, paper no. 1207, Houston, pp 577–594
Saitoh M (2010) Effect of local nonlinearity in cohesionless soil on optimal radius minimizing fixed-head pile bending by inertial and kinematic interactions. Acta Geotech 5(4):273–286
Banerjee PK, Davies TG (1978) The behavior of axially and laterally loaded single piles embedded in nonhomogeneous soils. Geotechnique 28(3):309–326
Poulos HG (1971) Behavior of laterally loaded piles: I—Single piles. J Soil Mech Found Div ASCE 97(5):711–731
Basu D, Salgado R, Prezzi M (2009) A continuum-based model for analysis of laterally loaded piles in layered soil. Géotechnique 59(2):127–140
Kuhlemeyer RL (1979) Static and dynamic laterally loaded piles. J Geotech Eng ASCE 105(2):289–304
Randolph MF (1981) The response of flexible piles to lateral loading. Geotechnique 31(2):247–259
Achmus M, Thieken K (2010) On the behavior of piles in non-cohesive soil under combined horizontal and vertical loading. Acta Geotech 5(3):199–210
Dobry R, Vicente E, O’Rouke MJ, Roesset R (1982) Horizontal stiffness and damping of single piles. J Geotech Eng Div ASCE 108(3):439–459
Poulos HG, Hull TS (1989) The role of analytical geomechanics in foundation engineering. In: Foundation engineering: current principles and practice (GSP 22). ASCE, pp 1578–1606
Kulhawy F, Chen Y (1995) A thirty year perspective of Brom’s lateral loading models, as applied to drilled shafts. In: Proceedings of Bengt Broms symposium in geotechnical engineering, Singapore, pp 225–240
Wang MC, Liao WP (1987) Active length of laterally loaded piles. J Geotech Eng ASCE 113(9):1044–1048
Velez A, George G, Krishnan R (1983) Lateral dynamic response of constrained head piles. J Geotech Eng ASCE 109(8):1063–1081
Gazetas G, Dobry R (1984) Horizontal response of piles in layered soils. J Geotech Eng ASCE 110(1):20–40
Krishnan R, Gazetas G, Velez A (1983) Static and dynamic lateral deflexion of piles in non-homogenous soil stratum. Geotechnique 33(3):307–325
Boominathan A, Ayothiraman R (2007) An experimental study on static and dynamic bending behavior of piles in soft clay. Geotech Geol Eng 25(2):177–189
Rocha M (1957) The possibility of solving soil mechanics problems by the use of models. In: Proceedings of 4th international conference on soil mechanics, London, vol 1, pp 183–188
Roscoe KH (1968) Soils and model tests. Proc Inst Mech Eng J Strain Anal Eng Des 3(1):57–64
Kagawa T (1978) On the similitude in model vibration tests of earth-structures. Proc Jpn Soc Civil Eng 275:69–77
Iai S (1989) Similitude for shaking table tests on soil-structure-fluid model in 1 g gravitational field. Jpn Soc Soil Mech Found Eng Soils Found 29(1):105–119
Kokusho T, Iwatate T (1979) Scaled model tests and numerical analyses on nonlinear dynamic response of soft grounds. Proc Jpn Soc Civil Eng 285:57–67
Reinsch CH (1971) Smoothing by spline functions II. Numer Math 16(5):451–454
Ishida T et al (1981) Static and dynamic mechanical properties of materials for model tests (Gifu Sand) under low confining stress. Research report of electrical power center research institute, no. 380045
Richart FE, Hall JR, Woods RD (1970) Vibrations of soils and foundations. Prentice-Hall, New Jersey
Pecker A (1995) Validation of small strain properties from recorded weak seismic motions. Soil Dyn Earthq Eng 14(6):399–408
Reese LC, Impe WFV (2001) Single piles and pile groups under lateral loading. A.A. Balkema, Great Britain
Kishida, H. and Nakai. S. (1977) Large deflection of a single pile under horizontal load. In: Proceedings of the 9th international conference on soil mechanics and foundation engineering, Tokyo, pp 87–92
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Goit, C.S., Saitoh, M., Oikawa, H. et al. Effects of soil nonlinearity on the active length of piles embedded in cohesionless soil: model studies. Acta Geotech. 9, 455–467 (2014). https://doi.org/10.1007/s11440-013-0257-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-013-0257-0