Abstract
Contact imaging is a compact lensless microscopy technique that allows observation of living cells placed directly on a charge-coupled device sensor. However, captured images exhibit low visibility in general. This work is aimed at integrating computational refocusing and high-frequency illumination into contact imaging to enhance the visibility of the captured images. Refocusing contributes to the synthesis of shallow depth-of-field images from the light field captured by moving a point light source. The visibility may be enhanced via high-frequency illumination. Naïve integration of both techniques requires several observations. Therefore, we propose an efficient integration from reduced observations by reformulating the computational refocusing applied in contact imaging. Furthermore, we developed a prototype system that demonstrates the effectiveness of the proposed method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cell cultivation and monitoring are fundamental tools in life science fields, such as biomedical and biomaterial engineering. An incubator and a microscope are used for culturing living cells and monitoring these cells, respectively. Placing a microscope inside an incubator is hard due to its size, hence, cell monitoring is performed only after these cells have been removed from the incubator. These operations impose stress on the cultured cells. Therefore, developing a device that can be housed in an incubator while continuously monitoring the living cells is essential.
Our goal is to develop a compact device that can be installed in an incubator for monitoring live cell imaging. The contact imaging technique enables us to capture an image of an object on the imaging sensor without using a lens. Figure 1 presents the conceptual illustration of the device we aim to develop. The device is a petri dish with a bare charge-coupled device (CCD) sensor, which is waterproof and, hence, safe for culture fluid. Cells will be cultivated on the CCD sensor and monitored continuously. Eliminating lenses contributes to the compactness of the imaging device, but some important functions based on optical techniques in microscopy cannot be directly applied to the contact imaging since the optics design is significantly different. We focus on two major functions associated with optical techniques, namely: (i) a shallow depth-of-field since sweeping the focus helps us to understand the three-dimensional (3D) structure of the thick subject, and (ii) visibility enhancement using optical techniques, such as dark field microscopy and phase contrast microscopy, especially for a transparent specimen. Checking the 3D alignment and shape of the cells are helpful for monitoring the cell cultivation. Although some technologies on contact imaging have been studied, such functions are currently unavailable.
In this work, we propose a computational method that provides a focusing function and visibility enhancement for contact imaging. We utilize two techniques namely, computational refocusing based on the capture of a light field and the separation of direct and global components via high-frequency illumination. The contributions of our paper are as follows. We propose:
-
1.
a design to capture a light field using a lensless system.
-
2.
an algorithm that integrates computational refocusing with the separation of direct and global components, to reduce the number of observations in contact imaging.
-
3.
a reformulation of the computational refocusing via the least squares sense for the integration.
This paper is organized as follows. Section 2 describes related work in computational microscopy. Section 3 describes the building blocks of the proposed method, i.e. contact imaging, the separation of direct and global components, and the computational refocusing of a captured light field. Section 4 describes the proposed method. Experimental results are presented in Sects. 5 and 6. Section 7 provides conclusions and future work.
2 Related Work
Lensless imaging allows the design of compact devices, such as FlatCam (Asif et al. 2015; Bimber and Koppelhuber 2017). Lensless imaging is therefore now widely studied in the field of live-cell imaging (Minzioni et al. 2017). The main techniques have been studied on shadow imaging, fluorescence, and super-resolution.
The simplest form, i.e., shadow imaging, relies on the characteristics of shadows and can be performed without an image reconstruction process (Ozcan and Mcleod 2016). Shadow lensless imaging is used for various applications, such as monitoring the culturing cell (Mudanyali et al. 2010; Wu and Ozcan 2017) and tracing the sperm (Daloglu and Ozcan 2017; Daloglu et al. 2017). One of these has focused on implementing a compact lensless device in an incubator (Kesavan et al. 2014). This type of imaging is also used for point-of-care cytometry and diagnostics applications (Seo et al. 2009), and for a high-throughput on-chip imaging platform that can rapidly monitor and characterize various cell types (Su et al. 2009). Reducing the cost, by excluding lenses, is also employed in fluorescence imaging for the direct observation of chemotactic transmigration (Heng et al. 2006). Moreover, some methods have been proposed to increase the resolution via illumination (Cui et al. 2008; Zheng et al. 2010; Lee et al. 2014), and with color-capable implementation (Lee et al. 2011)
A super-resolution method, which involves moving a point light source, has also been proposed (Bishara et al. 2010). For example, high-resolution lensless microscopes have been extensively investigated to achieve a wide field of view (Greenbaum et al. 2014; Isikman et al. 2012; Luo et al. 2015), implementing portable devices (Bishara et al. 2011), and observing the cell microstructure (Wang et al. 2017). Greenbaum et al. (2014) have implemented contact imaging that provides high-resolution holographic images of large-area pathology samples.
While the above techniques contribute to the observations at high pixel resolution, the axial resolution was significantly lower. Isikman et al. (2011) have developed a 3D lensless microscope which enables imaging a large volume of approximately \(15\,\hbox {mm}^{3}\) on a chip by sweeping the focus plane computationally. Such function is a powerful tool for high-throughput applications in, e.g., cell and developmental biology. However, this technique is limited because the bulk of the photons incident on an object should encounter at most a single scattering event before being detected. Thus, it is not applicable to observe the subject in a scattering media or scattering subjects.
From the viewpoint of computational photography, some studies have been conducted to improve the visibility where such scattering exists. For example, Nayar et al. (2006) have proposed to use high-frequency illumination to separate scattering components from reflected light. Achar et al. (2013) have developed a motion compensation method that can separate direct and global components by moving projector-camera systems and Gupta et al. (2011) have proposed a technique that separates direct-global components and mechanically sweeps focal plane. Tanaka et al. (2013) have investigated the contribution of the direct-global separation to the visibility enhancement. Levoy et al. (2004) have adapted confocal imaging to large-scale scenes by replacing the optical apertures with pairs of cameras and projector. Fuchs et al. (2008) have performed confocal imaging in translucent media improved by combining with the descattering procedure. Recently, Shimano et al. (2017) have proposed to adopt the direct-global separation to remove global component that makes microscopic image unclear.
Moreover, even in microscopy, the illumination pattern was changed to achieve a bright or dark field of phase shift imaging (Tian et al. 2014; Zheng et al. 2011; Liu et al. 2014; Guo et al. 2015a). Fourier ptychographic method has also been used to increase the visibility (Zheng et al. 2013; Guo et al. 2015b; Ou et al. 2013), and acquire a phase shift image using chromatic aberration (Waller et al. 2010). The structured illumination microscopy (SIM) is also a technique that utilizes illumination pattern for various purposes such as super-resolution, surface profiling, and phase imaging (Saxena et al. 2015). Especially, phase imaging is a technique for visibility enhancement for microscopy. Regarding the use of structured light, SIM is similar to the direct-global separation technique (Nayar et al. 2006), however, there are differences in principle, actual setting, and processes. The most significant difference is the principle: SIM stands on wave optics whereas direct-global separation stands on geometrical optics.
From the above, many techniques have been developed for lensless imaging and visibility enhancement. To the best of our knowledge, a study that simultaneously incorporates increasing axial resolution and separating scattering has yet to be reported for lensless imaging.
3 Building Blocks
3.1 Contact Imaging
Contact imaging is a compact lensless microscopy technique, which enables us to capture an image of a subject placed on or near the image sensor chip by illuminating this object from a single point light source. Although this configuration seems different from a common camera, the image captured by the device is equivalent to the image with a pinhole camera and a planar light source. Figure 2a illustrates the correspondence between a pinhole camera and this configuration. The point light source can be treated as a pinhole in front of the planar light source. Thus, the difference is just the position of the pinhole, which is between the object and the sensor or behind the object. As such, the image becomes the all-in-focus image of the subject.
As presented in Fig. 1, our first prototype of the device consists of a single-point light source and a petri dish with a hole. This hole is bonded to a bare CCD sensor, which is waterproof and, hence, safe for culture fluid. The subject is directly placed on the sensor, and the transmitted image of the subject will be captured.
3.2 Separating Direct and Global Components
According to Nayar et al. (2006), when the scene is lit by a light source, the radiance of each point in the scene can be described by direct and global components. These components result from direct illumination of the point by the source and illumination of the point by other points in the scene, respectively.
By capturing multiple images of the scene illuminated with the different high frequency patterns, these components can be separated by simple computations. Here, we suppose that a scene is illuminated by a stripe pattern.Footnote 1 The scene is illuminated with half the energy of the point light source. Therefore, the intensity of the global component is halved at each point, whereas the direct component is directly reduced by the illumination pattern. The direct and global components at \(\varvec{x}\) in an image can then be formulated as:
where \(\ddot{I}(\varvec{x})\): intensity of the pixel at \(\varvec{x}\) under high-frequency illumination, \(\alpha (\varvec{x})\): coefficient of the direct component, \(\beta \): coefficient of the global component, and \(D(\varvec{x})\) and \(G(\varvec{x})\) are the direct and global components, respectively. Note that \(\alpha (\varvec{x})\) corresponds to the illumination pattern, whereas \(\beta \) is usually taken as a constant. By collecting the observations with the high-frequency pattern shifted N times, the acquired images can then be formulated as:
where \(\ddot{I}_n(\varvec{x})\) and \(\alpha _n(\varvec{x})\) are the image and the coefficient corresponding to the n-th illumination pattern, respectively. Using vector representation, we express the above formulation as
For each pixel of the image, the direct and global components \({\varvec{X}}(\varvec{x})\) can be obtained by minimizing the mean square error as follows:
3.3 Computational Refocusing
In computational photography, the light-field (i.e., the 2D spatial and 2D angular distributions of light passing through the cells) is recorded via light field microscopy (Levoy et al. 2006; Lin et al. 2015). This field is then used for a computational refocusing process that synthesizes a flexible focus. We adopt this approach to implement a shallow depth-of-field function that elucidates, for observers, the 3D structure of thick subjects.
The 4D light field can be represented in several ways. In this work, we adopt a multi-view representation that depicts the light field as a 2D array of 2D images \(I_{m}(\varvec{x})\), where m denotes the viewpoint \((m=1,\dots ,M)\). According to previous work, the refocused image can be represented as the mean for each pixel in the shifted images:
where \(I_{m}(\varvec{x})\) denotes the m-th image of the captured light field, d is the depth of the focal plane, and \(\varDelta \varvec{x}_{m}\) is the disparity of the image.
4 Integration of Refocusing and Direct-Global Separation with Contact Imaging
By integrating the building blocks explained in the previous section, our system of contact imaging can simultaneously examine the visual enhancement resulting from direct-global separation and the computational refocusing. First, we describe the setup to capture the light field during lensless contact imaging for computational refocusing. Second, we explain a naïve integration to capture the light field under high-frequency illumination. Although this setup allows us to individually adopt the separation of the direct and global components and the computational refocusing, several \(N \times M\) observations (which are captured after prolonged periods) are required. Therefore, we propose a new efficient integration that allows simultaneous adoption of both methods, thereby contributing to reduced number of observations in M. We perform this integration by reformulating the computational refocusing method as an optimization problem. Subsequently, we explain the proposed algorithm that integrates the separation of direct and global components with the computational refocusing. The device proposed for contact imaging is then explained.
4.1 Capturing the Light Field Via Contact Imaging
For computational refocusing, the light field of the scene must be captured during contact imaging. In previous studies, the light field was captured by either a camera array, a micro-lens array, or a single camera mounted on a translation stage (Levoy et al. 2006; Lin et al. 2015). The structure of our device for contact imaging is lensless and therefore has a different structure from the devices used in those studies.
As explained in Sect. 3.1, the combination of the bare sensor and the point light source is equivalent to a combination of a pinhole camera and a planar light source as illustrated in Fig. 2a. According to the analogy between them, a system to capture a light field via contact imaging can also be considered. In the case of contact imaging, a pinhole is located at the position of the point light source. Whereas a single camera mounted on a translation stage sequentially captures images, the light field associated with contact imaging can be captured by moving the point light source, as illustrated in Fig. 2b. Note that we only move the pinhole, which is the point light source, but not the sensor in contact imaging. In this paper, \(I_{m}\) denotes the captured image of the scene illuminated from the m-th light position.
4.2 Naïve Integration with Contact Imaging
In our scenario, the direct and global components can be considered as illustrated in Fig. 3. The direct component reflects the boundary of cells clearly, whereas the global component reduces the visibility due to complex light path caused by scattering, reflection, and refraction by colliding with the subject. Therefore, we expect that the visibility can be enhanced in the direct component from the observation.
a Set a stripe mask between the point light source and the CCD to project the high-frequency pattern onto the subject. The recorded intensity, i.e., the mixture of direct and global components whose ratio is known, is then calculated and separated. b Red lines and blue lines represent the path of the direct component that is transmitted straight through the object and the paths of the global component that randomly propagate by colliding with the objects, respectively (Color figure online)
To separate the direct and global components, the target scene must be illuminated with a high-frequency pattern. For stable separation, a certain number of observations must be collected by shifting the pattern by a certain step. This shifting was controlled in previous methods by using either a display or a projector. However, such devices are unsuitable for this work, owing to the size restriction of our contact imaging. Therefore, we place a Ronchi ruling as a tiny stripe mask between the point light source and the CCD sensor to embed high-frequency illumination into the contact imaging. Separation of the direct and global components requires multiple images obtained under different illumination patterns, which are realized by e.g. mechanically shifting the stripe mask.
If sufficient observations are obtained by respectively shifting the stripe mask and the point light source, then the direct-global separation and the computational refocusing can be sequentially performed. As for observations, suppose that a set of images have been captured for a light position m and high-frequency illumination with various shifts n. \(\ddot{I}_{m,n}(\varvec{x})\) denotes the captured image at the m-th light position and n-th mask position. The direct and global components for each image in the set \(\left\{ \ddot{I}_{m,n}(\varvec{x})\right\} _{n=1}^{N}\) can be separated, and the components, \(D_{m}(\varvec{x})\) and \(G_{m}(\varvec{x})\) for the m-th light position can then be obtained.
where \(\ddot{{\varvec{I}}}_{m}(\varvec{x})=\begin{bmatrix} \ddot{I}_{m,1}(\varvec{x})&\cdots&\ddot{I}_{m,N}(\varvec{x})\\ \end{bmatrix}^{\top }\), and \({\varvec{C}}_{m}(\varvec{x})=\begin{bmatrix} \alpha _{m,1}(\varvec{x})&\cdots&\alpha _{m,N}(\varvec{x}) \\ \beta _{m}&\cdots&\beta _{m} \end{bmatrix}^{\top }\). \(\alpha _{m,n}(\varvec{x})\) is the coefficient of the direct component at the pixel \(\varvec{x}\) under illumination through the stripe mask at n under the point light source at m, and \(\beta _{m}\) is the coefficient of the global component. The coefficient \(\beta _{m}\) is usually taken as a constant as in Eq. (1). However, in our case, \(\beta _{m}\) varies since the point light source moves over a relatively large area during computational refocusing. \(\alpha _{m,n}(\varvec{x})\) can be preliminarily calibrated as the ratio of the captured image with and without the mask, under the light at m. \(\beta _{m}\) is also obtained as the average of \(\alpha _{m,n}(\varvec{x})\) over the image and n.
Here, \(D_{m}(\varvec{x})\) can be considered as an all-in-focus image with visibility enhancement. We denote by \(D(\varvec{x},d)\) the refocused image of the direct component associated with a given depth d. The computational refocusing can then be applied via \(\left\{ D_{m}(\varvec{x})\right\} _{m=1}^{M}\).
4.3 Changing the Illumination Pattern Without Shifting the Stripe Mask
The above method requires a mechanism for independent shifting of the stripe mask and the point light source. The algorithm of the integration is simple. However, a large device is needed to implement the mechanism and the acquisition of observations is time-consuming. These drawbacks are problematic as the device must be small enough for installation in an incubator, thereby reducing the number of observations required to observe living cells.
Actually, even if the stripe mask is fixed, the translation of the point light source changes the illumination pattern on the subject, as illustrated in Fig. 4. We utilize this fact to solve the aforementioned drawbacks by fixing the mask.
However, this does not allow us to adopt the separation of the direct and global components and the computational refocusing one by one. We can collect the images \(\ddot{I}_{m}(\varvec{x})\) by moving the light source to the position m with a fixed stripe mask. Figure 4a, b respectively illustrate the light paths of the illumination pattern where the position of the stripe mask and the point light source are controlled. A comparison of these paths reveals that the illumination patterns on the CCD sensor are the same, although the light paths through the cells are different. This indicates that the acquired images \(\ddot{I}_{n}(\varvec{x})\) and \(\ddot{I}_{m}(\varvec{x})\) in (a) and (b), respectively, are different. Therefore, owing to the disparities among the images, direct application of the method to these images should be avoided. Computationally, we can obtain a different result from Eq. (4) by ignoring the difference between these images, but the result would include artifacts associated with the disparities.
In this work, we propose an algorithm that applies both processes simultaneously, by calculating Eqs. (4) and (5) from a unified equation. These equations have different forms and must be unified via reformulation of the computational refocusing. Subsequent formulation and optimization of the unified cost function yields a refocused image from which the direct and global components can be obtained. The algorithm has no approximation, thereby contributing to reduced observations (i.e., from \(M \times N\) to M), and the result is free of artifacts.
4.4 Reformulation of the Computational Refocusing
Let \(\hat{R}(\varvec{x},d)\) be an ideal focused image of depth d, and \(I_{m}(\varvec{x})\) as previously stated is the all-in-focus image captured from various viewpoints m. According to the corresponding disparity \(\varDelta \varvec{x}_{m}\), the shifted image \(I_{m}(\varvec{x}-d\varDelta \varvec{x}_{m})\) is comparable to \(\hat{R}(\varvec{x},d)\). Therefore, a defocused component \(\epsilon _{m}(\varvec{x},d)\) can be taken as the difference between the disparity and the shifted image, and may be expressed as:
The least squares of the sum of the defocus components is given as:
This minimization is satisfied when \(\hat{R}(\varvec{x},d)\) equals the mean image of \(I_{m}(\varvec{x}-d\varDelta \varvec{x}_{m})\), which is expressed as,
As presented in Eq. (5), the refocused image \(R(\varvec{x},d)\) is usually formulated as a summation of the shifted images \(I_{m}(\varvec{x}-d\varDelta \varvec{x}_{m})\). Although this is slightly different from Eq. (10), the difference is simply divided by M. Thus, the computational refocusing can therefore be treated as a minimization problem of squared defocused components in the set of shifted images.
4.5 Integration in the Unified Formulation
According to the reformulation, we integrate Eqs. (4) and (10) using a unified formulation. Recall that \(D_{m}(\varvec{x})\) and \(G_{m}(\varvec{x})\) are introduced in Sect. 4.2 to denote the direct and global components associated with the light position m. \(D_{m}(\varvec{x})\), \(G_{m}(\varvec{x})\), and \(I_{m}(\varvec{x})\) are considered as all-in-focus images. For \(D(\varvec{x},d)\) in Eq. (7), let \(G(\varvec{x},d)\) be the refocused images of the global component at a depth d. The defocused component under high-frequency illumination in a light position m is denoted as \(\epsilon '_{m}(\varvec{x},d)\). This component can be expressed as the difference between the observed image \(\ddot{I}_{m}(\varvec{x}-d\varDelta \varvec{x}_{m})\) and the refocused direct and global components, i.e. \(D(\varvec{x},d)\) and \(G(\varvec{x},d)\), as follows: (See also Fig. 5 for reference.)
Finally, \(D(\varvec{x},d)\) and \(G(\varvec{x},d)\) can be estimated by minimizing the summation of \(\left\| \epsilon '_{m}(\varvec{x},d)\right\| ^2\) as follows:
where
and \({\varvec{C}}^+(\varvec{x},d) = \left( {\varvec{C}}(\varvec{x}, d)^\top {\varvec{C}}(\varvec{x},d)\right) ^{-1} {\varvec{C}} (\varvec{x},d)^\top \).
5 Quantitative Evaluation of the Algorithm Using Synthetic Data
To validate the results of the proposed algorithm quantitatively, we build an environment similar to the contact imaging to synthesize the images, adopt the naïve integration and the proposed method, and compare the results.
5.1 Simulation Environment
To synthesize the images of contact imaging, we have developed a physically based renderer. We have implemented a ray tracing renderer that can simulate scattering effects to solve the volume light transport equation (Jensen and Christensen 1998; Jensen and Wann 2001) by Monte Carlo approach. More specifically, the renderer simulates 64 millions of photons’ paths emitted from a virtual light source to a virtual image sensor plane, then calculates the influence of the photons on each pixel of the image sensor. In this simulation, embryo is assumed to be a participating medium which produces the scattering effects.
We synthesize an embryo with eight small spheres surrounded by one large sphere. To simulate the scattering, both extinction coefficient \(\sigma _t\) and scattering coefficient \(\sigma _s\) are set to be \(1.0\,\hbox {mm}^{-1}\) assuming no photon absorption during the scattering for a large sphere. Also, the parameter g of Henyey-Greenstein phase function which represents an average cosine of scatted direction was set to be 0.95. For small inner spheres, we set \(\sigma _t=\sigma _s=2.0\) and \(g=0.99\). Note, these parameters were empirically determined.
The resolution of the rendered image was (256, 256). By shifting the point light source and the stripe mask as \(M=1005\) and \(N=10\), we have rendered 10,050 images in total for naïve integration. For unified approach we only used 1005 images of \(n=4\).
5.2 Quantitative Evaluation
Figure 6 shows examples of rendered image with and without stripe mask, a result of direct-global separation from N images, a result of refocused image from M images with and without stripe mask, results of the naïve integration, and the proposed method. (a) and (b) are all-in-focus images under a point light source and a stripe mask. (c) and (d) are respectively the direct and global components obtained by moving the stripe mask without moving the point light source. (e) is a refocused image obtained by moving the light source without stripe mask. Under the stripe mask, the refocused images have about half intensity of (e) as shown in (f). Note that the stripe mask pattern is also blurred since it is placed far above the focus plane. (g) and (h) are respectively the refocused results obtained from the direct and global components such as (c) and (d). (i) and (j) are respectively the refocused direct and global components obtained by the proposed method, which only moves a point light source over the fixed stripe mask.
Synthetic data used for quantitative evaluation. a All-in-focus image under a point light source, b under a stripe mask. c, d are respectively the direct and global components obtained by moving the stripe mask without moving the point light source. e is a refocused image obtained by moving the light source without stripe mask. Under the stripe mask, a refocused image shown in f has about half intensity with e. Note that the stripe mask pattern is also blurred since it placed far above the focus plane. g, h are respectively the refocused results obtained from the direct and global components such as c, d. i, j are respectively the refocused direct and global components obtained by the proposed method, which only moves a point light source over the fixed stripe mask. Note that g, h are computed from MN images whereas the proposed method uses M images for i, j. Inputs and refocusing results can be also found in the Online Resource 1
By comparing (g, h) and (i, j), the results seem quite similar. As quantitative evaluation, we have calculated the normalized root mean-squared error (NRMSE) to compare (g) with (i), and (h) with (j). By taking the results of the naïve integration (g,h) as the denominator, NRMSE of the direct component (i) was 0.3% and the global component (j) was 1.3%. As for peak signal to noise ratio (PSNR), the direct component (i) was 79.04 dB and the global component (j) was 88.58 dB. Note that the proposed method only use 10% of the images from the naïve integration set. Although the global component has larger error than the direct component, it is presented that the proposed method can provide similar results with the naïve integration even if it does not move the stripe mask.
5.3 Quality Comparisons of the Results Produced from the Same Number of Images
As a quantitative evaluation, we evaluated the accuracy of the naïve integration and the proposed method. As the ideal output, we have prepared enough number of observations, where \(M=1005\) and \(N=10\), then adopted the naïve integration to obtain refocused direct and global components for various depths with 120 steps, i.e. Fig. 6g, h. Then, we also adopted the naïve integration and the proposed method with a limited number of observations. Evaluations have been made on different total number of observations: \(MN = 500\), 400, 300, 200, 100, 70, 50, 40, 30, and 20. For the proposed method, the stripe mask is supposed to be fixed, thus \(N=1\). On the other hand, the naïve integration requires the stripe mask to be moved, thus \(N=10\) and \(M= 50\), 40, 30, 20, 10, 7, 5, 4, 3, and 2. As well as the above, we have calculated NRMSE for the result and the ideal output, which is obtained from \(MN = 10{,}050\).
Figure 7 shows the results at a certain depth obtained from \(MN=500\), 300, 100, 40, and 20. Defocused effect seems natural when M is sufficiently large, but artifacts appear when M is small. In comparison with the naïve integration, the proposed method could produce more natural defocused effect since it could take 10 times larger number of M for observed image.
Comparing the results of the naïve integration and the proposed method. Each column show the results from the same number of images, where the proposed method can take 10 times more viewpoints than the naïve integration. Especially when MN is small, the proposed method achieved better quality than the the naïve integration. Refocusing results can be also found in the Online Resource 1
Figure 8 presents the box plot of NRMSE from all the refocused images, each of them has 120 samples. Overall, the proposed method is superior to the naïve integration especially when the number of input MN is small. For the direct component, the proposed method achieved greatly better result than the naïve integration. As for the global component, the NRMSE of the proposed method was mostly better than the naïve integration.
Quantitative comparison of the naïve integration and the proposed method with respect to the number of images used, where the proposed method can take 10 times more viewpoints than the naïve integration in this setting. NRMSE is evaluated for refocused images by comparing with the ideal output, then its distribution is shown by box-plot
Qualitatively, the proposed method achieved better refocused results than the naïve integration. According to the application, which is monitoring live cell, it is required to clearly image the embryo of which the individual cells are distinguishable. In that sense, the proposed method provides natural refocusing from \(M\ge 40\) observations whereas the naïve integration cannot. From the quantitative evaluation, NRMSE of the proposed method with \(M=(20,40,100)\) is mostly equivalently to the one of the naïve integration with \(MN=(100,200,400)\), respectively. This indicates that the proposed method works about five times more efficient than the naïve integration in terms of the acquisition time. This improvement can be significant for live cell imaging; the subjects are not fixed thus taking longer time for the observation may leads the artifacts caused by the disturbance of the subjects’ motion.
6 Experiments Using a Prototype
6.1 Experimental Setup
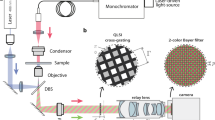
We have implemented contact imaging as presented in Fig. 9. For the ease of theoretical validation and implementation, the relevant equipment is simplified so that the point light source is moved along a 1D direction, which is orthogonal to the stripe pattern. However, the use of a checker pattern for movement of the source in a plane is desirable. We also use a fixed sample to validate the algorithm although our study is aimed at developing a device for observing living cells. For this reason, we prepare unstained embryos of a sea urchin (diameter: about \(100\,\upmu \hbox {m}\)) and a mouse (\(80\,\upmu \hbox {m}\)) at the cleavage stage in distilled water. In future work, the results will be experimentally validated using a fully equipped device and living cells.
The device is equipped with a CCD sensor (Panasonic MN34595PL) having a resolution of \(4656 \times 3480\) and a pixel pitch of \(1.335\,\upmu \hbox {m}\). The sensor is embedded in a petri dish with a hole. As a point light source, the device consists of a white LED and a pinhole (diameter: \(10\,\upmu \hbox {m}\)). The light source is set at a height of 14.9 mm above the sensor. High-frequency illumination is achieved using a mask with a stripe pattern with 40 line pairs per mm (lpmm). This mask is placed at a height of 2.6 mm above the CCD sensor.
As a mechanism for shifting the illumination pattern, the point light source is attached to a motorized linear stage. The observation is executed by moving the source from \(-\,5020\) to \(5020\,\upmu \hbox {m}\) in \(10\,\upmu \hbox {m}\) intervals, i.e., 1005 images are captured in total.
In this setting, whereas the depth-of-field is theoretically supposed to be about \(5150\,\upmu \hbox {m}\) with a light source of \(10\,\upmu \hbox {m}\) in diameter, it becomes about \(5.16\,\upmu \hbox {m}\) with the synthetic aperture of \(5020\,\upmu \hbox {m}\) in radius. Such a shallow depth-of-field function is meaningful to observe the 3D structure of the embryos with 80–\(100\,\upmu \hbox {m}\) in diameter.
Experimental setup for contact imaging with light field captured under high-frequency illumination. a A photograph of the prototype device. b Schematic illustration of the device. c An image captured by the device. The green rectangles indicate the samples focused on in the following experiment (Color figure online)
Experimental results. Samples 1 and 2 are sea urchin embryos, whereas samples 3 and 4 are mouse embryos. Column a shows the all-in-focus images that are captured by the first prototype. The sequential images b show the separated direct and global components. Images that are arranged in a lattice show the refocused images. The green straight line in the direct images shows the cells where the visibility is enhanced by applying our method. Refocusing results can be also found in the Online Resource 1 (Color figure online)
6.2 Experimental Results
Figure 10 presents the results of the proposed method that integrates the separation of direct and global components with the computational refocusing. In our experiment, we capture images with a resolution of \(4656 \times 3480\). The captured scene consists of many tiny embryos in a very wide field of view and, hence, we cropped the images around an embryo to a resolution of \(150 \times 150\) and adopt the proposed method. Note that the coefficient \(\beta _{m}\) are calculated for each of samples independently to be globally varied but it is assumed to be locally constant. The resultant images are shown in Fig. 9c. The figure consists of four rows of images and each row observes one embryo. Samples 1 and 2 are sea urchin embryos, whereas samples 3 and 4 are the mouse embryos. Column (a) in Fig. 10 shows the image captured by our first prototype, which uses only the point light source and the CCD sensor (i.e., without a stripe mask) shown in Fig. 1. This can be considered as the all-in-focus image. The sequential images Fig. 10b show the results of the proposed method. The upper and lower rows correspond to the separated direct and global components, respectively, and the refocused images are arranged horizontally.
The refocused images of the direct component elucidate the 3D structure of the cells in the embryo, whereas the all-in-focus images lack such depth information. The refocused images of the global component describe the light scattered in the cells. Compared with these images, the refocused images of the direct component more clearly captures organelles, such as membranes, thereby contributing to the monitoring of cell cultivation. These results demonstrate that the proposed method successfully integrates computational refocusing with the separation of the direct and global components.
The green straight lines in the sequential images (b) indicate the 3D structure of the cells determined by observing the direct component. The number represents the order of the stacking cells along d.
The all-in-focus image of sample 1 suggests that the embryo contains only six cells. However, the refocused images of the direct component reveals eight stacking cells. In sample 2, the embryo contains eight cells, as in the case of the direct component associated with sample 1. In the case of sample 3, the stacking mouse cells associated with direct components are revealed. These results confirm that our method is valid for different samples. The same holds true for sample 4. Therefore, we have verified that the direct and global separation is effective for enhancing the visibility in the images. A movie illustrating input images, refocusing of the separated direct and global components using our proposed method are provided in the Online Resource 1.
7 Conclusion
In this paper, we propose an efficient method for integrating both computational refocusing and the separation of direct and global components into contact imaging. This technique contributes important functions, such as a shallow depth-of-field and visibility enhancement for transparent subjects, while allowing the use of a compact imaging device. Experimental results also demonstrate that these functions elucidate the 3D structure of the subject.
The technical contributions of this paper are threefold. First, we have proposed a method to capture the light field via contact imaging system by moving the point light source. Second, we have reformulated the computational refocusing in the least-squares form by introducing the concept of a defocused component. Third, we have proposed an algorithm for integrating the computational refocusing and the separation of direct and global components into a unified formulation. This contributes to the efficient acquisition of observations and allows fixing of the stripe mask.
This work addresses the challenge of developing a compact microscope that can be installed in an incubator. We have built the prototype for verifying the principle of integrating computational refocusing and the separation of the direct and global components. However, the development of the device is incomplete as the actual prototype is too large to be installed in an incubator. The remaining size requirements can be satisfied by substituting the point light source (with a motorized linear stage) with another compact device such as a display. This will be considered as a part of future work. Other improvements are possible. This system still requires many observations to realize high-quality live-cell imaging, and can be optimized via e.g. multi-plex illumination. In this work, computational refocusing and direct-global separation are performed in 1D. For extending the method to 2D, such optimization will be significant. Further experimental validations are also desirable, and will be conducted in future work.
Notes
Using a two-dimensional (2D)- checkerboard pattern will have more natural effect, however, for the ease of theoretical validation and implementation, we only consider a one-dimensional (1D) pattern in this study.
References
Achar, S., Nuske, S., & Narasimhan, S. G. (2013). Compensating for motion during direct-global separation. In 2013 IEEE international conference on computer vision (pp. 1481–1488).
Asif, M. S., Ayremlou, A., Veeraraghavan, A., Baraniuk, R. G., & Sankaranarayanan, A. C. (2015). Flatcam: Replacing lenses with masks and computation. In 2015 IEEE international conference on computer vision workshop (ICCVW) (pp. 663–666).
Bimber, O., & Koppelhuber, A. (2017). Toward a flexible, scalable, and transparent thin-film camera. Proceedings of the IEEE, 105, 960–969.
Bishara, W., Sikora, U., Mudanyali, O., Su, T. W., Yaglidere, O., Luckhart, S., et al. (2011). Holographic pixel super-resolution in portable lensless on-chip microscopy using a fiber-optic array. Lab on a Chip, 11(7), 1276–1279.
Bishara, W., Su, T. W., Coskun, A. F., & Ozcan, A. (2010). Lensfree on-chip microscopy over a wide field-of-view using pixel super-resolution. Optics Express, 18(11), 11181–11191.
Cui, X., Lee, L. M., Heng, X., Zhong, W., Sternberg, P. W., Psaltis, D., et al. (2008). Lensless high-resolution on-chip optofluidic microscopes for caenorhabditis elegans and cell imaging. Proceedings of the National Academy of Sciences, 105(31), 10670–10675.
Daloglu, M. U., Luo, W., Shabbir, F., Lin, F., Kim, K. B. S., Lee, I., et al. (2017). Label-free 3D computational imaging of spermatozoon locomotion, head spin and flagellum beating over a large volume. Light: Science & Applications, 7, 17121.
Daloglu, M. U., & Ozcan, A. (2017). Computational imaging of sperm locomotion. Biology of Reproduction, 97(2), 182–188.
Fuchs, C., Heinz, M., Levoy, M., Seidel, H. P., & Lensch, H. P. A. (2008). Combining confocal imaging and descattering. Computer Graphics Forum, 27(4), 1245–1253. https://doi.org/10.1111/j.1467-8659.2008.01263.x.
Greenbaum, A., Zhang, Y., Feizi, A., Chung, P. L., Luo, W., Kandukuri, S. R., et al. (2014). Wide-field computational imaging of pathology slides using lens-free on-chip microscopy. Science Translational Medicine, 6(267), 267ra175.
Guo, K., Bian, Z., Dong, S., Nanda, P., Wang, Y. M., & Zheng, G. (2015a). Microscopy illumination engineering using a low-cost liquid crystal display. Biomedical Optics Express, 6(2), 574–579.
Guo, K., Dong, S., Nanda, P., & Zheng, G. (2015b). Optimization of sampling pattern and the design of fourier ptychographic illuminator. Optics Express, 23(5), 6171–6180.
Gupta, M., Tian, Y., Narasimhan, S. G., & Zhang, L. (2011). A combined theory of defocused illumination and global light transport. International Journal of Computer Vision, 98, 146–167.
Heng, X., Erickson, D., Baugh, L. R., Yaqoob, Z., Sternberg, P. W., Psaltis, D., et al. (2006). Optofluidic microscopy—a method for implementing a high resolution optical microscope on a chip. Lab on a Chip, 6(10), 1274–1276.
Isikman, S. O., Bishara, W., Mavandadi, S., Yu, F. W., Feng, S., Lau, R., et al. (2011). Lens-free optical tomographic microscope with a large imaging volume on a chip. Proceedings of the National Academy of Sciences of the United States of America, 108(18), 7296–301.
Isikman, S. O., Greenbaum, A., Luo, W., Coskun, A. F., & Ozcan, A. (2012). Giga-pixel lensfree holographic microscopy and tomography using color image sensors. PloS ONE, 7(9), e45. 044.
Jensen, H. W., & Christensen, P. H. (1998). Efficient simulation of light transport in scenes with participating media using photon maps. In Proceedings of the 25th annual conference on computer graphics and interactive techniques—SIGGRAPH ’98 (pp. 311–320). New York, NY: ACM Press. https://doi.org/10.1145/280814.280925.
Jensen, H. W., & Wann, H. (2001). Realistic image synthesis using photon mapping. Natick: A K Peters.
Kesavan, S. V., Momey, F., Cioni, O., David-Watine, B., Dubrulle, N., Shorte, S., et al. (2014). High-throughput monitoring of major cell functions by means of lensfree video microscopy. Scientific Reports, 4, 5942.
Lee, S. A., Erath, J., Zheng, G., Ou, X., Willems, P., Eichinger, D., et al. (2014). Imaging and identification of waterborne parasites using a chip-scale microscope. PloS ONE, 9(2), e89. 712.
Lee, S. A., Leitao, R., Zheng, G., Yang, S., Rodriguez, A., & Yang, C. (2011). Color capable sub-pixel resolving optofluidic microscope and its application to blood cell imaging for malaria diagnosis. PloS ONE, 6(10), e26. 127.
Levoy, M., Chen, B., Vaish, V., Horowitz, M., McDowall, I., & Bolas, M. (2004). Synthetic aperture confocal imaging. ACM Transactions on Graphics, 23(3), 825–834. https://doi.org/10.1145/1015706.1015806.
Levoy, M., Ng, R., Adams, A., Footer, M., & Horowitz, M. (2006). Light field microscopy. ACM Transactions on Graphics (TOG), 25(3), 924–934.
Lin, X., Wu, J., Zheng, G., & Dai, Q. (2015). Camera array based light field microscopy. Biomedical Optics Express, 6(9), 3179–3189.
Liu, Z., Tian, L., Liu, S., & Waller, L. (2014). Real-time brightfield, darkfield, and phase contrast imaging in a light-emitting diode array microscope. Journal of Biomedical Optics, 19(10), 106002.
Luo, W., Greenbaum, A., Zhang, Y., & Ozcan, A. (2015). Synthetic aperture-based on-chip microscopy. Light: Science & Applications, 4(3), e261.
Minzioni, P., Osellame, R., Sada, C., Zhao, S., Omenetto, F. G., Gylfason, K. B., et al. (2017). Roadmap for optofluidics. Journal of Optics, 19, 093003.
Mudanyali, O., Tseng, D., Oh, C., Isikman, S. O., Sencan, I., Bishara, W., et al. (2010). Compact, light-weight and cost-effective microscope based on lensless incoherent holography for telemedicine applications. Lab on a Chip, 10(11), 1417–28.
Nayar, S. K., Krishnan, G., Grossberg, M. D., & Raskar, R. (2006). Fast separation of direct and global components of a scene using high frequency illumination. In ACM SIGGRAPH 2006 papers, SIGGRAPH ’06 (pp. 935–944). New York, NY: ACM. https://doi.org/10.1145/1179352.1141977.
Ou, X., Horstmeyer, R., Yang, C., & Zheng, G. (2013). Quantitative phase imaging via fourier ptychographic microscopy. Optics Letters, 38(22), 4845–4848.
Ozcan, A., & Mcleod, E. (2016). Lensless imaging and sensing. Annual Review of Biomedical Engineering, 18, 77–102.
Saxena, M., Eluru, G., & Gorthi, S. S. (2015). Structured illumination microscopy. Advances in Optics and Photonics, 7(2), 241–275. https://doi.org/10.1364/AOP.7.000241.
Seo, S., Su, T. W., Tseng, D. K., Erlinger, A., & Ozcan, A. (2009). Lensfree holographic imaging for on-chip cytometry and diagnostics. Lab on a Chip, 9(6), 777–787.
Shimano, M., Bise, R., Zheng, Y., & Sato, I. (2017). Separation of transmitted light and scattering components in transmitted microscopy. In M. Descoteaux, L. Maier-Hein, A. Franz, P. Jannin, D. L. Collins, & S. Duchesne (Eds.), Medical image computing and computer-assisted intervention—MICCAI 2017 (pp. 12–20). Cham: Springer.
Su, T. W., Seo, S., Erlinger, A., & Ozcan, A. (2009). High-throughput lensfree imaging and characterization of a heterogeneous cell solution on a chip. Biotechnology and Bioengineering, 102(3), 856–868.
Tanaka, K., Mukaigawa, Y., Matsushita, Y., & Yagi, Y. (2013). Descattering of transmissive observation using parallel high-frequency illumination. IEEE international conference on computational photography (ICCP) (pp. 1–8). https://doi.org/10.1109/ICCPhot.2013.6528300.
Tian, L., Wang, J., & Waller, L. (2014). 3D differential phase-contrast microscopy with computational illumination using an led array. Optics Letters, 39(5), 1326–1329.
Waller, L., Kou, S. S., Sheppard, C. J., & Barbastathis, G. (2010). Phase from chromatic aberrations. Optics Express, 18(22), 22817–22825.
Wang, M., Feng, S., & Wu, J. (2017). Multilayer pixel super-resolution lensless in-line holographic microscope with random sample movement. Scientific Reports, 7, 12791.
Wu, Y., & Ozcan, A. (2017). Lensless digital holographic microscopy and its applications in biomedicine and environmental monitoring. Methods, 136, 4–16.
Zheng, G., Horstmeyer, R., & Yang, C. (2013). Wide-field, high-resolution fourier ptychographic microscopy. Nature Photonics, 7(9), 739–745.
Zheng, G., Kolner, C., & Yang, C. (2011). Microscopy refocusing and dark-field imaging by using a simple led array. Optics Letters, 36(20), 3987–3989.
Zheng, G., Lee, S. A., Yang, S., & Yang, C. (2010). Sub-pixel resolving optofluidic microscope for on-chip cell imaging. Lab on a Chip, 10(22), 3125–3129.
Acknowledgements
This study was partially supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant No. J26700013 and Japan Science and Technology Agency (JST) CREST Grant Number JPMJCR1764.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Dr. Mohit Gupta.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 1 (mp4 39133 KB)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kuniyoshi, F., Funatomi, T., Kubo, H. et al. Visibility Enhancement by Integrating Refocusing and Direct-Global Separation with Contact Imaging. Int J Comput Vis 127, 1162–1174 (2019). https://doi.org/10.1007/s11263-019-01173-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11263-019-01173-5