Abstract
A physical model to describe the contact between rubber and a rough surface with water as intermediate medium is presented. The Navier–Stokes equations are simplified and surface properties are approached by the Abbott–Firestone curve to generate an approximative description of the water squeeze out between a visco-elastic rubber block and a macro-rough surface. The model is used to describe the pattern dependent wet grip performance of vehicle tires at moderate water heights between pure wetgrip and full hydroplaning. Influence of surface macro-roughness, water height, tire pattern, and vehicle speed on braking performance is considered in particular. For validation purpose, braking tests on two different surfaces were done at an inner drum test bench. Test results show good agreement with the theory presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
There are various approaches to describe rubber friction of rough surfaces. Most of them try to model hysteretic friction on different length scales [1,2,3,4,5]. In [6], Persson proposes a method to describe wet grip with sealing effects. Water trapped in substrate pools smoothens the track and therefore reduces hysteretic friction. In [7, 8] the squeeze out of water between a solid track and rubber is described with viscosity effects. In [9] hysteretic friction of a rubber block moving on a rough surface is approached with a simplified visco-elastic contact. In [10] the model is expanded to wet conditions with the viscous squeeze out of a fluid film. On the other hand exist detailed finite element and finite volume models to describe the effects of tire profile and tread depth on hydroplaning behavior [11]. A more simple hydroplaning model of a slick tire is proposed in [12, 13]. Already small water heights of 1–3 mm have a significant impact on braking force transmission between track and tire, although no full hydroplaning occurs yet [14]. These effects could be seen in our tests especially for high vehicle speeds above 80 km/h. The theories for very thin waterfilms presented in [7, 10, 15] are based on viscous effects and will reach their boundaries at higher water heights. The theory presented in [16] is only valid at low vehicle speeds. For higher velocities and water heights inertia effects will be of major importance in the squeeze out process, as shown by Bathelt [17, p. 31]. The main focus of the model presented here is to predict wet grip performance for high vehicle speeds and moderate water heights, when no hydroplaning occurs yet. It has to be mentioned, that we aim to examine wet grip only at discrete speeds and not for the deceleration until zero. The combination of moderate water heights and high vehicle speed was already examined in [18]. He reduces the problem to a simple equation for the water height between tire and road. This is achieved, among other things, by neglecting squeeze out in the direction of travel and reducing track characteristics to two scalar values described as ’texture depth’ and ’connectivity factor’. In contrast to [18], less simplifying assumptions are to be made in this study in order to develop a physically more valid model.
To describe the pattern dependent impact of water height on the braking performance, a physical model of a single tread block is developed. Main goal is to calculate the inertia-driven squeeze out of water under a single tread block and thus the contact area between rubber and track. This allows a qualitative estimation of pattern effects independent of absolute friction levels. The underlying assumption is, that for small water heights the water squeezed out under a single tread block is consumed by the surrounding grooves. Rubber properties, track macro-roughness, and tire load are taken into account. To validate the model, braking tests with various pattern layouts on two different tracks where done at an inner drum test bench at KIT.
This paper is organized as follows: In Sect. 2 we give a detailed description of the physical model and an interpretation of the quantities calculated. In Sect. 3 we describe the setup for the braking tests at different parameter combinations and validate the simulation results with the test results. In Sect. 4 we summarize the new findings and give an outlook on possible improvements and enhancements of the model.
2 Model
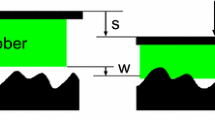
Considering the contact between an elastic rubber block and a macro-rough track (e.g., Asphalt) which is partly covered with water, we get the conditions shown in Fig. 1. The zero position of the \(x,y,z\)-coordinate system is placed in the medium road level. Track valleys are filled with water up to a height \(h(t)\). The surface area covered by water is called \(A_{\rm F}(h)\). Mean fluid pressure \(p_{\rm F}(t)\), defined as overpressure relative to ambient pressure, deforms the rubber in this area by a distance \(s^*(t)\), assuming that the mean water height \(h(t)\) is equal everywhere under the tread block. On the area \(A_{\rm R}(h)\) asperities penetrate the fluid film and contact between track and rubber is established on the largest length scale. Micro-roughness on smaller length scales and fluid viscosity determine the local friction coefficient on these asperities. We do not aim to predict the absolute friction coefficient on these asperities, but only how fast \(A_{\rm R}(h)\) increases during braking dependent on water height, speed, and pattern layout independently of the friction level on the asperities; therefore, roughness on smaller length scales is not considered in this approach. Where contact is established, the rubber is deformed by a distance \(s(x,y,h(t))+s^*(t)\). The mean contact pressure on the asperities is described by \(p_{\rm R}(t)\). The track profile is given by \(Z(x,y)\). Furthermore the relationship \(s(x,y,h(t))= Z(x,y)- h(t)\) is given. For the sake of clarity in the further model description the function arguments will only be written if they are of particular interest. The local problem description is now transformed into a global description by averaging the local rubber deformation \(s(x,y,h(t))\) over the area of contact \(A_{\rm R}(h)\) which leads to the mean rubber deformation
This relation is shown in Fig. 2. Thus we have a system with two degrees of freedom, described by the water height \(h(t)\) and the rubbber deformation \(s^*(t)\). Figure 3 shows a rectangular tread block with edge lengths \(B\) and \(L\) and surface area \(A\) on a rough track with an intermediate fluid. While the tread block sinks in all water has to be squeezed out through the boundary surface \(A_q(h)= 2(A_{q_x}(h)+ A_{q_y}(h))\). The fluid volume trapped between tread block and track is described as control volume \(V_{\rm C}(h)\) . The newly introduced sizes \(A_{\rm F}(h)\), \(A_{\rm R}(h)\), \(A_q(h)\) and \(\bar{s}(h)\) can be calculated from the Abbott–Firestone curve of the corresponding track and will represent the track influence on squeeze out in the equations derived later. The Abbott–Firestone curve is the cumulative probability density function of the surface profile height \(Z(x,y)\) and describes the material share \(x_a(z_a)\) dependent on the track height \(z_a\). The two tracks used in this paper are shown in Fig. 4. The mean texture depth MTD is 1 mm for asphalt and 0.2 mm for Safety-Walk™. Looking at the curve for asphalt, we can see for example that \(x_a(0\,{\rm mm})=50\%\), which means that for a water height of 0 mm 50% of the track is covered with water. Another example would be \(z_a= 1\,{\rm mm}\) for Asphalt, with \(x_a= 2\%\) which means roughly \(98\%\) of the track is covered with water. With this definition we can write
and
for rectangular block geometries. \(V_{\rm C}\) will be used later.
Sahlin et al. [19] used the Abbott–Firestone curve of different surfaces to determine surface dependent flow factors. They showed numerically that ‘the Abbot curve acts as an unambiguous two-dimensional surface classification in hydrodynamic lubrication with this homogenization approach’ [19]. Although the approach used here is different, we can use this as encouragement to capture the track influence on squeeze out with the Abbott–Firestone curve. When a load is applied to the tread block, the fluid is accelerated and flows through the boundary surface \(A_q(h)\). This flow will be calculated approximately through the Navier–Stokes equations. All viscous terms are neglected in a first step, since the considered average water height is between 0.5 and 3 mm and for these water heights inertia effects are dominant. Neglecting viscous terms also means that the shape of the boundary surface \(A_q(h)\) has no influence, only it’s size. This is of great importance, since the shape of the surface is an information with is not included in the Abbott curve. Furthermore, the velocity distribution \(\mathbf {v}_{\rm F}= (u(x), v(y), w(z))^T_{x,y,z}\) inside the fluid is calculated according to the analytical approximate solution for the fluid flow between a smooth elliptical rigid disc and a smooth rigid surface proposed in [17].
The linearity in \(x\)- and \(y\)-direction and the independence of z shown in Fig. 5 follows from the neglection of viscous terms inside the fluid. The fluid velocity \(w(z)\) in z-direction is neglected because the relation \(h(t)\ll B, L\) applies.
The relation between the velocities in \(x\)- and \(y\)-direction is set to \(\psi =f_{B}(h)\cdot f_{L}(h)^{-1} = L \cdot B^{-1}\) based on the analytical solution of an elliptical rigid disc according to [17]. We use this for velocity distribution for rectangular block geometries too, because the error caused by this approximation is small as shown in [17]. The fluid velocity coefficients \(f_{L}(h)\) and \(f_{B}(h)\) are functions of the water height \(h(t)\) and it’s time derivative \({\dot{h}}(t)\) as shown in Sect. 2.1.
2.1 Continuity Equation
Applying the continuity equation and the incompressibility of the fluid on our control volume \(V_{\rm C}(h)\) gives us

where \({\dot{V}}_{{\rm in}}\) is the volume flow in \(V_{\rm C}(h)\) and \({\dot{V}}_{{\rm out}}\) the volume flow out of \(V_{\rm C}(h)\). The volume change of our control volume is given by
with \({\dot{h}}(t)\) as time derivative of the water height \(h(t)\). The perpendicular velocities \(v_{{\rm out}_{\perp }, A_{q_x}}(y)\) and \(v_{{\rm out}_{\perp }, A_{q_y}}(x)\) at the outflow boundaries \(A_{q_x}(h)\) and \(A_{q_y}(h)\) are given by
and
which allows us to write
Inserting the relations from 9 and 14 in 8 leads to
and
The geometric factor \(C\) is very similar to the hydraulic diameter. For the derivation of the governing equations the factor \(\psi \) will be held variable, but is assumed to be time independent.
2.2 Energy Conservation
With the given simplifications we can now set up the energy balance for the fluid between tread block and track:
\({\dot{W}}_{{\rm in}}\) is the power entry through the vertical movement of the treadblock. \({\dot{W}}_{{\rm kin}}\) is the change of kinetic energy inside the fluid, \({\dot{W}}_{{\rm out}}\) describes the energy loss due to fluid flow over the boundaries of our control volume. \({\dot{W}}_{{\rm visc}}\) describes an approximation of the losses through viscous friction inside the fluid.
2.2.1 Energy Input
The energy input \({\dot{W}}_{{\rm in}}\) into the fluid is defined by the product of fluid pressure \(p_{\rm F}(t)\), fluid surface \(A_{\rm F}(h)\) and the sink in velocity \({\dot{h}}\).
The negative algebraic sign is caused by the fact, that \(h(t)\) and the resulting pressure \(p_{\rm m}(t)\) on the fluid point into opposite directions.
2.2.2 Change of Kinetic Energy
The change of kinetic energy \({\dot{W}}_{{\rm kin}}\) inside the fluid is defined by
\(\rho \) is the density of water. An equivalent expression is
where \(V_{\infty }\) is the possible infinite volume underneath the tread block. The fact, that for a lower waterheight the share of \(V_{\rm C}(h)\) in the complete volume is lower, is taken into account by the correction factor
which can be calculated from the Abbott curve, as shown in Eq. 2, and equals 1 above the highest asperity and 0 below the deepest valley. Applying the integration boundaries to Eq. 21 leads to
for a rectangular block under the assumption of symmetry in \(x\)- and \(y\)-direction. Taking Eqs. 16, 17 and Leibniz’ rule of integration into account leads to (see “Appendix B”)
\(G_1(h)\), \(G_2(h)\), \(G_3(h)\), \(K(h)\), \(\kappa (z)\) and later \(G_4(h)\) are track parameters which can be calculated from the Abbott–Firestone curve of the track used with Eqs. 2–4.
2.2.3 Energy Outflow
The energy outflow is defined by the water velocity \(v_{{\rm out}}(x,y)\) at the outflow and the mass flow density through the boundary surface \(A_q(h)\).
The fluid velocities \(v_{{\rm out}, A_{q_x}}(y)\) and \(v_{{\rm out}, A_{q_y}}(x)\) at the outflow boundaries \(A_{q_x}(h)\) and \(A_{q_y}(h)\) are defined similar to Eqs. 10 and 11 by
The mass outflow density \({\dot{m}}_{{\rm out}}\) is given by
Equations 10, 11, 28, 29 and 30 allow to simplify Eq. 27 to (see “Appendix C”)
The geometric factor C was already introduced in Eq. 15.
2.2.4 Viscous Losses
To take the damping effect of viscous losses in the fluid into account an additional term \({\dot{W}}_{{\rm visc}}\) is introduced. It describes the energy dissipation through viscous friction inside the fluid. In reality a combination of inertia and viscous driven flow would cause a complex velocity distribution inside the fluid. We neglect the influence of inertia for the calculation of the viscous losses, and later use the principal of superposition to add up inertia and viscous terms. We assume a flat track with a given water height \({\bar{h}}(h)\), which contains the same amount of water as a rough track at a water height \(h(t)\). This leads to
The \(x,y\)-plane describes a flat track and the equivalent water height \({\bar{h}}(h)\) is measured in \(z'\)-direction as shown in Fig. 6. The Velocity distribution \(\mathbf {v}(x,y,z') = (u(x,z'),v(y,z'), w(x,y,z'))^T_{x,y,z'}\) for a pure viscous flow in a thin water film is given by a Poiseuille flow [20]. The single entries are
and
where \(\mu \) is the dynamic viscosity of water. Again the velocity \(w(x,y,z')\) is neglected because of \({\bar{h}}(h)<<B, L\). Integrating over the water height \({\bar{h}}(h)\) leads to
The applicable boundary conditions are
and
The assumption of a purely viscous flow hence leads to a quadratic velocity distribution, which is shown in Fig. 6. We want to calculate the energy dissipation for a sink in velocity which is equal to the one caused by a purely inertia-driven flow described by Eqs. 6 and 7. This means the volume flow over the boundaries of \(V_{\rm C}(h)\) has to be same and therefore the relation
holds. Integrating leads to
and therefore
Using Eq. 36 gives us the velocity distributions
and
The second derivatives are
and
The energy loss in case of a pure viscous flow is calculated according to [Bathelt [17], p.45] as
2.3 Pressure Equilibrium
In a first step the rubber behavior is approached by a Kelvin–Voigt element. The modulus of elasticity \(E\) is set to 14 MPa. This value was chosen to achieve a contact area of \(~65\%\) under static load. This value equals the area of contact obtained from static footprint measurements on a Fujifilm prescale pressure sheet with the test tires. This value is at the upper level of rubber elasticity values since the model approach corresponds to an infinite number of parallel Kelvin–Voigt elements which are not coupled with each other. Shear stress between neighboring elements is neglected. The viscosity \(\eta \) is \(5\times 10^4\) Pa s. This value did not have a significant impact on the results, as long as it’s chosen large enough to prevent oscillations of the rubber block when it hits the asperities. The contact pressure \(p_{\rm F}(t)\) between fluid and rubber is calculated according to
where \(s_0\) describes the height of the undeformed tread block, respectively the height of the Kelvin–Voigt element. The contact pressure between rubber and track is given by
where \(\bar{s}(h)\) is the mean penetration depth given by Eq. 1. Fluid and track combined have to carry the tread block load \(F_z(t)\), which leads to
The mean pressure on a single tread block \(p_{\rm m}(t)\) is given by
2.4 Differential Equation System
Energy conservation and pressure equilibrium lead to a system of two coupled, non-linear and implicit differential equations with \(h(t)\) and \(s^*(t)\) as degrees of freedom. The state vector \({\mathbf{x}}\) is given by \((h(t), {\dot{h}}(t), s^*(t))^T\) and it’s time derivative by \(\dot{{\mathbf{x}}}=({\dot{h}}(t), {\ddot{h}}(t), \dot{s}^*(t))^T\). The resulting system of differential equations is
Equation 55 describes the fact that the entries of \({\mathbf{x}}\) are not independent, but the second entry of \({\mathbf{x}}\) is the time derivative of the first entry. It should be noted that for a more complex rubber model the state vector could be expanded to \((h(t), {\dot{h}}(t), s^*(t), \dot{s}^*(t))^T\). The initial water height \(h_0\) is given by the amount of water on the track. For the positioning of our coordinate system in Fig. 1 1 mm water height means the track contains \(1\) l/m2 if all asperities are covered with water. For lower water heights \(h_0\) is adjusted that it describes the corresponding volume (e.g \(0.5\,{\rm mm} \equiv 0.5\,{\rm l/m}^{2} \rightarrow h_0= 0.46\,{\rm mm}\) with Eq. 5 and \(V_{\rm C}=0.5\,{\rm mm}\,A\)). An initial rubber deformation of \(s^*_0=0\) is assumed. For the calculation of the initial sink in velocity \({\dot{h}}_0\) it is assumed, that the kinetic energy of a single tread block
is converted into kinetic energy \(W_{{\rm kin},F}\) of the fluid
\(\rho _{\rm R}\) is the density of rubber. \(\dot{y}_{\perp }\) describes is the vertical velocity of a tread block on an undisturbed circular path before it hits the fluid film. Since churning losses will occur a factor \(\gamma _{\rm T}\) is introduced which describes how much of the kinetic energy of the tread block is converted into fluid velocity \(\mathbf {v}_{\rm F}\). This leads to
and after some transformations to
If no churning losses occur \(\gamma _{\rm T}\) is set to one, otherwise \(\gamma _{\rm T}\in [0, 1]\). Without more detailed considerations we assume a churning loss of \(50\%\).
The differential equation system from Eqs. 53 to 55 is solved with ode15i of \(\textsc {Matlab}\)™. Figure 7 shows some of the calculated quantities for one of our patterns (BB, see Fig. 9a) at 120 km/h and 2 mm water height on an asphalt track. The main result is the water height \(h(t)\) under a tread block as shown in Fig. 7a. The dotted lines symbolize the highest peaks and lowest valleys of the track used. The chain dotted line shows the circular path of a tread block on an undeflected tire with constant radius. As shown in Fig. 7b, the simulation starts wit a fluid pressure of 0.3 MPa, which means the whole tread block load \(F_Z(t)\) is carried by the fluid film. When the first asperities penetrate the fluid film, the contact pressure between track and rubber \(p_{\rm R}(t)\) increases rapidly, which is caused by rubber damping and large deformation velocity. At the same time the fluid pressure \(p_{\rm F}(t)\) decreases, since an increasing part of the tire load \(F_z(t)\) is carried by the asperities. For \(t\rightarrow \infty \) the fluid pressure aims towards zero and the contact pressure \(p_{\rm R}(t)\) aims towards \(p_{\rm R}(t \rightarrow \infty )=p_{\rm m}(t)\cdot A\cdot A_{\rm R}(h(t \rightarrow \infty ))^{-1}\). Inserting \(h(t)\) in \(A_{\rm R}(h)\) and normalizing the result with \(A\), we obtain the time dependent relative area of contact between track and tread block which is shown in Fig. 7c. This value is averaged over the length of the footprint \(l_{\rm fp}\), which gives us the dimensionless scalar value
where \(t_{\rm c}\) describes the time the tread block is inside the contact patch. This value gives an idea how much contact between track and tread block is established during the simulation. Table 1 shows the sensitivity of \(A_{\rm rel}\) to a change of \(+\,10\%\) of the described parameters. The parameter \(\gamma _T\) describing the churning losses only has a very small influence on \(A_{\rm rel}\). Increasing the length respectively size of the footprint reduces the mean pressure acting on a single tread block and therefore aggravates the squeeze out, which leads to a smaller value of \(A_{\rm rel}\). An increased vertical load causes a faster squeeze out and therefore a larger contact area. Increasing the material stiffness E or the dynamic viscosity \(\eta \) decreases the area of contact. The effect of modified model parameters is rather similar for all water heights and speeds and is therefore not critical for the evaluation of pattern, speed, and water height influence. In Sect. 3 we compare \(A_{\rm rel}\) with maximum friction coefficients from braking tests. The underlying assumption is that the transmittable friction forces are proportional to the area of contact. This approach does not take into account that in the front part of the footprint fewer braking forces are transmitted compared to the rear part and therefore not only the total contact area, but also it’s distribution within the footprint is of importance for the transmittable braking forces.
3 Results/Validation
Braking tests on Asphalt and Safety-Walk™ at the inner drum test bench at KIT are performed for validation of the physical model. Figure 8 shows the topography of the two tracks used. The larger macro texture of the asphalt track is clearly visible and leads to the big differences between the Abbott curves shown in Fig. 4. The average friction level on wet for the compound used in this study is roughly 0.7 on asphalt and 1.0 on Safety-Walk™. This is caused by the different micro-texture, which is neither captured by the track measurement nor represented by the Abbott curve. Since we do not consider the micro-roughness for our model, this is not a problem. The test bench consists of a steel drum with an inside diameter of 3.8 m which is equipped with an Asphalt or Safety-Walk™ track and a hydraulically driven wheel suspension with built-in measuring hub. The drum rotates with a constant circumferential speed which corresponds to the driving speed. The tire is braked by the hydraulic wheel guide and the resulting forces are recorded with the measuring hub. While the tire is decelerated, the drum speed is kept constant. This allows the measurement of a friction coefficient at a discrete driving speed. For a detailed description of the test bench see [21]. Tires with the dimensions 245/45 r18 and different pattern layouts (BB = big blocks, SB = small blocks and SBv = small blocks with more void volume) were tested at speeds from 80 to 140 km/h and water heights of 1–3 mm. The schematic pattern layout is shown in Fig. 9. The direction of travel is vertical. For the detailed block geometries see “Appendix A”. The tire load was set to 4875 N with an inflation pressure of 2.1 bar. The test result used for model validation is the maximum friction coefficient \(\mu _{\max }\) measured during braking with varying the wheel slip at constant drum speed. Water heights were measured capacitively, which means 1 mm equals \(1\)l/m2. The same definition was used for the model.
In Fig. 10a test and simulation results are shown for a water height of 1 mm on Asphalt. The rating value for the test results is calculated by normalizing the measured maximum friction coefficients with the friction coefficient measured at 80 km/h for small blocks. The rating value for the model is calculated by normalizing \(A_{\rm rel}\) introduced in Eq. 62, with the value of \(A_{\rm rel}\) calculated for 80 km/h and small blocks. As one can see there is a good qualitative agreement for the decrease over velocity for all patterns. The difference predicted by the model between small blocks at \(25\%\) and \(35\%\) void volume is confirmed by the test. One reason is the larger surface pressure, which causes a faster squeeze out of water. The second reason is the slightly shorter squeeze out distance. The disadvantage of big blocks is underestimated by the model, which could be explained by the higher geometric stiffness in vertical direction of the big blocks. This effect is not captured by the model and will aggravate squeeze out because of the higher contact pressure \(p_{\rm R}(t)\). Therefore the penetration depth of the asperities is lower which is associated with a smaller contact area.
In Fig. 10b test and simulation results of the same three patterns are shown for a water height of 1 mm on Safety-Walk™ (For the track characteristic see Fig. 4). Again, all values are normalized with the test/simulation result at 80 km/h for small blocks. The pattern ranking (order of the patterns) matches well, except for small blocks with high void at 80 km/h. The decrease over velocity is slightly underestimated, except for the high void pattern. One reason could be, that the grooves start filling with water for the low void patterns, which aggravates the squeeze out effect.
The track dependent decrease of grip over velocity is clearly visible if we compare the two tracks. As expected the velocity dependence on Safety-Walk™ is much stronger, which can be explained by the poor drainage capability of the track and therefore slower squeeze out. This effect is captured by the model through the Abbott curve of the given track, which allows a detailed consideration of track properties.
In Fig. 11 we see the results of big blocks for 1 and 2 mm water height, scaled to the values at 80 km/h and 1 mm. On asphalt there is a good match between test and model. On Safety-Walk™ the spread between 1 and 2 mm is underestimated by the model. The reason might be, that for 2 mm the grooves start to fill and the underlying single block consideration reaches it’s boundaries. This can be verified by calculating the maximum amount of water which fits into the grooves. For a given tread depth of 7.5 mm and a relative void volume of \(25\%\), the maximum water height which can be taken by the grooves is roughly \(h_{\max }=0.25\cdot 7.5\,{\rm mm}=1.875\,{\rm mm}\), if we neglect the drainage volume of the track. For asphalt the maximum water height is larger, since the track macro-roughness provides additional drainage volume.
4 Conclusions
The introduced model allows a qualitative comparison of simple patterns for different tracks, water heights, and driving speeds. Impact of load and void level is included in the model and confirmed by the test results. The boundaries of the model are reached when tire grooves start to fill completely with water and the transition to hydroplaning occurs, which could be seen in the test results for 2 mm on Safety-Walk™. To capture the transition to hydroplaning, the consideration of the whole footprint would be necessary, including the time dependent flooding of the tire void. A quantitative prediction of grip would require the consideration of slip and a friction model that takes micro-roughness into account, which was not the goal of this study. The block deformation during braking is also expected to have an impact on squeeze out and will be considered in a future study by coupling the presented squeeze out model with a finite element simulation of a visco-elastic rubber block sliding on a macro-rough surface.
Change history
16 May 2021
A Correction to this paper has been published: https://doi.org/10.1007/s11249-021-01448-4
Abbreviations
- \(A\) :
-
Surface area of tread block
- \(A_{\rm F}(h)\) :
-
Area of contact between fluid and rubber
- \(A_q(h)\) :
-
Free area between track and tread block
- \(A_{q_x}(h)\) :
-
Free area between track and tread block parallel to y, z-plane
- \(A_{q_y}(h)\) :
-
Free area between track and tread block parallel to x, z-plane
- \(A_{\rm R}(h)\) :
-
Area of contact between track and rubber
- \(B\) :
-
Width of tread block
- \(C\) :
-
Geometric factor
- \(E\) :
-
Modulus of elasticity of Kelvin–Voigt element
- \(\eta \) :
-
Viscosity of Kelvin–Voigt element
- \(f_{L}(h)\) :
-
Water height dependent fluid velocity coefficient in x-direction
- \(f_{B}(h)\) :
-
Water height dependent fluid velocity coefficient in y-direction
- \(F_z(t)\) :
-
Load on tread block
- \(\gamma _{\rm T}\) :
-
Factor for churning losses
- \(G_1(h)\) :
-
Track parameter
- \(G_2(h)\) :
-
Track parameter
- \(G_3(h)\) :
-
Track parameter
- \(G_4(h)\) :
-
Track parameter
- \(h(t)\) :
-
Water height
- \({\dot{h}}(t)\) :
-
Initial change of water height
- \(h_0\) :
-
Initial water height
- \({\bar{h}}(h)\) :
-
Equivalent water height
- \(K(h)\) :
-
Track parameter
- \(\kappa (z)\) :
-
Correction factor for control volume \(V_{\rm C}\)
- \(L\) :
-
Length of tread block
- \({\dot{m}}_{{\rm out}}\) :
-
Mass flow density over the control volume boundaries
- \(\mu \) :
-
Dynamic viscosity of fluid
- \(p_{\rm F}(t)\) :
-
Mean fluid pressure
- \(p_{\rm m}(t)\) :
-
Mean pressure acting on tread block
- \(p_{\rm R}(t)\) :
-
Mean contact pressure at interface \(A_{\rm R}(h)\)
- \(\psi \) :
-
Relation between \(f_{L}\) and \(f_{B}\)
- \(\rho \) :
-
Density of water
- \(\rho _{\rm R}\) :
-
Density of rubber
- \(s(x,y,h(t))\) :
-
Local rubber deformation at interface \(A_{\rm R}(h)\)
- \(\bar{s}(h)\) :
-
Mean rubber deformation at interface \(A_{\rm R}(h)\)
- \(s^*(t)\) :
-
Additional rubber deformation at interface \(A_{\rm F}(h)\)
- \(\dot{s}^*(t)\) :
-
Time derivative of additional rubber deformation at interface \(A_{\rm F}(h)\)
- \(\mathbf {v}_{\rm F}\) :
-
Fluid velocity
- \(u(x)\) :
-
Fluid velocity in x-direction
- \(v(y)\) :
-
Fluid velocity in y-direction
- \(w(z)\) :
-
Fluid velocity in z-direction
- \(t_{\rm c}\) :
-
Contact time
- \(u(x,z')\) :
-
Fluid velocities x-direction in equivalent coordinate system
- \(v(y,z')\) :
-
Fluid velocities y-direction in equivalent coordinate system
- \(w(x,y,z')\) :
-
Fluid velocities z-direction in equivalent coordinate system
- \(v_{{\rm out}}(x,y)\) :
-
Fluid velocity at boundary surfaces
- \(v_{{\rm out}, A_{q_x}}(y)\) :
-
Fluid velocity at boundary surface \(A_{q_x}\)
- \(v_{{\rm out}, A_{q_y}}(x)\) :
-
Fluid velocity at boundary surface \(A_{q_y}\)
- \(v_{{\rm out}_{\perp }, A_{q_x}}(y)\) :
-
Perpendicular fluid velocity at boundary surface \(A_{q_x}\)
- \(v_{{\rm out}_{\perp }, A_{q_y}}(x)\) :
-
Perpendicular fluid velocity at boundary surface \(A_{q_y}\)
- \(V_{\rm C}(h)\) :
-
Control volume
- \({\dot{V}}_{{\rm in}}\) :
-
Volume flow in \(V_{{\rm in}}\)
- \(V_{\infty }\) :
-
Infinite volume under tread block
- \({\dot{V}}_{{\rm out}}\) :
-
Volume flow out \(V_{{\rm out}}\)
- \({\dot{W}}_{{\rm in}}\) :
-
Engery flow into \(V_{\rm C}\)
- \({\dot{W}}_{{\rm kin}}\) :
-
Change of kinetic energy inside \(V_{\rm C}\)
- \(W_{{\rm kin},F}\) :
-
Initial kinetic energy of fluid
- \({\dot{W}}_{{\rm out}}\) :
-
Energy flow out of \(V_{\rm C}\)
- \({\dot{W}}_{{\rm visc}}\) :
-
Viscous losses inside \(V_{\rm C}\)
- \({\mathbf{x}}\) :
-
State vector
- \(x_a\) :
-
Material share
- \(x,y,z'\) :
-
Coordinate system for equivalent water height
- \(\dot{y}_{\perp }\) :
-
Initial vertical velocity of tread block on an undisturbed circular path
- \(Z(x,y)\) :
-
Track profile
- \(z_a\) :
-
Track height
References
Heinrich, G., Klüppel, M.: Rubber friction, tread deformation and tire traction. Wear 265(7–8), 1052–1060 (2008)
Persson, B.N.J.: Theory of rubber friction and contact mechanics. J. Chem. Phys. 115(8), 3840–3861 (2001)
Wagner, P., Wriggers, P., Klapproth, C., et al.: Multiscale FEM approach for hysteresis friction of rubber on rough surfaces. Comput. Methods Appl. Mech. Eng. 296, 150–168 (2015)
Wagner, P., Wriggers, P., Veltmaat, L., et al.: Numerical multiscale modelling and experimental validation of low speed rubber friction on rough road surfaces including hysteretic and adhesive effects. Tribol. Int. 111, 243–253 (2017)
Wriggers, P., Reinelt, J.: Multi-scale approach for frictional contact of elastomers on rough rigid surfaces. Comput. Methods Appl. Mech. Eng. 198(21–26), 1996–2008 (2009)
Persson, B.N.J., Tartaglino, U., Albohr, O., et al.: Sealing is at the origin of rubber slipping on wet roads. Nat. Mater. 3(12), 882–885 (2004)
Persson, B.N.J., Prodanov, N., Krick, B.A., et al.: Elastic contact mechanics: percolation of the contact area and fluid squeeze-out. Eur. Phys. J. E 35(1), 5 (2012)
Persson, B.N.J.: Fluid dynamics at the interface between contacting elastic solids with randomly rough surfaces. J. Phys. Condens. Matter 22(26), 265004 (2010)
Kane, M., Cerezo, V.: A contribution to tire/road friction modeling: from a simplified dynamic frictional contact model to a “dynamic friction tester” model. Wear 342–343, 163–171 (2015)
Kane, M., Do, M.T., Cerezo, V., et al.: Contribution to pavement friction modelling: an introduction of the wetting effect. Int. J. Pavement Eng. 20(8), 965–976 (2019)
Seta, E., Nakajima, Y., Kamegawa, T., et al.: Hydroplaning analysis by FEM and hydroplaning analysis by FEM and FVM: effect of tire rolling and tire pattern on hydroplaning. Tire Sci. Technol. 28(3), 140–156 (2000)
Ong, G.P., Fwa, T.F.: Wet-pavement hydroplaning risk and skid resistance: modeling. J. Transp. Eng. 133(10), 590–598 (2007)
Ong, G., Fwa, T.: Prediction of wet-pavement skid resistance and hydroplaning potential. Transp. Res. Rec. 2005, 160–171 (2007)
Gnadler, R., Unrau, H.J., Fischlein, H., et al.: Umfangskraftverhalten von PKW-Reifen bei unterschiedlichen Fahrbahnzuständen. Automob. Z. 98(9), 458–466 (1996)
Persson, B.N.J., Volokitin, A.I., Tosatti, E.: Role of the external pressure on the dewetting of soft interfaces. Eur. Phys. J. E 11(4), 409–413 (2003)
Persson, B.N.J., Scaraggi, M.: On the transition from boundary lubrication to hydrodynamic lubrication in soft contacts. J. Phys. Condens. Matter 21(18), 185002 (2009)
Bathelt, H.: Analytische Behandlung der Strömung in der Aufstandsfläche schnell rollender Reifen auf nasser Fahrbahn. Dissertation, Technische Hochschule Wien, Wien (1971)
Thom, N.: Modeling surface water. Tire Technology International. www.tiretechnologyinternational.com (2018). Accessed 3 June 2019
Sahlin, F., Almqvist, A., Larsson, R., et al.: Rough surface flow factors in full film lubrication based on a homogenization technique. Tribol. Int. 40(7), 1025–1034 (2007)
Khonsari, M.M., Booser, E.R.: Applied Tribology: Bearing Design and Lubrication. Wiley, Hoboken (2017)
Gnadler, R., Unrau, H.J., Frey, M., et al.: Ermittlung von \(\mu \)-Schlupf-Kurven an PKW-Reifen, vol. 119. FAT-Schriftenreihe, Frankfurt (1995)
Funding
Financial support by Continental Reifen Deutschland GmbH is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
No potential conflict of interest was reported by the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised due to a retrospective Open Access order.
Appendices
Appendices
1.1 Appendix A: Pattern Geometries
Block geometries of the patterns used, void volume is equal to surface void. BB-tire contains 3 rows with the block geometry described, SB and SBv contain 5 rows, including the tire shoulder
Geometry | Abbrv. | Block length (mm) | Block width (mm) | Void volume (%) | Nr. of rows |
|---|---|---|---|---|---|
Big blocks | BB | 36.6 | 53.2 | 24.8 | 3 |
Small blocks | SB | 23.2 | 25.6 | 25.0 | 5 |
Small blocks | SBv | 20.8 | 25.6 | 35.3 | 5 |
1.2 Appendix B: Additional Information for Change of Kinetic Energy
Steps after Eq. 23
1.3 Appendix C: Additional Information for Change of Energy Outflow
Steps after Eq. 31
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Löwer, J., Wagner, P., Unrau, HJ. et al. Physical Model of Tire-Road Contact Under Wet Conditions. Tribol Lett 68, 25 (2020). https://doi.org/10.1007/s11249-019-1264-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11249-019-1264-6