Abstract
Reactive transport in fractured media is conceptualized as a multi-scale problem that couples a pore-scale component, which comprises Navier–Stokes flow, multi-component transport and aqueous equilibrium in the fracture, and a Darcy-scale component, which comprises multi-component diffusive transport, aqueous equilibrium and mineral reactions in the porous matrix. The model that implements this multi-scale approach builds on an existing pore-scale model and is able to capture complex fracture geometries with the embedded-boundary method. The embedded boundary acts as the interface between pore- and Darcy-scale domains. Adaptive mesh refinement is used to match resolutions at the interface while using coarser resolution away from the interface when not needed in the Darcy-scale domain. The new model is validated and then compared to results from a pore-scale model. Multi-scale model results are shown to be equivalent to pore-scale results under diffusion-controlled reactions in the pore scale and very fast dissolution in the Darcy scale. The multi-scale model provides a more accurate solution for a given resolution as it effectively sets the equilibrium concentrations as boundary conditions. The multi-scale model is capable to capture flow channelization observed in an experimental fractured core and, at the same time, limitations in the dissolution of calcite by diffusive transport through an altered porous layer. Discrepancies in effluent calcium concentrations between the multi-scale results and results from a reduced-dimension Darcy-scale model for this fractured core experiment are attributed to the solution of the flow field and the gradients that develop inside the fracture. Discrepancies in effluent magnesium concentrations exemplify the limitations of the approach because the multi-scale model requires calibration of reactive surface areas as Darcy-scale continuum models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Understanding fracture evolution is essential for many subsurface energy applications, including subsurface nuclear waste storage, fracking, shale gas production, CO\(_2\) sequestration, and geothermal energy extraction. Geochemical processes in particular play a significant role in the evolution of fractures through dissolution-driven widening, fines migration, and/or fracture sealing due to precipitation.
Conceptually, fractured systems have often been represented as being composed of fast flow paths—the fractures—and slow flow paths—the rock matrix—where aqueous geochemistry is dominated by reaction–diffusion processes (e.g., Steefel and Lichtner 1994, 1998a, b; MacQuarrie and Mayer 2005). Darcy-scale continuum models treat fractures as preferential flow paths with their permeability a function (often, a cubic law) of the fracture aperture (MacQuarrie and Mayer 2005). Mass exchange between the fracture and the porous matrix may be captured with dual porosity or multiple interacting continua models (Pruess 1992). Reaction rates affected by diffusion limitations through porous layers at fracture surfaces may be calculated of the reaction rate as a function of the thickness of the dissolving front (Deng et al. 2016) or with consideration of the layer of precipitate that coats the surface (Noiriel et al. 2007). Darcy-scale models of fractured domains have the limitation that they may oversimplify flow within the fracture and fail to capture transport limitation within the fracture toward its surfaces as well-mixed conditions need to be assumed in each grid cell of the model (Starchenko et al. 2016). These models do not provide an accurate estimation of fracture hydrodynamic properties at realistic fracture roughness, e.g., (Deng et al. 2013).
In contrast, pore-scale models are characterized by their ability to resolve the fracture surfaces explicitly (Starchenko et al. 2016). In pore-scale models, the interfaces between the different fluid and solid phases that make up porous media are resolved and it is therefore possible to solve for flow and reactive transport within the pore space. Pore-scale models can capture the diffusion boundary layers that develop around reactive surfaces and contribute to the formation of effective reaction rates (Li et al. 2008; Molins et al. 2014, 2017). They can also simulate the channelization of the flow path due to dissolution in transport-limited conditions (Szymczak and Ladd 2009). Pore-scale models, however, even when they use multi-resolution methods and high-performance computing capabilities, have a limit in their ability to resolve the fine-scale heterogeneity that characterizes natural porous media (Anovitz and Cole 2015). This is especially true in multi-mineral systems that display a very wide range of mineral reactivities at a range of spatial scales (Deng et al. 2016, 2017a). Fractured media are an extreme example of this, with a relative large pore space (the fracture) and a rock matrix with porosity at a much smaller scale. There is a sharp contrast—with a clear separation of scales—between the porosity in the fracture and in the rock matrix.
Multi-scale models seek to combine two or more scale representations within a single simulation framework (Scheibe et al. 2007, 2015b, a). Although multi-scale models are sensitive to the approach employed to segment the images of reconstructed porous media (Soulaine and Tchelepi 2016), they are especially suited to fractured media due to the large contrast between the fracture and the matrix. An approach for combining pore- and Darcy-scale representations that has quickly gained much traction in the earth sciences is the one conceptualized by the Darcy–Brinkman–Stokes equation (Golfier et al. 2002; Popov et al. 2009; Gulbransen et al. 2010; Yang et al. 2014; Soulaine and Tchelepi 2016; Soulaine et al. 2017). Darcy–Brinkman–Stokes equation describes flow in open pore space and in a porous continuum with a single equation. In the pore space, terms associated with porous-media flow become negligible, and in the porous continuum, the terms associated with pore-scale flow become negligible. Although these models have been extended for reactive transport (Golfier et al. 2002; Soulaine et al. 2017), they have not been specifically applied to fractured media. Because processes at different scale are solved in a single equation, this approach does not easily allow for different spatial and temporal discretization in the different portions of the domain.
Hybrid multi-scale models provide a different approach that makes it possible to consider different spatial and temporal discretizations in different portions of the domain. In this approach, pore- and Darcy-scale domains are separated and coupled by enforcing the continuity of pressures and mass fluxes at the pore/continuum interfaces (Battiato et al. 2011; Roubinet and Tartakovsky 2013; Yousefzadeh and Battiato 2017). Coupling between sub-domains can be accomplished by using finite-element spaces to determine interface conditions, such as in the mortar method (Balhoff et al. 2008; Mehmani et al. 2012). Although mortar methods also allow for a flexible approach to map discretizations across the interface, they add significant complexity in the code implementation. From a software development point of view, it may still be convenient however to use a hybrid approach. This allows for the use of existing capabilities that tackle one of the sub-problems and couple them to new capabilities that tackle the other.
The objective of this work is the development of a multi-scale model for the simulation of reactive transport processes in fractured media that captures diffusion limitations to fracture surfaces as in pore-scale models and diffusion limitations through porous layers around fracture surfaces. The model seeks to simulate processes in complex pore-scale geometries in 3 dimensions using multiple resolutions in different areas of the domain within a high-performance computing framework. Rather than developing it from scratch, we build on the existing Chombo-Crunch code base (Molins et al. 2012; Trebotich et al. 2014; Molins et al. 2014) to develop an overarching framework that includes a pore-scale model for the fracture, a Darcy-scale model for the rock matrix, a novel coupling approach based on an adaptive mesh refinement embedded-boundary method to provide the connection between the sub-domains, and a sequential iterative solver for the coupled problem. This model is described in the following section. Next, a set of simulations are presented to validate and demonstrate the features of the multi-scale approach, particularly in relation to pore-scale modeling with a focus on diffusion limitations in the fracture. In the last section, we use experimental data and results from a previously published reduced-dimension Darcy-scale model that also discusses the role of transport limitations through the porous matrix in fractured media.
2 Model Description
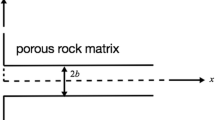
The fractured media domain (\(\varOmega \subset {R}^{3}\)) is composed of a pore-scale sub-domain (\(\varOmega _\mathrm{p}\)) and a Darcy-scale sub-domain (\(\varOmega _\mathrm{d}\)) that completely define it (\(\varOmega =\varOmega _\mathrm{p}\cup \varOmega _\mathrm{d}\)). The pore-scale domain is exclusively composed of pore space of arbitrary geometry, the fracture opening (Fig. 1). The Darcy-scale domain is composed of pore space and mineral phase that form a porous continuum, i.e., one can choose a representative elementary volume where bulk properties can be defined. The Darcy-scale domain comprises the porous matrix in which the fracture is embedded and where mineral dissolution–precipitation reactions are assumed to take place. Flow takes place preferentially in the fracture domain, and flow in the Darcy-scale domain is assumed negligible compared to pore-scale flow. While this assumption may not hold in all cases (e.g., Ling et al. 2018), especially if evolution of the media is considered over long time frames, it aligns with the focus of this manuscript on the study of diffusion limitations on rates. Thus, transport of geochemical species inside the porous matrix takes place by diffusion only.
The approach is to solve flow in the fracture (i.e., in pore-scale domain) to obtain the steady-state advective velocity. Once the steady-state velocity is obtained, the transient reactive transport problem is solved. The solution for each time step is obtained by solving sequentially the pore-scale problem and the Darcy-scale problem, updating the boundary conditions applied to the interface between the two sub-domains, and iterating the solution as needed until convergence for these boundary conditions, the coupling unknowns. The model builds on a previously developed embedded-boundary pore-scale solver (Molins et al. 2012; Trebotich et al. 2014; Molins et al. 2014) by adding a Darcy-scale reactive transport solver for the complementary embedded-boundary domain representing the porous-medium domain, and the framework that allows for the sequential, iterative solution of the pore-scale/Darcy-scale coupled problem. This framework also enforces the appropriate boundary conditions on the shared embedded boundary that represents the interface between the two sub-domains. Adaptive mesh refinement is used around the interface to match the resolution in pore-scale and Darcy-scale domains, and it allows for coarsening of the mesh where fine resolution is not necessary.
Conceptual diagram illustrating the multi-scale simulation approach depicting a sinusoidal fracture in a porous domain. The fracture opening is captured with the pore-scale embedded-boundary Cartesian-mesh domain (left). The porous matrix is captured with the complementary Darcy-scale embedded-boundary Cartesian-mesh domain (center). The interface between the sub-domains is used as connection between them by enforcing continuity of fluxes and concentrations to solve the coupled multi-scale problem (right)
2.1 Equations
Flow in the pore scale is described by the incompressible Navier–Stokes equations
where \(\rho \) is the fluid density, \(\nu \) is the dynamic viscosity, p is the fluid pressure, and \(\mathbf u \) is the fluid velocity.
Reactive transport in the pore-scale domain is described by the advection–diffusion equation and the law of mass action for aqueous complexation equilibrium
where \(N_\mathrm{c}\) is the number of components, \(N_\mathrm{x}\) is the number of aqueous complexation reactions, \(\psi _{i}\) is the total concentration of component i, \(c_{i}\) and \(\gamma _{i}\) are the concentrations and activity coefficients of the primary species, \(m_{j}\) and \(\gamma _{j}\) are the concentrations and activity coefficients of secondary species, and \(\xi _{ij}\) is the stoichiometric coefficient of primary species i in reaction j. Total concentrations are defined as the sum of the individual species concentrations times the corresponding stoichiometric coefficients (Eq. 5). Heterogeneous reactions are not considered in the pore scale, i.e., the solid phase is completely contained within the Darcy-scale domain.
Flow in the Darcy-scale domain is negligible (\(\mathbf q \simeq \mathbf 0 \)), and therefore, mass and momentum conservation equations for fluid flow are not solved. As a result, reactive transport in the Darcy-scale domain is obtained by solving the diffusion equation, coupled to the mass action law for aqueous complexation equilibrium and a kinetic rate expression for heterogeneous mineral dissolution–precipitation
where \(N_\mathrm{m}\) is the number of mineral reactions, \(\theta \) and \(\tau \) are the medium porosity and tortuosity, \(\varPsi _{i}\) is the total concentration of component i, \(C_{i}\) and \(\gamma {}_{i}\) are the concentrations and activity coefficients of the primary species, \(M_{j}\) and \(\gamma _{j}\) are the concentrations and activity coefficients of secondary species, \(\xi _{ik}\) is the stoichiometric coefficient of species i in mineral reaction k, \(A_{k}\) is the bulk reactive surface area of mineral k in units of area per unit volume, and \(r_{k}\) is the reaction rate in units of mass per unit surface per unit time. For calcite dissolution, the reaction rate may be calculated using a transition-state theory-type rate expression (Plummer et al. 1978; Chou et al. 1989):
where \(K_{\mathrm{CaCO}_{3}}\) is the solubility constant of calcite and \(Q_{\mathrm{CaCO}_{3}}\) is the ion activity product of the reaction. For dolomite dissolution, Deng et al. (2016) used:
where \(K_{\mathrm{CaMg}(\mathrm{CO}_{3})_2}\) is the solubility constant of dolomite and \(Q_{\mathrm{CaMg}(\mathrm{CO}_{3})_2}\) is the ion activity product of the reaction. The uppercase notation in Eqs. (6–11) indicates that these quantities apply to a porous-medium continuum, where both fluid and solid phases are assumed to coexist at each point in space, rather to each discrete phase separately as in a pore-scale description.
At the interface between pore-scale and Darcy-scale sub-domains, continuity of fluxes and concentrations is enforced such that
where the superscript EB indicates the embedded-boundary interface (Sect. 2.2).
An iterative method is employed to obtain the solution of the coupled problem, i.e., Eq. (3–5) + Eq. (6–11) + Eq. (12–13). This method entails solving each sub-problem subject to boundary conditions determined from the solution of the complementary sub-problem. That is, Darcy-scale concentrations at the interface are used as Dirichlet boundary conditions for the pore-scale problem, Eq. (12). Upon solution of the pore-scale sub-problem, concentration gradients are evaluated at the interface and used as Neumann boundary conditions for the Darcy-scale sub-problem, Eq. (13). Convergence in the coupling unknowns, i.e., the values of the boundary conditions, is used to determine whether the solution of the iterative problem has been achieved.
2.2 Methods and Software
A Cartesian grid is constructed that covers the entire domain. The interface between the pore-scale and the Darcy-scale domains is an arbitrary surface that intersects the cells that make up the Cartesian grid (Fig. 1). The equations in the cells intersected by the interface are discretized using the embedded-boundary method. The embedded-boundary (EB), or cut-cell, method refers to a finite volume discretization in irregular cells on a Cartesian grid that result from the intersection of a boundary and the rectangular cells of the grid. Conservative numerical approximations to the solution are found from discrete integration over the non-rectangular control volumes, or cut cells, with fluxes located at centroids of the edges or faces of a control volume. The embedded-boundary method has been used before to discretize reactive transport equations in complex pore-scale geometries (Molins et al. 2014; Trebotich et al. 2014). In the current model, the EB method is used to discretize equations (1–3) in the pore-scale domain and Eq. (6) in the Darcy-scale domain (see details in “Appendix A”).
An advantage of the embedded-boundary method is that it is amenable to adaptive mesh refinement (AMR) (Berger and Oliger 1984; Berger and Colella 1989). Block-structured AMR is a technique to add grid resolution efficiently and dynamically in areas of interest while leaving the rest of the domain at a coarser resolution. AMR has been combined with embedded-boundary methods to model inviscid and viscous compressible flow in complex geometries (Pember et al. 1995; Colella et al. 2006; Graves et al. 2013; Trebotich and Graves 2015). In the current model, AMR is used in combination with the EB approach to match mesh resolution at the interface between sub-domains without requiring fine resolution in parts of the domain where it is not necessary. Mesh refinement is adaptive in that it can be dynamically adjusted as the simulation is performed based on given criteria.
The model has been coded using the Chombo library package, which provides tools for the discretization and solution of partial differential equations in Cartesian grids using the embedded-boundary method and adaptive mesh refinement (Adams et al. 2015; Colella et al. 2003). A selection of solvers is available including geometric multi-grid and algebraic multi-grid methods. The latter was implemented using the PETSc software package (Balay et al. 2018). The geochemical problem is solved by CrunchFlow (Steefel et al. 2014). In the implementation, the pore-scale and Darcy-scale components are each an instantiation of a class that solves a reactive transport time step in a given embedded-boundary domain. A containment class controls how the two individual models communicate with each other and a driver routine performs the iterative solution.
3 Cross-Sectional Model Demonstrations
This section presents a validation of the multi-scale model against a model that solves the multi-scale problem with a single equation. Then, we build on this validation simulation (i) to contrast the multi-scale model with the pore-scale model, which allows us to discuss diffusion limitations to rates in the fracture opening, and (ii) to demonstrate the adaptive mesh embedded-boundary approach to interface the sub-models.
3.1 Two-Dimensional Planar Fracture
A 2D planar fracture is used as validation example by comparing the results from the multi-scale model against simulation results obtained with the multi-component reactive transport code CrunchFlow (Steefel et al. 2014). For this purpose, a 2D simulation domain is constructed with dimensions \(0.4\times 0.4\) cm in the center of which a 0.1-cm-wide straight channel representing a fracture is placed (Fig. 2a, Table 1). A mesh of \(128\times 128\) grid cells is employed to discretize the equations. The Poiseuille solution for flow between parallel plates is applicable in the channel. The reactive transport problem involves the transport of 6 components, including a non-reactive tracer, 9 complexation reactions, and a mineral dissolution reaction. A solution out of equilibrium with respect to calcite (Li et al. 2008), which also includes a non-reactive tracer (Table 2), is injected into the fracture at the constant flow rate of 0.04 cm/s. No-flow conditions are applied at the interface and the upper and lower side of the Darcy-scale domain. The effluent solution is allowed to be transported out of the domain across the outlet side of the domain. Initially, the solution everywhere in the domain is far from equilibrium with respect to calcite and the concentration of the non-reactive tracer is very low. Calcite present in the porous matrix dissolves, while reactants diffuse into the matrix and products diffuse into the fracture opening.
a Simulation domain of a planar fracture (in blue) embedded in a porous matrix (in light brown) used for the validation of the new multi-scale model, against an equivalent multi-scale CrunchFlow model (Sect. 3.1) and a pore-scale model (Sect. 3.2). In the multi-scale approach (b), calcite dissolution is calculated within the porous matrix and diffusive transport is solved for both in the fracture and in the matrix. Boundary conditions are applied at external boundaries of the multi-scale domain as shown in (a). In addition, in the hybrid multi-scale model, boundary conditions at the fracture surface for each sub-component are used as coupling unknowns in the sequential iterative solution as shown in (b). In the pore-scale approach (c), the domain only encompasses the fracture (in blue) with calcite dissolution calculated at the fracture surface as a Robin boundary condition (Eq. 14). The pore-scale and multi-scale models are compared under diffusion-limited rates at the fracture surface, i.e., the dissolution rate is faster than diffusion in the fracture and concentrations at the surface reach equilibrium with calcite (d)
The new multi-scale model simulates the processes as described in Sect. 2 treating the pore-scale and Darcy-scale domains separately. In contrast, the equivalent multi-scale CrunchFlow model solves the governing equations for the entire domain. While CrunchFlow does not solve for pore-scale flow, it can read in a flow solution from an external file. The flow field is prescribed directly: the Poiseuille solution in the fracture and a zero Darcy velocity in the porous matrix. Further, reactive transport at the pore scale can be simulated if porosity and tortuosity are set to 1 in the fracture opening (i.e., \(\theta =\tau =1\)), in which case Eq. (6) is mathematically equivalent to Eq. (3). For simplicity, and to avoid differences caused by the discretization of fluxes across the interface between domains in CrunchFlow, the tortuosity in the Darcy-scale domain is also set to 1. Parameters used in the simulation are summarized in Table 1.
The results from the reactive transport problem are compared along a cross section at \(x=0.2\) cm, perpendicular to the fracture axis, at times 5.8, 10.16, 20.31, 30.08 s (Fig. 3). Results show that concentration gradients develop on both sides of the interface between the fracture and rock matrix. Over time the non-reactive tracer starts diffusing into the matrix from the fracture. For reactive components, gradients are driven by the dissolution of calcite in the rock matrix. As a concentration gradient develops between the rock matrix and the influent solution, reaction products diffuse into the fracture and are carried out of the domain by advection (Fig. 3). Overall, very good agreement is found between result from the CrunchFlow equivalent multi-scale model and the newly developed multi-scale model both in space and in time. Because tortuosity in the matrix is set to 1, the concentration gradients are continuous across the interface.
Although this validation simulation is necessarily simple, it already highlights the differences between the multi-scale approach proposed in this manuscript and the pore-scale approach. In the pore-scale approach, diffusion control on rates exists only in the pore-scale domain (Fig. 2c). Thus, the relative importance between transport processes in the fracture and the dissolution rate at the surface determines the specific dissolution regime (Molins 2015). In the multi-scale approach, in contrast, concentration gradients develop on both sides of the interface. Thus, diffusion control exists both in the fracture and in the porous matrix (Fig. 3d). In the simulation results presented in this section, this control plays a role in the transient evolution of the concentrations from the initial conditions used.
Comparison between simulation results from the new model (Ch.) and the CrunchFlow (CF) equivalent multi-scale model at 4 different times along a transect perpendicular to the fracture surface at 0.2 cm—displayed as a vertical dashed line in (d)—for a a non-reactive tracer, b calcium, and c total carbon. d 2D calcium concentrations in the multi-scale model showing the interfaces between domains in horizontal dashed lines
3.2 Comparison with a Pore-Scale Model
Results from the multi-scale model are compared to a pore-scale model to test its ability to capture limitations to rates due to diffusive transport in the fracture only, not in the matrix. For this purpose, the simulation in Sect. 3.1 is modified to make the effective diffusion in the porous matrix arbitrarily small (Table 1). In these conditions, diffusion in the porous matrix is slow compared to the dissolution rate in the matrix and concentrations reach equilibrium. This reduces the multi-scale model to a pore-scale model in that it effectively sets the concentrations at the fracture surface, limiting the solution to the processes that take place in the fracture.
A pore-scale simulation is run with Chombo-Crunch (Molins et al. 2012; Trebotich et al. 2014; Molins et al. 2014) using the same fracture geometry, but with the domain limited to the fracture only (Fig. 2c). In the pore-scale model, dissolution rates are calculated as a Robin boundary condition at the fracture surface as a function of pore-scale concentrations (Molins et al. 2012):
where \(r_k\) has the same functional form as Eq. (9) but with pore-scale concentrations, i.e., \(c_i\).
With a diffusive Damköhler number (\(Da_{II}=k_{1}\gamma _{\mathrm{H}^{+}}a/D\)) equal to 890, the dissolution rate in the pore-scale simulation is diffusion-limited in the direction perpendicular to the fracture surface. This implies that the concentrations at the surface must be in equilibrium with the mineral. A strong driving force for reaction is maintained throughout the fracture with a fast flow rate (\(\mathrm{Pe} = 400\)).
Both multi-scale and pore-scale simulations are run to steady state, that is, until effluent concentrations no longer change significantly (Fig. 4b). Effluent concentrations are obtained by flux-averaging concentrations at the fracture outlet (Li et al. 2008; Molins et al. 2012, 2014, 2017).
Results show that under the conditions set above the multi-scale and pore-scale models are very close (Fig. 4). However, the pore-scale model yields a surface concentration slightly lower than that of the multi-scale model. This reveals a drawback in the pore-scale approach, namely that concentrations at the reactive surface cannot be exactly at equilibrium as the rate at the surface would be zero in the discretized form of the equations, i.e., at equilibrium \(Q_{\mathrm{CaCO}_3}=K_{\mathrm{CaCO}_3}\) thus \(r=0\) (Eq. 10). The discrepancy between the pore-scale surface concentration and the equilibrium concentration is thus dependent on the resolution. Indeed, results from additional pore-scale simulations at finer resolutions (\(256\times 256\) and \(512\times 512\)) indicate convergence toward multi-scale results (Fig. 4), i.e., equilibrium concentrations at the surface. This discrepancy, however, can lead to significant errors in integrated measures of reaction such as effluent concentrations (Fig. 4b).
This result serves as verification test for the multi-scale model, and it also shows that it can capture rates at pore scale more accurately than pore-scale models when they are fully controlled by transport in the pore scale. However, in the transition regime or under surface-limited reaction conditions (e.g., when the flow rate in the fracture is much faster), pore-scale and multi-scale model results are not necessarily equivalent. In this scenario, the concentration at the surface is not that at equilibrium with calcite. Therefore, bulk parameters that characterize reactive transport processes in the porous matrix such as reactive surface area and tortuosity would need to be calibrated such that the concentration at the surface satisfied the solution of the pore-scale model.
Computationally, the multi-scale approach entails the simulation of a pore-scale component and a Darcy-scale component and an sequential iteration of the two solutions to reach convergence of the overall solution. Further, in the simulations in this section the pore-scale domain is smaller than the multi-scale domain (Fig. 2). As a result, the multi-scale computational cost is higher than that of the pore-scale model. The pore-scale simulation used 0.070 s per transport time step, while the multi-scale simulations used 0.370 s per transport time step. Both simulations were carried out using 8 MPI processes on a machine with Intel\(^\circledR \) Xeon\(^\circledR \) E5-2600 v2 processors at 2.1 Hz. On average two iterations were required to converge for each transport time step, which implies that two pore-scale solutions and two Darcy-scale solutions were performed. Thus, the averaged cost per solution (0.0925 s) is slightly larger than that of the pore-scale model, which can be accounted for by the larger size of the Darcy-scale domain and the overhead associated with the coupling infrastructure.
3.3 Rough Fracture Surface
A central objective of the multi-scale model is the ability to simulate the complex geometries of natural fractured media. In these domains, the embedded-boundary method (Sect. 2.2) must be used to capture the interface accurately in a Cartesian grid. Further, it is also necessary to use fine resolution to accurately solve the Navier–Stokes equations for pore-scale flow (Eq. 1–2). As apparent from the simulations in Sect. 3.1, fluxes that control effective rates in the domain are determined by concentration gradients that develop in localized areas of the domain, near the interface in both sub-domains. To accurately quantify these rates, the model must be able to capture these gradients accurately. In the Darcy scale, away from the interface, concentration gradients are negligible as concentrations are near or at equilibrium (Sect. 3.1) and fine resolution is not needed. In order to capture concentration gradients accurately and match the resolution on both sides of the interface, adaptive mesh refinement (Sect. 2.2) is used.
To demonstrate the adaptive mesh refinement embedded-boundary approach, a sinusoidal fracture (as in Fig. 1) is placed in a domain of the same overall dimensions as in Sect. 3.1 with an average fracture aperture of 0.1 cm. For simplicity and taking advantage of the domain geometry, only half of the domain is simulated (Fig. 5). The geochemical problem is the same as in Sect. 3.1 with the porous matrix composed by calcite that dissolves as the solution out equilibrium with respect to calcite flows into the fracture and diffuses into the porous matrix.
Two criteria are used to determine whether additional mesh refinement is required in the porous matrix: one that placed this refinement in the location of the interface and another that does so where the difference between concentration values in adjacent cells exceeds a given threshold. However, because gradients develop near the interface, both criteria lead to refinement in the same area (Fig. 5). This refinement does not change with time.
The roughness of the fracture surface leads to velocity variations along the fracture length (Fig. 5). Where the fracture is narrow, flow is faster and the diffusive boundary layer is thinner. Where the fracture widens, slow flow zones form in the sine troughs and diffusive boundary layers become thicker.
4 Flow Channeling and Diffusive Transport Limitations in a 3D Fractured Domain
The simulations in the previous section demonstrate the capabilities of the new model in capturing processes accurately in arbitrary multi-scale domains. In 2-dimensional cross sections, however, the advantages of the model in capturing pore-scale flow are not fully apparent in that flow channelization within the fracture plane is not taken into account. Darcy-scale models can also capture this channelization by using the so-called cubic law to calculate a permeability from fracture apertures. In this way, the 3D problem becomes a 2D problem within the fracture plane. This cubic law simplification however has come into question (e.g., Starchenko et al. 2016). Further, in this approach, pore-scale transport processes perpendicular to the fracture plane that may control dissolution rates are not considered, i.e., well-mixed conditions are assumed within the fracture opening.
Deng et al. (2016) used these simplifications (i.e., cubic law and well-mixed conditions) to simulate a fractured core experiment of a dolomite sample from the Duperow formation. In this experiment, the core was subject to flow of a solution at high partial pressure of CO\(_2\), which resulted in both the evolution of the fracture geometry and the formation of an altered porous layer around the fracture surface (Deng et al. 2016). The model by Deng et al. (2016) included the impact of transport in this porous layer on the dissolution rate of calcite by tracking its thickness and accounting for diffusion in the reaction rate model.
Here we set out to explore the additional insights provided by the 3D multi-scale model on the effective dissolution rate and the effect of the Darcy-scale simplifications made in Deng et al. (2016). For this purpose, the results of the model in Deng et al. (2016) are used to generate the multi-scale domain (Table 1). The simulations only seek to reproduce results at a specific time point for a given fracture geometry and thickness of the altered layer (Fig. 6) rather than the formation and evolution of the altered layer. In particular, the simulations attempt to reproduce concentrations at 80 hours into the experiment. The fracture aperture is used to generate the geometry of the fracture aperture assuming fracture symmetry (Fig. 6). The thickness of the altered layer is used to assign the distribution of minerals in the porous matrix (i.e., the Darcy-scale domain). The altered layer is characterized by the absence of calcite, while dolomite is present uniformly everywhere in the porous matrix. The reactive surface area for calcite is set to be arbitrarily large as in Sect. 3.2 to ensure transport-limited rates (as in Deng et al. (2016)). The reactive surface area for dolomite is obtained from the literature (Xu et al. 2011), in contrast to the surface area used in Deng et al. (2016), which equals the interfacial area of the fracture surface. For the diffusion coefficient through the porous altered layer, the one corresponding to the best fit obtained by Deng et al. (2016) (\(D=2\times 10^{-10}\,{\text {m}}^2/{\text {s}}\)) is used.
The 3D domain for the multi-scale model is constructed from the aperture and altered layer thickness maps from Deng et al. (2016)
Multi-scale results show a non-uniform pattern for calcium concentrations. In the pore-scale domain, inlet concentrations extend further into the domain along the preferential flow path that develops on the right side of the fracture (Fig. 7b), while they are higher where flow is slower. In the porous matrix, a gradient is established between the area where calcite is dissolving and the fracture surface, i.e., across the altered layer (Fig. 7a). In the regions where pore-scale concentrations are higher, these gradients are small and concentrations in the altered layer are also high.
The mesh has \(64\times 160\times 32\) cells that cover the entire domain. However, for the pore-scale domain, this implies an equivalent resolution of \(128\times 320\times 64\) cells because an additional refinement level is used throughout. The resolution in the XY plane is coarser than that used by Deng et al. (2016) (\(168\times 429\)). As in Sect. 3.3, the criterion used for adaptive mesh refinement places the additional refinement near the surface and where concentration gradients are steep (Fig. 7d). In this simulation, this implies that AMR naturally captures the thickness of the altered layer in the porous matrix. If a criterion based only on geometry had been used, the additional refinement would have been available near a narrow zone around the fracture surface (as in the downstream end of the fractured domain (Fig. 7d)). However, the additional criterion based on difference in concentration values between adjacent cells makes it possible to have a zone with finer resolution also in the upstream end of the domain where the altered layer is thicker (Fig. 7d). The simulations were run using 512 MPI processes on 2.3 GHz Intel Haswell processors, with each time step taking 9.19 s on average. Initially, a little more than two iterations were necessary on average to reach convergence for the solution, but as the solution approached steady-state conditions, a single iteration sufficed.
Steady-state calcium concentrations in the 3D simulations of the Duperow fracture experiment a in the Darcy-scale domain and b the pore-scale domain. c A close-up view of the pore-scale domain shows concentration gradients within the fracture opening, and d a side view of the Darcy-scale domains shows the embedded boundary and the mesh refinement around the fracture surface, where it interfaces with the pore-scale domain and steep concentration gradients develop
Effluent concentrations of calcium from the multi-scale model are greater than those in the results of Deng et al. (2016) (Table 3). In contrast to the reduced-dimension model of Deng et al. (2016), the multi-scale model solves for transport processes in 3D inside the fracture space and is able to capture concentration gradients toward fracture surfaces (Fig. 7c). However, this effect seems to be minor and limited to a small area where the fracture aperture is the widest. Further, the multi-scale model solves the 3D Navier–Stokes equation considering directly the geometry of the fracture. If pore-scale concentrations are averaged over the fracture aperture and compared to the results by Deng et al. (2016), it can be observed that concentration contours are qualitatively similar to those from the reduced-order model. However, the 2D simplification introduced by the use of the cubic law for flow to the reduced-dimension model results in smoother calcium concentrations (Fig. 8b). The multi-scale model shows a more sharply defined preferential flow channel with lower calcium concentrations. For a given thickness of the altered layer, diffusive fluxes are larger when concentrations are lower in the fracture. Hence, the overall higher effective rate of calcite dissolution is evident from effluent concentrations (Table 3). Velocity distributions for both domains support this observation. Fluid velocities in the fracture from the multi-scale model display a sharper transition from low to high values than those obtained by the reduced-dimension model (Fig. 8c). While relatively more grid cells have low velocities in the reduced-dimension model, the multi-scale model can resolve much slower velocities (Fig. 8c). However, relatively more grid cells in the multi-scale model have faster flow velocities than in the reduced-dimension model (Fig. 8c).
The effective coefficient of diffusion in the matrix is a critical parameter controlling the effective rate of calcite dissolution. Deng et al. (2016) used it as calibration parameter to obtain a best fit. However, when D was estimated with Archie’s law based on porosities observed in the experiment using the literature coefficients, effluent calcium concentrations were lower than experimental measurements (Deng et al. 2016). An additional multi-scale simulation is performed here using the lower bound of the D value estimated with Archie’s law (\(D=4\times 10^{-11}\, \text {m}^2\)/s). Results from the multi-scale model are much closer than those obtained by the reduced-dimension model (Table 3) and do not match as well observed in the experiment. In fact, the difference between the multi-scale simulations with the two different values of D is larger than for the reduced-dimension model. This indicates the balance between transport in the fracture, and diffusion–reaction in the matrix is different in the multi-scale model and the reduced-dimension model. Hence, the harmonic average between surface rates and diffusion-limited rates used in the reduced-dimension model appears to capture more accurately the results of the multi-scale model when \(D=4\times 10^{-11}\,\text {m}^2\)/s when altered layer thickness are smaller.
Calcium concentrations at steady state in the fracture plane from a the multi-scale model, with results averaged over the fracture aperture, and b the reduced-dimension model of Deng et al. (2016). Fracture contact points are displayed in white in the multi-scale model results. c Normalized cumulative distribution function of the fluid velocity fields in the reduced-dimension (red) and multi-scale model (blue)
Effluent magnesium concentrations are lower than those simulated by Deng et al. (2016) or measured experimentally (Table 3). This is caused by the value of the reactive surface area used for dolomite. The value sourced from the literature is not sufficient to capture the effective rate of dolomite dissolution. The values of effluent magnesium concentration from the two simulations indicate that the rate is mostly controlled by the kinetics of the reaction, although partial diffusion control is also apparent. This shows a limitation of the multi-scale model, namely that it requires the use of bulk parameters as in Darcy-scale models.
5 Conclusions
The multi-scale model developed in this work makes it possible to capture limitations to dissolution rates both at the pore scale and at the Darcy scale. The former are closely related to flow within the fracture and the latter to transport through the porous matrix.
The model may be equivalent to a pore-scale model under certain conditions, namely when the solution in the porous matrix reaches equilibrium uniformly. Potential limitations of pore-scale models may be overcome by applying a Darcy-scale description in the areas where the spatial scales of medium heterogeneity are too fine to be resolved at the pore scale. This was the case of altered layers that formed around in the porous matrix in the Duperow fracture experiment in Deng et al. (2016). However, by using a continuum characterization for these media, the model must rely on bulk parameter values—e.g., reactive surface area—that add a source of uncertainty. The use of a surface area sourced from the literature for dolomite dissolution in the Duperow fracture simulation results in an under-estimation of effluent magnesium concentrations with respect to earlier modeling and experiments.
In spite of this limitation, the multi-scale model presents an advantage over Darcy-scale models, which rely on the cubic law to solve for flow in the fracture. This 2D simplification has already shown to produce results that diverged from those of a 3D pore-scale model when local inhomogeneities appeared during fracture evolution (Starchenko et al. 2016). Here, similar discrepancies were observed between the multi-scale and a reduced-dimension model (Deng et al. 2016). In a domain such as the Duperow fracture experiment, characterized by a preferential flow path, the multi-scale model—more specifically, its pore-scale component—provided a sharper velocity contrast and sharper concentration results.
While it was assumed that flow in the porous matrix is negligible, conceptually, the multi-scale model presented here could be extended to consider flow both in the fracture and in the porous matrix, with continuity of fluid fluxes and pressures at the interface. This could potentially be relevant in the scenarios similar to the Duperow fracture experiment where the porosity of the altered layer is large enough that flow in it may be significant.
From a code development perspective, a hybrid model that couples pore-scale and Darcy-scale representation presents some advantages. The model was implemented building upon existing capabilities by combining them with newly developed code. Numerical approaches available in the existing computational platform were taken advantage of. Specifically, the embedded-boundary method was successfully used to capture complex geometries of the interface between pore-scale and Darcy-scale domains. Adaptive mesh refinement provided a convenient efficient approach to match resolutions on both sides of the interface that avoided the use of computationally complex mortar methods. Further, it also added additional refinement where concentration gradients made it necessary.
Although the simulations presented in this work did not make it necessary, the fact that the two sub-problems are solved separately and coupled sequentially allows in practice for the use of different time stepping approaches in each sub-domain. This is generally not possible in models that combine multi-scale processes in a single equation such as the Darcy–Brinkman–Stokes. This feature of the multi-scale model presented in this manuscript could be especially useful when considering larger fractured domains in which fractures occupied a small portion volumetrically of the larger porous domain and required high resolution and small time steps. Further, in such domains, several additional levels of refinement could be used to transition from very fine pore-scale resolution in the fractures to relatively coarse resolution in porous-media domain that could span to several meters and beyond.
The simulations in this manuscript did not consider evolution of the media as a result of the reactions, and therefore, the pore-scale and Darcy-scale domains did not evolve over time. An embedded-boundary method for time-evolving domains developed by Miller and Trebotich (2012) and implemented in Molins et al. (2017) for pore-scale geometry evolution could however be applied in the multi-scale model. In this case, the model could capture both the evolution of the porous matrix and the displacement of the pore-scale/Darcy-scale interface as a result of dissolution and other relevant processes such as altered layer erosion, e.g., Deng et al. (2017b).
References
Adams, M., Colella, P., Graves, D.T., Johnson, J., Keen, N., Ligocki, T.J., Martin, D.F., McCorquodale, P., Modiano, D., Schwartz, P., Sternberg, T., Straalen, B.V.: Chombo Software Package for AMR Applications, Design Document. Lawrence Berkeley National Laboratory Technical Report LBNL-6616E (2015)
Ajo-Franklin, J., Voltolini, M., Molins, S., Yang, L.: Coupled processes in a fractured reactive system, American Geophysical Union (AGU), chap 9, pp. 187–205. https://doi.org/10.1002/9781119118657.ch9, https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/9781119118657.ch9 (2018)
Anovitz, L.M., Cole, D.R.: Characterization and analysis of porosity and pore structures. Rev. Mineral. Geochem. 80(1), 61–164 (2015). https://doi.org/10.2138/rmg.2015.80.04
Balay, S., Abhyankar, S., Adams, M.F., Brown, J., Brune, P., Buschelman, K., Dalcin, L., Eijkhout, V., Gropp, W.D., Kaushik, D., Knepley, M.G., May, D.A., McInnes, L.C., Mills, R.T., Munson, T., Rupp, K., Sanan, P., Smith, B.F., Zampini, S., Zhang, H., Zhang, H.: PETSc Users Manual. Argonne National Laboratory, ANL-95/11 - Revision 3.10. (2018). http://www.mcs.anl.gov/petsc. Accessed 18 Mar 2019
Balhoff, M.T., Thomas, S.G., Wheeler, M.F.: Mortar coupling and upscaling of pore-scale models. Comput. Geosci. 12(1), 15–27 (2008). https://doi.org/10.1007/s10596-007-9058-6
Battiato, I., Tartakovsky, D.M., Tartakovsky, A.M., Scheibe, T.: Hybrid models of reactive transport in porous and fractured media. Adv. Water Resour. 34(9), 1140–1150 (2011). https://doi.org/10.1016/j.advwatres.2011.01.012
Berger, M.J., Colella, P.: Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 82(1), 64–84 (1989)
Berger, M.J., Oliger, J.: Adaptive mesh refinement for hyperbolic partial differential equations. J. Comput. Phys. 53(3), 484–512 (1984). https://doi.org/10.1016/0021-9991(84)90073-1
Chou, L., Garrels, R.M., Wollast, R.: Comparative study of the kinetics and mechanisms of dissolution of carbonate minerals. Chem. Geol. 78(3–4), 269–282 (1989). https://doi.org/10.1016/0009-2541(89)90063-6
Colella, P., Graves, D., Ligocki, T., Modiano, D., Straalen, B.V.: EBChombo software package for Cartesian grid, embedded boundary applications. Technical Report, Applied Numerical Algorithms Group, Lawrence Berkeley National Laboratory. http://davis.lbl.gov/APDEC/designdocuments/ebchombo.pdf (2003) (unpublished)
Colella, P., Graves, D.T., Keen, B.J., Modiano, D.: A Cartesian grid embedded boundary method for hyperbolic conservation laws. J. Comput. Phys. 211(1), 347–366 (2006). https://doi.org/10.1016/j.jcp.2005.05.026
Deng, H., Ellis, B.R., Peters, C.A., Fitts, J.P., Crandall, D., Bromhal, G.S.: Modifications of carbonate fracture hydrodynamic properties by CO2-acidified brine flow. Energy Fuels 27(8), 4221–4231 (2013). https://doi.org/10.1021/ef302041s
Deng, H., Molins, S., Steefel, C., DePaolo, D., Voltolini, M., Yang, L., Ajo-Franklin, J.: A 2.5d reactive transport model for fracture alteration simulation. Environ. Sci. Technol. https://doi.org/10.1021/acs.est.6b02184 (2016)
Deng, H., Steefel, C., Molins, S., DePaolo, D.: Fracture evolution in multimineral systems: the role of mineral composition, flow rate, and fracture aperture heterogeneity. ACS Earth Space Chem. (2017a). https://doi.org/10.1021/acsearthspacechem.7b00130
Deng, H., Voltolini, M., Molins, S., Steefel, C., DePaolo, D., Ajo-Franklin, J., Yang, L.: Alteration and erosion of rock matrix bordering a carbonate-rich shale fracture. Environ. Sci. Technol. 51(15), 8861–8868 (2017b). https://doi.org/10.1021/acs.est.7b02063
Golfier, F., Zarcone, C., Bazin, B., Lenormand, R., Lasseux, D., Quintard, M.: On the ability of a Darcy-scale model to capture wormhole formation during the dissolution of a porous medium. J. Fluid Mech. 457, 213–254 (2002). https://doi.org/10.1017/S0022112002007735
Graves, D., Colella, P., Modiano, D., Johnson, J., Sjogreen, B., Gao, X.: A cartesian grid embedded boundary method for the compressible Navier–Stokes equations. Commun. Appl. Math. Comput. Sci. 8(1), 99–122 (2013). https://doi.org/10.2140/camcos.2013.8.99
Gulbransen, A.F., Hauge, V.L., Lie, K.A., ICT, S.: A multiscale mixed finite-element method for Vuggy and naturally fractured reservoirs. SPE J. 9, 395–403 (2010)
Li, L., Steefel, C.I., Yang, L.: Scale dependence of mineral dissolution rates within single pores and fractures. Geochim. Cosmochim. Acta 72(2), 360–377 (2008). https://doi.org/10.1016/j.gca.2007.10.027
Ling, B., Oostrom, M., Tartakovsky, A.M., Battiato, I.: Hydrodynamic dispersion in thin channels with micro-structured porous walls. Phys. Fluids 30(7), 076,601 (2018). https://doi.org/10.1063/1.5031776
MacQuarrie, K.T.B., Mayer, K.U.: Reactive transport modeling in fractured rock: a state-of-the-science review. Earth Sci. Rev. 72(3), 189–227 (2005). https://doi.org/10.1016/j.earscirev.2005.07.003
Mehmani, Y., Sun, T., Balhoff, M.T., Eichhubl, P., Bryant, S.: Multiblock pore-scale modeling and upscaling of reactive transport: application to carbon sequestration. Transport Porous Med. 95(2), 305–326 (2012). https://doi.org/10.1007/s11242-012-0044-7
Miller, G., Trebotich, D.: An embedded boundary method for the Navier-Stokes equations on a time-dependent domain. Commun. Appl. Math. Comput. Sci. 7(1), 1–31 (2012). https://doi.org/10.2140/camcos.2012.7.1
Molins, S.: Reactive interfaces in direct numerical simulation of pore scale processes. Rev. Mineral. Geochem. 80, 461–481 (2015)
Molins, S., Trebotich, D., Steefel, C.I., Shen, C.: An investigation of the effect of pore scale flow on average geochemical reaction rates using direct numerical simulation. Water Resour. Res. 48, W03527. https://doi.org/10.1029/2011WR011404 (2012)
Molins, S., Trebotich, D., Yang, L., Ajo-Franklin, J.B., Ligocki, T.J., Shen, C., Steefel, C.I.: Pore-scale controls on calcite dissolution rates from flow-through laboratory and numerical experiments. Environ. Sci. Technol. 48(13), 7453–7460 (2014)
Molins, S., Trebotich, D., Miller, G.H., Steefel, C.I.: Mineralogical and transport controls on the evolution of porous media texture using direct numerical simulation. Water Resour. Res. 53(5), 3645–3661 (2017)
Noiriel, C., Mad, B., Gouze, P.: Impact of coating development on the hydraulic and transport properties in argillaceous limestone fracture: dissolution in argillaceous limestone fracture. Water Resour. Res. 43, W09406. https://doi.org/10.1029/2006WR005379 (2007)
Pember, R.B., Bell, J.B., Colella, P., Curtchfield, W.Y., Welcome, M.L.: An adaptive cartesian grid method for unsteady compressible flow in irregular regions. J. Comput. Phys. 120(2), 278–304 (1995). https://doi.org/10.1006/jcph.1995.1165
Plummer, L.N., Wigley, T.M.L., Parkhurst, D.L.: The kinetics of calcite dissolution in CO2 -water systems at 5 degrees to 60 degrees C and 0.0 to 1.0 atm CO2. Am. J. Sci. 278(2), 179–216 (1978). https://doi.org/10.2475/ajs.278.2.179
Popov, P., Efendiev, Y., Qin, G. Multiscale modeling and simulations of flows in naturally fractured karst reservoirs. Commun. Comput. Phys. 6(1), 162–184. https://doi.org/10.4208/cicp.2009.v6.p16 (2009)
Pruess, K.: Brief Guide to the Minc-Method for Modeling Flow and Transport in Fractured Media. Technical Report LBL-32195, Lawrence Berkeley Lab., CA (United States), https://doi.org/10.2172/6951290, https://www.osti.gov/scitech/biblio/6951290 (1992)
Roubinet, D., Tartakovsky, D.M.: Hybrid modeling of heterogeneous geochemical reactions in fractured porous media: hybrid models for fractured and porous media. Water Resour. Res. 49(12), 7945–7956 (2013). https://doi.org/10.1002/2013WR013999
Scheibe, T.D., Tartakovsky, A.M., Tartakovsky, D.M., Redden, G.D., Meakin, P.: Hybrid numerical methods for multiscale simulations of subsurface biogeochemical processes. J. Phys. Conf. Ser. 78(012), 063 (2007). https://doi.org/10.1088/1742-6596/78/1/012063
Scheibe, T.D., Murphy, E.M., Chen, X., Rice, A.K., Carroll, K.C., Palmer, B.J., Tartakovsky, A.M., Battiato, I., Wood, B.D.: An analysis platform for multiscale hydrogeologic modeling with emphasis on hybrid multiscale methods. Groundwater 53(1), 38–56 (2015a). https://doi.org/10.1111/gwat.12179
Scheibe, T.D., Schuchardt, K., Agarwal, K., Chase, J., Yang, X., Palmer, B.J., Tartakovsky, A.M., Elsethagen, T., Redden, G.: Hybrid multiscale simulation of a mixing-controlled reaction. Adv. Water Resour. 83, 228–239 (2015b). https://doi.org/10.1016/j.advwatres.2015.06.006
Soulaine, C., Tchelepi, H.A.: Micro-continuum approach for pore-scale simulation of subsurface processes. Transport Porous Med. 113, 431–456 (2016). https://doi.org/10.1007/s11242-016-0701-3
Soulaine, C., Roman, S., Kovscek, A., Tchelepi, H.A.: Mineral dissolution and wormholing from a pore-scale perspective. J. Fluid Mech. 827, 457–483 (2017)
Starchenko, V., Marra, C.J., Ladd, A.J.C.: Three-dimensional simulations of fracture dissolution. J. Geophys. Res. Solid Earth 121(9), 6421–6444 (2016). https://doi.org/10.1002/2016JB013321
Steefel, C.I., Lichtner, P.C.: Diffusion and reaction in rock matrix bordering a hyperalkaline fluid-filled fracture. Geochim. Cosmochim. Acta 58(17), 3595–3612 (1994). https://doi.org/10.1016/0016-7037(94)90152-X
Steefel, C.I., Lichtner, P.C.: Multicomponent reactive transport in discrete fractures: I. Controls on reaction front geometry. J. Hydrol. 209(1–4), 186–199 (1998a). https://doi.org/10.1016/S0022-1694(98)00146-2
Steefel, C.I., Lichtner, P.C.: Multicomponent reactive transport in discrete fractures: II: Infiltration of hyperalkaline groundwater at Maqarin, Jordan, a natural analogue site. J. Hydrol. 209(1–4), 200–224 (1998b). https://doi.org/10.1016/S0022-1694(98)00173-5
Steefel, C.I., CaJ, Appelo, Arora, B., Jacques, D., Kalbacher, T., Kolditz, O., Lagneau, V., Lichtner, P.C., Mayer, K.U., Meeussen, J.C.L., Molins, S., Moulton, D., Shao, H., imnek, J., Spycher, N., Yabusaki, S.B., Yeh, G.T.: Reactive transport codes for subsurface environmental simulation. Comput. Geosci. 19(3), 445–478 (2014). https://doi.org/10.1007/s10596-014-9443-x
Szymczak, P., Ladd, A.J.C.: Wormhole formation in dissolving fractures. J. Geophys. Res. Solid Earth 114(B6), B06,203 (2009). https://doi.org/10.1029/2008JB006122
Trebotich, D., Graves, D.: An adaptive finite volume method for the incompressible Navier–Stokes equations in complex geometries. Commun. Appl. Math. Comput. Sci. 10(1), 43–82 (2015)
Trebotich, D., Adams, M.F., Molins, S., Steefel, C.I., Shen, C.: High-resolution simulation of pore-scale reactive transport processes associated with carbon sequestration. Comput. Sci. Eng. 16(6), 22–31 (2014). https://doi.org/10.1109/MCSE.2014.77
Xu, T., Spycher, N., Sonnenthal, E., Zhang, G., Zheng, L., Pruess, K.: TOUGHREACT Version 2.0: a simulator for subsurface reactive transport under non-isothermal multiphase flow conditions. Comput. Geosci. 37(6), 763–774 (2011). https://doi.org/10.1016/j.cageo.2010.10.007
Yang, X., Liu, C., Shang, J., Fang, Y., Bailey, V.L.: A unified multiscale model for pore-scaleflow simulations in soils. Soil Sci. Soci. Am. J. 78(1), 108 (2014). https://doi.org/10.2136/sssaj2013.05.0190
Yousefzadeh, M., Battiato, I.: Physics-based hybrid method for multiscale transport in porous media. J. Comput. Phys. 344, 320–338 (2017). https://doi.org/10.1016/j.jcp.2017.04.055
Acknowledgements
This work was supported by Laboratory Directed Research and Development (LDRD) funding from Berkeley Lab, provided by the Director, Office of Science, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Funding from the Exascale Computing Project (17-SC-20-SC), a collaborative effort of the U.S. Department of Energy Office of Science and the National Nuclear Security Administration, has enabled significant improvements in code performance and completion of this manuscript in a timely manner. Simulations used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract DE-AC02-05CH11231.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Embedded-Boundary Solution
Embedded-Boundary Solution
In the embedded-boundary method, in grid cells where the irregular domain intersects the Cartesian grid, finite volume discretizations must be constructed to obtain conservative discretizations of flux-based operations. First, the underlying description of space is given by rectangular control volumes on a Cartesian grid \(\Upsilon _i\). Given an irregular domain \(\varOmega \), we obtain control volumes \(V_i = \Upsilon _i \bigcap \varOmega \) (Fig. 9). The intersection of the boundary of the irregular domain with the Cartesian control volume is defined as \(A^B_i = \partial \varOmega \bigcap \Upsilon _i\). The conservative approximation of the divergence of a flux \(\mathbf {F}\) can now be defined by applying a discrete form of the divergence theorem
where D is the dimensionality of the problem, h is the mesh spacing, \(\kappa _i\) are the volume fractions, \(\alpha _i\) are the area fractions, and where \(\widetilde{F}_{i+\mathbf {e}^d/2}\) indicates that the flux has been interpolated to the face centroid using linear (2D) or bilinear (3D) interpolation of face-centered fluxes. For example, given the cell edge with outward normal \(\mathbf {e}^1\), with centroid \(\mathbf {x}\), the 2D linearly interpolated flux in the d direction (\(d\ne 1\)) is defined by
Left: example of an irregular geometry on a Cartesian grid. Middle: close-up view of embedded boundaries cutting regular cells. Right: single cut cell showing boundary fluxes. The shaded area represents the volume of cells excluded from the domain. Dots represent cell centers. Each x represents a centroid
In our multi-scale approach, two separate embedded-boundary domains are generated, one for the fracture and the other for the rock matrix. The embedded boundary captures the interface between the two domains. The two solutions are however obtained sequentially and separately from each other. The fluxes and concentrations used for boundary conditions are calculated at the embedded boundaries (Fig. 10) and exchanged iteratively after the solution for each problem has been obtained. That is, the fluxes obtained from the pore-scale solution at the embedded boundary (\(F^B\)) are passed as boundary conditions for the rock matrix solution. In turn, upon solution of the Darcy-scale problem concentrations are calculated at the embedded boundary and passed as boundary conditions for the pore-scale problem.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Molins, S., Trebotich, D., Arora, B. et al. Multi-scale Model of Reactive Transport in Fractured Media: Diffusion Limitations on Rates. Transp Porous Med 128, 701–721 (2019). https://doi.org/10.1007/s11242-019-01266-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-019-01266-2