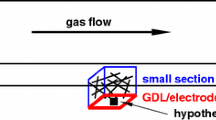
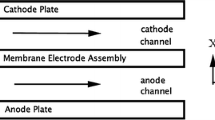
Abstract
In this work, we present a novel methodology for incorporating the effect of fibre surface morphology on liquid water transport in polymer electrolyte membrane fuel cell gas diffusion layers (GDLs). Roughness features presented on the surface of the fibre are analysed using atomic force microscopy and are found to significantly impact the capillary pressure of liquid water pathways propagating through the GDL. A threshold capillary pressure was defined as the largest capillary pressure exhibited by the liquid water phase during the invasion of the throat. The threshold capillary pressures observed in the presence of roughness features are significantly greater than those in the absence of roughness features. Two-dimensional circumferential roughness models in cylindrical and converging-diverging throats are established, and an interfacial meniscus advancing algorithm is presented to determine the resulting threshold capillary pressures required for liquid water penetration. Revised Young–Laplace equations, which are particularly useful for pore network modeling, are suggested for calculating threshold capillary pressures that account for the effect of the roughness of throats with intrinsic contact angles greater than \(90^{\circ }\).













Similar content being viewed by others
Abbreviations
- \(\alpha \) :
-
Angle of inclination (\(^{\circ }\))
- \(\beta \) :
-
Filling angle (\(^{\circ }\))
- \(\beta _\mathrm{t}\) :
-
Critical filling angle at threshold capillary pressure (\(^{\circ }\))
- \(\theta \) :
-
Intrinsic contact angle (\(^{\circ }\))
- \(\theta _\mathrm{e}\) :
-
Effective contact angle (\(^{\circ }\))
- \(\sigma \) :
-
Surface tension (\(\hbox {N}/\hbox {m}\))
- \(A_{{\text {AFM}}}\) :
-
Cross-sectional area of the partially imaged carbon fibre (\(\upmu \hbox {m}^{2}\))
- \(A_\mathrm{C}\) :
-
Cross-sectional area of the carbon fibre in the absence of roughness features (\(\upmu \hbox {m}^{2}\))
- \(A_\mathrm{r}\) :
-
Cross-sectional area of fibre roughness features protruding from the carbon fibre section (\(\upmu \hbox {m}^{2}\))
- l :
-
Length of the chord defining the base of the partial fibre (arc) (\(\upmu \hbox {m}\))
- \(L_\mathrm{C}\) :
-
Length between the centres of meniscus curvature and the adjacent roughness features (\(\upmu \hbox {m}\))
- \(r_\mathrm{m}\) :
-
Interfacial meniscus radius (\(\upmu \hbox {m}\))
- \(r_\mathrm{C}\) :
-
Carbon fibre radius (\(\upmu \hbox {m}\))
- \(r_\mathrm{e}\) :
-
Effective throat radius (\(\upmu \hbox {m}\))
- \(r_\mathrm{r}\) :
-
Unit roughness radius (\(\upmu \hbox {m}\))
- \(r_\mathrm{t}\) :
-
Throat radius in absence of roughness features (\(\upmu \hbox {m}\))
- \(P_\mathrm{C}\) :
-
Capillary pressure (\(\hbox {Pa}\))
- \(P_{{\text {defending}}}\) :
-
Pressure in the defending phase (\(\hbox {Pa}\))
- \(P_{{\text {invading}}}\) :
-
Pressure in the invading phase (Pa)
- Z :
-
Carbon fibre height profile (\(\upmu \hbox {m}\))
References
Alrwashdeh, S., Manke, I., Markötter, H., Klages, M., Göbel, M., Haußmann, J., Scholta, J., Banhart, J.: In-operando quantification of three dimensional water distribution in nanoporous carbon based layers in polymer electrolyte membrane fuel cells. ACS Nano (2017)
Bao, L., Yee, A.F.: Moisture diffusion and hygrothermal aging in bismaleimide matrix carbon fiber composites–part I: uni-weave composites. Compos. Sci. Technol. 62, 2099–2110 (2002)
Blunt, M.J.: Flow in porous media–pore-network models and multiphase flow. Curr. Opin. Colloid Interface Sci. 6, 197–207 (2001)
Bockris, J.O., Conway, B.E., White, R.E.: Modern Aspects of Electrochemistry. Springer, Berlin (2012)
Botelho, S.J., Bazylak, A.: The impact of fibre surface morphology on the effective thermal conductivity of a polymer electrolyte membrane fuel cell gas diffusion layer. J. Power Sources 269, 385–395 (2014)
Ceballos, L., Prat, M.: Invasion percolation with inlet multiple injections and the water management problem in proton exchange membrane fuel cells. J. Power Sources 195, 825–828 (2010)
Cindrella, L., Kannan, A., Lin, J., Saminathan, K., Ho, Y., Lin, C., Wertz, J.: Gas diffusion layer for proton exchange membrane fuel cells—a review. J. Power Sources 194, 146–160 (2009)
Dullien, F.A.: Porous Media: Fluid Transport and Pore Structure. Academic Press, Cambridge (2012)
Fazeli, M., Hinebaugh, J., Bazylak, A.: Investigating inlet condition effects on PEMFC GDL liquid water transport through pore network modeling. J. Electrochem. Soc. 162, F661–F668 (2015)
Gostick, J.T., Ioannidis, M.A., Fowler, M.W., Pritzker, M.D.: Pore network modeling of fibrous gas diffusion layers for polymer electrolyte membrane fuel cells. J. Power Sources 173, 277–290 (2007)
Gostick, J.T., Ioannidis, M.A., Fowler, M.W., Pritzker, M.D.: Wettability and capillary behavior of fibrous gas diffusion media for polymer electrolyte membrane fuel cells. J. Power Sources 194, 433–444 (2009)
Hinebaugh, J., Bazylak, A.: Condensation in PEM fuel cell gas diffusion layers: a pore network modeling approach. J. Electrochem. Soc. 157, B1382–B1390 (2010)
Hinebaugh, J., Fishman, Z., Bazylak, A.: Unstructured pore network modeling with heterogeneous PEMFC GDL porosity distributions. J. Electrochem. Soc. 157, B1651–B1657 (2010)
Hinebaugh, J., Bazylak, A., Mukherjee, P.P.: Multi-scale modeling of two-phase transport in polymer electrolyte membrane fuel cells. Woodhead Publishing, Cambridge (2012)
Lee, C., Hinebaugh, J., Banerjee, R., Chevalier, S., Abouatallah, R., Wang, R., Bazylak, A.: Influence of limiting throat and flow regime on oxygen bubble saturation of polymer electrolyte membrane electrolyzer porous transport layers. Int. J. Hydrog. Energy 42, 2724–2735 (2017)
Markicevic, B., Bazylak, A., Djilali, N.: Determination of transport parameters for multiphase flow in porous gas diffusion electrodes using a capillary network model. J. Power Sources 171, 706–717 (2007)
Mason, G., Morrow, N.R.: Effect of contact angle on capillary displacement curvatures in pore throats formed by spheres. J. Colloid Interface Sci. 168, 130–141 (1994)
O’Hayre, R.P., Cha, S., Colella, W., Prinz, F.B.: Fuel Cell Fundamentals. Wiley, New York (2006)
Raeesi, B., Morrow, N.R., Mason, G.: Effect of surface roughness on wettability and displacement curvature in tubes of uniform cross-section. Colloids Surf. Physicochem. Eng. Aspects 436, 392–401 (2013)
Ray, B.: Temperature effect during humid ageing on interfaces of glass and carbon fibers reinforced epoxy composites. J. Colloid Interface Sci. 298, 111–117 (2006)
Schulz, V.P., Becker, J., Wiegmann, A., Mukherjee, P.P., Wang, C.: Modeling of two-phase behavior in the gas diffusion medium of PEFCs via full morphology approach. J. Electrochem. Soc. 154, B419–B426 (2007)
Sinha, P.K., Wang, C.: Pore-network modeling of liquid water transport in gas diffusion layer of a polymer electrolyte fuel cell. Electrochim. Acta 52, 7936–7945 (2007)
Song, W., Gu, A., Liang, G., Yuan, L.: Effect of the surface roughness on interfacial properties of carbon fibers reinforced epoxy resin composites. Appl. Surf. Sci. 257, 4069–4074 (2011)
Tsakiroglou, C.D., Fleury, M.: Resistivity index of fractional wettability porous media. J. Pet. Sci. Eng. 22, 253–274 (1999)
Vielstich, W., Lamm, A., Gasteiger, H.A.: Handbook of Fuel Cells: Fundamentals, Technology, and Applications. Wiley, New York (2009)
Wang, C.: Fundamental models for fuel cell engineering. Chem. Rev. 104, 4727–4766 (2004)
Wang, C., Cheng, P.: Multiphase flow and heat transfer in porous media. Adv. Heat Transf. 30, 93–196 (1997)
Washburn, E.W.: The dynamics of capillary flow. Phys. Rev. 17, 273 (1921)
Weber, A.Z., Darling, R.M., Newman, J.: Modeling two-phase behavior in PEFCs. J. Electrochem. Soc. 151, A1715–A1727 (2004)
Wu, R., Zhu, X., Liao, Q., Wang, H., Ding, Y., Li, J., Ye, D.: A pore network study on water distribution in bi-layer gas diffusion media: effects of inlet boundary condition and micro-porous layer properties. Int. J. Hydrog. Energy 35, 9134–9143 (2010)
Xia, Y., Whitesides, G.M.: Soft lithography. Annu. Rev. Mater. Sci. 28, 153–184 (1998)
Yao, Y., Chen, S.: Effects of the longitudinal surface roughness on fiber pull-out behavior in carbon fiber-reinforced epoxy resin composites. J. Appl. Mech. 80, 021015 (2013)
Zenyuk, I.V., Medici, E., Allen, J., Weber, A.Z.: Coupling continuum and pore-network models for polymer-electrolyte fuel cells. Int. J. Hydrog. Energy 40, 16831–16845 (2015)
Zhu, X., Sui, P., Djilali, N.: Three-dimensional numerical simulations of water droplet dynamics in a PEMFC gas channel. J. Power Sources 181, 101–115 (2008)
Acknowledgements
Financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC), the NSERC Discovery Accelerator Program, the NSERC Canada Research Chairs Program, and the Canada Foundation for Innovation are gratefully acknowledged. Graduate scholarships to Hang Liu from the University of Toronto Connaught International Scholarship for Doctoral Students is gratefully acknowledged. Graduate scholarships to ChungHyuk Lee from the Pierre Rivard Hydrogenics Graduate Fellowship, C. W. Bowman Graduate Scholarship, William Dunbar Memorial Fellowship in Mechanical Engineering, and the Ontario Graduate Scholarship are also gratefully acknowledged. The authors would like to thank Dr. Roswitha Zeis for her valuable discussions. The authors also acknowledge Mr. Peter Krolla-Sidenstein at the Karlsruhe Institute of Technology in Karlsruhe, Germany, for his generous assistance in AFM imaging.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Liu, H., Hinebaugh, J., Chevalier, S. et al. Modeling the Effect of Fibre Surface Morphology on Liquid Water Transport in Polymer Electrolyte Membrane Fuel Cell Gas Diffusion Layers. Transp Porous Med 121, 437–458 (2018). https://doi.org/10.1007/s11242-017-0966-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-017-0966-1