1 Introduction

In recent years, several scientific disciplines have been facing a replication crisis: researchers fail to reproduce the results of previous experiments when copying the original experimental design. By investigating replication rates for the main reported effect in a representative sample of published papers, scientists have tried to assess the seriousness of the crisis in a systematic way. The outcome of these studies is sobering: the number of statistically significant findings and the observed effect sizes are often much lower than the theoretical expectation (for the fields of psychology, experimental economics and cancer biology, respectively: Open Science Collaboration 2015; Camerer et al. 2016; Nosek and Errington 2017). While the appropriate interpretation of replication failures is debatable (e.g., Maxwell et al. 2015), there is a shared sentiment that science is not as reliable as it is supposed to be and that something needs to change.

There are several causes of low replicability and hence a wide range of possible reforms to address the crisis. We identify three types of reforms that can be regarded as complementary rather than mutually exclusive. First, social reforms, which are inspired by the prevalence of questionable research practices (“QRPs”: Simmons et al. 2011) and more generally, the adverse effects of social and structural factors in science (Bakker et al. 2012; Nuijten et al. 2016; Romero 2017). Social reforms include educating researchers about statistical cognition and methodology (Schmidt 1996; Lakens 2019), but also creating greater incentives for replication work—for example by publishing and co-citing replications alongside original studies (Koole and Lakens 2012) or establishing a separate reward system for confirmatory research (Romero 2018). Second, there are methodological reforms such as pre-registering studies and their data analysis plan (Quintana 2015), sharing experimental data for “successful” as well as “failed” studies (van Assen et al. 2014; Munafò et al. 2017) and promoting multi-site experiments (Klein et al. 2014). By “front-staging” important decisions about experimental design and data analysis, these reforms address various forms of post-hoc bias (e.g., selective reporting, adding covariates) and increase the transparency and reliability of published research (see also Freese and Peterson 2018). Third, numerous authors identify “classical” statistical inference based on Null Hypothesis Significance Testing (NHST) as a major cause of the replication crisis (Cohen 1994; Goodman 1999a; Ioannidis 2005; Ziliak and McCloskey 2008) and suggest statistical reforms. Some of them remain within the frequentist paradigm and promote novel tools for hypothesis testing (Lakens et al. 2018b) or focus on effect sizes and confidence intervals instead of p-values (Fidler 2005; Cumming 2012, 2014). Others are more radical and propose to replace NHST by Bayesian inference (Goodman 1999b; Rouder et al. 2009; Lee and Wagenmakers 2014), likelihood-based inference (Royall 1997), or even purely descriptive data summaries (Trafimow and Marks 2015).

While science most likely needs a combination of these reforms to improve (e.g., Ioannidis 2005; Romero 2019), we study in this paper the case for statistical reform, and its interaction with various limitations in scientific research (e.g., insufficient sample size, selective reporting of results). In other words, we ask whether the replicability of published research would change if we replaced the conventional NHST method by Bayesian inference.

To address this question, we conduct a systematic computer simulation study that investigates the self-corrective nature of science in the context of statistical inference. A strong version of the self-corrective thesis (SCT, Laudan 1981) asserts that scientific method guarantees convergence to true theories in the long run: by staying on the path of scientific method, errors in published research will eventually be discovered, corrected and wed out (see also Peirce 1931; Mayo 1996). SCT can be operationalized in the context of statistical inference and the replication crisis in the sense that sequential replications of an experiment will eventually “reveal the truth” (Romero 2016).

SCT*:

Given a series of exact replications of an experiment, the meta-analytical aggregation of their effect sizes will converge on the true effect size as the length of the series of replications increases.

Arguably, validating SCT* in the precisely defined context of exact replications (i.e., experiments that copy the original design) would be a minimal condition for any of the more far-reaching claims that science eventually corrects errors and converges to the truth. Conversely, if SCT* fails—and the replication crisis provides some preliminary evidence that we should not take SCT* for granted—then claims to the general truth of SCT, and to science as a reliable source of knowledge, are highly implausible.

The truth or falsity of SCT* strongly depends on the conditions in which experimental research operates—in particular on the prevalent kind of publication bias, that is, the bias in the process of publishing scientific evidence and disseminating it to the scientific community. Since different statistical frameworks (e.g., NHST and Bayesian inference) classify the same set of experimental results in different qualitative categories, e.g., “strong evidence for the hypothesis”, “moderate evidence”, “inconclusive evidence”, etc., the dominant statistical framework will affect the form and extent of publication bias. This affects, in turn, the accuracy of the meta-analytic effect size estimates and the validity of SCT*.

Our paper studies the validity of SCT* in both statistical frameworks under various conditions that relate to the social dimension of science: in particular, the conventions and biases that affect experimental design and data reporting. We model publication bias in NHST as suppressing (a large percentage of) statistically non-significant results, and in Bayesian inference, as suppressing inconclusive evidence—that is, outcomes that yield Bayes factors in the interval \((\frac{1}{3}; 3)\). Then, under various imperfections that are typical of scientific practice, Bayesian inference yields more accurate effect size estimates than NHST, sometimes significantly so. This makes the long-run estimation of unknown effects more reliable. The results do not imply that Bayesian inference also outperforms other forms of frequentist inference, such as equivalence testing (Lakens et al. 2018b) or pure estimation-based inference (Cumming 2012, 2014)—they just highlight its advantages with respect to the traditional, and still widely endorsed, method of NHST.

The paper is structured as follows: Sect. 2 briefly explains the two competing statistical paradigms—frequentist inference with NHST and Bayesian inference. Section 3 describes the simulation model and the statistical and social factors it includes. Sections 4–6 present the results of multiple simulation scenarios that allow us to evaluate and contrast NHST and Bayesian inference in a variety of practically important circumstances. Finally, Sect. 7 discusses the general implications of the study and suggests projects for further research.

2 NHST and Bayesian inference

Suppose we would like to measure the efficacy of an experimental intervention—for example, whether on-site classes lead to higher student performance than remote teaching. In frequentist statistics, the predominant technique for addressing such a question is Null Hypothesis Significance Testing (NHST). At the basis stands a default or null hypothesis \(H_0\) about an unknown parameter of interest. Typically, this hypothesis makes a precise statement about this parameter (e.g., \(\mu = 0\)), or it claims that the parameter has the same value in two different experimental groups (e.g., \(\mu _1 = \mu _2\)). For example, the null hypothesis may claim that classroom and remote teaching do not differ in their effect on student grades. Opposed to the null hypothesis is the alternative hypothesis \(H_1\) which corresponds, in most practical applications, to the logical negation of the null hypothesis (e.g., \(\mu \ne 0\) or \(\mu _1 \ne \mu _2\)). To test such hypotheses against each other, researchers conduct a two-sided hypothesis test: an experimental design where large deviations in either direction from the “null value” count as evidence against the null hypothesis, and in favor of the alternative.Footnote 1

Suppose that the data in both experimental conditions (e.g., student grades for on-site and remote teaching) are Normally distributed with unknown variance. Then it is common to analyze them by a t-statistic, that is, a standardized difference between the sample mean in both groups. This statistic measures the divergence of the data from the null hypothesis \(H_0: \mu _1 = \mu _2\). If the value of t diverges largely from zero—and more precisely, if it falls into the most extreme 5% of the distribution—, we reject the null hypothesis and call the result “statistically significant” at the 5% level (\(p < .05\)). In the above example, such a result means evidence for the alternative hypothesis that classroom and remote teaching differ in their effect on student grades. Otherwise we state a “non-significant result” or a “non-effect” (\(p > .05\)). Similarly, a result in the 1%-tail of the distribution of the t-statistic is called “highly significant” (\(p < .01\)).

The implicit logic of NHST—to “reject” the null hypothesis and to declare a result statistically significant evidence if it deviates largely from the null value—has been criticized for a long time in philosophy, statistics and beyond. Critics claim, for example, that it conflates statistical and scientific significance, uses a highly counterintuitive and frequently misinterpreted measure of evidence (p-values) and makes it impossible to express support for the null hypothesis (e.g., Edwards et al. 1963; Hacking 1965; Spielman 1974; Ziliak and McCloskey 2008).

The shortcomings of NHST have motivated the pursuit of alternative models of statistical inference. The most prominent of them is Bayesian inference: probabilities express subjective degrees of belief in a scientific hypothesis (Bernardo and Smith 1994; Howson and Urbach 2006). p(H) quantifies prior degree of belief in hypothesis H whereas p(H|D), the conditional probability of H given D, quantifies posterior degree of belief in H—that is, the degree of belief in H after learning data D. While the posterior probability p(H|D) serves as a basis for inference and decision-making, the evidential import of a dataset D on two competing hypotheses is standardly described by the Bayes factor

$$\begin{aligned} BF_{10} (D):= & {} \frac{p(H_1|D) / p(H_0|D)}{p(H_1) / p(H_0)} = \frac{p(D|H_1)}{p(D|H_0)}. \end{aligned}$$

The Bayes factor is defined as the ratio between posterior and prior odds of \(H_1\) over \(H_0\) (Kass and Raftery 1995). Equivalently, it can be interpreted as the likelihood ratio of \(H_1\) and \(H_0\) with respect to data D—that is, as a measure of how much the data discriminate between the two hypotheses, and which hypothesis explains them better. Bayes factors \(BF_{10} > 1\) favor the alternative hypothesis \(H_1\), and Bayes factors in the range \(0< BF_{10} < 1\) favor the null hypothesis \(H_0\). Finally, note that the Bayes factors for the null and the alternative are each other’s inverse: \(BF_{01} = 1/BF_{10}\).

In this paper, we shall not enter into the foundational debate between Bayesians and frequentists (for surveys of arguments, see, e.g., Romeijn 2014; Sprenger 2006; Mayo 2018; van Dongen et al. 2019). We just note that while Bayesian inference avoids the typical problems of frequentist inference with NHST, it is not exempt from limitations. These include misinterpretation of Bayes factors, mindless use of “objective” or “default” priors (e.g., exclusive reliance on fat-tailed Cauchy priors in statistical packages), bias in favor of the null hypothesis, and potential mismatch between inference with Bayes factors and estimation based on the posterior distribution (e.g., Sprenger 2013; Kruschke 2018; Lakens et al. 2018a; Mayo 2018; Tendeiro and Kiers 2019).

3 Model description and simulation design

Romero (2016) presents a simulation model to study whether SCT* holds when relaxing ideal, utopian conditions for scientific inquiry in the context of frequentist statistics. This paper follows Romero’s simulation model, but we add the choice of the statistical framework (i.e., Bayesian vs. frequentist/NHST inference) as an exogenous variable to study how the validity of SCT* is affected by the statistical framework.

To examine the self-corrective abilities of Bayesian and frequentist inference, we first need to agree on a statistical model. In the behavioral sciences—arguably the disciplines hit most by the replication crisis—, many experiments collect data on a continuous scale and measure how the sample means \(\overline{X_1}\) and \(\overline{X_2}\) differ across two independent experimental conditions (e.g., treatment and control group). The means in each condition are assumed to follow a Normal distribution \(N(\mu _{1,2}, \sigma ^2)\), and the true effect size is described by the standardized difference of the unknown means: \(\delta = (\mu _1 - \mu _2)/\sigma\). Conventionally, a \(\delta\) around 0.2 is considered small, around 0.5 is considered medium, and around 0.8 is considered large. For both Bayesians and frequentists, the natural null hypothesis is \(H_0: \delta =0\), stating equal means in both groups. Frequentists leave the alternative hypothesis \(H_1: \delta \ne 0\) unspecified whereas Bayesians put a diffuse prior over the various values of \(\delta\), typically a Cauchy distribution such as \(H_1: \delta \sim \text {Cauchy}(0, \frac{1}{\sqrt{2}})\) (Rouder et al. 2009).

The value of \(\delta\) can be adequately estimated by Cohen’s d, which summarizes observed effect size by means of the standardized difference in sample means:

$$\begin{aligned} \text{Cohen's } d = \frac{\overline{X_1} - \overline{X_2}}{S_P} \end{aligned}$$

where \(S_P\) denotes the pooled standard deviation of the data.Footnote 2

Using the statistics software R, we randomly generate Normally distributed data for two independent groups. We study two conditions, one where the null hypothesis is (clearly) false and one where it is literally true. As a representative of a positive effect, we choose \(\delta = 0.41\), in agreement with meta-studies that consider this value typical of effect sizes in behavioral research (Richard et al. 2003; Fraley and Vazire 2014). The data are randomly generated with standard deviation \(\sigma =1\) in each group. For the first group, the mean is zero while for the second, the mean corresponds to the hypothesized effect size (either \(\delta =0\) or \(\delta =0.41\)). The sample size of each group is set to \(N=156\) since this corresponds to a statistical power of 95% (=5% type II error rate) for a true effect of \(\delta =0.41\). We then compute the observed effect size and repeat this procedure to simulate multiple replications of a single experiment. At the same time, we simulate a cumulative meta-analysis of the effect size estimates. Figure 1 shows the observed effect sizes from 10 replications and how they are aggregated into an overall meta-analytic estimate.Footnote 3,Footnote 4

Fig. 1
figure 1

Observed effect sizes with 95% confidence intervals in the exact replication of an experiment (left figure), and the corresponding aggregated effect size estimates (right figure). Data generated under the assumption \(\delta =0.41\)

Full size image

We expect that frequentist and Bayesian inference both validate SCT* under ideal conditions where various biases and imperfections are absent. The big question is whether Bayesian statistics improves upon NHST when we move to more realistic scenarios. In particular: Are the experiments sufficiently powered to detect an effect? Are the researchers biased in a particular direction? Are non-significant results systematically dismissed? The available evidence on published research suggests that the answers to these questions should not always be yes, leaving open whether SCT* will still hold in those cases. We model the relevant factors as binary variables, contrasting an ideal or utopian condition to a less perfect (and more realistic) condition. Let’s look at them in more detail.

3.1 Variable 1: sufficient versus limited resources

NHST is justified by its favorable long-run properties, spelled out in terms of error control: a true null hypothesis is rarely “rejected” by NHST and a true alternative hypothesis typically yields a statistically significant result. To achieve these favorable properties, experiments require an adequate sample size. Due to lack of resources and other practical limitations (e.g., availability of participants/patients, costs of trial, time pressure to finish experiments), the sample size is often too small to bound error rates at low levels. Since the type I error level—that is, the rate of rejecting the null hypothesis when it is true—is conventionally fixed at 5%, this means that the power of a test is frequently low and can even fall below 50% (e.g., Ioannidis 2005).

In our simulation study, we compare two cases: first, a condition where the type I error rate in a two-sample t-test is bound at the 5% level and power relative to \(\delta = 0.41\) equals 95%. This condition of sufficient resources corresponds to a sample size of N = 156. It is contrasted to a condition of limited resources that is typical of many experiments in behavioral research. In that condition, both experimental groups have sample size N = 36, resulting in a power of only 40%.

The Bayesian analogue to power analysis is to control the probability of misleading evidence (Royall 2000; Schönbrodt and Wagenmakers 2018), and to design an experiment such that the Bayes factor will, with high probability, state evidence for \(H_1\) when it is true, and mutatis mutandis for \(H_0\). For the parameters in our study, such a “Bayes factor design analysis” yields the sample size N = 190. To ensure a level playing field between both approaches, we use the same values (N = 156 and N = 36) for the frequentist and Bayesian scenarios. The simulation results for N = 190 instead of N = 156 in the sufficient resources condition are also qualitatively identical.

3.2 Variable 2: direction bias

Scientists sometimes conduct their research in a way that is shaped by selective perception and biased expectations. For example, feminist critiques of primatological research have pointed out that evidence on the mating behavior of monkeys and apes was often neglected when it contradicted scientists’ theoretical expectations (e.g., polyandrous behavior of females: Hrdy 1986; Hubbard 1990). More generally, researchers often exhibit confirmation bias (e.g., MacCoun 1998; Douglas 2009): their perception of empirical findings is shaped by the research program to which they are committed. There is also specific evidence that results are more likely to be published if they agree with previously found effects and exhibit positive magnitude (Hopewell et al. 2009; Lee et al. 2013). Effects that contradict one’s theoretical expectations and have a negative magnitude may either be suppressed as an act of self-censuring or be discarded in the peer-review process. Such direction bias is obviously detrimental to the impartiality and objectivity of scientific research, and we expect that it affects the accuracy of meta-analytic effect estimation and the validity of SCT*, too.

We model direction bias by a variable that can have two values: either all results are published, regardless of whether the effect is positive or negative (=no direction bias), or all results with negative effect size magnitude are suppressed (=direction bias present).

3.3 Variable 3: suppressing inconclusive evidence

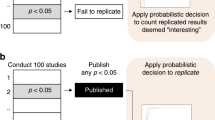
Statistically non-significant outcomes of NHST (\(p > .05\)) are in practice often filtered out and end up in the proverbial file drawer (Rosenthal 1979; Ioannidis 2005; Fanelli 2010). An epistemic explanation for this is that non-significant outcomes are ambiguous between supporting the null hypothesis and the study not having enough statistical power to find an effect. Due to this ambiguity, they are hard to package into a clear narrative and published much less frequently. In our model, we distinguish between a non-ideal condition where only results significant at the 5% level are published and an ideal condition where all results are published, also non-significant ones (i.e., results with a p-value exceeding .05). This dichotomous picture (which we relax when we extend the model) is in line with scientometric evidence for the increasing prevalence of statistically significant over non-significant findings (Fanelli 2012). The choice of 5% as a cutoff level is a well-entrenched convention in the behavioral sciences; that said, also “marginally significant” p-values (i.e., \(.05 \le p < .10\)) are often reported in economics and the biomedical sciences (De Winter and Dodou 2015; Lakens 2015; Bruns et al. 2019).

For the Bayesian, the inconclusiveness of findings is spelled out by means of the Bayes factor instead of the p-value. When the Bayes factor is close to 1, the evidence is inconclusive: the null hypothesis and the alternative are equally likely to explain the observed data. We set up the two conditions analogously to the frequentist case: in the ideal condition, all observed Bayes factors enter the meta-analysis, regardless of their value, whereas the non-ideal condition excludes all Bayes factors reporting weak evidence, that is, those values where neither the null hypothesis nor the alternative are clearly favored by the data.

Specifically, we use the range \(\frac{1}{3}< BF_{10} < 3\) for denoting inconclusive or weak evidence. This range is appropriate for two reasons. First, the qualitative meaning of the \(p<.05\) significance threshold corresponds to the Bayesian threshold \(\frac{1}{3}< BF_{10} < 3\). Frequentists consider p-values between .05 and .10 as weak or anecdotal evidence, as witnessed by formulations such as “marginally significant” and “trend”. Similarly, Bayesian researchers use a scale where the interval 1–3 corresponds to anecdotal or weak evidence for \(H_1\), 3–10 to moderate evidence, 10–30 to strong evidence, and so on (Jeffreys 1961; Lee and Wagenmakers 2014). Reversely for the ranges 1/3 to 1, 1/10 to 1/3, and so on. Second, Bayesian re-analysis of data with an observed significance level of \(p \approx .05\) often corresponds to a Bayes factor around \(BF_{10}=3\).Footnote 5 Wider ranges for inconclusive evidence, such as \(\frac{1}{6}< BF_{10} < 6\) (Schönbrodt and Wagenmakers 2018), are possible, but such proposals do not correspond to an interpretation of Bayes factors anchored in existing conventions.

To date, there has not yet been a systematic study of evidence filtering in Bayesian statistics. Hence, it is an open question whether in practice researchers would publish evidence for the null hypothesis when they have the necessary statistical tools to express it, e.g., Bayes factors. We return to this question in the discussion section.

4 Results: the baseline condition

Our simulations compare the performance of NHST and Bayesian inference in two types of situations: the baseline conditions and extensions of the model. The baseline conditions, numbered S1–S16, take the three variables described in Sect. 3 and the true effect size as independent variables. Table 1 explains which scenario corresponds to which combination of values of these variables. The model extensions explore a wider range of situations: we examine conditions where some, but not all negative results are published, and we contrast Bayesian and frequentist inference for a wider range of effect sizes (e.g., small effects such as \(\delta \approx 0.2\) or large effects such as \(\delta \approx 1\)).

Table 1 The 16 possible simulation scenarios
Full size table

As revealed by Fig. 2, there is no difference between Bayesian and frequentist inference as long as “negative results” (i.e., results with inconclusive evidence) are published. This is to be expected since the difference between Bayesian and frequentist analysis in our study consists in the way inconclusive evidence is explicated and filtered. Thus both frameworks yield the same result in S1–S8: when the alternative hypothesis is true, meta-analytic estimates are accurate (scenarios S1–S4); when the null hypothesis is true, both frameworks are vulnerable to direction bias (scenarios S7–S8). Indeed, when the alternative hypothesis is true, few experiments will yield estimates with a negative magnitude and the presence of direction bias will not compromise the meta-analytic aggregation substantively.

Fig. 2
figure 2

Meta-analytic effect size estimates for Bayesian inference (dark bars) and frequentist inference (light bars) in conditions S1–S8 after 25 reported experiments. Upper graph: scenarios S1–S4 where \(\delta = 0.41\), lower graph: scenarios S5–S8 where \(\delta =0\). All inconclusive evidence is published. The dashed line represents the true effect size, the error bars show one standard deviation

Full size image
Fig. 3
figure 3

Meta-analytic effect size estimates for Bayesian inference (dark bars) and frequentist inference (light bars) in conditions S9–S16 after 25 reported experiments. Left graph: scenarios S9–S12 where \(\delta = 0.41\), right graph: scenarios S13–S16 where \(\delta =0\). All inconclusive evidence is suppressed. The dashed line represents the true effect size, the error bars show one standard deviation

Full size image

Figure 3 shows the results of scenarios S9–S16 where a file drawer effect is operating and inconclusive, “non-significant” evidence is suppressed. To recall, this means that data from experiments with \(p \ge .05\) or with a Bayes factor in the range \(\frac{1}{3}< BF_{10} < 3\) do not enter the meta-analysis. In some of these scenarios, especially when the null hypothesis is true and direction bias is present, the frequentist excessively overestimates the actual effect size (e.g., \(d \approx 0.25\) in S15 and \(d \approx 0.55\) in S16 while in reality, \(\delta =0\)). The reason is that the frequentist conception of “significant evidence” filters out evidence for the null hypothesis and acts as an amplifier of direction bias: only statistically significant effect sizes with positive magnitude enter the meta-analysis (e.g., \(d \ge 0.47\) in S16). By contrast, the Bayesian also reports evidence that speaks strongly for the null hypothesis (i.e., \(d \approx 0\)) and obtains just a weak positive meta-analytic effect.

A similar diagnosis applies when the alternative hypothesis is true, regardless of direction bias. Consider scenarios S10 and S12. Due to the limited resources and the implied small sample size, only large effects meet the frequentist threshold \(p < .05\), leading to a substantial overestimation of the actual effect (\(d \approx 0.65\) in both scenarios, instead of the true \(\delta = 0.41\)). The overestimation in the Bayesian case, by contrast, is negligible for S10 and moderate for S12 (\(d \approx 0.5\)).

Thus, Bayesian inference performs considerably better when inconclusive evidence is not published, as it often happens in empirical research. There is thus a (partial) case for statistical reform: Bayesian analysis of experiments leads to more accurate meta-analytic effect size estimates when the experimental conditions are non-ideal and inconclusive evidence is suppressed.Footnote 6

The next two sections present two extensions that model other practically relevant situations.

5 Extension 1: the probabilistic file drawer effect

The preceding simulations have modeled the file drawer effect as the exclusion of all non-significant p-values. In practice, it will depend a lot on the context whether inconclusive evidence is published or not. Bakker et al. (2012) report studies according to which the percentage of unpublished research in psychology may be greater than 50%. Especially in conceptual replications and other follow-up studies it is plausible that evidence contradicting the original result may be discarded (e.g., by finding fault with oneself and repeating the experiment with a slightly different design or test population). Then, disciplines with an influential private sector such as medicine may be especially susceptible to bias in favor of significant evidence: as indicated by the effect size gap between industry-funded and publicly funded studies, sponsors are often disinterested in publishing research on an apparently ineffective drug (Wilholt 2009; Lexchin 2012).

By contrast, there is an increasing number of prestigious journals that accepts submissions according to the “registered reports” model: before starting to collect the data, the researcher submits a study proposal that is accepted or rejected based on the study’s theoretical interest and the experimental design.Footnote 7 This means that the paper will be published regardless of whether the results are statistically significant or not. Moreover, in large-scale replication projects such as Open Science Collaboration (2015) or Camerer et al. (2016) that examine the reproducibility of previous research, the evidence is published regardless of direction or size of the effect.

Taking all this together, we can expect that some proportion of statistically inconclusive studies will make it into print, or be made publicly available, while a substantial part of them will remain in the file drawer. We extend the results of the model analytically to investigate how the performance of frequentist and Bayesian inference depends on the proportion of inconclusive evidence that is actually published.

Fig. 4
figure 4

Difference between estimated and true effect size as a function of the probability of suppressing inconclusive evidence, that is, the prevalence of the file drawer effect. Left graph = frequentist analysis, right graph = Bayesian analysis

Full size image

Like in the baseline condition, we model the suppression of inconclusive evidence as not reporting non-significant results, i.e., \(p > .05\) and Bayes factors with weak, anecdotal evidence (\(\frac{1}{3}< BF_{10} < 3\)). Figure 4 plots effect size overestimation in both frameworks as a function of the probability of publishing studies with inconclusive evidence.

For the frequentist, estimates get more accurate when more statistically non-significant studies are published. Notably, when direction bias is present, publishing just a small proportion of those studies is already an efficient antidote to large overestimation. This is actually logical: when direction bias is present and statistically non-significant results are suppressed, only studies with extreme effects are published and including some non-significant results will already be a huge step toward more realistic estimates.

The accuracy of the Bayesian estimates, however, does not depend much on the probability of publishing inconclusive studies—the overestimation is more or less invariant under the strength of the file drawer effect. Indeed, the Bayesian estimates are already accurate when all inconclusive evidence is suppressed. Using Bayesian inference instead of NHST may act as a safeguard against effect size overestimation in conditions where the extent of publication bias is unclear and potentially large. As soon as 20–30% of statistically non-significant results are published, however, frequentist estimates become similarly accurate.

6 Extension 2: a wider range of effect sizes

While \(\delta =0.41\) may be a good long-term average for the effect size of true alternative hypotheses in behavioral research, true effect sizes will typically spread over a wide range, ranging from small and barely observable effects (\(\delta \approx 0.1\)) to very large and striking effects (e.g., \(\delta \approx 1\)). This also depends on the specific scientific discipline and the available means for filtering noise and controlling for confounders. To increase the generality of our findings, we examine a wider range of true effect sizes. We focus on those conditions where Bayesians and frequentists reach different conclusions—that is, scenarios S9–S16 where inconclusive evidence is suppressed. Figures 5 and 6 show for both frameworks how the difference between estimated and true effect size varies as a function of the true effect size.

Fig. 5
figure 5

Difference between estimated and true effect size as a function of the true effect size (measured by standardized means difference), for scenarios with direction bias and suppression of inconclusive evidence. Triangles = frequentist case, circles = Bayesian case, with linear interpolation

Full size image

When direction bias is present (Fig. 5), the Bayesian estimate comes closer to the true effect. Frequentists largely overestimate small effects due to the combination of direction bias and suppressing inconclusive evidence, but they estimate large effects accurately. This is to be expected since with increasing effect size, almost everything will be significant and fewer results will be suppressed. In these cases, the file drawer effect does not compromise the accuracy of the meta-analytic estimation procedure.

Fig. 6
figure 6

Difference between estimated and true effect size as a function of the true effect size (measured by standardized means difference), for scenarios with suppression of inconclusive evidence and no direction bias. Triangles = frequentist case, circles = Bayesian case, with linear interpolation

Full size image

Turning to the case of no direction bias, shown in Fig. 6, two observations are striking. First, the frequentist graph ceases to be monotonically decreasing: small effects are substantially overestimated while null effects are estimated accurately. This is because, in the case of N = 36, all results inside the range \(d \in [-0.47;0.47]\) yield a p-value higher than .05 and do not enter the meta-analysis. For a true small positive effect, we will therefore observe many more (large) positive than negative effects and obtain a heavily biased meta-analytic estimate. For a true null effect, however, positive and negative magnitude effects are equally likely to be published and the aggregated estimate will be accurate.Footnote 8 Similarly, when effects are big enough, few results will remain unpublished and the meta-analytic estimate will converge to the true effect size. The left graph in Fig. 7 visualizes these explanations by plotting the probability density function of d, and the range of suppressed observations.

Fig. 7
figure 7

Probability density functions for the standardized sample mean in a single experiment for \(N=36\) and different values of the real effect size. Full line: \(\delta =0.15\), dashed line: \(\delta =0.41\), dotted line: \(\delta =0\). The suppressed regions (i.e., observations that do not enter the meta-analysis because \(p > .05\) or \(\frac{1}{3}< BF_{10} < 3\)) are shaded in dark. Left graph: frequentist case, right graph: Bayesian case

Full size image

Second, the Bayesian underestimates some small effects. This phenomenon is due to a superposition of two effects. Unlike the frequentist, the Bayesian publishes large effects in both directions and observed effects close to the null value \({d} \approx 0\). Intermediate effect size estimates from single studies are not published and left out of the meta-analysis—see Fig. 7. For small positive effects such as \(\delta =0.1\) or \(\delta =0.2\), the Bayesian is more likely to obtain results that favor the null hypothesis with \(BF_{10} < \frac{1}{3}\), than results that favor the alternative with \(BF_{10} > 3\). However, for these scenarios, the underestimation does not affect the qualitative interpretation of the effect size in question.

All in all, omitting weak evidence in favor of either hypothesis leads to more accurate meta-analytic estimates than omitting statistically non-significant results. These observations are especially salient for small effects. SCT*—the thesis about the self-corrective nature of science in sequential replications of an experiment—therefore holds for a wider range of possible effect sizes when replacing NHST with Bayesian inference.

Our findings also agree with the distribution of effect sizes in the OSC replication project for behavioral research (Open Science Collaboration 2015): replications of experiments with large observed effects usually confirm the original diagnosis, while moderate effects often turn out to be small or inexistent in the replication.Footnote 9 While a more detailed and substantive analysis would require assumptions about the prevalence of direction bias and suppressing inconclusive evidence in empirical research, our findings are, at first sight, consistent with patterns observed in recent replication research.

7 Discussion

Numerous areas of science are struck by a replication crisis—a failure to reproduce past landmark results. Such failures diminish the reliability of experimental work in the affected disciplines and the epistemic authority of the scientists that work in them. There is a plethora of complementary reform proposals to leave this state of crisis behind. Three principled strategies can be distinguished. The first strategy, called statistical reform, blames statistical procedures, in particular in the continued use of null hypothesis significance testing (NHST). Were NHST to be abandoned and to be replaced by Bayesian inference, scientific findings would be more replicable. The opposed strategy, called social reform, contends that the current social structure of science, in particular career incentives which reward novel and spectacular findings, has been the main culprit in bringing about the replication crisis. Between these extremes is a wide range of proposals for methodological reform that combines elements of social interaction and statistical method techniques (multi-site experiments, data-sharing, compulsory preregistration, etc.).

In this paper, we have explored the scope of statistical reform proposals by contrasting Bayesian and frequentist inference with respect to a specific thesis about the self-corrective nature of science, SCT*: convergence to the true effect in a sequential replication of experiments. Validating SCT* is arguably a minimal adequacy condition for any statistical reform proposal that addresses the replication crisis. Our model focuses on a common experimental design—two independent samples with normally distributed data—and compares NHST and Bayesian inference in different conditions: an ideal scenario where resources are sufficient and all results are published, as well as less ideal (and more realistic) conditions, where experiments are underpowered and/or various biases affect the publication of a research finding.

Our results support a partially favorable verdict on the efficacy of statistical reform. When a substantial proportion of studies with inconclusive evidence are published, both Bayesian inference and frequentist inference with NHST lead to quite accurate meta-analytic estimates and validate SCT*. However, when inconclusive evidence is not published, but strong evidence for a null effect is, Bayesian inference leads to more accurate estimates. In these conditions, which are unfortunately characteristic of scientific practice, statistical reform in favor of Bayesian inference will improve the reproducibility of published studies, validate SCT* and make experimental research more reliable.

The advantage of Bayesian statistics is particularly evident for small effect sizes (\(\delta \approx 0.2\)), which the frequentist often misidentifies as moderate or relatively large effects. This finding is in line with observations that small effects are at particular risk of being overestimated systematically (Ioannidis 2008). This holds for experimental research (e.g., Open Science Collaboration 2015), but perhaps even more so for observational research. Especially in the context of regression analysis, slight biases due to non-inclusion of relevant variables are almost inevitable and they inflate effect size estimates and observed significance substantially (Bruns and Ioannidis 2016; Ioannidis et al. 2017).

Finally, we turn to the limitations of our study. First, our results do not prove that moving to Bayesian statistics is the best statistical reform: alternative frameworks within the frequentist paradigm (e.g., Cumming 2012; Lakens et al. 2018b; Mayo 2018) could improve matters, too. Assessing and comparing such proposals is beyond the scope of this paper.

Second, the claim in favor of Bayesian statistics depends crucially on the assumption that researchers would publish evidence for the null hypothesis when the statistical framework supports such a conclusion (compare Sect. 3). One could object to this assumption by saying that such studies would just count as “failed” and that the evidence would nonetheless be suppressed (e.g., think of a clinical trial showing that a particular medical drug does not cure the target disease). Such situations certainly occur, but on the other hand, the null hypothesis does often play a major role in scientific inference and hypothesis testing: it is simple, has higher predictive value and can express important theoretical relations such as additivity of factors, chance effects and absence of a causal connection (e.g., Gallistel 2009; Morey and Rouder 2011; Sprenger and Hartmann 2019, ch. 9). In such circumstances, evidence for the null is of major theoretical interest. Moreover, evidence for a point null hypothesis is often the target of medical research that assesses the equivalence of two treatments, i.e., those aiming at establishing “theoretical equipoise” (Freedman 1987). Such research is greatly facilitated by a statistical framework that allows for a straightforward quantification of evidence for the null hypothesis. We therefore conjecture that statistical frameworks where evidence for the null can be expressed on the same scale as evidence for the alternative would lead to more “null” results being reported. Being able to state strong evidence against the targeted alternative hypothesis (e.g., that a specific intervention works) will also make the allocation of future resources easier compared to just stating “failure to reject the null”.

Third, statistical reform does not cure all the problems of scientific inference. We have not discussed here which concrete steps for social reform (e.g., changing incentive structures and funding allocation schemes) would be most effective in complementing statistical reforms. The interplay of reform proposals on different levels is a fascinating topic for future research in the social epistemology of science. At this point, we can just observe that the file drawer effect seems to be particularly detrimental to reliable effect size aggregation, and that proposals for social and methodological reform should try to combat it. Compulsory pre-registration of experiments is a natural approach, but studying the efficacy of that strategy has to be left to future work.

Increasing the reliability of published research remains a complex and challenging task, involving reform of the scientific enterprise on various levels. What we have shown in this paper is that the choice of the statistical framework plays an important role in this process. Under the imperfect conditions where experimental research operates, adopting Bayesian principles for designing and analyzing experiments leads to more accurate effect size estimates compared to NHST, without incurring major drawbacks. Regardless of whether or not one likes Bayesian inference, it would be desirable to evaluate the model empirically—for example, by imposing the use of Bayesian statistics on an entire subdiscipline and then measuring how publication bias and replicability rates change. Such a project would not be easy to implement, but yield valuable insights about the mechanisms underlying the replication crisis.