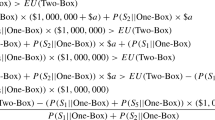Abstract
This paper has two main parts. In the first part, we motivate a kind of indeterminate, suppositional credences by discussing the prospect for a subjective interpretation of a causal Bayesian network (CBN), an important tool for causal reasoning in artificial intelligence. A CBN consists of a causal graph and a collection of interventional probabilities. The subjective interpretation in question would take the causal graph in a CBN to represent the causal structure that is believed by an agent, and interventional probabilities in a CBN to represent suppositional credences. We review a difficulty noted in the literature with such an interpretation, and suggest that a natural way to address the challenge is to go for a generalization of CBN that allows indeterminate credences. In the second part, we develop a decision-theoretic foundation for such indeterminate suppositional credences, by generalizing a theory of coherent choice functions to accommodate some form of act-state dependence. The upshot is a decision-theoretic framework that is not only rich enough to, so to speak, ground the probabilities in a subjectively interpreted causal network, but also interesting in its own right, in that it accommodates both act-state dependence and imprecise probabilities.

Similar content being viewed by others
Notes
Note that we take \(P^{do({\mathbf {S}}={\mathbf {s}})}\) to be a probability distribution over \({\mathbf {V}} - {\mathbf {S}}\) rather than over \({\mathbf {V}}\). A more common formulation is to take \(P^{do({\mathbf {S}}={\mathbf {s}})}\) to be a distribution over \({\mathbf {V}}\) and take the intervention principle to require that
$$\begin{aligned} P^{do({\mathbf {S}}={\mathbf {s}})}({\mathbf {V}}) = \left\{ \begin{array}{ll} \prod _{X\in {\mathbf {V}}- {\mathbf {S}}}P(X | \mathbf {Pa}_{\mathcal {G}}(X)) &{} \text {for values of } {\mathbf {V}} \text { consistent with } {\mathbf {S}} = {\mathbf {s}}, \\ 0 &{} \text {for values of } {\mathbf {V}} \text { inconsistent with } {\mathbf {S}} = {\mathbf {s}}. \end{array}\right. \end{aligned}$$Our formulation in the main text is entailed by and slightly weaker than this formulation. In particular, this formulation makes explicit that \(P^{do({\mathbf {S}}={\mathbf {s}})}({\mathbf {S}}={\mathbf {s}}) = 1\) while ours does not. We thank an anonymous referee for this observation. We adopt this weaker formulation because it is more convenient for our subsequent discussions. All our points remain valid under the stronger formulation.
The positivity of the observational distribution is needed for Proposition 1, because the intervention principle in Definition 1 puts constraints on an interventional probability distribution only if the relevant observational conditional probabilities are defined. As an illustration, here is a simple kind of situation in which failure of positivity can easily induce a counterexample to Proposition 1. Consider three binary variables X, Y, Z, among which X and Z are exogenous, meaning that neither of them is affected by any intervention of the other two variables. Suppose Y is affected by X and Z in such a way that if \(Z=0\), then the value of X does not make a difference to Y, whereas if \(Z=1\), then the value of X does. In other words, \(P^{do(X=0\wedge Z=0)}(Y) = P^{do(X=1\wedge Z=0)}(Y)\), while \(P^{do(X=0\wedge Z=1)}(Y) \ne P^{do(X=1\wedge Z=1)}(Y)\). However, if the observational distribution \(P^{do(\emptyset )}\) puts zero mass on \(Z=1\), then all that is needed to satisfy the intervention principle in Definition 1 is just a graph with an arrow from Z to Y but without an arrow from X to Y. In particular, given this graph, the intervention principle does not constrain \(P^{do(X=0\wedge Z=1)}(Y)\) or \(P^{do(X=1\wedge Z=1)}(Y)\), for \(P^{do(\emptyset )}(Y | Z=1)\) is undefined. So, despite the disequality \(P^{do(X=0\wedge Z=1)}(Y) \ne P^{do(X=1\wedge Z=1)}(Y)\), the arrow from X to Y is not needed to meet Definition 1.
A possible view to take here is that a CBN is individuated by its collection of interventional distributions, and so a mere change of the graph (e.g., to a proper supergraph) does not change the CBN. Then the simplest graph picked out by Propositions 1 and 2 is naturally regarded as the canonical form of the first element of a CBN. Under this view, the restriction is not a restriction on CBNs but rather a restriction to canonical forms. We thank an anonymous referee for raising this issue.
A closely related notion known as ’strong independence’ applies to convex sets of probability functions. Two variables X and Y are strongly independent if the set of probability functions is the convex hull of a set that satisfies complete independence (Cozman 2012). As we intimated earlier, we have no intention to enforce the requirement of convexity for credal sets in this paper.
In a way, this is similar to what Spirtes et al. (2000, pp. 42–43) suggested in their brief discussion of “Bayesian interpretations” of the formalism. However, in their suggestion the set of probability functions is explicitly indexed by a set of parameters that, following orthodox Bayesianism, are also treated as random variables.
We thank an anonymous referee for stressing these points. The referee also raises the following question. What if the agent has a prior or higher-order probability distribution over the set of probability functions? Should the prior be ignored or should it be used to integrate out parameters to form a single, precise probability function? This is an important question to which we cannot do justice here, in part because we are yet to make up our (group) mind about it. However, it is fair to say that for the reason elaborated earlier, unless we give up the subjective Markov condition, we cannot simply collapse the hierarchical structure into a precise distribution over the substantive variables and treat that single distribution as all there is to the agent’s doxastic state (though this single distribution may well be useful for other purposes). On the other hand, to ignore the prior seems obviously unreasonable. Presumably it is the whole hierarchical structure, consisting of the set and the distribution over the set, that is a proper representation of the credences in question, in which case a subjective Markov condition in some form may still be maintained (cf. Spirtes et al. 2000, pp. 42–43, as is mentioned in the previous note). A broadly similar representation was used in (Gärdenfors and Sahlin 1982), where each member of a set of probability functions is labeled with a degree of epistemic reliability. Our results in this paper do not cover credences with this additional complexity.
This corresponds to what is known as credal networks under complete independence. Two more commonly studied types are known as credal networks under strong independence, which is, roughly speaking, a convexized version of that under complete independence, and credal networks under epistemic irrelevance, which is importantly different (De Bock 2017).
Notice that in this example, the marginal of X contains two distributions, and so does the marginal of Y. However, the set \({\mathbf {K}}\) contains only two joint distributions of X and Y, rather than all four joint distributions that can be generated from the two marginal sets. That is, in our conception of a credal network, we do not require that the credal set include every joint distribution that can be generated by picking one member from each local marginal or conditional, and taking their product.
This reflects a rather common theme in the study of imprecise probabilities. Another most salient example is that the notion of stochastic independence is fruitfully generalizable in more than one way in the context of imprecise probabilities, as we mentioned before. We thank an anonymous referee for making this observation.
We thank an anonymous referee for pressing us on this point. Moreover, as the referee pointed out, it may be worth considering credal networks of an altogether different type, such as credal networks under epistemic irrelevance.
Here closure of a set of horse lotteries is defined with respect to the topology of state-wise convergence of distributions over the prize set (i.e., vNM lotteries).
In Seidenfeld et al. (2010), the non-indexed version of this axiom is formulated as two clauses:
- (a)::
-
If \(o_2\in O\) and \(o\in R(\{o_1\}\cup O)\), then \(o\in R(O)\), and
- (b)::
-
If \(o_1\in O\) and \(o\in R(O)\), then \(o\in R(\{o_2\}\cup O - \{o_1\})\).
It is not hard to see that the two clauses are equivalent to the simpler formulation: for any \(o_1\ne o\ne o_2\), if \(o\in R(\{o_1\}\cup O)\), then \(o\in R(\{o_2\}\cup O - \{o_1\})\). IC4 is an adaptation of this simpler formulation.
We suspect that we will need to add at least:
- IC6::
-
For every pair of constant horse lotteries \(o_1^j\) and \(o_2^k\), if \(C(\{o_1^j, o_2^k\}) = \{o_1^j, o_2^k\}\), then for any closed option set \(O \supseteq \{o_1^j, o_2^k\}\), \(o_1^j \in C(O)\) if and only if \(o_2^k \in C(O)\).
This is Sen’s (1977) property \(\beta \) restricted to constant horse lotteries. Since our notion of a coherent choice function is relative to a common, state-independent and index-independent utility, this axiom is obviously sound. Together with IC1(a), this axiom ensures an index-independent weak ordering of the prizes, which we believe is needed for the desired representation theorem.
We thank an anonymous referee for suggesting this direct proof rather than an indirect one as it was originally presented.
In SSK’s argument, \({\underline{p}}\) is taken to be equal to \(p_*\). The change here guarantees that \({\underline{p}}<1\) and so avoids the need to consider the case of \({\underline{p}}=1\) later in the argument.
References
Aizerman, M. A. (1985). New problems in general choice theory. Social Choice and Welfare, 2, 235–282.
Anscombe, F. J., & Aumann, R. J. (1963). A definition of subjective probability. The Annals of Mathematical Statistics, 34, 199–205.
Armendt, B. (1986). A foundation for causal decision theory. Topoi, 5, 3–19.
Augustin, T., Coolen, F. P. A., de Cooman, G., & Troffaes, M. C. M. (2014). Introduction to imprecise probabilities. Hoboken: Wiley.
Bradley, S., & Steele, K. (2014). Should subjective probabilities be sharp? Episteme, 11, 277–289.
Chandler, J. (2014). Subjective probabilities need not be sharp. Erkenntnis, 79(6), 1273–1286.
Couso, I., Moral, S., & Walley, P. (2000). A survey of concepts of independence for imprecise probabilities. Risk, Decision and Policy, 5, 165–181.
Cozman, F. (2000). Credal networks. Artificial Intelligence, 120, 199–233.
Cozman, F. (2012). Sets of probability distributions, independence, and convexity. Synthese, 186, 577–600.
Cozman, F., & Walley, P. (2001). Graphoid properties of epistemic irrelevance and independence. In Proceedings of the 2nd international symposium on imprecise probabilities and their applications (pp. 112–121).
Danks, D. (2014). Unifying the mind: Cognitive representations as graphical models. Cambridge, MA: MIT Press.
De Bock, J. (2017). Credal networks under epistemic irrelevance. International Journal of Approximate Reasoning, 85, 107–138.
De Bock, J., & de Cooman, G. (2015). Credal networks under epistemic irrelevance: The sets of desirable gambles approach. International Journal of Approximate Reasoning, 56, 178–207.
De Bock, J., & de Cooman, G. (2019). Interpreting, axiomatising and representing coherent choice functions in terms of desirability. In Proceedings of machine learning research (ISIPTA 2019) (Vol. 103, pp. 125–134).
Elga, A. (2010). Subjective probabilities should be sharp. Philosophers’ Imprint, 10(5), 1–11.
Gärdenfors, P., & Sahlin, N. (1982). Unreliable probabilities, risk taking, and decision making. Synthese, 53, 361–386.
Glymour, C. (2001). The mind’s arrows: Bayes nets and graphical causal models in psychology. Cambridge, MA: MIT Press.
Glymour, C., & Danks, D. (2007). Reasons as causes in Bayesian epistemology. Journal of Philosophy, 104(9), 464–474.
Gopnik, A., & Schulz, L. (2007). Causal learning: Psychology, philosophy, and computation. New York: Oxford University Press.
Hitchcock, C. (1996). Causal decision theory and decision-theoretic causation. Noûs, 30(4), 508–526.
Jeffrey, R. (1965). The logic of decision. New York: McGraw Hill.
Jeffrey, R. (1983). Bayesianism with a human face. In J. Earman (Ed.), Testing scientific theories (pp. 133–156). Minneapolis: University of Minnesota Press.
Joyce, J. (1999). The foundations of causal decision theory. Cambridge: Cambridge University Press.
Joyce, J. (2005). How degrees of belief reflect evidence. Philosophical Perspectives, 19, 153–179.
Joyce, J. (2010). A defense of imprecise credences in inference and decision making. Philosophical Perspectives, 24, 281–323.
Kadane, J. B., Schervish, M. J., & Seidenfeld, T. (2004). A Rubinesque theory of decision. IMS Lecture Notes Monograph, 45, 1–11.
Kaplan, M. (1996). Decision theory as philosophy. Cambridge: Cambridge University Press.
Kyburg, H. (1983). Epistemology and inference. Minneapolis: University of Minnesota Press.
Levi, I. (1974). On indeterminate probabilities. Journal of Philosophy, 71, 397–418.
Levi, I. (1980). The enterprise of knowledge. Cambridge, MA: MIT Press.
Meek, C., & Glymour, C. (1994). Conditioning and intervening. British Journal for the Philosophy of Science, 45, 1001–1021.
Menzies, P., & Price, H. (1993). Causation as a secondary quality. British Journal for the Philosophy of Science, 44, 187–203.
Pearl, J. (1988). Probabilistic reasoning in intelligent systems. San Mateo, CA: Morgan Kaufmann.
Pearl, J. (2009). Causality: Models, reasoning, and inference (2nd ed.). Cambridge: Cambridge University Press.
Price, H. (1991). Agency and probabilistic causality. British Journal for the Philosophy of Science, 42, 157–176.
Seidenfeld, T., Schervish, M. J., & Kadane, J. B. (1995). A representation of partially ordered preferences. Annals of Statistics, 23, 2168–2217.
Seidenfeld, T., Schervish, M. J., & Kadane, J. B. (2010). Coherent choice functions under uncertainty. Synthese, 172(1), 157–176.
Sen, A. (1977). Social choice theory: A re-examination. Econometrica, 45, 53–89.
Spirtes, P., Glymour, G., & Scheines, R. (2000). Causation, prediction and search (2nd ed.). Cambridge, MA: MIT Press.
Spohn, W. (2000). Bayesian nets are all there is to causal dependence. In M. C. Galavotti, et al. (Eds.), Stochastic dependence and causality (pp. 157–172). Stanford: CSLI Publications.
Stern, R. (2017). Interventionist decision theory. Synthese, 194(10), 4133–4153.
Sturgeon, S. (2008). Reason and the grain of belief. Noûs, 42, 139–165.
Van Camp, A. (2018). Choice functions as a tool to model uncertainty. PhD thesis, Faculty of Engineering and Architecture, Ghent University.
Van Camp, A., de Cooman, G., & Miranda, E. (2018). Lexicographic choice functions. International Journal of Approximate Reasoning, 92, 97–119.
von Neumann, J., & Morgenstern, O. (1947). Theory of games and economic behavior. Princeton: Princeton University Press.
Walley, P. (1991). Statistical reasoning with imprecise probabilities. New York: Chapman and Hall.
Williamson, J. (2001). Foundations for Bayesian networks. In D. Corfield & J. Williamson (Eds.), Foundations of Bayesianism (pp. 75–115). Berlin: Springer.
Woodward, J. (2003). Making things happen: A theory of causal explanation. Oxford: Oxford University Press.
Yule, G. U. (1903). Notes on the theory of association of attributes in statistics. Biometrika, 2, 121–34.
Zhang, J., & Spirtes, P. (2011). Intervention, determinism, and the causal minimality condition. Synthese, 182, 335–347.
Acknowledgements
This research was supported by the Research Grants Council of Hong Kong under the General Research Fund LU13600715, and by a Faculty Research Grant from Lingnan University. The research of the third author was supported by the Humanity and Social Science Youth Foundation of Ministry of Education of China (No. 16YJC72040001) and the MOE Project of Key Research Institute of Humanities and Social Sciences at Universities (No .17JJD720008).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In this appendix, we prove Propositions 1–5. A proof of Proposition 1 and Proposition 2 was given in Zhang and Spirtes (2011). We include a proof here for the sake of Propositions 3 and 4.
Proof of Proposition 1
Suppose for the sake of contradiction that there exist \(X, Y\in {\mathbf {V}}\) such that there is no arrow from X to Y in \({\mathcal {G}}\) (i.e., \(X\notin \mathbf {Pa}_{\mathcal {G}}(Y)\)), but there exist two distinct possible values, \(x_1\ne x_2\), for X and a value configuration \({\mathbf {z}}\) for \({\mathbf {Z}} = {\mathbf {V}} - \{X, Y\}\) such that
Since \(X\notin \mathbf {Pa}_{\mathcal {G}}(Y)\), \(\mathbf {Pa}_{\mathcal {G}}(Y)\subseteq {\mathbf {Z}}\). Then, since according to the intervention principle that defines the CBN, we have
where \({\mathbf {s}}\) is the value configuration of \(\mathbf {Pa}_{\mathcal {G}}(Y)\) that is consistent with \({\mathbf {Z}}={\mathbf {z}}\). (Recall that \(P^{do(\emptyset )}\) is assumed to be positive, so \(P^{do(\emptyset )}(Y | \mathbf {Pa}_{\mathcal {G}}(Y) = {\mathbf {s}})\) is defined.) Contradiction. \(\square \)
Proof of Proposition 2Footnote 15
Proof
Since \(({\mathcal {G}}, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is a CBN over \({\mathbf {V}}\), by Proposition 1, it contains \({\mathcal {G}}_I\) as a subgraph. If \({\mathcal {G}}={\mathcal {G}}_I\), the desired conclusion follows. Otherwise, \({\mathcal {G}}\) contains arrows that do not satisfy the condition in Proposition 1. Since \({\mathcal {G}}\) is finite, the number of such arrows is finite. Let these arrows be ordered as \(E_1, ..., E_m\), and let \({\mathcal {G}}_j\) (\(1\le j\le m\)) denote the graph resulting from taking away the set of arrows \(\{E_1, ..., E_j\}\) from \({\mathcal {G}}\). Obviously \({\mathcal {G}}_m = {\mathcal {G}}_I\). Let \({\mathcal {G}}_0 = {\mathcal {G}}\). We show by induction that for all \(0\le j\le m\), \(({\mathcal {G}}_j, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is a CBN over \({\mathbf {V}}\).
The base case is trivial. Suppose \(({\mathcal {G}}_k, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is a CBN over \({\mathbf {V}}\), we now argue that \(({\mathcal {G}}_{k+1}, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is also a CBN over \({\mathbf {V}}\). Note that the only difference between \({\mathcal {G}}_{k}\) and \({\mathcal {G}}_{k+1}\) is that the former, but not the latter, contains the arrow \(E_{k+1}\). Let \(X\rightarrow Y\) denote the arrow \(E_{k+1}\). To show that \(({\mathcal {G}}_{k+1}, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is a CBN, it suffices to show that for every \(V\in {\mathbf {V}}\), \(P^{do(\emptyset )}(V|\mathbf {Pa}_{{\mathcal {G}}_{k+1}}(V)) = P^{do(\emptyset )}(V|\mathbf {Pa}_{{\mathcal {G}}_k}(V))\), because \(({\mathcal {G}}_k, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is a CBN by the inductive hypothesis. This is obviously the case for every \(V\ne Y\), which has the exact same parents in both \({\mathcal {G}}_{k+1}\) and \({\mathcal {G}}_k\). Regarding Y, \(\mathbf {Pa}_{{\mathcal {G}}_k}(Y) = \mathbf {Pa}_{{\mathcal {G}}_{k+1}}(Y)\cup \{X\}\). Since the arrow \(X\rightarrow Y\) does not satisfy the condition in Proposition 1, it follows that for every value configuration \({\mathbf {s}}\) for \({\mathbf {S}}=\mathbf {Pa}_{{\mathcal {G}}_{k+1}}(Y)\), value configuration \({\mathbf {t}}\) for \({\mathbf {T}} = {\mathbf {V}}-\{X, Y\} - \mathbf {Pa}_{{\mathcal {G}}_{k+1}}(Y)\), and distinct values \(x_1\ne x_2\) for X, we have
On the other hand, since \(({\mathcal {G}}_k, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is a CBN, for both \(i=1, 2\) we have
because \(\mathbf {Pa}_{{\mathcal {G}}_k}(Y) = {\mathbf {S}}\cup \{X\}\). Hence, for any distinct values \(x_1, x_2\) for X and any value configuration \({\mathbf {s}}\) for \(\mathbf {Pa}_{{\mathcal {G}}_{k+1}}(Y)\),
Thus, \(P^{do(\emptyset )}(Y|\mathbf {Pa}_{{\mathcal {G}}_k}(Y)) = P^{do(\emptyset )}(Y|\mathbf {Pa}_{{\mathcal {G}}_{k+1}}(Y)\cup \{X\}) = P^{do(\emptyset )}(Y|\mathbf {Pa}_{{\mathcal {G}}_{k+1}}(Y))\). Therefore, for every \(V\in {\mathbf {V}}\), \(P^{do(\emptyset )}(V|\mathbf {Pa}_{{\mathcal {G}}_{k+1}}(V)) = P^{do(\emptyset )}(V|\mathbf {Pa}_{{\mathcal {G}}_k}(V))\), which implies that \(({\mathcal {G}}_{k+1}, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is also a CBN.
Therefore, \(({\mathcal {G}}_j, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is a CBN over \({\mathbf {V}}\) for all \(0\le j\le m\). The desired conclusion follows since \({\mathcal {G}}_m = {\mathcal {G}}_I\). \(\square \)
Proof of Proposition 3
By the definition of a CCN (Definition 2), for every \(\{P^{do({\mathbf {S}}={\mathbf {s}})}\}\in \mathbf {CK}\), \(({\mathcal {G}}, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is a CBN. Then the argument for Proposition 1 can be used here to establish the desired conclusion.
Proof of Proposition 4
Again, for every \(\{P^{do({\mathbf {S}}={\mathbf {s}})}\}\in \mathbf {CK}\), \(({\mathcal {G}}, \{P^{do({\mathbf {S}}={\mathbf {s}})}\})\) is a CBN. Therefore, if an arrow in \({\mathcal {G}}\) does not satisfy the condition in Proposition 3, then the argument for Proposition 2 can be applied for every \(\{P^{do({\mathbf {S}}={\mathbf {s}})}\}\in \mathbf {CK}\), establishing that the DAG resulting from taking away the arrow from \({\mathcal {G}}\) still constitutes a CBN with every \(\{P^{do({\mathbf {S}}={\mathbf {s}})}\}\in \mathbf {CK}\), and so still constitutes a CCN with \(\mathbf {CK}\). \(\square \)
Proof of Proposition 5
The proof is a generalization of a simplified version of SSK’s argument for their uniqueness result (Seidenfeld et al. 2010, pp. 161–162). Consider an arbitrary vector \(\langle P^1, \dots , P^m\rangle \) of distributions over \(\Omega \). Each \(P^j\) can itself be written as a probability vector with n coordinates. Let \(p_*\) be the smallest positive coordinate in the m probability vectors, and let \({\underline{p}}=\frac{1}{2}p_*\).Footnote 16 Let a denote the vNM lottery \({\underline{p}}B\oplus (1-{\underline{p}})W\). For each \(k = 1,\dots , n\) and \(j = 1, \dots , m\), define option \(o_k^j\) (i.e., option \(o_k\) with index j) as follows, where \(p_k^j\) denotes the kth coordinate of the probability vector \(P^j\), namely, \(P^j(w_k)\)—the probability mass \(P^j\) assigns to state \(w_k\):
Let \(O_{\langle P^1, \dots , P^m\rangle } = \{o_k^j \mid k = 1, \dots , n; j=1, \dots , m \}\cup \{{\mathbf {a}}^1\}\), where \({\mathbf {a}}^1\) denotes the constant horse lottery (with index 1) that assigns to each state the vNM lottery a. Suppose C is a coherent choice function over \({\mathcal {H}}^\dag \) that is represented by a set of vectors of probability distributions \({\mathbf {Q}}\) over \(\Omega \) and a (state-independent and index-independent) utility function u over the set of vNM lotteries. Without loss of generality, suppose \(u(B) = 1\) and \(u(W)=0\) (recall that a strict preference of B to W is assumed), so that \(u(a) = {\underline{p}}\). We now show that \(\langle P^1, \dots , P^m\rangle \in {\mathbf {Q}}\) if and only if \({\mathbf {a}}^1\in C(O _{\langle P^1, \dots , P^m\rangle })\).
(Only if) Suppose \(\langle P^1, \dots , P^m\rangle \in {\mathbf {Q}}\). With respect to \(\langle P^1, \dots , P^m\rangle \) and u, the expected utility of \(\{{\mathbf {a}}^1\}\) is obviously \(u(a) = {\underline{p}}\). Consider now any \(o_k^j\in O_{\langle P^1, \dots , P^m\rangle }\), its expected utility with respect to \(\langle P^1, \dots , P^m\rangle \) and u is given by
Thus, every option in \(O_{\langle P^1, \dots , P^m\rangle }\) has the same expected utility with respect to \(\langle P^1, \dots , P^m\rangle \) and u. Since C is represented by \({\mathbf {Q}}\) and u, and \(\langle P^1, ..., P^m\rangle \in {\mathbf {Q}}\), \(C(O _{\langle P^1, \dots , P^m\rangle }) = O _{\langle P^1, \dots , P^m\rangle }\), and so \({\mathbf {a}}^1\in C(O _{\langle P^1, \dots , P^m\rangle })\).
(If) Suppose \({\mathbf {a}}^1\in C(O _{\langle P^1, \dots , P^m\rangle })\). Consider any vector \(\langle Q^1, \dots , Q^m\rangle \) that is different from \(\langle P^1, \dots , P^m\rangle \). Then there exists \(1\le j\le m\) such that \(P^j\ne Q^j\), which implies that there exists \(1\le k\le n\) such that \(P^j(w_k)=p^j_k < q^j_k=Q^j(w_k)\). Note also that by definition, \({\underline{p}}<1\). Then the expected utility of option \(o_k^j\) with respect to \(\langle Q^1, \dots , Q^m\rangle \) and u is given by
whereas the expected utility of \({\mathbf {a}}^1\) remains \({\underline{p}}\) with respect to \(\langle Q^1, \dots , Q^m\rangle \) and u. Therefore, for every \(\langle Q^1, \dots , Q^m\rangle \ne \langle P^1, \dots , P^m\rangle \), \({\mathbf {a}}^1\) is not acceptable in \(O _{\langle P^1, \dots , P^m\rangle }\) with respect to \(\langle Q^1, \dots , Q^m\rangle \) and u. But by supposition, \(\{{\mathbf {a}}^1\}\in C(O _{\langle P^1, \dots , P^m\rangle })\), which means that \(\{{\mathbf {a}}^1\}\) is acceptable with respect to \({\mathbf {Q}}\) and u. It follows that \(\langle P^1, \dots , P^m\rangle \in {\mathbf {Q}}\).
What we have shown is that whether an arbitrary vector of probability distributions is in the set that represents a given coherent choice function over \({\mathcal {H}}^\dag \) is fully determined by the choice function. Therefore, the set of vectors of probability distributions that represents a given coherence choice function is unique. \(\square \)
Rights and permissions
About this article
Cite this article
Zhang, J., Seidenfeld, T. & Liu, H. Subjective causal networks and indeterminate suppositional credences. Synthese 198 (Suppl 27), 6571–6597 (2021). https://doi.org/10.1007/s11229-019-02512-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-019-02512-2