Abstract
I show that the social stratification of academic science can arise as a result of academics’ preference for reading work of high epistemic value. This is consistent with a view on which academic superstars are highly competent academics, but also with a view on which superstars arise primarily due to luck. I argue that stratification is beneficial if most superstars are competent, but not if most superstars are lucky. I also argue that it is impossible to tell whether most superstars are in fact competent or lucky, or which group a given superstar belongs to, and hence whether stratification is overall beneficial.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Academic superstars are a familiar phenomenon. These academics write the papers that everyone reads and talks about, they make media appearances, give presidential addresses, and they win grants and awards. The work of an academic superstar generally attracts more attention than that of the average academic.
Attention can be quantified in various ways, e.g., number of papers published, citations to those papers, awards received, etc. It is a well-established empirical fact that, regardless of which metric is used, the vast majority of academics receives little attention (if any), while a rare few receive a great deal (Price 1965; Cole and Cole 1973).Footnote 1
This fact has been called the social stratification of science (or academia) (Cole and Cole 1973). Stratification is important in studying the social epistemology of science. If some academic work receives more attention than other work, this influences the flow of information in an academic community. This may affect, e.g., the consensus that an academic community settles on for a particular question.
In this paper I raise the question whether the phenomenon of stratification serves the aims of academic science.Footnote 2 I argue that the answer to this question depends largely on how one thinks academic superstars are distinguished from academic nobodies. In particular, what are the roles of competence and luck in distinguishing the two groups?
I start by introducing some toy models which illustrate the different roles that competence and luck might play (Sect. 2). In this section important concepts such as “competence”, “luck”, “attention”, and “superstars” are left at an intuitive level (to be made more precise later).
In Sect. 3 I develop a formal model focusing on how academics decide which papers to read. In Sect. 4 I develop the idea that papers may differ in “epistemic value” and that small differences in epistemic value can lead to large differences in attention; large enough to match the pattern of stratification described above.
Section 5 returns to the notion of competence. I show that the model is consistent with a scenario in which stratification in science is purely competence-based. I argue that on this view stratification serves the aims of academic science, because it makes it easier to identify competent academics, whose past and future work is likely to be of high epistemic value.
In contrast, Sect. 6 focuses on the less optimistic lessons that can be drawn from the model. I show that the model is also consistent with a scenario in which stratification is determined by a large component of randomness. Because they cannot be distinguished by their past performance, it is impossible to separate the lucky superstars from the competent ones. But the epistemic benefit of stratification derives exactly from the ability to identify competent academics, or so I argue. It follows that stratification either hinders the aims of academic science, or, if it does help, it is impossible to show this.
2 Some intuitions for competence and luck
The purpose of this section is to develop some intuitions for the notions of competence and luck as they will be used in this paper. Consider the following toy models.
Toy Model 1
Suppose a group of scientists are interested in the same experiments. Suppose also that each scientist has a fixed amount of time to perform experiments; perhaps they are all in a one-year post-doc and they need to produce a paper at the end of it. Suppose further that the more competent a scientist is, the more replications she can perform in that time. And suppose finally that the work of a scientist who has performed more replications receives more attention. It follows that the superstarsFootnote 3 in this toy model are exactly the most competent scientists.
Here, differences in productivity among the scientists are the result of differences in competence. Contrast a case in which differences in productivity among scientists are entirely random.
Toy Model 2
Consider again a group of scientists who have a fixed amount of time to perform experiments. But now suppose that the equipment available to each scientist restricts their productivity so that each scientist can perform exactly n replications in the available time. However, the equipment is not perfectly reliable, so that each replication succeeds (yields usable data) with probability \(\alpha \), and fails with probability \(1-\alpha \).
Suppose as before that the work of those scientists who performed more replications receives more attention. Since in this toy model the only difference between the scientists is in the probabilistic behavior of their equipment, the superstars are those lucky scientists for whom all n replications succeed (which happens with probability \(\alpha ^n\) if the success probabilities are independent).
What is the difference between these two toy models? From an external perspective, not much. A group of scientists perform some experiments, and those who come up with more replications receive more attention.
Intuitively, the difference from an internal perspective is that there is something systematic about differences in competence that does not exist when the differences are due to luck. In the first toy model, we should expect the same scientists to perform the most replications next year. Whereas in the second model, all scientists are equally likely to have a lot of successful replications in the next year, except insofar as their differential productivity in the previous year has affected their employment or funding situation.
This will be the key difference between competence and luck in the discussion of competent and lucky superstars in Sects. 5 and 6. Competent superstars are those for whom good past academic work is predictive of good future academic work, while lucky superstars are those for whom good past academic work is not indicative of the value of their future work.Footnote 4
The next toy model includes both factors—competence and luck—at the same time. It seems plausible that in such a situation, the systematic contribution of competence outweighs the unsystematic contribution of luck. But Proposition 1, below, shows that this is not necessarily the case.
Toy Model 3
Suppose as before that scientists have time to perform n replications, each of which succeeds or fails independently from the others with some fixed probability. Competence is reflected in the value of that probability. Suppose further that there are just two types of scientists: average scientists, whose success probability for each replication is \(\alpha \), and good scientists, whose success probability is \(\beta \) (\(0< \alpha< \beta < 1\)). As before the superstars are those scientists for whom all n replications succeed.
Let p denote the proportion of good scientists. It seems plausible that good scientists are rare: most scientists are of average quality. It turns out that if good scientists are sufficiently rare, the chance that a given superstar is a good scientist may be arbitrarily small.
To make this more precise, suppose one draws a scientist at random from the group. Let g denote the proposition that the scientist drawn is a good scientist and let s denote the proposition that the scientist is a superstar.
Proposition 1
For all \(\varepsilon > 0\) there exists a proportion of good scientists \(p \in (0,1)\) such that \(\Pr (g\mid s) \le \varepsilon \).
Proof
Let \(\varepsilon > 0\). Assume \(\varepsilon < 1\) (otherwise the result is trivial). Choose \(p = \frac{\alpha ^n \varepsilon }{\beta ^n (1 - \varepsilon ) \, + \, \alpha ^n \varepsilon }\). Since the superstars are those for whom all replications succeed, \(\Pr (s\mid g) = \beta ^n\) and \(\Pr (s\mid \lnot g) = \alpha ^n\). Therefore
\(\square \)
Note that while competence and luck are both present in Toy Model 3, their effects are modulated by how they affect the number of replications each scientist is able to perform. That is, whether a given scientist becomes a superstar is not directly a function of how competent or lucky they are, but rather a function of how their competence or luck translates into replications.
These toy models have a number of unrealistic features. The idea that whether a scientist becomes a superstar depends only on the number of replications they perform is one of them. While this assumption will be dropped in the next section, I retain the idea that competence and luck do not affect superstar status directly, but rather via what I will call the “epistemic value” of papers. In the next two sections I make the notions of epistemic value, attention, and superstars more precise, and show how small differences in epistemic value among papers can generate the characteristic pattern of social stratification in science. This is consistent with either competence, luck, or a combination of both being responsible for creating differences in epistemic value between papers. I return to discussing competence and luck explicitly in Sects. 5 and 6.
3 A model of academics reading papers
This section presents a formal model of information exchange in an academic community. The guiding idea is that each academic does some experiments and publishes the results in a paper. Academics may then choose to read each other’s papers depending on their interests. The model focuses on the “short run”, that is, academics’ reading behavior in the context of one research project or paper.
Viewing the academics as nodes and the choice to read a paper as a (directed) edge yields a network. In Sect. 4 the idea of “attention for academic work” is given a precise interpretation using a concept from network theory: the in-degree. Because the structure of this network depends on the academics’ choices, this is a model of (strategic) network formation in the sense of Jackson and Wolinsky (1996).Footnote 5
The purpose of this model is to show that certain small differences among papers are sufficient to generate patterns in the resulting network that are similar to those observed in real academic networks. That is, most academic work receives little or no attention, while a small amount of work receives a great deal of attention (a phenomenon I called stratification in the Sect. 1).
The results obtained from the model show that the mechanisms of competence and luck I outlined in Sect. 2 are (at least in principle) sufficient for generating the pattern of stratification observed empirically. This secures the foundations for the subsequent discussion of these mechanisms: if either competence or luck can create these patterns, we may legitimately ask if either or both of them do.
It may be remarked that the characteristic pattern of social stratification in science already has a standard generating mechanism in the literature. This mechanism is described by so-called preferential attachment models (Barabási and Albert 1999). In a preferential attachment model new papers cite older papers proportional to the number of citations that older paper already has.
It can be shown that this generates a power law distribution of citations with an exponent equal to three (Barabási and Albert 1999). This is very close to what is observed in real citation data (Redner 1998, cf. footnote 1). While this is illuminating in many contexts (for example, in relating citations to other social phenomena where power laws occur), it does not address the question at issue in this paper for the following reason.
Preferential attachment models do not include any features that distinguish papers from one another (other than their number of citations). So these models can only explain how existing differences in citations get exacerbated, not where these differences came from. In particular, the epistemic dimension of science (or: its content) is abstracted away entirely. The model of this paper, at minimum, introduces a way of talking about this.
Consider an academic community, modeled as a set I. Each element \(i\in I\) represents an individual academic. I is best thought of as consisting of academics at a similar stage in their career, e.g., a group of post-docs. I is assumed to be finite.
Each academic, as part of her own research, performs some “experiments”.Footnote 6 Suppose there are m experiments one might do. Each academic’s research involves doing each of these experiments some (possibly zero) number of times. Write n(i, j) to denote the number of times academic i performs experiment j.
The set of results of academic i’s experiments is called her information set \(A_i\). Experiments are modeled as random variables, with different experiments corresponding to different probability distributions, so an information set is a set of random variables. Information set \(A_i\) thus contains n(i, j) random variables for each experiment j.
The number of random variables of each type is the main feature I use to distinguish information sets. On a strict interpretation, this is a modest generalization of the number of replications that I used in Sect. 2. But there is an alternative interpretation on which the experiments refer to different categories academics might use to evaluate each other’s work (e.g., Kuhn’s accuracy, simplicity, and fruitfulness), and the number of replications of each experiment gives the score of the academic’s work in that category. More on this in Sect. 4.
Each academic publishes her information in a paper. In this “short run” model, each academic publishes a single paper, and this paper contains all the information in her information set.Footnote 7
A generalization of my model would have separate sets of academics and papers, with an information set for each paper. This allows for academics who publish multiple papers, and academics without papers. For example, if I is a group of post-docs, senior academics may be included without papers: their reading choices may influence who among the post-docs becomes a superstar, but their own papers are irrelevant. Results qualitatively similar to those presented in Sect. 4 can be derived for this generalization.
Academics can read each other’s papers. Reading a paper means learning the information in the information set of the academic who wrote the paper.Footnote 8 The only information that is transferred is that in the information set of the academic whose paper is being read: the academic who wrote the paper does not learn anything as a result of this interactionFootnote 9, nor is there any second-hand transfer of information.Footnote 10
What (strategic) decisions do the academics need to make, and what do they know when they make them? Each academic needs to decide which papers to read. I do not consider the order in which the different academics make their decisions. That is, academics do not know what other academics are reading, or if they do, they ignore this information. But I do allow that individual academics make their decisions sequentially: after reading a paper they may use what they have learned in deciding what to read next (or whether to stop reading). After all, often one only becomes interested in reading a paper after reading some other paper, and such a decision can be made on short notice.
In contrast, due to the time and cost involved in designing and running an experiment, which experiments to run is not changed as easily. I assume that in the “short run”, which this model focuses on, it cannot be changed at all. The type and number of experiments performed by each academic is taken as fixed. The model can be viewed as looking only at the time associated with a single research project: doing some experiments and exchanging results with epistemic peers. More on the import of this assumption in Sects. 5 and 6.
Academics are assumed to know, before choosing to read a paper, how many replications of each type of experiment it contains (that is, they know the values n(i, j) for all i and j). My justification for this assumption is as follows.Footnote 11 The time required to search for papers on a certain subject (perhaps looking at some titles and abstracts) is negligible compared to the time required to actually read papers and obtain the information in them. Idealizing somewhat, I suppose that the title and abstract contain enough information to determine the type and number of experiments, but not enough to learn the results in full detail. Alternatively, in relatively small academic communities this assumption may be justified because everyone knows what everyone else is working on through informal channels.
So academics choose sequential decision procedures (Wald 1947), which specify what to read as a function of information gained from their own research and papers they have already read. Because that information takes the form of random variables, the decision procedure itself is also random. A simple example illustrates this.
Example 1
Suppose that there are two possible worlds, a and b. Suppose that there is one experiment and each academic has performed that experiment once. In world a, the experiment outputs either a zero or a one, each with probability 1 / 2. In world b the experiment always outputs a one. So upon observing a zero an academic is certain to be in world a.
Consider an academic who initially thinks she is equally likely to be in either world and uses the decision procedure “read papers until you are at least \(99\%\) certain which world you are in”. Assume world a is the actual world. Then she reads no papers with probability 1 / 2 (if her own experiment yields a zero), one paper with probability 1 / 4 (if she saw a one but the first paper she reads has a zero), and so on. So a decision procedure does not specify which papers to read, but it specifies the probability of reading them.
In the next section I put some constraints on the way academics choose a sequential decision procedure.
4 Superstars in the model
How do academics choose which papers to read? One might want to assume that academics have some form of utility function which they maximize. But this has a number of problems: whether (expected) utility maximization can provide a good model of rationality is controversial; and even if it is a good model of rationality academics may not act rationally so the descriptive power of the model may be poor.
Moreover, one would need to argue for the specific form of the utility function, requiring a detailed discussion of academics’ goals. For example, if academics aim only at truth an epistemic utility function may be needed, and it is not clear what that should look like (Joyce 1998; Pettigrew 2016). If they aim only at credit or recognition (as in Strevens 2003), a pragmatic utility function is needed. If they aim at both truth and credit (as seems likely) these two types of utility function must be combined (Kitcher 1993, Chap. 8; see also Bright 2016 for a comparison of these three types of utility function), and if they have yet other goals things get even more complicated.
Here I take a different approach. I state two assumptions, or behavioral rules, that constrain academics’ choices to some extent (although they still leave a lot of freedom). I then show that these assumptions are sufficient for the appearance of superstars in the model.
For those who think that, despite the problems I mentioned, academics’ behavior should be modeled using (Bayesian) expected utility theory, I show that a wide range of utility functions would lead academics to behave as the assumptions require (see theorems 1 and 2). For those who are impressed by the problems of that approach, I argue that one should expect academics to behave as the assumptions require even if they are not maximizing some utility function.
The first assumption relies on the notion that a paper may have higher epistemic value than another. I first state the formal definition of higher epistemic value and the assumption before discussing how they are intended to be interpreted.
Consider the information sets (i.e., papers) of two academics, i and \(i^\prime \). Say that academic i’s paper is of higher epistemic value than academic \(i^\prime \)’s paper if academic i has performed at least as many replications of each experiment as academic \(i^\prime \), and more replications overall. Formally, \(A_i\) is of higher epistemic value than \(A_{i^\prime }\) (written \(A_{i^\prime }\sqsubset A_i\)) if \(n(i,j) \ge n(i^\prime ,j)\) for all experiments j, with \(n(i,j) > n(i^\prime ,j)\) for at least one j.Footnote 12
The “higher epistemic value” relation is a partial order. For example, if academic i has performed experiment 1 ten times and experiment 2 zero times, and academic 2 has performed experiment 1 zero times and experiment 2 five times, neither paper has higher epistemic value than the other.
Assumption 1
(Always Prefer Higher Epistemic Value). If academic i’s paper has higher epistemic value than academic \(i^\prime \)’s (\(A_{i^\prime }\sqsubset A_i\)) then other academics prefer to read academic i’s paper over academic \(i^\prime \)’s.
On a strict interpretation, Always Prefer Higher Epistemic Value requires that academics prefer to read papers that contain more replications (of those experiments that they are interested in reading about in the first place). For example in the medical sciences, where the number of replications might refer to the number of patients studied, a higher number of replications would correspond to more reliable statistical tests, and would as such be preferable.
The strict interpretation, however, probably has limited application. Academics presumably care about more than just the quantity of data in a paper when they judge its epistemic value (although it should be noted that Always Prefer Higher Epistemic Value will usually not fix academics’ preferences completely, leaving at least some room for other considerations to play a role). For example, an important consideration may be what, if any, theoretical advances are made by the paper. How could such a consideration be incorporated in the model?
One suggestion is to consider the theoretical advances made by the paper as an additional experiment, and to define the number of replications of the additional experiment as a qualitative measure of the importance of the theoretical advances. Assuming that academics will mostly agree on the relative importance of theoretical advances this idea can be made to fit the structure of the model.
This suggests a looser interpretation of the notion of higher epistemic value in Always Prefer Higher Epistemic Value (one I alluded to in Sect. 3). On this interpretation the different “experiments” are categories academics use to judge the epistemic value of papers, and “replications” are just a way to score papers on these categories. Always Prefer Higher Epistemic Value then says that academics will not read a paper if another paper is available that scores at least as well or better on all categories.Footnote 13
The loose interpretation makes a more complete picture of academics’ judgments of epistemic value possible, at the cost of some level of formal precision. But on either interpretation Always Prefer Higher Epistemic Value may be unrealistically simple. Given that there is, to my knowledge, no research trying to model academics’ decisions what to read, Always Prefer Higher Epistemic Value should be read as a tentative first step. Future research may fruitfully explore improved or alternative ways of making the factors that go into such decisions formally precise.
The second assumption gets its plausibility from the observation that there is a finite limit to how many papers an academic can read, simply because it is humanly impossible to read more. More formally, there exists some number N (say, a million) such that for any academic the probability (as implied by her decision procedure) that she reads more than N papers is zero.
But rather than making this assumption explicitly, I assume something strictly weaker: that the probability of reading a very large number of papers is very small.
Assumption 2
(Bounded Reading Probabilities). Let \(p_{i,A,n}\) denote the probability that academic i reads the papers of at least n academics with information set A.Footnote 14 For every \(\varepsilon > 0\), there exists a number N that does not depend on the academic or the size of the academic community, such that \(n\cdot p_{i,A,n} \le \varepsilon \cdot p_{i,A,1}\) for all \(n > N\).Footnote 15
So Bounded Reading Probabilities says that for very high numbers, the probability of reading that number of papers is very small, independent of the academic reading or the size of the academic community. If, as I suggested above, no academic ever reads more than a million papers, then \(p_{i,A,n} = 0\) for all i and A whenever n is greater than a million, and so the assumption would be satisfied.
As I indicated, these assumptions are not only independently plausible, but are also satisfied by Bayesian academics (who maximize expected utility) under quite general conditions. The most important of these conditions is that reading a paper has a fixed cost c. This cost reflects the opportunity cost of the time spent reading the paper.Footnote 16
The relation between my assumptions and Bayesian rationality is expressed in the following two theorems. The proofs are given in Heesen (2016, Sect. 3).
Theorem 1
If \(c > 0\) and if each replication of an experiment is probabilistically independent and has a positive probability of changing the academic’s future choices, then the way a fully Bayesian rational academic chooses what to read satisfies Always Prefer Higher Epistemic Value.
Theorem 2
If \(c > 0\) and if each replication of an experiment is probabilistically independent, then a community of fully Bayesian rational academics with the same prior probabilities over possible worlds and the same utility functions chooses what to read in a way that satisfies Bounded Reading Probabilities.
Now consider the graph or network formed by viewing each academic as a node, and drawing an arrow (called an arc or directed edge in graph theory) from node i to node \(i^\prime \) whenever academic i reads academic \(i^\prime \)’s paper.Footnote 17
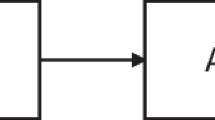
In order to study social stratification in this network, I need a metric to identify superstars. A natural idea suggests itself: rank academics by the number of academics who read their work. In the network, the number of academics who read i’s work is simply the number of arrows ending at i. In graph-theoretical terms, this is the in-degree of node i. This idea is illustrated in Fig. 1.
If, as the empirical evidence suggests, science is highly stratified, then one should expect large differences in in-degree among academics. Theorem 3, below, says that this is exactly what happens in my model.
The theorem relates the average in-degrees of academics (denoted, e.g., \(\mathbb {E}\left[ d(A)\right] \) for the average in-degree of an academic with information set A).Footnote 18 In particular, it relates the average in-degrees of academics with information sets A and B to that of academics with information sets \(A\sqcup B\) and \(A\sqcap B\). An academic has information set \(A\sqcup B\) if she has performed each experiment as many times as an academic with information set A or an academic with information set B, whichever is higher (whereas an academic with information set \(A\sqcap B\) takes the lower value for each experiment).Footnote 19
For example, if information set A contains twelve replications of experiment 1 and eight replications of experiment 2 and information set B contains ten replications of each experiment then \(A\sqcup B\) contains twelve replications of experiment 1 and ten replications of experiment 2 (and \(A\sqcap B\) contains ten and eight replications, respectively). Or, on the loose interpretation, if the paper represented by information set A makes a greater theoretical advance than the paper represented by information set B, but B contains valuable empirical work as well, then information set \(A\sqcup B\) indicates a paper containing as great a theoretical advance as A, and empirical work as valuable as that in B.Footnote 20
Theorem 3
(Stratified In-Degrees). Let I be an academic community satisfying Always Prefer Higher Epistemic Value and Bounded Reading Probabilities. If I is large enough, then for any two information sets A and B such that at least one academic in I has information set \(A\sqcup B\)
Moreover, if neither A nor B is identical to \(A\sqcup B\) Footnote 21 and \(\mathbb {E}\left[ d(A\sqcup B)\right] > 0\) then the above inequality can be strengthened to
What the theorem says is that if the set of academics is sufficiently large, the number of times a given paper is read increases rapidly—on average, faster than linearly—in the epistemic value of the information set. See Heesen (2016, Sect. 2.5) for a proof.
What do I mean by “faster than linearly”? The following corollary makes this more precise.Footnote 22 Suppose that (part of) the academic community only performs replications of some subset E of the experiments (where E contains at least two experiments).
Let \(A_E(n)\) denote an information set containing n replications of each of the experiments in E (and nothing else). Let \({\hat{n}}\) be the highest value of n such that at least one academic in I has information set \(A_E(n)\). Say that I is dense in E if for each combination of number of replications of the experiments in E some academic has performed exactly that number of replications.Footnote 23 The corollary (proven in Heesen 2016, Sect. 2.6) shows that in dense communities the average number of times a paper is read increases exponentially in n.
Corollary 1
(Exponential In-Degrees). Let I be an academic community satisfying Always Prefer Higher Epistemic Value and Bounded Reading Probabilities. Let E be a subset of the experiments (\(\left| E\right| \ge 2\)) and suppose that I is dense in E. If I is large enough, then for all n (with \(1 \le n \le {\hat{n}}\)),
The theorem and its corollary show that the pattern of stratification in my model reflects the pattern that can be seen in empirical metrics of stratification, e.g., using citation metrics. That is, most papers have few citations, while a rare few have a great number of citations (Price 1965; Redner 1998). This pattern is seen to arise from academics’ preference for papers of high epistemic value. Thus this preference can be viewed as a sufficient condition for these patterns to arise.
5 A competence-based view of academic superstars
In this section I show that the results from the previous section are consistent with a purely competence-based view of academic superstars. I argue for two consequences of this insight. First, one should not be too quick in concluding that particular patterns of stratification could not have resulted from differences in competence. Second, if the competence-based view is correct stratification has some important benefits. The next section considers the flip side of these arguments.
Stratified In-Degrees, the main result of Sect. 4, identified differences in the epistemic value of papers as a source of differences in the number of times they get read (their in-degree in the network). Because differences in competence can create differences in epistemic value, the result is consistent with a view on which only the most competent academics become superstars.
Toy Model 1 in Sect. 2 illustrates this. Differences in competence can create differences in the number of replications each academic is able to do, and by Stratified In-Degrees the most competent academics will be superstars.
Speaking more generally, on any interpretation of competence on which more competent academics tend to write papers of higher epistemic value (on either the strict or the loose interpretation), the competent academics will be the superstars. By Exponential In-Degrees, differences in epistemic value may be enlarged exponentially in terms of the amount of attention paid to academic work, as measured in, e.g., citation or productivity metrics.
This casts some suspicion on research that uses linear models to argue that differences in citation metrics or productivity metrics cannot be explained by differences in competence (e.g., Cole and Zuckerman 1987; Prpić 2002; Medoff 2006; Knobloch-Westerwick and Glynn 2013). Their line of reasoning is roughly as follows:
-
1.
There are differences in citation or productivity metrics that correlate with measurable characteristics of academics such as academic affiliation (Medoff 2006) or gender (Cole and Zuckerman 1987; Prpić 2002; Knobloch-Westerwick and Glynn 2013).
-
2.
In a linear model that controls for competence, this correlation is not explained away.
-
3.
Therefore, differences in competence cannot explain all differences in citation or productivity metrics.
They would thus use the results of regression analyses to reject the competence-based view of superstars I outlined. But this conclusion is too quick. The fact that a model in which competence and citations (or productivity) stand in a linear relation cannot explain all of the variance in citations does not rule out the possibility that a model using a nonlinear relation can. According to my results this may be exactly what is needed.
I do not claim to have shown that their conclusion is incorrect: I think it is quite plausible that characteristics of academics other than competence affect citations and productivity. I merely caution against basing this conclusion on linear models.
For the remainder of this section, suppose that the competence-based view of superstars I outlined is correct (cf. Cole and Cole 1973; Rosen 1981; Strevens 2006). That is, papers of high epistemic value tend to get read the most, competent academics tend to produce papers of high epistemic value, and therefore academic superstars are more competent than academic nobodies.
On this view, the social stratification of science has a number of benefits for academics and academic institutions. I identify three of them.
First, stratification greatly simplifies the maintenance of consensus in an academic community. Without a relatively high degree of consensus, scientific progress might be impossible, as the following quote argues.Footnote 24
Scientific progress is in part dependent upon maintaining consensus by vesting intellectual authority in stars. Without consensus, scientists would go off in hundreds of different directions, and science might lose its cumulative character. The stars in a particular field determine which ideas are acceptable and which are not. (Cole and Cole 1973, p. 78)
So stratification seems necessary for progress. But “[i]t is only when the scientific community sees those exercising authority as deserving of it that the authority will be accepted” (Cole and Cole 1973, p. 80). If the competence-based view of superstars is correct, academics can rest assured that those exercising authority are in fact deserving of it.
Second, stratification can be of use to grant-awarding agencies such as the NSF and the NIH. In evaluating a research proposal, an important question is whether the academic who submitted it will be able to carry it out successfully. These agencies thus have an interest in estimating the academic competence of those submitting proposals.
On the competence-based view of superstars, this is easy. Citation metrics and publication counts provide straightforward measures of competence.Footnote 25 Agencies like the NSF or the NIH use this information, presumably for this reason.
Third, stratification may be used by academics themselves to identify competent academics. Even if academics who work on very similar things are able to judge each other’s competence directly, they still lack the time and the expertise to judge the competence of academics outside their small range of collaborators and competitors.
This suggests an explanation for the Matthew effect, the observation that when two academics make the same discovery (either independently or collaboratively), the academic who is already a superstar receives more recognition for it (Merton 1968). On Merton ’s own view, it is a result of the fact that academics pay more attention to papers written by superstars. According to Merton , this fact aids the efficiency of communication in science, but the Matthew effect itself is a pathology.
Strevens (2006) goes a step further by arguing that differential recognition is justified. The idea is that the mere presence of a superstar’s name makes a paper more trustworthy. In this way the superstar earns the additional recognition. So the Matthew Effect is not a pathology.
The competence-based view of superstars endorses both suggestions. If academics use the names of superstars to identify papers to read outside their own subfield, they will identify papers of high epistemic value, aiding the efficiency of communication. And because superstars can be trusted to be competent, putting more trust in papers written by superstars is also justified.
It is worth noting how the model and the Matthew effect interact here. The idea is that whenever a paper by a young academic is published, its epistemic value determines how many academics in the immediate academic community of the author will read it. Papers of high epistemic value stand out, and their authors stand out from their peers.
This is where the “short run” analysis of the model stops. In the longer run, the Matthew effect takes over. The differences in recognition already present in the group of young academics are exacerbated as academics further afield notice the work of the ones that stood out and ignore the work of the others. If the initial differences in recognition are the result of differences in competence, the larger subsequent differences in recognition—driven by the Matthew effect—continue to track competence.
6 A role for luck
I have suggested that differences in epistemic value might be responsible for the social stratification of science (in combination with the Matthew effect). If this is correct, it does not follow that the competence-based view of superstars is correct. In this section I consider the possibility that luck is partially or wholly responsible for differences in epistemic value. I argue that the mere fact that this is possible has consequences for evaluating stratification.
To see that luck by itself could produce the patterns typical of socially stratified academic science, we need only consider Toy Model 2 from Sect. 2 again. Here, differences in epistemic value between papers are generated purely randomly, yet by Stratified In-Degrees and Exponential In-Degrees these differences are sufficient for extremely stratified patterns of attention.
Moreover, Toy Model 3 and Proposition 1 suggested that, at least in some circumstances, luck can drown out competence.
The consequences drawn in this section regarding luck do not depend on the particular interpretation of luck given in Sect. 2. Any alternative interpretation suffices as long as it (a) can generate differences in epistemic value (on either the strict or the loose interpretation), and (b) academics who have produced work of high epistemic value in the past are not particularly likely to do so again in the future (although the Matthew effect may create an impression to the contrary).
What conclusions can one draw about individual superstars in light of the possibility of lucky superstars? Suppose one thought that academics who produced work of high epistemic value in the past are likely to do so again in the future. Strevens seems to endorse this when he writes “I do not need to argue, I think, that a discovery produced by a scientist with a demonstrated record of success has more initial credibility than a discovery produced by an unknown” (Strevens 2006, p. 166).
I have argued that it is possible that the “demonstrated record of success” was obtained through luck. This does not show that one would be mistaken to assign more credibility to a discovery made by an academic with such a record. But it does show that that record is not in itself a decisive argument for this assignment of credibility. (This is essentially the first argument of Sect. 5 run in reverse.)
If an academic becomes a superstar through luck, independent of competence (cf. footnote 4), then the epistemic value of her past work is not predictive of her future work. In fact, her past performance is indistinguishable from that of a highly competent academic, while her future performance is (probabilistically) indistinguishable from that of an average academic.
This undermines the second and third benefits of stratification I identified in Sect. 5. According to the second benefit, grant-awarding agencies can use stratification to assess the competence of academics. According to the third benefit, academics themselves can do the same, assessing in particular academics outside their own subfield. But these assessments may go awry if there are lucky superstars. In the worst case (see Proposition 1), the vast majority of these assessments are mistaken.
What about the first benefit, according to which stratification is a necessary condition for maintaining consensus, which is itself a necessary condition for scientific progress? The possibility of lucky superstars undermines the argument that those able to affect what counts as the consensus in an academic community are particularly well-suited for that position. While competent superstars may be better judges of future work that challenges or reaffirms the consensus, there is no reason to expect lucky superstars to be. If academics thought most superstars were lucky rather than competent, they might no longer rely on superstars’ opinions to determine the direction of the field, effectively destroying consensus and progress.
However, that point does not affect the claim that stratification may be necessary for progress. If most academics believe that superstars are competent—as they seem to do—consensus and the possibility of progress are maintained (albeit through a kind of “noble lie” if in fact most superstars are lucky). Perhaps this is the only way to maintain consensus and the possibility of progress, as Cole and Cole (1973, pp. 77–83) suggest. This is the only purported benefit of stratification I found in the literature that does not rely on the competence-based view.
Is it true that consensus and progress are impossible without stratification? This is a hard question to answer, as modern academic science has always been highly stratified. One might construct a model to investigate under what conditions consensus and progress are possible in a non-stratified academic community, but that is beyond the scope of this paper. I offer some informal remarks instead.
The absence of stratification may well prevent academics from judging those outside their own subfield. But it does not seem to prevent academics in small communities (say, up to a hundred or so) from learning to trust (or distrust) each other (Holman and Bruner 2015, Sect. 5). Consensus and progress would seem to be possible within such communities.
Aggregating the results of these communities would be harder. For one, it may be impossible to tell for those outside a community whether a given academic is representative of it. And the communities may be less interested in unifying their results with those of other communities. Governments and grant-giving agencies may need to play a more active role to extract socially useful information from such a decentralized academic environment.
These considerations certainly do not show that non-stratified academic science would be particularly effective. But they show that it is not obviously true that stratification is necessary for consensus and progress. A more sustained argument is needed to settle this question one way or the other.
In the absence of such an argument, all the benefits of stratification that I have identified rely on the possibility of using the stratification of science to pick out particular academics as highly competent. But if there is a role for luck, not all superstars are highly competent. Worse, because they are indistinguishable by past performance, it is impossible to tell a lucky superstar from a competent one.
The problem could be mitigated if there was a way to show that most superstars are in fact highly competent. This might appear to be a testable proposition. Take a random sample of superstars and a random sample of nobodies, and measure the epistemic value of their next paper. If stratification mostly tracks competence, the superstars should produce more valuable work than the nobodies, whereas if stratification mostly tracks luck, their work should be of similar epistemic value. Evidence of the former would suggest that using stratification to assess competence is a mostly reliable mechanism, and so the identified benefits mostly hold.
The problem is that the only way to measure epistemic value is via other academics’ assessment. The Matthew effect establishes that academics rate the work of superstars more highly than that of nobodies even when they are of similar epistemic value.Footnote 26 So regardless of whether stratification in fact tracks competence or luck, superstars would appear to produce more valuable work than nobodies.
Thus the Matthew effect makes it impossible to determine whether superstars are mostly competent or mostly lucky. Because the benefits of stratification depend on the assumption that most superstars are competent (in the absence of an argument that stratification is necessary for progress), it is impossible to prove that stratification is beneficial, at least in the ways identified in the literature. This is not an argument that stratification is not beneficial; merely that it cannot be shown to be.
Having stated this conclusion, I return briefly to some of the assumptions of the model. I assumed that academics prefer to read papers of high epistemic value and that academics know the epistemic value of the papers produced in the community before they read them.
While these assumptions may be unrealistic, it seems unlikely that relaxing them would change the conclusion. I reason as follows. The benefits of stratification depend on the assumption that superstars are competent. Competent academics are more likely to produce papers of high epistemic value. Relaxing either of the assumptions just mentioned would make the correlation between epistemic value and stratification weaker rather than stronger. As a result, superstars are less likely to be highly competent. So relaxing these assumptions does not make it easier to prove that stratification is beneficial.
7 Conclusion
I have used a formal model to show that a preference for reading papers of high epistemic value is sufficient to produce social stratification in science.
The model is consistent with a competence-based view of superstars. In particular, small differences in competence are sufficient to produce extreme stratification. On this basis, I caution against those who would conclude (based on linear models) that the stratification actually observed is too extreme to be explained by competence.
On a competence-based view of superstars, stratification has a number of benefits to academics and academic institutions. All but one of these benefits, however, assume that stratification can reliably be used to identify highly competent academics. The remaining one I found to be underargued.
Luck may also give rise to superstars. In fact, there is some reason to believe that if luck and competence both give rise to superstars, lucky superstars are more common than competent ones. Because they are indistinguishable by past performance, the possibility of lucky superstars prevents the reliable identification of competence via stratification.
Due to the Matthew effect, it is impossible to measure the ratio of competent to lucky superstars. Since the benefits of stratification rely on that ratio being high, it is impossible to show that stratification has the benefits hitherto ascribed to it.
I conclude by raising a few questions for future work. First, what happens if the model is changed to explicitly consider longer periods of time? While I have described informally a situation in which multiple iterations of the model are used successively, interacting with the Matthew effect, capturing these interactions in a formal model can make my claims more precise.
Second, what would a science without stratification look like? Under what circumstances are consensus and progress possible? Explicitly considering an alternative picture of science or academia may also bring into focus other potential benefits or harms of stratification. Formal models are ideally suited to investigate counterfactuals like these.
Notes
For example, the distribution of citations follows a “power law”: the number of papers that gets cited n times is proportional to \(n^{-\alpha }\) for some \(\alpha \). Redner (1998) estimates \(\alpha \) to be around 3.
Some care should be taken in using the phrase “the aims of academic science”. Academic science is not a monolithic enterprise, uniformly directed at some aim or set of aims. Here I seek to identify ways in which stratification may be beneficial or harmful to groups of academics and academic institutions, as distinct from the ways individual academics may be helped or harmed by their own place in this stratified social structure. This introduction uses “the aims of academic science” as a shorthand for that. In the rest of the paper I will be more specific.
If the scientists are post-docs, most likely none of them are superstars in an absolute sense. The “superstars” in this community are relative: their work receives more attention than that of the other post-docs in this group. In an absolute sense, “rising stars” might be a more appropriate name. Cf. my discussion of the Matthew effect in Sect. 5.
Although Louis Pasteur’s claim that “Fortune favors only the prepared mind” suggests otherwise. See McKinnon (2014) and Merton and Barber (2004, Chap. 9) for discussion of the relation between competence and luck. The kind of luck that results from competence counts as competence as far as this paper is concerned. My aim is to take seriously the implications of the possibility of a kind of luck that is independent from competence.
Contrast this with recent philosophical work on epistemic networks, which compared the performance of different network structures on various epistemic desiderata (Zollman 2010; Grim et al. 2013). In this work the network structures being compared are fixed in advance, rather than formed endogenously. Such work is thus complimentary to the type of model considered here. However, this paper differs from Jackson and Wolinsky (1996) in that pairwise stability and other notions of equilibrium are not a key issue. This is because forming an edge in my model is a unilateral act (an academic does not need another academic’s permission to read her paper). In the terminology of Zollman (2013, Sect. 2), this is a “one way, one pays” information transmission model without second-hand communication.
While I use the word “experiment” to refer to individual research units, I do not intend to restrict the model to academic fields that perform experiments. One “experiment” could be one collision of particles in particle physics, one subject examined in a medical or psychological study, or one text studied in a corpus analysis.
Thus, information sets are characteristics that differentiate the academics (nodes) in the network. Information sets consist of random variables. This generalizes Anderson (2016), where academics’ information consists of deterministic bits (called “skills” by Anderson ). Anderson ’s model in turn generalizes the early network formation models (Jackson and Wolinsky 1996; Bala and Goyal 2000), where information is additive and each node has exactly one unit of it. Creating a model of strategic network formation with heterogeneous nodes and stochasticity constitutes the main technical innovation of this paper (discussed in more detail in Heesen 2016).
Academics learn each other’s experimental results (or evidence) not each other’s conclusions as expressed, say, in a posterior probability. In this sense my model differs from that of Aumann (1976). If academics only learn each other’s posterior on some set of possible worlds, they may not actually learn anything substantial (Geanakoplos and Polemarchakis 1982, Proposition 3).
Zollman (2013, Sect. 2) calls this “one way” information transmission. In contrast, “two way” information transmission occurs when an edge in the network allows information to flow in both directions, such as may happen when two academics meet at a conference. But since information is transmitted through reading in the present model, “one way” transmission seems like the more appropriate assumption.
That is, if academic i has read academic \(i^\prime \)’s paper, and then a third academic reads academic i’s paper, the third academic only learns the contents of the information set of academic i, not of academic \(i^\prime \). In this way my model differs from other information transmission models, e.g., those by Jackson and Wolinsky (1996) and Bala and Goyal (2000). There are two reasons for this. First, academic i’s paper presumably focuses on reporting academic i’s experimental results, not those she learned from others. Second, even if some iterated transfer of information happened, and the third academic learned something interesting about academic \(i^\prime \)’s work this way, one might expect her to then read the paper by academic \(i^\prime \) as well.
Cf. Sect. 6, where I argue that dropping this assumption does not affect the conclusions I draw there.
The reason for the “\(\sqsubset \)” notation is that this relation among information sets is closely related to the usual set-theoretic relation of inclusion “\(\subset \)”. See Heesen (2016, Sect. 2.2) for more on this.
More formally, academics only read papers on the Pareto frontier. But note that the Pareto frontier may change with each paper that is read. Any paper may eventually get read by a given academic; Always Prefer Higher Epistemic Value merely requires that the academic first reads any papers of higher epistemic value than that paper.
An academic has information set A if her information set contains the same number of realizations of each experiment as A does. See Heesen (2016, Sect. 2.2) for more on what this means formally.
Note that the assumption distinguishes the number of times the academic reads a paper with a given information set. This is because for technical reasons, I need to distinguish between cases where \(p_{i,A,1}\) is zero (i.e., the academic never reads any papers with information set A) and cases where \(p_{i,A,1}\) is positive. But for interpreting the assumption this is mostly irrelevant, because the number of papers with a given information set an academic reads is always less than the total number of papers she reads.
More formally, the graph of interest is \(G = (I,\{(i,i^\prime ) \in I^2\mid i\) reads \(i^\prime \})\), where I is the set of nodes and \(\{(i,i^\prime ) \in I^2\mid i\) reads \(i^\prime \}\) is the set of arcs.
Recall that an academic has information set A if her information set contains the same number of realizations of each experiment as A does.
\(\mathbb {E}\left[ d(A)\right] \) denotes an average in two senses. First, it averages over all academics with information set A. Second, it takes the mean over all the possible graphs that may arise due to the probabilistic nature of individual academics’ decisions to form connections.
Formally, \(A_{i^{\prime \prime }} = A_i \sqcup A_{i^\prime }\) if \(n(i^{\prime \prime },j) = \max \{n(i,j),n(i^\prime ,j)\}\) for all j, and \(A_{i^{\prime \prime }} = A_i \sqcap A_{i^\prime }\) if \(n(i^{\prime \prime },j) = \min \{n(i,j),n(i^\prime ,j)\}\) for all j. These notions are closely related, but not identical, to the standard set-theoretic notions of union and intersection. See Heesen (2016, Sect. 2.2) for details.
How often does this happen? In social sciences like psychology and economics one frequently sees empirical work included in papers whose primary contribution is theoretical, or vice versa. This could be interpreted as at least attempting to create situations like that described in the main text.
That is, if neither A nor B contains the same number of replications of each experiment as \(A\sqcup B\).
Thanks to Dominik Klein for suggesting that I include a corollary along these lines.
More formally, I is dense in E if for any combination of numbers \(n_1,\ldots ,n_m\) (where \(1\le n_j\le {\hat{n}}\) if \(j\in E\) and \(n_j = 0\) if \(j\notin E\)) there is an academic \(i\in I\) such that \(n(i,j)=n_j\) for all j.
Kuhn (1962) makes a similar point.
At least relatively speaking. If citation metrics or publication metrics were used as if they provided a numerical scale of competence, differences in competence would likely be exaggerated, as I showed above. But the competence-based view supports judgments like “Academic i is among the \(10\,\%\) most cited in her field, therefore she is among the \(10\,\%\) most competent”.
If I am right that epistemic value can only be measured by academics’ assessments, how could Merton (1968) establish the Matthew effect in the first place? He noted that if a superstar and a nobody co-authored a paper together, the superstar received more credit than the nobody; this obviously controls for epistemic value. He also noted that if a superstar and a nobody made the same discovery independently, the superstar received more credit; this arguably also controls for epistemic value. However, these strategies are not helpful in the measurement problem I describe.
References
Anderson, K. A. (2016). A model of collaboration network formation with heterogeneous skills. Network Science, 4(2), 188–215. ISSN 2050-1250. doi:10.1017/nws.2015.33. http://journals.cambridge.org/article_S2050124215000338.
Aumann, R. J. (1976). Agreeing to disagree. The Annals of Statistics, 4(6), 1236–1239. ISSN 00905364. http://www.jstor.org/stable/2958591.
Bala, V., & Goyal, S. (2000). A noncooperative model of network formation. Econometrica, 68(5), 1181–1229. ISSN 1468-0262. doi:10.1111/1468-0262.00155.
Barabási, A., & Albert, R. (1999). Emergence of scaling in random networks. Science, 286(5439), 509–512. ISSN 00368075. http://www.jstor.org/stable/2899318.
Bright, L. K. (2016). On fraud. Philosophical Studies, forthcoming. ISSN 1573-0883. doi:10.1007/s11098-016-0682-7.
Cole, J. R., & Cole, S. (1973). Social stratification in science. Chicago: University of Chicago Press. ISBN 0226113388.
Cole, J. R., & Zuckerman, H. (1987). Marriage, motherhood and research performance in science. Scientific American, 256(2), 119–125. ISSN 0036-8733. doi:10.1038/scientificamerican0287-119.
de Solla Price, D. J. (1965). Networks of scientific papers. Science, 149(3683), 510–515. ISSN 00368075. http://www.jstor.org/stable/1716232.
Geanakoplos, J. D., & Polemarchakis, H. M. (1982). We can’t disagree forever. Journal of Economic Theory, 28(1), 192–200. ISSN 0022-0531. doi:10.1016/0022-0531(82)90099-0. http://www.sciencedirect.com/science/article/pii/0022053182900990.
Good, I. J. (1967). On the principle of total evidence. The British Journal for the Philosophy of Science, 17(4), 319–321. ISSN 00070882. http://www.jstor.org/stable/686773.
Grim, P., Singer, D. J., Fisher, S., Bramson, A., Berger, W. J., Reade, C., Flocken, C., & Sales, A. (2013). Scientific networks on data landscapes: Question difficulty, epistemic success, and convergence. Episteme, 10, 441–464. ISSN 1750-0117. doi:10.1017/epi.2013.36. http://journals.cambridge.org/article_S1742360013000361.
Heesen, R. (2016). Network formation with heterogeneous nodes and stochasticity. Technical Report CMU-PHIL-191, Carnegie Mellon University. http://www.cmu.edu/dietrich/philosophy/docs/tech-reports/191_Heesen.pdf.
Holman, B., & Bruner, J. P. (2015). The problem of intransigently biased agents. Philosophy of Science, 82(5), 956–968. ISSN 00318248. http://www.jstor.org/stable/10.1086/683344.
Jackson, M. O., & Wolinsky, A. (1996). A strategic model of social and economic networks. Journal of Economic Theory, 71(1), 44–74. ISSN 0022-0531. doi:10.1006/jeth.1996.0108. http://www.sciencedirect.com/science/article/pii/S0022053196901088.
Joyce, J. M. (1998). A nonpragmatic vindication of probabilism. Philosophy of Science, 65(4), 575–603. ISSN 00318248. http://www.jstor.org/stable/188574.
Kitcher, P. (1993). The advancement of science: Science without legend. Objectivity without Illusions. Oxford: Oxford University Press. ISBN 0195046285.
Knobloch-Westerwick, S., & Glynn, C. J. (2013). The Matilda effect–role congruity effects on scholarly communication: A citation analysis of communication research and journal of communication articles. Communication Research, 40(1), 3–26. doi:10.1177/0093650211418339.
Kuhn, T. S. (1962). The structure of scientific revolutions. Chicago: The University of Chicago Press.
McKinnon, R. (2014). You make your own luck. Metaphilosophy, 45(4-5), 558–577. ISSN 1467-9973. doi:10.1111/meta.12107.
Medoff, M. H. (2006). Evidence of a Harvard and Chicago Matthew effect. Journal of Economic Methodology, 13(4), 485–506. doi:10.1080/13501780601049079.
Merton, R. K. (1968). The Matthew effect in science. Science, 159(3810), 56–63. ISSN 00368075. http://www.jstor.org/stable/1723414.
Merton, R. K., & Barber, E. (2004). The travels and adventures of serendipity: A study in sociological semantics and the sociology of science. Princeton: Princeton University Press.
Pettigrew, R. (2016). Accuracy and the Laws of Credence. Oxford: Oxford University Press.
Prpić, K. (2002). Gender and productivity differentials in science. Scientometrics, 55(1), 27–58. ISSN 0138-9130. doi:10.1023/A:1016046819457.
Redner, S. (1998). How popular is your paper? An empirical study of the citation distribution. The European Physical Journal B: Condensed Matter and Complex Systems, 4(2), 131–134. ISSN 1434-6028. doi:10.1007/s100510050359.
Rosen, S. (1981). The economics of superstars. The American Economic Review, 71(5), 845–858. ISSN 00028282. http://www.jstor.org/stable/1803469.
Strevens, M. (2003). The role of the priority rule in science. The Journal of Philosophy, 100(2), 55–79. ISSN 0022362X. http://www.jstor.org/stable/3655792.
Strevens, M. (2006). The role of the Matthew effect in science. Studies in History and Philosophy of Science Part A, 37(2), 159–170. ISSN 0039-3681. doi:10.1016/j.shpsa.2005.07.009. http://www.sciencedirect.com/science/article/pii/S0039368106000252.
Wald, A. (1947). Sequential analysis. New York: Wiley.
Zollman, K. J. S. (2010). The epistemic benefit of transient diversity. Erkenntnis, 72(1), 17–35. ISSN 01650106. http://www.jstor.org/stable/20642278.
Zollman, K. J. S. (2013). Network epistemology: Communication in epistemic communities. Philosophy Compass, 8(1), 15–27. ISSN 1747-9991. doi:10.1111/j.1747-9991.2012.00534.x.
Acknowledgments
Thanks to Kevin Zollman, Teddy Seidenfeld, Katharine Anderson, Tomas Zwinkels, Liam Bright, Aidan Kestigian, Conor Mayo-Wilson, Dominik Klein, the anonymous reviewers, and audiences at the Congress on Logic and Philosophy of Science in Ghent, Philosophy and Theory of Artificial Intelligence in Oxford, the Society for Exact Philosophy in Pasadena, and Agent-Based Modeling in Philosophy in Munich for valuable comments and discussion. This work was partially supported by the National Science Foundation under Grant SES 1254291
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Heesen, R. Academic superstars: competent or lucky?. Synthese 194, 4499–4518 (2017). https://doi.org/10.1007/s11229-016-1146-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-016-1146-5