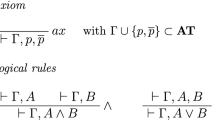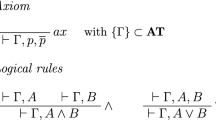Abstract
This paper shows that, for the Hertz–Gentzen Systems of 1933 (without Thinning), extended by a classical rule T1 (from the Stoics) and using certain axioms (also from the Stoics), all derivations are analytic: every cut formula occurs as a subformula in the cut’s conclusion. Since the Stoic cut rules are instances of Gentzen’s Cut rule of 1933, from this we infer the decidability of the propositional logic of the Stoics. We infer the correctness for this logic of a “relevance criterion” and of two “balance criteria”, and hence (in contrast to one of Gentzen’s 1933 results) that a particular derivable sequent has no derivation that is “normal” in the sense that the first premiss of each cut is cut-free. We also infer that Cut is not admissible in the Stoic system, based on the standard Stoic axioms, the T1 rule and the instances of Cut with just two antecedent formulae in the first premiss.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Bobzien, S., Stoic syllogistic. In Oxford Studies in Ancient Philosophy, volume 14, OUP, Oxford, 1996, pp. 133–192.
Bobzien, S., Stoic logic. In B. Inwood, (ed.), The Cambridge Companion to Stoic Philosophy, CUP, 2003, pp. 85–123.
Dyckhoff, R., Contraction-free sequent calculi for intuitionistic logic, Journal of Symbolic Logic 57:795–807, 1992.
Dyckhoff, R., Implementation of Stoic propositional logic, 2017.
Gentzen, G., Über die Existenz unabhängiger Axiomensysteme zu unendlichen Satzsystemen, Mathematische Annalen 107:329–350, 1933.
Gentzen, G., Untersuchungen über das logische Schließen, Mathematische Zeitschrift 39:176–210, 405–431, 1935.
Leitsch, A., and S. Hetzl, Personal communication, January 2018.
Milne, P., On the completeness of non-Philonian Stoic logic, History and Philosophy of Logic 16:39–64, 1995.
Milne, P., Unpublished MS, 2012.
Moriconi, E., Early structural reasoning. Gentzen 1932, Review of Symbolic Logic 8:662–679, 2015.
Read, S., Relevant Logic, Blackwell, 1988.
Schroeder-Heister, P., Resolution and the origins of structural reasoning: early proof-theoretic ideas of Hertz and Gentzen, Bull. Symbolic Logic 8:246–265, 2001.
Sextus Empiricus, Against the Logicians, Translated by Richard Bett, Cambridge Texts in the History of Philosophy, Cambridge Univ. Press, 2005.
Acknowledgements
Susanne Bobzien thanks All Souls College, Oxford, for support; Roy Dyckhoff thanks the University of St Andrews for an Honorary position. Both are grateful to Alex Leitsch and Stefan Hetzl for their contribution [7], and to two anonymous referees for their helpful remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
Presented by Heinrich Wansing
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bobzien, S., Dyckhoff, R. Analyticity, Balance and Non-admissibility of \(\varvec{Cut}\) in Stoic Logic. Stud Logica 107, 375–397 (2019). https://doi.org/10.1007/s11225-018-9797-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11225-018-9797-5