Abstract
In the modern age, rankings data are ubiquitous and they are useful for a variety of applications such as recommender systems, multi-object tracking and preference learning. However, most rankings data encountered in the real world are incomplete, which prevent the direct application of existing modelling tools for complete rankings. Our contribution is a novel way to extend kernel methods for complete rankings to partial rankings, via consistent Monte Carlo estimators for Gram matrices: matrices of kernel values between pairs of observations. We also present a novel variance-reduction scheme based on an antithetic variate construction between permutations to obtain an improved estimator for the Mallows kernel. The corresponding antithetic kernel estimator has lower variance, and we demonstrate empirically that it has a better performance in a variety of machine learning tasks. Both kernel estimators are based on extending kernel mean embeddings to the embedding of a set of full rankings consistent with an observed partial ranking. They form a computationally tractable alternative to previous approaches for partial rankings data. An overview of the existing kernels and metrics for permutations is also provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Motivation
Permutations play a fundamental role in statistical modelling and machine learning applications involving rankings and preference data. A ranking over a set of objects can be encoded as a permutation; hence, kernels for permutations are useful in a variety of machine learning applications involving rankings such as recommender systems, multi-object tracking and preference learning. It is of interest to construct a kernel in the space of the data in order to capture similarities between datapoints and thereby influence the pattern of generalisation. A kernel input is required for the maximum mean discrepancy (MMD) two-sample test (Gretton et al. 2012), kernel principal component analysis (kPCA) (Schölkopf et al. 1999), support vector machines (Boser et al. 1992; Cortes and Vapnik 1995), Gaussian processes (GPs) (Rasmussen and Williams 2006) and agglomerative clustering (Duda and Hart 1973), among others.
Our main contributions are: (1) a novel and computationally tractable way to deal with incomplete or partial rankings by first representing the marginalised kernel (Haussler 1999) as a kernel mean embedding of a set of full rankings consistent with an observed partial ranking. We then propose two estimators that can be represented as the corresponding empirical mean embeddings; (2) a Monte Carlo kernel estimator that is based on sampling independent and identically distributed rankings from the set of consistent full rankings given an observed partial ranking; (3) an antithetic variate construction for the marginalised Mallows kernel that gives a lower variance estimator for the kernel Gram matrix. The Mallows kernel has been shown to be an expressive kernel; in particular, Mania et al. (2016) show that the Mallows kernel is an example of a universal and characteristic kernel, and hence, it is a useful tool to distinguish samples from two different distributions, it achieves the Bayes risk when used in kernel-based classification/regression (Sriperumbudur et al. 2011). Jiao and Vert (2015) have proposed a fast approach for computing the Kendall marginalised kernel; however, this kernel is not characteristic (Mania et al. 2016) and hence has limited expressive power.
The resulting estimators are used for a variety of kernel machine learning algorithms in the Experiments section. In particular, we present comparative simulation results demonstrating the efficacy of the proposed estimators for an agglomerative clustering task, a hypothesis test task using the maximum mean discrepancy (MMD) (Gretton et al. 2012) and a Gaussian process classification task. For the latter, we extend some of the existing methods in the software library GPy (GPy 2012).
Since the space of permutations is an example of a discrete space, with a non-commutative group structure, the corresponding reproducing kernel Hilbert spaces (RKHS) have only recently being investigated; see Kondor et al. (2007), Fukumizu et al. (2009), Kondor and Barbosa (2010), Jiao and Vert (2015) and Mania et al. (2016). First, we provide an overview of the connection between kernels and certain semimetrics when working on the space of permutations. This connection allows us to obtain kernels from given semimetrics or semimetrics from existing kernels. We can combine these semimetric-based kernels to obtain novel, more expressive kernels which can be used for the proposed Monte Carlo kernel estimator.
2 Definitions
We first briefly introduce the theory of permutation groups. A particular application of permutations is to use them to represent rankings; in fact, there is a natural one-to-one relationship between rankings of n items and permutations (Stanley 2000). For this reason, we sometimes use ranking and permutation interchangeably. In this section, we state some mathematical definitions to formalise the problem in terms of the space of permutations.
Let \(\left[ n\right] =\left\{ 1,2,\ldots ,n\right\} \) be a set of indices for n items, for some \(n \in \mathbb {N}\). Given a ranking of these n items, we use the notation \(\succ \) to denote the ordering of the items induced by the ranking, so that for distinct \(i, j \in \left[ n \right] \), if i is preferred to j, we will write \(i \succ j\). Note that for a full ranking, the corresponding relation \(\succ \) is a total order on \(\{1,\ldots , n\}\).
We now outline the correspondence between rankings on \(\left[ n \right] \) and the permutation group \(S_n\) that we use throughout the paper. In words, given a full ranking of [n], we will associate it with the permutation \(\sigma \in S_n\) that maps each ranking position \(1,\ldots ,n\) to the correct object under the ranking. More mathematically, given a ranking \(a_1 \succ \cdots \succ a_n\) of \(\left[ n \right] \), we may associate it with the permutation \(\sigma \in S_n\) given by \(\sigma (j) = a_j\) for all \(j =1,\ldots ,n\). For example, the permutation corresponding to the ranking on [3] given by \(2\succ 3\succ 1\) corresponds to the permutation \(\sigma \in S_3\) given by \(\sigma (1)=2,\sigma (2)=3,\sigma (3)=1\). This correspondence allows the literature relating to kernels on permutations to be leveraged for problems involving the modelling of ranking data.
In the next section, we first review some semimetrics on \(S_n\) because of the existing relationship between semimetrics with an additional property and kernels. We state such relationship in Theorem 1.
2.1 Metrics for permutations and properties
Definition 1
Let \(\mathcal {X}\) be any set and \(d:\mathcal {X}\times \mathcal {X}\rightarrow \mathbb {R}\) is a function, which we write d(x, y) for every \(x,y \in \mathcal {X}\). Then d is a semimetric if it satisfies the following conditions, for every \(x,y\in \mathcal {X}\) (Dudley 2002):
-
(i)
\(d(x,y)=d(y,x)\), that is, d is a symmetric function.
-
(ii)
\(d(x,y)=0\) if and only if \(x=y\).
A semimetric is a metric if it satifies:
-
(iii)
\(d(x,z)\le d(x,y)+d(y,z)\) for every \(x,y, z \in \mathcal {X}\), that is, d satisfies the triangle inequality.
The following are some examples of semimetrics on the space of permutations \(S_n\) (Diaconis 1988). All semimetrics in bold have the additional property of being of negative type. Theorem 1 shows that negative-type semimetrics are closely related to kernels. This is because the semimetric can be written as the Hilbert space norm of a feature embedding and the kernel is the inner product for such feature embedding.
-
(1)
Spearman’s footrule
$$\begin{aligned} d_f(\sigma ,\sigma ') = \sum _{i=1}^n |\sigma (i) - \sigma '(i)|= \Vert \sigma -\sigma '\Vert _1. \end{aligned}$$ -
(2)
Spearman’s rank correlation
$$\begin{aligned} d_{\rho }(\sigma ,\sigma ')= \sum _{i=1}^n (\sigma (i) -\sigma '(i))^2= \Vert \sigma -\sigma '\Vert ^2_2. \end{aligned}$$ -
(3)
Hamming distance
$$\begin{aligned}d_H(\sigma ,\sigma ') = \# \{i | \sigma (i) \not = \sigma '(i) \}. \end{aligned}$$It can also be defined as the minimum number of substitutions required to change one permutation into the other.
-
(4)
Cayley distance
$$\begin{aligned} d_C(\sigma , \sigma ') = \sum _{j=1}^{n-1}X_j(\sigma \circ (\sigma ')^{-1}), \end{aligned}$$where the composition operation of the permutation group \(S_n\) is denoted by \(\circ \) and \(X_j(\sigma \circ (\sigma ')^{-1})= 0\) if j is the largest item in its cycle and is equal to 1 otherwise (Irurozki et al. 2016b). It is also equal to the minimum number of pairwise transpositions taking \(\sigma \) to \(\sigma '\). Finally, it can also be shown to be equal to \(n-C(\sigma \circ (\sigma ')^{-1})\) where \(C(\eta )\) is the number of cycles in \(\eta \).
-
(5)
Kendall distance
$$\begin{aligned} d_{\tau }(\sigma , \sigma ') = n_d(\sigma , \sigma '), \end{aligned}$$where \(n_d(\sigma , \sigma ')\) is the number of discordant pairs for the permutation pair \((\sigma , \sigma ')\). It can also be defined as the minimum number of pairwise adjacent transpositions taking \(\sigma ^{-1}\) to \((\sigma ')^{-1}\).
-
(6)
\(l_p\) distances
$$\begin{aligned} d_p(\sigma , \sigma ')= & {} \left( \sum _{i=1}^n |\sigma (i) - \sigma '(i)|^p\right) ^{\frac{1}{p}}= \Vert \sigma -\sigma '\Vert _p,\, \\&\quad \mathrm{with} \,p\ge 1. \end{aligned}$$ -
(7)
\( l_{\infty }\) distances
$$\begin{aligned} d_{\infty }(\sigma , \sigma ') ={\mathop {_{1\le i \le n}}\limits ^{\text{ max }}}|\sigma (i) - \sigma '(i)|= \Vert \sigma -\sigma '\Vert _{\infty }. \end{aligned}$$
Definition 2
A semimetric is said to be of negative type if for all \(n\ge 2\), \(x_1,\ldots ,x_n\in \mathcal {X}\) and \(\alpha _1,\ldots , \alpha _n\in \mathbb {R}\) with \(\sum _{i=1}^n \alpha _i=0\), we have
In general, if we start with a Mercer kernel for permutations, that is, a symmetric and positive-definite function \(k : S_n \times S_n \rightarrow \mathbb {R}\), the following expression gives a semimetric d that is of negative type
Berlinet and Thomas-Agnan (2004) and Shawer-Taylor and Cristianini (2004) provide in-depth treatments about Mercer kernels and reproducing kernel Hilbert spaces (RKHS); see “Appendix A” for a short overview. A useful characterisation of semimetrics of negative type is given by the following theorem, which states a connection between negative-type metrics and a Hilbert space feature representation or feature map \(\varPhi \).
Theorem 1
(Berg et al. 1984) A semimetric d is of negative type if and only if there exists a Hilbert space \(\mathcal {H}\) and an injective map \(\varPhi :\mathcal {X}\rightarrow \mathcal {H}\) such that \(\forall x,x' \in \mathcal {X}\), \(d(x,x')=\Vert \varPhi (x)-\varPhi (x')\Vert _{\mathcal {H}}^2\).
Once the feature map from Theorem 1 is found, we can directly take its inner product to construct a kernel. For instance, Jiao and Vert (2015) propose an explicit feature representation for Kendall kernel given by
They show that the inner product between two such features is a positive-definite kernel. The corresponding metric, given by Kendall distance, can be shown to be the square of the norm of the difference of feature vectors. Hence, by Theorem 1, it is of negative type.
Analogously, Mania et al. (2016) propose an explicit feature representation for the Mallows kernel, given by
where \(\bar{\varPhi }(\sigma )_{s_i}=2\mathbb {I}_{\left\{ \sigma (a_i)<\sigma (b_i)\right\} -1}\) when \(s_i=(a_i,b_i)\) and \(\bar{\varPhi }(\sigma )_{\emptyset }=2^{\frac{1}{2}\left( {\begin{array}{c}n\\ 2\end{array}}\right) }(1+\exp {(-v)})^{\frac{1}{2}\left( {\begin{array}{c}n\\ 2\end{array}}\right) }\).
In the following proposition, an explicit feature representation for the Hamming distance is introduced and we show that it is a distance of negative type.
Proposition 1
The Hamming distance is of negative type with
where the corresponding feature representation is a matrix given by
Proof
The Hamming distance can be written as a square difference of indicator functions in the following way
where each indicator is one whenever the given entry of the permutation is equal to the corresponding element of the identity element of the group. Let the \(\ell \)th feature vector be \(\phi _{\ell }(\sigma )=\left( \mathbb {I}_{\left\{ \sigma (1)=\ell \right\} },\ldots ,\mathbb {I}_{\left\{ \sigma (n)=\ell \right\} }\right) \), then
This is the trace of the difference of the product of the feature matrices \(\varPhi (\sigma )-\varPhi (\sigma ')\), where the difference of feature matrices is given by
This is the square of the usual Frobenius norm for matrices, by Theorem 1, and the Hamming distance is of negative type. \(\square \)
Another example is Spearman’s rank correlation, which is a semimetric of negative type since it is the square of the usual Euclidean distance (Berg et al. 1984).
The two alternative definitions given for some of the distances in the previous examples are handy from different perspectives. One is an expression in terms of either an injective or non-injective feature representation, whilst the other is in terms of the minimum number of operations to change one permutation to the other. Other distances can be defined in terms of this minimum number of operations, and they are called editing metrics (Deza and Deza 2009). Editing metrics are useful from an algorithmic point of view, whereas metrics defined in terms of feature embeddings are useful from a theoretical point of view. Ideally, having a particular metric in terms of both algorithmic and theoretical descriptions gives a better picture of which are the relevant characteristics of the permutation that the metric takes into account (Fig. 1). For instance, Kendall and Cayley distances algorithmic descriptions correspond to the bubble and quick sort algorithms, respectively (Knuth 1998).
Another property shared by most of the semimetrics in the examples is the following
Definition 3
Let \(\sigma _1,\sigma _2\in S_n\), \((S_n,\circ )\) denote the symmetric group of degree n with the composition operation, a right-invariant semimetric (Diaconis 1988) satisfies
In particular, if we take \(\eta =\sigma _1^{-1}\), then \(d(\sigma _1,\sigma _2)=d(e,\sigma _2\circ \sigma _1^{-1})\), where e corresponds to the identity element of the permutation group.
This property is inherited by the distance-induced kernel from Sect. 2.2, Example 7. This symmetry is analogous to translation invariance for kernels defined in Euclidean spaces.
2.2 Kernels for \(S_n\)
If we specify a symmetric and positive-definite function or kernel k, it corresponds to defining an implicit feature space representation of a ranking data point. The well-known kernel trick exploits the implicit nature of this representation by performing computations with the kernel function explicitly, rather than using inner products between feature vectors in high or even infinite-dimensional space. Any symmetric and positive-definite function uniquely defines an underlying Reproducing Kernel Hilbert Space (RKHS); see the supplementary material Appendix A for a brief overview about the RKHS. Some examples of kernels for permutations are the following
-
1.
The Kendall kernel (Jiao and Vert 2015) is given by
$$\begin{aligned} \displaystyle {k_\tau (\sigma , \sigma ^\prime ) = \frac{n_c(\sigma , \sigma ^\prime ) - n_d(\sigma , \sigma ^\prime )}{\left( {\begin{array}{c}d\\ 2\end{array}}\right) }}, \end{aligned}$$where \(n_c(\sigma , \sigma ^\prime )\) and \( n_d(\sigma , \sigma ^\prime )\) denote the number of concordant and discordant pairs between \(\sigma \) and \(\sigma ^\prime \), respectively.
-
2.
The Mallows kernel (Jiao and Vert 2015) is given by
$$\begin{aligned} \displaystyle {k_{\lambda }(\sigma , \sigma ^\prime ) = \exp (-\lambda n_d(\sigma , \sigma ^\prime ))}. \end{aligned}$$ -
3.
The Polynomial kernel of degree m (Mania et al. 2016) is given by
$$\begin{aligned} \displaystyle { k_{P}^{(m)}(\sigma , \sigma ^\prime ) = (1 + k_{\tau }(\sigma , \sigma ^\prime ))^m}. \end{aligned}$$ -
4.
The Hamming kernel is given by
$$\begin{aligned} \displaystyle {k_H(\sigma , \sigma ^\prime ) = \text {Trace}\left[ \left( \varPhi (\sigma )\varPhi (\sigma '\right) ^T\right] }. \end{aligned}$$ -
5.
An exponential semimetric kernel is given by
$$\begin{aligned} \displaystyle {k_{\text{ exp }}(\sigma , \sigma ^\prime ) = \exp \left\{ -\lambda d(\sigma , \sigma ^\prime )\right\} }, \end{aligned}$$where d is a semimetric of negative type.
-
6.
The diffusion kernel (Kondor and Barbosa 2010) is given by
$$\begin{aligned} \displaystyle {k_{\beta }(\sigma , \sigma ^\prime ) = \exp \left\{ \beta q(\sigma \circ \sigma ^\prime )\right\} }, \end{aligned}$$where \(\beta \in \mathbb {R}\) and q is a function that must satisfy \(q(\pi )=q(\pi ^{-1})\) and \(\sum _{\pi }q(\pi )=0\). A particular case is \(q(\sigma ,\sigma ')=1\) if \(\sigma \) and \(\sigma '\) are connected by an edge in some Cayley graph representation of \(S_n\), and \(q(\sigma ,\sigma ')=-\text {degree}_{\sigma }\) if \(\sigma =\sigma '\) or \(q(\sigma ,\sigma ')=0\) otherwise.
-
7.
The semimetric or distance-induced kernel (Sejdinovic et al. 2013): if the semimetric d is of negative type, then, a family of kernels k, parameterised by a central permutation \(\sigma _0\), is given by
$$\begin{aligned} \displaystyle k_d(\sigma ,\sigma ')= \frac{1}{2}\left[ d(\sigma ,\sigma _0)+d(\sigma ',\sigma _0)-d(\sigma ,\sigma ')\right] . \end{aligned}$$
If we choose any of the above kernels by itself, it will generally not be complex enough to represent the ranking data’s generating mechanism. However, we can benefit from the allowable operations for kernels to combine kernels and still obtain a valid kernel. Some of the operations which render a valid kernel are the following: sum, multiplication by a positive constant, product, polynomial and exponential (Berlinet and Thomas-Agnan 2004).
In the case of the symmetric group of degree n, \(S_n\), there exist kernels that are right invariant, as defined in Equation (4). This invariance property is useful because it is possible to write down the kernel as a function of a single argument and then obtain a Fourier representation. The caveat is that this Fourier representation is given in terms of certain matrix unitary representations due to the non-Abelian structure of the group (James 1978). Even though the space is finite, and every irreducible representation is finite-dimensional (Fukumizu et al. 2009), these Fourier representations do not have closed-form expressions. For this reason, it is difficult to work on the spectral domain in contrast to the \(\mathbb {R}^n\) case. There is also no natural measure to sample from such as the one provided by Bochner’s theorem in Euclidean spaces (Wendland 2005). In the next section, we will present a novel Monte Carlo kernel estimator for the case of partial rankings data.
3 Partial rankings
Having provided an overview of kernels for permutations, and reviewed the link between permutations and rankings of objects, we now turn to the practical issue that in real data sets, we typically have access only to partial ranking information, such as pairwise preferences and top-k rankings. Partial rankings can be obtained from pairwise comparisons data given certain assumptions. For instance, a classic generative model for pairwise comparisons that can be used to obtain topk rankings is the Bradley–Terry model (Bradley and Terry 1952) and its extension to multiple comparisons, the Plackett–Luce model (Luce 1959; Plackett 1974). See (Chen et al. 2017) for details on how to obtain a topk partial ranking given pairwise comparisons from the Bradley–Terry model and (Caron et al. 2014) for a nonparametric Bayesian extension of the Plackett–Luce model and references therein. In the following, as Jiao and Vert (2015), we assume that our data are partial rankings of the following types
Definition 4
(Exhaustive partial rankings, top-krankings) Let \(n \in \mathbb {N}\). A partial ranking on the set [n] is specified by an ordered collection \(\varOmega _1 \succ \cdots \succ \varOmega _l\) of disjoint non-empty subsets \(\varOmega _1,\ldots ,\varOmega _l \subseteq [n]\), for any \(1 \le l \le n\). The partial ranking \(\varOmega _1 \succ \cdots \succ \varOmega _l\) encodes the fact that the items in \(\varOmega _i\) are preferred to those in \(\varOmega _{i+1}\), for \(i=1,\ldots ,l-1\). A partial ranking \(\varOmega _1 \succ \cdots \succ \varOmega _l\) with \(\cup _{i=1}^l \varOmega _i = [n]\) termed exhaustive, as all items in [n] are included within the preference information. A top-k partial ranking is a particular type of exhaustive ranking \(\varOmega _1 \succ \cdots \succ \varOmega _{l}\), with \(|\varOmega _1| = \cdots = |\varOmega _{l-1}| = 1\), and \(\varOmega _{l} = [n] \setminus \cup _{i=1}^{l-1} \varOmega _i\). We will frequently identify a partial ranking \(\varOmega _1 \succ \cdots \succ \varOmega _l\) with the set \(R(\varOmega _1,\ldots ,\varOmega _l) \subseteq S_n\) of full rankings consistent with the partial ranking. Thus, \(\sigma \in R(\varOmega _1,\ldots ,\varOmega _l)\) iff for all \(1\le i< j \le l\), and for all \(x \in \varOmega _i, y \in \varOmega _j\), we have \(\sigma ^{-1}(x) < \sigma ^{-1}(y)\). When there is potential for confusion, we will use the term “subset partial ranking” when referring to a partial ranking as a subset of \(S_n\), and “preference partial ranking” when referring to a partial ranking with the notation \(\varOmega _1 \succ \cdots \succ \varOmega _l\).
Several interpretations are compatible with this definition; for instance, scenarios in which no preference information is known about items within a particular \(\varOmega _i\) are possible, as well as are scenarios where the preferences of all items in a particular \(\varOmega _i\) are ties. Thus, for many practical problems, we require definitions of kernels between subsets of partial rankings rather than between full rankings, to be able to handle data sets containing only partial ranking information. A common approach (Tsuda et al. 2002) is to take a kernel K defined on \(S_n\), and use the marginalised kernel, defined on subsets of partial rankings by
for all \(R, R^\prime \subseteq S_n\), for some probability distribution \(p \in \mathscr {P}(S_n)\). Here, \(p(\cdot |R)\) denotes the conditioning of p to the set \(R \subseteq S_n\). If some prior information about the distribution of complete rankings is available, it can be used to define a kernel over partial rankings with a non-uniform distribution. For instance, let \(\sigma \in S_n\) be a permutation, its probability mass function under a Mallows distribution (Mallows 1957), given a metric \(d : S_n \times S_n \rightarrow \mathbb {R}\), a location parameter \(\sigma _0 \in S_n\), and a scale parameter \(\theta > 0\), is
with normalising constant \(\psi (\theta )=\sum _{\sigma \in S_n}\exp {\left\{ -\theta d(\sigma ,\sigma _0)\right\} } \times \mathbb {I}_{\left\{ \sigma \in R\right\} }.\) This family of probability distributions has been extensively studied for the full rankings case, when \(R=S_n\); see Fligner and Verducci (1986), Mukherjee (2016) and Busse et al. (2007) for mixtures of Mallows distributions. The R package “PerMallows” (Irurozki et al. 2016) provides random number generators based on different algorithms to sample from a Mallows distribution parameterised by different distance functions. These sampling procedures are not straightforwardly applicable to the partial rankings case. There have been various extensions for topk partial rankings such as Lebanon and Mao (2008), who propose a nonparametric estimator based on kernel smoothing; Chierichetti et al. (2018), who extended the Mallows model by defining a distance measure directly over topk rankings; and Vitelli et al. (2017), who developed a Bayesian framework for inference using a Metropolis–Hastings algorithm, among others. We assume that we do not have any prior information about the generative process of full rankings; hence, we only deal with the case of the marginalised kernel from Equation (5), in which we take the probability mass function to be uniform over each of the partial rankings denoted by \(R,R'\). The corresponding kernel is given by
Jiao and Vert (2015) also use this kernel and called it the convolution kernel (Haussler 1999) between partial rankings. In general, the use of a marginalised kernel quickly becomes computationally intractable, with the number of terms in the right-hand side of Eq. (5) growing super-exponentially with n, for a fixed number of items in the partial rankings R and \(R^\prime \); see “Appendix E” for a table that illustrates such growth. An exception is the Kendall kernel case for two interleaving partial rankings of k and m items or a top-k and top-m ranking. In this case, the sum can be tractably computed and it can be done in \(\mathcal {O}(k \log k + m \log m)\) time (Jiao and Vert 2015).
We propose a variety of Monte Carlo methods to estimate the marginalised kernel of Eq. (5) for the general case, where direct calculation is intractable.
Definition 5
The Monte Carlo estimator approximating the marginalised kernel of Eq. (5) is defined for a collection of partial rankings \((R_i)_{i=1}^I\), given by
for \(i,j = 1,\ldots ,I\), where \(((\sigma ^{(i)}_n)_{m=1}^{M_i})_{i=1}^I\) are random permutations and \(\left( (w^{(i)}_m)_{m=1}^{M_i}\right) _{i=1}^I\) are random weights. Note that this general setup allows for several possibilities:
-
For each \(i=1\ldots ,I\), the permutations \((\sigma ^{(i)}_m)_{m=1}^{M_i}\) are drawn exactly from the distribution \(p(\cdot |R_i)\). In this case, the weights are simply \(w^{(i)}_n = 1\) for \(m=1,\ldots ,M_i\).
-
For each \(i=1,\ldots ,I\), the permutations \((\sigma ^{(i)}_m)_{m=1}^{M_i}\) drawn from some proposal distribution \(q(\cdot |R_i)\) with the weights given by the corresponding importance weights\(w^{(i)}_n = p(\sigma ^{(i)}_n|R) / q(\sigma ^{(i)}_n|R)\) for \(m=1,\ldots ,M_i\).
An alternative perspective on the estimator defined in Eq. (7), more in line with the literature on random feature approximations of kernels, is to define a random feature embedding for each of the partial rankings \((R_i)_{i=1}^I\).
More precisely, let \(\mathcal {H}_K\) be the (finite-dimensional) Hilbert space associated with the kernel K on the space \(S_n\), and let \(\varvec{\varPhi }\) be the associated feature map, so that \(\varPhi (\sigma ) = K(\sigma , \cdot ) \in \mathcal {H}_K\) for each \(\sigma \in S_n\). Then observe that we have \(K(\sigma , \sigma ^\prime ) = \langle \varvec{\varPhi }(\sigma ), \varvec{\varPhi }(\sigma ^\prime ) \rangle \) for all \(\sigma , \sigma ^\prime \in S_n\). We now extend this feature embedding to partial rankings as follows. Given a partial ranking \(R \subseteq S_n\), we define the feature embedding of R by
With this extension of \(\varvec{\varPhi }\) to partial rankings, we may now directly express the marginalised kernel of Eq. (5) as an inner product in the same Hilbert space \(\mathcal {H}_K\)
for all partial rankings \(R, R^\prime \subseteq S_n\). If we define a random feature embedding of the partial rankings \((R_i)_{i=1}^I\) by
then the Monte Carlo kernel estimator of Eq. (7) can be expressed directly as
for each \(i,j \in \{1,\ldots , I\}\). This expression of the estimator as an inner product between randomised embeddings will be useful in the sequel.
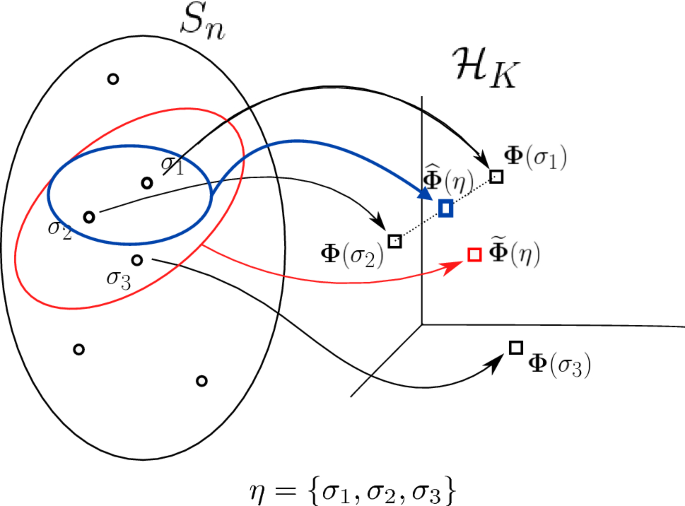
We provide an illustration of the various RKHS embeddings at play in Fig. 2, using the notation of the proof of Theorem 3. In this figure, \(\eta \) is a partial ranking, with three consistent full rankings \(\sigma _1, \sigma _2, and \sigma _3\). The extended embedding \(\widetilde{\varvec{\varPhi }}\) applied to \(\eta \) is the barycentre in the RKHS of the embeddings of the consistent full rankings, and a Monte Carlo approximation \(\widehat{\varvec{\varPhi }}\) to this embedding is also displayed.
Visualisation of the various embeddings discussed in the proof of Theorem 3. \(\sigma _1, \sigma _2 and \sigma _3\) are permutations in \(S_n\), which are mapped into the RKHS \(\mathcal {H}_K\) by the embedding \(\varvec{\varPhi }\). \(\eta \) is a partial ranking subset which contains \(\sigma _1, \sigma _2, \sigma _3\), and its embedding \(\widetilde{\varvec{\varPhi }}(\eta )\) is given as the average of the embeddings of its full rankings. The Monte Carlo embedding \(\widehat{\varvec{\varPhi }}(\eta )\) induced by Equation (7) is computed by taking the average of a randomly sampled collection of consistent full rankings from \(\eta \)
Theorem 2
Let \(R\subseteq S_n\) be a partial ranking, and let \(\left( \sigma _m\right) _{m=1}^{M}\) independent and identically distributed samples from \(p(\cdot \mid R)\). The kernel Monte Carlo mean embedding,
is an unbiased estimator of the marginalised kernel embedding
Proof
Note that the RKHS in which these embeddings take values is finite-dimensional, and the Monte Carlo estimator is the average of iid terms, each of which is equal to the true embedding in expectation. Thus, we immediately obtain unbiasedness of the Monte Carlo embedding. \(\square \)
Theorem 3
The Monte Carlo kernel estimator from Eq. (7) does define a positive-definite kernel; further, it yields unbiased estimates of the off-diagonal elements and consistent for the diagonal elements of the kernel matrix.
Proof
We first deal with the positive-definiteness claim. Let \(R_1, \ldots , R_I \subseteq S_n\) be a collection of partial rankings, and for each \(i=1,\ldots ,I\), let \((\sigma ^{(i)}_{m}, w^{(i)}_{m})_{m=1}^{M_i}\) be an i.i.d. weighted collection of complete rankings distributed according to \(p(\cdot | R_i)\). To show that the Monte Carlo kernel estimator \(\widehat{K}\) is positive definite, we observe that by Eq. (8), the \(I \times I\) matrix with (i, j)th element given by \(\widehat{K}(R_i, R_j)\) is the Gram matrix of the vectors \((\widehat{\varvec{\varPhi }}(R_i))_{i=1}^I\) with respect to the inner product of the Hilbert space \(\mathcal {H}_K\). We therefore immediately deduce that the matrix is positive semidefinite. Furthermore, the Monte Carlo kernel estimator is unbiased for the off-diagonal elements and consistent for the diagonal elements of the kernel matrix; see Appendix C in the supplementary material for the proof. \(\square \)
We highlight that whilst the mean embedding estimator in Eq. (9) is unbiased, the corresponding kernel estimator is consistent for the diagonal elements of the kernel matrix and unbiased for the off-diagonal elements. Having established that the Monte Carlo estimator \(\widehat{K}\) is itself a kernel, we note that when it is evaluated at two partial rankings \(R, R^\prime \subseteq S_n\), the resulting expression is not a sum of iid terms; the following result quantifies the quality of the estimator through its variance.
Theorem 4
The variance of the Monte Carlo kernel estimator evaluated at a pair of partial rankings \(R_i, R_j\), with \(M_i, N_j\) Monte Carlo samples, respectively, is given by
The proof is given in the supplementary material, “Appendix D”. We have presented some theoretical properties of the embedding corresponding to the Monte Carlo kernel estimator which confirm that it is a sensible embedding. In the next section, we present a lower variance estimator based on a novel antithetic variates construction.
4 Antithetic random variates for permutations
A common, computationally cheap variance-reduction technique in Monte Carlo estimation of expectations of a given function is to use antithetic variates (Hammersley and Morton 1956), the purpose of which is to introduce negative correlation between samples without affecting their marginal distribution, resulting in a lower variance estimator. Antithetic samples have been used when sampling from Euclidean vector spaces, for which antithetic samples are straightforward to define. Ross (2006) defines the antithetic of a full ranking by reversing the order of the original permutation. We give a definition of antithetic permutations for partial rankings in terms of distance maximisation and show that this coincides with the definition of Ross (2006) in the case of full rankings. We begin with a preliminary lemma, before giving the full definition of antithetic permutations given a fixed partial ranking.
Lemma 1
Let \(R \subseteq S_n\) be a top-k partial ranking, let \(\sigma \in R\). Then, there exists a unique solution to the problem
Moreover, it can be calculated directly; if the preference partial ranking corresponding to R is given by \(a_1 \succ \cdots \succ a_k\), so that the full ranking \(\sigma \in R\) satisfies \(\sigma (1) = a_1,\ldots ,\sigma (k) = a_k\), then the unique distance-maximising permutation \(\sigma ^\prime \) is given by
In this case, we have \(d_{\tau }(\sigma , \sigma ^\prime ) = \left( {\begin{array}{c}n-k\\ 2\end{array}}\right) \).
See “Appendix B” for the proof.
Definition 6
(Antithetic permutations) Let \(R \subseteq S_n\) be a top-k partial ranking. The antithetic operator \(A_{R} : R \rightarrow R\) maps each permutation \(\sigma \in R\) to the permutation in R of maximal Kendall distance from \(\sigma \). \(A_R(\sigma )\) is said to be antithetic to \(\sigma \).
This definition of antithetic samples for permutations has parallels with the standard notion of antithetic samples in vector spaces, in which typically a sampled vector \(x \in \mathbb {R}^d\) is negated to form \(-x\), its antithetic sample; \(-x\) is the vector maximising the Euclidean distance from x, under the restrictions of fixed norm. We note here also that the computational cost of generating an antithetic permutation via the method described in Lemma 1 is no greater than the cost associated with generating an independent permutation.
Proposition 1
Let R be a partial ranking and \(\left\{ \sigma ,A_{R}({\sigma })\right\} \) be an antithetic pair from R, \(\sigma \) is distributed uniformly in the region R. Let \(d_{\tau }:S_n\rightarrow \mathbb {R}^{+}\) be the Kendall distance and \(\sigma _0\in R\) a fixed permutation, let \(X=d_{\tau }(\sigma ,\sigma _0)\) and \( Y= d_{\tau }(A_{R}({\sigma }),\sigma _0)\), then X and Y have negative covariance.
Proposition 1 is useful because one of the main tasks in statistical inference is to compute expectations of a function of interest, denoted by h. Once the antithetic variates are constructed, the functional form of h determines whether or not the antithetic variate construction effectively produces a lower variance estimator for its expectation. The proof of this proposition is presented after the relevant lemmas are proved. If h is a monotone function, we have the following corollary.
Corollary 2
Let h be a monotone increasing (decreasing) function. Then, the random variables \(h\left( X\right) \) and \(h\left( Y\right) \) have negative covariance.
Proof
The random variable Y from Proposition 1 is equal in distribution to \(Y{\mathop {=}\limits ^{d}}C-X\), where C is a constant which specialises depending on whether \(\sigma \) is a full ranking or an exhaustive partial ranking; see the proof of Proposition 1 in the next section for the specific form of the constant for each case. By Chebyshev’s integral inequality (Fink and Jodeit 1984), the covariance between a monotone increasing (decreasing) and a monotone decreasing (increasing) functions is negative. \(\square \)
The next theorem presents the antithetic empirical feature embedding and corresponding antithetic kernel estimator. Indeed, if we take the inner product between two embeddings, this yields the kernel antithetic estimator which is a function of a pair of partial rankings subsets. In this case, the h function from above is the kernel evaluated in each pair, and this is an example of a U-statistic (Serfling 1980, Chapter 5).
Theorem 5
Let \(R_i\subseteq S_n\) be a partial ranking, \(S_n\) denotes the space of permutations of \(n\in \mathbb {N}\), \((\sigma _m^{(i)},A_{R_i}({\sigma _m^{(i)}}))_{m=1}^{M_i}\) are antithetic pairs of i.i.d. samples from the region \(R_i\). The kernel antithetic Monte Carlo mean embedding
is a unbiased estimator of the embedding that corresponds to the marginalised kernel. The corresponding antithetic kernel estimator is
using M antithetic pairs of samples \((\sigma ^{(i)}_m, A_{R_i}(\sigma ^{(i)}_m))_{m=1}^{M}\) from region \(R_i\) and N antithetic pairs of samples
\((\sigma ^{(j)}_n, A_{R_j}(\sigma ^{(j)}_n))_{n=1}^{N}\), from \(R_j\).
Proof
Since the antithetic kernel embedding is a convex combination of the Monte Carlo kernel embedding, unbiasedness follows. \(\square \)
In the next section, we present the main result about the kernel estimator from Eq. (10), namely, that it has lower asymptotic variance than the Monte Carlo kernel estimator from Eq. 7 if we use the Mallows kernel.
4.1 Variance of the antithetic kernel estimator
We now establish some basic theoretical properties of antithetic samples in the context of marginalised kernel estimation. In order to do so, we require a series of lemmas to derive the main result in Theorem 6 that guarantees that the antithetic kernel estimator has lower asymptotic variance than the Monte Carlo kernel estimator for the marginalised Mallows kernel.
The following result shows that antithetic permutations may be used to achieve coupled samples which are marginally distributed uniformly on the subset of \(S_n\) corresponding to a top-k partial ranking.
Lemma 2
If \(R \subseteq S_n\) is a top-k partial ranking, then if \(\sigma \sim \text {Unif}(R)\), then \(A_{R}(\sigma ) \sim \text {Unif}(R)\).
See “Appendix B” for the proof. Lemma 2 establishes a base requirement of an antithetic sample—namely, that it has the correct marginal distribution. In the context of antithetic sampling in Euclidean spaces, this property is often trivial to establish, but the discrete geometry of \(S_n\) makes this property less obvious. Indeed, we next demonstrate that the condition of exhaustiveness of the partial ranking in Lemma 2 is necessary.
Example 1
Let \(n=3\), and consider the partial ranking \(2 \succ 1\). Note that this is not an exhaustive partial ranking, as the element 3 does not feature in the preference information. There are three full rankings consistent with this partial ranking, namely \(3 \succ 2 \succ 1\), \(2 \succ 3 \succ 1\), and \(2 \succ 1 \succ 3\). Encoding these full rankings as permutations, as described in the correspondence outlined in Sect. 2, we obtain three permutations, which we, respectively, denote by \(\sigma _A, \sigma _B, \sigma _C \in S_3\). Specifically, we have
Under the right-invariant Kendall distance, we obtain pairwise distances given by
Thus, the marginal distribution of an antithetic sample for the partial ranking \(2 \succ 1\) places no mass on \(\sigma _B\), and half of its mass on each of \(\sigma _A\) and \(\sigma _C\), and is therefore not uniform over R.
We further show that the condition of right invariance of the metric d is necessary in the next example.
Example 2
Let \(n=3\), and suppose d is a distance on \(S_3\) such that, with the notation introduced in Example 1, we have
Note that d is not right invariant, since
where \(\nu \in S_3\) is given by \(\nu (1) = 1, \nu (2) = 3, \nu (3) =2\). Then, note that an antithetic sample for the kernel associated with this distance and the partial ranking \(1 \succ 2\) is equal to \(\sigma _B\) with probability 2 / 3 and the other two full rankings with probability 1 / 6 each and therefore does not have a uniform distribution.
Examples 1 and 2 serve to illustrate the complexity of antithetic sampling constructions in discrete spaces. Finally, we remark that an alternative phrasing of Lemma 2 is that the pushforward of the distribution \(\text {Unif}(R)\) through the function \(A_R\) is again \(\text {Unif}(R)\). Whilst it may be possible to design distributions such that \(p(\cdot |R)\) has this property for each top-k ranking \(R \subseteq S_n\), many commonly used non-uniform distributions over permutations, such as Mallows models, do not satisfy this property.
We now begin direct calculation with antithetic permutations and partial rankings. We primarily focus on the case of top-k rankings, as calculation turns out to be particularly tractable in this case and also due to the fact that top-k rankings feature in many applications of interest. The following two lemmas state some useful relationships between the distance between two permutations \((\sigma ,\nu )\) and the corresponding pair \((A_{R}({\sigma }),\nu )\) in both the unconstrained and constrained cases which correspond to not having any partial ranking information and having partial ranking information, respectively.
Lemma 3
Let \(\sigma , \nu \in S_n\). Then, \(d_{\tau }(\sigma , \nu ) = \)\(\left( {\begin{array}{c}n\\ 2\end{array}}\right) - d_{\tau }(A_{S_n}(\sigma ), \nu )\).
Proof
This is immediate from the interpretation of the Kendall distance as the number of discordant pairs between two permutations; a distinct pair \(i,j \in [n]\) is discordant for \(\sigma , \nu \) iff they are concordant for \(A_{S_n}(\sigma ), \nu \). \(\square \)
In fact, Lemma 3 generalises in the following manner.
Lemma 4
Let R be a top-k ranking \(a_1 \succ \cdots \succ a_l \succ [n] \setminus \{a_1, \ldots , a_l\}\), and let \(\sigma , \nu \in R\). Then \(d_{\tau }(\sigma , \nu ) = \left( {\begin{array}{c}n-l\\ 2\end{array}}\right) - d_{\tau }(A_{R}(\sigma ), \nu )\).
See “Appendix B” for the proof. Next, we show that it is possible to obtain a unique closest element in a given partial ranking set R, denoted by \(\varPi _R(\nu )\), with respect to any given permutation \(\nu \in S_n,\nu \notin R\). This is based on the usual generalisation of a distance between a set and a point (Dudley 2002). We then use such closest element in Lemmas 6 and 7 to obtain useful decompositions of distances identities. Finally, in Lemma 8 we verify that the closest element is also distributed uniformly on a subset of the original set R.
Lemma 5
Let \(R \subseteq S_n\) be a top-k partial ranking, let \(\nu \in S_n\) be arbitrary. There is a unique closest element in R to \(\nu \). In other words, \(\arg \min _{\sigma \in R}d_{\tau }(\sigma , \nu )\) is a set of size 1.
See “Appendix B” for the proof.
Definition 7
Let \(R \subseteq S_n\) be a top-k partial ranking. Let \(\varPi _R : S_n \rightarrow R\) be the map that takes a permutation to the corresponding Kendall-closest permutation in R; by Lemma 5, this is well defined.
Lemma 6
Let \(\sigma \in R\), and \(\nu \in S_n\). We have the following decomposition of the distance \(d(\sigma , \nu )\)
See “Appendix B” for the proof.
Lemma 7
Let \(\sigma \in R\), and let \(\nu \in R^\prime \). We have the following relationship between \(d_{\tau }(A_{R}(\sigma ), \nu )\) and \(d_{\tau }(\sigma , \nu )\)
See “Appendix B” for the proof.
Lemma 8
Let \(R, R^\prime \subseteq S_n\) be top-k rankings, in preference notation given by
If \(\nu \sim \text {Unif}(R^\prime )\), then \(\varPi _R(\nu )\) is a full ranking with distribution \(\text {Unif}(R^{\prime \prime })\), where \(R^{\prime \prime } \subseteq R\) is the partial ranking given by
where \(\{b_{i_1},\ldots ,b_{i_q}\} = \{b_1,\ldots ,b_m\} \setminus \{a_1,\ldots , a_l\}\), and \(i_{j} < i_{j+1}\) for all \(j=1,\ldots ,q-1\).
See “Appendix B” for the proof.
Having introduced the antithetic operator for a top-k partial ranking R, \(A_R : R \rightarrow R\) and the projection map \(\varPi _R : S_n \rightarrow R\), we next study how these operations interact with one another.
Lemma 9
Let \(R^{\prime \prime } \subseteq R \subseteq S_n\) be top-k partial rankings. Then for \(\sigma \in R\), we have
See “Appendix B” for the proof.
Finally, the last lemma states the most general identity for a distance, which involves the antithetic operator, the closest element map given a partial rankings set R and a subset of it, denoted by \(R''\).
Lemma 10
Let \(R^{\prime \prime } \subseteq R \subseteq S_n\) be top-k partial rankings, given in preference notation by
Let \(\alpha \) be the number of unranked elements under R, and let \(\beta \) be the additional number of elements ranked under \(R^{\prime \prime }\) relative to R. Then for \(\sigma \in R\), we have
See “Appendix B” for the proof.
Proof of Proposition 1
Case\(\sigma _0\in S_n\) be the fixed permutation, then
This holds true since
\(d_{\tau }(A_{R}({\sigma }),\sigma _0)={n \atopwithdelims ()2}-d_{\tau }(\sigma ,\sigma _0), \forall \sigma \in S_n\), \(\forall n \in \mathbb {N}\) by Lemma 3.
Case\(\mathbf {\emptyset \subset R}\): Let \(\sigma _0\in R\), we have that
\(d_{\tau }(A_{R}({\sigma }),\sigma _0)={n-k\atopwithdelims ()2}\)\(-d_{\tau }(\sigma ,\sigma _0)\)\(\forall \sigma _0\in R\) by Lemma 4. \(\square \)
In general, if \(\sigma _0\notin R\), by Lemma 7, \(d_{\tau }(A_{R}({\sigma }),\sigma _0)=\)
\(d_{\tau }(\sigma , \sigma _0) + \left( {\begin{array}{c}n-k\\ 2\end{array}}\right) - 2d_{\tau }(\sigma , \varPi _{R_i}(\sigma _0))\).
After proving all the relevant Lemmas, we now present our main result regarding antithetic samples, namely, that this scheme provides negatively correlated pairs of samples.
Theorem 6
Consider the antithetic kernel estimator for the Mallows kernel evaluated on a pair of partial rankings \(R_i, R_j\) using M antithetic pairs of samples \((\sigma ^{(i)}_m, A_{R_i}(\sigma ^{(i)}_m))_{m=1}^{M}\) from region \(R_i\) and N antithetic pairs of samples \((\sigma ^{(j)}_n, A_{R_j}(\sigma ^{(j)}_n))_{n=1}^{N}\), from \(R_j\). The asymptotic variance of this estimator is lower than the kernel estimator using 2M (respectively, 2N) i.i.d. samples from \(R_i\) (respectively, \(R_j\)).
Proof
It has been shown previously that the antithetic kernel estimator is unbiased (in the off-diagonal case), so showing that it has lower MSE in the antithetic case which is equivalent to showing that its second moment is smaller in the antithetic case than in the i.i.d. case. The second moment is given by
We identify three types of terms in the above sum: (i) those where \(n \not = n^\prime \) and \(m \not = m^\prime \); (ii) those where \(n=n^\prime \) but \(m\not =m^\prime \), or \(m=m^\prime \) but \(n\not =n^\prime \); (iii) those where \(n=n^\prime \) and \(m=m^\prime \).
We remark that in case (i), the 16 terms that appear in the summand all have the same distribution in the antithetic and i.i.d. case, so terms of the form (i) contribute no difference between antithetic and i.i.d.. There are \(\mathcal {O}(N^2 M + M^2 N)\) terms of the form (ii) and \(\mathcal {O}(NM)\) terms of the form (iii). We thus refer to terms of the form (ii) as cubic terms and terms of the form (iii) as quadratic terms. We observe that due to the proportion of cubic terms to quadratic terms diverging as \(N,M \rightarrow \infty \), it is sufficient to prove that each cubic term is less in the antithetic case than the i.i.d. case to establish the claim of lower MSE.
Thus, we focus on cubic terms. Let us consider a term with \(n=n^\prime \) and \(m\not =m^\prime \). The term has the form
Of the sixteen terms appearing in the expectation above, there are only two distinct distributions they may have. The two types of terms are given below:
and
Terms of the form in Eq. (12) have the same distribution in the antithetic and i.i.d. cases, so we can ignore these. However, terms of the form in Eq. (13) have differing distributions in these two cases, so we focus in on these. We deal specifically with the case where \(K_{\lambda }(\sigma , \nu ) = \exp (-\lambda d_{\tau }(\sigma , \nu ))\), so we may rewrite the expression in Eq. (13) as
We now decompose the distances \(d_{\tau }(\sigma _n, \nu _m)\), \(d_{\tau }(\widetilde{\sigma }_n, \nu _{m^\prime })\) using the series of lemmas introduced before. First, we use Lemma 6 to write
We give a small example illustrating some of the variables at play in this decomposition in Fig. 3.
An example of the variables appearing in the decomposition in Eq. (15)
Now, writing \(R_3 \subseteq R_1\) for the partial ranking described by Lemma 8, we have that \(\varPi _{R_1}(\nu _m), \varPi _{R_1}(\nu _{m^\prime }) \overset{\mathrm {i.i.d.}}{\sim } \mathrm {Unif}(R_3)\). Therefore, the distances in Eq. (15) may be decomposed further
We now consider each term and argue as to whether the distribution is different in the antithetic and i.i.d. cases, recalling that in the i.i.d. case, \(\widetilde{\sigma }_n\) is drawn from \(R_1\) independently from \(\sigma _n\), whilst in the antithetic case, \(\widetilde{\sigma }_n = A_{R_1}(\sigma _n)\).
-
Each of the terms \(d_{\tau }(\varPi _{R_1}(\nu _{m}), \nu _{m})\) and
\(d_{\tau }(\varPi _{R_1}(\nu _{m^\prime }), \nu _{m^\prime })\) has the same distribution under the i.i.d. case and antithetic case. Further, in both cases, \(d_{\tau }(\varPi _{R_1}(\nu _{m}), \nu _{m})\) is independent of \(\varPi _{R_1}(\nu _m)\), and \(d_{\tau }(\varPi _{R_1}(\nu _{m^\prime }), \nu _{m^\prime })\) is independent of \(\varPi _{R_1}(\nu _{m^\prime })\), so these two terms are independent of all others appearing in the sum in both cases.
-
Each of the terms \(d_{\tau }(\varPi _{R_3}(\sigma _n), \varPi _{R_1}(\nu _m))\) and
\(d_{\tau }(\varPi _{R_3}(\widetilde{\sigma }_n), \varPi _{R_1}(\nu _{m^\prime }))\) has the same distribution under the i.i.d. case and the antithetic case and is independent of all other terms in both cases.
-
We deal with the terms \(d_{\tau }(\sigma _n, \varPi _{R_3}(\sigma _n))\) and
\(d_{\tau }(\widetilde{\sigma }_n, \varPi _{R_3}(\widetilde{\sigma }_n))\) using Lemma 10. More specifically, under the i.i.d. case, these two distances are clearly i.i.d.. However, under the antithetic case, the lemma tells us that the sum of these two distances is equal to the mean under the distribution of the i.i.d. case almost surely. Thus, in the antithetic case, this random variable has the same mean as in the i.i.d. case, but is more concentrated (strictly so iff \(d(\sigma _n, \varPi _{R_3}(\sigma _n))\) is not a constant almost surely, which is the case iff \(R_1 \not = R_3\)).
Thus, \(d_{\tau }(\sigma _n, \nu _m) + d_{\tau }(\widetilde{\sigma _n}, \nu _{m^\prime })\) has the same mean under the i.i.d. and antithetic cases, but is strictly more concentrated when \(R_1 \not = R_3\) This holds true iff the partial rankings \(R_1\) and \(R_2\) do not concern exactly the same set of objects. Thus, by a conditional version of Jensen’s inequality, since \(\exp (-\lambda x )\) is strictly convex as a function of x, we obtain the variance result. \(\square \)
4.2 The antithetic kernel estimator and kernel herding
In this section, having established the variance-reduction properties of antithetic samples in the context of Monte Carlo kernel estimation, we now explore connections to kernel herding (Chen et al. 2010). Kernel herding is a deterministic approach to numerical integration, in which quadrature points are selected according to a distance-minimisation algorithm taking place in a particular Hilbert space.
More precisely, given an integration problem of the form \(\mathbb {E}_{X \sim \mu }[f(X)]\), for some domain \(\mathcal {X}\), a function \(f:\mathcal {X} \rightarrow \mathbb {R}\) and probability measure \(\mu \in \mathscr {P}(\mathcal {X})\), kernel herding proceeds by first selecting a kernel \(K : \mathcal {X}^2 \rightarrow \mathbb {R}\). Successively, the reproducing kernel Hilbert space is chosen \(\mathcal {H}_K = \overline{\mathrm {span}\{K(x, \cdot ) | x \in \mathcal {X}\}}\) with inner product defined as the unique continuous linear extension of \(\langle K(x, \cdot ), K(y, \cdot ) \rangle _{\mathcal {H}_K} = K(x, y)\) for all \(x,y \in \mathcal {X}\), and with corresponding embedding \(\phi _K : \mathcal {X} \rightarrow \mathcal {H}_K\) given by \(\phi _K(x) = K(x, \cdot )\) for all \(x \in \mathcal {X}\). An initial quadrature point \(x_1 \in \mathcal {X}\) is then specified, and then, additional quadrature points are selected iteratively according to the following rule: given m quadrature points \(x_{1:m}\), the next quadrature point \(x_{m+1}\) is selected by
Our main result in this section makes clear the connection between kernel herding and our antithetic construction.
Theorem 7
The antithetic variate construction of Theorem 5 is equivalent to the optimal solution for the first two steps of a kernel herding procedure in the space of permutations.
Proof
Let R be a partial ranking of n elements. We calculate the sequence of herding samples from the uniform distribution \(p(\cdot | R)\) over full rankings consistent with R associated with the exponential semimetric kernel \(K_{\text {exp}}(\sigma , \sigma ^\prime ) = \exp (-\lambda d(\sigma , \sigma ^\prime ))\), for a metric d of negative definite type. Following Chen et al. (2010), we note that the herding samples from \(p(\cdot | R)\) associated with the kernel K, with RKHS embedding \(\phi : S_n \rightarrow \mathcal {H}\), are defined iteratively by
where \(\mu _p\) is the RKHS mean embedding of the distribution p. Since p is uniform over its support, any ranking \(\sigma \) in the support of \(p(\cdot | R)\) is a valid choice as the first sample in a herding sequence. Given such an initial sample, we then calculate the second herding sample, by considering the herding objective as follows
which, as a function of \(\sigma _2\), is equal to \(2K_{\text {exp}}(\sigma _1, \sigma _2) = 2\exp (-\lambda d(\sigma _1, \sigma _2))\), up to an additive constant. Thus, selecting \(\sigma _2\) to minimise the herding objective is equivalent to maximising \(d(\sigma _1, \sigma _2)\), which is exactly the definition of the antithetic sample to \(\sigma _1\). \(\square \)
After this result, one would like to do a herding procedure for more than two steps. However, the solution is not the same as picking k herding samples simultaneously. Specifically, the following counterexample, illustrated in Fig. 4, clearly shows why. The left plot shows the result of solving the herding objective for 2 samples—the result is an antithetic pair of samples for the region R. If a third sample is selected greedily, with these first two samples fixed, it will yield a different result than if the herding objective is solved for 3 samples simultaneously, as illustrated in the right of the figure.
Remark 3
Theorem 7 says that if we first pick a point uniformly at random from R, then put it into the herding objective and then select the second deterministically to minimise the herding objective and this is equivalent to the antithetic variate construction of Definition 6. Alternatively, we could pick the second point uniformly at random from R, independently from the first point. This second scheme will produce a higher value of the herding objective on average.
After the two estimators for kernel matrices have been constructed, we use them in some experiments to assess their performance in the next section.
5 Experiments

In this section, we use the Monte Carlo and antithetic kernel estimators for a variety of machine learning unsupervised and supervised learning tasks: a nonparametric hypothesis test, an agglomerative clustering algorithm and a Gaussian process classifier.
Definition 6 states the antithetic permutation construction with respect to a given permutation for Kendall’s distance. In order to consider partial rankings data, we should respect the observed preferences when obtaining the antithetic variate. Algorithm 1 describes how to sample an antithetic permutation and simultaneously respect the constraints imposed by the observed partial ranking. Namely, the antithetic permutation has the observed preferences fixed in the same locations as the original permutation and only reverses the unobserved locations. This corresponds to maximising the Kendall distance between the permutation pair whilst respecting the constraints and ensures that both permutations have the right marginals as stated in Lemmas 1 and 2.
5.1 Data sets
Synthetic data set The synthetic data set for the nonparametric hypothesis test experiment, where the null hypothesis is \(H_0:P=Q\) and the alternative is \(H_1:P\ne Q\), is the following: the data set from the P distribution is a mixture of Mallows distributions (Diaconis 1988) with the Kendall and Hamming distances. The central permutations are given by the identity permutation and the reverse of the identity, respectively, with lengthscale equal to one. The data set from the Q distribution is a sample from the uniform distribution over \(S_n\), where \(n = 6\).
Sushi data set This data set contains rankings about sushi preferences given by 5000 users (Kamishima et al. 2009). The users ranked 10 types of sushi, and the labels correspond to the user’s region This data set is used for the Gaussian and ten for the agglomerative clustering task.
5.2 Agglomerative clustering
In this experiment, we used both the full and a censored version of the sushi data set from Sect. 5.1. We used various distances for permutations to compute the estimators for the semimetric matrix between pairs of partial rankings subsets. In order to compute our estimators, we censored the data set by storing the \(topk=4\) partial rankings per user. The Monte Carlo and antithetic kernel estimators were used to obtain negative-type semimetric matrices using the relationship from Equation (2) in the following way:
These matrices were then used as an input to the average linkage agglomerative clustering algorithm (Duda and Hart 1973). The tree purity measure is reported, and it provides way to asses the tree produced by the agglomerative clustering algorithm. It can be computed in the following way: when a dendrogram and all correct labels are given, pick uniformly at random two leaves which have the same label c and find the smallest subtree containing the two leaves. The dendrogram purity is the expected value of \(\frac{\#\text {leaves with label c in subtree}}{\#\text {leaves in the subtree}}\) per class. If all leaves in the class are contained in a pure subtree, the dendrogram purity is one. Hence, values close to one correspond to high-quality trees.
In Table 1, the true and estimated purities using the full rankings and the partial rankings data sets are reported. We assumed that the true labels are given by the user’s region, and there are ten different possible regions. The true purity corresponds to an agglomerative clustering algorithm using the Gram matrix obtained from the full rankings. We can compute the Gram matrix for the full rankings because we have access to all of the users’ rankings over the ten different types of sushi. The antithetic Monte Carlo estimator outperforms the vanilla Monte Carlo estimator in terms of average purity since it is closer to the true purity. It also has a lower standard deviation when estimating the marginalised Mallows kernel.
5.3 Nonparametric hypothesis test with MMD
Let P and Q be probability distributions over \(S_n\), the null hypothesis is \(H_0: P = Q\) versus \(H_1:P \ne Q\) using samples \(\sigma _1,\ldots ,\sigma _{n}{\mathop {\sim }\limits ^{\text {i.i.d.}}} P\) and \(\sigma '_1,\ldots ,\sigma '_{m}{\mathop {\sim }\limits ^{\text {i.i.d.}}} Q\). We can estimate a pseudometric between P and Q and reject \(H_0\) if the observed value of the statistic is large. The following is an unbiased estimator of the \(MMD^2\) (Gretton et al. 2012)
This statistic depends on the chosen kernel as can be seen in Eq. (18). If the kernel is characteristic (Sriperumbudur et al. 2011), then the \(MMD^2\) is a proper metric over probability distributions. Analogously, we can compute an MMD squared estimator for partial rankings sets, such that \(R_1,\ldots ,R_{n}{\mathop {\sim }\limits ^{\text {i.i.d.}}} P\) and \(R'_1,\ldots ,R'_{m}{\mathop {\sim }\limits ^{\text {i.i.d.}}} Q\), in the following way
We used the synthetic data sets for P and Q described in Sect. 5.1 to asses the performance of the Monte Carlo and antithetic kernel estimators in a nonparametric hypothesis test. The data sets consist of rankings over \(n=10\) objects, and we censored them to obtain top\(-k\) partial rankings with \(k=3\). We then computed the MMD squared statistic for the samples using the samples from the two populations. Since the non-asymptotic distribution of the statistic from Eq. (19) is not known, we performed a permutation test (Alba Fernández et al. 2007) in order to estimate consistently the null distribution and compute the p value. We did this repeatedly as we varied the number of observations for a fixed number of Monte Carlo samples to see the effect of the sample size in the p value computations. Specifically, Fig. 5 and Table 2 show how the p value computed with the antithetic kernel estimator has lower variance as we vary the number of observations in our data set. Both p values converge to zero since the samples from both populations come from different distributions. In Table 2, we report the standard deviations of the estimated p values. The p value obtained with the antithetic kernel estimator has lower variance across all sample sizes.
5.4 Gaussian process classifier
In this experiment, two different kernels were used to compute the estimators for the Gram matrix between different pairs of partial rankings subsets. The matrix was then provided as the input to a Gaussian process classifier (Neal 1998). The Python library GPy (2012) was extended with custom kernel classes for partial rankings which compute both the Monte Carlo and antithetic kernel estimators for partial rankings subsets. Previously, it was only possible to do pointwise evaluations of kernels, but our implementation allows to compute the kernels over pairs of partial ranking subsets by storing the sets in a tensor first.
We used the sushi data set from Sect. 5.1 with the labels binarised in East Japan or West Japan regions. We selected a random subset of the observations of size 100 and used 80%, for the training set and 20% for the test set. In the Mallows kernel case, we used the median distance heuristic (Takeuchi et al. 2006; Schölkopf and Smola 2002) with the Kendall distance to compute the bandwidth parameter and a scale parameter of 9.5. We performed a grid search over different values of the scale parameter and picked the one that had the largest classification accuracy for the test set.
In Table 3, the results of running the Gaussian process classifier are reported using the marginalised Mallows kernel, the marginalised Gaussian kernel and the marginalised Kendall kernel as well as the corresponding estimators. Since the Mallows kernel is based on the Kendall distance, it is a kernel specifically tailored for permutations and it is the best in terms of predictive performance. In contrast, the Gaussian kernel is a kernel that is suitable for Euclidean spaces and it does not take into account the data type, and it still exhibits good predictive performance. The Kendall kernel does take into account the data type; however, it performs the worst. The full model corresponds to using the Gram matrix computed with the full rankings, and MC and antithetic refer to the Gram matrix obtained with the Monte Carlo and antithetic kernel estimators. We observe that the test and train loglikelihoods obtained with the antithetic kernel estimator have lower variance as expected.
6 Conclusion
We addressed the problem of extending kernels to partial rankings by introducing a novel Monte Carlo kernel estimator and explored variance-reduction strategies via an antithetic variates construction. Our schemes lead to a computationally tractable alternative to previous approaches for partial rankings data. The Monte Carlo scheme can be used to obtain an estimator of the marginalised kernel with any of the kernels reviewed herein. The antithetic construction provides an improved version of the kernel estimator for the marginalised Mallows kernel. Our contribution is noteworthy because the computation of most of the marginalised kernels grows super-exponentially with respect to the number of elements in the collection; hence, it quickly becomes intractable for relatively small values of the number of ranked items n. An exception is the fast approach for computing the convolution kernel proposed by Jiao and Vert (2015), which is only valid for Kendall kernel. Mania et al. (2016) have showed that the Kendall kernel is not characteristic using non-commutative Fourier analysis to show that it has a degenerate spectrum. For this reason, using other kernels for permutations might be desirable depending on the task at hand.
One possible direction for future work includes the use of explicit feature representations for traditional random features schemes to further reduce the computational cost of the Gram matrix. Another possible application is to use our method with pairwise preference data where users are not necessarily consistent about their preferences. In this type of data, we could still extract a partial ranking from a given user, then sample from the space of the corresponding full rankings consistent with this observed partial ranking and obtain our Monte Carlo kernel estimator. This would benefit from our framework because having a partial ranking is in general more informative that having pairwise comparisons or star ratings.
Another natural direction for future work is to develop variance-reduction sampling techniques for a wider variety of kernels over permutations, and to the extent the theoretical analysis of these constructions to discrete graphs more generally.
References
Aronszajn, N.: Theory of reproducing kernels. Trans. Am. Math. Soc. 68(3), 337–404 (1950)
Berg, C., Christensen, J.P.R., Ressel, P.: Harmonic Analysis on Semigroups. Springer, New York (1984)
Berlinet, A., Thomas-Agnan, C.: Reproducing Hilbert Spaces for Probability and Statistics. Kluwer Academic Publishers, Dordrecht (2004)
Boser, B.E., Guyon, I.M., Vapnik, V.N.: A training algorithm for optimal margin classifiers. In: ACM workshop on Computational Learning Theory (1992)
Bradley, R.A., Terry, M.E.: Rank analysis of incomplete block designs. Biometrika 39, 324–345 (1952)
Busse, L.M., Orbanz, P., Buhmann, J.M.: Cluster analysis of heterogeneous rank data. In: International Conference on Machine Learning (2007)
Caron, F., Teh, Y.W., Murphy, T.B.: Bayesian nonparametric Plackett–Luce models for the analysis of preferences for college degree programmes. Ann Appl Stat 8, 1145–1181 (2014)
Chen, Y., Fan, J., Ma, C., Wang, K.: Spectral method and regularized MLE are both optimal for top-k ranking (2017). arXiv:1707.09971
Chen, Y., Welling, M., Smola, A.: Super-Samples from Kernel Herding. In: UAI (2010)
Chierichetti, F., Dasgupta, A., Haddadan, S., Kumar, R., Lattanzi, S.: Mallows models for top-k lists. In: Advances in Neural Information Processing Systems (2018)
Cortes, C., Vapnik, V.N.: Support-vector networks. J. Mach. Learn. 20, 273–297 (1995)
Deza, M.M., Deza, E.: Encyclopedia of Distances. Springer, Berlin, Heidelberg (2009)
Diaconis, P.: Group Representations in Probability and Statistics. Institute of Mathematical Statistics lecture notes (1988)
Duda, R.O., Hart, P.E.: Pattern Classification and Scene Analysis. Wiley, New York (1973)
Dudley, R.: Real Analysis and Probability. Cambridge University Press, Cambridge (2002)
Fernández, V.A., Gamero, M.D.J., García, J.M.: A test for the two-sample problem based on empirical characteristic functions. Comput. Stat. Data Anal. 52, 3730–3748 (2007)
Fink, A.M., Jodeit, M.: On Chebyshev’s other inequality. Inequal. Stat. Probab. 5, 115–120 (1984)
Fligner, M.A., Verducci, J.S.: Distance based ranking models. J R Stat Soc Ser B 48, 359–369 (1986)
Fukumizu, K., Sriperumbudur, B., Gretton, A., Schölkopf, B.: Characteristic kernels on groups and semigroups. In: Neural Information processing systems (2009)
GPy. since 2012. GPy: A Gaussian process framework in python. http://github.com/SheffieldML/GPy
Gretton, A., Borgwardt, K.M., Rasch, M.J., Schölkopf, B., Smola, A.: A Kernel two sample test. J. Mach. Learn. Res. 13, 723–773 (2012)
Hammersley, J.M., Morton, K.W.: A new Monte Carlo technique: antithetic variates. Math. Proc. Camb. Philos. Soc. 52, 449–475 (1956)
Haussler, D.: Convolution Kernels on Discrete Structures (1999)
Irurozki, E., Calvo, B., Lozano, J.A.: PerMallows: an R package for Mallows and Generalized Mallows models. J. Stat. Softw. (2016a)
Irurozki, E., Calvo, B., Lozano, J.A.: Sampling and learning Mallows and Generalized Mallows models under the Cayley distance. Methodol. Comput. Appl. Probab. 20, 1–35 (2016b)
James, G.D.: The Representation Theory of the Symmetric Groups. Springer, Berlin (1978)
Jiao, Y., Vert, J.P.: The Kendall and Mallows Kernels for permutations. In: International conference for Machine learning (2015)
Kamishima, T., Akaho, S.: Efficient clustering for orders. In: Zighed, D.A., Tsumoto, S., Ras, Z.W., Hacid, H. (eds.) Mining Complex Data, pp. 261–279. Springer, Berlin (2009)
Knuth, D.: The Art of Computer Programming, vol. 3. Addison-Wesley, Boston (1998)
Kondor, R., Barbosa, M.: Ranking with kernels in Fourier space. In: Conference on Learning Theory (2010)
Kondor, R., Howard, A., Jebara, T.: Multi-object tracking with representations of the symmetric group. In: AISTATS (2007)
Lebanon, G., Mao, Y.: Non-parametric modeling of partially ranked data. J. Mach. Learn. Res. 9, 2401–2429 (2008)
Luce, R.D.: Individual Choice Behavior: A Theoretical Analysis. Wiley, New York (1959)
Mallows, C.L.: Non-null ranking models. Biometrika 44, 114–130 (1957)
Mania, H., Ramdas, A., Wainwright, M.J., Jordan, M.I., Recht, B.: On kernel methods for covariates that are rankings (2016)
Mukherjee, S.: Estimation in exponential families. Ann. Stat. 44, 853–875 (2016)
Neal, R.M.: 1998. Regression and Classification Using Gaussian Process Priors. Bayesian Statistics 6
Plackett, L.R.: The analysis of permutations. J. R. Stat. Soc. Ser. C (1974)
Rasmussen, C.E., Williams, C.K.I.: Gaussian Processes for Machine Learning. MIT Press, Cambridge (2006)
Ross, S.M.: Simulation Fourth Edition, Statistical Modeling and Decision Science. Academic, Cambridge (2006)
Schölkopf, B., Smola, A.: Learning with Kernels: Support Vector Machines, Regularisation, Optimisation and Beyond. MIT press, Cambridge (2002)
Schölkopf, B., Smola, A.J., Müller, K.R.: Kernel principal component analysis. In: Schölkopf, B., Burges, C.J.C., Smola, A.J. (eds.) Advances in Kernel Methods. MIT Press, Cambridge (1999)
Sejdinovic, D., Sriperumbudur, B., Gretton, A., Fukumizu, K.: Equivalence of distance-based and RKHS-based statistics in hypothesis testing. Ann. Stat. 41, 2263–2291 (2013)
Serfling, R.J.: Approximation Theorems of Mathematical Statistics. Wiley, New York (1980)
Shawer-Taylor, J., Cristianini, N.: Kernel Methods for Pattern Analysis. Cambridge University Press, Cambridge (2004)
Sriperumbudur, B.K., Fukumizu, K., Lanckriet, G.R.G.: Universality, characteristic Kernels and RKHS embedding of measures. J. Mach. Learn. Res. 12, 2389–2410 (2011)
Stanley, R.P.: Enumerative Combinatorics, vol. 1. Cambridge University Press, Cambridge (2000)
Takeuchi, I., Le, Q.V., Sears, T.D., Smola, A.: Nonparametric quantile estimation. J. Mach. Learn. Res. 7, 1231–1264 (2006)
Tsuda, K., Kin, T., Asai, K.: Marginalised kernels for biological sequences. Bioinformatics 18, S268–S275 (2002)
Vitelli, V., Sørensen, Ø., Crispino, M., Frigessi, A., Arjas, E.: Probabilistic preference learning with the mallows rank model. J. Mach. Learn. Res. 18, 158-1 (2017)
Wendland, H.: Scattered Data approximation. Cambridge University Press, Cambridge (2005)
Acknowledgements
We thank the anonymous reviewers for their valuable comments which have improved the quality of our manuscript and Ryan Adams, for insightful discussions. Maria Lomeli and Zoubin Ghahramani acknowledge support from the Alan Turing Institute (EPSRC Grant EP/N510129/1), EPSRC Grant EP/N014162/1, and donations from Google and Microsoft Research. Arthur Gretton thanks the Gatsby Charitable Foundation for financial support. Mark Rowland acknowledges support by EPSRC Grant EP/L016516/1 for the Cambridge Centre for Analysis.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Reproducing kernel Hilbert spaces
A reproducing kernel Hilbert space (RKHS) (Berlinet and Thomas-Agnan 2004) over a set \(\mathcal {X}\) is a Hilbert space \(\mathcal {H}\) consisting of functions on \(\mathcal {X}\) such that for each \(x\in \mathcal {X}\) there is a function \(k_x\in \mathcal {H}\) with the property
The function \(k_x(\cdot )=k(x,\cdot )\) is called the reproducing kernel of \(\mathcal {H}\) (Aronszajn 1950). The space \(\mathcal {H}\) is endowed with an inner product \(\langle \cdot {,}\cdot \rangle _{\mathcal {H}}\) and a norm can be defined based on it such that \(\Vert f\Vert _{\mathcal {H}}:=\sqrt{\langle \cdot {,}\cdot \rangle _{\mathcal {H}}}\). In order to be a Hilbert space, it needs to contain all limits of Cauchy sequences, i.e. it has to be complete. In the case of the symmetric group of degree n, \(\mathcal {X}=S_n\), the space is finite-dimensional which guarantees that it is complete. Finally, any symmetric and positive-definite function \(k_x:\mathcal {X}\times \mathcal {X}\rightarrow \mathbb {R}\) uniquely determines an RKHS. Alternatively, a function \(k:\mathcal {X}\times \mathcal {X}\rightarrow \mathbb {R}\) is called a kernel if there exists a Hilbert space \(\mathcal {H}\) and a map \(\phi :\mathcal {X}\rightarrow \mathcal {H}\) such that \(\forall x,y \in \mathcal {X}\), \(k(x,y)=\langle \phi (x),\phi (y) \rangle _{\mathcal {H}}\). The function \(\phi \) is usually referred to as the feature representation of x. Even though the RKHS induced by the kernel is unique, there can be more than one feature representations that define the same kernel.
Proofs
Lemma 1
Let \(R \subseteq S_n\) be a top-k partial ranking, let \(\sigma \in R\). Then, there exists a unique solution to the problem
Moreover, it can be calculated directly; if the preference partial ranking corresponding to R is given by \(a_1 \succ \cdots \succ a_k\), so that the full ranking \(\sigma \in R\) satisfies \(\sigma (1) = a_1,\ldots ,\sigma (k) = a_k\), then the unique distance-maximising permutation \(\sigma ^\prime \) is given by
In this case, we have \(d_{\tau }(\sigma , \sigma ^\prime ) = \left( {\begin{array}{c}n-k\\ 2\end{array}}\right) \).
Proof
We use the interpretation of Kendall’s tau distance as counting numbers of discordant pairs. From this perspective, it straightforwardly follows that all permutations in R can be at most distance \(\left( {\begin{array}{c}n-k\\ 2\end{array}}\right) \) from one another, since any pair of items involving one of the top-k items must necessarily be concordant for any two permutations in R. It also follows straightforwardly that there is a unique permutation in R for which this distance is realised, given when all pairs of items not in the top-k have the opposite ordering to that under \(\sigma \), from which the formula in the statement follows. \(\square \)
Lemma 2
If \(R \subseteq S_n\) is a top-k partial ranking, then if \(\sigma \sim \text {Unif}(R)\), then \(A_{R}(\sigma ) \sim \text {Unif}(R)\).
Proof
The proof is immediate from Lemma 1, since \(A_R\) is bijective on R. \(\square \)
Lemma 4
Let R be a top-k ranking \(a_1 \succ \cdots \succ a_l \succ [n] \setminus \{a_1, \ldots , a_l\}\), and let \(\sigma , \nu \in R\). Then \(d_{\tau }(\sigma , \nu ) = \left( {\begin{array}{c}n-l\\ 2\end{array}}\right) - d_{\tau }(A_{R}(\sigma ), \nu )\).
Proof
As for the proof of Lemma 3, we use the “discordant pairs” interpretation of the Kendall distance. Note that if a distinct pair \(\{ x, y \} \in [n]^{(2)}\) has at least one of \(x, y \in \{a_1,\ldots ,a_l\}\), then by virtue of the fact that \(\sigma , A_R(\sigma ), \nu \in R\), any pair of these permutations is concordant for x, y. Now observe that any distinct pair \(x,y \in [n] \setminus \{a_1, \ldots , a_l\}\) is discordant for \(\sigma , \nu \) iff it is concordant for \(A_R(\sigma ), \nu \), from the construction of \(A_R(\sigma )\) described in Lemma 1. The total number of such pairs is \(\left( {\begin{array}{c}n-l\\ 2\end{array}}\right) \), so we have \(d_{\tau }(\sigma , \nu ) + d_{\tau }(A_R(\sigma ), \nu ) = \left( {\begin{array}{c}n-l\\ 2\end{array}}\right) \), as required. \(\square \)
Lemma 5
Let \(R \subseteq S_n\) be a top-k partial ranking, let \(\nu \in S_n\) be arbitrary. There is a unique closest element in R to \(\nu \). In other words, \(\arg \min _{\sigma \in R}d_{\tau }(\sigma , \nu )\) is a set of size 1.
Proof
We use the interpretation of the Kendall distance as the number of discordant pairs between two permutations. Let R be the top-k partial ranking given by \(x_1 \succ \cdots \succ x_k \succ [n] \setminus \{x_1,\ldots ,x_k\}\), and let \(X = \{x_1,\ldots , x_k\}\). We decompose the Kendall distance between \(\sigma \in R\) and \(\nu \) as follows:
As \(\sigma \) varies in R, only some of these terms vary. In particular, it is only the third term that varies with \(\sigma \), and it is minimised at 0 by the permutation \(\sigma \) in R which is in accordance with \(\nu \) on the set \([n] \setminus X\). \(\square \)
Lemma 6
Let \(\sigma \in R\), and \(\nu \in S_n\). We have the following decomposition of the distance \(d(\sigma , \nu )\)
Proof
We compute directly with the discordant pairs definition of the Kendall distance. Again, let R be the partial ranking \(x_1 \succ \cdots \succ x_k\), and let \(X = \{x_1,\ldots , x_k\}\). We decompose the Kendall distance between \(\sigma \in R\) and \(\nu \) as before:
By the construction of \(\varPi _R(\nu )\) in the proof of Lemma 5, we have that
i.e. the first two terms of the decomposition in Equation (22). Similarly, we have
and so the result follows. \(\square \)
Lemma 7
Let \(\sigma \in R\), and let \(\nu \in R^\prime \). We have the following relationship between \(d_{\tau }(A_{R}(\sigma ), \nu )\) and \(d_{\tau }(\sigma , \nu )\)
Proof
We begin by observing that, by Lemma 6, we have
and
Now, from Lemma 4, we have that \(d(A_R(\sigma ), \varPi _R(\nu )) = \left( {\begin{array}{c}n-k\\ 2\end{array}}\right) - d(\sigma , \varPi _R(\nu ))\). Hence, the result follows. \(\square \)
Lemma 8
Let \(R, R^\prime \subseteq S_n\) be top-k rankings, in preference notation given by
If \(\nu \sim \text {Unif}(R^\prime )\), then \(\varPi _R(\nu )\) is a full ranking with distribution \(\text {Unif}(R^{\prime \prime })\), where \(R^{\prime \prime } \subseteq R\) is the partial ranking given by
where \(\{b_{i_1},\ldots ,b_{i_q}\} = \{b_1,\ldots ,b_m\} \setminus \{a_1,\ldots , a_l\}\), and \(i_{j} < i_{j+1}\) for all \(j=1,\ldots ,q-1\).
Proof
We first show that \(\varPi _R\) maps \(R^\prime \) into \(R^{\prime \prime }\). This is straightforward, as given \(\nu \in R^\prime \), we first observe that \(\varPi _R(\nu ) \in R\), and so the full ranking \(\varPi _R(\nu )\) is consistent with the partial ranking
Next, since \(\varPi _R(\nu )\) is concordant with \(\nu \) for all pairs outside the set \(\{a_1,\ldots , a_l\}\), \(\varPi _R(\nu )\) must be consistent with the partial ranking
Putting these two facts together shows that the full ranking \(\varPi _R(\nu )\) must be consistent with the partial ranking
Thus, given \(\nu \sim \text {Unif}(R^\prime )\), the distribution of \(\varPi _R(\nu )\) is supported on \(R^{\prime \prime }\). To show that it is uniform, we now argue that equally many rankings in \(R^\prime \) are mapped to each ranking in \(R^{\prime \prime }\). To see this, we observe that the pre-image of a ranking in \(R^{\prime \prime }\) is the set of all rankings in \(R^{\prime }\) which are concordant with it on all pairs in \([n] \setminus \{a_1,\ldots ,a_l, b_1,\ldots , b_m\}\). The number of such rankings is independent of the selected ranking in \(R^{\prime \prime }\), and so the statement of the lemma follows. \(\square \)
Lemma 9
Let \(R^{\prime \prime } \subseteq R \subseteq S_n\) be top-k partial rankings. Then for \(\sigma \in R\), we have
Proof
We begin by introducing preference-style notation for R and \(R^{\prime \prime }\). Let R be the top-k ranking given by \(a_1 \succ \cdots \succ a_l \succ [n] \setminus \{a_1,\ldots ,a_l\}\), and let \(R^{\prime \prime }\) be the partial ranking given by \(a_1 \succ \cdots \succ a_l \succ a_{l+1} \succ \cdots \succ a_m \succ [n] \setminus \{a_1,\ldots ,a_m\}\). Let \(\sigma \in R\), and let the elements of \([n] \setminus \{a_1,\ldots ,a_m\}\) be given by \(b_1,\ldots ,b_q\), with indices chosen such that \(\sigma \) corresponds to the full ranking
Then, the ranking \(A_{R^{\prime \prime }}(\varPi _{R^{\prime \prime }}(\sigma ))\) is given by
and a straightforward calculation shows that this is also the case for \(\varPi _{R^{\prime \prime }}(A_R(\sigma ))\), as required. \(\square \)
Lemma 10
Let \(R^{\prime \prime } \subseteq R \subseteq S_n\) be top-k partial rankings, given in preference notation by
Let \(\alpha \) be the number of unranked elements under R, and let \(\beta \) be the additional number of elements ranked under \(R^{\prime \prime }\) relative to R. Then for \(\sigma \in R\), we have
Proof
Again, we denote \(\{b_1, \ldots , b_q\} = [n] \setminus \{a_1,\ldots ,a_m\}\), with indices chosen such that \(\sigma \) corresponds to the full ranking \( a_1 \succ \cdots \succ a_m \succ b_1 \succ \cdots \succ b_q\). From earlier arguments, we have
Now observe that for \(a_i, a_j\) with \(l+1 \le i < j \le m\), this pair is discordant for the pair of rankings \(\sigma , \varPi _{R^{\prime \prime }}(\sigma )\) iff \(a_j \succ a_i\) under \(\sigma \) iff \(a_i \succ a_j\) w.r.t \(A_R(\sigma )\) iff \(a_i, a_j\) are concordant for the pair of rankings \(A_R(\sigma ), \varPi _{R^{\prime \prime }}(A_R(\sigma ))\). Hence, we have
By analogous reasoning, we have
Altogether, these statements yield the result of the lemma. \(\square \)
Expectation of the Kernel Monte Carlo estimator
Proof
For distinct \(i,j =1,\ldots , I\), let \(\left\{ \sigma _n^{(i)}\right\} _{n=1}^{N_i}\) be an independent and identically distributed (i.i.d.) sample from \(p(\sigma \mid R_i)\) and \(\left\{ \sigma _m^{(j)}\right\} _{m=1}^{N_j}\) be an i.i.d. sample from \(p(\sigma \mid R_j)\). Then,
By linearity of expectation, since the samples are identically distributed, the expectation in the summand above reduces to
as required. Hence, the kernel Monte Carlo estimator is unbiased for the off-diagonal elements of the kernel matrix. In the diagonal case the expectation is biased but consistent since,
\(\square \)
Variance of Kernel Monte Carlo estimator with i.i.d. samples
Proof
The variance of the Kernel Monte Carlo estimator with uniform weights is the following:
If we use the law of total variance, then
So the variance for the Monte Carlo kernel estimator is given by
\(\square \)
Factorial growth of the space of consistent full rankings for a given partial ranking
See Table 4.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lomelí, M., Rowland, M., Gretton, A. et al. Antithetic and Monte Carlo kernel estimators for partial rankings. Stat Comput 29, 1127–1147 (2019). https://doi.org/10.1007/s11222-019-09859-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11222-019-09859-z