The stochastic topic block model for the clustering of vertices in networks with textual edges

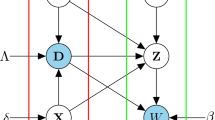
Abstract

Due to the significant increase of communications between individuals via social media (Facebook, Twitter, Linkedin) or electronic formats (email, web, e-publication) in the past two decades, network analysis has become an unavoidable discipline. Many random graph models have been proposed to extract information from networks based on person-to-person links only, without taking into account information on the contents. This paper introduces the stochastic topic block model, a probabilistic model for networks with textual edges. We address here the problem of discovering meaningful clusters of vertices that are coherent from both the network interactions and the text contents. A classification variational expectation-maximization algorithm is proposed to perform inference. Simulated datasets are considered in order to assess the proposed approach and to highlight its main features. Finally, we demonstrate the effectiveness of our methodology on two real-word datasets: a directed communication network and an undirected co-authorship network.

Appendix

1.1 Appendix 1: Optimization of R(Z)

The VEM update step for each distribution $R(Z_{ij}^{dn}), A_{ij}=1$, is given by

$$\begin{aligned} \begin{aligned} \log R(Z_{ij}^{dn})&= \mathrm {E}_{Z^{\backslash i,j,d,n},\theta }[\log p(W|A, Z, \beta ) \\&\quad + \log p(Z|A, Y, \theta )] + \mathrm {const}\\&= \sum _{k=1}^{K} Z_{ij}^{dnk}\sum _{v=1}^{V}W_{ij}^{dnv}\log \beta _{kv}\\&\quad + \sum _{q,r}^{Q}Y_{iq}Y_{jr}\sum _{k=1}^{K}Z_{ij}^{dnk}\mathrm {E}_{\theta _{qr}}[\log \theta _{qrk}] + \mathrm {const}\\&= \sum _{k=1}^{K}Z_{ij}^{dnk}\left( \sum _{v=1}^{V}W_{ij}^{dnv}\log \beta _{kv} \right. \\&\left. \quad +\sum _{q,r}^{Q}Y_{iq}Y_{jr}\left( \psi (\gamma _{qrk})-\psi \left( \sum _{k=1}^{K}\gamma _{qrk}\right) \right) \right) \\&\quad + \mathrm {const}, \end{aligned} \end{aligned}$$

(9)

where all terms that do not depend on $Z_{ij}^{dn}$ have been put into the constant term $\mathrm {const}$. Moreover, $\psi (\cdot )$ denotes the digamma function. The functional form of a multinomial distribution is then recognized in (9)

$$\begin{aligned} R(Z_{ij}^{dn})={\mathcal {M}}\left( Z_{ij}^{dn};1,\phi _{ij}^{dn}=\left( \phi _{ij}^{dn1},\dots , \phi _{ij}^{dnK}\right) \right) , \end{aligned}$$

where

$$\begin{aligned} \phi _{ij}^{dnk} \propto \left( \prod _{v=1}^{V} \beta _{kv}^{W_{ij}^{dnv}}\right) \prod _{q,r}^{Q}\exp \left( \psi (\gamma _{qrk}-\psi \left( \sum _{l=1}^{K}\gamma _{qrl}\right) \right) ^{Y_{iq}Y_{jr}}{.} \end{aligned}$$

$\phi _{ij}^{dnk}$ is the (approximate) posterior distribution of words $W_{ij}^{dn}$ being in topic k.

1.2 Appendix 2: Optimization of $R(\theta )$

The VEM update step for distribution $R(\theta )$ is given by

$$\begin{aligned} \begin{aligned} \log R(\theta )&= \mathrm {E}_{Z}[\log p(Z|A, Y, \theta )] + \mathrm {const}\\&= \sum _{i \ne j}^{M}A_{ij}\sum _{d=1}^{D_{ij}}\sum _{n=1}^{N_{ij}^{d}}\sum _{q,r}^{Q}Y_{iq}Y_{jr}\\&\quad \times \sum _{k=1}^{K}\mathrm {E}_{Z_{ij}^{dn}}\left[ Z_{ij}^{dnk}\right] \log \theta _{qrk}\\&\quad + \sum _{q,r}^{Q}\sum _{k=1}^{K}(\alpha _k - 1)\log \theta _{qrk} + \mathrm {const}\\&= \sum _{q,r}^{Q}\sum _{k=1}^{K}\left( \alpha _{k} + \sum _{i \ne j}^{M} A_{ij}Y_{iq}Y_{jr}\sum _{d=1}^{N_{ij}^{d}}\sum _{n=1}^{N_{ij}^{dn}}\phi _{ij}^{dnk}-1\right) \\&\qquad \log \theta _{qrk} + \mathrm {const}. \end{aligned} \end{aligned}$$

We recognize the functional form of a product of Dirichlet distributions

$$\begin{aligned} \begin{aligned} R(\theta )= \prod _{q,r}^{Q}\mathrm {Dir}(\theta _{qr};\gamma _{qr}=(\gamma _{qr1},\dots , \gamma _{qrK})), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \gamma _{qrk} = \alpha _{k} + \sum _{i \ne j}^{M} A_{ij}Y_{iq}Y_{jr}\sum _{d=1}^{N_{ij}^{d}}\sum _{n=1}^{N_{ij}^{dn}}\phi _{ij}^{dnk}. \end{aligned}$$

1.3 Appendix 3: Derivation of the lower bound $\tilde{{\mathcal {L}}}\left( R(\cdot ); Y, \beta \right)$

The lower bound $\tilde{{\mathcal {L}}}\left( R(\cdot ); Y, \beta \right)$ in (7) is given by

$$\begin{aligned}&\tilde{{\mathcal {L}}}\left( R(\cdot ); Y, \beta \right) \nonumber \\&\quad = \sum _{Z}\int _{\theta }R(Z,\theta ) \log \frac{p(W, Z, \theta |A, Y,\beta )}{R(Z,\theta )} \mathrm{d}\theta \nonumber \\&\quad = \mathrm {E}_{Z}[\log p(W|A, Z, \beta )] \nonumber \\&\qquad + \mathrm {E}_{Z, \theta }[\log p(Z|A, Y, \theta )] + \mathrm {E}_{\theta }[\log p(\theta )]\nonumber \\&\qquad - \mathrm {E}_{Z}[\log R(Z)]-\mathrm {E}_{\theta }[\log R(\theta )] \nonumber \\&\quad =\sum _{i \ne j}^{M}A_{ij}\sum _{d=1}^{D_{ij}}\sum _{n=1}^{N_{ij}^{dn}}\sum _{k=1}^{K}\phi _{ij}^{dnk}\sum _{v=1}^{V}W_{ij}^{dnv}\log \beta _{kv} \nonumber \\&\qquad + \sum _{i \ne j}^{M}A_{ij}\sum _{d=1}^{D_{ij}}\sum _{n=1}^{N_{ij}^{dn}} \sum _{q,r}^{Q}Y_{iq}Y_{jr}\nonumber \\&\qquad \times \sum _{k=1}^{K}\phi _{ij}^{dnk}\left( \psi (\gamma _{qrk})-\psi \left( \sum _{l=1}^{K}\gamma _{qrl}\right) \right) \\&\qquad + \sum _{q,r}^{Q}\left( \log \varGamma \left( \sum _{l=1}^{K}\alpha _{k}\right) - \sum _{l=1}^{K}\log \varGamma (\alpha _{l})\right. \nonumber \\&\qquad \left. +\sum _{k=1}^{K}(\alpha _{k}-1)\left( \psi (\gamma _{qrk})-\psi \left( \sum _{l=1}^{K}\gamma _{qrl}\right) \right) \right) \nonumber \\&\qquad - \sum _{i \ne j}^{M}A_{ij}\sum _{d=1}^{D_{ij}}\sum _{n=1}^{N_{ij}^{dn}}\sum _{k=1}^{K}\phi _{ij}^{dnk}\log \phi _{ij}^{dnk}\nonumber \\&\qquad - \sum _{q,r}^{Q}\left( \log \varGamma \left( \sum _{l=1}^{K}\gamma _{qrl}\right) - \sum _{l=1}^{K}\log \varGamma (\gamma _{qrl})\right. \nonumber \\&\qquad \left. +\sum _{k=1}^{K}(\gamma _{qrk}-1)\left( \psi (\gamma _{qrk})-\psi \left( \sum _{l=1}^{K}\gamma _{qrl}\right) \right) \right) .\nonumber \end{aligned}$$

(10)

1.4 Appendix 4: Optimization of $\beta$

In order to maximize the lower bound $\tilde{{\mathcal {L}}}\left( R(\cdot ); Y, \beta \right)$, we isolate the terms in (10) that depend on $\beta$ and add Lagrange multipliers to satisfy the constraints $\sum _{v=1}^{V}\beta _{kv}=1,\forall k$

$$\begin{aligned} \tilde{{\mathcal {L}}}_{\beta }= & {} \sum _{i \ne j}^{M}A_{ij}\sum _{d=1}^{D_{ij}}\sum _{n=1}^{N_{ij}^{dn}}\sum _{k=1}^{K}\phi _{ij}^{dnk}\sum _{v=1}^{V}W_{ij}^{dnv}\log \beta _{kv}\\&+ \sum _{k=1}^{K}\lambda _{k}\left( \sum _{v=1}^{V}\beta _{kv}-1\right) . \end{aligned}$$

Setting the derivative, with respect to $\beta _{kv}$, to zero, we find

$$\begin{aligned} \beta _{kv}\propto \sum _{i \ne j}^{M}A_{ij}\sum _{d=1}^{D_{ij}}\sum _{n=1}^{N_{ij}^{dn}}\phi _{ij}^{dnk}W_{ij}^{dnv}. \end{aligned}$$

1.5 Appendix 5: Optimization of $\rho$

Only the distribution $p(Y|\rho )$ in the complete data log-likelihood $\log p(A, Y|\rho , \pi )$ depends on the parameter vector $\rho$ of cluster proportions. Taking the log and adding a Lagrange multiplier to satisfy the constraint $\sum _{q=1}^{Q}\rho _{q}=1$, we have

$$\begin{aligned} \log p(Y|\rho ) = \sum _{i=1}^{M}\sum _{q=1}^{Q}Y_{iq}\log \rho _{q}. \end{aligned}$$

Taking the derivative with respect $\rho$ to zero, we find

$$\begin{aligned} \rho _{q} \propto \sum _{i=1}^{M}Y_{iq}. \end{aligned}$$

1.6 Appendix 6: Optimization of $\pi$

Only the distribution $p(A|Y, \pi )$ in the complete data log-likelihood $\log p(A, Y|\rho , \pi )$ depends on the parameter matrix $\pi$ of connection probabilities. Taking the log we have

$$\begin{aligned}&\log p(A|Y, \pi )\\&\quad = \sum _{i \ne j}^{M}\sum _{q,r}^{Q}Y_{iq}Y_{jr}\Big (A_{ij}\log \pi _{qr} +(1-A_{ij})\log (1-\pi _{qr})\Big ). \end{aligned}$$

Taking the derivative with respect to $\pi _{qr}$ to zero, we obtain

$$\begin{aligned} \pi _{qr} = \frac{ \sum _{i \ne j}^{M}\sum _{q,r}^{Q}Y_{iq}Y_{jr}A_{ij}}{ \sum _{i \ne j}^{M}\sum _{q,r}^{Q}Y_{iq}Y_{jr}}. \end{aligned}$$

1.7 Appendix 7: Model selection

Assuming that the prior distribution over the model parameters $(\rho , \pi , \beta )$ can be factorized, the integrated complete data log-likelihood $\log p(A, W, Y|K, Q)$ is given by

$$\begin{aligned} \begin{aligned}&\log p(A, W, Y|K, Q)\\&\quad = \log \int _{\rho ,\pi ,\beta } p(A, W, Y, \rho , \pi , \beta |K, Q) \mathrm{d}\rho \mathrm{d}\pi \mathrm{d}\theta \\&\quad = \log \int _{\rho ,\pi ,\beta } p(A, W, Y|\rho , \pi , \beta , K, Q)\\&\qquad \times p(\rho |Q)p(\pi |Q)p(\beta |K)\mathrm{d}\rho \mathrm{d}\pi \mathrm{d}\beta . \end{aligned} \end{aligned}$$

Note that the dependency on K and Q is made explicit here, in all expressions. In all other sections of the paper, we did not include these terms to keep the notations uncluttered. We find

$$\begin{aligned}&\log p(A, W, Y|K, Q)\nonumber \\&\quad = \log \int _{\rho , \pi , \beta }\left( \sum _{Z}\int _{\theta }p(A, W, Y, Z, \theta |\rho , \pi , \beta , K, Q)\mathrm{d}\theta \right) \nonumber \\&\qquad \times p(\rho |Q)p(\pi |Q)p(\beta |K)\mathrm{d}\rho \mathrm{d}\pi \mathrm{d}\beta \nonumber \\&\quad = \log \int _{\rho , \pi , \beta } \left( \sum _{Z}\int _{\theta }p(W, Z, \theta |A, Y, \beta , K, Q)p(A, Y|\rho , \pi , Q)\mathrm{d}\theta \right) \nonumber \\&\qquad \times p(\rho |Q)p(\pi |Q)p(\beta |K)\mathrm{d}\rho \mathrm{d}\pi \mathrm{d}\beta \nonumber \\&\quad = \log \int _{\rho , \pi , \beta }p(W|A, Y, \beta , K, Q) p(A|Y, \pi , Q)p(Y|\rho , Q)\\&\qquad \times p(\rho |Q)p(\pi |Q)p(\beta |K)\mathrm{d}\rho \mathrm{d}\pi \mathrm{d}\beta \nonumber \\&\quad = \log \int _{\beta }p(W|A, Y, \beta , K, Q)\nonumber \\&\qquad \times p(\beta |K) \mathrm{d}\beta + \log \int _{\pi } p(A|Y, \pi , Q)p(\pi |Q)\mathrm{d}\pi \nonumber \\&\qquad + \log \int _{\rho }p(Y|\rho , Q)p(\rho |Q)\mathrm{d}\rho .\nonumber \end{aligned}$$

(11)

Following the derivation of the ICL criterion, we apply a Laplace (BIC-like) approximation on the second term of Eq. (11). Moreover, considering a Jeffreys prior distribution for $\rho$ and using Stirling formula for large values of M, we obtain

$$\begin{aligned}&\log \int _{\pi } p(A|Y, \pi , Q)p(\pi |Q)\mathrm{d}\pi \\&\quad \approx \max _{\pi }\log p(A|Y, \pi , Q) - \frac{Q^2}{2}\log M(M-1), \end{aligned}$$

as well as

$$\begin{aligned}&\log \int _{\rho }p(Y|\rho , Q)p(\rho |Q)\mathrm{d}\rho \\&\quad \approx \max _{\rho } \log p(Y|\rho , Q) - \frac{Q-1}{2}\log M. \end{aligned}$$

For more details, we refer to Biernacki et al. (2000). Furthermore, we emphasize that adding these two approximations leads to the ICL criterion for the SBM model, as derived by Daudin et al. (2008)

$$\begin{aligned} \begin{aligned} ICL_{SBM}&= \max _{\pi }\log p(A|Y, \pi , Q)\\&\quad - \frac{Q^2}{2}\log M(M-1) + \max _{\rho } \log p(Y|\rho , Q)\\&\quad - \frac{Q-1}{2}\log M \\&= \max _{\rho , \pi } \log p(A,Y|\rho , \pi , Q)\\&\quad - \frac{Q^2}{2}\log M(M-1) - \frac{Q-1}{2}\log M. \end{aligned} \end{aligned}$$

In Daudin et al. (2008), $M(M-1)$ is replaced by $M(M-1)/2$ and $Q^2$ by $Q(Q+1)/2$ since they considered undirected networks.

Now, it is worth taking a closer look at the first term of Eq. (11). This term involves a marginalization over $\beta$. Let us emphasize that $p(W|A, Y, \beta , K, Q)$ is related to the LDA model and involves a marginalization over $\theta$ (and Z). Because we aim at approximating the first term of Eq. (11), also with a Laplace (BIC-like) approximation, it is crucial to identify the number of observations in the associated likelihood term $p(W|A, Y, \beta , K, Q)$. As pointed out in Sect. 2.4, given Y (and $\theta$), it is possible to reorganize the documents in W as $W=({\tilde{W}}_{qr})_{qr}$ is such a way that all words in ${\tilde{W}}_{qr}$ follow the same mixture distribution over topics. Each aggregated document ${\tilde{W}}_{qr}$ has its own vector $\theta _{qr}$ of topic proportions and since the distribution over $\theta$ factorizes ($p(\theta )=\prod _{q,r}^{Q}p(\theta _{qr}))$, we find

$$\begin{aligned} \begin{aligned}&p(W|A, Y, \beta , K, Q)\\&\quad = \int _{\theta } p(W |A, Y, \theta , \beta , K, Q)p(\theta |K, Q)\mathrm{d}\theta \\&\quad = \prod _{q,r}^{Q}\int _{\theta _{qr}}p({\tilde{W}}_{qr}|\theta _{qr}, \beta , K, Q)p(\theta _{qr}| K)\mathrm{d}\theta _{qr} \\&\quad = \prod _{q,r}^{Q} \ell ({\tilde{W}}_{qr}|\beta , K, Q), \end{aligned} \end{aligned}$$

where $\ell ({\tilde{W}}_{qr}|\beta , K, Q)$ is exactly the likelihood term of the LDA model associated with document ${\tilde{W}}_{qr}$, as described in Blei et al. (2003). Thus

$$\begin{aligned}&\log \int _{\beta }p(W|A, Y, \beta , K, Q) p(\beta |K) \mathrm{d}\beta \nonumber \\&\quad = \log \int _{\beta } p(\beta |K) \prod _{q,r}^{Q} \ell ({\tilde{W}}_{qr}|\beta , K, Q)\mathrm{d}\beta . \end{aligned}$$

(12)

Applying a Laplace approximation on Eq. (12) is then equivalent to deriving a BIC-like criterion for the LDA model with documents in $W=({\tilde{W}}_{qr})_{qr}$. In the LDA model, the number of observations in the penalization term of BIC is the number of documents [see Than and Ho (2012) for instance]. In our case, this leads to

$$\begin{aligned}&\log \int _{\beta }p(W|A, Y, \beta , K, Q) p(\beta |K) \mathrm{d}\beta \nonumber \\&\quad \approx \max _{\beta } \log p(W|A, Y, \beta , K, Q) - \frac{K(V-1)}{2}\log Q^2.\nonumber \\ \end{aligned}$$

(13)

Unfortunately, $\log p(W|A, Y, \beta , K, Q)$ is not tractable and so we propose to replace it with its variational approximation $\tilde{{\mathcal {L}}}$, after convergence of the C-VEM algorithm. By analogy with $ICL_{SBM}$, we call the corresponding criterion $BIC_{LDA|Y}$ such that

$$\begin{aligned} \log p(A, W, Y|K, Q) \approx BIC_{LDA|Y} + ICL_{SBM}. \end{aligned}$$