Abstract
The first major scientific discovery of the Space Age was that the Earth is enshrouded in toroids, or belts, of very high-energy magnetically trapped charged particles. Early observations of the radiation environment clearly indicated that the Van Allen belts could be delineated into an inner zone dominated by high-energy protons and an outer zone dominated by high-energy electrons. The energy distribution, spatial extent and particle species makeup of the Van Allen belts has been subsequently explored by several space missions. Recent observations by the NASA dual-spacecraft Van Allen Probes mission have revealed many novel properties of the radiation belts, especially for electrons at highly relativistic and ultra-relativistic kinetic energies. In this review we summarize the space weather impacts of the radiation belts. We demonstrate that many remarkable features of energetic particle changes are driven by strong solar and solar wind forcings. Recent comprehensive data show broadly and in many ways how high energy particles are accelerated, transported, and lost in the magnetosphere due to interplanetary shock wave interactions, coronal mass ejection impacts, and high-speed solar wind streams. We also discuss how radiation belt particles are intimately tied to other parts of the geospace system through atmosphere, ionosphere, and plasmasphere coupling. The new data have in many ways rewritten the textbooks about the radiation belts as a key space weather threat to human technological systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many of the space systems on which modern human society depends operate in the region from altitudes of a few hundred km to ∼40,000 km above Earth’s surface. This region of space is filled with the populations of energetic particles that we collectively call the radiation belts. The fact that the Earth is surrounded by toroids of very energetic protons and electrons was the first great discovery of the Space Age in 1958 (see Van Allen et al. 1958, 1959). From the first realization that the terrestrial magnetic field could “trap” high-energy particles, we have come today to a much more sophisticated understanding of what are appropriately often dubbed the “Van Allen Radiation Zones” (see Summers et al. 2012).
More or less from the first discovery of the radiation belts, it was recognized that intense populations of penetrating particles could be highly damaging to electronic systems in space as well as to spacecraft structural material and spacefaring human beings (Van Allen 1966). Thus, from the earliest days of the space era it was realized that the Earth’s radiation belts were a challenge to be reckoned with when it came to flying satellites and human missions in near-Earth orbits. Today we recognize that radiation belt particles are one of the most pervasive and persistent threats that constitute what we comprehensively term space weather (Baker and Lanzerotti 2016).
This chapter is intended to provide a brief overview of radiation belt space weather impacts. A more thorough treatment of such impacts is provided in the companion chapter by Luntama et al. (2017, this issue). The further intention of this paper is to describe from a scientific perspective our present understanding of radiation belt structure, dynamics, and coupling to other parts of the geospace system. In providing such a scientific survey, the goal is to characterize as completely as possible the increasing importance of radiation belt effects on technological systems.
2 Overview of Radiation Belt Space Weather Impacts
Figure 1 shows a schematic cutaway diagram of the Earth’s radiation belts. Closest to the Earth’s surface is the inner Van Allen zone. This belt extends from just above the dense atmosphere out to an equatorial altitude of about 10,000 km above the Earth’s surface. The inner Van Allen belt is comprised dominantly of very energetic protons (ranging up to multiple GeV energies). Recent work using the Relativistic Electron-Proton Telescope (REPT) instruments on NASA’s Van Allen Probes Mission (see Baker et al. 2013b) has shown fascinating temporal and spatial behavior for the inner zone proton population (see Selesnick et al. 2014). These results demonstrate that protons with energies from ∼10 MeV to ∼100 MeV are quite stable in time near the geocentric radial distance of \(r\sim1.5R_{\mathrm{E}}\) (Earth radii = 6372 km) at which the inner zone proton fluxes peak. However, an outer “shoulder” of the radial distribution from \(1.7 \leq r \leq2.5 R_{\mathrm{E}}\) shows tremendous temporal variability for protons with \(E\lesssim60\ \text{MeV}\). These variable proton fluxes are probably due primarily to evolution of trapped solar energetic protons (Selesnick et al. 2014).
The inner Van Allen zone also has copious fluxes of low-and medium-energy electrons (Fennell et al. 2015; Li et al. 2015) as revealed by Van Allen Probes and other spacecraft data sets. However, the Van Allen Probes era (September 2012 → present) has provided many new discoveries about inner magnetospheric ultra-relativistic electrons with energies \(E \gtrsim2.5\ \text{MeV}\). In particular, initial results after major storm intervals surprisingly showed essentially no detectable prompt ultra-relativistic electron fluxes in the region \(L \lesssim2.8\) (Baker et al. 2014a), but over longer time scales these electrons did eventually move inward from locations beyond this radial distance to \(L\lesssim 2.5\). The paucity of very energetic electrons in the inner magnetosphere immediately following major magnetic storms is quite striking (Foster et al. 2016; Baker et al. 2016) and the consequences for space weather effects will be discussed further in this chapter (see also Boyd et al. 2016; Baker et al. 2016; and Kim et al. 2016).
As shown by the leftmost label in Fig. 1, the space weather concerns for the inner radiation belt zone are several. The intense, high-energy trapped protons are extremely damaging to space systems (Vette 1966) and are quite hard to shield against. There are also the variable, trapped solar energetic particles in the inner zone that can cause dose and single-event effects (see Lorentzen et al. 2002; Baker 2002). The inner zone also has trapped galactic cosmic rays (see Klecker et al. 1995; Cummings et al. 1993). Finally, the trapped energetic electrons with \(E\lesssim1\ \text{MeV}\) (Fennell et al. 2015; Claudepierre et al. 2017) also represent a further significant source causing total dose effects.
The so-called “slot region” of the radiation belts extends from roughly \(L\sim2.0\) to \(L\sim3.0\) depending on energy and particle species. (L is the geocentric distance in Earth radii at which a dipole magnetic field line crosses the magnetic equatorial plane). The slot is a region often relatively devoid of energetic electrons. However, during strong geomagnetic storm periods, the gap between the inner and outer zone can be filled to a large degree by moderate (and even high) energy electrons (Fennell et al. 2005, 2012; Turner et al. 2016; see also Fig. 6). For example, in the intense “Halloween” storm period of late-October and November 2003, the slot region was filled with multi-MeV electrons for several weeks (Baker et al. 2004a). Thus, as indicated in Fig. 1, the slot region can present several space weather concerns including low- and medium-energy electron enhancements, multi-MeV electrons (on rare occasions), and strong solar energetic particle events (again on relatively rare occasions).
Finally, the outer Van Allen radiation belt represents in many ways the most pervasive space weather risks to operating spacecraft. As shown in Fig. 1, the outer zone is broad in spatial extent (from \(r\sim3R_{\mathrm{E}}\) to \(r\gtrsim6.5 R_{\mathrm{E}}\)). It is comprised of mildly to highly relativistic electrons (∼100 keV to ≳10 MeV) and varies widely in particle intensity. Commercial, military, and scientific satellites operating in medium-Earth orbit (MEO) and geostationary Earth orbit (GEO) number in the multiple hundreds worldwide. All of these operating spacecraft are subject to outer Van Allen belt space weather impacts.
The record of operating spacecraft over the Space Age is laden with examples of anomalies and outright satellite failures due to space weather effects (Allen 2002). Many operational problems occur in the so-called South Atlantic Anomaly (SAA) region as shown here in Fig. 2. As illustrated in the diagram, the Earth’s surface magnetic field is weakest over Brazil and eastward into the South Atlantic Ocean region. This is due to the offset, tilted dipole nature of Earth’s intrinsic magnetic field (Cain 1966). Trapped particles mirroring along magnetic field lines, especially high-energy protons in the inner zone, can approach closest to the Earth’s surface in the SAA weak field region. Thus, this is the place where low-Earth orbit (LEO) spacecraft encounter the most intense particle fluxes. Figure 2 shows that the TOPEX (U.S./French Ocean Surface Topography mission) and TERRA (flagship Earth Observing System-1 satellite at 705 km altitude) spacecraft suffered a very large number of electronic anomalies and upsets in the SAA (Allen 2002), probably due to single-event effects from inner zone protons.
Figure 3 shows a schematic diagram (Baker 2002) of a spacecraft at some location within the Earth’s magnetosphere. At relatively high altitudes, the spacecraft can be subject to a variety of effects. Both solar energetic particles (SEPs) and trapped energetic protons can cause significant energy deposition insensitive electronics on board a given spacecraft. Similarly, galactic cosmic ray nuclei can pass through electrical components and induce radiation degradation effects. As illustrated in Fig. 3, these ion interactions effects are termed “single event effects” (SEE).
A schematic diagram showing spacecraft anomaly mechanisms: (a) single-event ion effects; (b) Deep-dielectric charging due to high-energy electrons; and (c) Surface charging due to low-to-medium energy electrons (from Baker 2002)
Another effect of the space environment is called “deep-dielectric charging” and is indicated in Fig. 3b. Electrons with energies of hundred of keV (and up to multiple MeV energies) can penetrate shielding and bury themselves in dielectric materials inside spacecraft subsystems. As shown by Fig. 4, if the build up of buried charge is fast enough (and the leakage of charge out of the dielectric material is slow enough, then a powerful discharge can occur. This can damage materials and sensitive electronic components.
Illustration of the deep-dielectric discharge mechanism that can cause severe spacecraft operational anomalies. Sequence is upper left downward and then to the right in the diagram (see Hastings and Garrett 1996)
A third kind of space weather impact within the radiation belts is shown in Fig. 3c. This is called “surface charging”. If the space system is subject to hot plasma in its vicinity and photo-electrons are not able to carry charge away promptly from surface insulator and dielectric material (as happens in solar eclipse conditions or on the dark side of a space vehicle) there can be a powerful build-up of charge on parts of the spacecraft surface. When the charge buildup is great enough, there can be a sudden discharge that can produce material damage and/or can produce a significant electromagnetic disturbance around the spacecraft. This can cause phantom signals or changes of state in memory systems, and even permanent damage to electronics.
Obviously, from the above brief description it is clear that the radiation belts can cause a wide variety of impacts on space systems. Thus, having a deeper understanding of radiation belt structure, dynamics, and temporal trends is crucial for our technological society. This chapter describes our current knowledge of these radiation belt aspects.
3 Radiation Belt Morphology and Trends
This section discusses our present understanding of the temporal and spatial properties of the radiation belts as they relate to space weather effects. We begin with a description of the inner zone properties and impacts. This is followed by a description of the slot region and then outer zone structure and dynamics.
3.1 Inner Zone Electrons
The inner radiation belt was the first region that was accessible to early satellite measurements. Unfortunately, very early on, before comprehensive measurements of the natural radiation there had been completed, there was a succession of high-altitude nuclear tests that injected populations of electrons into these regions (Van Allen et al. 1959). Many of the injected electrons were lost fairly rapidly but some were still present many years later because they were injected into regions where the electron loss rates were quite low (Van Allen 1966). The STARFISH event was one of those that generated enduring electrons because of the L-position where its electron belt formed. This made it difficult to specify what the natural electron environment was and what the sources were during the early times in space science (see Gombosi et al. 2017, this issue). This was compounded by the fact that the inner zone protons are of high energy and can penetrate electron sensors, contaminating many of the attempted electron measurements. The early electron radiation models (Vette 1966; Teague and Vette 1972, 1974; Teague et al. 1976; Sawyer and Vette 1976; Vette 1991) for the inner zone were built on a very limited set of observations and there was concern that their electron fluxes did not represent the real flux levels (Daly et al. 1996; Barth et al. 2003).
Recently, the NASA Van Allen probes mission made measurements in the inner zone and, subsequently, upper limits on the electron fluxes there were developed (Li et al. 2015; Fennell et al. 2015, 2016) as shown in Fig. 5. These new measurements corrected for much of the proton backgrounds using capabilities built into the sensors (Claudepierre et al. 2015; Fennell et al. 2016; Blake et al. 2013; Baker et al. 2013b). As a result, they showed that real electron fluxes >0.5 MeV are indeed significantly lower than the commonly used radiation model fluxes. They also showed that there were essentially no (or very few) \(E > 1\ \text{MeV}\) electrons present, at least in the early Van Allen Probes mission time frame. Selesnick (2015) showed that the neutron albedo generated electron fluxes are too low to account for the observed \(E < 1\ \text{MeV}\) inner zone electrons, indicating that a different source was responsible for the inner zone electron fluxes. However, his calculations also indicated that the process could generate multi-MeV electrons at low flux levels, below the upper limits set by the Van Allen Probe measurements.
Upper limit electron flux estimates for \(L=1.5\) from the Van Allen Probes mission (MagEIS and REPT) compared to CRRES observations and the electron models AE8MAX and AE9mean (after Fennell et al. 2015)
As is noted below for Fig. 13, and is shown here in Fig. 6 from the pre-Van Allen Probe era, there are episodic incursions of \(E \geq 1\ \text{MeV}\) electrons into the low-L regions and even into the inner zone, but their presence is not the norm. Figure 6 shows HEO3 satellite (Fennell et al. 2012) measurements for > 1.5 and >3 MeV electrons and >15 MeV protons in the \(1.75 < L < 7\) region during the 1998 through 2011 period that includes solar sunspot cycle 23. The figure shows multiple instances of the electrons penetrating to \(L < 3\) and a few to \(L \leq 2\). The Halloween storm of 2003 (Day 304) accelerated and transported >1.5 and >3 MeV electrons through the slot region \((2 < L <3)\) and into the inner zone (see also Baker et al. 2004a; Baker et al. 2007) while other large storms during solar cycle 23 accelerated and transported electrons to \(L\sim2\). See also Fig. 7 from Van Allen Probes measurement.
MagEIS equatorially mirroring electron fluxes showing the injection/transport of 1.06 MeV electrons into the inner zone during the June 2015 storm period (after Claudepierre et al. 2017)
Horne et al. (2005) and Shprits et al. (2006) have speculated that the erosion of the plasmasphere to low L could create temporary conditions that are conducive to local acceleration there. If MeV electrons can be accelerated, injected, or transported deep in the inner zone where the electron lifetimes typically exceed hundreds of days (Van Allen 1964; Roberts 1968) and they can persist for years at observable levels as happened with the electrons injected into the belts by the STARFISH event. These lifetimes are generally controlled by plasmaspheric hiss (Summers et al. 2007) however losses can be enhanced by chorus and EMIC waves during periods where the plasmasphere is strongly eroded.
June 2015 was the most recent period where MeV electrons were injected into the inner zone (Claudepierre et al. 2017) as shown in Fig. 7. These electrons persisted for months at \(L\sim1.75\). As Fig. 8 shows, \(E<800\ \text{keV}\) electrons can be transported to low L-values and into the inner radiation zone during storms (see Baker et al. 2007). The lower the energy, the more common are such injections to the lowest L-values. Note, for example, that the 36 keV to 460 keV electrons in Fig. 8 were injected to \(L<2\) multiple times during the ∼2 years of data shown. In fact, many of these injections caused electron enhancements at <1.5 and, during the March 2015 storm, enhanced fluxes were observed down to \(L\sim1.2\) especially at energies <460 keV. Such penetrations of electrons into the inner zone where their lifetimes are long can be a hazard for satellites orbiting there from both the total dose perspective and from the subsurface/internal charging perspective. So, while the occurrence of >1 MeV electrons in the inner zone is relatively rare, they can become an enhanced hazard when they occur and their populations can persist for months (Shprits, 2009).
Electron locally mirroring flux history for \(1.2 < L < 5\) during the July 2014–August 2016 period. The electron energies range from 36 keV to 2.645 MeV as noted in the panel legends. The sudden flux enhancements or injections to low \(L\) values is easily seen at the lower energies (<900 keV) whereas at > MeV energies they do not penetrate deeply into the slot region
Turner et al. (2016) investigated “sudden particle enhancements at low \(L\)” (SPELLS) as slot filling events and as a source of inner zone electrons. The study found that the enhancements occurred much more often for electrons \(E < 600\ \text{keV}\) than for those \(E > 600\ \text{keV}\) as shown in Fig. 9, reproduced from that paper. Turner and colleagues argue that these electron enhancements or injections are most likely the dominant source for most of the electrons in the inner zone. These more common enhancements of the 100–800 keV electrons, as shown in Fig. 8, can penetrate thermal control material and wiring insulation to become a significant electrostatic discharge threat to space systems. For example, 300 keV electrons have sufficient range to penetrate typical thermal blanket material and deposit their charge on underlying insulators where it can build up to high-voltage breakdown levels as shown in Fig. 4.
Number of low \(L\) electron flux enhancements as a function of energy that penetrated to \(L < 2.7\) and those which were slot filling during the Sep. 2012 to Feb. 2016 period (after Turner et al. 2016)
A clear result of these studies found that the quiet-time phase space density radial profiles in the inner zone are characterized by positive slopes with increasing \(L\) (or \(L^{*}\)) for \(L < 2\) and beyond for the electrons with the lowest magnetic moments as shown in Fig. 10 (Fennell et al. 2015). Figure 10 also indicates that a peak in the radial profiles develops near \(L\sim2\) at the larger magnetic moment values. Turner et al. (2016) showed the peak in the phase space density radial profiles develops in this region as the electrons injected into and through the slot region began to decay away. Radial flux profiles also remained stable in the \(L < 1.8\) inner radiation zone, as can be seen by comparing Figs. 10 and 11. Figure 11 is excerpted from a longer movie (O’Brien et al. 2016) and shows the radial profiles for equivalently constant magnetic moments, with clear dynamical variations in phase space density radial profiles at low \(L\). The Fig. 11 frame is a snapshot of the PSD radial profiles observed following the 17 March 2013 storm time injection (see Baker et al. 2014b). This can be contrasted with the quiet time radial profiles in Fig. 10. The post-storm 20 March 2013 radial profiles do not show a peak near \(L=2\) and indicate there is a source of electrons external to the slot region that were transported inward to low \(L\). This indicates that the electrons transported to low \(L\) are most likely the source of the inner zone electrons.
Quiet time phase space density radial profile of quiet time inner zone electrons for a range of constant first adiabatic invariant (after Fennell et al. 2015)
Phase space density (PSD) radial profiles at constant \(\xi\) in the inner zone and slot region for 20 March 2013. \(\xi = M/\gamma^{2}\) where \(M\) is the first adiabatic invariant and \(\gamma\) is the sine of the equatorial pitch angle (after O’Brien et al. 2016)
Features still in need of further examination are the PSD radial profiles at \(L < 2\). First impressions, from examining many intervals of the PSD radial profiles (Fennell et al. 2015; Turner et al. 2016; O’Brien, private communication), are that for \(L < 2\) the PSD profiles are relatively constant in shape and levels over time. This means that the electron losses there are being well matched by inward transport. Electron lifetime estimates indicate that at \(L < 1.5\) they are consistent with losses from atmospheric scattering (Walt 1966). So, the processes of inward transport of electrons must balance the estimated loss rates. In any case, the transport, buildup and penetration of electron fluxes through the slot region and into the inner zone represent a time dependent threat from the subsurface/internal charging perspective that cannot be ignored. Since inner zone is within the high-density plasmasphere, surface charging is not a threat there even though there are significant and variable fluxes of ≤80 keV electrons there as shown in Fig. 8.
3.2 Slot Region Electrons
The region \(2 \leq L \leq 3\) is known as the electron slot. It is a transition region between the outer and the inner radiation zones. The slot region’s flux levels are highly time dependent and the spatial structure is strongly energy dependent (Turner et al. 2015 and 2016; Reeves et al. 2016; Zhao et al. 2016). During extended quiet periods the electron fluxes can decay to low levels, especially at the higher energies, giving rise to PSD radial profiles that peak in the \(2 < L < 3\) range for electrons with \(E \leq \text{MeV}\). Both of these features are clearly seen in Fig. 8. The electron lifetimes are energy dependent with the dominant loss being from pitch angle scattering by waves. Inside the plasmasphere hiss scattering of the electrons is the dominant loss mechanism (Lyons and Thorne 1973; Lyons et al. 1972; Abel and Thorne 1998a, 1998b; Meredith et al. 2009). The energetic electrons (0.2–1.5 MeV) that are transported into the slot region decay fairly rapidly (Abel and Thorne 1998a, 1998b; Fennell et al. 2012; Claudepierre et al. 2017).
What has been notable is that ultra-relativistic electrons, ≥2.5 MeV, seldom penetrate deeply into the slot region at \(L\) values < 2.8 over prompt time scales following acceleration/injection events (Baker et al. 2014a; Foster et al. 2016) as is evident from Figs. 6, 9, and 12. (On longer ∼ weeks to months scales, however, gradual inward radial diffusion does seem to move these electron energies inwards of this radial distance to \(L \sim 2.5\).) While this penetration limit has been observed multiple times preceding and during the Van Allen Probes mission, at this point the processes that are responsible for this condition are still under discussion. Three that have been considered are: (1) A balance between diffusive radial transport and scattering losses that limit the ability of highly relativistic electrons to penetrate to low \(L\) values during storms of the Van Allen Probes era (Lyons and Thorne (1973); Baker et al. 2014a); (2) localized precipitation of MeV electrons through wave mode coupling and wave–particle interactions induced by VLF transmitter signals at their maximum outward extent near \(L=2.8\) (Foster et al. 2016); and (3) the effect of VLF transmitter-induced waves on the coherency of the wave–particle interactions, creating an earthward limit to the local acceleration of electrons to MeV energies. (Regarding this latter possibility, see as well the discussion on possible anthropogenic VLF transmission effects within Gombosi et al., this issue.) Whatever the mechanism, the fact that high fluxes of multi-MeV electrons are seldom present deep in the slot means that the threat of internal charging and highly penetrating radiation dose is minimal throughout that region most of the time. In fact, as Fig. 12 shows, it takes large storms to position the peak of the MeV electron fluxes at \(L< 3\). The figure also implies that there is a linkage between the plasmapause position and the \(L\) of maximum MeV fluxes. Thus, high fluxes of MeV electrons will populate the outer edge of the slot region for large storms, as measured by Dst or by the plasmapause erosion. When this occurs, deep dielectric charging will become a hazard for satellites orbiting there.
The mechanisms that cause injections of the lower energy electrons into and through the slot region (see Russell and Thorne 1970) have been investigated by Thorne et al. (2005), Zhao and Li (2013), and Turner et al. (2015, 2016). Zhao and Li modeled the transport into the slot region and inner zone as diffusive transport using a 1-D radial diffusion model. However, they used diffusion coefficients that were much larger than the usual Kp-dependent electromagnetic diffusion values and concluded that the usual Kp dependent coefficients cannot be simply extended to the slot region and inner zone. Turner et al. (2015, 2016) and others (Sergeev et al. 1998; Runov et al. 2014; Takahashi et al. 2003) considered how magnetosonic waves and compressional fast mode waves might be responsible for the sudden enhancements in the electron fluxes at low \(L\)-values in the plasmasphere. After examining the electric and magnetic field fluctuations during an injection of electrons to low \(L\), Turner et al. (2015) proposed that Pi2 cavity mode waves could explain the electron flux enhancements inside the plasmasphere. They also speculated that the upper energy limit to the enhancements could result from the radial gradient of the PSD combined with the efficiency of the interaction with the waves. Thus, sudden enhancements of energetic electrons associated with substorm activity and injections at higher \(L\) shells can penetrate very deep into the inner magnetosphere and may ultimately play an activity-dependent role in the formation of the inner zone population as discussed above. In any case, as noted previously, the intense but variable hundreds of keV electron fluxes can be a hazard from the vehicle charging perspective which can include surface charging during those intervals when the plasmasphere is eroded to \(L < 3\).
3.3 Inner Zone and Slot Region Protons
Only the more energetic ions/protons in space are of concern from a space weather hazard perspective. Very high energy protons and ions can penetrate shielding, depositing their energy in electronic devices. The hazardous proton populations of the inner zone and slot regions have two fundamental sources. In the inner zone the primary source is the neutron albedo process, which has been well defined (Selesnick et al. 2007 and references therein). The outer edges of the inner zone and the lower part of the slot region also host energetic protons and ions that consist of entrapped solar particles (Selesnick et al. 2007; Lorentzen et al. 2002; Mazur et al. 2005). Protons with \(E > 3\ \text{MeV}\) are a primary contributor to solar array degradation while >15 MeV protons contribute to single event effects (e.g. Fig. 2) and non-ionizing radiation damage to electronic parts within satellites that orbit in or traverse these regions. In addition to the trapped population, there are also episodic solar particle events, with associated energetic solar ions. Those ions that eventually reach the Earth can penetrate deeply into the inner magnetosphere where they can cause single event upsets, as in Fig. 14, and enhance the radiation damage to satellite solar arrays and electronic parts, similar to that shown in Fig. 13 (Marvin and Gorney 1991. Figure 6 shows multiple incidences of >15 MeV solar protons penetrating to low \(L\) combined with the presence of the protons from cosmic ray albedo neutron decay (CRAND) at very low \(L\) and inherent variability of the proton fluxes in the \(2.5 < L < 4\) region in response to magnetic storms (Lorentzen et al. 2002; Mazur et al. 2005).
Solar Energetic Particle (SEP) events are the mechanism by which very high-energy protons appear in the outer zone region of the radiation belts. However, these events are very short-lived (hours in duration), as the high-energy protons with such large gyro-radii are not able to be stably trapped at these locations. As mentioned earlier, they can often penetrate to the inner zone where stronger magnetic fields in a more rigid topology can entrain these particles for very long times. In general, highly energetic protons (multi-MeV energies) are not considered to be a regular feature in the outer zone.
3.4 Outer Zone Electrons
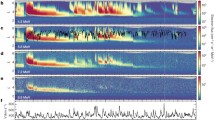
The characteristics and dynamics of ultra-relativistic and MeV electron fluxes in Earth’s outer radiation belt are strongly influenced by geomagnetic storm time processes, leading both to significant electron loss and local acceleration deep within the inner magnetosphere (Ukhorskiy et al. 2014; Reeves et al. 2013). The outer Van Allen belt is highly variable on essentially all temporal scales and shows tremendous variability as well as significant variations in the outer belt spatial extent. This is well illustrated by Fig. 14 adapted from Li et al. (2006). The main (lower) panel of the figure shows integral fluxes of \(2\lesssim E \lesssim6\ \text{MeV}\) electrons measured by sensors on board the LEO spacecraft called the Solar, Anomalous, and Magnetospheric Particle Explorer (SAMPEX) mission (see Baker et al. 1993). The data are color-coded representations of electron flux from \(L=2.0\) to \(L=7.0\) (vertical axis) versus time (horizontal axis) from 1992 to 2013. The color bar to the left is the log of electron flux (electrons/cm2-s-sr). The upper panel of Fig. 14 shows in black the smoothed sunspot number over the period 1992–2013 while the red trace shows the solar wind speed (km/sec) measured upstream of the Earth’s magnetosphere.
As is evident from the figure, the outer Van Allen belt (as monitored from the ∼500 km altitude of SAMPEX) typically extends from \(L \sim3.0\) to roughly \(L=6.5\). However, the belt’s spatial extent was highly variable over the ∼ 20-year SAMPEX lifetime. Also, the peak electron flux levels varied widely as a function of time. For example, in 1994, the peak >2 MeV electron fluxes were over 104 electrons/cm2-s-sr, while in 2008–2009 the electron flux was often barely above background levels (∼ \(10^{0}\) electrons/cm2-s-sr). As is obvious from inspection of the figure, a main controller of the electron fluxes in the outer belt is the solar wind speed impacting Earth’s magnetosphere (Baker et al. 1979, 1986), Kellerman et al. (2013), Kellerman and Shprits (2012). Indeed, solar wind speeds with \(V\gtrsim 500\ \text{km/sec}\) generally are associated with high outer radiation belt electron “content” (Baker 2004). On the other hand, persistent solar wind speeds of \(V\lesssim300\ \text{km/sec}\) can lead to virtual disappearance of the outer belt (for electron energies \(E \gtrsim 1\ \text{MeV}\)). This occurred quite prominently in the profound solar minimum of 2008–09.
The inner “edge” of the outer zone — as is obvious in Fig. 14 — shows considerable variability in spatial location. During particularly strong solar wind forcing conditions, the inward extent of the outer zone population can appear to reach down to \(L\sim2.5\). This is typically a rare and brief circumstance. During truly extreme forcing events such as the Halloween Storm events of late 2003 (see Baker et al. 2004a), the slot region can be filled with multi-MeV electrons for weeks of time. An event of great strength was also seen in late 2004 (see Fig. 13).
It has long been clear that large increases in multi-MeV electrons can cause significant spacecraft operational anomalies. For example, Fig. 15 (taken from Baker et al. 1987a) shows that star-tracker anomalies were observed on an operational geostationary Earth orbit (GEO) spacecraft whenever the counting rate for \(E\sim3\ \text{MeV}\) electrons reached or exceeded 7 counts/sec. The vertical arrows show the precise timing relationship between the star tracker problems and the enhanced electron flux episodes during this 1980–82 period.
Temporal correspondence between star tracker anomalies onboard a geostationary orbit spacecraft (vertical arrows) and enhancements in \(E \sim3\ \text{MeV}\) electron fluxes measured by sensors on the same spacecraft (from Baker et al. 1987a)
Another example drawn from SAMPEX for the 2003 Halloween storm experience is shown here in Fig. 16. This figure from Baker et al. (2004b) shows that dozens of spacecraft operational anomalies occurred during the Halloween Storm (Oct.–Nov. 2003) period. Some of these anomalies were onboard spacecraft in distant locales (e.g., Genesis and Mars Odyssey), but most anomalies were seen on near-Earth spacecraft (GOES, RHESSI, ADEOS, NOAA-17, POLAR) and were due to the highly elevated radiation belt electron population (Baker et al. 2004b).
Color-coded electron fluxes measured by the SAMPEX spacecraft (see Fig. 13) for Days 290 through 335 of 2003 in an \(L\) versus time format. Times of severe operational anomalies for various spacecraft are indicated by the red arrows and boxes
The extent and quality of observations of the radiation belts improved dramatically with the successful launch of the Radiation Belt Storm Probes (RBSP, renamed the Van Allen Probes mission in November 2012). The Van Allen Probes have a very comprehensive particle and fields detection payload (see Mauk et al. 2013). The higher energy electron measurements from the REPT instruments (Baker et al. 2013a) give unprecedented information throughout the inner and outer Van Allen belts. From the outer radiation belt standpoint, the REPT measurements show beautifully the spatial and temporal properties of electrons from \(E\sim1\ \text{MeV}\) to \(E\gtrsim10\ \text{MeV}\). Figure 16, for example shows combined data from the Van Allen Probes A and B spacecraft for \(E=1.8\ \text{MeV}\) (1.6–2.0 MeV channel). Each panel shows color-coded flux levels for one-year periods. The vertical axis is \(L\)-value (\(2\leq L\leq6\)) in each case and each horizontal axis shows one year of time starting with 1 September 2012 (upper left) to 1 September 2016 (lower right). There are fascinating acceleration, transport, dropout, and recovery features seen in the data. Particularly strong storm events (such as October 2012, March 2015, and June 2015) are evident. See Reeves et al. (2013) and Baker et al. (2016) for details of these coronal mass ejection (CME)-driven events Thorne et al. (2013b). Also, note the very weak outer belt structures during much of 2014 as seen in panel (b) of the figure. The most recent year of data shown (1 September 2015 to 1 September 2016) is particularly notable for the frequency and intensity of the \(E\sim1.8\ \text{MeV}\) electron enhancements.
Examination of the inward extent of relativistic electrons in Fig. 17 and the earlier Fig. 14 demonstrate visually the striking conclusions of Baker et al. (2014a) and Baker et al. (2016). Those studies found that in recent times since the launch of Van Allen Probes in August 2012, the Earthward extent of the outer belt of highly relativistic electrons appears to encounter an almost impenetrable barrier at an equatorial radial distance \((L)\) near 2.8 \(R_{\mathrm{E}}\), such that almost no electrons with \(E \geq 2.5\ \text{MeV}\) are seen inside this position in the hours and days following major disturbances and their associated inward injections and/or in-situ acceleration events. Slow radial diffusion to locations inwards of \(L=2.8\) does occur at longer time scales, but in no instance over four years of data do we see electrons with \(E\gtrsim1\ \text{MeV}\) penetrate inside \(L\sim2.5\). The greatest “intrusions” observed were for the March and June 2015 storms (see Baker et al. 2016; Foster et al. 2016). The nearly “impenetrable” barrier to inward injection or diffusive transport of relativistic electrons over prompt time intervals is one of the most unexpected findings of the Van Allen Probes era (see Baker et al. 2014a). The finding has important and nuanced space weather implications when considering the temporal response of the outer belt’s inner edge, with the general conclusion that locations in the \(L=2.5\) to 2.8 range can be expected to have almost complete protection from prompt increases in ultra-relativistic electrons. However, over longer time scales of weeks to months typically associated with slower diffusion effects, these locations will gradually see the impacts of these extremely energetic electrons in the absence of further storm time or injection associated events.
The features for \(E\sim1.8\ \text{MeV}\) in Fig. 17 are amplified in the \(E=4.2\ \text{MeV}\) channels of REPT shown here as Fig. 18, and demonstrate once again that the “impenetrable” barrier to inward prompt injection holds across multiple energy levels. In particular, the 4.2 MeV electron fluxes (in identical format to Fig. 16) show a virtual absence of electrons for much of 2014 (see panel (b)). Numerous instances in 2013, 2015, and 2016, however show the fascinating “3-belt” structure indicative of the relativistic electron “storage ring” property reported by Baker et al. (2013a). Again – and even more strikingly at these higher energies — the outer zone electrons approach \(L\sim2.8\) (Baker et al. 2014a; Kellerman et al. 2014). However, in no cases do these highly energetic electrons pass through the impenetrable barrier either by direct injection or by radial diffusion, although on occasion these electrons later slowly penetrate inwards to \(L=2.5\) — e.g. by mid June 2015 (difficult to see on this plot scale) following the March 17, 2015 great storm. Clearly, the dynamic behavior of these electrons is far richer than previously thought, and more studies are under way to further explore these features and to quantify associated space weather effects across the range of natural injection and diffusion processes and characteristic scales.
Similar to Fig. 16 but for \(E\sim4.2\ \text{MeV}\) electrons from the REPT instruments
4 Radiation Belt Acceleration, Transport, and Loss
4.1 Particle Diffusion Across Invariant Parameters
Around the time of the early Van Allen-led space missions in the late 1950s (as mentioned previously), theorists asserted that classical and relativistic physics laws have important and inherent consequences for the behavior of charged particles in the presence of a background magnetic field. In particular, for the approximate dipole field present in the terrestrial inner magnetosphere, particles under non-disturbed conditions undergo three quasi-periodic motions, each associated with an adiabatic invariant and a corresponding spatial and temporal characteristic scale. Further, particles that obey all three invariant motions define a stable drift shell encircling Earth, allowing trajectory predictions. The three invariants, arranged from strongest to weakest and from shortest time scale to longest time scale, are particle gyration in a homogeneous magnetic field, bounce gyrocenter motion along the field lines, and drift-bounce gyrocenter motion around Earth (Shulz and Lanzerotti 1974). As Ukhorskiy and Sitnov (2013) point out, for relativistic ∼1 MeV electrons in the center of the outer belt (\(L \sim4\text{--}5\)), these motion invariants are well decoupled as they are separated by approximately six orders of magnitude: gyration frequency on ∼kHz scales, bounce frequency on ∼Hz scales, and gradient-curvature drift frequency on ∼mHz scales (Schulz and Lanzerotti 1974).
However, nature often provides non-adiabatic conditions e.g. during injection events, strong plasma wave generation at appropriate frequencies, or during strong non-dipole magnetic dipolarizations. The Van Allen-led early missions and a large number of subsequent observational experiments (e.g. CRRES, AMPTE, SAMPEX, Van Allen Probes) revealed that these highly dynamic conditions can often provide strong and variable particle forcing on time scales less than the characteristic invariant time scale, leading to direct violation of one (or often more) of the invariant particle motion laws. Intervals with these types of violations can therefore cause particle intensities across the radiation belts to vary significantly with time (see early review by Roederer 1968), with direct associated space weather impacts. In particular, large amplitude perturbations in electric and magnetic fields along particle orbits can violate invariants. Plasma waves, often (but not always) separately excited by differing energy pathways in the plasma, have associated electrostatic and electromagnetic fields that can resonantly interact with quasi-periodic particle motions to amplify their energy and alter their densities.
In the case where the radiation belt particle energy and density is small compared to other plasma populations, one can consider the forces mentioned as external, and quasi-linear theory then allows a modeling of the action of these forces as particle diffusion in the three adiabatic invariants, with various formulations to describe the effective diffusion coefficients caused by the external forcing. Historically, Ukhorskiy and Sitnov (2013) note that this quasi-linear particle diffusion theory was well established within the first decade after initial radiation belt discoveries, but non-linear modifications to this diffusion framework did not occur until much later in the 1980s and 1990s.
Excellent summaries of adiabatic invariant particle motion theory as well as violations of that theory are given by a number of previous works including Dungey (1965), Trakhtengerts (1966), Walt (1971), and the previously referenced Ukhorskiy and Sitnov (2013). As this article is devoted to a description of radiation belt space weather effects, however, we focus here on recent results with new insights into the general space weather consequences of dynamic, non-adiabatic particle motions. We also note that recent results have implied that multiple cycles of energy exchange between waves and particles may be involved in relativistic particle acceleration, since unstable plasmas use the energy of other particles for the ultimate acceleration energy source (Shklyar 2017). These situations make it complex to assess the full life cycle of particle acceleration, with associated implications and impacts on quasi-linear and non-linear particle invariant diffusion theories for radiation belt dynamics. Such topics remain at the heart of current theoretical research (e.g. Albert et al. 2016).
4.2 Radial Diffusion
A long recognized scenario for transport of energetic electrons from acceleration or injection zones is radial diffusion, caused when the first two adiabatic invariants are preserved in the outer zone whereas the third and slowest gradient curvature drift invariant is violated by particle–wave processes through the presence of ultralow-frequency (ULF) waves in the Pc-5 range between ∼1.67 and ∼6.67 mHz (Jacobs et al. 1964). Efficient interactions occur when the driving ULF wave frequency is an integer multiple of the azimuthal drift frequency (Schulz and Lanzerotti 1974). Extensions to the pure azimuthal drift based radial diffusion framework have been pursued more recently by Elkington et al. (1999, 2003) through inclusion of drift-resonant electron interactions with ULF toroidal and/or poloidal wave modes in a manner that inherently accommodates an asymmetric geomagnetic field. The general effect of third invariant violation is to cause a net change in the particle’s radial coordinate, causing a net gain/loss in particle energy as the particle diffuses inwards/outwards. ULF waves in this frequency range can be produced by internal processes including both mirror (Hasegawa 1969) and drift (e.g. Chen and Hasegawa 1991) instabilities embedded in the inner magnetospheric plasma. ULF wave power can also be generated by external forcing events including magnetopause shear flow instabilities (e.g. Claudepierre et al. 2008), solar wind pressure variations (Kivelson and Southwood 1988), and transient ion foreshocks (Hartinger et al. 2013). It is important to note that ULF driven radial diffusion is inherently stochastic in nature rather than coherent, as typical ULF driving wave fields are rarely monochromatic and span a range of ∼mHz frequencies.
A number of observational studies have attempted to calculate the effective total radial diffusion coefficient, itself a measure of the radial diffusion rate. This rate, \(D_{\mathrm{LL}}\), includes effects from perturbations in both the induced electric field and magnetic field, and various theoretical formulations (Fälthammar 1965; Fei et al. 2006) have been established to provide quantitative estimates. Many observational studies have been conducted using these frameworks with a notable focus on establishing when electric and/or magnetic field effects are dominant, and a recent comprehensive summary is provided by Ali et al. (2016). Notably, the work of Tu et al. (2012) using THEMIS and GOES data, along with the work of Ozeke et al. (2012, 2014) using AMPTE and GOES data, determined that, contrary to earlier expectations, electric field effects in radial diffusion dominate over magnetic field effects when setting radial diffusion coefficient amplitudes. In fact, Ali et al. (2015, 2016), using Van Allen Probes observations, finds that the radial diffusion electric component is on average larger than the magnetic component by one to two orders of magnitude for almost all \(L^{*}\) and \(Kp\) values. Thus, it appears that electric field perturbations in the ULF range are substantially more effective in driving radial diffusion of charged particles in the inner magnetosphere.
For space weather purposes, typical radial diffusion coefficients range from 10−2 to 10−4 days−1 for low Kp, setting a time scale of hundreds to thousands of days for these slow processes to effect the distribution of energetic particles. Thus, as referred to earlier, the slow movement of the inner edge of the outer belt in Fig. 17 seen in ultra-relativistic electrons between March and June 2015 is an example of observations compatible with inward radial diffusion of an accelerated population created earlier by stormtime injection or by local acceleration processes (cf. later discussion in this section). However, radial diffusion coefficients can be as high as 100 days−1 during times of heightened geomagnetic activity (Ali et al. 2016), allowing for events during which radial diffusion is arguably the dominant acceleration process in the heart of the outer radiation belt.
4.3 Role of Substorms
The role of geomagnetic storms versus substorms and high-energy radiation belt acceleration has been studied for decades. While the exact definitions of the two types of geomagnetic disturbance can be debated, they each represent fundamentally different forms of energy transfer into the Earth’s magnetosphere as a result of solar wind driving. Long-term studies of correlations between radiation belt electron content and solar wind speed show a repeatable ‘triangular distribution’ (Baker et al. 2004b; Reeves et al. 2011), indicating that large enhancements of outer belt relativistic electron flux can occur at any solar wind speed — from the lowest to the highest velocities (Fig. 19). These distributions can be clarified by plotting in terms of occurrence rate contours (e.g. Fig. 1, Kellerman and Shprits 2012), yet still the outcome shows that the relationship between relativistic electron flux and solar wind drivers is not linear. Not only can enhancements occur over a wide range of solar wind speeds, the contents of the radiation belts can also change unpredictably from one geomagnetic storm to the next. Reeves et al. (2003) studied the response of high-energy electrons to almost 300 storms over an 11-year period. The result was a varied distribution, with the highest likely response being one of no change between pre- and post-storm flux levels. An almost equal likelihood existed of the total population increasing or decreasing with any given storm. These results were replicated even when very small storms or non-storm events (\(Dst > -50\ \text{nT}\)) were taken into account (Anderson et al. 2015). Thus, geomagnetic storms and solar wind speed are not good predictors of energetic electron enhancement events, and electron response does not necessarily scale with the strength of a storm. Several recent studies during the Van Allen Probes era have in fact shown cases of strong outer belt relativistic electron enhancements during non-storm times (Schiller et al. 2014; Su et al. 2014). Both papers noted the increase in chorus wave power during the acceleration periods, but did not explicitly make the connection to substorm activity.
Outer belt radiation belt content index vs. solar wind speed (after Baker et al. 2004b)
If strong enhancement events cannot be predicted by strength of a geomagnetic storm (measured by the Dst index) or solar wind speed alone, what then determines an efficient acceleration event? Several studies have attempted to bring light to this subject by examining both individual case studies and the statistics of many enhancements. Meredith et al. (2002) looked at several example periods of outer belt electron acceleration during both strong and weak storm conditions and determined that prolonged substorm activity is a requirement for effective enhancement of relativistic electrons. Kataoka and Miyoshi (2010) found that the main controller of outer belt electron fluxes was IMF orientation: weaker southward Bz resulted in weaker enhancement events. The authors note that northward or weak southward IMF orientation suppresses the amount of substorm activity generated. Comparing modeled electron fluxes at GEO with measurements, Li et al. (2011) concluded that high-speed solar wind is not a necessary condition for MeV electron enhancements at geosynchronous orbit — only a southward orientation of the IMF is absolutely required. More recently, a superposed epoch analysis of both efficient and inefficient acceleration events from Van Allen Probes data has provided a statistical look at the underlying causes (Li et al. 2015). The comprehensive study found three main contributions to efficient acceleration events: (1) prolonged southward Bz, (2) high solar wind speed, and (3) low solar wind dynamic pressure. By examining global chorus wave distributions, the study also clearly shows that intense chorus waves are present for far longer periods during the efficient enhancements.
The common thread throughout this previous work is one of substorm-driven energy being introduced into the ring current region, thus driving relativistic electron enhancements. The acceleration can be achieved via resonant wave–particle interactions with VLF chorus waves, as discussed in a following section. In a quasi-linear interaction scenario, the enhancement progresses in a step-wise pattern, with lower energies appearing first, and high energies taking longer to be produced. This common picture has been noted as far back as Baker et al. (1979) where lower energy electron enhancements at GEO were seen to be closely related to solar wind speed variations, while >1 MeV electrons exhibited a similar profile but with a significant delay in time. The same delay pattern can often be observed, with the time lag increasing as energy does, in the Van Allen Probes data (e.g. Baker et al. 2016). In order for the process to be efficient at producing the very highest energy tail of the radiation belt population, VLF chorus (and thus, their source of energy in the form of plasmasheet particles) need to be continually energized over a long duration (many hours to days), as during High Intensity Long Duration Continuous AE Activity events (Gonzalez and Tsurutani 1987; Tsurutani et al. 1995). A recent case of where this mechanism was not put into place properly showed a failure of relativistic and ultra-relativistic electrons to appear, despite the high solar wind speeds and space weather models predicting enhancements of relativistic electron (Jaynes et al. 2015). The relativistic accelerator process, described in a schematic reprinted here as Fig. 20, requires both source (10’s keV) and seed (100’s keV) electrons to drive chorus waves and provide a base population for acceleration to much higher energies.
Schematic of the relativistic accelerator mechanism in Earth’s inner magnetosphere (reprinted from Jaynes et al. 2015)
The developments throughout the Van Allen Probes era have built on the foundational studies of this topic published over the preceding decades. The emerging picture is one of substorms (with or without geomagnetic storms) playing the dominant role in producing Earth’s high-energy radiation belt population through the intermediary of chorus wave generation. This is a particularly important paradigm to consider as the need for more accurate space weather forecasting models becomes pressing.
4.4 Wave–Particle Interactions (Linear, Nonlinear)
4.4.1 Acceleration by ULF Waves
It has long been known that there is a direct correlation between ULF wave power in the inner magnetosphere and relativistic electron acceleration (Rostoker et al. 1998; Mathie and Mann 2000). ULF waves can accelerate radiation belt particles through two different mechanisms: inward radial diffusion and drift-resonance interaction. The first mechanism was extensively discussed in Sect. 4.2. and can accelerate outer belt electrons on timescales of hours or longer. The second mechanism has been continuously studied for the past 20 years, yet, despite these efforts, it is still unclear what extent of the overall acceleration is driven by drift-resonance. The resonance that can take place between a relativistic electron and the appropriate frequency ULF wave is fundamentally dependent upon the wave period matching the drift period (or multiples thereof) of the electron. This phase-coherent interaction is possible both with toroidal mode ULF waves, detailed nicely in Elkington et al. (1999), as well as poloidal mode (Claudepierre et al. 2013) as shown in Fig. 21. Section 4.2 already covered these processes thoroughly.
Evidence of drift-resonance interaction between poloidal mode ULF wave (b) and 57–80 keV electrons (blue and green trace in (a)). From Claudepierre et al. (2013)
4.4.2 Local Acceleration by VLF Chorus
VLF waves in particular have a strong interaction potential with radiation belt electrons, and can cause significant acceleration characterized by a fundamentally local nature. During this local acceleration process, both a source of energy for wave growth and a population of energetic seed electrons are required. New observations are shedding considerable light on the interdependence and necessity of these requirements for local acceleration. In particular, recent Van Allen Probes observations indicate that rapid (<1 hour) energization of seed electrons to MeV energies is associated with (substorm) injections of 10s keV to 100s keV electrons into the inner magnetosphere and the subsequent enhancement of VLF chorus band waves in the inner magnetosphere (e.g. Foster et al. 2014a).
The acceleration of electrons to MeV energies in the core of the outer zone of the radiation belt involves the local acceleration (Horne and Thorne 1998; Reeves et al. 2013; Thorne et al. 2013a; Summers et al. 1998) of a seed population of energetic electrons (e.g. Jaynes et al. 2015) in interactions with (very low frequency) VLF chorus waves. Thorne et al. (2013a) demonstrated that quasi-linear modeling of this local acceleration process could reproduce the observed recovery of the inner radiation belt electrons. Li et al. (2014) modeled the recovery of the radiation belt over the course of ∼24 hours by quasi-linear interactions with VLF chorus. Foster et al. (2014a) described Van Allen Probes observations of substorm electron injection and chorus amplification associated with the rapid recovery of the MeV electron population following a storm time depletion of radiation belt electrons. Lower energy injected electrons in the ∼10 to 80 keV range provide a source of free energy for VLF waves growth and subsequently are driven into the loss cone, precipitating into the atmosphere (e.g. Foster and Rosenberg 1976). At the same time, the high-energy tail of the electron distribution gains perpendicular energy from the waves and is accelerated (Summers et al. 1998; Albert 2002; Omura et al. 2007).
A detailed example is given by Van Allen Probes dual spacecraft particle and wave observations spanning a substorm during the large March 17, 2013 storm with onset near 15:50 UT, as shown in Figs. 22 and 23. Lower energy injected electrons (50 keV, Fig. 23 panel a) arrive promptly at the Van Allen Probe A position near \(L^{*} = 4.7\). The effects of their involvement in chorus amplification are already seen at this time, as particle distribution is driven toward loss cone pitch angles. Panel c of Fig. 23 shows the development of strong chorus wave activity in step with the electron injections. The multi-MeV radiation belt electron population (panel d) that had been significantly depleted earlier in the storm increases by 10x during the substorm interval (with respect to that measured before the substorm 1 hour earlier by Van Allen Probe B).
Storm–time changes in the 2.6 MeV electron fluxes observed at \(L^{*} = 4.0\) with the REPT instruments on both Van Allen Probes delineate the event time history of relativistic electron loss and recovery. Storm onset was at 06:15 UT on 17 March 2013 and prompt stepwise radiation belt energization accompanied substorm injections at 15:50 UT and 22:15 UT. Diamonds indicate the sequential observations by Probes A and B at \(L^{*} = 4.0\) (after Foster et al. 2017)
Local acceleration involves the enhancement of VLF chorus by lower energy injected electrons, and the subsequent energization of a seed population of higher energy electrons by the amplified waves. (a) RBSP-A MagEIS observations of injected >50 keV and (b) >150 keV electrons and (c) associated chorus emissions observed by EMFISIS-A are shown for the 15:50 UT substorm interval on March 17, 2013. The lower panel (d) shows the growing enhancement of 2.6 MeV electrons resulting from the local acceleration of the near-relativistic seed population (after Foster et al. 2017)
It should be noted here that ultra-relativistic electron acceleration in the outer belt can also take place under the influence of fast magnetosonic waves which are thought to take their energy from enhanced/unstable proton ring current distributions at 10 s of keV energies, as demonstrated by several studies using GOES and CRRES observations among others (Perraut et al. 1982; Meredith et al. 2008; Chen et al. 2016; Balikhin et al. 2015). For example, the production of electron butterfly distributions has recently been observed in Van Allen Probes data during a 2015 storm and was linked to parallel acceleration caused by Landau resonance with magnetosonic waves (Li et al. 2016). Details on this rich and non-linear process are still a matter of current research and are a good example of the importance of wave–particle interactions on the outer belt (e.g. Thorne 2010).
The rapid increase in MeV electron fluxes associated with substorm injections suggests that nonlinear processes, with associated rapid interaction time scales, play a significant role in the local acceleration process (Foster et al. 2017). Wave-electron interactions during the generation of VLF rising tones are strongly non-linear, leading the formation of a highly coherent wave structure. As a result, a fraction of the relativistic electron seed population at resonant energies can be trapped by waves, leading to significant non-adiabatic energy exchange. Direct observations show that chorus elements consist of a sequence of wave subpackets (e.g. Santolík et al. 2014) each spanning multiple wave cycles and delineating a single cycle of continuous wave growth and damping (Fig. 24).
For the strong VLF lower-band chorus rising tone seen at 16:56:30 in the lower panel, by RBSP-A during the March 17, 2013 storm, subpacket analysis of the single 180-msec chorus element is shown in the upper panel. The magnitude of the wave magnetic field in the plane perpendicular to B for individual wave cycles is shown in black. Clear modulation of the wave amplitude identifies a sequence of subpackets within the rising tone chorus element, each spanning multiple wave cycles. The instantaneous wave frequency determined from individual wave cycles is shown in blue (adapted from Foster et al. 2017)
For phase trapped resonant electrons with near-relativistic initial energies, well-developed subpackets at and around \(1/4\) \(f_{\mathrm{ce}}\) result in strong (>100 keV) energy gain through nonlinear relativistic turning acceleration (RTA) (Omura et al. 2007) for electrons with relativistic initial energies (Foster et al. 2017). Electrons with initial energy 100s keV–3 MeV can be accelerated by 50 keV–200 keV in resonant interactions with a single VLF rising tone on a time scale of 10–100 msec (Foster et al. 2017).
To illustrate the effect of nonlinear RTA acceleration on the evolution of the relativistic electron flux spectrum, we have iteratively applied the calculated nonlinear energy gain profile (Fig. 25) to the observed initial electron flux profile for the 17 March 2015 event. The evolution of the ratio of the modeled electron flux profile at \(L^{*}=4\) over 30 cycles of nonlinear RTA modeling indicates a 10x flux enhancement confined to low MeV energies and centered near 2 MeV. For electrons with 0.5 sec bounce period, and assuming that strong chorus waves are encountered only 1 percent of the time, the 30 cycles modeled would occur over 1500 sec. or ∼30 min the approximate characteristic time for the relativistic electron acceleration observed in this event. The good agreement between theory and observations indicates the efficiency of nonlinear interactions with chorus rising tones for accelerating a seed population of energetic electrons to MeV energies.
a) The ratio of the modeled electron flux increase at \(L^{*}=4\) after 30 cycles of nonlinear RTA acceleration to the initial profile indicates a 10x flux enhancement confined to los-MeV energies and centered near 2 MeV. (b) The electron flux increase determined as the ratio of RBSP-A to RBSP-B observations shows good qualitative agreement with the RTA theoretical predictions (Foster et al. 2017)
In aggregate, these observationally based calculations reinforce the conclusion that nonlinear acceleration processes are likely a fundamentally important part of local acceleration to relativistic levels, and that the very rapid time scales involved set a considerably faster minimum time scale for in-situ space weather effects at these energies than previously considered.
Energy gain for a single RTA interaction with the chorus rising tone shown in Fig. 24 is shown as a function of initial electron energy; B) the observed electron flux increase ratio at \(L^{*}=4\) is shown as the black curve. The nested blue curves indicate the iterative application of the RTA nonlinear energy gain to the observed initial electron flux profile over 30 cycles with 5% trapping ratio.
4.5 Shock Acceleration
Solar wind shocks are another process that produces significant space weather, through extremely fast acceleration of ultra-relativistic electrons deep within the radiation belts and inside the plasmasphere. Explosive eruptions on the Sun launch a supersonic blast wave of high-density particles that stream through the background solar wind. This solar wind shock front sweeps up the interplanetary magnetic field along its path, carrying significant particle and magnetic energy to Earth orbit in about one day’s time. The high-speed solar wind shock strikes a sledgehammer blow to the protective barrier of Earth’s magnetic field on the dayside, launching a powerful magnetosonic pulse that tears through the magnetosphere from front to back at speeds approaching 1000 km/sec. The strong electric field associated with this shock-induced pulse efficiently accelerates radiation belt electrons (Fig. 26). As the electrons circle the Earth, those with azimuthal velocity matching the magnetosonic pulse propagation speed can stay in the shock induced electric field for ∼100 sec, and gain significant energy (up to millions of electron volts) (e.g. Foster et al. 2015).
Relativistic electron flux increases in the 3.6 MeV channel from the REPT instrument on the Van Allen Probes A and B is shown. In the bottom panels, measurements electron flux in the 3.6 MeV REPT channel are shown as functions of pitch angle and time from each of the two Probes. The shock-driven electric field at each spacecraft is included in the upper panels for reference (after Foster et al. 2015)
Thus, prompt acceleration by impulsive shock-induced electric fields and subsequent ULF wave processes (Fig. 27) comprise a significant mechanism on space weather time scales of ∼10s to ∼100s of seconds for enhancing relativistic electron populations inside the plasmasphere and in the heart of the outer zone (e.g. Foster et al. 2015; Kanekal et al. 2016; Li et al. 1993; Blake et al. 1992). Of significance for space weather effects, shock acceleration can introduce nearly instantaneous, significant fluxes of ultra-relativistic electrons deep within the slot region where other electron acceleration processes are not operative (Blake et al. 1992).
Sequential Van Allen Probes A and B orbits during a shock event are shown. Arrows indicate the 20:22 UT time of shock observation at each spacecraft. At shock time, Probe B was at \(L^{*}\sim5\) and Probe A was further inward near \(L^{*}\sim3.3\). Rapid acceleration of 3.6 MeV electrons and subsequent periodic drift echoes were seen at each location (after Foster et al. 2015)
4.6 Solar Wind Drivers
Many studies have focused on the response of energetic electrons in the outer radiation belt to upstream solar wind conditions. It has been long recognized that energetic particles at geosynchronous Earth orbit (GEO) are modulated by solar wind forcing (e.g., Paulikas and Blake 1979; Baker et al. 1979, 1986, 1990; Blake et al. 1997; Reeves 1998; Mathie and Mann 2001; O’Brien et al. 2001; Li, 2001, 2004; Li et al. 2005, 2011; Lyatsky and Khazanov 2008a, 2008b; Borovsky and Denton 2009; Reeves et al. 2011; Boynton et al. 2013; Simms et al. 2016; Kellerman et al. 2015). Paulikas and Blake (1979), for example, analyzed energetic electron data from ATS-1, ATS-5 and ATS-6 spacecraft and found a pronounced positive correlation between the electron fluxes and solar wind speed. Concurrently and independently, Baker et al. (1979) found strong solar wind speed correlations with GEO electron fluxes as well. Baker et al. (1986), using data from the Spectrometer for Energetic Electrons (SEE) onboard two operational GEO satellites, showed a very good correlation between highly relativistic electrons and solar wind stream structures. Blake et al. (1997), based on measurements from a GEO satellite and the WIND spacecraft, presented a study of the correlation between relativistic electrons at GEO and properties of solar wind drivers during a solar minimum period. Their results indicated that relativistic electron enhancements are associated with a solar wind speed increase, but also with solar wind density increases and southward turnings of the IMF. Li (2001), using a model based on the radial diffusion equation, quantitatively predicted the electron fluxes at GEO based on solar wind velocity and IMF properties. They found a linear correlation of 0.9 between predicted and measured values for the period 1995–1996. The solar wind speed was found to be the most important factor in their prediction model.
Figure 28 is taken from Baker et al. (1979). It shows the temporal relationships between fluxes of moderate energy electrons (\(E \sim200\ \text{keV}\)) and highly relativistic electrons (\(E\sim1.5\ \text{MeV}\)) as compared to concurrent upstream solar wind speed. As is evident, the low-to-moderate energy electron fluxes at GEO track the solar wind speed quite closely in time while the very energetic electron fluxes are delayed by ∼2 days in time.
Top panel: Daily average fluxes of \(E\sim200\ \text{keV}\) and \(E\sim1.4\ \text{MeV}\) electrons at GEO for October 1976. Bottom panel: Solar wind speeds for the same period of time. Data show that ∼200 keV electrons track solar wind driver very closely in time while E 1 MeV electrons are delayed by 2–3 days (from Baker et al. 1979)
As mentioned in Sect. 4.2, Reeves et al. (2011) examined the relationship between relativistic electron fluxes at GEO and solar wind speed using LANL-GEO data from 1989 to 2010. Their results showed a triangle-shaped distribution of electron fluxes versus solar wind speed, indicating that the radiation belt electron fluxes can be high for essentially any concurrent solar wind speed. Li et al. (2011) emphasized that geomagnetic activity driven by a southward orientation of IMF is a necessary condition for MeV electron enhancements at GEO. Boynton et al. (2013), using the nonlinear autoregressive moving average approach, studied the relation between electron fluxes at GEO and various solar wind parameters. Their results suggested that for lower energy electrons, the solar wind speed is the most strongly controlling factor of electron fluxes at GEO. On the other hand, for MeV electrons, the solar wind speed 2 days preceding was found to be the most important factor in electron flux enhancements. This is consistent with the Baker et al. (1979) results shown in Fig. 28 here. Also, Wing et al. (2016), (Blake et al. 1992; Li et al. 1993) using information theory, investigated the solar wind driver for 1.8–3.5 MeV electrons at GEO. They showed that various solar wind parameters are causally related to 1.8–3.5 MeV electron fluxes at GEO while among all parameters the solar wind speed has shown to have the highest peak information transfer. These previous studies show the important role of solar wind on the dynamics of relativistic electrons at GEO.
There also have been statistical studies focusing on the electrons in the whole outer radiation belt and their relation to the solar wind parameters (e.g., Li et al. 1997a, 1997b; Baker et al. 1999; Iles et al. 2002; Vassiliadis et al. 2002; Mann et al. 2004; Rigler et al. 2007; Li et al. 2009). Iles et al. (2002), using >750 keV and >1 MeV electron data from two microsatellites, STRV-1a and 1b, which were in highly elliptical, near-equatorial orbits, studied the correlation between total relativistic electron content in the outer belt and solar wind and geomagnetic parameters during geomagnetic storms at the first six months of 1995. They found that the main requirements for relativistic electron enhancements were fast solar wind speed and fluctuating or southward IMF Bz. Baker et al. (2004b) constructed the radiation belt electron content index (RBC), which is a robust estimate of total relativistic electrons in the outer radiation belt, and showed that the RBC is well correlated with solar wind speed and the Dst index. The RBC index has proven very useful in its correlation with times of severe space weather anomalies as shown in Fig. 29.
The driving of magnetospheric processes by the solar wind has also been shown to be critical in radiation belt electron dynamics (e.g., Baker et al. 1990; Reeves 1998; Reeves et al. 2003; Li et al. 2009; Zhao and Li 2013; Jaynes et al. 2015). Geomagnetic storms and substorms play essential roles in transport and acceleration of radiation belt electrons. Reeves (1998) studied relativistic electron enhancement events at GEO from 1992 to 1995. He found correlation between maximum electron flux and minimum Dst, though geomagnetic storms were found to not necessarily cause flux enhancements. Li et al. (2009) analyzed total relativistic electron flux variations in the outer radiation belt during 18 storms from 1990 to 1991 and studied the statistical roles of storms and substorms on the radiation belt electron population. Substorm activity was well correlated with the net increases of total electron fluxes in the outer belt. Jaynes et al. (2015), using data from Van Allen Probes, studied the importance of source and seed populations in radiation belt electron variations and showed the crucial role of substorms in radiation belt electron acceleration. Most recently, Forsyth et al. (2016) examined the total radiation belt electron content variations following substorms and showed increases of total radiation belt electron content following substorms with a time lag of 1–3 days (see Baker et al. 1979, 2004b).
As the above review shows, the roles of solar wind and magnetospheric processes on the radiation belt electrons have been extensively studied. However, due to the limitations of observations, most previous studies only focused on relativistic electrons at GEO or on a very limited energy range. With the launch of Van Allen Probes, which provide clean radiation belt electron measurements in a wide \(L\) range with very fine energy resolution, researchers have been able to study the correlation between radiation belt electrons and solar wind parameters/geomagnetic indices and its dependence on the energy of electrons and \(L\) shell for the first time. Also, the majority of previous studies only examined the correlation between various parameters and radiation belt electron fluxes. However, these studies cannot rule out the influence of adiabatic effects in their statistical analyses, which can greatly affect the measured electron fluxes during geomagnetic storms especially at higher \(L\) shells.
In a very recent paper, Zhao et al. (2017), using data from the Magnetic Electron Ion Spectrometer (MagEIS) (Blake et al. 2013) and the Relativistic Electron–Proton Telescope (REPT) (Baker et al. 2013b) instruments of the Energetic Particle, Composition, and Thermal Plasma (ECT) suites (Spence et al. 2013) on the Van Allen Probes, have studied the relation between radiation belt electron phase space density (PSD) and solar wind parameters/geomagnetic indices while focusing on its dependence on the first adiabatic invariant \(\mu\) and \(L^{*}\) for a wide \(\mu\) and \(L^{*}\) range. Using the electron PSD instead of fluxes, they excluded the influence of the adiabatic effect and thus the actual effects of solar wind/magnetospheric processes on radiation belt electrons are appropriately highlighted. Besides the radiation belt electron PSD, Zhao et al. (2017) also show that the solar wind and magnetospheric processes play important roles in radiation belt electron acceleration by analyzing the relation between electron PSD enhancements and solar wind/geomagnetic parameters. Examples of such correlations are shown here in Fig. 30 from Zhao et al. (2017). Furthermore, the important role of substorms on radiation belt electron PSD enhancements and their prolonged effects are unveiled by this most recent work.
A scatterplot of dependences on (a) solar wind speed, (b) southward IMF Bz, (c) SYM-H index, and (d) AL index for electrons with the \(\mu=1000\ \text{MeV/G}\). These are phase space density by (PSD) enhancements at \(L^{*}=4.5\) using REPT data from the Van Allen Probes (from Zhao et al. 2017)
4.7 Loss Mechanisms
Despite decades of radiation belt research and monitoring, quantifying the total loss from the belts during both quiet and active times is a daunting task. Yet a part of this loss, in the form of precipitation to the atmosphere, contributes to the overall space weather effects on satellites and other technology in low to medium Earth orbit. There are many processes, usually acting in concert, which produce irreversible losses in the radiation belts. Several of these, such as the complimentary ring current expansion and inward magnetopause motion during active times, are discussed in the next section. Several different wave–particle interactions drive pitch angle scattering of relativistic and ultra-relativistic electrons and protons, which can result in loss from part or all of the full pitch angle distribution. We refer the readers to comprehensive reviews written previously on the subject (Summers et al. 2007; Thorne et al. 2010).
In addition, the Van Allen Probes era has produced a multitude of new studies on particle loss through wave–particle interactions. Notably, three main wave modes are likely responsible for the vast majority of particle losses in the inner magnetosphere by way of pitch angle scattering. VLF chorus can interact with lower energy electrons (up to ∼30 keV) to scatter them into the loss cone, which results in the optical consequence called diffuse aurora (Thorne et al. 2010). The more incoherent VLF hiss waves are resonant with a wide variety of electron energies, but pitch angle diffusion timescales vary drastically, and hiss are only present inside the high density of the Earth’s plasmasphere or plasmaspheric plumes (see next section). Recent work has been done to better parameterize the distribution and intensity of hiss wave power with respect to the plasmapause location, over varying local time and geomagnetic conditions (Malaspina et al. 2016). Finally, EMIC waves are known to interact strongly with highly energetic electrons in the MeV range, particularly during active storm times (Albert 2003; Summers and Thorne 2003). EMIC waves occur in frequency bands and new studies indicate that the H+-band is most efficient at scattering up to a few MeV, while the He+- and O+-bands are more significant for higher energies (Ni et al. 2015). Interestingly, Usanova et al. (2014) showed that EMIC waves primarily affect only the lower pitch angles, essentially leaving the core distribution unchanged.
The task of implementing newly parameterized waves in existing radiation belt models is a daunting one, but much progress has been made over the last several years (e.g. Orlova et al. 2014, 2016; Agapitov et al. 2015; Spasojevic et al. 2015; Drozodov et al. 2017). Still, these models cannot always predict the outcome in event-specific instances, since less is known about which loss mechanism may play a larger role at a given time.
One of the difficulties in determining the dominant loss mechanisms during a particular event is the lack of direct measurements of the precipitating particle population. The loss can be observed as a decay or a dropout of near-equatorial magnetosphere particles, but the low-altitude measurement is rarely available; thus, the loss could be an apparent loss to other energies or equatorial locations, rather than a true loss from the system. Several platforms are ideal for filling in this measurement gap. LEO CubeSats, for example, can make substantial contributions to our understanding of precipitation. The Colorado Student Space Weather Experiment (CSSWE) CubeSat (Li et al. 2012) measured radiation belt particles in the loss cone at low altitudes simultaneously with the Van Allen Probes mission, and characterized the precipitating portion of several radiation belt loss events (Li et al. 2013; Blum et al. 2013; Schiller et al. 2014; Jaynes et al. 2014). The Balloon Array for RBSP Relativistic Electron Losses (BARREL) mission of opportunity (Millan et al. 2013) was designed to fly at very low (sub-orbital) altitudes to quantify and constrain precipitation timescales, amounts, and locations. To date, they have flown four separate campaigns in conjunction with NASA’s Van Allen Probes. A major accomplishment of the mission was to find a distinct coherence between hiss wave modulation and variation in precipitation observed on the balloons (Breneman et al. 2015), leading to an enhanced understanding of overall radiation belt loss. The two generations of Focused Investigations of Relativistic Electron Burst Intensity, Range, and Dynamics (FIREBIRD) CubeSats (Spence et al. 2012) had the objective to spatially and temporally constrain microbursts, a type of magnetospheric wave thought to be responsible for sudden relativistic electron precipitation (Lorentzen et al. 2001). The second flight (FIREBIRD II) did indeed measure microburst precipitation and has provided the first in-situ confirmation of these spatial scales (Crew et al. 2016).
A sensor-fusion technique for studying loss from the radiation belts in detail incorporates in-situ wave measurements with conjunction observations from the ground using incoherent scatter radar instrumentation. Incoherent or Thomson scatter radars (Evans 1969) use radar scatter at VHF to UHF frequencies from thermal electron density fluctuations to directly probe the plasma state vector for the cold, dense plasma (∼0.1–0.4 eV) at the foot of inner magnetospheric field lines. Analysis of the very weak backscattered signal yields full ionospheric altitude profiles of ion and electron temperature, ion composition, electron density, and line-of-sight velocity. In particular, the electron density profile deep in the ionosphere at altitudes below 100 km is directly enhanced by precipitating medium energy particles >10 s of keV beyond those levels provided by solar EUV illuminations. With appropriate assumptions, inversion techniques can convert the radar observed ionospheric electron density profile to provide estimates of the incoming particle energy distribution (e.g. Semeter and Kamalabadi 2005). These can then be correlated with in-situ wave activity on orbiting platforms that are in magnetic conjunction with the ground based radar field of view to assess radiation belt loss and impacts on the dynamic atmosphere-ionosphere system. These impacts on such things as global circulation patterns and the production of molecules such as NOx are of intense interest in the middle atmosphere modeling community (cf. Sect. 5.3).
Another long-established technique for examining radiation belt losses to the atmosphere uses the relative ionospheric opacity meter (riometer), a broadband HF ground radio receiver system examining >25 keV electron precipitation levels through induced changes in received transionospheric signals originating from the relatively constant cosmic noise background (e.g. Hargreaves 1969). The mechanism behind the riometer principle involves enhanced electron density produced in the D region ionosphere, causing increased electron collision rates with sufficient frequency to attenuate HF radio waves transiting the atmosphere. Riometers can be used in event and statistical studies (e.g., Baker et al. 1981; Spanswick et al. 2007) and can also be used in infer temporal evolution of population fluxes from the overlying magnetosphere (Kellerman et al. 2015). Riometer technology has evolved from simpler wide beam systems to analog and now digital beam forming, wide frequency capture imaging systems, with the latter providing much better measurement precision and/or much higher spatial resolution for temporal and spatial precipitation loss studies (e.g., Honary et al. 2011).
5 Radiation Belt Coupling
5.1 Ring Current and Plasmasphere Coupling
The ring current is a westward-directed electric current carried by a toroidal population of ions surrounding Earth, often overlapping with both the outer radiation belt and the plasmasphere. The ring current varies in density and structure, but often exists between 2 and 9 \(R_{\mathrm{E}}\). Changes in composition can occur suddenly during times of geomagnetic storms and heightened geomagnetic activity; the source of ring current plasma can very during these times, with ionospheric outflow becoming dominant over protons of solar wind origin during storm times. For excellent reviews on the ring current, see Daglis et al. (1999) and Daglis and Kozyra (2002) along with Keika et al. (2013) summarizing work on inner magnetospheric O+ energization and associated ring current injection/pressure effects.
The Dst index is a measure of the ring current strength as measured from a network of ground-based magnetometer stations, and is central in space weather investigations. The so-called “Dst effect” (Li et al. 1997a, 1997b; Kim and Chan 1997) appears as adiabatic changes in electron populations during times of dramatic magnetic field changes that manifest as variations in the Dst index. The result can be a sudden loss or enhancement in radiation belt fluxes that appears to be real, but is in fact an entirely adiabatic reaction that eventually reverses as the Dst index recovers. The real loss and acceleration during the main phase of storms can therefore be very difficult to separate from this Dst effect, as all mechanisms are likely taking place concurrently.
Enhancements in the stormtime ring current can have direct impacts on radiation belt losses in two ways: through wave–particle interactions or through increased magnetopause shadowing due to diamagnetic effects. Electromagnetic ion-cyclotron (EMIC) waves are driven by unstable ring current proton distributions (e.g. Anderson and Hamilton 1993) and are able to produce losses of the very highest-energy radiation belt electrons and protons (Meredith et al. 2003). The other mechanism involves a pumping of the partial ring current by enhanced convection and repeated small-scale injections (Gkioulidou et al. 2014), thereby diamagnetically expanding electron drift orbits to a point where magnetopause shadowing (West et al. 1972) can have a greater effect on the core population (Ukhorskiy et al. 2006) and lead to dramatic dropout features in the observations (Shprits et al. 2006). This process irreversibly alters the content of the outer radiation belt region, and can lead to almost total drainage of the preexisting populations (Turner et al. 2014).
Acceleration events of relativistic electrons can also be influenced by ring current dynamics. Sustained periods of electron injections can build up and maintain the source and seed populations, which are required to produce relativistic and ultra-relativistic electrons. Chorus wave growth, which plays a central role in relativistic electron enhancements, is driven by temperature anisotropies in ring current energy electrons (Sudan 1964; Kennel and Petschek 1966). See Sect. 4.4 for more details on this process.
The plasmasphere is a cold, dense toroidal plasma population that typically extends from the ionosphere out to an extremely variable outer boundary known as the plasmapause (e.g., Carpenter and Lemaire 2004). The plasmapause varies in local time, and can be as low as 2 \(R_{\mathrm{E}}\) or as far out as >6 RE, depending on geomagnetic activity (Chappell 1972). There is often much structure observed in the plasmapause/plasmasphere boundary layer, including persistent features such as the duskside bulge and plume region (Darrouzet et al. 2009). Plasmaspheric densities are often dramatically restructured during large geomagnetic storm events due to e.g. coronal interaction region or coronal mass ejection impacts. Afterwards, several processes act to refill the pre-storm population from the ionosphere through e.g. field-aligned diffusion, charge exchange, and cross-field transport. During recovery phases, the rate of field-aligned refilling is quite slow (∼days) and therefore variability in local plasmaspheric densities can be accordingly quite high during dynamic conditions associated with repeated storms. Even after more than five decades of study (see review by Singh and Horwitz 1992), plasmasphere refilling dynamics and their impacts on overall plasmasphere structuring are still a subject of intense study with many unsolved problems (Gallagher and Comfort 2016).
The dynamic plasmasphere has long been recognized as a key agent in radiation belt configurations due to multiple interaction pathways between the cold plasma and more energetic particles. Early work showed a clear correlation between the plasmapause location and innermost extent of the multi-MeV electron outer radiation belt (Li et al. 2006). However, more recent detailed observations across a wide range of energies have revealed that the relationship between the plasmapause and relativistic electrons is complex and highly energy- and activity-dependent (Reeves et al. 2016). The plasmapause can provide both a protective effect as well as causing greater loss rates, depending on the energy of the electrons and their location within the magnetic field. The primary loss mechanism for radiation belt electrons within the plasmasphere is by cyclotron resonance interactions with VLF hiss waves. This wave mode is fairly efficient at pitch angle scattering relativistic electrons into the loss cone (Thorne et al. 1973). At lower L-shells, the resonance is more favorable for higher energies (Summers et al. 2007) and thus the outer radiation belt can be quickly carved out by the location of the plasmasphere and the hiss contained within. Several models have attempted to quantify this loss rate in a parameterized sense (e.g. Orlova et al. 2014), but event-specific studies have also shown faster loss rates for relativistic electrons than previously predicted (Jaynes et al. 2014), thus this is still an open question.
The lifetimes for relativistic electrons due to hiss scattering vary with magnetic field strength, magnetic local time, electron energy, and geomagnetic activity. In addition to this constant loss mechanism, radial diffusion is at work in this region, although it acts much more slowly here than in the outer belt region. Therefore, the dynamics inside the plasmasphere are a complicated balance of inward diffusion and slow scattering losses, highly dependent on the location and portion of the population being observed. There are times when the plasmasphere can retreat quickly, allowing for acceleration at very high energies to take place just outside the plasmapause boundary at low L-shells. After a time, the plasmasphere can refill to higher radial distances, effectively enveloping the newly accelerated electrons in a protective shell, as during the formation of the third belt in September 2012 (Baker et al. 2013a). Deep inside the plasmasphere, ultra-relativistic electrons can have lifetimes of 10’s to 100’s of days. Coupled with very slow diffusion rates, this means that a so-called remnant belt can persist for a long time untouched inside the plasmasphere (Fig. 31).
A long-lived remnant belt of ultra-relativistic energies protected by a refilled plasmasphere. Reprinted from Baker et al. (2013a)
5.2 Ionosphere Coupling
5.2.1 Ionospheric Plasma in the Magnetosphere
In the inner magnetosphere at \(L\) shells \(<{\sim}4\), high density solar-produced ionospheric plasma is redistributed upward along closed magnetic field lines until a diffusive equilibrium (Angerami and Thomas 1964) is reached between ion species partial pressures and gravity. The underlying ionosphere is the source of the overlying plasmasphere and the plasmasphere can be considered as the high-altitude extension of the topside F region ionosphere. Disturbance effects observed in the ionosphere and magnetosphere during geomagnetic disturbances, and their space weather effects, have a direct relation to processes occurring in the plasmasphere boundary layer (PBL) (Carpenter and Lemaire 2004), the boundary between the corotating field lines of the plasmasphere and the outer magnetosphere. This section discusses space weather phenomena observed near this outer boundary of the coupled plasmasphere–mid-latitude ionosphere with an emphasis on related effects in the radiation belts. The dense low energy plasmas of the ionosphere and plasmasphere play a significant role in modulating the wave–particle interactions (WPI) that are very important for both radiation belt energization and loss. In general, an increase in density inhibits local acceleration, and an increase in heavy ions generates EMIC waves that produce loss of relativistic electrons. Interactions with waves of both natural (e.g. Thorne et al. 2013a) and anthropogenic origin (e.g. Foster et al. 2016) are important. The redistribution of low energy plasma of ionospheric origin into the high-latitude outer magnetosphere (cf. Foster 2016) creates density gradients and localized structure that influence radiation belt space weather effects.
5.2.2 Cold Plasma Redistribution
The theoretical study of Summers et al. (1998) pointed out the importance cold plasma density in modulating the interactions of magnetospheric waves and electrons. Figure 32A, based on that work, describes the relationship of cold plasma density structure in the magnetosphere to regions where RB interactions with VLF chorus, hiss, and EMIC waves would be important. The plasmaspheric plume, the plasmapause, and the characteristics of the plasmasphere boundary layer are important regions in this regard.
(A) Schematic representation of cold plasma density structures in the magnetospheric equatorial plane (the plasmapause and plasmaspheric plume) indicates their relationship to the regions where electron interactions with different wave modes are important (after Summers et al. 1998). (B) The orbits of the Van Allen Probes spacecraft intersect the plume and the plasmapause (shown with mapped GPS TEC observations) facilitating the investigation of these significant space weather wave particle interactions
During disturbed conditions, magnetosphere–ionosphere coupling processes at the plasmasphere boundary layer drive a large-scale redistribution of cold ionospheric/plasmaspheric plasma through the geospace system. Foster (1993) investigated the disturbed mid-latitude ionosphere using scanning observations with the Millstone Hill incoherent scatter radar that provided a two-dimensional picture of the evolution of ionospheric F region structure. Spatially extended sunward convecting density enhancements seen immediately equatorward of the dusk-sector ionospheric trough were termed storm-enhanced density (SED). SED was observed as a continuous plume of ionospheric plasma spanning a large portion of the postnoon to midnight sector (Fig. 33A). The study concluded that SED plasma was transported sunward (westward) in the sub-auroral polarization stream (SAPS, Foster and Vo 2002) at speeds of ∼1 km/s. SED flows at ionospheric altitudes provide significant heavy ion fluxes into the high latitude F-region cusp ionosphere with magnitude \({\geq} 1.0 \times 10^{14}\ \text{m}^{-2}\,\text{s}^{-1}\) (Foster et al. 2004, 2014b; Erickson et al. 2011; Makarevich et al. 2009, 2011). In this way a continuous stream of ionospheric plasma is carried in the convective flow channel from low latitudes in the evening sector to the cusp and into the polar cap at noon (Fig. 33B) creating a tongue of ionization (TOI, Foster et al. 2005) stretching across the polar cap to the midnight sector. In general, an increase in density inhibits local acceleration, and an increase in heavy ions generates EMIC waves that produce loss of relativistic electrons.
(A) Azimuth scan observations with the Millstone Hill radar provide a spatial “snapshot” of a continuous stream of plasma carried from low latitudes in the evening sector to the cusp and polar cap. The observations of ionospheric electron density were made over a ∼30 minute interval near the noon meridian and are plotted in latitude//longitude coordinates with north at the top. (B) Aggregation of 5 minutes of northern hemisphere GPS TEC observations provided global imagery of a nearly-identical feature some 30+ years later during a March 2013 storm. Presented in polar local time geodetic coordinates with noon at the top, the plume extending poleward from North America is seen to stretch anti-sunward across polar latitudes and to merge into the auroral oval in the midnight sector. The orbital track of a DMSP satellite crossing polar latitudes is shown as a black line. (C) Space based imagery of the outer extent of the plasmasphere depicts the erosion and sunward extension of the cold plasma plume. An IMAGE EUV snapshot looking down on the plasmasphere and plume from above north polar latitudes is shown. (D) GPS TEC observations, when mapped along the magnetic field into the magnetospheric equatorial plane, reveal plasma boundaries closely reproducing the evolution of the geospace plume at magnetospheric heights, indicating its full sunward extension to the magnetopause
A geospace system perspective of SED has been provided with distributed ground-based Global Positioning System (GPS) observations of TEC (Foster et al. 2002) and with space-based imagery of the outer plasmasphere by the IMAGE EUV instrument (Goldstein and Sandel 2005). Combining these ground and space-based plasma imaging techniques, Foster et al. (2002) demonstrated that the ionospheric SED plume was magnetically connected to the low altitude signature of a drainage plume (plasmaspheric tail) associated with the stormtime erosion of the outer plasmasphere (Figs. 33C and 33D). Outflowing cold ionospheric plasma can have large effects on the radiation belts due to mechanisms such as inhibition of local relativistic acceleration processes through detuning of cyclotron resonances which depend on cold plasma density (Abel and Thorne 1998a, 1998b). The O+ rich ion content of these flows also is a source of EMIC waves that are known to be highly efficient loss mechanisms for relativistic particles (e.g. Jordanova et al. 2008).
The combination of ground based (e.g. radar or GPS TEC) observations with in situ Van Allen Probes or MMS observations of waves and electrons, as depicted in Fig. 33B, has addressed the radiation belt associated space weather effects of SAPS (fundamental magnetosphere–ionosphere electrodynamic coupling agent) and cold plasma plumes in the \(L=4-8+\) region in the post-noon sector (e.g. Foster et al. 2014a; Erickson et al. 2016). Substorms also influence SAPS occurrence (e.g., Makarevich et al. (2009, 2011) leading to plume-related space weather effects.
The characteristic interrelationship of outer plasmaspheric M–I coupling phenomena to the density structure at the PBL and their relationship to the inward extent of MeV RB electrons are shown in Fig. 34 for disturbed storm-recovery conditions.
The relationship of the SAPS, the ring current, and the geospace plume were observed by Van Allen Probe A as its near-equatorial outbound orbit crossed the plasmasphere boundary layer at 18 MLT during the 17 March 2015 storm. (A) In situ plasma density observations identified the plume near its point of formation near \(L\sim3\). (B) Strong radially outward electric fields (red curve; azimuthal component is shown in blue) were observed across the SAPS flow channel responsible for the sunward advection of outer plasmaspheric ions in the geospace plume. (C) A ‘nose’ of hot ring current O+ ions extended across the region of SAPS electric field. Ring current pressure gradients associated with the hot ions drive the SAPS convection. (D) The Earthward extent of the recovering outer zone multi-MeV electrons falls within the region of SAPS, ring current, plume PBL interactions
Very sharp cold plasma density gradients can develop in the mid-latitude ionosphere as the result of strong M–I coupling effects during magnetic disturbances. Plasma transport in combination with flow-dependent collisional ion-neutral recombination can produce a deep low-density ionospheric trough associated with strong SAPS flows (Schunk and Walker 1969; Anderson et al. 1991). An example of the steep ionospheric density gradients observed during a major storm is shown in Fig. 35 using GPS TEC observations.
The TEC gradients across the poleward edge of the SED plume observed over the central US at two times during the 20 November 2003 storm are shown. TEC in excess of 180 TECu is observed equatorward of the PBL gradients. The steep decreases in TEC with latitude across the PBL extend over ∼2 deg of latitude with a characteristic gradient of −85 TECu per deg of latitude. Such gradients constitute a severe space weather hazard for positioning and navigation systems
The magnetosphere–ionosphere coupling effects producing the sharp ionospheric density gradients do not only affect the ionosphere, but, owing to their electrodynamic nature, map along magnetic field lines into the outer plasmasphere. At these locations, they are associated with steep electron density gradients seen along the outer edge of the erosion plume in the dusk sector (e.g. Figure 34). The cold plasma density gradient at the plasmapause fundamentally controls the stability of injected electrons for wave–particle interactions generating VLF chorus rising tones. Importantly, in those nonlinear interactions, the ∼50 keV electrons give up perpendicular energy to the VLF waves and are rapidly precipitated into the atmosphere. This process was illustrated in the study of Foster and Rosenberg (1976) as shown in Fig. 36.
(A) Cyclotron interactions between 20–80 keV electrons and VLF waves on field lines near the cold plasma density gradient at the PBL (B) lead to the generation of VLF chorus rising tones and scatter substorm-injected electron (C) into the atmospheric loss cone. (D) The cyclotron resonant energy drops sharply into the energy range of the injected electrons as the cold plasma density increases. (E) Bursts of precipitating electrons (seen with a balloon-borne X-ray detector) are correlated on a one-to-one basis with bursts of chorus rising tones (Foster and Rosenberg 1976)
Simultaneously, plasma wave effects in the form of discrete chorus rising tones within the inner magnetosphere undergo nonlinear interactions with the high-energy tail of the electron population, rapidly accelerating electrons to multi-MeV energies (Foster et al. 2017). These effects constitute important space weather features. Figure 23 (above) illustrates the rapid recovery of the MeV RB electron population observed simultaneously with the M–I coupling and density structure shown in Fig. 34. Multi-MeV electron fluxes increased by a factor of 10 over 1-hour interval in the low-density region immediately outside the PBL in association with ∼100 keV electron injection and the generation of strong VLF chorus rising tones.
The examples provided in this section have concentrated on the processes associated with the interaction of lower energy and relativistic electrons with VLF chorus and the effect of ambient cold density on those processes. A similar scenario could be presented for the density dependence of the electron interactions with VLF hiss and EMIC waves at other regions in the inner magnetosphere. More generally, results of these recent studies underline the fundamental conclusion that the dynamic variations of the highest energy radiation belt electrons are closely coupled to the characteristics of the lowest energy (ionospheric) particle populations.
5.3 Middle Atmospheric Coupling
Part of the radiation belt electron population is continuously lost to the Earth’s atmosphere. When wave–particle interactions scatter electrons into the bounce loss cone, they penetrate to low-enough altitudes (∼100 km) and deposit their energy in collisions with atmospheric gas molecules instead of mirroring back to higher altitudes. This process, termed “electron precipitation”, takes place in the auroral and sub-auroral latitudes, is strongly driven by the solar wind and geomagnetic storms (as radiation belt processes are in general), and leads to ionization and dissociation of atmospheric molecules (see Baker et al. 1987b).
Energetic electron precipitation from the outer radiation belt (from now on denoted RBE) is one of the several populations of energetic particles ionizing the atmosphere (e.g. Verronen and Rodger 2015). In addition to RBE, CME-driven solar proton events (SPE) and substorm-driven auroral electron (AE) precipitation are also important. At high-latitude (\(L = 2\text{--}7\)) mesospheric altitudes, RBE ionization dominates over AE and protons (except during strong SPEs which, however, are infrequent) while mesospheric ionization caused by solar ultraviolet and X-ray radiation and galactic cosmic rays is typically marginal. The energy of an electron determines its atmospheric penetration depth and the altitude region of ionization. Thus, RBE with energy between about 30 keV and 1 MeVs is most important for mesospheric altitudes (90–50 km) (see Fig. 37).
Energetic particle precipitation (EPP) can lead to important changes in the neutral composition of the atmosphere at high polar latitudes (Sinnhuber et al. 2012). Most studied have been the production of a) odd hydrogen HOx (H + OH + HO2) through chemistry associated with ion pair production, water cluster ion formation, and subsequent recombination; and b) odd nitrogen NOx (N + NO + NO2) through dissociation of molecular nitrogen via charged particle impact and ion chemistry. Production of HOx and NOx is important because these species participate in catalytic chemical reactions that play a key role in the ozone balance of the mesosphere and stratosphere, respectively. Both short-term (days) and longer-term (weeks) ozone depletion has been observed after strong precipitation events, e.g. SPEs (Reid et al. 1991; Jackman et al. 2001; Seppälä et al. 2004).
Most of the precipitating electrons deposit their energy in the mesosphere-lower thermosphere (MLT) region. Unlike HOx, which can directly affect ozone at mesospheric altitudes, the produced NOx needs to be transported from MLT down to the upper stratosphere in order to have an impact on ozone. The NOx descent can only take place in the winter pole, inside the polar vortex, which restricts mixing with low-NOx air in the lower latitudes. In the absence of solar radiation, NOx has a long chemical lifetime and is thus subject to transport. Many observational studies have shown NOx descent to take place during individual winters (Callis and Lambeth 1998; Siskind et al. 2000; Randall et al. 2009; Päivärinta et al. 2013), and a decadal analysis of satellite data has shown that NOx descent is in fact occurring over every winter, in both hemispheres (Funke et al. 2014a, 2014b). The amount of NOx, however, varies from year-to-year with respect to electron forcing and polar vortex dynamics, the South typically having more NOx in the stratosphere than the North (Fig. 38).
EPP-produced, excess NOy (\(\text{NO}_{x} + \text{NO}_{x}\) converted to other nitrogen species, in ppmv mixing ratio) descent observed between 2002 and 2012 by the MIPAS instrument. Upper panel: latitudes between 70 and 90 degrees South. Lower panel: the same but for North. Adopted from Funke et al. (2014b)
Direct, mesospheric impacts of RBE have been recently quantified using satellite-based OH observations. At geomagnetic latitudes between 55 and 72 degrees, there is a clear and robust connection between satellite-based measurements of RBE fluxes and mesospheric OH concentration (Verronen et al. 2011; Andersson et al. 2012), with strong RBE significantly increasing night-time OH (Fig. 39). Impacts are observed down to about 50 km altitude but not below, which indicates that even during the strongest RBE periods the fluxes of MeV electrons are too low to enhance OH above its background concentration. The strongest effects are seen during the declining phase of the solar cycle while practically no effect was seen during the geomagnetically record-low year of 2009. The longitudinal distribution of the OH response follows the geomagnetic latitudes in both hemispheres and indicates a more inhomogeneity in the Southern Hemisphere polar region (Andersson et al. 2014b), similar to those seen in satellite-based RBE flux observations. While there is a stronger OH signature in the sector poleward of the South Atlantic Anomaly (SAA) region when compared to other longitudes, the SAA region itself shows no OH response. This indicates negligible fluxes of >100 keV RBE in the SAA region.
Relation between OH concentration at 71–78 km and count rate of precipitating electrons in the outer radiation belt as observed by the MLS/Aura and MEPED/POES instruments, respectively. Shown are daily mean data in March 2005 and April 2006 (blue dots). Horizontal and vertical blue lines mark the standard error of the mean. The red solid and dashed lines mark a line fit and its estimated standard deviation \(r\) is the correlation coefficient. The counts/s measured by the MEPED instrument can be converted to “normal” electron flux units (cm−2 s−1 sr−1) by multiplying the count rate by 100. Reproduced from Verronen et al. (2011)
Connected to the OH response discussed above, there are also studies analyzing the response of mesospheric ozone from satellite-based measurements, considering both daily variability during RBE events (individual as well statistical) and long-term variability over (partial) solar cycle (Verronen et al. 2013; Andersson et al. 2014a). Unlike in the case of HOx, the ozone response is not strictly limited to the magnetic latitudes of the radiation belts but is observed over a more extended area in the polar cap region. This is because, in addition to chemistry, ozone is also affected by atmospheric dynamics on daily time scales. During strong RBE events, mesospheric ozone can decrease by tens of percent due to RBE driven HOx enhancements (Fig. 40). The magnitude and duration of the ozone effect depends on the RBE event but also on the atmospheric state, e.g., the effect is relatively larger in the winter pole. The higher frequency of the events during solar active years leads to ozone variability by up to tens of percent on solar cycle timescales as well.
Short-term RBE effects on mesospheric ozone at geomagnetic latitudes between 55 and 65 degrees, North and South. Results are from a superposed epoch analysis of the 60 largest RBE events between 2002 and 2012. Relative ozone anomalies from the GOMOS instrument are shown in color scale, and count rates of 100–300 keV electrons (ECR) from the MEPED/POES instrument with the black line. Day zero marks the beginning of RBE events. Reproduced from Andersson et al. (2014a)
It has been suggested for a long time that the RBE contributes to polar NOx production in the MLT region (Callis et al. 1996, 1998). However, distinguishing the contribution of RBE to the mesospheric NOx budget is not straightforward using observations only. This is because the RBE-NOx produced in the mesosphere is mixing in with large amounts of NOx produced by auroral electrons above the mesopause. Both descend from MLT to the upper stratosphere during winter months. For specific years, there are studies reporting increases in mesospheric NOx ranging from 100% to orders of magnitude due to in-situ production by RBE (Clilverd et al. 2009; Newnham et al. 2011). Over decadal time scales, however, the majority of mesospheric NOx enhancement in wintertime has been reported to be due to descent of auroral NOx from the lower thermosphere (Sinnhuber et al. 2011), with considerable in-situ production occurring above 70 km only (Sinnhuber et al. 2016). Nevertheless, any NOx produced by RBE below the mesopause is more likely to descend to the upper stratosphere and affect ozone, because at the mesopause the wintertime mean circulation changes vertical direction to from downward below to upward above (Smith et al. 2011).
Understanding the response of upper stratospheric ozone on the descending NOx has been challenging because of its relatively large overall variability due to atmospheric dynamics (e.g. Päivärinta et al. 2013). Nevertheless, satellite observations has been shown that polar upper stratospheric ozone can be depleted locally by 40–60% during winters of exceptionally strong NOx descent (Randall et al. 1998, 2005). A recent study using satellite data between 1979 and 2014 has revealed a long-term response of Southern Hemispheric stratospheric ozone to RBE activity over the solar cycle, with an average ozone depletion of about 10–15% at 30–45 km altitude (Damiani et al. 2016). Another study, using observations between 2005 and 2010, reported 5–10% negative EPP response of Southern Hemispheric polar ozone at 25–50 km over the winter months (Fytterer et al. 2015). All these studies, however, discuss the combined ozone effect due to EPP total without separating the RBE contribution.
In atmospheric simulations, RBE impact can be separated. However, there have been serious issues with the quality and characteristics of available satellite-based data. Most useful long-term data sets of RBE fluxes have been provided by the instruments aboard the POES satellites, but even these data have restrictions concerning their applicability to atmospheric modeling (Rodger et al. 2010a). The measurement setup allows only part of the bounce loss cone fluxes (i.e. fluxes of precipitating electrons) to be measured, with a limited energy resolution. Based on ground-based ionospheric observations, it has been suggested that precipitating fluxes might be underestimated by as much as a factor of 10 (Hendry et al. 2012; Clilverd et al. 2012). On the other hand, the underestimation seems to be restricted to low-to-medium geomagnetic activity periods because a comparison of modeled and observed concentrations of mesospheric OH indicates a reasonable agreement during geomagnetic storms (Verronen et al. 2013). Contamination by energetic protons is another issue that has to be carefully considered (Rodger et al. 2010a). Despite these difficulties, precipitation models have been created based on the POES (and other) data for 3-D, long-term atmospheric applications. For example, the AIMOS model uses statistical maps of precipitation, scaled with observed electron fluxes to provide global RBE (and other EPP) forcing data from year 2002 onwards (Wissing and Kallenrode 2009). Recently, a RBE model driven by geomagnetic indices has been created for multi-decadal climate simulations (Van de Kamp et al. 2016) as a part of the solar forcing recommendation for Coupled Model Intercomparison Project Phase 6 (CMIP6) (Matthes 2016). An example of the model output, in Fig. 41, shows RBE forcing patterns on a world map and demonstrates the variability from solar maximum to minimum. To date, there are a few atmospheric modeling studies addressing the separate impact of RBE on the upper stratospheric and mesospheric composition (Codrescu et al. 1997; Semeniuk et al. 2011; Arsenovic et al. 2016). All these studies, ranging from monthly to solar-cycle time scales, suggest a considerable RBE contribution to EPP-driven polar stratospheric NOx and ozone variability. In the mesosphere, it is already evident that RBE is the main driver of HOx and ozone response. Although the work is still on-going, especially in terms of simulating the climate effects over several solar-cycles, uncertainties in the RBE forcing remain such that the assessment of its importance would benefit from improved satellite-based flux observations and their representation in models.
Yearly average, zonal mean mesospheric ionization rates due to RBE, calculated using the model by Van de Kamp et al. (2016). The model provides data at \(L\) shells 2 to 10, white areas indicate no data
Ozone is one of the most important minor species in the middle atmosphere. It is a strong absorber of solar UV radiation and long-wave radiation from the surface, and thus important to the temperature balance and dynamics. It has been suggested that the polar ozone variability caused by energetic particle precipitation (including RBE), could connect to the troposphere and cause regional variability of up to 5 K in ground-level wintertime average temperatures over the solar cycle, in regions of Europe and North America (Rozanov et al. 2005; Seppälä et al. 2009; Baumgaertner et al. 2011; Maliniemi et al. 2013). The most likely physical explanation is the so-called top-down mechanism (Gray et al. 2010; Maycock and Misios 2015). It connects ozone and dynamical changes in the stratosphere to modulation of the North Atlantic Oscillation, which is a large-scale mode (i.e., pattern) of climate variability around the North Atlantic. Although the RBE-climate connection has been reproduced in some climate simulations, so far the magnitude of the ground-level temperature variations have been underestimated compared to observations, and the details of the complex chemical-dynamical mechanism are not yet fully understood. A recent summary by Clilverd et al. (2016) gives a more detailed discussion on the proposed ground-level climate effects of RBE.
In summary, there is now a wealth of evidence of RBE effects in polar, wintertime atmosphere. In the mesosphere, substantial amounts of HOx are produced, and this causes ozone response in time scales ranging from days to the solar cycle. NOx production is probably an important addition to the indirect effect on upper stratospheric ozone through NOx descent. The combination of ozone responses in both the mesosphere and stratosphere is likely needed to understand the suggested coupling to the troposphere and regional climate variability over the solar cycle.
6 Summary and Future Directions
As described in this chapter, the Earth’s radiation belts were the first great discovery of the Space Age. With the realization that near-Earth space was filled with very energetic particles, there was recognition of the deleterious effects that could be produced in spacecraft and biological systems flying in space. The space weather impacts of the radiation belts have only increased over the past six decades as humans have used space more and more intensively for communication, navigation, reconnaissance, weather forecasting, and countless other applications. Deeper physical understanding of the radiation belts and their temporal variations has become a pressing requirement in the modern age.
In this chapter we have reviewed the structure and dynamics of the radiation belts from a scientific perspective. We have described our present understanding of the acceleration, transport, and loss of particles across the inner Van Allen zone, the slot region, and the outer Van Allen belt. We have shown how recent comprehensive observations have revealed new and unexpected aspects of the radiation belt properties. While many features of the radiation belts depend on external forcing of the system by the ambient solar wind near Earth, there still is a pressing requirement to make continual observations throughout the belts. The complexity and diversity of responses of both inner and outer zone properties are quite striking and, thus, we still do not have the knowledge to predict radiation belt properties at key locations based solely upon solar and solar wind forcing parameters.
As described in this chapter, the radiation belts are an integral part of the overall magnetospheric environment of Earth. As such, the Van Allen belts are intimately coupled to the ring current, plasmasphere, ionosphere, and magnetotail regions of our planet. The ebb and flow of cold plasmas and the electromagnetic waves these plasmas support play an essential role in the acceleration and loss of radiation belt particles. We also are finding new evidence that human activities such as powerful ground-based radio transmitters can directly affect the structure and dynamics of the radiation belts.
Quite importantly, there is ample evolving evidence that the loss of radiation belt particles into the Earth’s atmosphere can have profound effects on the chemistry and electrodynamic state of our planet. This means that the coupling from the radiation belts into the mesosphere and stratosphere must be actively considered as contributing to the richly varying properties of the overall atmospheric system. This fact amplifies the importance of studying and monitoring the state of Earth’s radiation belts now and into the future.
References
B. Abel, R.M. Thorne, Electron scattering loss in Earth’s inner magnetosphere 1. Dominant physical processes. J. Geophys. Res. 103(A2) (1998a). doi:10.1029/97JA02919
B. Abel, R.M. Thorne, Electron scattering loss in Earth’s inner magnetosphere 2. Sensitivity to model parameters. J. Geophys. Res. 103(A2) (1998b). doi:10.1029/97JA02920
O.V. Agapitov, A.V. Artemyev, D. Mourenas, F.S. Mozer, V. Krasnoselskikh, Empirical model of lower band chorus wave distribution in the outer radiation belt. J. Geophys. Res. 120, 10425 (2015)
J.M. Albert, Nonlinear interaction of outer zone electrons with VLF waves. Geophys. Res. Lett. 29(8) (2002). doi:10.1029/2001GL013941
J.M. Albert, Evaluation of quasi-linear diffusion coefficients for EMIC waves in a multispecies plasma. J. Geophys. Res. 108(A6), 1249 (2003). doi:10.1029/2002JA009792
J.M. Albert, M.J. Starks, R.B. Horne, N.P. Meredith, S.A. Glauert, Quasi-linear simulations of inner radiation belt electron pitch angle and energy distributions. Geophys. Res. Lett. 43, 2381–2388 (2016). doi:10.1002/2016GL067938
A.F. Ali, S.R. Elkington, W. Tu, L.G. Ozeke, A.A. Chan, R.H.W. Friedel, Magnetic field power spectra and magnetic radial diffusion coefficients using CRRES magnetometer data. Rev. Geophys. Space Phys. 120, 973–995 (2015). doi:10.1002/2014JA020419
A.F. Ali, D.M. Malaspina, S.R. Elkington, A.N. Jaynes, A.A. Chan, J. Wygant, C.A. Kletzing, Electric and magnetic radial diffusion coefficients using the Van Allen probes data. J. Geophys. Res. Space Phys. 121, 9586–9607 (2016). doi:10.1002/2016JA023002
J.H. Allen, Historical and recent solar activity and geomagnetic storms affecting spacecraft operations, in Proc. GOMAC, Modern Space Syst. Issues, Monterey, CA (2002)
B.J. Anderson, D.C. Hamilton, Electromagnetic ion cyclotron waves stimulated by modest magnetospheric compressions. J. Geophys. Res. 98(A7) (1993). doi:10.1029/93JA00605
P.C. Anderson, R.A. Heelis, W.B. Hanson, The ionospheric signatures of rapid subauroral ion drifts. J. Geophys. Res. 96(A4), 5785–5792 (1991). doi:10.1029/90JA02651
B.R. Anderson, R.M. Millan, G.D. Reeves, R.H.W. Friedel, Acceleration and loss of relativistic electrons during small geomagnetic storms. Geophys. Res. Lett. 42, 10,113–10,119 (2015). doi:10.1002/2015GL066376
M.E. Andersson, P.T. Verronen, S. Wang, C.J. Rodger, M.A. Clilverd, B. Carson, Precipitating radiation belt electron and enhancements of mesospheric hydroxyl during 2004–2009. J. Geophys. Res. 117(D09), 304 (2012). doi:10.1029/2011JD017246
M.E. Andersson, P.T. Verronen, C.J. Rodger, M.A. Clilverd, A. Seppälä, Missing driver in the Sun–Earth connection from energetic electron precipitation impacts mesospheric ozone. Nat. Commun. 5 (2014a). doi:10.1038/ncomms6197
M.E. Andersson, P.T. Verronen, C.J. Rodger, M.A. Clilverd, S. Wang, Longitudinal hotspots in the mesospheric OH variations due to energetic electron precipitation. Atmos. Chem. Phys. 14, 1095–1105 (2014b). doi:10.5194/acp-14-1095-2014
J.J. Angerami, J.O. Thomas, Studies of planetary atmospheres: 1. The distribution of electrons and ions in the Earth’s exosphere. J. Geophys. Res. 69(21), 4537–4560 (1964). doi:10.1029/JZ069i021p04537
P. Arsenovic, E. Rozanov, A. Stenke, B. Funke, J.M. Wissing, K. Mursula, F. Tummon, T. Peter, The influence of Middle Range Energy Electrons on atmospheric chemistry and regional climate. J. Atmos. Sol.-Terr. Phys. 20 (2016). doi:10.1016/j.jastp.2016.04.008
D.N. Baker, How to cope with space weather. Science 297, 1486–1487 (2002). doi:10.1126/science.1074956
D.N. Baker, Specifying and forecasting space weather threats to human technology, in Effects of Space Weather on Technology Infrastructure, ed. by I.A. Daglis (Kluwer, New York, 2004), pp. 1–25
D.N. Baker, L.J. Lanzerotti, Space weather. Am. J. Phys. 84, doi.org/10.1119/1.4938403 (2016)
D.N. Baker, P.R. Higbie, R.D. Belian, E.W. Hones, Do Jovian electrons influence the terrestrial outer radiation zone? Geophys. Res. Lett. 6, 531–534 (1979). doi:10.1029/GL006i006p00531
D.N. Baker, P. Stauning, E.W. Hones Jr., P.R. Higbie, R.D. Belian, Near equatorial, high-resolution measurements of electron precipitation and L≅6.6. J. Geophys. Res. 86, 2295 (1981)
D.N. Baker, J.B. Blake, R.W. Klebesadel, P.R. Higbie, Highly relativistic electrons in the Earth’s outer magnetosphere: 1. Lifetimes and temporal history 1979–1984. J. Geophys. Res. 91(A4), 4265–4276 (1986)
D.N. Baker, R.D. Belian, P.R. Hibgie, J.B. Blake, Deep dielectric charging effects due to high energy electrons in Earth’s outer magnetosphere. J. Electrost. 20(3) (1987a). doi:10.1016/0304-3886(87)90082-9
D.N. Baker, J.B. Blake, D.J. Gorney, P.R. Higbie, R.W. Klebesadel, J.H. King, Highly relativistic magnetospheric electrons: a role in coupling to the middle atmosphere? Geophys. Res. Lett. 14, 1027-10–1027-30 (1987b). doi:10.1029/GL014i010p01027
D.N. Baker, R.L. McPherson, T.E. Cayton, R.W. Klebesadel, Linear prediction filter analysis of relativistic electron properties at 6.6 RE. J. Geophys. Res. 95(A9), 15133–15140 (1990). doi:10.1029/JA095iA09p15133
D.N. Baker, G.M. Mason, O. Figueroa, G. Colon, J.G. Watzin, R.M. Aleman, An overview of the Solar, Anomalous, and Magnetospheric Particle Explorer (SAMPEX) mission. IEEE Trans. Geosci. Remote Sens. 31(3), 531–541 (1993). doi:10.1109/36.225519
D.N. Baker, S.G. Kanekal, J.B. Blake, B. Klecker, G. Rostoker, Satellite anomalies linked to electron increase in the magnetosphere. Eos 75(35), 401–405 (1994). doi:10.1029/94EO01038
D.N. Baker, S.G. Kanekal, T.I. Pulkkinen, J.B. Blake, Equinoctial and solstitial averages of magnetospheric relativistic electron: a strong semiannual modulation. Geophys. Res. Lett. 26(20), 3193–3196 (1999). doi:10.1029/1999GL003638
D.N. Baker, S.G. Kanekal, X. Li, S.P. Monk, J. Goldstein, J.L. Burch, An extreme distortion of the Van Allen belt arising from the ‘Hallowe’en’ solar storm in 2003. Nature 432, 878–881 (2004a). doi:10.1038/nature03116
D.N. Baker, S.G. Kanekal, J.B. Blake, Characterizing the Earth’s outer Van Allen zone using a radiation belt content index. Space Weather 2, S02003 (2004b). doi:10.1029/2003SW000026
D.N. Baker, S.G. Kanekal, R.B. Horne, N.P. Meredith, S.A. Glauert, Low-altitude measurements of 2–6 MeV electron trapping lifetimes at \(1.5\leq L \leq 2.5\). Geophys. Res. Lett. 34(20), L20110 (2007). doi:10.1029/2007GL031007
D.N. Baker, S.G. Kanekal, V.C. Hoxie, M.G. Henderson, X. Li, H.E. Spence, S.R. Elkington, R.H. Friedel, J. Goldstein, M.K. Hudson, G.D. Reeves, R.M. Thorne, C.A. Kletzing, S.G. Claudepierre, A long-lived relativistic electron storage ring embedded within the Earth’s outer Van Allen Radiation Zone. Science 340, 186–190 (2013a). doi:10.1126/science.1233518
D.N. Baker, S.G. Kanekal, V.C. Hoxie, S. Batiste, M. Bolton, X. Li, S.R. Elkington, S. Monk, R. Reukauf, S. Steg, J. Westfall, C. Belting, B. Bolton, D. Braun, B. Cervelli, The Relativistic Electron–Proton Telescope (REPT) instrument on Board the Radiation Belt Storm Probes (RBSP) spacecraft: characterization of Earth’s radiation belt high-energy particle Populations. Space Sci. Rev. 179 (2013b). doi:10.1007/s11214-012-9950
D.N. Baker, A.N. Jaynes, V.C. Hoxie, R.M. Thorne, J.C. Foster, X. Li, J.F. Fennell, J.R. Wygant, S.G. Kanekal, P.J. Erickson, W. Kurth, W. Li, Q. Ma, Q. Schiller, L. Blum, D.M. Malaspina, A. Gerrard, L.J. Lanzerotti, An impenetrable barrier to ultra-relativistic electrons in the Van Allen Radiation Belt. Nature 515, 531–534 (2014a). doi:10.1038/nature13956
D.N. Baker, A.N. Jaynes, Z. Li, M.G. Henderson, S.G. Kanekal, G.D. Reeves, H.E. Spence, S.G. Claudepierre, J.F. Fennell, M.K. Hudson, R.M. Thorne, J.C. Foster, P.J. Erickson, D.M. Malaspina, J.R. Wygant, A. Boyd, C.A. Kletzing, A. Drozdov, Y.Y. Shprits, Gradual diffusion and punctuated phase space density enhancements of highly relativistic electrons: Van Allen Probes observations. Geophys. Res. Lett. 41(5), 1351–1358 (2014b)
D.N. Baker, A.N. Jaynes, S.G. Kanekal, J.C. Foster, P.J. Erickson, J.F. Fennell, J.B. Blake, H. Zhao, Z. Li, S.R. Elkington, M.G. Henderson, G.D. Reeves, H.E. Spence, C.A. Kletzing, J.R. Wygant, Highly relativistic radiation belt electron acceleration, transport, and loss: large solar storm events of March and June 2015. J. Geophys. Res. Space Phys. 121(7), 6647–6660 (2016). doi:10.1002/2016JA022502
M.A. Balikhin, Y.Y. Shprits, S.N. Walker, L. Chen, N. Cornilleau-Wehrlin, I. Dandouras, O. Saantolik, C. Carr, K.H. Yearby, B. Weiss, Observations of discrete harmonics emerging from equatorial noise. Nat. Commun. 6, 7703 (2015). doi:10.1038/ncomms8703
J.L. Barth, C.S. Dyer, E.G. Stassinopoulos, Space, atmospheric and terrestrial radiation environment. IEEE Trans. Nucl. Sci. 50, 466–482 (2003)
A.J.G. Baumgaertner, A. Seppälä, P. Jöckel, M.A. Clilverd, Geomagnetic activity related NOx enhancements and polar surface air temperature variability in a chemistry climate model: modulation of the NAM index. Atmos. Chem. Phys. 11, 4521–4531 (2011). doi:10.5194/acp-11-4521-2011
J.B. Blake, W.A. Kolasinski, R.W. Fillius, E.G. Mullen, Injection of electrons and protons with energies of 10 s of MeV into \(L < 3\) on March 24, 1991. Geophys. Res. Lett. 19, 821–824 (1992). doi:10.1029/92GL00624
J.B. Blake, D.N. Baker, N. Turner, K.W. Ogilvie, R.P. Lepping, Correlation of changes in the outer-zone relativistic electron population with upstream solar wind and magnetic field measurements. Geophys. Res. Lett. 24(8) (1997). doi:10.1029/97GL00859
J.B. Blake et al., The Magnetic Electron Ion Spectrometer (MagEIS) instruments aboard the Radiation Belt Storm Probes (RBSP) spacecraft. Space Sci. Rev. 179 (2013). doi:10.1007/s11214-013-9991-8
L.W. Blum, Q. Schiller, X. Li, R. Millan, A. Halford, L. Woodger, New conjunctive CubeSat and balloon measurements to quantify rapid energetic electron precipitation. Geophys. Res. Lett. 40, 5833–5837 (2013). doi:10.1002/2013GL058546
J.E. Borovsky, M.H. Denton, Relativistic-electron dropouts and recovery: a superposed epoch study of the magnetosphere and the solar wind. J. Geophys. Res. 114, A02201 (2009). doi:10.1029/2008JA013128
A.J. Boyd, H.E. Spence, C.-L. Huang, G.D. Reeves, D.N. Baker, D.L. Turner, S.G. Claudepierre, J.F. Fennel, J.B. Blake, Y.Y. Shprits, Statistical properties of the radiation belt seed population. J. Geophys. Res. 121(8), 7636–7646 (2016)
R.J. Boynton et al., The analysis of electron fluxes at geosynchronous orbit employing a NARMAX approach. J. Geophys. Res. 118 (2013). doi:10.1002/jgra.50192
A.W. Breneman et al., Observations of a global coherence scale modulation of radiation belt electron loss resulting from plasmaspheric hiss. Nature 523, 193–195 (2015). doi:10.1038/nature14515
J.C. Cain, Models of the Earth’s magnetic field, in Radiation Trapped in the Earth’s Magnetic Field, ed. by B. McCormac (Gordon and Breach, Newark NJ, 1966)
L.B. Callis, J.D. Lambeth, NOy formed by precipitating electron events in 1991 and 1992: descent into the stratosphere as observed by ISAMS. Geophys. Res. Lett. 25, 1875–1878 (1998). doi:10.1029/98GL01219
L.B. Callis, R.E. Boughner, D.N. Baker, R.A. Mewaldt, J.B. Blake, R.S. Selesnick, J.R. Cummings, M. Natarajan, G.M. Mason, J.E. Mazur, Precipitation electrons: evidence for effects on mesospheric odd nitrogen. Geophys. Res. Lett. 23, 1901–1904 (1996). doi:10.1029/96GL01787
L.B. Callis, M. Natarajan, D.S. Evans, J.D. Lambeth, Solar atmospheric coupling by electrons (SOLACE) 1. Effects of the May 12, 1997 solar event on the middle atmosphere. J. Geophys. Res. 103, 28,405–28,419 (1998)
D.L. Carpenter, J. Lemaire, The plasmasphere boundary layer. Ann. Geophys. 22, 4291–4298 (2004). doi:10.5194/angeo-22-4291
C.R. Chappell, Recent satellite measurements of the morphology and dynamics of the plasmasphere. Rev. Geophys. 10(4), 951–979 (1972). doi:10.1029/RG010i004p00951
L. Chen, A. Hasegawa, Kinetic theory of geomagnetic pulsations: 1. Internal excitations by energetic particles. J. Geophys. Res. 96(A2), 1503–1512 (1991). doi:10.1029/90JA02346
L. Chen, J. Sun, Q. Lu, X. Gao, Z. Xia, Z. Zhima, Generation of magnetosonic waves over a continuous spectrum. J. Geophys. Res. Space Phys. 121, 1137–1147 (2016). doi:10.1002/2015JA022089
S.G. Claudepierre, S.R. Elkington, M. Wiltberger, Solar wind driving of magnetospheric ULF waves: pulsations driven by velocity shear at the magnetopause. J. Geophys. Res. 113, A05218 (2008). doi:10.1029/2007JA012890
S.G. Claudepierre, I.R. Mann, K. Takahashi, J.F. Fennell, M.K. Hudson, J.B. Blake, J.L. Roeder, J.H. Clemmons, H.E. Spence, G.D. Reeves, D.N. Baker, H.O. Funsten, R.H.W. Friedel, M.G. Henderson, C.A. Kletzing, W.S. Kurth, R.J. MacDowall, C.W. Smith, J.R. Wygant, Van Allen, Probes observation of localized drift resonance between poloidal mode ultra-low frequency waves and 60 keV electrons. Geophys. Res. Lett. 40, 4491–4497 (2013). doi:10.1002/grl.50901
S.G. Claudepierre, T.P. O’Brien, J.B. Blake, J.F. Fennell, J.L. Roeder, J.H. Clemmons, M.D. Looper, J.E. Mazur, T.M. Mulligan, H.E. Spence, G.D. Reeves, R.H.W. Friedel, M.G. Henderson, B.A. Larsen, A background correction algorithm for Van Allen Probes MagEIS electron flux measurements. J. Geophys. Res. Space Phys. 120(7) (2015). doi:10.1002/2015JA021171
S.G. Claudepierre, T.P. O’Brien, J.F. Fennell, J.B. Blake, J.H. Clemmons, M.D. Looper, J.E. Mazur, J.L. Roeder, D.L. Turner, G.D. Reeves, H.E. Spence, The hidden dynamics of relativistic electrons (0.7–1.5 MeV) in the inner zone and slot region. J. Geophys. Res. Space Phys. 122(3) (2017). doi:10.1002/2016JA023719R
M.A. Clilverd, A. Seppälä, C.J. Rodger, M.G. Mlynczak, J.U. Kozyra, Additional stratospheric NOx production by relativistic electron precipitation during the 2004 spring NOx descent event. J. Geophys. Res. 114 (2009). doi:10.1029/2008JA013472
M.A. Clilverd, C.J. Rodger, D. Danskin, M.E. Usanova, T. Raita, T. Ulich, E.L. Spanswick, Energetic particle injection, acceleration, and loss during the geomagnetic disturbances which upset Galaxy 15. J. Geophys. Res. 117(A12), 213 (2012). doi:10.1029/2012JA018175
M.A. Clilverd, C.J. Rodger, M.E. Andersson, A. Seppälä, P.T. Verronen, Linkages between the radiation belts, polar atmosphere and climate, in Electron Precipitation Through Wave Particle Interactions, Waves, Particles, and Storms in Geospace, ed. by G. Balasis, I.A. Daglis, I.R. Mann (Oxford University Press, Oxford, 2016)
M.V. Codrescu, T.J. Fuller-Rowell, R.G. Roble, D.S. Evans, Medium energy particle precipitation influences on the mesosphere and lower thermosphere. J. Geophys. Res. 102(A9) (1997). doi:10.1029/97JA01728
A.B. Crew, H.E. Spence, J.B. Blake, D.M. Klumpar, B.A. Larsen, T.P. O’Brien, S. Driscoll, M. Handley, J. Legere, S. Longworth, K. Mashburn, E. Mosleh, N. Ryhajlo, S. Smith, L. Springer, M. Widholm, First multipoint in situ observations of electron microbursts: initial results from the NSF FIREBIRD II mission. J. Geophys. Res. Space Phys. 121(6), 5272–5283 (2016). doi:10.1002/2016JA022485
J.R. Cummings, A.C. Cummings, R.A. Mewaldt, R.S. Selesnick, E.C. Stone, T.T. Von Rosenvinge, J.B. Blake, SAMPEX measurements of heavy ions trapped in the magnetosphere. IEEE Trans. Nucl. Sci. 40(6) (1993)
I.A. Daglis, J.U. Kozyra, Outstanding issues of ring current dynamics. J. Atmos. Sol.-Terr. Phys. 64(2) (2002)
I.A. Daglis, R.M. Thorne, W. Baumjohann, S. Orsini, The terrestrial ring current: origin, formation, and decay. Rev. Geophys. 37(4), 407–438 (1999). doi:10.1029/1999RG900009
E.J. Daly, J. Lamaire, D. Heynderickx, D.J. Rodgers, Problems with models of the radiation belts. IEEE Trans. Nucl. Sci. 43(2) (1996). doi:10.1109/23.490889
A. Damiani, B. Funke, M.L. Santee, R.R. Cordero, S. Watanabe, Energetic particle precipitation: a major driver of the ozone budget in the Antarctic upper stratosphere. Geophys. Res. Lett. 43, 3554–3562 (2016). doi:10.1002/2016GL068279
F. Darrouzet et al., Plasmaspheric density structures and dynamics: properties observed by the CLUSTER and IMAGE missions. Space Sci. Rev. 145(55) (2009). doi:10.1007/s11214-008-9438-9
A.Y. Drozodov, Y.Y. Shprits, M.E. Usanova, N.A. Aseev, A.C. Kellerman, H. Zhu, EMIC wave parameterization in the long-term VERB code simulation. J. Geophys. Res. 122, 8488 (2017)
J.W. Dungey, Effects of the electromagnetic perturbations on particles trapped in the radiation belts. Space Sci. Rev. 4, 199 (1965)
S.R. Elkington, M.K. Hudson, A. Chan, Acceleration of relativistic electrons via drift-resonant interaction with toroidal-mode Pc-5 ULF oscillations. Geophys. Res. Lett. 26(21), 3273–3276 (1999). doi:10.1029/1999GL003659
S.R. Elkington, M.K. Hudson, A.A. Chan, Resonant acceleration and diffusion of outer zone electrons in an asymmetric geomagnetic field. J. Geophys. Res. 108(A3), 1116 (2003). doi:10.1029/2001JA009202
P.J. Erickson et al., Multipoint MMS observations of fine-scale SAPS structure in the inner magnetosphere. Geophys. Res. Lett. 43 (2016). doi:10.1002/2016GL069174
P.J. Erickson, F. Beroz, M.Z. Miskin, Statistical characterization of the American sector subauroral polarization stream using incoherent scatter radar. J. Geophys. Res. 116, A00J21 (2011). doi:10.1029/2010JA015738
J.V. Evans, Theory and practice of ionosphere study by Thomson scatter radar. Proc. IEEE 57(4), 496–530 (1969)
C.-G. Fälthammar, Effects of time-dependent electric fields on geomagnetically trapped radiation. J. Geophys. Res. 70(11), 2503–2516 (1965). doi:10.1029/JZ070i011p02503
Y. Fei, A.A. Chan, S.R. Elkington, M.J. Wiltberger, Radial diffusion and MHD particle simulations of relativistic electron transport by ULF waves in the September 1998 storm. J. Geophys. Res. 111, A12209 (2006). doi:10.1029/2005JA011211
J.F. Fennell, J.B. Blake, R. Friedel, S.G. Kanekal, The energetic electron response to magnetic storms: HEO satellite observations, in The Inner Magnetosphere: Physics and Modeling, ed. by T. Pulkkinen, Friedel. Geophysical Monograph, vol. 155 (2005). doi:10.1029/155GM10
J.F. Fennell, S.G. Kanekal, J.L. Roeder, Storm responses of radiation belts during solar cycle 23: HEO satellite observations, in Dynamics of the Earth’s Radiation Belts and Inner Magnetosphere, ed. by D. Summers, I.R. Mann, D.N. Baker, M. Schulz. Geophysical Monograph Series, vol. 199 (American Geophysical Union, Washington, D.C., 2012). doi:10.1029/2012GM001356
J.F. Fennell, S.G. Claudepierre, J.B. Blake, T.P. O’Brien, J.H. Clemmons, D.N. Baker, H.E. Spence, G.D. Reeves, Van Allen Probes show that the inner radiation zone contains no MeV electrons: ECT/MagEIS data. Geophys. Res. Lett. 42(5), 1283–1289 (2015). doi:10.1002/2014GL062874
J.F. Fennell, J.B. Blake, S. Claudepierre, J. Mazur, S.G. Kanekal, P. O’Brien, D.N. Baker, W. Crain, D. Mabry, J. Clemmons, Current energetic particle sensors. J. Geophys. Res. 121(9) (2016). doi:10.1002/2016JA022588
C. Forsyth, I.J. Rad, K.R. Murphy, M.P. Freeman, C.-L. Huang, H.E. Spence, A.J. Boyd, J.C. Coxon, C.M. Jackman, N.M.E. Kalmoni, C.E.J. Watt, J. Geophys. Res. (2016). Virtual issue. doi:10.1002/2016JA0022620
J.C. Foster, Storm-time plasma transport at middle and high latitudes. J. Geophys. Res. 98(A2), 1675–1689 (1993). doi:10.1029/92JA02032
J.C. Foster, Cold plasma redistribution throughout geospace. Sci. China, Technol. Sci. 59(9), 1340–1345 (2016). doi:10.1007/s11431-016-6047-9
J.C. Foster, T.J. Rosenberg, Electron precipitation and VLF emissions associated with cyclotron resonance interactions near the plasmapause. J. Geophys. Res. 81(13), 2183–2192 (1976). doi:10.1029/JA081i013p02183
J.C. Foster, H.B. Vo, Average characteristics and activity dependence of the subauroral polarization stream. J. Geophys. Res. 107(A12), 1475 (2002). doi:10.1029/2002JA009409
J.C. Foster, P.J. Erickson, A.J. Coster, J. Goldstein, F.J. Rich, Ionospheric signatures of plasmaspheric tails. Geophys. Res. Lett. 29(13) (2002). doi:10.1029/2002GL015067
J.C. Foster, A.J. Coster, P.J. Erickson, F.J. Rich, B.R. Sandel, Stormtime observations of the flux of plasmaspheric ions to the dayside cusp/magnetopause. Geophys. Res. Lett. 31(8) (2004). doi:10.1029/2004GL020082
J.C. Foster, A.J. Coster, P.J. Erickson, J.M. Holt, F.D. Line, W. Rideout, M. McCready, A. van Eyken, R.J. Barnes, R.A. Greenwald, F.J. Rich, Multiradar observations of the polar tongue of ionization. J. Geophys. Res. 110(A9), A09S31 (2005). doi:10.1029/2004JA010928
J.C. Foster, P.J. Erickson, D.N. Baker, S.G. Claudepierre, C.A. Kletzing, W. Kurth, G.D. Reeves, S.A. Thaller, H.E. Spence, Y.Y. Shprits, Prompt energization of relativistic and highly relativistic electrons during a substorm interval: Van Allen Probes observations. Geophys. Res. Lett. 41(1), 20–25 (2014a). doi:10.1002/2013GL058438
J.C. Foster, P.J. Erickson, A.J. Coster, S. Thaller, J. Tao, J.R. Wygant, J.W. Bonnell, Storm time observations of plasmasphere erosion flux in the magnetosphere and ionosphere. Geophys. Res. Lett. 41(3), 762–768 (2014b). doi:10.1002/2013GL059124
J.C. Foster, J.R. Wygant, M.K. Hudson, A.J. Boyd, D.N. Baker, P.J. Erickson, H.E. Spence, Shock-Induced Prompt Relativistic Electron Acceleration in the Inner Magnetosphere. J. Geophys. Res. 120(3) (2015). doi:10.1002/2014JA020642
J.C. Foster, P.J. Erickson, D.N. Baker, A.N. Jaynes, E.V. Mishin, J.F. Fennell, Z. Li, M.G. Henderson, S.G. Kanekal, Observations of the impenetrable barrier, the plasmapause, and the VLF bubble during the 17 March 2015 storm. J. Geophys. Res. Space Phys. 121(6), 5537–5548 (2016). doi:10.1002/2016JA022509
J.C. Foster, P.J. Erickson, Y. Omura, D.N. Baker, C.A. Kletzing, S.G. Claudepierre, Van Allen Probes observations of prompt MeV radiation belt electron acceleration in non-linear interactions with VLF Chorus. J. Geophys. Res. Space Phys. 122(1) (2017). doi:10.1002/2016JA023429
B. Funke, M. López-Puertas, L. Holt, C.E. Randall, G.P. Stiller, T. von Clarmann, Hemispheric distributions and interannual variability of NOy produced by energetic particle precipitation in 2002–2012. J. Geophys. Res. 119, 13.565–13.582 (2014a). doi:10.1002/2014JD022423
B. Funke, M. López-Puertas, G.P. Stiller, T. von Clarmann, Mesospheric and stratospheric NOy produced by energetic particle precipitation during 2002–2012. J. Geophys. Res. 119, 4429–4446 (2014b). doi:10.1002/2013JD021404
T. Fytterer, M.G. Mlynczak, H. Nieder, K. Perot, M. Sinnhuber, G. Stiller, J. Urban, Energetic particle induced intra-seasonal variability of ozone inside the Antarctic polar vortex observed in satellite data. Atmos. Chem. Phys. 15, 3327–3338 (2015). doi:10.5194/acp-15-3327-2015
D.L. Gallagher, R.H. Comfort, Unsolved problems in plasmasphere refilling. J. Geophys. Res. Space Phys. 121, 1447–1451 (2016). doi:10.1002/2015JA022279
M. Gkioulidou, A.Y. Ukhorskiy, D.G. Mitchell, T. Sotirelis, B.H. Mauk, L.J. Lanzerotti, The role of small-scale ion injections in the buildup of Earth’s ring current pressure: Van Allen Probes observations of the 17 March 2013 storm. J. Geophys. Res. Space Phys. 119, 7327–7342 (2014). doi:10.1002/2014JA020096
J. Goldstein, B.R. Sandel, The global pattern of evolution of plasmaspheric drainage plumes, 1–22, in Inner Magnetosphere Interactions: New Perspectives from Imaging, ed. by J. Burch, M. Schultz (AGU Press, Washington, DC, 2005). doi:10.1029/159GM02
T.I. Gombosi, D.N. Baker, A. Balogh, P.J. Erickson, J.D. Huba, L.J. Lanzerotti, Anthropogenic space weather. Space Sci. Rev. 212(3–4), 985–1039 (2017), this issue. doi:10.1007/s11214-017-0357-5
W.D. Gonzalez, B.T. Tsurutani, Criteria of interplanetary parameters causing intense magnetic storms (\(Dst < -100\ \text{nT}\)). Planet. Space Sci. 35, 1101–1109 (1987). doi:10.1016/0032-0633(87)90015-8
L.J. Gray, J. Beer, M. Geller, J.D. Haigh, M. Lockwood, K. Matthes, U. Cubasch, D. Fleitmann, G. Harrison, L. Hood, J. Luterbacher, G.A. Meehl, D. Shindell, B. van Geel, W. White, Solar influences on climate. Rev. Geophys. 48, 75 RG4001 (2010). doi:10.1029/2009RG000282
J.K. Hargreaves, Auroral absorption of HF radio waves in the ionosphere: a review of results from the First Decade of Riometry. Proc. IEEE 57(8), 1348–1371 (1969)
M.D. Hartinger, D.L. Turner, F. Plaschke, V. Angelopoulos, H. Singer, The role of transient ion foreshock phenomena in driving Pc5 ULF wave activity. J. Geophys. Res. Space Phys. 118, 299–312 (2013). doi:10.1029/2012JA018349
A. Hasegawa, Drift mirror instability in the magnetosphere. Phys. Fluids 12, 2642 (1969)
D. Hastings, H. Garrett, Spacecraft–Environment Interactions (Cambridge University Press, Cambridge, 1996)
A.T. Hendry, C.J. Rodger, M.A. Clilverd, N.R. Thomson, S.K. Morley, T. Raita, Rapid radiation belt losses occurring during high speed solar wind stream driven storms: importance of energetic electron precipitation, in Dynamics of the Earth’s Radiation Belts and Inner Magnetosphere, ed. by D. Summers, I.R. Mann, D.N. Baker, M. Schulz. American Geophysical Union Monograph, vol. 199 (American Geophysical, Union, 2012), pp. 213–223. doi:10.1029/2012GM001299
F. Honary, N. Borisov, M. Beharrell, A. Senior, Temporal development of the magnetic zenith effect, 116(A6) (2011). doi:10.1029/2010JA0116029
R.B. Horne, R.M. Thorne, Potential waves for relativistic electron scattering and stochastic acceleration during magnetic storms. Geophys. Res. Lett. 15, 3011–3014 (1998). doi:10.1029/98GL01002
R.B. Horne, R.M. Thorne, S.A. Glauert, J.M. Albert, N.P. Meredith, R.R. Anderson, Timescale for radiation belt electron acceleration by whistler mode chorus waves. J. Geophys. Res. 110, A03225 (2005). doi:10.1029/2004HA010811
R.H.A. Iles et al., The relativistic electron response in the outer radiation belt during magnetic storms. Ann. Geophys. 20, 957–965 (2002)
C.H. Jackman, R.D. McPeters, G.J. Labow, E.L. Fleming, C.J. Praderas, J.M. Russell, Northern hemisphere atmospheric effects due to the July 2000 solar proton events. Geophys. Res. Lett. 28, 2883–2886 (2001)
J.A. Jacobs, Y. Kato, S. Matsushita, V.A. Troitskaya, Classification of geomagnetic micropulsations. J. Geophys. Res. 69, 180–181 (1964). doi:10.1029/JZ069i001p00180
A.N. Jaynes, X. Li, Q.G. Schiller, L.W. Blum, W. Tu, B. Ni, J. Bortnik, D.N. Baker, S.G. Kanekal, J.B. Blake, J. Wygant, Evolution of relativistic outer belt electrons during an extended quiescent period. J. Geophys. Res. Space Phys. 119, 9558–9566 (2014). doi:10.1002/2014JA020125
A.N. Jaynes, D.N. Baker, H.J. Singer, J.V. Rodriguez, T.M. Loto’aniu, A.F. Ali, S.R. Elkington, Z. Li, S.G. Kanekal, S.G. Claudepierre, J.F. Fennell, W. Li, R.M. Thorne, C.A. Kletzing, H.E. Spence, G.D. Reeves, Source and seed populations for relativistic electrons: Their roles in radiation belt changes. J. Geophys. Res. Space Phys. 120(9) (2015). doi:10.1002/2015JA021234
V.K. Jordanova, J. Albert, Y. Miyoshi, Relativistic electron precipitation by EMIC waves from self-consistent global simulations. J. Geophys. Res. 113, A00A10 (2008). doi:10.1029/2008JA013239
S.G. Kanekal, D.N. Baker, J.F. Fennell, A. Jones, Q. Schiller, I.G. Richardson, X. Li, D.L. Turner, S. Califf, S.G. Claudepierre, L.B. Wilson III., A. Jaynes, J.B. Blake, G.D. Reeves, H.E. Spence, C.A. Kletzing, J.R. Wygant, Prompt acceleration of magnetospheric electrons of ultrarelativistic energies by the 17 March 2015 interplanetary shock. J. Geophys. Res. (2016). virtual issue. doi:10.1002/2016JA022596
R. Kataoka, Y. Miyoshi, Why are relativistic electrons persistently quiet at geosynchronous orbit in 2009? Space Weather 8, s08002 (2010). doi:10.1029/2010SW000571
K. Keika, L.M. Kistler, P.C. Brandt, Energization of O+ ions in the Earth’s inner magnetosphere and the effects on ring current buildup: a review of previous observations and possible mechanisms. J. Geophys. Res. Space Phys. 118, 4441–4464 (2013). doi:10.1002/jgra.50371
A.C. Kellerman, Y.Y. Shprits, On the influence of solar wind conditions on the outer-electron radiation belt. J. Geophys. Res. (2012). doi:10.1029/2011JA017253
A.C. Kellerman, Y.Y. Shprits, D.L. Turner, A Geosynchronous Radiation-belt Electron Empirical Prediction (GREEP) model. Space Weather 11, 463–475 (2013). doi:10.1002/swe.29974
A.C. Kellerman, Y.Y. Shprits, D. Kondrashov, D. Subbotin, R.A. Makarevich, E. Donovan, T. Nagai, Three-dimensional data assimilation and reanalysis of radiation belt electrons: Observations of a four-zone structure using five spacecraft and the VERB code. J. Geophys. Res., Space Phys. 119 (2014). doi:10.1002/2014JA020171
A.C. Kellerman, Y.Y. Shprits, R.A. Makarevich, E. Spanswick, E. Donovan, G. Reeves, Characterization of the energy-dependent response of riometer absorption. J. Geophys. Res. Space Phys. 120, 615–631 (2015). doi:10.1002/2014JA020027
C.F. Kennel, H.E. Petschek, Limit on stably trapped particle fluxes. J. Geophys. Res. 71(1), 1–28 (1966). doi:10.1029/JZ071i001p00001
H.-J. Kim, A.A. Chan, Fully adiabatic changes in storm time relativistic electron fluxes. J. Geophys. Res. 102(A10), 22107–22116 (1997). doi:10.1029/97JA01814
K.-C. Kim, Y.Y. Shprits, J.B. Blake, Fast injection of the relativistic electrons into the inner zone and the formation of the Split-zone structure during the Bastille Day storm in July 2000. J. Geophys. Res. 121(9) (2016)
M.G. Kivelson, D.J. Southwood, Hydromagnetic waves and the ionosphere. Geophys. Res. Lett. 15(11) (1988). doi:10.1029/GL015i011p01271
B. Klecker, M.C. McNab, J.B. Blake, D.C. Hamilton, D. Hovestadt, H. Kaestle, Charge state of anomalous cosmic ray nitrogen, oxygen, and neon: SAMPEX observations. Astrophys. J. 442 (1995)
X. Li, Quantitative prediction of radiation belt electrons at geostationary orbit based on solar wind measurements. Geophys. Res. Lett. 28(9) (2001)
X. Li, Variations of 0.7–6.0 MeV electrons at geosynchronous orbit as a function of solar wind. Space Weather 2 (2004). doi:10.1029/2003W000017
X. Li, I. Roth, M. Temerin, J.R. Wygant, M.K. Hudson, J.B. Blake, Simulation of the prompt energization and transport of radiation belt particles during the March 14, 1991 SSC. Geophys. Res. Lett. 20(22), 2423–2426 (1993). doi:10.1029/93GL02701
X. Li, D.N. Baker, M. Temerin, D. Larson, R.P. Lin, G.D. Reeves, M. Looper, S.G. Kanekal, R.A. Mewaldt, Are energetic electrons in the solar wind the source of the outer radiation belt? Geophys. Res. Lett. 24(8) (1997a)
X. Li, D.N. Baker, M. Temerin, T.D. Cayton, E.G.D. Reeves, R.A. Christensen, J.B. Blake, M.D. Looper, R. Nakamura, S.G. Kanekal, Multisatellite observations of the outer zone electron variation during the November 3–4, 1993, magnetic storm. J. Geophys. Res. 102(A7), 14123–14140 (1997b). doi:10.1029/97JA01101
X. Li, D.N. Baker, M. Temerin, G. Reeves, R. Friedel, C. Shen, Energetic electrons, 50 keV to 6 MeV, at geosynchonous orbit: their responses to solar wind variations. Space Weather 3(4) (2005). doi:10.1029/2004SW000105
X. Li, D.N. Baker, T.P. O’Brien, L. Xie, Q.G. Zong, Correlation between the inner edge of outer radiation belt electrons and the innermost plasmapause location. Geophys. Res. Lett. 33(14) (2006). doi:10.1029/2006GL026294
X. Li, A.B. Barker, D.N. Baker, W.C. Tu, T.E. Sarris, R.S. Selesnick, R. Friedel, C. Shen, Modeling the deep penetration of outer belt electrons during the “Halloween” magnetic storm in 2003. Space Weather 7(2) (2009)
X. Li, M. Temerin, D.N. Baker, G.D. Reeves, Behavior of MeV electrons at geosynchronous orbit during last two solar cycles. J. Geophys. Res. 116, A11207 (2011). doi:10.1029/2011JA016934
X. Li, S. Palo, R. Kohnert, D. Gerhardt, L. Blum, Q. Schiller, D. Turner, W. Tu, N. Sheiko, C.S. Cooper, Colorado student space weather experiment: differential flux measurements of energetic particles in a highly inclined low Earth orbit, in Dynamics of the Earth’s Radiation Belts and Inner Magnetosphere (American Geophysical Union, Washington, D.C., 2012). doi:10.1029/2012GM001313
X. Li, Q. Schiller, L. Blum, S. Califf, H. Zhao, W. Tu, D.L. Turner, D. Gerhardt, S. Palo, S.G. Kanekal, D.N. Baker, J. Fennell, J.B. Blake, M. Looper, G.D. Reeves, H. Spence, First results from CSSWE CubeSat: characteristics of relativistic electrons in the near-Earth environment during the October 2012 magnetic storms. J. Geophys. Res. Space Phys. 118(10), 6489–6499 (2013). doi:10.1002/2013JA019342
W. Li et al., Radiation belt electron acceleration by chorus waves during the 17 March 2013 storm. J. Geophys. Res. Space Phys. 119, 6 (2014). doi:10.1002/2014ja019945
X. Li, R.S. Selesnick, D.N. Baker, A.N. Jaynes, S.G. Kanekal, Q. Schiller, L. Blum, J. Fennell, J.B. Blake, Upper limit on the inner radiation belt MeV electron intensity. J. Geophys. Res. 120(2), 1215–1228 (2015). doi:10.1002/2014JA020777
J. Li, B. Ni, Q. Ma, L. Xie, Z. Pu, S. Fu, R.M. Thorne, J. Bortnik, L. Chen, W. Li, D.N. Baker, C.A. Kletzing, W.S. Kurth, G.B. Hospodarsky, J.F. Fennell, G.D. Reeves, H.E. Spence, H.O. Funsten, D. Summers, Formation of energetic electron butterfly distributions by magnetosonic waves via Landau resonance. Geophys. Res. Lett. 43(7) (2016). doi:10.1002/2016gl067853
K.R. Lorentzen, M.D. Looper, J.B. Blake, Relativistic electron microbursts during the GEM storms. Geophys. Res. Lett. 28(13), 2573–2576 (2001). doi:10.1029/2001GL012926
K.R. Lorentzen, J.E. Mazur, M.D. Looper, J.F. Fennell, J.B. Blake, Multisatellite observations of MeV ion injections during storms. J. Geophys. Res. 107(A9), 1231 (2002). doi:10.1029/2001JA000276
J.P. Luntama et al. 2017, this issue
W. Lyatsky, G.V. Khazanov, A new polar magnetic index of geomagnetic activity. Space Weather 6(6) (2008a). doi:10.1029/2007SW000382
W. Lyatsky, G.V. Khazanov, Effects of solar wind density on relativistic electrons at geosynchronous orbit. Geophys. Res. Lett. 35 (2008b)
L.R. Lyons, R.M. Thorne, Equilibrium structure of radiation belt electrons. J. Geophys. Res. 78, 2142–2149 (1973). doi:10.1029/JA078i013p02142
L.R. Lyons, R.M. Thorne, C.F. Kennel, Pitch angle diffusion of radiation belt electrons within the plasmasphere. J. Geophys. Res. 77(19), 3455–3474 (1972)
R.A. Makarevich, A.C. Kellerman, Y.V. Bogdanova, A.V. Koustov, Time evolution of the subauroral electric fields: a case study during a sequence of two substorms. J. Geophys. Res. 114, A04312 (2009). doi:10.1029/2008JA013944
R.A. Makarevich, A.C. Kellerman, J.C. Devlin, H. Ye, L.R. Lyons, Yo. Nishimura, SAPS intensification during substorm recovery: a multi-instrument case study. J. Geophys. Res. 116, A11311 (2011). doi:10.1029/2001JA016916
D.M. Malaspina, A.N. Jaynes, C. Boule, J. Bortnik, S.A. Thaller, R.E. Ergun, C.A. Kletzing, J.R. Wygant, The distribution of plasmaspheric hiss wave power with respect to plasmapause location. Geophys. Res. Lett. 43, 7878–7886 (2016). doi:10.1002/2016GL069982
V. Maliniemi, T. Asikainen, K. Mursula, A. Seppälä, QBO dependent relation between electron precipitation and wintertime surface temperature. J. Geophys. Res., Atmos. 118, 6302–6310 (2013). doi:10.1002/jgrd.50518
I.R. Mann, T.P. O’Brien, D.K. Milling, Correlations between ULF wave power, solar wind speed, and relativistic electron flux in the magnetosphere: solar cycle dependence. J. Atmos. Sol.-Terr. Phys. 66(2) (2004). doi:10.1016/j.jastp.2003.10.002
D.C. Marvin, D.J. Gorney, Solar proton events of 1989: effects on spacecraft solar arrays. J. Spacecr. Rockets 28, 713–719 (1991). doi:10.2514/3.26304
R.A. Mathie, I.R. Mann, A correlation between extended intervals of ULF wave power and storm-time geosynchronous relativistic electron flux enhancements. Geophys. Res. Lett. 27, 3261 (2000). doi:10.1029/2000GL003822
R.A. Mathie, I.R. Mann, On the solar wind control of Pc5 ULF pulsation power at mid-latitudes: implications for MeV electron acceleration in the outer radiation belt. J. Geophys. Res. 106, A12 (2001). doi:10.1029/2001JA000002
K. Matthes, Solar forcing for CMIP6 (v3.2). Geosci. Model Dev. Discuss. 10, 2247–2302 (2016). doi:10.5194/gmd-2016-91
B.H. Mauk, N.J. Fox, S.G. Kanekal, R.L. Kessel, D.G. Sibeck, A. Ukhorskiy, Science objectives and rationale for the radiation belt storm probes mission. Space Sci. Rev. 179 (2013). doi:10.1007/s11214-012-9908-y
A.C. Maycock, S. Misios, Top-down versus bottom-up mechanisms for solar-climate coupling, in Earth’s Climate Response to a Changing Sun, ed. by T. Dudok de Wit et al. (EDP Sciences, Les Ulis Cedex A, 2015), pp. 237–246. www.edpsciences.org
J.E. Mazur et al., The creation of new ion radiation belts associated with solar energetic particle events and interplanetary shocks, in Solar Eruptions and Energetic Particles, ed. by M. Gopalswamy, Torsti. Geophys. Monogr. Ser., vol. 165 (AGU, Washington, D.C., 2005), p. 345
N.P. Meredith, R.B. Horne, R.H.A. Iles, R.M. Thorne, D. Heynderickx, R.R. Anderson, Outer zone relativistic electron acceleration associated with substorm-enhanced whistler mode chorus. J. Geophys. Res. 107(A7) (2002). doi:10.1029/2001JA900146
N.P. Meredith, R.M. Thorne, R.B. Horne, D. Summers, B.J. Fraser, R.R. Anderson, Statistical analysis of relativistic electron energies for cyclotron resonance with EMIC waves observed on CRRES. J. Geophys. Res. 108, 1250 (2003). doi:10.1029/2002JA009700
N.P. Meredith, R.B. Horne, R.R. Anderson, Survey of magnetosonic waves and proton ring distributions in the Earth’s inner magnetosphere. J. Geophys. Res. 113, A06213 (2008). doi:10.1029/2007JA012975
N.P. Meredith, R.B. Horne, S.A. Glauert, D.N. Baker, S.G. Kaneka, J.M. Albert, Relativistic electron loss timescales in the slot region. J. Geophys. Res. 114, A03222 (2009). doi:10.1029/2008JA013889
R.M. Millan, M.P. McCarthy, J.G. Sample, D.M. Smith, L.D. Thompson, D.G. McGaw, L.W. Woodger, J.G. Hewitt, M.D. Comess, K.B. Yando, A.X. Liang, B.A. Anderson, N.R. Knezek, W.Z. Rexroad, J.M. Scheiman, G.S. Bowers, A.J. Halford, A.B. Collier, M.A. Cliverd, R.P. Lin, M.K. Hudson, The balloon array for RBSP relativistic electron losses (BARREL). Space Sci. Rev. (2013). doi:10.1007/s11214-013-9971-z
D.A. Newnham, P.J. Espy, M.A. Clilverd, C.J. Rodger, A. Seppälä, D.J. Maxfield, P. Hartogh, K. Holmén, R.B. Horne, Direct observations of nitric oxide produced by energetic electron precipitation into the Antarctic middle atmosphere. Geophys. Res. Lett. 38, L20104 (2011). doi:10.1029/2011GL048666
B. Ni, X. Cao, Z. Zou, C. Zhou, Z. Gu, J. Bortnik, J. Zhang, S. Fu, Z. Zhao, R. Shi, L. Xie, Resonant scattering of outer zone relativistic electrons by multiband EMIC waves and resultant electron loss tie scales. J. Geophys. Res. 120, 7357–7373 (2015). doi:10.1002/2015JA021466
T.P. O’Brien et al., Which magnetic storms produce relativistic electrons at geosynchronous orbit. J. Geophys. Res. 106, 15533–15544 (2001). doi:10.1029/2001JA000052
T.P. O’Brien, K.R. Lorentzen, I.R. Mann, N.P. Meredith, J.B. Blake, J.F. Fennell, M.D. Looper, D.K. Milling, R.R. Anderson, Energization of relativistic electrons in the presence of ULF power and MeV microbursts: evidence for dual ULF and VLF acceleration. J. Geophys. Res. 108(A8), 1329 (2003). doi:10.1029/2002JA009784
T.P. O’Brien, S.G. Claudepierre, T.B. Guild, J.F. Fennell, D.L. Turner, J.B. Blake, J.H. Clemmons, J.L. Roeder, Inner zone and slot electron radial diffusion revisited. Geophys. Res. Lett. 43 (2016). doi:10.1002/2016GL069749
Y. Omura, N. Furuya, D. Summers, Relativistic turning acceleration of resonant electrons by coherent whistler mode waves in a dipole magnetic field. J. Geophys. Res. 112, A06236 (2007). doi:10.1029/2006JA012243
K. Orlova, M. Spasojevic, Y. Shprits, Activity-dependent global model of electron loss inside the plasmasphere. Geophys. Res. Lett. 41, 3744–3751 (2014). doi:10.1002/2014GL060100
K. Orlova, Y. Shprits, M. Spasojevic, New global loss model of energetic and relativistic electrons based on Van Allen Probes measurements. J. Geophys. Res. 121, 1308 (2016)
L.G. Ozeke, I.R. Mann, K.R. Murphy, I.J. Rae, D.K. Milling, S.R. Elkington, A.A. Chan, H.J. Singer, ULF wave derived radiation belt radial diffusion coefficients. J. Geophys. Res. 117, A04222 (2012). doi:10.1029/2011JA017463
L.G. Ozeke, I.R. Mann, K.R. Murphy, I.J. Rae, D.K. Milling, Analytic expressions for ULF wave radiation belt radial diffusion coefficients. J. Geophys. Res. Space Phys. 119, 1587–1605 (2014). doi:10.1002/2013JA019204
S.-M. Päivärinta, A. Seppälä, M.E. Andersson, P.T. Verronen, L. Thölix, E. Kyrölä, Observed effects of solar proton events and sudden stratospheric warmings on odd nitrogen and ozone in the polar middle atmosphere. J. Geophys. Res., Atmos. 118, 6837–6848 (2013). doi:10.1002/jgrd.50486
G.A. Paulikas, J.B. Blake, Effects of the solar wind on magnetospheric dynamics: energetic electrons at the synchronous orbit, in Quantitative Modeling of Magnetospheric Processes. Geophys. Monogr. Ser., vol. 21 (AGU, Washington, D.C., 1979)
S. Perraut, A. Roux, P. Robert, R. Gendrin, J.-A. Sauvaud, J.-M. Bosqued, G. Kremser, A. Korth, A systematic study of ULF waves above \(f _{H+}\) from GEOS 1 and 2 measurements and their relationships with proton ring distributions. J. Geophys. Res. 87(A8), 6219–6236 (1982). doi:10.1029/JA087iA08p06219
C.E. Randall, D.W. Rusch, R.M. Bevilacqua, K.W. Hoppel, J.D. Lumpe, Polar Ozone and Aerosol Measurement (POAM) II stratospheric NO2, 1993–1996. J. Geophys. Res. 103 (1998). doi:10.1029/98JD02092
C.E. Randall, V.L. Harvey, G.L. Manney, Y. Orsolini, M. Codrescu, C. Sioris, S. Brohede, C.S. Haley, L.L. Gordley, J.M. Zawodny, J.M. Russell, Stratospheric effects of energetic particle precipitation in 2003–2004. Geophys. Res. Lett. 32 (2005). doi:10.1029/2004GL022003
C.E. Randall, V.L. Harvey, D.E. Siskind, J. France, P.F. Bernath, C.D. Boone, K.A. Walker, NOx descent in the Arctic middle atmosphere in early 2009. Geophys. Res. Lett. 36 (2009). doi:10.1029/2009GL039706
G.D. Reeves, Relativistic electrons and magnetic storms: 1992–1995. Geophys. Res. Lett. 25( 11) (1998)
G.D. Reeves, K.L. McAdams, R.H.W. Friedel, T.P. O’Brien, Acceleration and loss of relativistic electrons during geomagnetic storms. Geophys. Res. Lett. 30, 1529 (2003). doi:10.1029/2002GL016513
G.D. Reeves, S.K. Morley, R.H.W. Friedel, M.G. Henderson, T.E. Cayton, G. Cunningham, J.B. Blake, R.A. Christensen, D. Thomsen, On the relationship between relativistic electron flux and solar wind velocity: Paulikas and Blake revisited. J. Geophys. Res. 116, A02213 (2011). doi:10.1029/2010JA015735
G.D. Reeves, H.E. Spence, M.G. Henderson, S.K. Morley, R.H.W. Friedel, H.O. Funsten, D.N. Baker, Electron acceleration in the heart of the Van Allen radiation belts. Science 341(6149) (2013). doi:10.1126/science.1237743
G.D. Reeves, R.H.W. Friedel, B.A. Larsen, R.M. Skoug, H.O. Funsten, S.G. Claudepierre, J.F. Fennell, D.L. Turner, M.H. Denton, H.E. Spence, J.B. Blake, D.N. Baker, Energy dependent dynamics of keV to MeV electrons in the inner zone, outer zone, and slot regions. J. Geophys. Res. 121(1), 397–412 (2016). doi:10.1002/2015JA021569
G.C. Reid, S. Solomon, R.R. Garcia, Response of the middle atmosphere to the solar proton events of August–December, 1989. Geophys. Res. Lett. 18 (1991)
E.J. Rigler, M. Wiltberger, D.N. Baker, Radiation belt electrons respond to multiple solar wind inputs. J. Geophys. Res. 112, A06208 (2007). doi:10.1029/2006JA012181
C.S. Roberts, Cyclotron-resonance and bounce resonance scattering of electrons trapped in the Earth’s magnetic field, in Earth’s Particle and Fields, ed. by B.M. McCormack (Reinhold, New York, 1968), pp. 317–336
C.J. Rodger, M.A. Clilverd, J.C. Green, M.M. Lam, Use of POES SEM-2 observations to examine radiation belt dynamics and energetic electron precipitation into the atmosphere. J. Geophys. Res. Space Phys. 115 (2010a). doi:10.1029/2008JA014023
J.G. Roederer, Experimental evidence on radial diffusion of geomagnetically trapped particles, in Earth’s Particles and Fields, ed. by B.M. McCormac (1968)
G. Rostoker, S. Skone, D.N. Baker, On the origin of relativistic electrons in the magnetosphere associated with some geomagnetic storms. Geophys. Res. Lett. 25, 3701–3704 (1998). doi:10.1029/98GL02801
E. Rozanov, L. Callis, M. Schlesinger, F. Yang, N. Andronova N, V. Zubov, Atmospheric response to NOy source due to energetic electron precipitation. Geophys. Res. Lett. 32 (2005). doi:10.1029/2005GL023041
A. Runov et al., Diamagnetic oscillations ahead of stopped dipolarization fronts. J. Geophys. Res. Space Phys. 119 (2014). doi:10.1002/2013JA019384
C.T. Russell, R.M. Thorne, On the structure of the inner magnetosphere. Cosm. Electrodyn. 1, 67–89 (1970)
O. Santolík, C.A. Kletzing, W.S. Kurth, G.B. Hospodarsky, S.R. Bounds, Fine structure of large-amplitude chorus wave packets. Geophys. Res. Lett. 41, 293–299 (2014). doi:10.1002/2013GL058889
D.M. Sawyer, J.I. Vette, AP-8 trapped proton environment for solar maximum and solar minimum (Goddard Space Flight Center, Greenbelt, Md, 1976). NASA WDC-A-R&S 76-06, NASA-TM-X-72605
Q. Schiller, X. Li, L. Blum, W. Tu, D.L. Turner, J.B. Blake, A nonstorm time enhancement of relativistic electrons in the outer radiation belt. Geophys. Res. Lett. 41, 7–12 (2014). doi:10.1002/2013GL058485
M. Schulz, L.J. Lanzerotti, Particle diffusion in the radiation belts, in Physics and Chemistry in Space, vol. 7 (Springer, New York, 1974)
R.W. Schunk, J.C.G. Walker, Thermal diffusion in the topside ionosphere for mixtures which include multiply-charged ions. Planet. Space Sci. 17 (1969)
R.S. Selesnick, High-energy radiation belt electrons from CRAND. J. Geophys. Res. 120(4) (2015). doi:10.1002/2014JA010963
R.S. Selesnick, M.D. Looper, R.A. Mewaldt, A theoretical model of the inner proton radiation belt. Space Weather 5(S04003) (2007). doi:10.1029/2006SW000275
R.S. Selesnick, D.N. Baker, A.N. Jaynes, X. Li, S.G. Kanekal, M.K. Hudson, B.T. Kress, Observations of the inner radiation belt: CRAND and trapped solar protons. J. Geophys. Res. 119 (2014). doi:10.1002/2014JA020188
K. Semeniuk, V.I. Fomichev, J.C. McConnell, C. Fu, S.M.L. Melo, I.G. Usoskin, Middle atmosphere response to the solar cycle in irradiance and ionizing particle precipitation. Atmos. Chem. Phys. 11 (2011). doi:10.5194/acp-11-5045-2011
J. Semeter, F. Kamalabadi, Determination of primary electron spectra from incoherent scatter radar measurements of the auroral \(\mathbf{E} \) region. Radio Sci. 40, RS2006 (2005). doi:10.1029/2004RS003042
A. Seppälä, P.T. Verronen, E. Kyrölä, S. Hassinen, L. Backman, A. Hauchecorne, J.L. Bertaux, D. Fussen, Solar proton events of October–November 2003: Ozone depletion in the Northern Hemisphere polar winter as seen by GOMOS/Envisat. Geophys. Res. Lett. 31 (2004). doi:10.1029/2004GL021042
A. Seppälä, C.E. Randall, M.A. Clilverd, E. Rozanov, C.J. Rodger, Geomagnetic activity and polar surface air temperature variability. J. Geophys. Res. 114 (2009). doi:10.1029/2008JA014029
V. Sergeev, M.A. Shukhtina, R. Rasinkangas, A. Korth, G.D. Reeves, H.J. Singer, M.F. Thomsen, L.I. Vagina, Event study of deep energetic particle injections during substorm. J. Geophys. Res. 103(A5), 9217–9234 (1998)
D.R. Shklyar, Energy transfer from lower to higher energy electrons mediated by whistler waves in the radiation belts. J. Geophys. Res. 122 (2017). doi:10.1002/2016JA023263
Y.Y. Shprits, R.M. Thorne, R. Friedel, G.D. Reeves, J. Fennell, D.N. Baker, S.G. Kanekal, Outward radial diffusion driven by losses at magnetopause. J. Geophys. Res. 111, A11214 (2006). doi:10.1029/2006JA011657
M. Shulz, L.J. Lanzerotti, Particle Diffusion in the Radiation Belts (Springer, Berlin, 1974)
L.E. Simms, M.J. Engebretson, V. Pilipenko, G.D. Reeves, M. Clilverd, Empirical predictive models of daily relativistic electron flux at geostationary orbit: Multiple regression analysis. J. Geophys. Res. 121(4) (2016). doi:10.1002/2016JA022414
N. Singh, J.L. Horwitz, Plasmasphere refilling: recent observations and modeling. J. Geophys. Res. 97, 1049–1079 (1992). doi:10.1029/91JA02602
M. Sinnhuber, S. Kazeminejad, J.M. Wissing, Interannual variation of NOx from the lower thermosphere to the upper stratosphere in the years 1991–2005. J. Geophys. Res. 116 (2011). doi:10.1029/2010JA015825
M. Sinnhuber, H. Nieder, N. Wieters, Energetic particle precipitation and the chemistry of the mesosphere/lower thermosphere. Surv. Geophys. 33 (2012). doi:10.1007/s10712-012-9201-3
M. Sinnhuber et al., The response of mesospheric NO to geomagnetic forcing in 2002–2012 as seen by SCIAMACHY. J. Geophys. Res. Space Phys. 65(121), 3603–3620 (2016). doi:10.1002/2015JA022284
D.E. Siskind, G.E. Nedoluha, C.E. Randall, M. Fromm, J.M. Russell, An assessment of Southern Hemisphere stratospheric NOx enhancements due to transport from the upper atmosphere. Geophys. Res. Lett. 27 (2000)
A.K. Smith, R.R. Rolando, D.R. Marsh, J.H. Richter, WACCM simulations of the mean circulation and trace species transport in the winter mesosphere. J. Geophys. Res. 116, D20115 (2011). doi:10.1029/2011JD016083
E. Spanswick, E. Donovan, R. Friedel, A. Korth, Ground based identification of dispersionless electron injections. Geophys. Res. Lett. 34, L03101 (2007). doi:10.1029/2006GL02839
M. Spasojevic, Y.Y. Shprits, K. Orlova, Global empirical models of plasmaspheric hiss using Van Allen Probes. J. Geophys. Res. 120, 10370 (2015)
H.E. Spence, J.B. Blake, A.B. Crew, S. Driscoll, D.M. Klumpar, B.A. Larsen, J. Legere, S. Longworth, E. Mosleh, T.P. O’Brien, S. Smith, L. Springer, M. Widholm, Focusing on size and energy dependence of electron microbursts from the Van Allen radiation belts. Space Weather (2012). doi:10.1029/2012SW000869
H.E. Spence, G.D. Reeves, D.N. Baker, J.B. Blake, M. Bolton, S. Bourdarie, A.A. Chan, S.G. Claudepierre, J.H. Clemmons, J.P. Cravens, S.R. Elkington, J.F. Fennell, R.H.W. Friedel, H.O. Funsten, J. Goldstein, Science goals and overview of the energetic particle, composition, and thermal plasma (ECT) Suite on NASA’s Radiation Belt Storm Probes (RBSP) mission. Space Sci. Rev. 179 (2013). doi:10.1007/s11214-013-0007-5
Z. Su, F. Xiao, H. Zheng, Z. He, H. Zhu, M. Zhang, C. Shen, Y. Wang, S. Wang, C.A. Kletzing, W.S. Kurth, G.B. Hospodarsky, H.E. Spence, G.D. Reeves, H.O. Funsten, J.B. Blake, D.N. Baker, Nonstorm time dynamics of electron radiation belts observed by the Van Allen Probes. Geophys. Res. Lett. 41, 229–235 (2014). doi:10.1002/2013GL058912
R.N. Sudan, Plasma electromagnetic instabilities. Phys. Fluids 6(1) (1964). doi:10.1063/1.1724508
D. Summers, R.M. Thorne, Relativistic electron pitch-angle scattering by electromagnetic ion cyclotron waves during geomagnetic storms. J. Geophys. Res. 108, 1143 (2003). doi:10.1029/2002JA009489
D. Summers, R.M. Thorne, F. Xiao, Relativistic theory of wave–particle resonant diffusion with application to electron acceleration in the magnetosphere. J. Geophys. Res. 103(20), 487 (1998)
D. Summers, B. Ni, N.P. Meredith, Timescales for radiation belt electron acceleration and loss due to resonant wave–particle interactions: 2. Evaluation for VLF chorus, ELF hiss, and electromagnetic ion cyclotron waves. J. Geophys. Res. 112, A04207 (2007). doi:10.1029/2006JA011993
D. Summers, I.R. Mann, D.N. Baker, M. Schulz, Dynamics of the Earth’s Radiation Belts and Inner Magnetosphere. AGU Monograph, vol. 199 (2012)
K. Takahashi, D.-H. Lee, M. Nose, R.R. Anderson, W.J. Hughes, CRRES electric field study of the radial mode structure of Pi2 pulsations. J. Geophys. Res. 108(A5), 1210 (2003). doi:10.1029/2002JA009761
M.J. Teague, J.I. Vette, The inner zone electron Model AE-5, NSSDC 72-10, NASA TMX-69987, Goddard Space Flight Center, Greenbelt MD (1972)
M.J. Teague, J.I. Vette, A model of the trapped electron population for solar minimum (Goddard Space Flight Center, Greenbelt, Md, 1974). NSSDC 74-03, NASA TMS-69909
M.J. Teague, K.W. Chan, J.I. Vette, AE 6: A model environment of trapped electrons for solar maximum (Goddard Space Flight Center, Greenbelt, Md, 1976). NSSDC/WDC-a-R&S 76-04, NASA TMX-72597
R.M. Thorne, Radiation belt dynamics: the importance of wave–particle interactions. Geophys. Res. Lett. 37, L22107 (2010). doi:10.1029/2010GL044990
R.M. Thorne, E.J. Smith, R.K. Burton, R.E. Holzer, Plasmaspheric hiss. J. Geophys. Res. 78(10), 1581–1596 (1973). doi:10.1029/JA078i010p01581
R.M. Thorne, T.P. O’Brien, Y.Y. Shprits, D. Summers, R.B. Horne, Timescale for MeV electron microburst loss during geomagnetic storms. J. Geophys. Res. 110, A09292 (2005). doi:10.1029/2004JA010882
R.M. Thorne, B. Ni, X. Tao, R.G. Horne, N.P. Meredith, Scattering by chorus waves as the dominant cause of diffuse auroral precipitation. Nature 467 (2010). doi:10.1038/nature09467
R.M. Thorne, W. Li, B. Ni, Q. Ma, J. Bortnik, L. Chen, D.N. Baker, H.E. Spence, G.D. Reeves, M.G. Henderson, C.A. Kletzing, W.S. Kurth, G.B. Hospodarsky, J.B. Blake, J.F. Fennell, S.G. Claudepierre, S.G. Kanekal, Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414 (2013a). doi:10.1038/nature12889
R.M. Thorne et al., Evolution and slow decay of an unusual narrow ring of relativistic electrons near \(L\sim3.2\) following the September 2012 magnetic storm. Geophys. Res. Lett. 40, 3507–3511 (2013b). doi:10.1002/grl.50627
V.Y. Trakhtengerts, Stationary states of the Earth’s outer radiation zone. Geomagn. Aeron. 6, 827 (1966)
B.T. Tsurutani, W.D. Gonzalez, A.L.C. Gonzalez, F. Tang, J.K. Arballo, M. Okada, Interplanetary origin of geomagnetic activity in the declining phase of the solar cycle. J. Geophys. Res. 100(A11), 21717–21733 (1995). doi:10.1029/95JA01476
W. Tu, S.R. Elkington, X. Li, W. Liu, J. Bonnell, Quantifying radial diffusion coefficients of radiation belt electrons based on global MHD simulation and spacecraft measurements. J. Geophys. Res. 117, A10210 (2012). doi:10.1029/2012JA017901
D.L. Turner, V. Angelopoulos, S.K. Morley, M.G. Henderson, G.D. Reeves, W. Li, D.N. Baker, C.-L. Huang, A. Boyd, H.E. Spence, S.G. Claudepierre, J.B. Blake, J.V. Rodriguez, On the cause and extent of outer radiation belt losses during the 30 September 2012 dropout event. J. Geophys. Res. 119(3), 1530–1540 (2014). doi:10.1002/2013JA019446
D.L. Turner, S.G. Claudepierre, J.F. Fennell, T.P. O’Brien, J.B. Blake, C. Lemon, M. Gkioulidou, K. Takahashi, G.D. Reeves, S. Thaller, A. Breneman, J.R. Wygant, W. Li, A. Runov, V. Angelopoulos, Energetic electron injections deep into the inner magnetosphere associated with substorm activity. Geophys. Res. Lett. 42(7), 2079–2087 (2015). doi:10.1002/2015GL063225
D.L. Turner, T.P. O’Brien, J.F. Fennell, S.G. Claudepierre, J.B. Blake, A.N. Jaynes, D.N. Baker, S.G. Kanekal, M. Gkioulidou, M.G. Henderson, G.D. Reeves, Investigating the source of near-relativistic and relativistic electrons in Earth’s inner radiation belt. J. Geophys. Res. 122(1) (2016). doi:10.1002/2016JA023600
L.V. Tverskaya, N.N. Pavlov, J.B. Blake, R.S. Selesnick, J.F. Fennell, Predicting the L-position of the storm-injected relativistic electron belt. Adv. Space Res. 31(4), 1039–1044, doi.org/10.1016/S0273-1177(02)00785-8 (2002)
A.Y. Ukhorskiy, M.I. Sitnov, Dynamics of radiation belt particles. Space Sci. Rev. 179(1), 545–578 (2013). doi:10.1007/s11214-012-9938-5
A.Y. Ukhorskiy, B.J. Anderson, P.C. Brandt, N.A. Tsyganenko, Storm time evolution of the outer radiation belt: transport and losses. J. Geophys. Res. Space Phys. 111, A11S03 (2006). doi:10.1029/2006JA011690
A.Y. Ukhorskiy, M.I. Sitnov, R.M. Millan, B.T. Kress, D.C. Smith, Enhanced radial transport and energization of radiation belt electrons due to drift orbit bifurcations. J. Geophys. Res. Space Phys. 119, 163–170 (2014)
M.E. Usanova, A. Drozdov, K. Orlova, I.R. Mann, Y. Shprits, M.T. Robertson, D.L. Turner, D.K. Milling, A. Kale, D.N. Baker, S.A. Thaller, G.D. Reeves, H.E. Spence, C. Kletzing, J. Wygant, Effect of EMIC waves on relativistic and ultrarelativistic electron populations: ground-based and Van Allen Probes observations. Geophys. Res. Lett. 41(5), 1375–1381 (2014). doi:10.1002/2013GL059024
J.A. Van Allen, Lifetimes of geomagnetically-trapped electrons at several MeV energy. Nature 203, 1006–1007 (1964)
J.A. Van Allen, Spatial distribution and time decay of the intensities of geomagnetically trapped electrons from the high altitude nuclear burst of July 1962, in Radiation Trapped in the Earth’s Magnetic Field, ed. by B.M. McCormac (Dordrecht-Holland, Reidel, 1966), pp. 575–592
J.A. Van Allen, G.H. Ludwig, E.C. Ray, C.E. McIlwain, Observation of high intensity radiation by satellites 1958 alpha and gamma. Jet Propuls. 28(9), 588–592 (1958)
J.A. Van Allen, C.E. McIlwain, G.H. Ludwig, Satellite observations of electrons artificially injected into the geomagnetic field. J. Geophys. Res. 64, 877 (1959)
M. Van de Kamp, A. Seppälä, M.A. Clilverd, C.J. Rodger, P.T. Verronen, I.C. Whittaker, A model providing long-term datasets of energetic electron precipitation during geomagnetic storms. J. Geophys. Res., Atmos. 121(20), 2015JD024212 (2016)
D. Vassiliadis, A.J. Klimas, S.G. Kanekal, D.N. Baker, R.S. Weigel, Long-term average, solar-cycle, and seasonal response of magnetospheric energetic electrons to the solar wind speed. J. Geophys. Res. 107 (2002). doi:10.1029/2001JA000506
P.T. Verronen, C.J. Rodger, M.A. Clilverd, S. Wang, First evidence of mesospheric hydroxyl response to electron precipitation from the radiation belts. J. Geophys. Res. 116(D7) (2011). doi:10.1029/2010JD014965
P.T. Verronen, M.E. Andersson, C.J. Rodger, M.A. Clilverd, S. Wang, E. Turunen, Comparison of modeled and observed effects of radiation belt electron precipitation on mesospheric hydroxyl and ozone. J. Geophys. Res. 118 (2013). doi:10.1002/jgrd.50845
P.T. Verronen, C.J. Rodger, Atmospheric ionization by energetic particle precipitation, in Earth’s Climate Response to a Changing Sun, ed. by T. Dudok de Wit et al. (EDP Sciences, Les Ulis Cedex, 2015), pp. 261–266. Chap. 4.5. www.edpsciences.org
J.I. Vette, Models of the Trapped Radiation Environment, Vol. I: Inner Zone Protons and Electrons, NASA SP-3024 (Goddard Space Flight Center, Greenbelt, MD, 1966)
J.I. Vette, The AE-8 Trapped Electron Model Environment (Goddard Space Flight Center, Greenbelt, Md, 1991). NSSDC/WDC-A-R&S 91-24
M. Walt, Loss rates of trapped electrons by atmospheric collisions, in Radiation Trapped in the Earth’s Magnetic Field, ed. by Reidel, B.M. McCormac. Astrophysics and Space Science Library, vol. 5, Dordrecht (1966), p. 337
M. Walt, Radial diffusion of trapped particles and some of its consequences. Rev. Geophys. 9(1) (1971). doi:10.1029/RG009i001p00011
H.I. West, R.M. Buck, J.R. Walton, Shadowing of electron azimuthal-drift motions near the noon magnetopause. Nat. Phys. Sci. 240, 6–7 (1972). doi:10.1038/physci240006a0
S. Wing, J.R. Johnson, E. Camporeale, G.D. Reeves, Information theoretical approach to discovering solar wind drivers of the outer radiation belt. J. Geophys. Res. 121(10) (2016). doi:10.1002/2016JA022711
J.M. Wissing, M.-B. Kallenrode, Atmospheric Ionization Module Osnabruck (AIMOS): A 3-D model to determine atmospheric ionization by energetic charged particles from different populations. J. Geophys. Res. 114(A6) (2009). doi:10.1029/2008JA013884
H. Zhao, X. Li, Modeling energetic electron penetration into the slot region and inner radiation belt. J. Geophys. Res. Space Phys. 118, 6936–6945 (2013). doi:10.1002/2013JA019240
H. Zhao, X. Li, D.N. Baker, S.G. Claudepierre, J.F. Fennell, J.B. Blake, B.A. Larsen, R.M. Skoug, H.O. Funsten, R.H.W. Friedel, G.D. Reeves, H.E. Spence, D.G. Mitchell, L.J. Lanzerotti, Ring current electron dynamics during geomagnetic storms based on the Van Allen Probes measurements. J. Geophys. Res. 121(4), 3333–3346 (2016). doi:10.1002/2016JA022358
H. Zhao, D.N. Baker, A.N. Jaynes, X. Li, S.R. Elkington, S.G. Kanekal, H.E. Spence, A.J. Boyd, C.-L. Huang, C. Forsyth, On the relation between radiation belt electrons and solar wind parameters/geomagnetic indices: dependence on the first adiabatic invariant and l*. J. Geophys. Res. 122(2), 1624–1642 (2017). doi:10.1002/2016JA023658
Author information
Authors and Affiliations
Corresponding author
Additional information
The Scientific Foundation of Space Weather
Edited by Rudolf von Steiger, Daniel Baker, André Balogh, Tamás Gombosi, Hannu Koskinen and Astrid Veronig
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Baker, D.N., Erickson, P.J., Fennell, J.F. et al. Space Weather Effects in the Earth’s Radiation Belts. Space Sci Rev 214, 17 (2018). https://doi.org/10.1007/s11214-017-0452-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11214-017-0452-7