Abstract
We review the morphology and dynamics of the electrical current systems of the terrestrial magnetosphere and ionosphere. Observations from the Active Magnetosphere and Planetary Electrodynamics Response Experiment (AMPERE) over the three years 2010 to 2012 are employed to illustrate the variability of the field-aligned currents that couple the magnetosphere and ionosphere, on timescales from minutes to years, in response to the impact of solar wind disturbances on the magnetosphere and changes in the level of solar illumination of the polar ionospheres. The variability is discussed within the context of the occurrence of magnetic reconnection between the solar wind and terrestrial magnetic fields at the magnetopause, the transport of magnetic flux within the magnetosphere, and the onset of magnetic reconnection in the magnetotail. The conditions under which the currents are expected to be weak, and hence minimally contaminate measurements of the internally-produced magnetic field of the Earth, are briefly outlined.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Motivation and Scope
Measurements of the magnetic field surrounding the Earth are of scientific interest to two communities of researchers: those studying the internal source of the magnetic field and its variation over many years, and those for whom perturbations on time-scales of minutes to days (or longer) are indicative of the interaction between the solar wind with the magnetosphere. This review arises from a discussion between internal and external field scientists hosted by the International Space Science Institute in Bern.
The electrical currents in the magnetosphere and ionosphere flow in large part due to the interaction of the terrestrial magnetic field with the solar wind. These currents define the structure of the geomagnetic environment, which responds to a variety of external stimuli on a wide range of timescales. Changes in solar wind pressure on timescales of minutes and days affect the size of the magnetosphere and the strength of the magnetopause currents that separate the interplanetary and terrestrial magnetic fields. Variations in the strength and orientation of the interplanetary magnetic field (IMF) on timescales of minutes and hours control the level of interconnection between the interplanetary medium and the terrestrial field, modifying the structure of and circulation within the magnetosphere. Within the magnetosphere many currents close through the polar ionosphere, the conductance of which is determined by the level of insolation, which itself varies diurnally, seasonally, and with the 11-year solar cycle. The magnetic perturbations associated with currents flowing on the magnetopause, along magnetic field lines, in the ionosphere, and within the inner magnetosphere provide a rich source of information regarding the dynamics of the magnetosphere. They also result in an extremely noisy magnetic environment that hinders study of the internally-produced magnetic field of the Earth. The aim of the present paper is to review the processes that give rise to these magnetic disturbances and to provide guidance as to when “quiet” geomagnetic conditions can be expected.
Several recent papers have reviewed the external electric current systems of the Earth and planets. Cowley (2000) outlined the basic physical processes that give rise to current systems within the terrestrial solar wind–magnetosphere coupled system, while Baumjohann et al. (2010) reviewed the formation of currents throughout the solar system. Ganushkina et al. (2015) described the observed morphology of the current systems and the measurements used to characterise them. Lockwood (2013) provided an overview of the current systems and the geomagnetic indices which are used to monitor their intensity and variability, with the aim of determining changes in interplanetary conditions over the last dozen or so solar cycles (150 years or more). Also of interest to this topic is the review of Milan (2015) which describes our present understanding of solar wind–magnetosphere–ionosphere coupling, that is the dynamics of the magnetosphere in response to solar wind driving, which in turn are responsible for many of the current systems within the magnetosphere.
The aim of the current paper is to review the processes that give rise to current variability on timescales of years, months, days, and hours in response to changes in the interplanetary medium. To do so, we will describe the behaviour of the field-aligned currents (FACs) that flow into and out of the ionosphere in the polar regions, observed over 3 years by the Active Magnetosphere and Planetary Electrodynamics Response Experiment (AMPERE). These FACs, also named Birkeland currents in honour of Kristian Birkeland (Birkeland 1908), were first identified in an average sense by Iijima and Potemra (1976a,b, 1978) using a single polar-orbiting spacecraft. AMPERE assimilates observations from 66 satellites of the Iridium® telecommunications constellation to characterise the spatial distribution of FACs in both northern and southern hemispheres with a cadence of a few minutes. As the FACs are a component of the larger current system, changes in the FACs can be used to infer changes in the other components. This new dataset has provided fresh impetus to the study of temporal variations of magnetospheric currents, especially as our understanding of magnetospheric dynamics has progressed significantly since the current systems were first identified.
When describing magnetospheric structure and dynamics two main paradigms are used: \(\mathbf{B}\), \(\mathbf{v}\) and \(\mathbf{E}\), \(\mathbf{j}\). In the former, magnetic field and plasma velocity are the dominant fundamental physical parameters, and electric current and electric field arise from these as secondary quantities. In the latter, the electric field and current are seen as the primary parameters. As argued by Parker (1996) and Vasyliunas (2005), the \(\mathbf{B}\), \(\mathbf{v}\) paradigm is more satisfactory from a dynamical point of view, whereas the \(\mathbf{E}\), \(\mathbf{j}\) approach relies on assumptions of stationarity (for instance, magnetic field lines are not equipotentials if \(\partial / \partial t \ne 0\)). We adopt the \(\mathbf{B}\), \(\mathbf{v}\) paradigm in our discussion, but mention the \(\mathbf{E}\), \(\mathbf{j}\) interpretation when it is the customary point of view. Fundamental to the \(\mathbf{B}\), \(\mathbf{v}\) picture is the assumption that the magnetic field is frozen into the plasma, which can be treated as a magnetised fluid, except in regions of the magnetosphere where the gyroradii of the particles are comparable to the scale size of spatial gradients in the field, such as sites of high magnetic field shear including the magnetopause and the neutral sheet of the magnetotail where magnetic reconnection occurs, and in the inner magnetosphere where hot plasma drifts across the field. In regions where the frozen-in condition holds, the motion of the plasma deforms the magnetic field, which in turn exerts tension and pressure forces back on the plasma.
We now briefly recap the main features of the current systems, but the interested reader should refer to the aforementioned reviews for full details.
1.2 Magnetospheric Current Systems
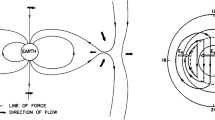
Figure 1 presents a schematic overview of the magnetic field configuration and the current systems in the northern hemisphere of the magnetosphere. Without the presence of exterior current systems, the Earth’s magnetic field would be approximately dipolar (with minor contributions from the higher orders of interest to internal field modellers). In general, currents flow where the field is distorted into a non-dipolar configuration, that is where there are spatial gradients in the magnetic field such that \(\nabla \times \textbf{B} \ne 0\), as required by Ampère’s law. The magnetopause separates the weaker magnetic field in the magnetosheath from the stronger field within the magnetosphere, so here the Chapman–Ferraro currents flow, dawn-to-dusk across the nose of the magnetosphere and dusk-to-dawn across the magnetotail magnetopause (Chapman and Ferraro 1931). In the equatorial plane of the magnetotail, where the magnetic field reverses from sunwards to antisunwards, the cross-tail current flows from dawn-to-dusk, connecting with the magnetotail Chapman–Ferraro currents at the flanks. The inner magnetosphere is inflated away from a dipolar configuration by the pressure of hot plasma, the magnetic perturbation being associated with the westward-flowing ring current (Chapman and Ferraro 1931, 1941).
A schematic of the magnetic field configuration and current systems of the terrestrial magnetosphere. (a) Open (red) and closed (blue) magnetic field lines. Open field lines comprise the magnetotail lobes (only northern lobe shown for clarity); the footprint of the lobe field lines in the ionosphere are the northern and southern polar caps. A field line newly-reconnected with the IMF at the dayside magnetopause is shown at the left. (b) Northern hemisphere Chapman–Ferraro currents (green) flow from dawn (\(Y < 0\)) to dusk (\(Y > 0\)) across the dayside magnetopause and from dusk to dawn across the magnetotail magnetopause. The cross-tail current (magenta) flows from dawn to dusk and connects into the magnetopause current of the magnetotail. The substorm current wedge (cyan), present during substorm expansion phase, is a diversion of the near-Earth cross-tail current into and out of the ionosphere post- and pre-midnight, respectively. (c) The ring current (magenta) flows westwards around the Earth. The region 1 (blue), region 2 (red), and partial ring current form the convection circuit, associated with the Dungey cycle. Region 1 field-aligned currents flow into (out of) the ionosphere at dawn (dusk), closing across the magnetopause in the same direction as the Chapman–Ferraro current. The region 2 flows into (out of) the ionosphere at dusk (dawn) and closes through the partial ring current
If the interior of the magnetosphere was static, no other currents would flow. However, the open magnetosphere model of Dungey (1961) implies that the magnetic fields of the Earth and the interplanetary medium are interconnected, causing an internal circulation or convection of magnetic field and plasma—the Dungey cycle—as the solar wind flows past the magnetosphere. Magnetic reconnection occurs at the magnetopause (see Fig. 1a), especially when the IMF is directed southwards (IMF \(B_{Z} < 0\), antiparallel to the subsolar terrestrial field), to form open magnetic field lines that are dragged antisunwards across the poles to form the magnetotail lobes (e.g., Ness 1965; Speiser and Ness 1967). Re-closure of these open field lines by magnetic reconnection occurring in the equatorial plane of the magnetotail produces sunward flows in the outer magnetosphere, resupplying the dayside magnetosphere with closed magnetic flux. Motion of plasma in the Dungey cycle is associated with an electric field that points in general from dawn-to-dusk across magnetosphere, which, as will be discussed below, maps to the ionosphere along magnetic field lines.
Figure 2a presents a schematic of the electrodynamics of the northern hemisphere polar ionosphere. As described by Cowley (2000), the Dungey cycle is communicated to the ionosphere along the convecting magnetic field lines, producing a horizontal drift of the ionospheric plasma. In the ionospheric polar cap—the footprint of the open magnetic field lines constituting the magnetotail lobes—the drift is antisunwards. Ionospheric return flow from the nightside to the dayside at auroral latitudes maps to the sunwards flow in the outer magnetosphere. The ionospheric plasma drags behind the convection in the magnetosphere due to friction with the neutral atmosphere, causing a bend-back of the magnetic field lines, with kinks at the ionosphere and (on open field lines) at the magnetopause. This drag is proportional to the electron density of the ionosphere as this controls the collisional cross-section of interaction between the plasma and the neutrals. The kinks in the field lines are associated with field-perpendicular currents, which in the ionosphere are horizontal Pedersen currents and at the magnetopause merge with the Chapman–Ferraro currents. In the \(\mathbf{E}\), \(\mathbf{j}\) paradigm these are referred to as the magnetopause solar wind dynamo or generator and the ionospheric load.
A schematic of the current systems in the polar ionosphere of the northern hemisphere. (a) The purple circle indicates the open/closed field line boundary (OCB) encircling the polar cap. Black arrows indicate streamlines of the typical twin-cell ionospheric convection pattern. The region 1 field-aligned currents (blue) are coincident with the OCB at the poleward edge of the auroral zone, while the region 2 FACs (red) are near the equatorward edge of the auroral zone (these correspond to the red/blue currents in Fig. 1). Region 0 FACs (magenta) flow in the cusp throat of the convection pattern (the polarity of the R0 FACs is drawn here for IMF \(B_{Y} > 0\)). The ionospheric conductance is enhanced (grey shading) in the auroral zone and sunward of the solar terminator. Pedersen currents (green) flow horizontally between upwards and downwards FACs where the conductance is high, and to a lesser degree across the polar cap where the conductance is low. The electric field in the ionosphere points in the same direction as the Pedersen currents; the convection streamlines are equipotentials of the associated electrostatic potential pattern. Hall currents in the high conductance auroral zones form the eastward and westward auroral electrojets; weaker Hall currents flow sunwards across the polar cap. Magnetic perturbations on the ground associated with these Hall currents are known as the DP2 pattern. Substorm current wedge FACs (cyan) and the interconnecting substorm electrojet are present during substorm intervals, producing DP1 pattern magnetic perturbations. DPY perturbations are associated with closure of the region 0 FACs. (b) The distribution of upward (red) and downward (blue) FACs deduced by Iijima and Potemra (1976b), and the demarcation into regions 0, 1, and 2 (red/blue is used here to correspond to the colour-coding of AMPERE current density maps). (c) The ionospheric convection pattern when dayside reconnection is ongoing and the polar cap is expanding (the polar cap flux, \(F_{PC}\), is increasing). The purple circle indicates the OCB, the red, dashed portion of which is the ionospheric footprint of the dayside reconnection X-line (or merging gap). Black arrows are convection streamlines and green arrows indicate the motion of the OCB to lower latitudes (After Cowley and Lockwood 1992). (d) Similar to (c) but for ongoing nightside reconnection and a contracting polar cap
Birkeland currents flow along magnetic field lines to connect all these regions (Zmuda et al. 1966, 1967; Boström 1964, 1967; Cummings and Dessler 1967; Zmuda and Armstrong 1974; Iijima and Potemra 1976a,b, 1978; Braithwaite and Rostoker 1981). Figure 2b shows the FAC structure deduced by Iijima and Potemra (1976b), which are associated with convective flows in the magnetosphere. Within the polar cap, open magnetic field lines are tilted antisunwards by the flow of the solar wind, whereas in the return flow region field lines are tilted sunwards due to pressure from the magnetotail driving the sunwards convection of closed flux. At the polar cap boundary (PCB or open/closed field line boundary, OCB), the opposite bend-back of the field lines on either side of this convection reversal produces a shear in the magnetic field that is associated with a current flowing upwards or downwards. These currents, out of the ionosphere at the dusk PCB and opposite at dawn, are known as region 1 (R1) currents and connect with the cross-field currents at the magnetopause (the dynamo) and in the ionosphere (the load). Similar shears exist at the equator edge of the convection pattern, and the associated region 2 (R2) FACs flow out of the ionosphere at dawn and into the ionosphere at dusk. These FACs are flowing along magnetic field lines which map to the inner magnetosphere where they enhance the nightside portion of the ring current, named the partial ring current (Vasyliunas 1970; Wolf 1970; Egeland and Burke 2012).
A further current system sits poleward of the R1/R2 system near midday, termed the region 0 (R0) current. The polarity of the R0 current depends on the \(B_{Y}\) component of the IMF, being upwards (downwards) in the northern hemisphere for \(B_{Y} > 0\) (\(B_{Y} < 0\)) and opposite in the southern hemisphere (Wilhjelm et al. 1978; Iijima et al. 1978; Erlandson et al. 1988; Papitashvili et al. 2002; Milan et al. 2015). This current system is associated with east-west flows in the dayside polar cap caused by magnetic tension forces on newly-reconnected field lines.
The above description of the ionospheric currents is formulated in terms of magnetic field line bending and ionospheric drag (i.e., the \(\mathbf{B}\), \(\mathbf{v}\) paradigm). An alternative description (\(\mathbf{E}\), \(\mathbf{j}\)) can be given in terms of the downwards mapping of the magnetospheric electric field along magnetic field lines and the ionospheric conductance (Boström 1964). Consideration of the motions of positive and negative charged particles in the collisional ionosphere shows that currents will flow both parallel and perpendicular to the electric field, known as Pedersen and Hall currents, respectively. The Pedersen and Hall conductances are proportional to the electron density of the ionosphere, that is the density of charge carriers. Divergence or convergence of the electric field and hence Pedersen currents at shears in the convection pattern indicate where current must flow upwards or downwards, out of and into the ionosphere, to maintain current continuity.
Hence the region 1 and region 2 currents connect the polar ionosphere to the magnetopause and inner magnetosphere. We will refer to this circuit (MP-R1-I-R2-PRC-R2-I-R1-MP, where MP, PRC and I refer to magnetopause, partial ring current and ionosphere, respectively) as the convection circuit. The magnitude of the current in the convection circuit is expected to be controlled by two factors: the strength of convection in the magnetosphere and the conductance of the polar ionosphere (e.g., Ridley 2007; Milan 2013, 2015; Coxon et al. 2016). The former is determined by the rate of magnetic reconnection at the magnetopause and in the magnetotail, and Coxon et al. (2014a) have demonstrated a relationship between R1/R2 magnitude and proxies for dayside and nightside reconnection rates. The conductance is produced by two processes: firstly, insolation of the polar regions, which differs between the dayside and nightside of the planet and in general between the northern and southern hemispheres; and secondly, impact ionisation of the atmosphere by precipitation of auroral charged particles from the magnetosphere, which are in part associated with the R1/R2 currents themselves. Pedersen currents flow to close the R1/R2 currents across the auroral zones. The associated Hall currents flow as the eastward and westward auroral electrojets at dusk and dawn, respectively.
Current systems comprise the differential flow of positive and negative charge carriers, though in practice this is difficult to measure directly. Rather, their location and strength is determined from the magnetic perturbations that they produce. Networks of magnetometer stations monitor the perturbations produced by ionospheric currents, the ring current, and to a lesser degree the magnetopause currents. Pedersen currents are generally assumed to produce little ground magnetic perturbation due to a cancellation by the magnetic perturbations produced by the R1/R2 FACs that they close (Fukushima 1976), though this is not always a good approximation (Laundal et al. 2016). However, the Hall currents produce magnetic perturbations that are readily measured.
The magnetic perturbations measured on the ground can be rotated to produce equivalent current maps: for instance, southward-directed perturbations are known to be produced by westward-directed ionospheric currents. Care must be taken when interpreting such equivalent currents as gradients in conductance and the contribution of distant currents affect the results. However, characteristic patterns of ground magnetic perturbations have been identified and ascribed to different aspects of the currents shown in Fig. 2a. At high latitudes these comprise the DP1, DP2, and DPY patterns. Identified by Obayashi (1967) and Nishida (1968), DP2 is produced by the Hall current electrojets which dominate in the dawn and dusk auroral zones (that is, northwards and southwards perturbations at dusk and dawn, respectively), whereas DP1 is a largely nightside auroral zone pattern of southwards-directed perturbations associated with substorms (see Sect. 1.3 for further discussion). In other words, DP2 is associated with the strength of the R1/R2 currents and general magnetospheric convection, whereas DP1 is produced by the substorm electrojet and substorm current wedge. DPY occurs in the dayside auroral and polar cap regions and is produced by ionospheric currents associated with the R0 FAC region; like R0, the sense of this current pattern depends on the orientation of the \(B_{Y}\) component of the IMF (Svalgaard 1973; Feldstein 1976; Wilhjelm et al. 1978). At low latitudes magnetometer stations are sensitive to magnetic perturbations from the ring current and dayside magnetopause (e.g., Akasofu and Chapman 1961; Kamide and Fukushima 1971; Kamide 1974).
To simplify analysis and interpretation of these magnetometer measurements, observations from different geographical regions are compiled into geomagnetic indices, which each aim to capture an aspect of the behaviour of a particular current system. The indices of interest to this study are the 1-min cadence auroral upper and auroral lower electrojet indices (AU and AL) of Davis and Sugiura (1966), and the 1-h storm-time disturbance index (Dst) described by Sugiura (1964); the 1-min symmetric H-component (Sym-H) index (Iyemori 1990) is similar to Dst, but at higher temporal resolution.
AU and AL are the positive and negative envelopes of north-south magnetic perturbations measured by magnetometers at auroral latitudes, sensitive to the DP1 and DP2 current systems. If the eastward and westward electrojets are of similar strength then AU and AL should be equal and opposite and can be considered as a measure of the strength of the DP2 pattern and hence the large-scale Dungey convection. When the DP1 pattern is active it appears as an additional negative excursion of AL, taken to be the signature of substorm activity. Care must be taken when interpreting variations in AU and AL as the magnetometers from which they are compiled are fixed, whereas the current patterns can move in latitude, as will be discussed in the next section. The Dst and Sym-H indices summarise the north-south magnetic perturbations measured by a longitudinal network of low latitude magnetometers, and are sensitive to the magnitude of the ring current and the dayside magnetopause current.
1.3 Magnetospheric Dynamics
We now briefly describe the time-dependent behaviour of the magnetosphere observed in response to driving by the solar wind interaction, including substorms (Akasofu and Chapman 1961; Akasofu 1964), an episodic enhancement of nightside auroral activity typically reoccurring every few hours, and geomagnetic storms (e.g., Akasofu et al. 1963; Gosling et al. 1990; Gonzalez et al. 1994, 1999), infrequent but significant perturbations of geospace which accompany solar wind disturbances.
Following a southwards turning of the IMF such that low-latitude magnetopause reconnection is favoured, closed magnetic flux from the dayside magnetosphere is converted to open magnetic flux, causing the magnetotail lobes and polar caps to inflate. Continued inflation cannot be maintained as pressure builds in the equatorial plane of the magnetotail and reconnection is eventually initiated. This causes the magnetotail to deflate and newly-closed flux to return to the dayside. Hence, the Dungey cycle is composed of somewhat decoupled dayside and nightside contributions: accumulation of open magnetic flux controlled promptly by changes in the interplanetary medium, and a delayed re-closure of open flux, where the factors that control the delay are poorly understood. The increase and subsequent decrease of the open magnetic flux content of the magnetosphere, and hence the cross-sectional area of the polar caps, has lead this to be known as the expanding/contracting polar cap (ECPC) model (e.g., Siscoe and Huang 1985; Lockwood 1991; Cowley and Lockwood 1992; Milan 2015, and references therein). The ionospheric convection patterns associated with the expansion and contraction phases are shown in Figs. 2c and d. The amount of open or polar cap magnetic flux in the magnetosphere, \(F_{PC}\), is controlled by the rate of opening at the magnetopause, the dayside reconnection rate \(\mathrm{\varPhi }_{D}\), and the rate of closure in the magnetotail, the nightside reconnection rate \(\mathrm{\varPhi } _{N}\),
whereas the rate of transport of magnetic flux across the polar cap, also known as the cross-polar cap potential or transpolar voltage, \(\mathrm{\varPhi }_{PC}\), is
The convection pattern shown in Fig. 2a is that expected when both dayside and nightside reconnection are active together. Averaged over a sufficient length of time, two to three hours,
indicating that \(F_{PC}\) is constant on long time-scales.
The ECPC has been identified with the substorm cycle (Lockwood and Cowley 1992; Milan et al. 2003, 2007). Substorms are typically divided into three phases (McPherron 1970; Rostoker et al. 1980). The gradual motion of the auroral oval to lower latitudes as open flux accumulates and the polar caps expand is known as the substorm growth phase; the magnetotail response, including vivid nightside auroral displays (and enhancements in ionospheric conductance) that expand polewards as the polar cap contracts, is known as the substorm expansion phase. The recovery phase marks the return to pre-substorm conditions. An important component of the substorm expansion phase is disruption of the near-Earth portion of the cross-tail current. This is inferred from the observed formation of a substorm current wedge (SCW) during expansion phase (Boström 1964; Atkinson 1967; McPherron et al. 1973), a pair of upward/downward FACs on either side of the midnight meridian, with westward current closure in the substorm electrojet across the nightside auroral ionosphere. Although it is possible to show that on average the SCW has this simple up/down FAC structure (e.g., Clausen et al. 2013a), substorm currents can be highly filamentary (Ohtani et al. 1990; Murphy et al. 2013; Forsyth et al. 2014).
Thus, the substorm cycle contributes to the DP1 and DP2 ionospheric current signatures and the associated FAC systems. During substorm growth and expansion phases dayside and nightside reconnection drive convection which enhances the DP2 current system. In addition, during expansion phase, the formation of the SCW results in DP1 perturbations. This leads to the characteristic signature of substorms in AU and AL: positive and negative excursions of AU and AL during growth phase and an enhanced negative excursion of AL during the expansion phase. Moreover, as the polar cap expands and contracts during growth and expansion phases, respectively, the auroral zones and R1/R2 current systems are observed to move equatorwards then polewards (e.g., Milan et al. 2003, 2007; Clausen et al. 2012; Coxon et al. 2014b). The growth and expansion phases are accompanied by enhanced FACs on the dayside and nightside, respectively (Anderson et al. 2014), as the locations of greatest ionospheric flow vorticity (and hence divergence of Pedersen currents) shift (cf. Figs. 2c and d). The expansion phase is also associated with a current system consistent with the SCW (Clausen et al. 2013a). The size that the polar cap attains prior to onset of the expansion phase then determines the intensity of the substorm in terms of auroral brightness, convection response, and the magnitudes of ionospheric and field-aligned currents (Milan et al. 2009a,b; Grocott et al. 2009; Clausen et al. 2013b; Coxon et al. 2014b).
Substorm expansion phase is associated with sunward convection of plasma from the magnetotail towards the inner magnetosphere, where it can contribute to the ring current. A significant enhancement of the ring current is known as a geomagnetic storm. The exact relationship between substorms and geomagnetic storms is unclear, but it is well-known that intervals of strong solar wind driving (mainly due to periods of prolonged, strongly southwards IMF) which are associated with intense substorm activity in general lead to the onset of a geomagnetic storm. Storm-times are sometimes accompanied by intense quasi-periodic substorm-like events known as sawteeth events (Belian et al. 1995). There is still debate regarding whether sawteeth events are a class of behaviour of there own (e.g., Fung et al. 2016) or are just intense substorms (e.g., Pulkkinen et al. 2007).
After driving has subsided, the ring current recovers to quiet levels over a period of days as the enhanced plasma density of the inner magnetosphere drains away, either into the ionosphere through precipitation, out across the magnetopause, or through charge-exchange with the neutral exosphere (Liemohn et al. 2001).
The ring current produces a southwards (negative) perturbation in low latitude magnetograms, though it is possible that the cross-tail current also contributes, which itself is dependent on the open magnetic flux content of the tail lobes. Definitions vary, but a negative deflection in Sym-H to \(-50~\mbox{nT}\) is considered a weak storm, to \(-100~\mbox{nT}\) a moderate storm, and in excess of \(-200~\mbox{nT}\) is a strong storm. When the solar wind pressure is high, the dayside magnetopause is pushed inwards towards the Earth and the associated Chapman–Ferraro current produces a northwards (positive) perturbation at low latitudes. The conditions in the solar wind that lead to enhancement of the ring current are often preceded by a solar wind shock, so the characteristic Sym-H signature of a geomagnetic storm is a positive perturbation (the storm initial phase), a rapid negative excursion lasting several hours (the storm main phase) as the ring current builds, followed by a several-day return to quiescent conditions (the storm recovery phase). The shock arrival and positive excursion of Sym-H is also known as a sudden storm commencement (e.g., Curto et al. 2007). There is some evidence for feedback between the intensity of the ring current and the deflation of the magnetotail lobes during the storm recovery phase (Milan 2009; Milan et al. 2009a,b).
2 Observations
2.1 Datasets
The Active Magnetosphere and Planetary Electrodynamics Experiment (AMPERE) infers maps of field-aligned current density in the northern and southern polar regions at a 10 min cadence, fitting a spherical harmonic expansion to the horizontal magnetic perturbations measured by the 66 spacecraft of the Iridium® telecommunications constellation (Anderson et al. 2000, 2002; Waters et al. 2001; Green et al. 2006). The spacecraft are arranged in six polar orbital planes uniformly spaced in local time, eleven spacecraft to each orbit at an altitude of 780 km. Each AMPERE map comprises observations of current density on a grid of 24 magnetic local time bins and 50 geomagnetic colatitude bins. Due to limitations of the onboard magnetometers, only relatively strong currents can be sensed (above approximately \(0.1~\upmu \mbox{A}\,\mbox{m}^{-2}\)). Figure 3a shows an example AMPERE map taken from the northern hemisphere at 01:40 UT on 10 April 2011. The main feature to note is the presence of a well-defined R1/R2 current system, comprising up/down pairs of current sheets at dawn and dusk, similar to the pattern identified by Iijima and Potemra (1976a). Although AMPERE current maps are available every 2 mins, each map is formed from Iridium observations within a 10-min sliding window. Hence we use 10 min cadence data in this study.
(a) An example AMPERE current density map from the northern hemisphere at 01:40 UT, 10 April 2011. Reds and blues indicates upwards and downwards currents. The colours saturate at \(\pm 0.5~\upmu \mbox{A}\,\mbox{m}^{-2}\). The black circle and cross represent an automated identification of the boundary between R1 and R2 currents. (b) The same current density map, pre-processed such that it is centred on the pole and the R1/R2 boundary has a colatitude of \(20^{\circ }\). This is represented by vector \(\mathbf{J}\). (c) and (d) The first- and second-most significant eigenFACs, \(\mathbf{F}_{1}\) and \(\mathbf{F}_{2}\), produced by the principal component analysis of all available northern hemisphere maps from 2010 to 2012. (e) A reconstruction of \(\mathbf{J}\) from a linear combination of \(\mathbf{F}_{1}\) and \(\mathbf{F}_{2}\). (f) The same as (e) but the contribution of \(\mathbf{F}_{2}\) has been multiplied by −1
The OMNI dataset (King 1991; King and Papitashvili 2005) provides solar wind and interplanetary magnetic field time-series, propagated from upstream monitors to the bow shock. We use 1-min OMNI measurements of the solar wind speed, \(V_{SW}\), proton number density \(N_{SW}\), and the geocentric solar magnetic (GSM) IMF components. There have been several attempts to predict the magnetopause reconnection rate, \(\mathrm{\varPhi }_{D}\), from upstream conditions and in this study we use the parameterisation of Milan et al. (2012), in which
where \(\theta \) is the IMF clock angle, \(B_{YZ}^{2}=B_{Y}^{2}+B_{Z} ^{2}\), and \(L_{eff}\) is an effective length scale given by
where \(R_{E}\) is the radius of the Earth. Together, Eqs. (4) and (5) indicate that the rate of reconnection is proportional to the magnetic flux carried by the solar wind (given by the solar wind electric field \(V_{SW} B_{YZ}\)), the width of the channel of solar wind that impinges on the magnetopause (\(L_{eff}\)), and is largest when the IMF is directed southwards.
OMNI also conveniently provides 1-min geomagnetic indices, from which we use the auroral electrojet indices AU and AL (Davis and Sugiura 1966), and the ring current index Sym-H (Iyemori 1990), similar to the Dst index (Sugiura 1964).
2.2 Analysis Method
To simplify the interpretation of the AMPERE observations, we employ a method of data reduction known as principal component analysis (PCA). PCA performs eigen decomposition of the covariance matrix of a set of observations to find basis vectors that represent the dominant coherent modes of variation within the dataset. Milan et al. (2015) performed PCA on the AMPERE observations from 2010 to 2012, and we use the same technique here. We now give a brief description of the application of PCA to AMPERE data, but refer to Milan et al. (2015) for more detail.
The AMPERE current maps are pre-processed prior to analysis: the R1/R2 current system is automatically detected in each map and the current densities are projected onto a \(24\times 40\) grid such that the boundary between the R1 and R2 FACs is a circle centred on the pole with a radius of \(20^{\circ }\). As an example, Fig. 3a has superimposed a circle of radius \(\mathrm{\varLambda }=18.5^{\circ }\) that indicates the fitted location of the R1/R2 boundary, with a cross marking the centre of the circle. Figure 3b shows the resampled map, which can be represented as a vector \(\mathbf{J}\) of 960 elements. AMPERE maps for which the currents are too weak, such that the R1/R2 signature cannot be identified with confidence, are discarded from the analysis, constituting approximately 21 % of the dataset. The time-series of \(\mathrm{\varLambda }\) can be used to monitor the latitudinal position of the R1/R2 currents, a proxy for the size of the polar cap or polar cap flux, \(F_{PC}\).
PCA decomposes a collection of such maps—in the present analysis 123,340 northern hemisphere maps from 2010 to 2012—into orthogonal basis vectors, or eigenFACs, \(\mathbf{F}_{1}, \mathbf{F}_{2}, \ldots, \mathbf{F}_{960}\), each a 960-element vector. The two most significant eigenFACs are presented in Figs. 3c and d: \(\mathbf{F} _{1}\) which can be seen to correspond to the R1/R2 system and \(\mathbf{F}_{2}\), a system of currents concentrated on the dayside, which we identify as the R0 current system.
Any of the original maps can be reconstructed as a linear combination of the \(\mathbf{F}_{i}\)s
where \(\alpha_{1}\), \(\alpha_{2}\), etc. are coefficients to be determined. Due to the orthogonality of the eigenFACs, the contribution of each eigenFAC \(\mathbf{F}_{i}\) to a particular current map \(\mathbf{J}\) can be determined by finding the projection or inner product
For \(\mathbf{J}\) of Fig. 3b, \(\alpha_{1}=3.4\) and \(\alpha_{2}=-1.1\). Figure 3e shows the reconstruction of \(\mathbf{J}\) as the truncated series \(\alpha_{1} \mathbf{F}_{1} + \alpha_{2} \mathbf{F}_{2}\) (cf. Eq. (6)). Comparing Figs. 3b and e we see that these two terms are sufficient to capture the essential features of the original map, including the magnitude of the R1/R2 currents and the polarity of the R0 current. In this case the R0 current in the polar cap is downward, representative of westward flows in the ionospheric convection throat, which is expected for IMF \(B_{Y} < 0\), consistent with contemporaneous solar wind observations.
For interest, in Fig. 3f we show a reconstruction of \(\mathbf{J}\) in which the sign of \(\alpha_{2}\) has been reversed. We see a reversal of the R0 polarity, as expected, but also a change in the location of the cross-over of the R1 and R2 currents at noon and at midnight, showing that PCA also captures this anticipated behaviour.
Time-series of \(\mathbf{J}\)s can be reduced to time-series of \(\alpha_{1}\) and \(\alpha_{2}\), which allow us to straight-forwardly monitor the individual temporal behaviours of the R1/R2 currents and the R0 currents. These are the parameters that we will explore in the rest of this study.
2.3 Long-Term Variability
Fig. 4 presents \(\alpha_{1}\) and \(\alpha_{2}\) for all current maps in the northern and southern hemispheres for the years 2010 to 2012. The total current flowing in each eigenFAC is determined for each map of each day; the day’s results are then summarised by a vertical bar that encompasses the 10 % and 90 % percentiles. Vertical red and blue lines show summer and winter solstices in the two hemispheres. The right hand axis of each panel shows the spatially-integrated absolute value of \(\alpha_{i} \mathbf{F}_{i}\), i.e. the total current flowing into and out of each hemisphere.
(a) and (b) The long-term behaviour of R1/R2 (\(\alpha_{1}\)) and R0 (\(\alpha_{2}\)) current systems in the northern hemisphere for the years 2010 to 2012. The data are presented as vertical lines which encompass the 10 % and 90 % percentile variation of the magnitude of \(\alpha_{i}\) on each day of observation. The right hand axis indicates the total current represented by \(\alpha_{i}\). Red and blue vertical lines indicate summer and winter solstices. Green ticks at the bottom of (b) indicate the times of sector structure boundary crossings in the solar wind. (c) and (d) Similar to (a) and (b) but for the southern hemisphere
The northern hemisphere R1/R2 eigenFAC varies in magnitude between 0.75 and 8 MA. If 2 MA flows in the convection circuit, then this corresponds to a total of 8 MA flowing into and out of the polar ionosphere. The current magnitude varies significantly from day to day, though there are long-term variations. For instance, the currents are somewhat depressed around the winter solstices. The southern hemisphere R1/R2 currents show similar variability, though their magnitudes are overall lower than in the northern hemisphere. Again, the currents are lower around winter solstice, especially in 2010 and 2011.
The R0 currents, on the other hand, show a considerably stronger seasonal variation. At summer solstice, the current magnitudes are \(\pm 4~\mbox{MA}\) in the northern hemisphere and \(\pm 3~\mbox{MA}\) in the southern hemisphere. At winter solstice, the magnitudes do not rise above \(\pm 0.5~\mbox{MA}\). In 2010 and 2011, the R0 currents change polarity (\(\alpha_{2}<0\) and \(\alpha_{2}>0\)) with a roughly 27 day periodicity, the polarity being opposite in the two hemispheres. In 2012, the frequency of the polarity reversals doubles.
In Fig. 5 we zoom in to an 80-day interval, day 110 to day 190, in 2010. Panels a and b show the R1/R2 current magnitude, \(\alpha_{1}\), from the northern and southern hemispheres respectively, panel c shows the upper and lower auroral electrojet indices AU and AL, and panel d presents Sym-H. The lower panels show the upstream solar wind conditions: panel e is the north-south component of the interplanetary magnetic field (IMF \(B_{Z}\)), and panels f and g are the solar wind speed and density, respectively. Finally, panel h presents an estimate of the magnetopause reconnection rate, \(\mathrm{\varPhi } _{D}\), from Eq. (4), which is expected to be a proxy for the rate of magnetospheric convection as quantified by the cross-polar cap potential, Eqs. (2) and (3). Five periods of enhanced R1/R2 FACs, labelled \(i\) to \(v\), are identified by vertical green lines.
The 80-day period from 20 April (day 110) to 9 July (day 190) 2010. Vertical green lines labelled \(i\) to \(v\) are discussed in the text. (a) and (b) The contribution of the R1/R2 current system, \(\alpha_{1}\), for the northern and southern hemispheres. (c) and (d) the upper and lower auroral electrojet indices, AU and AL, and Sym-H ring current index. (e) The north-south component of the interplanetary magnetic field, IMF \(B_{Z}\). (f) and (g) The solar wind velocity and proton number density. (h) The predicted dayside reconnection rate, \(\mathrm{\varPhi }_{D}\), from Eq. (4)
During this period, the solar wind velocity, \(V_{SW}\), varies between 300 and \(700~\mbox{km}\,\mbox{s}^{-1}\). Enhancements in \(V_{SW}\) tend to occur suddenly (e.g., at the time of event \(i\), Fig. 5f), followed by a gradual diminishment over the subsequent week or so. These features, stream interaction regions, are caused by fast solar wind catching up preceding slow solar wind. As the interface between fast and slow wind travels outwards from the Sun, the fast solar wind scoops up the plasma ahead of it, resulting in elevated solar wind density at the time of the velocity step (Fig. 5g). The interplanetary magnetic field is also bunched up within the density enhancements, so these tend to be times of elevated IMF \(B_{Z}\) magnitude (see especially event \(i\), Fig. 5e).
There appears to be a tendency for the dayside reconnection rate, \(\mathrm{\varPhi }_{D}\) (Fig. 5h), and solar wind density to peak at approximately the same time. However, close examination of the highlighted events, especially \(\mathit{iii}\) and \(\mathit{iv}\), reveals that the peaks are often displaced. Both enhanced \(N_{SW}\) and high \(\mathrm{ \varPhi }_{D}\) are associated with periods when the solar wind speed increases—the arrival of solar wind disturbances—but the association is not exact: \(\mathrm{\varPhi }_{D}\) is more closely controlled by the amplitude and orientation of the IMF.
Despite Fig. 4 showing a general seasonal anticorrelation in the magnitude of the northern and southern FACs, in Figs. 5a and b we see a good correspondence between FAC magnitudes at the level of day-to-day variability. In both hemispheres, the overall FAC magnitude follows closely the variation in the predicted dayside reconnection rate, \(\mathrm{\varPhi }_{D}\). This is enhanced when the IMF has a significant southwards component (\(B_{Z} < 0\)), but also when the solar wind velocity is high. Figure 6 shows the correspondence between 1-h averages of \(\mathrm{\varPhi }_{D}\) and \(\alpha_{1}\) for the period covered in Fig. 5, with a coefficient of correlation of 0.74; if 1-day averages are used, the correlation increases to 0.87.
(a) Correlation between hourly-averages of \(\mathrm{\varPhi } _{D}\) and \(\alpha_{1}\) for the 80-day period from 20 April (day 110) to 9 July (day 190) 2010 in the northern hemisphere (as shown in Fig. 5). The coefficient of correlation is \(r=0.74\). (b) Correlation between hourly-averages of \(\mathrm{\varPhi }_{D}\) and AU for the same period; \(r=0.75\). (c) The occurrence distribution of values of \(\mathrm{\varPhi }_{D}\) when the R1/R2 current system was successfully fitted during pre-processing (black line) and when it was not successfully fitted (grey bars)
Returning to Fig. 5 and comparing the auroral electrojet indices AU and AL with \(\mathrm{\varPhi }_{D}\) or \(\alpha_{1}\), we note that periods of enhanced solar wind driving and R1/R2 currents are also periods of enhanced electrojet activity. The correlation coefficient between 1-h averages of \(\mathrm{\varPhi }_{D}\) and AU is 0.75 (Fig. 6), rising to 0.91 for 1-day averages.
Finally, we turn to Sym-H in Fig. 5d. The two highlighted events with the largest peaks in \(\mathrm{\varPhi }_{D}\), \(i\) and \(\mathit{iii}\), are accompanied by negative excursions in Sym-H, storm main phases, indicating enhancement of the magnitude of the ring current. Events \(\mathit{iv}\) and \(v\) also show modest depressions in Sym-H. The occurrence of spikes in the solar wind density, especially around the times of events \(i\), \(\mathit{ii}\), \(\mathit{iii}\), and \(v\), produce positive excursions in Sym-H, storm initial phases, associated with enhanced and inwardly compressed magnetopause currents.
2.4 Geomagnetic Storm and Substorm Behaviour
We continue to zoom in on the data, focussing on the period around event \(\mathit{iii}\) of Fig. 5 in Fig. 7. The solar wind conditions indicate that this period corresponds to the arrival of a coronal mass ejection (CME) at the Earth. CMEs are eruptions of coronal material from the solar atmosphere, accompanied by a large magnetic flux rope. As it propagates outwards from the Sun faster than the ambient solar wind speed, the CME accumulates a dense sheath of plasma, which in this event arrives during day 148 (Fig. 7g). The flux rope or magnetic cloud arrives during day 149, with large IMF magnitudes in both \(B_{Y}\) and \(B_{Z}\) (Fig. 7e). Characteristically, the field components rotate slowly during the passage of the cloud, revealing it’s twisted flux rope structure—in this case \(B_{Z}\) rotates from positive to negative to positive again, while \(B_{Y}\) rotates from negative to positive. In this event, faster solar wind follows the sheath and cloud, peaking near \(600~\mbox{km}\,\mbox{s}^{-1}\) on day 151 (Fig. 7f). The predicted dayside reconnection rate has a day-long maximum associated with the magnetic cloud (Fig. 7h). After the magnetic cloud the magnitude of IMF \(B_{Z}\) fluctuations decreases significantly, however the elevated solar wind speed keeps \(\mathrm{\varPhi }_{D}\) sporadically high until the start of day 153.
The 6-day period encompassing a geomagnetic storm, from 28 May to 2 June 2010 (days 148 to 153). (a) and (b) The contributions of the R1/R2 and R0 current systems, \(\alpha_{1}\) and \(\alpha_{2}\), for the northern hemisphere. (c) and (d) The upper and lower auroral electrojet indices, AU and AL, and Sym-H ring current index. (e) The east-west and north-south components of the interplanetary magnetic field, IMF \(B_{Y}\) (blue) and \(B_{Z}\) (red). (f) and (g) The solar wind velocity and proton number density. (h) The predicted dayside reconnection rate, \(\mathrm{\varPhi }_{D}\), from Eq. (4)
The Sym-H index (Fig. 7d) indicates that the main phase of a weak geomagnetic storm occurs on day 149 in response to the magnetic cloud of the CME. The high solar wind density beforehand produces positive excursions in Sym-H, the initial phase. Sym-H recovers gradually to near quiet-time levels by the start of day 154.
The AU and AL indices (Fig. 7c) show continuous activity on day 149. There is more sporadic but significant substorm activity throughout days 150 to 152, driven by the fluctuating \(\mathrm{\varPhi } _{D}\) during this period. Two isolated substorms occur on day 148 before the commencement of the storm.
Figures 7a and b show the R1/R2 and R0 current magnitudes in the northern hemisphere throughout the period. As before, the R1/R2 current follows the shape of \(\mathrm{\varPhi }_{D}\) and AU/AL very closely. The magnitude and polarity of the R0 current reflect changes in IMF \(B_{Y}\), as seen most clearly during the magnetic cloud passage on day 149.
Because the substorm activity during the recovery phase of the geomagnetic storm is continuous, it is difficult to study the detailed response to solar wind driving. Instead we focus on the two isolated substorms occurring on day 148, and the main phase on day 149 in Fig. 8. Figure 8d presents \(\mathrm{\varPhi }_{D}\), and Fig. 8c and d shows the response of AU/AL, including three substorms numbered 1 to 3 (blue and red shading indicating the approximate durations of growth and expansion phases). Figure 8a presents the magnitude of the R1/R2 current, showing two 2-h to 3-h enhancements on day 148 associated with the substorms and the day-long enhancement during the main phase of the storm on day 149. Figure 8b shows the radius of the R1/R2 current system that was calculated as part of the pre-processing of the current maps described in Sect. 2.2. During quiescent periods the radius is 15∘ or lower. During the substorms this rises to 20∘, and reaches 25∘ near the peak of the storm. Missing data in Figs. 8a and b indicate times when the current magnitudes were too weak for the pre-processing to confidently identify the R1/R2 current system.
The 2-day period that precedes and encompasses the main phase of the storm shown in Fig. 7, 28 and 29 May (days 148 and 149) 2010. Blue and red shading indicates the approximate times of the growth and expansion/recovery phases of three substorms numbered 1 to 3. (a) The contribution of the R1/R2 current system, \(\alpha_{1}\), for the northern hemisphere. (b) The radius of the circle fitted to the R1/R2 boundary in the current density maps during pre-processing, \(\mathrm{\varLambda }\), taken as a proxy for the size of the polar cap or \(F_{PC}\). (c) The electrojet indices AU and AL. (d) The predicted dayside reconnection rate, \(\mathrm{\varPhi }_{D}\), from Eq. (4)
During the periods highlighted by blue shading \(\mathrm{\varPhi }_{D}\) rises to between 30 and 50 kV and the radius of the current systems increases, which we identify as the accumulation of open magnetic flux in the magnetosphere by magnetopause reconnection—these are substorm growth phases. At these times, AU and AL diverge from 0, indicating that the eastwards and westwards electrojets are enhanced. The end of each growth phase is marked by the onset of bays in AL, substorm expansion phase onset. After onset the radius of the current systems decreases over the next 2 to 3 h (red shading) as reconnection in the tail reduces the open flux content. In the case of the first substorm, onset occurs at approximately the same time that dayside reconnection ceases; in the second case, dayside reconnection continues for some time after onset, leading to a re-intensification in AL. During the prolonged and extreme driving associated with the main phase of the storm on day 149, re-intensifications in AL occur with a 30 min quasi-period.
Figure 9 focusses on the second substorm of Fig. 8, showing the raw (un-pre-processed) current density maps from the northern hemisphere at 30-min intervals through the substorm. Prior to the growth phase of the substorm (Fig. 9a) currents are concentrated on the dayside and located at high latitudes. As the growth phase proceeds (Figs. 9c and d) the currents move to lower latitudes, indicating that dayside reconnection is causing the polar cap to expand (see Eq. (1) with \(\mathrm{\varPhi }_{D}>0\), \(\mathrm{ \varPhi }_{N}=0\)), and the R1/R2 system develops, indicating that ionospheric convection associated with the reconnection is enhancing (see Eq. (2) with \(\mathrm{\varPhi }_{D}>0\), \(\mathrm{\varPhi } _{N}=0\)), though currents are still strongest on the dayside. During the expansion phase and re-intensification, when both dayside and nightside reconnection are active (Figs. 9d, e, and f) the R1/R2 pattern is clear at all local times, indicating that convection is strongest at this time (see Eq. (2) with \(\mathrm{ \varPhi }_{D} \approx \mathrm{\varPhi }_{N}>0\)), and the currents remain at the same latitude, indicating that the polar cap size is not changing significantly (see Eq. (1) with \(\mathrm{\varPhi }_{D} \approx \mathrm{\varPhi }_{N}>0\)). Strong currents are observed on the nightside at this time, though the pattern does not obviously conform to the simple up/down FACs straddling the midnight meridian expected in the simple substorm current wedge model. During the recovery phase, when dayside reconnection has ceased, the currents weaken and retreat to higher latitudes (see Eqs. (1) and (2) with \(\mathrm{\varPhi }_{D}=0\), \(\mathrm{\varPhi }_{N}>0\)). After the substorm (Fig. 9i) the currents return to their original configuration (cf. Fig. 9a).
The electrojet indices AU and AL for the 5-h period encompassing the second substorm in Fig. 8, 10 to 15 UT on 28 May 2000, and the AMPERE current density observations at 30-min intervals. Expansion phase onset is observed in AL shortly after 11:30 UT, followed by a reintensification at around 12:15 UT. Red and blue indicate upwards and downwards currents. The colours saturate at \(\pm 1~\upmu \mbox{A}\,\mbox{m}^{-2}\). Black circles indicate fits to the boundary between R1 and R2 currents
3 Discussion
We have investigated the response of the R1/R2 and R0 field aligned current systems, the ionospheric electrojets, and the ring current, to solar wind–magnetosphere coupling on a range of temporal scales. The observations show clearly that the magnitude of the FAC systems is controlled by a combination of the rate of magnetospheric (and hence ionospheric) convection, driven by magnetic reconnection occurring at the magnetopause and in the magnetotail, and the level of ionospheric conductance. We discuss these findings below.
3.1 Solar Wind–Magnetosphere Coupling and R1/R2 Currents
Magnetic reconnection at the magnetopause and in the magnetotail give rise to magnetospheric and ionospheric convection (Dungey 1961; Cowley and Lockwood 1992). Hall and Pedersen currents in the ionosphere are proportional to the speed of convection (equivalent to an electric field) and the conductance of the ionosphere. The magnitude of these horizontal currents tends to maximise in the auroral zones for two reasons. Firstly, the ionospheric conductance is greater in the auroral zone than in the polar cap due to impact ionisation by auroral precipitation. Secondly, the speed in the sunward flow regions, coincident with the auroral zones, tends to be faster than the antisunward flow in the polar cap due to the relative widths of these regions.
It is the divergence of these horizontal currents, especially the Pedersen currents, that leads to the requirement of field-aligned currents to provide current continuity (e.g., Milan 2013). As will be discussed below, magnetotail reconnection tends to lag behind its magnetopause counterpart, but averaged over a sufficiently long time (e.g. the 3-h substorm cycle), \(\mathrm{\varPhi }_{D}\) can be used as a proxy for the cross-polar cap potential (transpolar voltage) \(\mathrm{\varPhi }_{PC}\) (see Eqs. (2) and (3)), a measure of the convection strength. Indeed, over the 80-day period presented in Fig. 5, we found a correlation of \(r=0.74\) between hourly-averaged \(\mathrm{\varPhi }_{D}\) and \(\alpha_{1}\) (rising to \(r=0.87\) for daily averages).
The Hall currents flowing in the auroral zones, the westwards and eastwards electrojets, produce magnetic perturbations on the ground that are quantified by the AU and AL indices (though the latter is also affected by the substorm electrojet). Unsurprisingly, the strengths of the electrojets and R1/R2 FACs are related, and we found a correlation of 0.75 (0.91) between hourly (daily) averages of \(\mathrm{\varPhi }_{D}\) and AU. The relationship between R1/R2 FACs and the electrojets will be complicated by variations in the ratio of Hall to Pedersen conductance produced by the energy spectrum of precipitating particles. Moreover, AU and AL measure the greatest magnetic perturbation in the auroral zone, which will only indirectly be related to the total FAC magnitude. However, our results show that on a gross scale, a fair correlation exists.
The R2 currents connect into the inner magnetosphere and contribute to the partial ring current which augments the symmetric ring current. Hence, variations in R2 magnitude are expected to produce perturbations in Sym-H in addition to the depression caused by the storm-time enhancement in plasma density in the inner magnetosphere. Indeed, comparing Figs. 7 a and d there is some evidence for depressions in Sym-H being associated with enhancements in \(\alpha _{1}\).
3.2 Substorms
Substorms comprise two main phases, the growth phase associated with the opening of magnetic flux at the magnetopause and the expansion phase when flux is closed in the magnetotail (Lockwood and Cowley 1992). Of less interest, the recovery phase marks the return to more quiescent conditions. In a typical substorm, the opening of flux precedes the closure, and the polar caps, the footprints of the open magnetic field lines of the magnetotail lobes, first expand and then contract. Although not shown in Fig. 8, the expansion and contraction are equal in both northern and southern hemispheres. The redistribution and transport of magnetic flux caused by the expansion and contraction are responsible for the ionospheric convection pattern (Figs. 2c and d, Cowley and Lockwood 1992) that is associated with the R1/R2 current system. Reconnection at the magnetopause and in the magnetotail are largely independent so the growth and expansion phases can occur separately in time, or can overlap. Hence, currents are elevated during both growth and expansion phases, as seen in the two isolated substorms in Fig. 8: even after dayside reconnection has ceased, convection and R1/R2 currents can persist for up to two hours. In this way, the correspondence between dayside reconnection and currents is somewhat decoupled, partially explaining why the correlation between \(\mathrm{\varPhi }_{D}\) and \(\alpha_{1}\) is not higher in Sect. 2.4. In the case where dayside and nightside reconnection occur together, steady magnetospheric convection can ensue (e.g., Sergeev et al. 1996; Walach and Milan 2015). In the substorm of Fig. 9 this overlap persisted for a few 10s of minutes, but in some cases it can continue for several hours.
This substorm behaviour has previously been noted by Coxon et al. (2014b), who showed the increase in R1/R2 current magnitude during substorm growth phase, an enhancement in current at expansion phase onset, and a gradual decrease in current magnitude as the substorm proceeds. The enhancement at substorm onset can be attributed to several factors. Firstly, the onset of nightside reconnection while dayside reconnection is still ongoing will lead to higher convection speeds (Eq. (2)) and hence currents. Secondly, substorms are associated with significant precipitation which enhances the ionospheric conductance. Thirdly, substorms are associated with the formation of the substorm current wedge (SCW) with additional field-aligned currents diverting current from the magnetotail into the nightside ionosphere. Clausen et al. (2013a) showed that on average the formation of the SCW enhances the nightside portions of the region 1 current system, though it is also known that the substorm FACs can be highly filamentary (e.g., Forsyth et al. 2014), on spatial scales much finer than can be resolved with AMPERE, and evolve with time during the expansion phase (e.g., Sergeev et al. 2014). Indeed, we found no clear signature of a SCW in the substorm presented in Fig. 9. As discussed by Milan et al. (2015), principal component analysis fails to reveal a basis function that obviously corresponds to the SCW, though several basis functions do display correlated changes around substorm onset. This suggests that the current systems associated with substorms are highly variable, both temporally and spatially. In this case, our present analysis using PCA is not sensitive to substorm currents, other than enhancements of the R1/R2 currents.
3.3 R0 Currents
Figure 7 shows a clear correspondence between changes in IMF \(B_{Y}\) and the R0 current as measured by \(\alpha_{2}\), as previously demonstrated by Milan et al. (2015), confirming that these cusp currents are associated with magnetic tension forces on newly-opened magnetic field lines.
Figure 4 reveals that \(\alpha_{2}\) varies in polarity with a roughly 27 day periodicity during 2010 and 2011, and at double this frequency in 2012. This suggests that the solar wind sector structure, in which the Earth experiences 2 or 4 periods of predominant IMF \(B_{Y} < 0\) and \(B_{Y} > 0\) per solar rotation (Wilcox and Ness 1965), plays a significant role in controlling the polarity of the R0 FAC and the associated DPY current (Svalgaard 1973). During 2010 and 2011, the warping of the heliospheric current sheet was such that two sectors predominated, changing to four in 2012. Green marks at the bottom of Figs. 4b and d show the times of sector boundary crossings (http://www.leif.org/research/), the frequency of which doubled in 2012.
Figure 7 shows that \(\alpha_{2} > 0\) in the northern hemisphere when IMF \(B_{Y} > 0\). Figure 4 indicates that, ignoring the seasonal dependence in the magnitude of \(\alpha_{2}\), the polarity of the R0 currents in the northern and southern hemispheres tends to be opposite, as is to be expected as magnetic tension forces act in opposite directions on open field lines connected to the north and the south.
As will be discussed in Sect. 3.4, the R0 currents are highly seasonally dependent, being strongest in summer months. The strength of the current is indicative of the conductance of the ionosphere at the footprints of the newly-opened field lines, or equivalently, the ionospheric drag imposed on east-west convecting field lines.
3.4 Seasonal and Interhemispheric Variations
Superimposed on the day-to-day variability of the currents produced by solar wind–magnetosphere coupling, there is a seasonal dependence that leads to stronger FACs around summer solstice. The seasonal variation in FAC magnitude is most clearly observed in \(\alpha_{2}\), the strength of the R0 currents. Coxon et al. (2016) previously reported a seasonal variation in monthly averages of overall FAC magnitude, but their analysis was not able to separate the contributions from the R0 and R1/R2 current systems. Their conclusion was that seasonal variations in solar illumination of the polar regions lead to ionospheric conductance variations that controlled the FAC magnitudes. This was further supported by their observation that current magnitudes also displayed a diurnal variation that was consistent with the offset of the geomagnetic and geographic poles in each hemisphere—that is a 24-h back-and-forth rocking of the auroral zones relative to the solar terminator. Our finding that this manifests itself more in the R0 currents concentrated near the dayside, than the R1/R2 currents which straddle both dayside and nightside, lends further weight to this argument. Furthermore, the R1/R2 currents are located in the auroral zones, where precipitation of charged particles modifies the conductance and the variation associated with photo-ionisation will be somewhat masked.
The seasonal control of FAC magnitude should lead to quasi-sinusoidal variations in anti-phase in the northern and southern hemispheres. However, Coxon et al. (2016) noted that month-to-month variations in average solar wind–magnetosphere coupling (\(\mathrm{\varPhi }_{D}\)) could disturb this pattern, as can be observed in our data as well (e.g. higher average R1/R2 currents around March 2012 in Fig. 4a). On time-scales of hours and days, the R1/R2 FAC magnitude, \(\alpha_{1}\), in both the northern and southern hemispheres vary in tandem, in close association with changes in \(\mathrm{\varPhi }_{D}\) (e.g. Fig. 5).
Coxon et al. (2016) also noted that, averaged over several years, the FAC magnitudes as measured by AMPERE are higher in the northern hemisphere than in the southern hemisphere, as is readily apparent in Fig. 4. At present, it is not clear if this difference is instrumental (for instance, there are significant differences in the coverage of the two polar regions by the orbits of the Iridium spacecraft) or real. However, spacecraft observations of the strength of the ionospheric electrojets in the two hemispheres tentatively support such an interhemispheric asymmetry.
There has been discussion of other mechanisms that can create localised interhemispheric differences in the FAC patterns (e.g., Østgaard et al. 2016). These include: asymmetries in the solar wind dynamo acting at the northern or southern magnetopause introduced by the \(B_{X}\) component of the IMF (e.g., Laundal and Østgaard 2009; Reistad et al. 2014); ionospheric conductance gradients near the solar terminator in each hemisphere (e.g., Benkevich et al. 2000); and the “penetration” of the \(B_{Y}\) component of the IMF into the magnetosphere (e.g., Tenfjord et al. 2015). Observations so far suggest that these are second order effects in comparison to the large-scale conductance asymmetry already noted, but further investigation is merited.
3.5 Quiet Times
Studies of the structure of the internal magnetic field of the Earth are sensitive to contamination by the magnetic perturbations produced by solar wind–magnetosphere coupling. These contaminations can be minimised by selecting periods when it is expected that the external current systems will be relatively inactive. Based upon our observations and discussion, we conclude that:
-
1.
The R0 current system is weak near winter solstice (Figs. 4b and d) and when IMF \(B_{Y} \approx 0\) (Fig. 7b).
-
2.
The R1/R2 current system is weakest near winter solstice (Fig. 4) and when the conditions in the interplanetary medium are unfavourable for dayside reconnection (Figs. 5 and 6).
-
3.
Both R0 and R1/2 current systems appear weaker in the southern hemisphere (Figs. 4c and d).
In Fig. 6a, when \(\mathrm{\varPhi }_{D} \approx 0\) the average \(\alpha_{1} \approx 1.6\), suggesting that 0.4 MA flows in the convection circuit of the magnetosphere (see Sect. 2.3) even during exceptionally weak driving conditions, though we note that this value may be an overestimate. Firstly, the period under consideration in Fig. 6 encompasses spring and summer months when the northern hemisphere ionospheric conductance will be elevated. Secondly, measurements of \(\alpha_{1}\) are only available from current density maps which have been successfully pre-processed prior to the application of principal component analysis (see Sect. 2.2). This introduces a bias in Fig. 6a to periods when the R1/R2 currents are well-defined. Figure 6c shows the proportion of the time that maps were successfully or unsuccessfully pre-processed for different levels of \(\mathrm{\varPhi }_{D}\). For \(\mathrm{\varPhi }_{D} < 10~\mbox{kV}\), 20 % of maps could not be pre-processed, indicating very weak R1/R2 currents. Figure 6c also shows that \(\mathrm{\varPhi } _{D} < 10~\mbox{kV}\) and currents are weak for the majority (\(\approx 60~\%\)) of the time.
The AU index is also well-correlated with \(\mathrm{\varPhi }_{D}\) (Fig. 6b), and hence the magnitude of the R1/R2 current system. This is to be expected as it also monitors a part of the convection circuit. Clearly \(\mathrm{\varPhi }_{D}\) and the electrojet indices are useful parameters for deducing when the influence of external currents systems will be minimal.
4 Conclusions
We have reviewed the main features of the magnetospheric and ionospheric current systems, and related their variability to solar wind–magnetosphere coupling. The currents that define the shape of the magnetosphere, at the magnetopause and across the central plane of the magnetotail are present at all times, though with varying strength. Currents that are associated with magnetic flux transport and the circulation of plasma within the magnetosphere–ionosphere are more variable, being associated with magnetic reconnection occurring at the magnetopause.
Southward turnings of the IMF produce a prompt enhancement of the convection circuit, but the system decays more slowly, on the timescale of the substorm cycle. Extreme and prolonged solar wind driving produces an enhancement of the ring current, a geomagnetic storm, that can take days to dissipate. The form of the solar wind disturbance determines the response of the magnetosphere to driving. The presence of fast and/or slow solar wind, an associated solar wind density enhancement and possibly a shock, and the duration and orientation of a magnetic cloud, all combine to determine the magnitude, onset, and duration of perturbations to currents at the magnetopause, in the convection circuit, and in the inner magnetosphere.
Moreover, insolation of the polar ionospheres, itself variable diurnally, seasonally, and with the solar cycle, modulates the response of the current systems, which can differ significantly between the northern and southern hemispheres. All these factors conspire to produce a highly variable electromagnetic environment.
We have illustrated these behaviours with Birkeland current density maps produced by the AMPERE technique, which exploits engineering magnetometers used for attitude-control onboard the satellites of the Iridium® telecommunications constellation. This novel use of “non-scientific” data for the study of the solar-terrestrial system has provided a significant advance of our understanding of magnetosphere–ionosphere coupling. We have presented observations from just the first three years of the AMPERE dataset, though at the time of writing data are available from six year period 2010–2016. It is to be hoped that these data will continue to be collected in the coming years, so that solar cycle variations in geospace can be investigated. The power of the AMPERE dataset should lend impetus for the development of future constellation missions for space weather monitoring.
References
S.-I. Akasofu, The development of the auroral substorm. Planet. Space Sci. 12, 273–282 (1964). doi:10.1016/0032-0633(64)90151-5
S.-I. Akasofu, S. Chapman, The ring current, geomagnetic disturbance, and the Van Allen radiation belts. J. Geophys. Res. 66, 1321–1350 (1961). doi:10.1029/JZ066i005p01321
S.-I. Akasofu, S. Chapman, D. Venkatesan, The main phase of great magnetic storms. J. Geophys. Res. 68, 3345–3350 (1963). doi:10.1029/JZ068i011p03345
B.J. Anderson, K. Takahashi, B.A. Toth, Sensing global Birkeland currents with Iridium® engineering magnetometer data. Geophys. Res. Lett. 27, 4045–4048 (2000). doi:10.1029/2000GL000094
B.J. Anderson, K. Takahashi, T. Kamei, C.L. Waters, B.A. Toth, Birkeland current system key parameters derived from Iridium observations: method and initial validation results. J. Geophys. Res. 107, 1079 (2002). doi:10.1029/2001JA000080
B.J. Anderson, H. Korth, C.L. Waters, D.L. Green, V.G. Merkin, R.J. Barnes, L.P. Dyrud, Development of large-scale Birkeland currents determined from the Active Magnetosphere and Planetary Electrodynamics Response Experiment. Geophys. Res. Lett. 41, 3017–3025 (2014). doi:10.1002/2014GL059941
G. Atkinson, Polar magnetic substorms. J. Geophys. Res. 72, 1491–1494 (1967). doi:10.1029/JZ072i005p01491
W. Baumjohann, M. Blanc, A. Fedorov, K.-H. Glassmeier, Current systems in planetary magnetospheres and ionospheres. Space Sci. Rev. 152, 99–134 (2010). doi:10.1007/s11214-010-9629-z
R.D. Belian, T.E. Cayton, G.D. Reeves, Quasi-periodic, substorm associated, global flux variations observed at geosynchronous orbit, in Space Plasmas: Coupling Between Small and Medium Scale Processes, ed. by M. Ashour-Abdalla, T. Chang, P. Dusenbery (AGU, Washington, 1995), p. 143
L. Benkevich, W. Lyatsky, L.L. Cogger, Field-aligned currents between conjugate hemispheres. J. Geophys. Res. 102, 27,727–27,737 (2000)
K. Birkeland, Elementary perturbations, in The Norwegian Aurora Polaris Expedition 1902–1903, vol. 1, On the Cause of Magnetic Storms and the Origin of Terrestrial Magnetism (H. Aschehoug, Oslo, 1908), pp. 61–160, part I, chap. II
B. Boström, A model of the auroral electrojets. J. Geophys. Res. 69, 4983–4999 (1964). doi:10.1029/JZ069i023p04983
B. Boström, Desirable magnetic-field measurements in the high-latitude magnetosphere. Space Sci. Rev. 7, 191–197 (1967)
K.S. Braithwaite, G. Rostoker, DP 2 current system in the ionosphere and magnetosphere. Planet. Space Sci. 29, 485–494 (1981)
S. Chapman, V.C.A. Ferraro, A new theory of magnetic storms. Terr. Magn. 36, 77–97 (1931)
S. Chapman, V.C.A. Ferraro, The geomagnetic ring-current: its radial stability. Terr. Magn. 46, 1–6 (1941)
L.B.N. Clausen, J.B.H. Baker, J.M. Ruohoniemi, S.E. Milan, B.J. Anderson, Dynamics of the region 1 Birkeland current oval derived from the Active Magnetosphere and Planetary Electrodynamics Response Experiment (AMPERE). J. Geophys. Res. 117, A06233 (2012). doi:10.1029/2012JA017666
L.B.N. Clausen, J.B.H. Baker, J.M. Ruohoniemi, S.E. Milan, J.C. Coxon, S. Wing, S. Ohtani, B.J. Anderson, Temporal and spatial dynamics of the region 1 and 2 Birkeland currents during substorms. J. Geophys. Res. Space Phys. 118, 3007–3016 (2013a). doi:10.1002/jgra.50288
L.B.N. Clausen, S.E. Milan, J.B.H. Baker, J.M. Ruohoniemi, K.-H. Glassmeier, J.C. Coxon, B.J. Anderson, On the influence of open magnetic flux on substorm intensity: ground- and space-based observations. J. Geophys. Res. Space Phys. 118, 2958–2969 (2013b). doi:10.1002/jgra.50308
S.W.H. Cowley, Magnetosphere–ionosphere interactions: a tutorial review, in Magnetospheric Current Systems, ed. by S. Ohtani et al.Geophys. Monogr. Ser., vol. 118 (AGU, Washington, 2000), pp. 91–106. doi:10.1029/GM118p0091
S.W.H. Cowley, M. Lockwood, Excitation and decay of solar wind-driven flows in the magnetosphere–ionosphere system. Ann. Geophys. 10, 103–115 (1992)
J.C. Coxon, S.E. Milan, L.B.N. Clausen, B.J. Anderson, H. Korth, The magnitudes of the Birkeland currents observed by AMPERE and their role in solar wind–magnetosphere–ionosphere coupling. J. Geophys. Res. Space Phys. 119, 9804–9815 (2014a). doi:10.1002/2014JA020138
J.C. Coxon, S.E. Milan, L.B.N. Clausen, B.J. Anderson, H. Korth, A superposed epoch analysis of the Region 1 and Region 2 Birkeland currents observed by AMPERE during substorms. J. Geophys. Res. Space Phys. 119, 9834–9846 (2014b). doi:10.1002/2014JA020500
J.C. Coxon, S.E. Milan, J.A. Carter, L.B.N. Clausen, B.J. Anderson, H. Korth, Seasonal and diurnal variations in AMPERE observations of the Birkeland currents compared to modelled results. J. Geophys. Res. Space Phys. 121, 4027–4040 (2016). doi:10.1002/2015JA022050
W.D. Cummings, A.J. Dessler, Field-aligned currents in the magnetosphere. J. Geophys. Res. 72, 1007–1013 (1967). doi:10.1029/JZ072i003p01007
J.J. Curto, T. Araki, L.F. Alberca, Evolution of the concept of Sudden Storm Commencements and their operative identification. Earth Planets Space 59, i–xii (2007)
T.N. Davis, M. Sugiura, Auroral electrojet activity index AE and its universal time variations. J. Geophys. Res. 71, 785–801 (1966)
J.W. Dungey, Interplanetary magnetic fields and the auroral zones. Phys. Rev. Lett. 6, 47–48 (1961)
A. Egeland, W.J. Burke, The ring current: a short biography. Hist. Geo- Space Sci. 3, 131–142 (2012). doi:10.5194/hgss-3-131-2012
R.E. Erlandson, L.J. Zanetti, T.A. Potemra, P.F. Bythrow, R. Lundin, Dependence of region 1 Birkeland currents near noon. J. Geophys. Res. 93, 9804–9814 (1988). doi:10.1029/JA093iA09p09804
Y.I. Feldstein, Magnetic field variations in the polar region during magnetically quiet periods and interplanetary magnetic fields. Space Sci. Rev. 18, 777 (1976)
C. Forsyth, A.N. Fazakerley, I.J. Rae, C.E.J. Watt, K. Murphy, J.A. Wild, T. Karlsson, R. Mutel, C.J. Owen, R. Ergun, A. Masson, M. Berthomier, E. Donovan, H.U. Frey, J. Matzka, C. Stolle, Y. Zhang, In situ spatiotemporal measurements of the detailed azimuthal substructure of the substorm current wedge. J. Geophys. Res. 119, 927–946 (2014). doi:10.1002/2013JA019302
N. Fukushima, Generalized theorem for no ground magnetic effect of vertical currents connected with Pedersen currents in the uniform conducting ionosphere. Rep. Ionos. Space Res. 30, 35–50 (1976)
S.F. Fung, J.A. Tepper, X. Cai, Magnetospheric state of sawtooth events. J. Geophys. Res. Space Phys. 121, 7860–7869 (2016). doi:10.1002/2016JA022693
N.Y. Ganushkina, M.W. Liemohn, S. Dubyagin, I.A. Daglis, I. Dandouras, D.L. De Zeeuw, Y. Ebihara, R. Ilie, R. Katus, M. Kubyshkina, S.E. Milan, S. Ohtani, N. Østgaard, J.P. Reistad, P. Tenfjord, F. Tofoletto, S. Zaharia, O. Amariutei, Defining and resolving current systems in geospace. Ann. Geophys. 33, 1369–1402 (2015). doi:10.5194/angeo-33-1369-2015
W.D. Gonzalez, J.A. Joselyn, Y. Kamide, H.W. Kroehl, G. Rostoker, B.T. Tsurutani, V.M. Vasyliunas, What is a geomagnetic storm? J. Geophys. Res. 99, 5771–5792 (1994). doi:10.1029/93JA02867
W.D. Gonzalez, B.T. Tsurutani, A.L. Clúa de Gonzalez, Interplanetary origin of geomagnetic storms. Space Sci. Rev. 88, 529–562 (1999). doi:10.1023/A:1005160129098
J.T. Gosling, S.J. Bame, D.J. McComas, J.L. Phillips, Coronal mass ejections and large geomagnetic storms. Geophys. Res. Lett. 17, 901–904 (1990). doi:10.1029/GL017i007p00901
D.L. Green, C.L. Waters, B.J. Anderson, H. Korth, R.J. Barnes, Comparison of large-scale Birkeland currents determined from Iridium and SuperDARN data. Ann. Geophys. 24, 941–959 (2006). doi:10.5194/angeo-24-941-2006
A. Grocott, J.A. Wild, S.E. Milan, T.K. Yeoman, Superposed epoch analysis of the ionospheric convection evolution during substorms: onset latitude dependence. Ann. Geophys. 27, 591–600 (2009)
T. Iijima, T.A. Potemra, The amplitude distribution of field-aligned currents at northern high latitudes observed by Triad. J. Geophys. Res. 81, 2165–2174 (1976a). doi:10.1029/JA081i013p02165
T. Iijima, T.A. Potemra, Field-aligned currents in the dayside cusp observed by Triad. J. Geophys. Res. 81, 5971–5979 (1976b). doi:10.1029/JA081i034p05971
T. Iijima, T.A. Potemra, Large-scale characteristics of field-aligned currents associated with substorms. J. Geophys. Res. 83, 599–615 (1978). doi:10.1029/JA083iA02p00599
T. Iijima, T.A. Potemra, N.A. Saflekos, Field-aligned currents in the south polar cusp and their relationship to the interplanetary magnetic field. J. Geophys. Res. 83, 5595–5603 (1978). doi:10.1029/JA083iA12p05595
T. Iyemori, Storm-time magnetospheric currents inferred from mid-latitude geomagnetic field variations. J. Geomagn. Geoelectr. 42, 1249–1265 (1990)
Y. Kamide, Association of DP and DR fields with the interplanetary magnetic field variation. J. Geophys. Res. 79, 49–55 (1974). doi:10.1029/JA079i001p00049
Y. Kamide, N. Fukushima, Analysis of magnetic storms with DR indices for equatorial ring-current field. Radio Sci. 6, 277–278 (1971). doi:10.1029/RS006i002p00277
J.H. King, Long-term solar wind variations and associated data sources. J. Geomagn. Geoelectr. 43, 865–880 (1991)
J.H. King, N.E. Papitashvili, Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. 110, A02209 (2005). doi:10.1029/2004JA010804
K.M. Laundal, N. Østgaard, Asymmetric auroral intensities in the Earth’s Northern and Southern hemispheres. Nature 460, 491–493 (2009)
K.M. Laundal, J. Gjerloev, N. Østgaard, J. Reistad, S. Haaland, K. Snekvik, P. Tenfjord, S. Ohtani, S.E. Milan, The impact of sunlight on high-latitude equivalent currents. J. Geophys. Res. Space Phys. 121, 2715–2726 (2016). doi:10.1002/2015JA022236
M.W. Liemohn, J.U. Kozyra, C.R. Clauer, A.J. Ridley, Computational analysis of the near-Earth magnetospheric current system during two-phase decay storms. J. Geophys. Res. 106, 29531–29542 (2001)
M. Lockwood, On flow reversal boundaries and transpolar voltage in average models of high latitude convection. Planet. Space Sci. 3, 397–409 (1991)
M. Lockwood, Reconstruction and prediction of variations in the open solar magnetic flux and interplanetary conditions. Living Rev. Sol. Phys. 10 (2013). URL (accessed 1 May): http://www.livingreviews.org/lrsp-2013-4
M. Lockwood, S.W.H. Cowley, Ionospheric convection and the substorm cycle, in Substorms 1: Proceedings of the First International Conference on Substorms, vol. 1 (European Space Agency, Kiruna, 1992), pp. 99–109
R.L. McPherron, Growth phase of magnetospheric substorms. J. Geophys. Res. 75, 5592–5599 (1970). doi:10.1029/JA075i028p05592
R.L. McPherron, C.T. Russell, M.P. Aubry, Satellite studies of magnetospheric substorms on August 15, 1968. 9. Phenomenological model for substorms. J. Geophys. Res. 78, 3131–3149 (1973)
S.E. Milan, Both solar wind–magnetosphere coupling and ring current intensity control of the size of the auroral oval. Geophys. Res. Lett. 36, L18101 (2009). doi:10.1029/2009GL039997
S.E. Milan, Modelling Birkeland currents in the expanding/contracting polar cap paradigm. J. Geophys. Res. 118, 5532–5542 (2013). doi:10.1002/jgra.50393
S.E. Milan, Sun et Lumière: solar wind–magnetosphere coupling as deduced from ionospheric flows and polar auroras, in Magnetospheric Plasma Physics: The Impact of Jim Dungey’s Research, ed. by D. Southwood et al. (Springer, Berlin, 2015)
S.E. Milan, M. Lester, S.W.H. Cowley, K. Oksavik, M. Brittnacher, R.A. Greenwald, G. Sofko, J.-P. Villain, Variations in polar cap area during two substorm cycles. Ann. Geophys. 21, 1121–1140 (2003)
S.E. Milan, G. Provan, B. Hubert, Magnetic flux transport in the Dungey cycle: a survey of dayside and nightside reconnection rates. J. Geophys. Res. 112, A01209 (2007). doi:10.1029/2006JA011642
S.E. Milan, A. Grocott, C. Forsyth, S.M. Imber, P.D. Boakes, B. Hubert, A superposed epoch analysis of auroral evolution during substorm growth, onset and recovery: open magnetic flux control of substorm intensity. Ann. Geophys. 27, 659–668 (2009a)
S.E. Milan, J. Hutchinson, P.D. Boakes, B. Hubert, Influences on the radius of the auroral oval. Ann. Geophys. 27, 2913–2924 (2009b)
S.E. Milan, J.S. Gosling, B. Hubert, Relationship between interplanetary parameters and the magnetopause reconnection rate quantified from observations of the expanding polar cap. J. Geophys. Res. 117, A03226 (2012). doi:10.1029/2011JA017082
S.E. Milan, J.A. Carter, H. Korth, B.J. Anderson, Principal Component Analysis of Birkeland currents determined by the Active Magnetosphere and Planetary Electrodynamics Response Experiment. J. Geophys. Res. Space Phys. 120, 10415–10424 (2015). doi:10.1002/2015JA021680
K.R. Murphy, I.R. Mann, I.J. Rae, C.L. Waters, H.U. Frey, A. Kale, H.J. Singer, B.J. Anderson, H. Korth, The detailed spatial structure of field-aligned currents comprising the substorm current wedge. J. Geophys. Res. Space Phys. 118, 7714–7727 (2013). doi:10.1002/2013JA018979
N.F. Ness, The Earth’s magnetic tail. J. Geophys. Res. 70, 2989–3005 (1965). doi:10.1029/JZ070i013p02989
A. Nishida, Geomagnetic DP-2 fluctuations and associated magnetospheric phenomena. J. Geophys. Res. 73, 5549 (1968)
T. Obayashi, The interaction of the solar wind with the geomagnetic field during disturbed conditions, in Solar-Terrestrial Physics, ed. by J.W. King, W.S. Newman (Academic Press, London, 1967)
S. Ohtani, S. Kokubun, R. Nakamura, R.C. Elphic, C.T. Russell, D.N. Baker, Field-aligned current signatures in the near-tail region: 2. coupling between the region 1 and region 2 systems. J. Geophys. Res. 95, 18913–18927 (1990). doi:10.1029/JA095iA11p18913
N. Østgaard, J.P. Reistad, P. Tenfjord, K.M. Laundal, K. Snekvik, S.E. Milan, S. Haaland, Mechanisms that produce auroral asymmetries in the conjugate hemispheres, in Auroral Dynamics and Space Weather, ed. by Y. Zhang, L.J. Paxton. AGU Geophysical Monograph, vol. 215 (2016), pp. 133–143
V.O. Papitashvili, F. Christiansen, T. Neubert, A new model of field-aligned currents derived from high-precision satellite magnetic field data. Geophys. Res. Lett. 29, 1683 (2002). doi:10.1029/2001GL014207
E.N. Parker, The alternative paradigm for magnetospheric physics. J. Geophys. Res. 101, 10587–10625 (1996)
T.I. Pulkkinen, N. Partamies, R.L. McPherron, M. Henderson, G.D. Reeves, M.F. Thomsen, H.J. Singer, Comparative statistical analysis of storm time activations and sawtooth events. J. Geophys. Res. 112, A01205 (2007). doi:10.1029/2006JA012024
J.P. Reistad, N. Østgaard, K.M. Laundal, S. Haaland, P. Tenfjord, K. Snekvik, K. Oksavik, S.E. Milan, Intensity asymmetries in the dusk sector of the poleward auroral oval due to IMF Bx. J. Geophys. Res. Space Phys. 119, 9497–9507 (2014). doi:10.1002/2014JA020216
A.J. Ridley, Effects of seasonal changes in the ionospheric conductances on magnetospheric field-aligned currents. Geophys. Res. Lett. 34, L05101 (2007). doi:10.1029/2006GL028444
G. Rostoker, S.-I. Akasofu, J. Foster, R. Greenwald, Y. Kamide, K. Kawasaki, A. Lui, R. McPherron, C. Russell, Magnetospheric substorms—definitions and signatures. J. Geophys. Res. 85, 1663–1668 (1980). doi:10.1029/JA085iA04p01663
V.A. Sergeev, R.J. Pellinen, T.I. Pulkkinen, Steady magnetospheric convection: a review of recent results. Space Sci. Rev. 75, 551–604 (1996)
V.A. Sergeev, A.V. Nikolaev, M.V. Kubyshkina, N.A. Tsyganenko, H. Singer, J. Rodriguez, V. Angelopoulos, R. Nakamura, S.E. Milan, J.C. Coxon, B. Anderson, H. Korth, Event study combining magnetospheric and ionospheric perspectives of the substorm current wedge modeling and dynamics. J. Geophys. Res. Space Phys. 119, 9714–9728 (2014). doi:10.1002/2014JA020522
G.L. Siscoe, T.S. Huang, Polar cap inflation and deflation. J. Geophys. Res. 90, 543–547 (1985)
T.W. Speiser, N.F. Ness, The neutral sheet in the geomagnetic tail: its motion, equivalent currents, and field line connection through it. J. Geophys. Res. 72, 131–141 (1967). doi:10.1029/JZ072i001p00131
M. Sugiura, Hourly values of the equatorial Dst for IGY, in, in Annales of the International Geophysical Year, vol. 35 (Pergamon, Oxford, 1964), pp. 945–948
L. Svalgaard, Polar cap magnetic variations and their relationship with the interplanetary magnetic sector structure. J. Geophys. Res. 78, 2064 (1973)
P. Tenfjord, N. Østgaard, K. Snekvik, K.M. Laundal, J. Reistad, S. Haaland, S.E. Milan, How the IMF \(B_{Y}\) induces a \(B_{Y}\) component in the closed magnetosphere and how it leads to asymmetric currents and convection patterns in the two hemispheres. J. Geophys. Res. Space Phys. 120, 9368–9384 (2015). doi:10.1002/2015JA021579
V.M. Vasyliunas, Mathematical models of magnetospheric convection and its coupling to the ionosphere, in Particles and Fields in the Magnetosphere, ed. by B.M. McCormac (Reidel, New York, 1970), pp. 60–71
V.M. Vasyliunas, Relation between magnetic fields and electric currents in plasmas. Ann. Geophys. 23, 2589–2597 (2005). doi:10.5194/angeo-23-2589-2005
M.-T. Walach, S.E. Milan, Are steady magnetospheric convection events prolonged substorms? J. Geophys. Res. Space Phys. 120, 1751–1758 (2015). doi:10.1002/2014JA020631
C.L. Waters, B.J. Anderson, K. Liou, Estimation of global field-aligned currents using the iridium® system magnetometer data. Geophys. Res. Lett. 28, 2165–2168 (2001). doi:10.1029/2000GL012725
J.M. Wilcox, N.F. Ness, Quasi-stationary corotating structure in the interplanetary medium. J. Geophys. Res. 70, 5793–5805 (1965)
J. Wilhjelm, E. Friis-Christensen, T.A. Potemra, The relationship between ionospheric and field-aligned currents in the dayside cusp. J. Geophys. Res. 83, 5586–5594 (1978). doi:10.1029/JA083iA12p05586
R.A. Wolf, Effects of ionospheric conductivity on convective flow of plasma in the magnetosphere. J. Geophys. Res. 75, 4677–4698 (1970)
A.J. Zmuda, J.C. Armstrong, The diurnal variation of the region with vector magnetic changes associated with field-aligned currents. J. Geophys. Res. 79, 2501–2502 (1974). doi:10.1029/JA079i016p02501
A.J. Zmuda, J.H. Martin, F.T. Heuring, Transverse magnetic disturbances at 1100 kilometres in the auroral region. J. Geophys. Res. 71, 5033–5045 (1966). doi:10.1029/JZ071i021p05033
A.J. Zmuda, F.T. Heuring, J.H. Martin, Dayside magnetic disturbances at 1100 km in the auroral oval. J. Geophys. Res. 72, 1115–1117 (1967). doi:10.1029/JZ072i003p01115
Acknowledgements
SEM and JAC were supported by were supported by the Science and Technology Facilities Council (STFC), UK, grant ST/N000749/1. MTW was supported by an STFC studentship. The work at the Birkeland Centre for Space Centre, University of Bergen, Norway, was supported by the Research Council of Norway/CoE under contract 223252/F50. We thank the AMPERE team and the AMPERE Science Center for providing the Iridium-derived data products; AMPERE products are available at http://ampere.jhuapl.edu. The OMNI data, including solar wind parameters and geomagnetic indices, were obtained from the GSFC/SPDF OMNIWeb interface at http://omniweb.gsfc.nasa.gov. We acknowledge the International Space Science Institute Bern for holding the Workshop on “Earth’s Magnetic Field” held in Bern in May 2015 that initiate this review article.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Milan, S.E., Clausen, L.B.N., Coxon, J.C. et al. Overview of Solar Wind–Magnetosphere–Ionosphere–Atmosphere Coupling and the Generation of Magnetospheric Currents. Space Sci Rev 206, 547–573 (2017). https://doi.org/10.1007/s11214-017-0333-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11214-017-0333-0