Applications of Electrified Dust and Dust Devil Electrodynamics to Martian Atmospheric Electricity

Abstract

Atmospheric transport and suspension of dust frequently brings electrification, which may be substantial. Electric fields of 10 kV m⁻¹ to 100 kV m⁻¹ have been observed at the surface beneath suspended dust in the terrestrial atmosphere, and some electrification has been observed to persist in dust at levels to 5 km, as well as in volcanic plumes. The interaction between individual particles which causes the electrification is incompletely understood, and multiple processes are thought to be acting. A variation in particle charge with particle size, and the effect of gravitational separation explains to, some extent, the charge structures observed in terrestrial dust storms. More extensive flow-based modelling demonstrates that bulk electric fields in excess of 10 kV m⁻¹ can be obtained rapidly (in less than 10 s) from rotating dust systems (dust devils) and that terrestrial breakdown fields can be obtained. Modelled profiles of electrical conductivity in the Martian atmosphere suggest the possibility of dust electrification, and dust devils have been suggested as a mechanism of charge separation able to maintain current flow between one region of the atmosphere and another, through a global circuit. Fundamental new understanding of Martian atmospheric electricity will result from the ExoMars mission, which carries the DREAMS (Dust characterization, Risk Assessment, and Environment Analyser on the Martian Surface)—MicroARES (Atmospheric Radiation and Electricity Sensor) instrumentation to Mars in 2016 for the first in situ electrical measurements.

1 Charge Separation in Dust

It has long been known that dust lofted or transported can become highly electrified. Strong effects were reported on a gold leaf electrometer connected to a roof-level electrode which was exposed to a dust storm in Lahore in 1847, together with the generation of sparks (Baddeley 1860). An accompanying characteristic of the Dust Bowl disaster in the US Great Plains during the 1930s was severe static electricity, audible on domestic medium wave radios and able to cause electric shocks, with earthing chains necessary on automobiles. Under fair weather conditions, the magnitude of the vertical terrestrial atmospheric electric field is about 100 V m⁻¹, sustained by distant thunderstorm and disturbed weather electrification. Dust storms are considerably electrified in comparison. Quantitatively, electric fields exceeding 100 kV m⁻¹ have been measured during blowing sand, dust storms and dust devils (Rudge 1913; Demon et al. 1953; Freier 1960; Crozier 1964; Harris 1967; Stow 1969; Kamra 1972; Schmidt et al. 1998; Renno et al. 2004; Jackson and Farrell 2006; Kok and Renno 2006, 2008a, 2008b; Williams et al. 2009). As an example, Fig. 1 shows the variation in electric field during the passage of a dust devil in the Sahara desert, opportunistically obtained during measurements undertaken for another purpose (Freier 1960).

Fig. 1

Variation of electric field with time beneath the passage of a dust devil in the Sahara desert. (Reproduced from Freier 1960 with permission of Wiley)

As discussed later in this paper (Sect. 3), it is generally accepted that dust electrification is due to contact and triboelectric charging between blowing particles during these phenomena. The details of the charge transfer mechanism remain incomplete, but several experiments and observations (Freier 1960; Inculet et al. 2006; Duff and Lacks 2008) suggest that on average, during collisions, the smallest grains acquire negative charge with respect to larger particles. In general, the smallest particles are brought into suspension and transported aloft into the atmosphere by local turbulence, whereas the larger particles stay close to the surface. This gravitational charge separation is consistent with increase of the atmospheric electric field observed during dusty phenomena.

Laboratory and theoretical work (Kok and Renno 2006, 2008a, 2008b) suggest that intense electric fields can influence charged particle dynamics through changing their trajectories and reducing the threshold friction speed necessary for initiating their motion. This facilitates the lifting of particles from the surface, so increasing the concentration of saltating grains at a given wind speed. Electric forces may therefore play a further role in the evolution of dust events, including dust devils.

Observations of dust electrification are sparse in literature, both because this field of study is relatively young and because of the difficulty in sampling stochastic dust activity. There is renewed interest in dust electrification due to its consequences for human activities such as the breakdown of power transmission lines, electrical alignment of atmospheric particles (Ulanowski et al. 2007), volcanic plume electrification (Mather and Harrison 2006) and planetary exploration (Helling et al. 2016). In this latter case, the presence of electric discharges or electromagnetic noise can potentially affect communications or communications equipment, but substantial electric fields have also been argued to affect atmospheric chemistry and planet habitability (Atreya et al. 2006; Delory et al. 2006) and the possible development of life (Miller 1953), in particular for Mars. New measurements from the ExoMars 2016 space mission (Bettanini et al. 2014) using the DREAMS-MicroARES (acronym formed from Dust characterization, Risk Assessment, and Environment Analyser on the Martian Surface, and Atmospheric Radiation and Electricity Sensor) instrument will provide the first direct measurements of the electric properties of Martian atmosphere. This is likely to mark a hugely important step change in the knowledge of Martian atmospheric electricity.

This paper therefore presents a pre-MicroARES view of the electrical properties of dusts and dust devils, with particular reference to Mars. To do this, Sect. 2 first briefly summarises knowledge on Martian atmospheric electricity. Section 3 then provides an overview of particle electrification mechanisms concerning dust. Section 4 reports the results of some of the most recent observations of dust electrification during dust storms/devils in terrestrial deserts both close to the surface and aloft. Section 5 provides an overview of modelling of dust devils, and Sect. 6 describes the DREAMS-MicroARES sensor to be used on the forthcoming ExoMars mission.

2 The Martian Electrical Environment

2.1 Atmospheric Electricity on Mars

Atmospheres electrify to varying extents, depending on the charged particles they contain and whether winds, convection or other meteorological processes can actively separate local charge (Harrison et al. 2008; Aplin 2006). The consequences of electrification include the motion of charged particles and ions under the action of electric fields, and electrical discharges where substantial accumulations of charge occur. In the Martian atmosphere, cosmic rays and ultra violet radiation generate molecular cluster ions which, together with free electrons, make the atmosphere electrically conductive. With active charge separation therefore, current flow can potentially occur, and a planetary electrical system analogous to the terrestrial global atmospheric electric circuit has accordingly been considered (Fillingim 1998; Farrell and Desch 2001; Aplin 2006). The abundance of dust in Mars’ atmosphere (and remote sensing of its dust devils), combined with knowledge that terrestrial dust electrification is common has led to the expectation that Martian dust devils can become electrified.

The basis for electrical activity on Mars has been assumed to be similar to electrical activity in Earth’s atmosphere. This has been considered through the global circuit concept introduced for the Earth in the early 20th century by Wilson (1921), Harrison (2011). A global circuit relies on the existence of several key characteristics: a global generator (lightning, discharges, etc.), conductive surfaces (the ionosphere and the rocky surface) overall forming a spherical capacitor system (Rycroft et al. 2008, 2012). Lightning is a key indicator of planetary atmospheric electricity which can be remotely sensed. For example, at Earth, VLF signals propagating in the surface-ionosphere waveguide allow location of lightning events, and high frequency “sferic” (>3 MHz) emissions can be detected by Earth-orbiting spacecraft (Herman et al. 1973). Global circuits may prevail on a number of solar system bodies including Mars (Aplin 2006; Aplin et al. 2008).

The case for Martian atmospheric electricity has taken a unique path motivated by a strong astrobiological context. After the initial tribo-electricity experiments of Eden and Vonnegut (1973), Mills (1977) mixed grains in a low pressure CO₂ gas and created impressive electrical activity (glow and spark discharges) in order to gain insights into the environment that may have created ambiguities in the Viking lander biological experiments. It was concluded that this active dust-created electrical environment could make Martian dust storms an effective ‘scavenger’ of organic material. To date though, there have been no direct measurements of the atmospheric electrical environment on Mars. Indirect evidence of electrification however exists from the apparent adhesion of dust to the wheels of the Mars Pathfinder and Sojourner rovers, suggested to be electrostatic in origin (Farrell et al. 1999; Ferguson et al. 1999) and from laboratory measurements using Martian analogue materials (e.g. Krauss et al. 2003; Aplin et al. 2012).

Given the lack of in situ measurements, there are three strong but circumstantial arguments that dust storms in the low pressure CO₂ atmosphere of Mars may be electrical in nature:

• (1) Laboratory experiments (Farrell et al. 2015) of the breakdown from mixing sand grains all display measurable electrical effects. These not only include the early glow-creating laboratory experiments by Eden and Vonnegut (1973) and Mills (1977), but also a later set of dust mixing studies in a low pressure CO₂ gas performed by Krauss et al. (2003, 2006) and pre-glow and spark discharge studies by Farrell et al. (2015).

• (2) Modelling studies (see Sect. 5) suggest that an electron avalanche and collisional plasma can be created when dust storm E-fields stress the low pressure CO₂ gas.

• (3) Measurements in terrestrial desert environments reveal that dust devils and dust features can generate large electric fields (Freier 1960; Crozier 1964; Farrell et al. 2004; Renno et al. 2004; Delory et al. 2006; Jackson and Farrell 2006; Seran et al. 2013; Esposito et al. 2015, 2016). If this same electrical generator process occurred in a lower pressure atmosphere (like that at Mars), there would be the initiation of enhanced electron impact ionization and atmospheric breakdown.

In terms of arguments against Martian atmospheric electricity, Ruf et al. (2009) reported the possible remote-sensed detection of lightning emission at 8 GHz from Mars using a terrestrial-based radio telescope. Given the detection, the electric dipole moment to account for the discharge was found to be relatively large. However, subsequent work (Anderson et al. 2012) could not confirm the initial ∼8 GHz observation. Also, a sensitive 4–5 MHz radio system aboard Mars Express carried out an unsuccessful search for lightning RF discharges, in close proximity to the planet (Gurnett et al. 2010).

These remote sensing observations do not confirm impulsive lightning events from Mars. However, instead of intense impulsive cloud-to-ground discharges known at Earth, laboratory experiments suggest the effects may be more subtle, with mixing of particles creating dark Townsend (gas ionization) discharges, low current glows, and local weaker but numerous spark discharges. In other words, the Martian system may be continually discharging (or ‘leaking’) at low current levels into the low-pressure atmosphere, thereby avoiding the excessively large accumulation of charge which leads to impulsive lightning events. In situ measurement systems offer the possibility to resolve this apparent fundamental difference in our understanding of the terrestrial and Martian systems.

2.2 Ion Balance in Atmospheres

On Mars, the main permanent ionization source is the bombardment by cosmic rays and the cascade of ions and electrons generated when they collide with neutral atoms and molecules. The maximum ion production rate by cosmic rays is at the surface because the atmospheric thickness of Mars is not sufficient to allow cosmic rays to deposit all their energy in the atmosphere, hence most of the energy reaches the surface. During day-time photo-ionization by solar EUV and soft X-rays can also contribute with an efficiency increasing with altitude while, at night, energetic electron precipitation from the magnetic tail of the planet may also provide a supplementary source of ionization.

Since the initial work of Whitten et al. (1971), progresses in laboratory measurements of ion-neutral reactions as well as radio-electric observations of the electron density profiles (Patzold et al. 2005) have allowed several authors to build more detailed models of ionized species in the Martian lower atmosphere. According to Molina-Cuberos et al. (2002) the most abundant ions below ∼50 km are hydronium ions $\mathrm{H}_{3}\mathrm{O}^{+}(\mathrm{H}_{2}\mathrm{O})_{n}$ while $\mathrm{O}_{2}^{+}$ dominates above ∼70 km. The main negative ion species are water clusters of $\mathrm{CO}_{3}^{-}$, $\mathrm{NO}_{2}^{-}$, $\mathrm{NO}_{3}^{-}$ reaching a density of about 4500 ions cm⁻³ at the surface. At 35 km the electron density reaches a peak of ${\sim} 10^{2}~\mbox{e}\,\mbox{cm}^{- 3}$ and after a decrease with altitude, a secondary peak of ${\sim}70~\mbox{e}\,\mbox{cm}^{- 3}$ appears at ∼5 km. This secondary peak may significantly impact the negative conductivity at ground level. Although not indicated in the paper, this secondary peak close to the surface might be due to photo-electron production from UV impacts on the surface (Grard 1995).

An atmosphere’s electrical conductivity depends on the local concentrations of ions and electrons and ion species it contains. The total conductivity $\sigma$ is given by

$$ \sigma = e ( \mu_{ +} n_{ +} + \mu_{ -} n_{ -} + \mu_{e} n_{e} ) $$

(1)

where $n_{+}$, $n_{-}$, and $n_{e}$ are the number concentrations per unit volume of positive ions, negative ions and free electrons respectively, and $\mu_{+}$, $\mu_{-}$, and $\mu_{e}$ are their associated electrical mobility (the drift speed per unit electric field). The concentrations of ions and electrons are determined by the production rates by ionization and photoelectron emission, and their losses by recombination and attachment to other particles. In the presence of a dust-laden atmosphere, the concentration of ions and electrons (and therefore the electrical conductivity) will be reduced. The ratio of ions to electrons depends on the concentration of atmospheric electrophilic species; on Mars both negative $\mathrm{CO}_{2}^{-}$ ions and electrons are thought to be present (e.g. Aplin 2006). The ion and electron concentrations are governed by a set of rate equations for ion production and loss, written separately for positive ions, negative ions and electrons by Tripathi et al. (2008) as

$$\begin{aligned} \frac{dn_{ +}}{dt} &= q - \alpha n_{ +} n_{ -} - \alpha_{e}n_{ +} n_{e} - n_{ +} \sum _{j} \beta_{j}^{ +} N_{j} , \end{aligned}$$

(2)

$$\begin{aligned} \frac{dn_{ -}}{dt} &= q - \alpha n_{ +} n_{ -} - n_{ -} \sum_{j} \beta_{j}^{ -} N_{j} - Fn_{ -} , \end{aligned}$$

(3)

$$\begin{aligned} \frac{dn_{e}}{dt} &= q_{e} + Fn_{ -} - \alpha_{e}n_{ +} n_{e} - n_{e}\sum_{j} \beta_{j}^{e}N_{j} , \end{aligned}$$

(4)

assuming no transport of ionization. In Eqs. (2) to (4), the volumetric ion and electron production rates are $q$ and $q_{e}$ respectively, the ion-ion and ion-electron recombination coefficients are $\alpha$ and $\alpha_{e}$, and the negative ion detachment rate to yield electrons is $F$. The positive ion-particle attachment coefficient to particles of concentration $N$ carrying $j$ elementary charges is $\beta_{j}^{ +}$, that for negative ion attachment to particles $\beta_{j}^{ -}$, and that for electron attachment to particles $\beta_{j}^{e}$. Theoretical formulations for recombination and attachment coefficients exist (e.g. Harrison and Tammet 2008; Tripathi et al. 2008), and the electron detachment rate can be found from thermodynamic considerations.

2.3 Martian Conductivity Profiles and Relaxation Timescales

Solution of the ion balance equations with time gives the variations in ion and electron concentrations, which, when the production and loss rates are equal, become steady-state concentrations. If the ion production rates are known or can be calculated as a function of height (for example from information about the cosmic ray energies and the atmospheric density profile), and assumptions are made about the vertical profile of particles, the steady state ion and electron concentrations can be found. In turn, this allows calculation of the electrical conductivity, $\sigma$. An important parameter which can be determined from $\sigma$ is the charge relaxation timescale, $\tau$, given by

$$ \tau = \frac{\varepsilon_{0}}{\sigma} $$

(5)

where $\varepsilon_{0}$ is the permittivity of free space. This defines the timescale for the decay of charge on a particle in a medium with conductivity $\sigma$, as if the particle were considered to be of a finite capacitance and connected to a distant fixed potential through the medium. It therefore provides a characteristic timescale for charge to be sustained on a particle. In the Earth’s lower atmosphere, timescales of 10 s to 100 s are typical, which allows electrification to develop with moderately active electrical processes such as those in terrestrial dust storms, thunderstorms or volcanic plumes.

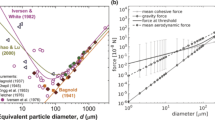
Figure 2(a) shows calculations from Tripathi et al. (2008) for the vertical profile of electrical conductivity in the Martian atmosphere, under different assumptions of aerosol loading. It is immediately apparent that the electrical conductivity is usually two orders of magnitude greater than that for Earth. Only when the Martian atmosphere is assumed to contain a dust storm does its lower atmosphere have an electrical conductivity comparable to that of Earth. (This has practical consequences for testing Martian atmospheric electrical instrumentation on Earth, see Sect. 6). The associated relaxation times are shown in Fig. 2(b). This indicates that, for charge to be sustained on particles in the Martian atmosphere for timescales appreciably greater than one second, a dust storm conductivity environment would be required. The combination presented by a dust devil generating particle electrification in a low conductivity environment may therefore offer unique circumstances on Mars for active charge generation.

Fig. 2

Profiles of (a) atmospheric electrical conductivity $\sigma$ and (b) the associated charge relaxation timescale $\varepsilon_{0}/\sigma$, for Mars (from Tripathi et al. 2008) and Earth (from Nicoll 2012). In the Martian case, three scenarios of conductivity profile are considered, for a clear atmosphere, an aerosol-laden atmosphere, and a dust storm of opacity 5. In the terrestrial case, the total conductivity is considered to be twice the positive conductivity, under the quiet solar conditions observed by Gringel (1978)

The effect of including the aerosols in the electrical model of the lower Martian atmosphere very substantially reduces the free electron concentration at low altitude. It decreases by more than two orders of magnitude compared to the simple model of ion-neutral chemistry of Molina-Cuberos et al. (2002) to be less than ${\sim} 0.5~\mbox{e}\,\mbox{cm}^{-3}$ at ground with the ${\sim} 100~\mbox{e}\,\mbox{cm}^{-3}$ peak at 35 km lifted to ∼45 km, and also reduced by two orders of magnitude at ${\sim} 1~\mbox{e}\,\mbox{cm}^{-3}$.

Michael et al. (2007, 2008) comprehensively modelled the role of aerosols on the charged particle distribution and conductivity in the lower atmosphere using aerosol properties (Chassefière et al. 1995). These studies were performed for both night-time and daytime conditions when dust particles are photo-ionized by low energy (∼6 eV) solar UV that reach the Martian surface and produce a photo-electron population whose properties were taken from the work of Grard (1995). A role for dust particles, in particular close to the surface, is clearly emphasized by this study.

At night aerosols become charged by attachment of positive or negative ions. More aerosols become charged close to the surface than at higher altitudes, and the dust content from Phobos 2 spacecraft data indicates an average decrease of conductivity by a factor of two over the whole range of altitudes (Chassefière et al. 1995).

2.3.1 Tribo-Electric Charging Processes

The build-up of intense electric fields in the Martian atmosphere is expected to result from charge exchange between particles colliding in a turbulent environment (see Fig. 3).

Fig. 3

An artist’s impression of an electrified dust devil at Mars (from Farrell et al. 2004)

In order to understand the differences between Earth and Mars charging processes, the combined system must be considered, where the E-field is generated by the competing tribo-electric charging currents and atmospheric dissipation currents. This can be expressed as

$$ - \varepsilon_{0}\frac{dE}{dt} = - J_{\mathrm{tribo}} + J_{\mathrm{diss}} = - n_{\mathrm{dust}}q_{\mathrm{dust}}v_{\mathrm{dust}} + \bigl[ \sigma E + n_{0}\exp ( \alpha_{\mathrm{T}}d )e\mu_{e}E \bigr] $$

(6)

where $n_{0}$ is the nominal near-surface electron content, $\alpha_{\mathrm{T}}$ is Townsend’s first coefficient representing the number of electron impact ionizations per unit distance, $d$ is the extent of the driving E-field in the dust devil, and $\mu_{e}$ is the electron mobility. The last two terms in square brackets represent the atmospheric dissipation currents, the first of which is the nominal dissipation current and the second an enhanced current associated with the electron avalanche process for a gas under electrical stress. In the following subsections, these different terms are compared for both Earth and Mars.

2.3.2 Tribo-Electric Current Generation, $J_{\mathrm{tribo}}$

The mixing of dust grains creates electricity via tribo-electric processes with the grain polarity being a function of the particle mass and composition. Forward et al. (2009a, 2009b) found, for particles of identical composition, that smaller grains tend to charge negatively and larger grains tend to charge positively. As discussed more extensively in Sect. 3, they argued that the mass-size dependency involves the collisional transfer of electrons trapped in defect-created meta-states upon contact or rubbing, with the net exchange of electrons statistically favouring the smaller grains due to their increase likelihood of defect region ‘rubbing’ with larger grains (see Fig. 3 in Forward et al. 2009a, 2009b). In the centre of a convective feature, the grains become stratified in the upward flow of warm air. Small negative grains tend to lift upward and large positive grains remain lower in such features, giving rise to the large-scale dipole moment and E-field like that measured within terrestrial dust devils (Freier 1960; Crozier 1964; Farrell et al. 2004; Renno et al. 2004; Delory et al. 2006; Jackson and Farrell 2006).

The dust load for a nominal terrestrial dust devil has been estimated to be up to ${\sim}10^{- 3}~\mbox{kg}\,\mbox{m}^{- 3}$ (Metzger et al. 2011). Assuming a dust devil primarily contains particles of ${\sim} 5~\upmu \mbox{m}$ diameter carrying −5 fC per particle with an upward flux of ${\sim} 2\times 10^{9}~\mbox{m}^{2}\,\mbox{s}^{-1}$ (Farrell et al. 2004; 2006b), an estimate of the associated upward tribo-charging current source would be ${\sim} 10^{-5}~\mbox{A}\,\mbox{m}^{- 2}$. Similar mass-dependent tribo-charging and mass stratification process are anticipated for Mars. However, given that dust devils on Mars can be larger, larger tribo-charging current sources can be anticipated.

2.3.3 Atmospheric Dissipation Currents, $J_{\mathrm{diss}}$

The large contrast between terrestrial and Martian dust devil electrification lies in the nature of the response by the atmosphere. At Earth, for typical disturbed electric field values, the atmosphere does not initiate the electron avalanche process, and the dissipation currents are defined primarily by conduction (i.e. proportional to $\sigma E$). For the terrestrial atmosphere with conductivity ${\sim}50~\mbox{fS}\,\mbox{m}^{-1}$ only a modest removal of current will occur in a dust devil having $E \sim~100~\mbox{kV}\,\mbox{m}^{-1}$, with the competing dissipation current at $J_{\mathrm{diss}} \sim 10^{-8}~\mbox{A}\,\mbox{m}^{- 2}$. This current is far less than the driving tribo-electric current, and is not the process limiting the development of dust devil electric field. It is likely that it is the efficiency of the dust lifting process itself which limits the electric fields generated.

In contrast, in a 6 hPa CO₂ atmosphere like that at Mars, the nominal value of the atmospheric conductivity is predicted to be about ∼100 times greater than that at Earth (Farrell et al. 2015), with $\sigma \sim 10^{-12}~\mbox{S}\,\mbox{m}^{-1}$ (see Fig. 2). However, even at modest E-field values of 10 kV m⁻¹, electron avalanche processes will develop, with the exponential increase of electron currents directed along the driving E-field (Delory et al. 2006; Jackson et al. 2010). In the low-pressure Martian atmosphere, the mean free path for electrons under the driving E-field is larger, thereby creating more energetic electron-CO₂ impacts compared to the case of the denser Earth-like pressure. This greater number of electron impact ionizations will lead to the exponential increase in electron content.

In essence, the stress of even a modest E-field at Mars initiates the electron avalanche process, creating a substantial dissipation current that increases itself exponentially with increasing driving E-field. As found in recent laboratory work (Farrell et al. 2015; see Fig. 4), the dissipation current can become comparable to the driving $J_{\mathrm{tribo}}$, creating a situation where the E-field becomes limited by the atmospheric dissipation (i.e. $d E/dt \sim 0$ in Eq. (6)). These dissipation currents can take the form of the Townsend dark discharge or a glow or even a spark if breakdown is reached. This visual effect was reported by Eden and Vonnegut (1973), Mills (1977) and Krauss et al. (2003). The atmosphere at Mars therefore creates a substantial and significant competing dissipation current that act to deplete the development of large separated charge centres.

Fig. 4

Effective electron conductivity measured in a representative Martian environment, as a function of an electric field maintained between two plates with a varying separation (from left to right in the figure) of 60, 40, 20, and 8 mm. The different current regimes (nominal, Townsend, and spark) are delineated. (Reprinted from Farrell et al. 2015, with permission of Elsevier)

2.3.4 Lightning

Given the possibility of strong dissipation currents that limit the growth of storm charge centres, it seems that large impulsive ‘dissipation’ currents via lightning would be unlikely. However, Jackson et al. (2008) and Kok and Renno (2009) found that the same dust grains responsible for the charging current, $J_{\mathrm{tribo}}$, can also absorb electrons from the dissipation currents. This electron absorption would then reduce dissipation currents and thus could lead to anomalously large charge centres in the convective feature, thus requiring impulsive breakdown as a means to remediate excessive charge. Clearly, resolving which of these competing electrical processes dominates requires in situ measurements.

2.3.5 Implications for Dust and Climate

The existence of a planetary electric field with very intense local enhancements and possibly significant breakdown currents may have a significant influence on the physics and chemistry of the surface material. A detailed description of the expected impacts of electrification on processes relevant to the climate of Mars is presented in Kok and Renno (2008b).

Dust is the most important source of local heating in the Martian atmosphere and is known to control in large part the thermal structure of the troposphere. Many studies in the past have focused on identifying and further characterizing the processes at work in levitating dust from the surface of Mars. Well-established work (Bagnold 1962) indicated that direct wind lifting on Mars typically occurs at wind speeds exceeding 25 ms⁻¹ near the surface (Greeley et al. 1992), a condition that is difficult to reach, according to current general circulation models. Instead, several other mechanisms have been proposed and explored in laboratories that provide the necessary lifting strength without requiring winds as strong as the standard theory predicts. The proposed mechanisms comprise sand blasting process and levitation induced by electrostatic forces. Considering the potential electrical force exerted on micron size dust particles by electric fields predicted inside dust devils or dust storms, electrification may potentially contribute to the global transport of dust at a level comparable as the drag force due to the wind (Berthelier et al. 2000). Studies have explored the more specific impacts of electrification on the lifting processes of dust from the surface of Mars, unveiling the unexpected role of electrification in the trajectories of saltating particles, an effect first suggested by Schmidt et al. (1998) and Zheng et al. (2003). A major effect concerns the limitation imposed by electric forces on the height of the saltation layer. Contrary to the standard theory, the observed height does not increase with increasing wind speed, as it simultaneously leads to development of a downward-pointing electric force exerted over the saltating particles (Kok and Renno 2008a, 2008b). A related effect is the emergence of a positive lifting feedback loop as a charge gradient exists between the positively charged particles lying at the surface and the negatively charged saltating particles. This phenomenon leads to a significant reduction of the shear velocity and thus aids hydrodynamic forces in lifting particles from the surface (Kok and Renno 2008a, 2008b). Direct lifting by the electric force may also occur in parallel, and thus establishes a combination of effects that can contribute significantly to dust lifting and potentially ultimately atmospheric dust loading on Mars. This remains something which global modelling of the Martian atmosphere has yet to consider quantitatively.

3 Contact and Tribo-Electrification of Environmental Dust and Sand

The importance of particle–particle interactions in the electrification of dust clouds and structures such as dust devils highlights the understanding needed in contact and tribo-electrification. This section now reviews understanding of the physical process(es) of contact and tribo-electrification. The discussion is based principally on laboratory studies, but also presents contemporary models and theories considering mineral dust and sand, because of their relevance to dust devils.

3.1 Definitions, History and Background

It is worth discussing the terminology regarding particulate electrification, since even this can be a source of confusion. Contact electrification was originally used as a broad term for electrostatic charge transfer resulting from contact, including contact modes such as detachment, sliding, rolling, impact, etc. Tribo-electrification was later used to describe this phenomenon resulting from ‘rubbing’. Currently both contact- and tribo-electrification are widely and interchangeably used in the literature. Conventionally (though not formally) contact electrification has since become associated with ‘contact and macroscopic separation leading to charge transfer’ (e.g. McCarty and Whiteside 2008), whereas tribo-electrification is typically used where emphasis is placed upon (empirical) dependence on composition (i.e. the triboelectric series) and impact velocity, and it is also interchangeably used with ‘frictional electrification’.

Despite the importance of contact electrification and the amount of research in this field, there is little agreement upon the core mechanism of charge transfer. Generally it is now thought that there are several competing process occurring, rather than one single mechanism being responsible, and that this is dependent upon the nature of the interacting surfaces and especially the surface chemistry. On the most fundamental level one may consider contact electrification to occur via charge exchange with the transfer of electrons and/or ions. There are several models involving each of these processes which have been successfully applied in respective experimental cases. A complete picture for all materials in all cases still eludes researchers and has been a source of active debate for decades (McCarty and Whiteside 2008; Harper 1998; Lowell and Rose-Innes 1980).

3.2 Experimental Studies of the Phenomenon

Numerous contact or tribo-electrification studies have used macroscopic contacting surfaces, often involving an insulator and a metal electrode (McCarty and Whiteside 2008). Here, however, focus will be placed on granular materials (sand/dust). Typical methods for quantifying electrification of coarse granular material (sand) involve removal and direct measurement of the electric charge, often using a combination of a Faraday cup and electrometer. The specifics of transport and collection vary, including; cascades, fountains, fluidized beds, blow-away experiments, aerosolizers or single particle impact studies (Matsusaka et al. 2010; Sickafoose et al. 2001; Poppe et al. 2000; Kok and Lacks 2009; Merrison et al. 2012).

3.2.1 Surface Charge Density

Techniques involving direct electric charge extraction are ineffective when dealing with dust sized (micrometer) particulates since they are typically well suspended and difficult to extract (e.g. into a Faraday cup). Suspended particles may also only be slightly charged, and, in contact with a surface, they may not be electrically conductive enough to allow rapid charge extraction. For fine suspended dust other techniques have typically been used to quantify particulate electrification. They rely upon the application of an electric field and the drift of electrified dust grains. The field induced drift velocity can be determined using optical or laser systems to study particle trajectories (Kunkel 1950; Merrison et al. 2012; Mazumder et al. 1991) or by extracting dust onto a surface (Merrison et al. 2012). The field-induced drift velocity will be proportional to the electrical force and therefore the electric charge and polarity of the dust grains.

In determining order of magnitude limits for expected values of contact electrification there has been considerable success using the ratio of charge to surface area. In a variety of experimental techniques and over a broad range of grain sizes (μm–mm) the electrification has been seen to be of order 0.1 mC m⁻² (Poppe et al. 2000; Lowell 1986; Merrison et al. 2004; Nieh and Nguyen 1988). In many granular electrification studies the electrified surface area is taken as the (total) surface area of the grain; since the contact area is not known, this possibly explains the lower level of electrification seen in such cases e.g. ${\sim}10^{-3}~\mbox{mC}\,\mbox{m}^{-2}$ (Sickafoose et al. 2001; Gross et al. 2001).

3.2.2 Specific Charge

Many workers, however, still express electrification in terms of the specific charge (i.e. the charge per unit mass, $Q/m$), due often to experimental convenience. There is less success in establishing expected/limiting values. In aeolian sand transport studies values have been quoted of order 60 μC kg⁻¹, (Schmidt et al. 1998; Zheng et al. 2003, 2004; Qu et al. 2004; Bo et al. 2014). In gas-solid pipe flows continuous sand transport is performed while measuring the current to metal pipe, here values of order 3 mC kg⁻¹ have been measured (Matsusaka et al. 2010). In metal oxides charges after blow-off exceeding ${\pm}200~\mbox{mC}\,\mbox{kg}^{-1}$ have been seen (Oguchi and Tamatani 1993) (see the section on wind tunnel experiments).

3.2.3 Practical Experimental Limitations

Another common cause for observing reduced electrification in charge collection systems is charge leakage via surface water, which is related to ambient humidity (Nieh and Nguyen 1988). In dust collection experiments electrostatic aggregation can also de-electrify suspended dust, especially when in high concentrations and after long suspension times (Merrison et al. 2012). In relatively recent studies using Atomic Force Microscopy (AFM) techniques and well prepared surfaces, significantly higher values were reported, although in these no account was made for lateral spreading of charge (Horn et al. 1993).

In many cases electrical breakdown can limit the charge on grains during separation, e.g. dielectric breakdown in terrestrial surface air is at an electric field of around $3\times 10^{5}~\mbox{V}\,\mbox{m}^{-1}$. (The lower surface pressure on Mars yields a smaller breakdown voltage there (Laughton and Warne 2004)). This could provide a quantitative explanation for the experimentally observed upper surface charge concentration $Q$ and has been supported experimentally in detailed investigation using polymer micro-spheres (50–500 μm radius $r$) where $Q/r^{2}$ is seen to be constant, of order 0.1 mC m⁻². Electrical breakdown has also been directly observed in some experiments (McCarty et al. 2007; Harper 1998; Matsuyama and Yamamoto 1997; Horn et al. 1993; Matsusaka et al. 2010). The observed charging will therefore in many cases be limited (by dielectric breakdown) to values less than 0.1 mC m⁻².

Even lacking a detailed physical understanding of the electrification process, there is therefore general agreement on the order of magnitude of the electrification and this is sufficient in most cases to quantify the effect of electrification on, for example, entrainment and transport of sand and dust.

3.3 Particulate Size Dependence

It is widely accepted that particulates of the same composition and of differing size will show a tendency for larger particulates to electrify positively and smaller ones to electrify negatively, upon contact and separation. In experimental studies the electric fields generated by terrestrial dust devils support the idea that suspended dust becomes electrified negatively with respect to the sand/sand-bed (Schmidt et al. 1998; Zheng et al. 2003; Qu et al. 2004). This size dependence has been best demonstrated in laboratory experiments involving sand cascading (Lacks et al. 2008; Kok and Lacks 2009; Lacks and Levandovsky 2007, Forward et al. 2009a, 2009b; Bilici et al. 2014). However, not all experimental studies reproduce this behaviour (Trigwell et al. 2003; Sowinski et al. 2010; Kunkel 1950). It should also be noted that in many of these electrification studies multiple particle interactions are involved, including particle-wall interactions (Aplin et al. 2012), and material purity (surface composition) is not well controlled. A more complex charge exchange behaviour can therefore often not be ruled out.

In laboratory experiments of sand transport in the absence of dust, it has been seen that sand may electrify either positively or negatively depending on the size distribution within the sand bed (Bo et al. 2014; Zheng et al. 2003, Kok and Renno 2008a, 2008b). Laboratory experiments have also shown that dust re-suspension in the absence of sand shows little net (size dependent) dust electrification (Merrison et al. 2012), however the role of dust aggregates (acting like large sand-sized particles) could possibly complicate this behaviour. This complexity makes describing/predicting contact electrification for example within a Martian dust devil problematic. Modelling has been unsuccessful in satisfactorily explaining this size dependence in contact electrification, although several promising models are being pursued. For example, one model is based upon electron transfer through so-called high energy electron surface states (Lacks and Sankaran 2011; Apodaca et al. 2010; Bo et al. 2014). It would be extremely useful here to experimentally identify the precise charge/polarity dependence of contact electrification with grain size: this has yet to be done.

3.4 Material and Humidity Dependence

Attempts to apply a single model (i.e. involving either electron or ion transfer) for all cases of contact electrification have failed. Although the use of various so called tribo-electric series have been empirically useful (and widely published) there are many cases where electrification does not follow such tribo-series, and examples exist of circular tribo-series (Harper 1998) wherein a repeating sequence of materials paradoxically generates increasing values on the tribo-series. Also the tribo-series cannot explain electrification of like materials with different sized particles (Lacks and Sankaran 2011). This suggests that there is not one single electrification process occurring (McCarty and Whiteside 2008).

It is however apparent that material properties are crucial in applying models of contact electrification. For contacting metals, electron transfer models have been extremely successful in reproducing observed electrification based upon differences in electron work function (e.g. Matsusaka et al. 2010). Similarly for insulators containing mobile ions, modelling involving ion exchange has provided a consistent picture and even allowed control in contact electrification (Diaz and Felix-Navarro 2004; Law et al. 1995; Mizes et al. 1990). Contact electrification in (non-ionic) insulating materials though, remains problematic. Currently most researchers assume that contacting (non-ionic) insulators involve electron transfer (Lowell and Rose-Innes 1980; Grzybowski et al. 2005).

Experimentally, a typical problem is purity, especially the presence of surface contamination. Since the number concentration of charges at the surface involved in electrification is low compared to the concentration of molecules/atoms, even low concentrations of impurities (of order ppm) can in principle dominate the electrification process. This makes studies of contact electrification technically challenging.

Under ambient terrestrial conditions layers of water molecules are invariably present at surfaces and can play role in electrification by enabling ion or electron transport. Since humidity and surface ions such as $\mathrm{H}^{+}$ and $\mathrm{OH}^{-}$, are ubiquitous, models have been proposed to describe electrification of insulating materials (not containing ions) in which for example $\mathrm{OH}^{-}$ accumulate on surfaces with water layers. In experiments using polymers and bound/unbound ions (Diaz and Felix-Navarro 2004) contact electrification was seen to be eliminated at 0 % RH (relative humidity) and rise to a maximum at 30–40 % RH, supporting this ion exchange model. Again, however, there are experimental cases in which contact electrification has been observed despite the absence of surface water (low humidity/vacuum) (Harper 1998; Lowell and Rose-Innes 1980) and also with well-prepared dry surfaces (e.g. Horn et al. 1993; Gady et al. 1998). Hence, despite advances made (Diaz and Felix-Navarro 2004; Law et al. 1995; Mizes et al. 1990) involving ion transfer (and the use of charge control agents), this model still cannot be applied in all cases of contact electrification.

In the case of real planetary silicate minerals, ions will likely be present at the surfaces (e.g. OH⁻, alkali metals, halide ions, etc.), and, terrestrially, water vapour (and therefore H⁺, OH⁻) will also be present and allow ion-transfer models to be applied. Generally, however, most current modelling of aeolian (contact/tribo-) electrification involves electron transfer (only) (Lacks and Sankaran 2011).

3.5 Models and Theories for Dust and Sand Electrification

For mineral dust and sand it is likely that both electron and/or ion transfer mechanisms may be relevant. Here material transfer is considered to be a form of ion transfer (Tanoue et al. 1999). For non-ionic insulators (e.g. polymers and possibly including mineral sand or dust) most researchers attempt to employ electron exchange models (Lowell and Rose-Innes 1980). However contact electrification does not correlate with surface or bulk electron properties such as dielectric constant, atomic properties, ionization energy, electron affinity or electro-negativity (Wiles et al. 2003). Despite this, some success has been achieved with electron transfer models involving electron donor/acceptors or so called high energy electron states in insulator-insulator contact, (also known as a molecular ion state model) (Lowell and Rose-Innes 1980; Bailey 2001; Duke and Fabish 1978). Similar electron transfer models involving so-called high energy surface electron states (likely due to impurities/contamination) are used in describing size dependent electrification (Lacks and Sankaran 2011; Bo et al. 2014).

Specific electron transfer models have been developed for electrification in metal-insulator contact, for example; involving an effective potential difference (Davies 1969) or performing quantum chemical (electron state) calculations (Shirakawa et al. 2008). Other models have also studied multiple surface impacts; one involved a capacitance charging model including charge relaxation (electrical discharge) (Matsusyama and Yamamoto 2006).

Despite these advances in electron transfer models, similar success and progress has also been achieved using ion exchange models specifically involving (proton exchange) which not only works well for ionic or ion doped materials, but also where water layers may be involved relating to chemical properties such as pH and/or zeta potential (Diaz and Felix-Navarro 2004; Law et al. 1995; Mizes et al. 1990). It has even been argued that there is ‘never electron transfer with insulators’ (Harper 1998), however this has not been demonstrated experimentally and is not widely accepted.

Based on an ion transfer (entropy driven) model, an order of magnitude calculation can be performed assuming a concentration of mobile ion groups (e.g. H⁺, OH⁻, metal ions, halide ions, etc.) of, for example, around 0.1 nm² generating around 3000 e μm⁻², this is in reasonable agreement with the expected upper limit (Diaz and Felix-Navarro 2004). This still corresponds to a surface concentration of <1 %. Experimental tests have yet to be performed of the temperature dependence in electrification which could verify the entropy driven model.

3.6 Wind Tunnel Experiments

On the scale of laboratory wind tunnels it has proved difficult to generate and therefore measure electric fields produced by sand/dust transport. It has been more practical to measure and determine the electrification of single grains (and distributions) and then apply modelling to predict electric field generation.

The electrification of saltating sand grains has been studied using wind tunnels in an extensive series of experiments, which also combined modelling with theory, involving determining the effects on grain trajectories of applied electric fields. In these experiments sand grain electrification was measured in a conventional manner using an Faraday cup type electrode to collect the charge of impacting grains and an electrometer to quantify the discharging current (Bo et al. 2014).

Grain electrification distribution was typically seen to be bipolar and broadly in the range from −300 to $+600~\upmu \mbox{C}\,\mbox{kg}^{-1}$. In the earliest wind tunnel studies the average electrification was seen to be negative (Zheng et al. 2003; Qu et al. 2004; Zhang et al. 2004), however in a more recent study the net charge is seen to be positive and also a higher degree of electrification (agreeing with field experiments of Schmidt et al. 1998), Bo et al. (2014). This discrepancy was interpreted as due to interaction (charge exchange) with finer grains (non-saltating) within the wind tunnel sand bed. Notably a (broad) grain size distribution was used, which was not representative of those seen in the field. From this work it seems that there is a dependence of the measured electrification on the grain size of both the saltating and non-saltating grains, as well as on wind speed and height (increasing strongly with height).

Based on this sand electrification work electric fields have been predicted to be generally less than 50 kV m⁻¹ and typically a few kV m⁻¹ (Bo et al. 2013a, 2013b), this is below values at which significant effects would be expected on saltation and below (upper limit for) value measured in the field (Farrell et al. 2004; Schmidt et al. 1998; Renno et al. 2004). It should be noted however, that the models applied did not include dust entrainment, i.e. fine, suspended fraction which may have enhanced the electric field.

For fine (suspended) dust grains the techniques based on measuring their electrical discharge current to an electrode is difficult and ineffective due to: the small charge degree, the particles not being ballistic (having low impact velocity) and not liberating electrical charge rapidly. An alternative technique has been applied in a series of wind tunnel studies of dust electrification. Here an electric field is applied in order to drift dust grains out of suspension and collect them on electrodes. The quantity of dust collected can then be quantified either optically or by mass. By determining the amount of collected dust as a function of applied electric field, the average electrification per grain can be established (Merrison et al. 2012; Merrison et al. 2004).

It was found that the degree of electrification of re-suspended dust is typically of the order of $10^{3}$ to $10^{4}~\mbox{e}/\mbox{grain}$ for μm scale particles (or around 0.1 mC m⁻²). In the absence of sand the net electrification of the dust was seen to be close to zero (therefore not expected to generate an electric field). However, dust aggregates (agglomerates) are also seen to become electrified and may show the electrostatic behaviour of real dust clouds, even in the absence of larger sand particles. Specifically in wind tunnel studies, it was found that electrification is affected by competing processes of aggregation (electrostatic self-assembly), causing reduced charge and aggregate dispersion causing electrification.

Xie and Han (2012) performed experiments in a wind tunnel to investigate the effect of relative humidity on aeolian E-field. The working section of the chamber was $20~\mbox{m} \times 1.3~\mbox{m} \times 1.3~\mbox{m}$. A sand bed of $8~\mbox{m} \times 12~\mbox{cm}$ was deposited in the chamber. Sand particles were collected in the Badain Jaran desert in China. The electric field was measured with a KDY-IV field mill. At a given wind speed, they measured the aeolian electric fields at different air relative humidity (RH) and sand relative moisture conditions. They observed the electric field linearly increased with increasing relative humidity up to a critical value and then exponentially decrease. This critical RH value was observed to increase with the wind speed. For a wind speed of 14 m s⁻¹ the critical RH was 32.7 %.

Wind tunnels have been more extensively used to investigate the influence of applied electric fields upon sand transport (saltation). Several groups have reported reduction in the threshold for saltation and enhanced transport rates of sand due to applied electric fields (Kok and Renno 2006, Rasmussen et al. 2009), typically at electric fields above around 100 kV m⁻¹. This work has mainly been based upon the assumption of a conductive sand bed (surface). However, recently it has been experimentally demonstrated that, for the case in which the sand bed is insulating, the application of an electric field in fact significantly increases the threshold shear stress for saltation (Holstein-Rathlou 2012). This is due to dielectric attraction, entirely analogous in its operation to diamagnetic chain formation in the presence of an applied magnetic field.

3.7 Charging and Radioactivity in Volcanic Plumes

Theoretical studies of triboelectric charging of single particle systems demonstrate that the particle size distribution determines the magnitude and size of charging (Lacks and Levandovsky 2007). Laboratory studies of electrical charging of volcanic ash systems confirm that the particle size distribution plays an important role in the electrical charging of terrestrial volcanic plumes (Houghton et al. 2013; Cimarelli et al. 2014) and indicate that the composition of the particulate matter making up the plume also affects electrical charging. The factors that affect triboelectric charging in terrestrial volcanic plumes, namely the particle size distribution, particle composition and relative humidity, are expected to have similar effects in the aeolian Martian environment. While recent work has contributed significantly to the understanding of triboelectric charging in terrestrial volcanic plumes, further investigation is required to fully understand this process and the effects of the particle size distribution, material composition and ambient conditions on charging.

Alpha and beta particles are emitted following the radioactive decay of the uranium, thorium and potassium radioisotopes, leaving a residual charge on the particle from which they have been emitted (Clement and Harrison 1992). Studies of ash collected from the 2010 Eyjafjallajökull and 2011 Grimsvötn eruptions demonstrate that radioactive decay is only seen in larger particles (Aplin et al. 2014). This size dependence means that for terrestrial volcanic plumes, charging associated with radioactive decay is only likely to occur near the vent itself, as the larger particles containing radioisotopes are rapidly removed by gravitational settling. The composition and size of particles in Martian dust storms are expected to determine whether or not radioactive decay contributes to charging in Martian dust storms; larger particles are expected to be lost first from the dust cloud.

During volcanic eruptions, magma fragmentation can contribute to plume charging near the vent (Gilbert et al. 1991; James et al. 2008). Charged species are ejected from cracked surfaces following material fracture, and the loss of these charged species results in the formation of charged fragments. However, particle fragmentation is not expected to occur in Martian dust storms.

Clearly there is much more research needed in this area before we reach an understanding of these disparate electrification processes. For wind tunnel investigations it would be informative to perform electrification studies which involve both sand and dust grains (i.e. using an extremely broad size distribution from 1 μm–1 mm) in order to gain an understanding of the interplay of electrification and field generation processes.

4 Atmospheric Observations of Dust Electrification

Atmospheric electrical parameters can be sensed in a variety of ways. The most commonly measured quantity is the vertical electric field,¹ but the air conductivity, charge density and vertical conduction current have also been routinely observed at some measurement sites. Many of these techniques have developed rapidly as electronic systems have improved, as exceptionally good performance—very often ultra-low leakage current—is required from the signal processing electronics across a wide range of conditions. A widely used fast-response instrument for electric field measurement is the field mill, which operates by the alternate exposure and screening of a sensing electrode using a rotating shutter followed by phase-sensitive detection. A field mill can be orientated with its sensing surface upwards or downwards for the vertical component of the field, although spherical geometries have also been used in dust devil studies, to obtain the horizontal field component (Ravichandran and Kamra 1999). Vertical electric fields can also be measured using passive (long horizontal wire) antennas or other electrodes which come into electrical equilibrium with the potential of the surrounding air. These can have a slow response because of the low conductivity of atmospheric air: a radioactive coating can increase the air conductivity and the associated time response. The position of a sensing instrument mounted above the surface acts to distort the local electric field, and calibration to the electric field over a flat undisturbed surface is needed. The negligible distortion of a long wire antenna provides one possible reference technique to calibrate atmospheric electric field measurements, which has been used for over a century (Harrison 1997, 2013; Bennett and Harrison 2006).

Another approach used in high field conditions is to measure the so-called point discharge current, which is the current flowing into a vertically facing sharpened vertical point under the influence of the atmospheric electric field (Marlton et al. 2013). Techniques for measurement of air conductivity and conduction current density are not discussed further here, but summaries of the associated methods required are given in Harrison (2004), Aplin and Harrison (2001) and Bennett and Harrison (2008).

4.1 Surface Measurements

As introduced in Sect. 1, Freier (1960) was one of the first researchers to measure electric fields in dust devils. It was found that the electric field was upward pointing in dust devils. Freier’s findings were later confirmed by Crozier (1964, 1970). These pioneering measurements of dust devil electric fields are consistent with results of more recent measurements also indicating upward pointing electric fields in dust devils (e.g., Farrell et al. 2004; Renno et al. 2004).

In dust storms the near surface electric field is stronger and in the opposite direction to the downward pointing fair weather electric field (e.g., Latham 1964). This suggests that dust particles become negatively charged after colliding with the larger sand particles and the surface (e.g., Schonland 1953; Latham 1964; Kok and Renno 2008a, 2008b; Renno et al. 2003). Schmidt et al. (1998) reported that the electric field is also upward pointing in saltation alone (that is, without dust lifting). Indeed, Schmidt et al. (1998) reported upward pointing electric fields of 160 kV m⁻¹ at a few cm above the surface during saltation in sand dunes. Electric fields of this magnitude could have significant effects on saltation and therefore dust lifting.

4.1.1 Recent Measurements of Electric Fields in Dust-Devils

Except for the measurements of Schmidt et al. (1998), all previous measurements summarized above were made using grounded instruments. Since grounded instruments typically measure the difference in potential between the ground and their sensing elements, rather than the electric field at the sensor height, measurements with these grounded instruments must be interpreted carefully. The presence of grounded instruments distorts the electric fields being measured and the instrument configuration must be calibrated on site (e.g. Sullivan 2013). In addition, the impact of charged dust or sand particles introduces noise on grounded instruments by the effect of electric currents between the instruments and the ground (Sullivan 2013).

Schmidt et al. (1998) used a cylindrical field mill isolated from the ground to measure the electric fields in the saltation layer directly (Johnston et al. 1986). Since charge transfer by the collision of charged particles with isolated field mills vanishes as soon as the field mills reach the same potential as the charged particles, the errors produced by these collisions also vanish. Renno et al. (2008) developed an isolated cylindrical field mill for making measurements of the electric fields in saltation, dust storms and dust devils. This new instrument is capable of measuring the electric fields accurately even when the instrument is subject to the impact of charged particles (Renno and Rogacki 2013).

Here we report results of measurements with this instrument in the Aerosols-Climate Interaction (ACI) project site at the Owens Lake salty playa, in California (Halleaux and Renno 2014). Figure 5 shows four electric field sensors installed at the ACI project site at the Owens Lake playa. Figure 6 indicates that, in mid-March, a saltation event triggered an order-of-magnitude increase in PM2.5 aerosol concentration. The hourly mean value of the electric field exceeded 10 kV m⁻¹ during this event. This value is two orders of magnitude larger than the fair weather electric field.

Fig. 5

ACI Project site at the Owens Lake playa with electric field sensors mounted at 0.5, 1.5, 2, and 3 m above the surface. The results reported here are from measurements of the electric field at 3 m above the ground. The PM2.5 aerosol concentration is measured at approximately 3.5 m above the ground, and saltation is measured at 7 cm above the ground

Fig. 6

PM2.5 aerosol concentration (upper panel), near surface electric field strength (middle panel), as well as electric field direction and indication of saltation events in blue (lower panel) at ACI project site in the Owens Lake in 2014. The measurements of the electric field strength and direction presented in Fig. 6 were made at 10 Hz. (Upward and downward pointing electric fields are defined as electric fields within approximately 30^∘ of the vertical. Saltation is measured with a Sensit sensor placed at about 7 cm above the surface e.g. Halleaux and Renno (2014). Saltation events are defined as those time periods in when the impact rate at the sensor is greater than 10⁻⁴ particles/second. Saltation intensity refers to the normalized number of impacts on the Sensit sensor per unit time.)

Figure 6(c) indicates that, in general, the electric field is downward pointing, but that when saltation and therefore dust lifting occurs the electric field points upward. The few exceptions occur when saltation is weak and during stormy weather when charged clouds are also present.

Figure 7 shows the results of measurements of PM2.5 aerosol concentration, electric field and saltation during a day of intense saltation and dust lifting. The measurements indicate that, in general, the electric field changes its polarity to upwards when saltation occurs. The exceptions to this occurred during periods when saltation was weak or when charged clouds were also present above the site.

Fig. 7

PM2.5 aerosol concentration (upper panel), near surface electric field strength (middle panel), as well as electric field direction and saltation events (lower panel) at the ACI project site in the Owens Lake on a day of active saltation and dust lifting events (May 10, 2014)

4.1.2 Measurements of Electric Fields in Dust Storms

Measurements of electric fields during dust storms are sparse in the literature but show both upward (Rudge 1913; Harris 1967; Stow 1969; Zhang et al. 2004) and downward (Demon et al. 1953) electric field directions.

Kamra (1972) performed measurements of the potential gradient between the surface and at 1 m above, in several US locations using a 500 μCi Polonium probe as a potential sensing probe. (The use of radioactivity enhances the time response of the sensor, without adding the mechanical complexity of a field mill.) The potential of the radioactive probe was measured by a Keithley model 600B electrometer, a laboratory grade device. During dust storms, this instrument recorded both upward and downward E-fields depending on the nature of soil in the measurement site. In particular, Kamra observed that dust storms dominated by clay minerals produced only negative potential gradients, while, when silica dominated in the dust storm, both polarities of potential gradients were produced.

During measurements in the Sahel with a Mission Instruments field mill, Williams et al. (2009) observed E-fields directed both downward and upward. Very recently, Esposito et al. (2016) carried out several measurements in the West Sahara (Merzouga region, Morocco) during the dust storm season in 2013 and 2014. They performed simultaneous measurements of atmospheric electric field, using a Campbell CS110 field mill, mounted at 2 m and directed toward the surface, atmospheric dust abundance and size distribution (in the range 0.265–34 μm), sand saltation rate (with the Sensit sensors), wind speed and direction at six different heights, air and soil temperature, pressure, relative humidity, soil moisture content and solar irradiance. They observed predominantly negative electric fields, i.e. with the same sign of fair weather E-field, with some sporadic and short inversions in polarity (Fig. 8). This was observed both during dust storms and dust devils (Fig. 9).

Fig. 8

Typical dust storm measured in the Sahara desert in July 2013 (Esposito et al. 2016)

Fig. 9

Properties of a dust devil observed in the Sahara desert in July 2014. Upper panel: rate of impact of particles. Second panel: dust particle concentration. Third panel: wind direction. Fourth panel: wind speed. Fifth panel: electric field. Bottom panel: atmospheric pressure

The relation between humidity and particle charging mentioned in Sect. 3.4 was observed by Esposito et al. (2016) during dust storms monitored in the Sahara desert. By a statistical analysis of the data, they found a linear relationship between the concentration of dust entered in suspension and atmospheric electric field. The slope of this linear trend was observed to increase when relative humidity reached a critical value. This value seemed to depend also on the content of soil moisture and was around 20 % in the 2013 campaign and 30 % in 2014 where the soil was drier (Fig. 10).

Fig. 10

Relationship between atmospheric electric field and concentration of dust emitted during several dust storms observed in the West Sahara in 2013 (upper) and 2014 (lower) field campaigns by Esposito et al. (2016). The slope of the linear trend increases when relative humidity exceeds a critical value. This value depends also on the moisture content of the soil emitting dust grains

The increase in the slope indicates that, for each value of dust concentration a lower E-field is observed for relative humidity larger than the critical value. Taken together, all these observations suggest there are complex mechanisms underlying natural dust electrification, and that different effects should be expected in different regions on Earth and Mars.

4.2 Measurements of Particle Charging Aloft

Although measurements of dust electrification in different circumstances have been made at and near Earth’s surface, measurements made aloft are rare in comparison, due to the difficulties associated with measurement platforms and lack of suitable instrumentation. Of the handful of airborne studies which do exist, all have focused on passive dust layers, which are typically isolated from the surface, travelling many hundreds of km from their source regions. As yet, no attempt has been made to measure electrification in dust storms or dust devils above the surface, which is certainly something that should be attempted in future to establish the in situ charge structure. Of the measurements that do exist, Gringel and Mühleisen (1978) were amongst the first to publish measurements of electrical conductivity, $\sigma$, measured by a Gerdien condenser, made from a free balloon platform through a 2 km thick layer of Saharan dust off the west coast of Africa. Their data show a clear decrease in the conductivity (caused by the attachment of ions to the dust particles) within the layer, dropping by a factor of two compared to its clean air value at the same altitude. These findings are to be expected from a passive dust layer where no active charge generation or charge separation occurs. This is in accordance with Ohm’s law, which governs charge conservation in the fair weather atmosphere, and states that the vertical conduction current, $J_{c}$, is equal to the product of the electrical conductivity and the local atmospheric electric field $E_{z}$, ($J_{c} = \sigma E_{z}$). In the case of no active charge generation, $J_{c}$ through the dust layer should be continuous, therefore any decrease in conductivity (caused by ion-aerosol attachment) will lead to an increase in the local electric field within the dust layer. This hypothesis is supported by measurements through aerosol layers (e.g. Markson 2007), which are similar to dust layers in terms of the presence of large particles, and show clear increases in $E_{z}$ inside the layer, as a result of the conductivity decrease.

Following on from the work of Gringel and Mühleisen (1978), Nicoll et al. (2011) made a series of instrumented balloon flights from the Cape Verde Islands, near the west coast of Africa, which frequently experiences elevated layers of dust transported from the Sahara in the so-called “Saharan Air Layer”, which can reach altitudes of 5–7 km. Simultaneous measurements of dust particle concentration and space charge, $\rho$, were obtained by two small sensors attached to standard balloon-carried meteorological radiosondes. The space charge sensor measures the net charge (i.e. the difference between positive and negative charge) carried by the dust particles and comprises a small spherical electrode connected to a sensitive electrometer circuit, measuring the voltage on the electrode.

Figure 11 shows measurements from one of the instrumented balloon flights from Sal, Cape Verde, which shows two distinct layers of dust particles at 2 km and 4 km (with particle diameters up to 2.6 μm). Measurements from the charge sensor show weak charge on the dust particles in both layers (up to 10 pC m⁻³). Particle–particle charging (i.e. triboelectric charging) of dust grains is likely to have originated near the surface during the initial lofting of the dust, but this charge will decay quickly (within several minutes) due to recombination with ions. This therefore suggests the presence of a continual charging (albeit weak) mechanism which is active in elevated dust layers, likely to be related to tribo-electrification of the dust particles (Houghton et al. 2013). Such an effect has also been observed in elevated layers of volcanic ash from the eruption of Eyjafjallajökull in Iceland in 2010 (Harrison et al. 2010). The effect of such charge on long range transport of dust and ash is as yet unknown, but may have implications for modification of deposition speed as well as particle–particle agglomeration rates and particle wet removal by droplets.

Fig. 11

Vertical profile of total aerosol particle concentration (grey) and magnitude of space charge density (black) measured on a specially instrumented radiosonde flight through Saharan dust layers from Sal, Cape Verde. Adapted from Nicoll et al. (2011) “© IOP Publishing Ltd. CC BY-NC-SA”

4.3 Particle Electrification Observed in Volcanic Plumes

A special case of particle electrification aloft is that associated with charge separation in volcanic plumes. Observations have shown that charging of terrestrial volcanic plumes can occur up to hundreds of kilometres from the eruption site (Harrison et al. 2010; Hatakeyama 1949). The presence of charge in the Earth’s electrically conductive atmosphere indicates that self-charging occurs in the plume and is attributed to triboelectric charging. Observations of volcanic lightning during the Eyjafjallajökull eruption in 2010 demonstrate that ambient atmospheric conditions also contribute to electrical charging of terrestrial volcanic plumes (Bennett et al. 2010), known as the ash-rich ice electrification system (ARIES) mechanism (Aplin et al. 2016). Convective processes, as in the ARIES mechanism, are expected to contribute to charging of dust storms on Mars, but without the enhancement associated with the presence of ice.

5 Models of charge exchange between particles

Simulations of the particle charging mechanism derive from laboratory measurements and have been developed in order to understand a number of different phenomena. The basic studies are described below and applications to dust devils follow.

Melnik and Parrot (1998) were interested in the conditions required for electric discharge in dust disturbances on Mars. Their charging mechanism assumed that the average charge on a particle was proportional to the particle size. They adopted the relation that each collision resulted in charge exchange between particles of $\Delta q = 1~\mbox{fC}/\upmu \mbox{m}$, with the larger particle losing electrons to the smaller particle.

Desch and Cuzzi (2000) proposed an alternate mechanism of charging where both particle size and composition influenced the amount of charge exchange between the colliding particles. While their simulations were conducted in order to understand the mechanisms for lightning generation in the solar nebula, the concepts are transferrable to particle collisions within dust storms or dust devils. The important parameter in their study is the contact potential difference between the two colliding particles. The contact potential of a material is the energy needed to remove an electron from that material. When two particles of differing material collide, the electrons will migrate to the material with the higher contact potential. For metals, this quantity is directly related to the work function. For insulators, the contact potential energy is more difficult to determine from intrinsic properties of the material, but potential differences between two materials can be found from the triboelectric series (Faraday 1855). A formula was derived to calculate the charge exchange, which is a function of potential difference and the mutual capacitance of the two materials. See Sect. 3.2 of Desch and Cuzzi (2000) for the full derivation, resulting in

$$ \Delta q = f_{1} \Delta \varPhi - (1-f_{2})q_{\mathrm{tot}} $$

(7)

where $f_{1} = (c_{12}c_{21} -c_{11}c_{22})/(c_{11} + c_{12} + c_{21} + c_{22})$ and $f_{2} = (c_{11} + c_{12})/(c_{11} + c_{12} + c_{21} + c_{22})$ are functions of the mutual capacitances, $c_{ij}$. ($\varPhi$ is the potential.) When mixing large insulator particles with small metallic particles, $f_{2}$ approaches unity and the charge exchange can be rewritten as a function of potential difference and particle size as

$$ \Delta q \sim 2668 (\Delta \varPhi/ 2~\mbox{V}) (r_{f} /0.5~\mbox{ }\upmu \mbox{m})e, $$

(8)

where $r_{f} = (r_{\mathrm{L}}^{-1} + r_{\mathrm{S}}^{-1})^{-1} \sim r_{\mathrm{S}}$ is the reduced radius, and $e$ is the elementary charge. (The approximate potential difference between a metal and an insulator is 2 V.)

Kok and Renno (2008a, 2008b) modelled charge exchange between sand particles and the Earth’s surface employing the Desch and Cuzzi charging mechanism, with an additional term for collisions between particle pairs of similar composition,

$$ \Delta \varPhi_{\mathrm{eff}} = (r_{\mathrm{L}} - r_{\mathrm{S}})/(r_{\mathrm{L}} + r_{\mathrm{S}}), $$

(9)

where $S$ is a scaling factor determined by calibrating the model with field measurements ($S = 6 \pm 4~\mbox{V}$). Their study was applied to reconcile discrepancies between classical saltation theory and terrestrial observations of the phenomenon. By including the electric force in the equation of motion for particles in saltation, they found that the wind stress needed to lift particles is reduced and the particle trajectories remain closer to the surface with a reduced horizontal speed.

Kok and Renno (2009) applied their terrestrial saltation model to explore saltation with charged particles on Mars. They concluded that the breakdown E-field in the Martian saltation layer is ${\sim}43~\mbox{kV}\,\mbox{m}^{-1}$, but their modelling could only achieve fields of ${\sim}15\mbox{--}20~\mbox{kV}\,\mbox{m}^{-1}$. Therefore, electric discharges in the saltation layer seem unlikely, but this does not prohibit discharges from occurring in larger scale phenomena such as dust storms and dust devils.

5.1 Applications of the Charge Exchange Mechanism to Dust Devils

The Melnik-Parrot and Desch-Cuzzi grain charging processes described above were applied to a comparative analytical study of dust devils on Earth and Mars in the work of Farrell et al. (2003). They created an electrodynamic model of a dust devil by applying the methodology used for modelling terrestrial thunderstorms, e.g. see Mathpal et al. (1980) to the induction electrification process between graupel and water/ice in terrestrial thunderstorms. The time derivative of the electric field, $E$, is related to rate of charging on the larger grains, $Q'_{\mathrm{L}}$, by

$$ E'' + \sigma E'/\varepsilon_{0} = -n_{\mathrm{L}} \Delta v Q_{\mathrm{L}}'/\varepsilon_{0} $$

(10)

where $\sigma$ is the local atmospheric conductivity, $n_{\mathrm{L}}$ is the particle number density, $\Delta v$ is the relative velocity between the large/small grains ($\Delta v = v_{\mathrm{L}} - v_{\mathrm{S}} < 0$), and $\varepsilon_{0}$ is the permittivity of free space. Here $Q'_{\mathrm{L}}$ is based on triboelectric processes (for dust devils) rather than induction processes (for thunderstorms) and is proportional to the charge exchange per collision, $\Delta q$, as $Q_{\mathrm{L}}' = v \Delta q$, where $v$ is the grain collision frequency. The model is applied to both Earth and Mars by varying the atmospheric conductivity appropriately. Results from their simulations are shown in Fig. 12.

Fig. 12

Comparison of the size-only grain charging mechanism from (a) Melnik and Parrot with the (b) Desch and Cuzzi grain charging mechanism which also includes the effects of grain composition (from Figs. 2 and 3 in Farrell et al. 2003)

A number of aspects become evident from Fig. 12. First, exponentially growing E-fields develop in both the terrestrial and Martian dust devils due to the tribocharging and subsequent mass (and charge) separation within the convective cloud. The electric fields in the Martian case are always lower than in the terrestrial case due to greater dissipation leakage current which removes charge from the stratified grains. Additionally, the Desch and Cuzzi charging results in electric fields consistently lower than those produced using Melnik and Parrot. The two cases are approximately equal for the Desch and Cuzzi $\Delta \varPhi = 2~\mbox{V}$ which represents the compositional difference of a metal and an insulator (i.e., simulating the collision between a metallic grain and a basaltic grain).

A follow-up study by Farrell et al. (2006a) added the acceleration term to Eq. (10), such that the right hand size becomes: $-n_{\mathrm{L}}( Q_{\mathrm{L}}'\Delta v + Q_{\mathrm{L}} \Delta v')/\varepsilon_{0}$. The $Q_{\mathrm{L}}'\Delta v$ acceleration term depends on the lifting process associated with the fluid, and the addition of this term links the electrostatic effects to the fluid properties of the medium, particularly the wind speed. The effects are seen only during the early dust devil formation period, but are evident as a rapid rise in E-field value by as much as a factor of 10 over that shown in Fig. 12 in the first ten seconds. As time progresses, the $Q_{\mathrm{L}}'\Delta v$ term primarily drives the system and the E-field asymptotes to approach results similar to the cases shown in Fig. 12.

5.2 Simulation Codes Integrating Particle Charging with Vortex Dynamics

Melnik & Parrot (1998) conducted a simulation where a number of particles of like composition but differing sizes were placed in a box and subjected to wind movement. These particles were then placed in a larger simulation domain ($50~\mbox{m} \times 100~\mbox{m}$) where the wind vortex was halted and further particle movement was controlled by the forces of gravity, air drag, and the electrostatic field. The redistribution of charge was tracked over time until an electric field built up to 20 kV m⁻¹, the breakdown field for the Martian atmosphere. The maximum electric field seen in the simulation reached ∼10 kV m⁻¹ in the first 2 s; the breakdown field was reached in 6.6 s. A second set of simulations tracking the movement of the electric field as particles roll up a hill (under the influence of a wind parallel to the surface) were also conducted. The electric field at the top of the hill reached the Martian breakdown value in about 13.5 s; growth of the electric field was exponential and much more regular than in the wind vortex case. In both wind environments, the amount of time to reach the breakdown field could be considerably lengthened (by greater than a factor of 10) by decreasing the number of particles involved, the amount of charge exchange upon collision, or the wind velocity. Over these longer timescales other processes (e.g. recombination of charges through subsequent collisions) are likely to occur, which could prevent the electric field increasing to breakdown strength.

Huang et al. (2008) numerically simulated a dust devil in a cylindrical domain of radius 100 m and height 200 m, in a terrestrial environment. They modelled the entire process iteratively beginning with development of the convective vortex from local surface heating, lifting of sand grains and their subsequent movement due to gravity and vortex winds, and applying a specified charge-to-mass ratio (Huang and Zheng 2001) on each grain in order to calculate the resulting electric field from Coulomb’s law. The closest fit to the observations of Farrell et al. (2004) employed charge-to-mass ratios of ${-}120~\upmu \mbox{C}\,\mbox{kg}^{-1}$, 60 μC kg⁻¹, and 57 μC kg⁻¹ for sand grains of diameter 0.15 mm, 0.2 mm, and 0.25 mm, respectively. The maximum E-field within the dust devil was reached in about 80 seconds of simulation time.

Motivated by the detection of ULF magnetic radiation emitted in terrestrial dust devils (Houser et al. 2003; Farrell et al. 2004), Farrell et al. (2006b) developed the Macroscopic Triboelectric Simulation (MTS). MTS is a 3-D particle code which quantifies charging associated with swirling, mixing dust grains. Grains of pre-defined sizes and compositions are placed in simulation box ($2~\mbox{m} \times 2~\mbox{m} \times 1~\mbox{m}$) and allowed to move under the influence of winds and gravity. The model tracks the movement of individual grains in the prevailing winds, and charge exchange upon grain-grain collision. An illustration of the model and a 3-D perspective of the grains during a simulation are shown in Fig. 13 and Fig. 14.

Fig. 13

Illustration of the forces on the grains in the Macroscopic Triboelectric Simulation model. Along the $z$-direction, grains are subject to an imposed constant upward wind and the downward gravitational force. In the horizontal plane, the prevailing winds are defined by a pattern of cyclostrophic balance between the outward centripetal force and inward pressure gradient force. (The $z$ and $xy$ motions are not coupled.) (From Farrell et al. 2006b)

Fig. 14

3-D perspective of the grain motion in an MTS simulation. The plots correspond to (a) 10 time steps, (b) 300 time steps, and (c) 499 time steps, where each timestep is approximately 1 ms (adapted from Fig. 4 in Farrell et al. 2006b)

The grains are initially placed in distinct clumps in close proximity to one another surrounding the box centre. Grain sizes are randomly generated but constrained such that the radius ranges 0.05–10 μm with a median value near 0.1 μm. To explore the Desch and Cuzzi compositional charging effects, the smaller grains ($r < 2~\upmu \mbox{m}$) are given a metallic composition (conductors) and the less abundant larger grains are modelled as silicates (insulators), with the potential difference between the two populations of $\Delta \varPhi = 1.6~\mbox{V}$. The motion of the smaller grains traces the wind pattern, while gravitational effects on the larger grains force them into a less circular wind pattern and they move towards the walls of the box as they fall. The distribution of charge on each of the grains at the point in the simulation before the grains reach the walls of the box ($t= 0.5~\mbox{s}$) is shown in Fig. 15(a).

Fig. 15

(a) Distribution of grain charge as a function of grain radius from an MTS simulation. The smaller metallic grains charge negatively and the large silicate grains charge positively as prescribed by the D&C charging mechanism. Additionally, and particularly evident with the metallic grains is the increase in grain capacity to hold charge with increasing particle radius. (b) The magnetic field generated as a function of time over the course of the same simulation (from Farrell et al. 2006b)

The spatial distribution of the charged grains establishes a distinct current system involving the relative displacement of negative and positive charge in the dust devil; the transverse part of this current is responsible for a time-variable magnetic field, and the vertical part is responsible for a large-scale vertical electrostatic E-field. The assumption of solenoidal current flow has allowed the magnetic effects of dust devils to be modelled (Kurgansky et al. 2007), which can explain some aspects of the ULF magnetic observations.

The MTS work described above used prescribed winds and the results were scaled up to the size of a real (terrestrial size) dust devil. Barth et al. (2015) applied the MTS simulations to Martian dust devils by incorporating the MTS-charged dust grains into their Mars Regional Atmospheric Modeling System (MRAMS; see Chap. 7 for additional description). The charged grains shown in Fig. 15 were partitioned into the MRAMS radius bins and a log-normal function was fitted to the charge values in each radius bin as shown in Fig. 16. Then the first and second moments of the charge distribution were added as tracers so that the charge on the dust particle tracers could be reconstructed at any MRAMS grid point.

Fig. 16

The MTS model returns charge values on individual dust grains. For each size-bin in MRAMS (Mars Regional Atmospheric Modeling System) the charge values were binned and fit to a log-normal function (from Barth et al. 2015, with permission of Elsevier)

As dust devils developed in the MRAMS Large Eddy Simulations (LES), the temporal/spatial change in charge distribution within the simulated Martian dust devil could be tracked and resulting E-fields were calculated. They found that the magnitude of the resulting E-field had strong dependence on particle size, amount of charge, and amount of dust lifted; the range of E-field values (mV m⁻¹ to kV m⁻¹) was in general, more modest than in previous studies (an example is shown in Fig. 17). As this study was a first look at the charge environment, a number of processes were not yet included. However, with this code one can examine the dust devil E-field in three dimensions, make estimates of the overall dipole moment, and get new insights on the development of higher order moments that form in regions of inhomogeneous fluid flows.

Fig. 17

Time and vertical variation of the electric field (V/m) an observer would see if traveling within the dust devil at the minimum pressure point, as generated by the MRAMS-MTS model (from Barth et al. 2015, with permission of Elsevier)

5.3 Breakdown Effects

Large E-fields like those measured in situ in terrestrial dust devils have been found which exceed 50 kV m⁻¹ (Farrell et al. 2004; Renno et al. 2004; Jackson and Farrell 2006). These same electrical convective features placed in the low pressure Martian atmosphere are expected to initiate atmospheric breakdown. Specifically, as the E-fields grow in the Martian dust devil, the atmospheric currents transition from nominal flows described by $J = \sigma E$ to the creation of a current-enhancing electron avalanche from Eq. (6) as

$$ J_{a} = n_{0}\exp \bigl( \alpha_{\mathrm{T}} ( E )d \bigr)ev_{e}E $$

(11)

where $n_{0}$ is the initial electron density, $\alpha_{\mathrm{T}}$ is Townsend’s first coefficient defining the number of ionizing events per unit length, and $v_{e}$ is the electron drift velocity in the gas. In the electron avalanche, those electrons with energy greater than 14.5 eV can ionize a CO₂ molecule via electron impact ionization to thus create extra electrons that get accelerated by the driving E-field. The population of electrons above 14.5 eV and their overall drift speed increases with electric field (Nighan 1970).

Farrell et al. (2015) noted that the electron avalanche represents a substantial modification of the atmospheric conductivity. At low E-fields, the atmospheric conductivity is represented as a bulk isotropic quantity, $\sigma$, where electron and ion mobility are assumed to be nearly equal. In contrast, within the electron avalanche itself, the electron conductivity is exponentially greater than that from the positive ion component, and is highly directional. As such, electrical dissipation of any charged object has to be examined based on the flow of fast beam-like electrons vs slow ions reaching the surface. Negatively charged dust grains immersed within the electron avalanche will not quickly dissipate their surface charge but instead reach a negative charge equilibrium state consistent with current balance to the grain surfaces. The interruption of dissipation of the negative dust grains is likely to act to reinforce the overall dust charge build-up in the convective feature.

Delory et al. (2006) modelled the electron avalanche process and growth in electron density in a dust feature and found that in dipole electric fields greater than 15 kV m⁻¹ the mean free path for electron impact ionization of less than a metre leads to substantial ionization. These energized electrons can then interact with CO₂ and $\mathrm{H}_{2}\mathrm{O}$, via dissociative attachment creating CO, $\mathrm{O}^{-}$, OH, and $\mathrm{H}^{-}$ (see Fig. 18). The dust devil-created CO and OH interactions are then suspected to generate hydrogen peroxide at concentrations well above those predicted via photochemistry (Atreya et al. 2006). These excesses of hydrogen peroxide become adsorbed onto aerosols and ultimately end up in the regolith, giving the $\mathrm{H}_{2}\mathrm{O}_{2}$ a longer lifetime than the chemically formed $\mathrm{H}_{2}\mathrm{O}_{2}$, which is photochemically dissociated during the day with a mean lifetime of 6 hours. Implications of this longer lifetime are that $\mathrm{H}_{2}\mathrm{O}_{2}$ could be an effective oxidiser (Encrenaz et al. 2012). The energetic electrons in the avalanche also can possibly create methane loss via dissociative attachment (Farrell et al. 2006c).

Fig. 18

Electron chemistry associated with (a) CO₂ and (b) H₂O, in the vicinity of an electrified dust devil or storm (after Delory et al. 2006)

5.3.1 Atmospheric Chemistry Effects and Breakdown

Delory et al. (2006) were the first to suggest that catalytic production of hydrogen peroxide can be triggered by electrostatic fields generated in the Martian dust devils and dust storms as well as near the surface within the saltation layer. The origin of this hydrogen peroxide enhancement lies in the possibility for electrons, after acceleration by large electric fields, to ionize CO₂ and $\mathrm{H}_{2}\mathrm{O}$ molecules, dissociating them and thereby releasing hydroxyl radicals as oxidizers of the Martian atmosphere. Atreya et al. (2006) predict that the $\mathrm{HO}_{x}$ enhancement factor can be up to 100 in electric fields reaching the breakdown limit (∼20 kV m⁻¹). However, no dedicated laboratory measurement to date has been performed in support of these assertions and the chemical implications for such catalytic production of oxidizer remain difficult to reconcile with our present understanding of Martian chemistry (Lefèvre and Forget 2009). The electron avalanche process including dust/electron absorption losses and the active conversion to $\mathrm{O}^{-}$ via electron dissociative attachment have been the focus of several later modelling studies (Jackson et al. 2008, 2010; Kok and Renno 2009). All of these models indicate that electron avalanche processes could develop, leading to electron impact excitation and new chemical products. However, each varied in the intensity of the electron impact ionization and chemical production. Delory et al. (2006) and Atreya et al. (2006) predicted an electron avalanche and plasma content having values below 1 part in $10^{14}$. Kok and Renno (2009) suggested that the activity could be of lower intensity when including grain charge dissipation effects. Jackson et al. (2010) found that the final equilibrium values for the plasma (electrons, $\mathrm{O}^{-}$, $\mathrm{CO}_{2}^{+}$) depend upon the assumed saturation process, with the most optimistic case to be 1 part in $10^{4}$, and in the least ideal case to be 1 part in $10^{13}$. These models all uniformly suggest the electron avalanche and ionization process is very mild, producing ions at concentrations ≪1 % of atmospheric gas densities. While electron dissociative processes are considered a loss process for methane (Farrell et al. 2006c), laboratory work has suggested that electrical activity associated with CO₂ and water could stimulate methane formation (Robledo-Martinez et al. 2012). Specifically, the electrons dissociate CO₂ and $\mathrm{H}_{2}\mathrm{O}$ into CO/O⁻ and OH/H⁻, with the CO and $\mathrm{H}_{2}$ then create methane and water. Farrell et al. (2015) concluded that the added energetic electrons in the atmosphere associated with relatively modest dust-generated E-fields act to create new chemistry, and in the case of the methane, can act to both destroy and create this critical biomarker. An obvious remaining question regarding methane is which process dominates at any given time, and how do these competing processes act to affect the overall global methane stability. To date, models have described the development of a bulk E-field, and its effect on storm-size chemistry. However, one can imagine the E-fields near individual dust particles to be amplified via the converging field near a local point source. A 5 micron particle charged to ${\sim}\,{-}$2.5 fC will have a local surface potential of −5 V (Farrell et al. 2015). However, in its immediate vicinity the local E-field values can become very large. For example, within 30 μm the E-fields exceed about 27 kV m⁻¹, and within 10 μm in excess of 250 kV m⁻¹. Thus very active local chemistry in the vicinity of these particles could be expected. Specifically, the electrons will initially collect or be removed on an individual small lofted particle depending upon the particle charge state and current balance to the particle in the electron avalanche flow. However, as these particles reach their negative equilibrium charge state, the electrons in the flow will be locally accelerated (i.e., redirected) about the particle. This effect will stimulate local chemistry in the near-grain environment. In equilibrium, the negative charged particles will also have a cloud of positive $\mathrm{CO}_{2}^{+}$ ions about it, but will tend to reject the $\mathrm{O}^{-}$ ions. The $\mathrm{O}^{-}$ ions should then congregate near the positively charged surface and in the vicinity of the larger positively charged grains near the bottom of the dust devil. The $\mathrm{O}^{-}$ ion is highly reactive and should modify near-surface chemistry. These avenues have yet to be fully examined.

6 Measurements of Martian Atmospheric Electricity

To provide a thorough picture of the atmospheric electricity on Mars, three principal parameters need to be measured in situ. These are the electrical conductivity, the DC atmospheric electric field and the AC electric fields associated with electromagnetic wave emissions. The atmospheric electric fields are directly related to atmospheric charging and discharging processes, and are characterized by large amplitudes, extending from DC to frequencies representative of the dynamics of charging and discharging processes.

The electrical conductivity of an atmosphere is an essential parameter of its global electric circuit. It also provides information on the ionization processes that control the electrical state of the atmosphere and on the major charged particles species, free electrons, positive and negative ions that are present in the medium. The conductivities associated with either positively or negatively charged species have to be measured separately to gain the relevant information. From model calculations (Sect. 2.3), the anticipated conductivities range from $10^{-12}~\mbox{S}\,\mbox{m}^{-1}$ to $10^{-10}~\mbox{S}\,\mbox{m}^{-1}$.

The quasi-DC electric fields provide direct evidence of the charging mechanisms and of their temporal variations. Based on the properties of the Martian atmosphere, measurements of the quasi DC electric fields should ideally cover the wide range from a few mV m⁻¹ to ${\sim}10~\mbox{kV}\,\mbox{m}^{-1}$ in order to encompass all situations of interest, from the faint electrification due to photo-electrons charging to potential electrical breakdown. Impact charging processes are directly associated with winds and thus their temporal variations at a fixed location should arise from e.g. the motion of dust devils and/or turbulence in the wind flow with a frequency of the order of 10 Hz. On the other hand, following observations in thunderstorms, discharge processes and the resulting redistribution of charges give rise to large amplitude variations as rapid as 0.5 to 1 ms. Ideally, therefore, in situ measurements should cover a frequency range up to ∼2 kHz.

Measuring the small amplitude AC electric fields will provide information on the electromagnetic wave emissions and the impact of charged dust grains on the lander. Electromagnetic waves can originate from atmospheric processes, such as the EM waves emitted by filamentary discharge currents in case of atmospheric breakdown or the Schumann resonances that result from the trapping of these waves in the surface-ionosphere resonator. They may also arise from totally different phenomena in the distant ionized environment of Mars through interactions with the solar wind. To achieve these observations AC electric fields have to be measured in the frequency range from a few Hz to more than 3 kHz, with a sensitivity of better than $\upmu \mbox{V}\,\mbox{m}^{-1}\,\mbox{Hz}^{- 1/2}$. This upper limit of 3 kHz is estimated from the greatest frequency signals expected, those of transverse resonances at ∼1500 Hz (Simões et al. 2009), and consideration of sampling requirements.

Several proposals have been made for an atmospheric electricity package on the surface of Mars (Berthelier et al. 2000; Farrell et al. 2000, 2004; Renno et al. 2004). The upcoming ExoMars Entry Descent Module (EDM) will carry the DREAMS package to the surface, which includes the MicroARES sensor that will provide an opportunity for the first-ever in situ measurements of Martian atmospheric electricity. These observations are likely to provide great insights into the Mars atmospheric electricity-chemistry-astrobiology interconnection. MicroARES is motivated by two fundamental science questions which are well addressed by in situ measurements: (1) is there an electric field on Mars?, and (2) are Martian dust devils electrified?

Ideally, an array of field mills could be deployed to answer these questions, operating indefinitely to sample a wide range of conditions. However, the very tight constraints imposed on the dimensions, mass and power of the sensors on the EDM surface payload restrict the electric field measurements to a short time window of only a few days, during which there is some expectation of dust storms. As on Earth, the planetary large scale electric field of atmospheric origin is essentially vertical and this component is of primary interest. MicroARES is based on a simplified version of the standard double probe technique used to measure electric field in space. Rather than deploying a boom with two sensors, MicroARES was designed to measure the potential with respect to the lander ground, using a single spherical electrode positioned 30 cm above the lander’s upper surface. Previous balloon flights of double-probe instruments together with numerical models have shown that the intended MicroARES configuration provides reliable measurements of the local atmospheric potential at the position of the electrode and higher frequency variations of electrostatic or electromagnetic origin.

6.1 MicroARES Electric Sensor

The MicroARES electric field sensor integrated in the ExoMars/DREAMS experiment (Esposito et al. 2014, 2015; Bettanini et al. 2014) will measure electrical properties of the Martian atmosphere. A modified version of this sensor has also been developed and tested in desert conditions, demonstrating its capability to measure electric fields found in terrestrial conditions, and under a simulated Martian conductivity environment. Because of the fundamental scientific results in planetary atmospheric electricity anticipated from the ExoMars/MicroARES measurements, the sensor to be deployed is described in some detail here.

In its final configuration, the sensor consists of a 27 cm mast supporting a 3 cm spherical electrode (see Fig. 19). The electrode is free to float electrically to a local potential, from which the local electric field can be derived using known electrical characteristics of the input stage. For weight and power consumption reasons, the reference electrode is the lander chassis. The spherical sensing electrode system has been designed upon the presumption that the Martian atmospheric conductivity lies between $10^{-10}$ and $10^{- 13}~\mbox{S}\,\mbox{m}^{-1}$. Measurements of the conductivity itself can also be made, from determining the charging time to restore the equilibrium potential of the electrode after bringing it to a fixed potential (e.g. Aplin 2005; Bennett and Harrison 2006).

Fig. 19

Photograph of electrode

The configuration used for the electrode-atmosphere interaction and associated electronic system is summarised in Figure 20. The interaction of the sensing electrode with the atmosphere can be modelled by a very simple RC circuit characterized by the sheath impedance ($R_{\mathrm{s}}$ and $C_{\mathrm{s}}$). Accurate modelling of the sheath around the electrode is therefore important in order to derive the conductivity from the measurement of $R_{\mathrm{s}}$ alone and vice-versa. Two methods can be used to achieve this, firstly a mathematical model approach (Molina-Cuberos et al. 2010, §2.2; Berthelier et al. 2000, §3.2), where the spherical electrode is considered immersed in a collisional and weakly ionized medium, and secondly an empirical approach of modelling of the equipotential lines around the electrode in order to retrieve the coefficients $k_{e}$ and $k_{\phi}$ which link the sheath resistance to the atmospheric conductivity (Seran et al. 2013).

Fig. 20

Concept of the electrode—atmosphere interaction used in the MicroARES measurement system. The sheath around the electrode is represented by the Resistance Capacitance combination of $R_{\mathrm{s}}$ and $C_{\mathrm{s}}$, and the input parameters of the electronic pre-amplifier by $R_{\mathrm{i}}$ and $C_{\mathrm{i}}$. RL (Relay Low range: 25 G$\Omega$) and RH (Relay High range: 10 G$\Omega$) are range setting resistances, which can be switched in successively (RL first, then RH) as necessary as the electric field increases

For the MicroARES sensor, the first approach is used, using

$$\begin{aligned} \begin{aligned} R_{\mathrm{s}}\cdot C_{\mathrm{s}} &= \frac{\varepsilon_{0}}{ \sigma}\quad \mbox{with} \\ C_{\mathrm{s}} &=4\pi r_{e} \varepsilon_{0}\quad \mbox{and}\quad R_{\mathrm{s}} = \frac{1}{4\pi\sigma r_{e}} \end{aligned} \end{aligned}$$

(12)

where $r_{e}$ is the electrode radius, $\varepsilon_{0}$ is the permittivity of free space and $\sigma$ is the local atmospheric conductivity. Further simulations of the electrode coupling with its environment will enable a comparison of the two approaches. With the Martian atmospheric conductivity assumptions, $R_{\mathrm{s}}$ will be between $10^{10}~\Omega$ and $10^{13}~\Omega$.

The input of the preamplifier is also modelled using a RC circuit. The $R_{\mathrm{i}}$ value is around $10^{14}~\Omega$ (based on the input impedance of the LMC6041 operational amplifier used combined with some leakage across the board), and the circuit has been optimised to maximize this parameter since $R_{\mathrm{s}}$ and $R_{\mathrm{i}}$ form a potential divider at the input. To allow measurement of the DC potential of the electrode regardless of the atmospheric conductivity, $R_{\mathrm{s}}$ has to be negligible compared to $R_{\mathrm{i}}$. For large electric fields, dividers formed by the $R_{\mathrm{L}}$ and $R_{\mathrm{H}}$ grounding resistors can be activated using controllable high impedance relays, similar to the method used for terrestrial measurements by Harrison and Aplin (2000), using the same model of operational amplifier. The $R_{\mathrm{L}}$ and $R_{\mathrm{H}}$ values of 25 G$\Omega$ and 10 G$\Omega$ respectively have been chosen to suit the Martian atmospheric conductivity assumption and the corresponding sheath resistance $R_{\mathrm{s}}$.

The range of measurable frequencies extends from DC to 3.2 kHz for sensor potential values ranging across ±100 V, corresponding to vertical electric fields of ${\pm}300~\mbox{V}\,\mbox{m}^{-1}$. At low frequencies, the electrode is coupled to the undisturbed plasma through the resistance of its surrounding sheath, to measure the DC electric fields. Above a cut-off frequency, which depends on the sheath resistance and electrode capacitance, the preamplifier is capacitance coupled to the ambient atmosphere (see Fig. 20). The high sheath resistance makes it necessary to use high input impedance (${>} 10^{14}~\Omega$), low leakage current (${<}10^{-14}~\mbox{A}$) electronic preamplifiers.

To cope with possible large electric fields exceeding the normal range of voltages applied to the electrode, the high impedance relay can switch in a parallel input resistance to the preamplifier (Fig. 20). This resistance is significantly smaller than the anticipated value of the electrode sheath resistance, which will therefore produce a potential divider, lowering the potential to lie within the input voltage range of the preamplifier. In practice there are two different shunt resistances that can be switched independently, $10~\mbox{G}\Omega$ and $25~\mbox{G}\Omega$. The measurements performed with these two shunt resistances allows the sheath resistance to be determined, which in disturbed conditions, may differ from that obtained in quiet conditions.

A further measurement possible is that of the atmospheric conductivity through the relaxation technique: the sensor potential is displaced from the local floating potential and then allowed to recover its equilibrium potential. The time constant for this charging (or discharging) process $\tau = \varepsilon_{0} /\sigma$ readily provides the local electric conductivity $\sigma$, provided that the conductive area of the lander is much larger than that of the sensor. This condition ensures that the return current collected by the lander to counterbalance the current collected by the polarized sensor does not entail any significant variation of the lander potential with respect to the atmosphere, and ensures that the lander ground stays constant with respect to the ambient medium.

6.2 MicroARES Tests in the Terrestrial Atmosphere

MicroARES can also be used for the measurement of the electric properties of Earth’s atmosphere, and this provides a test opportunity. A terrestrial version of MicroARES (Fig. 21) was developed and operated in the Sahara desert (at Merzouga, Morocco) for a week in July 2014 during the local dust storm season. It operated during the field campaign described in Sect. 4.1 and fully reported in Esposito et al. (2016). As Fig. 2 shows, however, the atmospheric conductivity profiles are very different between Earth and Mars, with the surface atmospheric conductivity at Mars comparable with that of the terrestrial stratosphere. Although space instrumentation can be tested using stratospheric balloons (Fulchignoni et al. 2004), use at this altitude would not be practical, not least as there would be no prospect of obtaining a ground connection. Since the Earth’s atmospheric conductivity² at sea-level is about 100 times smaller than that near the surface on Mars, the antenna-atmosphere coupling will generate a greater sheath resistance of up to $10^{15}~\Omega$, which will cause the signal to be almost fully attenuated and the electrode will not be able to maintain itself at the floating local potential because of the small bias current flow to the input amplifier.

Fig. 21

Terrestrial adaptation of MicroARES antenna as used in the Sahara desert

Since the standard MicroARES configuration will not properly measure the Earth’s DC electric field, possible solutions for a test system are to either change the relay resistances and the pre-amplifier input resistance or to change the antenna. Given the fact that the input resistance is an intrinsic property of the design, increasing it is clearly not possible. Therefore, the antenna needs to be adapted to the Earth atmospheric properties instead.

For atmospheric conductivity roughly 100 times smaller than that on Mars, an electrode roughly 100 times larger is needed in order to keep $R_{\mathrm{s}}$ at the same order of magnitude. For the tests undertaken in the Sahara, for which there were numerous practical issues, a 60 cm side copper cube constructed from 0.8 mm thickness sheets was used. Its $2.16~\mbox{m}^{2}$ surface area was equivalent to a 41.6 cm radius sphere, around 30 times larger than the original antenna. Thus, by calculation, the associated $C_{\mathrm{s}}$ becomes around 46 pF, and $R_{\mathrm{s}}$ (with assumed atmospheric conductivity of 50 fS m⁻¹) will be around 3.5 T $\Omega$ instead of 100 T $\Omega$. With this modified sheath resistance, the input relays are expected to provide switching of the input stage as originally planned, and the pre-amplifier input resistance should not significantly affect the measurements. The mast height was also increased to 50 cm, which lowers the parasitic capacity to a few pF. A further consequence is that the centre of the cube is now located at 80 cm from the ground, which will lead to a greater measured potential (Fig. 21).

As the cube antenna and Earth atmosphere have different electrical properties from the anticipated Martian input configuration, some different post-processing is required. The response time of the instrument input is inversely proportional to the conductivity ($\tau = \varepsilon_{0} /\sigma = 1/R_{\mathrm{p}} C_{\mathrm{p}}$), hence the expected response time on Earth with this cube antenna will be ∼200 s. The two main consequences of this are that the signal is highly deformed, which can be corrected numerically, and that, in the conductivity measurement mode, a switching sequence as rapid as 4 s is no longer possible. Since the post-processing correction depends on $\sigma$, its determination is performed with the signal correction. The instrument can only record 20 min worth of data, so it is restarted, with the signal correction applied every 20 min.

To reconstruct the input response, the instrument input stage parameters are needed accurately. The model employed for the electronics is that presented in

Figure 20, with $R_{\mathrm{i}} =10~\mbox{T}\Omega$, $C_{\mathrm{i}} =2~\mbox{pF}$ (preamplifier) + 6 pF (antenna), $R_{\mathrm{L}} =25~\mbox{G}\Omega$ and $R_{\mathrm{H}} =10~\mbox{G}\Omega$. The antenna-atmosphere coupling depends on two parameters, $C_{\mathrm{s}}$ and $R_{\mathrm{s}}$, but the measurements only provide one parameter, the atmospheric conductivity $\sigma$. Since the equations describing the instrument input depend on these variables separately, an equivalent radius to a spherical electrode (41.6 cm) is assumed to derive $C_{\mathrm{s}}$ and $R_{\mathrm{s}}$ from the conductivity.

The signal distortion at each zeroing of the instrument is clearly visible on Fig. 22. Note that at every restart (switching on and off of the signal processing board), the input of the preamplifier is connected to ground and then consequently discharged, so the slow response time of the atmospheric coupling is exaggerated.

Fig. 22

Time series of the MicroARES unprocessed signal. Measurements were acquired in the Sahara desert, Morocco in July 2014

In order to correct the signal the response is modelled with the assumptions made previously. The data reconstruction depends on the determination of $\sigma$ (for the values of $R_{\mathrm{s}}$ and $C_{\mathrm{p}}$) and the initial potential condition i.e. $U_{e}(0)$. On Mars, $\sigma$ would have been provided by the conductivity measurement mode, during calm weather, and the relay operation during stormy weather (the quick response time allows computation of the ratio before and after relay operations to easily determine $R_{\mathrm{s}}$ and $\sigma$), but for Earth measurements it is not available directly, without the post processing. The data reconstruction also relies on the assumption that, during the 6 s reset time, the electric field is steady, thus allowing a good approximation of $U_{e}(0)$ during each 20 min of measurement.

Determination of $\sigma$ has been achieved by iterating its value in the input inversion equations, at every switching cycle of the instrument visible on Fig. 22, so that the derivative and potential changes before and after the switch are minimized (see Fig. 23). Comparison of the reconstructed electric field with that obtained from an adjacent commercial field-mill (Fig. 24) demonstrates the effectiveness of this technique, with a correlation of 0.9 during calm weather and 0.75 during stormy weather.

Fig. 23

Discontinuity smoothing with simultaneous determination of conductivity. The time axis is local time

Fig. 24

Electric field samples made at 1 Hz: comparison during calm (upper panel: 10th July 2014) and disturbed (lower panel: 12th July 2014) weather. Note that the electric field intensity measured during fair (calm) weather by MicroARES at 80 cm from the ground is smaller than the value measured by the reference field mill that was placed at 2 m from the ground. This is in agreement with the expected atmospheric electric field vertical profile

As explained, the MicroARES measurement sequence and post-processing also allow the retrieval of conductivity, which is generally not possible with commercial field-mills alone running in a standard mode. Figure 25 shows the retrieved conductivity for 9–13th July 2014; the scale chosen emphasises the variability. The increase of conductivity during dust events implies that the dust is contributing to the conductivity, as discussed for dense aerosol concentrations by Dhanorkar and Kamra (1997).

Fig. 25

Conductivity inferred with MicroARES instrument in terrestrial desert conditions from 9–13th July 2014

7 Conclusions

Dusty environments on Earth can, as shown here, readily become electrified, and, by analogy and theoretical consideration, the Martian atmosphere also seems likely to contain electrified dust. Central to developing an improved understanding of this dust electrification is the understanding of charge exchange between the substances concerned, and possible breakdown effects. Ultimately, bulk measurements made in natural dust storms on Earth and Mars need to be reconciled with laboratory measurements of electrification at a particle level and the modelled electric field structures they present under the appropriate electrodynamic conditions.

Measurements of terrestrial dust electrification at the surface and aloft indicate that particle charging in dust storms is a common, and, perhaps, even a universal phenomenon to a greater or lesser extent. The use of field mill measurements in dust devils shows that electric fields of order 10 kV m⁻¹ are readily observed, which are associated with the pressure minimum and wind speed maximum (e.g. Fig. 8). Larger values to ∼100 kV m⁻¹ have also been reported. The magnitude of the field appears to be reduced with increasing humidity (Fig. 10), which is likely to be related to the properties of the contact electrification process when water layers at the molecular level are present (Sect. 3.4).

Several modern experimental techniques are proving to be extremely informative with regard to contact electrification processes, notably, as mentioned, atomic force microscopy (AFM) (Matsusaka et al. 2010; Horn et al. 1993, Gady et al. 1998). This approach promises to provide a more detailed (atomic scale) understanding of electrification and has already led to the discovery that net surface electrification in fact is made up of a ‘mosaic’ of highly electrified regions of positive and negative patches (Baytekin et al. 2011). Both processes of electron and ion transfer can be involved in contact electrification, depending on the surface conditions or composition. In the terrestrial environment, surface water layers will typically be expected on particles facilitation ion exchange irrespective of surface composition.

For the electrostatics in dust devils, specific studies aimed at understanding and quantifying the dust or sand electrification interactions are of direct practical use. Several laboratory (and wind tunnel) based studies are currently being performed (Bo et al. 2014; Lacks and Sankaran 2011, Merrison et al. 2012). To allow modelling of electrification within a dust devil, a deeper understanding is needed in the size dependence of contact electrification. This is probably only likely to be achieved by pursuing more advanced laboratory experiments, applying detailed physical models (possibly involving both electron and ion transfer processes). Detailed and novel field studies could also contribute here.

Modelling of dust devils has shown that, by linking the flow dynamics produced by the balance between centripetal and pressure gradient forces (i.e. cyclostrophic balance) with theoretically derived inter-particle charge exchange processes, leads to electric fields comparable with those observed (Fig. 12). This includes a rapid initial rise in the electric field. At extreme electric fields, the dynamics of the charged particles can be influenced by the field (Kok and Renno 2008a, 2008b), providing a feedback on the electrification or a means by which the effectiveness of dust uplift is enhanced. Ultimately the growth of the field is limited by breakdown processes, which are dependent on the chemical composition of the atmosphere concerned.

Within the Martian atmosphere there are good arguments to expect electrification of dust devils and dust storms, in the absence of any direct electrical measurements to date. The DREAMS-MicroARES instrument due to land on Mars in 2016 will provide these first direct measurements, and with them, an important and substantial change in the knowledge of its planetary electrical environment.