The Variation of Geomagnetic Storm Duration with Intensity

Abstract

Variability in the near-Earth solar wind conditions can adversely affect a number of ground- and space-based technologies. Such space-weather impacts on ground infrastructure are expected to increase primarily with geomagnetic storm intensity, but also storm duration, through time-integrated effects. Forecasting storm duration is also necessary for scheduling the resumption of safe operating of affected infrastructure. It is therefore important to understand the degree to which storm intensity and duration are correlated. The long-running, global geomagnetic disturbance index, $\mathit{aa}$, has recently been recalibrated to account for the geographic distribution of the component stations. We use this $\mathit{aa}_{H}$ index to analyse the relationship between geomagnetic storm intensity and storm duration over the past 150 years, further adding to our understanding of the climatology of geomagnetic activity. Defining storms using a peak-above-threshold approach, we find that more intense storms have longer durations, as expected, though the relationship is nonlinear. The distribution of durations for a given intensity is found to be approximately log-normal. On this basis, we provide a method to probabilistically predict storm duration given peak intensity, and test this against the $\mathit{aa}_{H}$ dataset. By considering the average profile of storms with a superposed-epoch analysis, we show that activity becomes less recurrent on the 27-day timescale with increasing intensity. This change in the dominant physical driver, and hence average profile, of geomagnetic activity with increasing threshold is likely the reason for the nonlinear behaviour of storm duration.

1 Introduction

A geomagnetic storm is a significant disturbance in the Earth’s magnetic field (e.g. Gonzalez et al., 1994) due to specific sets of conditions in the near-Earth solar wind. Southward-orientated interplanetary magnetic field (IMF) can reconnect with the geomagnetic field of the dayside magnetosphere resulting in the storage of energy in the lobes of the magnetotail (Dungey, 1961). Reconnection associated with disturbances in the magnetotail current sheet releases the stored energy and currents in the upper atmosphere are enhanced. This can result in adverse effects in a number of ground- and space-based technologies, as well as posing a threat to the health of astronauts and flight crew and passengers (Baker, 1998). In particular, this substorm cycle of tail lobe energy storage and release can result in enhanced ionospheric currents which can in turn lead to geomagnetically induced currents (GICs), a quasi-DC signal, flowing through ground infrastructure such as power grids and pipelines (Patel et al., 2016; Cannon et al., 2016). An induced DC current in AC power transformers may create a half cycle saturation leading to degradation and breakdown. Thus geomagnetic storms can affect today’s technologically centred society to great disruption and at great cost (Eastwood et al., 2017; Oughton et al., 2017; Riley et al., 2018; Cannon et al., 2016).

GICs result from rapidly varying local geomagnetic fields, on the timescale of minutes or less. Therefore geomagnetic indices (e.g. $\mathit{Dst}$, $\mathit{AE}$ and $\mathit{Kp}$), which summarise global geomagnetic variability on the timescale of hours, do not directly relate to the GIC drivers. However, there is coupling across these timescales and spatial scales, with the largest GICs occurring during geomagnetic storms (Trichtchenko and Boteler, 2004, 2007).

Space-weather forecasting often focuses on estimating the onset and intensity of geomagnetic storms (Abunina et al., 2013; Lundstedt, Gleisner, and Wintoft, 2003; Joselyn, 1995). But storm duration can also be an important secondary factor through time-integrated effects (Mourenas, Artemyev, and Zhang, 2018; Balan et al., 2016). Indeed, Lockwood et al. (2016) showed that the time-integrated value of solar wind forcing, which measures the net geomagnetic disturbance, was influenced both by the amplitude and duration of storms. Therefore, a forecast of storm duration would be beneficial in the development of mitigation plans for sensitive infrastructure and services, in terms of estimating when normal operations can resume. Thus it is important to quantify the relationship between storm intensity and duration.

Surveys of the largest geomagnetic storms in the $\mathit{Dst}$ index have included estimates of storm duration (Echer, Gonzalez, and Tsurutani, 2008; Balan et al., 2016), though the relation with storm intensity was not explicitly quantified. Using the $\mathit{Dst}$ index, Yokoyama and Kamide (1997) showed that the average duration of main and recovery phases of storms increased with storm intensity across three broad categories (weak, moderate and strong) for 8 years of observations. A similar analysis was presented in Hutchinson, Wright, and Milan (2011) for Solar Cycle 23 but concluded that storm main phase duration increases with intensity to a point, but then the relationship reverses for storms more intense than a peak $\mathit{SYM}$–$H$ index disturbance of $-150~\mbox{nT}$. Recently, Walach and Grocott (2019) analysed the $\mathit{SYM}$–$H$ index between 2010 and 2016 in a similar way to Hutchinson, Wright, and Milan (2011) but concluded that there was no clear ordering of intensity by storm duration. Conversely, Vennerstrom et al. (2016) used the $\mathit{aa}$ index to demonstrate an increase in average storm duration across five peak intensity levels. The weakest storms had a median duration of 6 hours and the most intense storms 30 hours, noting that the duration of the most intense storms ranged from 12 to 93 hours. Xie et al. (2008) showed that, for large storms, preconditioning of the magnetospheric system by prior solar wind conditions can increase storm duration but found no evidence that it increases peak amplitude.

The long-running, global geomagnetic disturbance index, $\mathit{aa}$ (Mayaud, 1971), has recently been recalibrated to account for the geographic distribution of the component stations (Lockwood et al., 2018a). In this study, we use this $\mathit{aa}_{H}$ index to analyse the relationship between geomagnetic storm intensity and storm duration over the past 150 years, further adding to our understanding of the climatology of geomagnetic activity. In particular, we construct and test a simple probabilistic forecast of storm duration based on storm intensity.

2 Data

Changes in magnetospheric current systems can result in magnetic fluctuations which can be measured at a number of stations around the world with ground-based magnetometers. These measurements are compiled into a variety of indices, including $\mathit{aa}$, $\mathit{Kp}$, $\mathit{Dst}$ and $\mathit{AE}$, which measure different properties of global geomagnetic activity. The $\mathit{aa}$ index, created by Mayaud (1971), is based on the $k$ values devised by Bartels, Heck, and Johnston (1939). The $k$ values are made by ranking the range of variation in the observed horizontal or vertical field component (whichever gives the larger value) in each 3-hour period into one of 10 categories. These categories are defined by quasi-logarithmic limits based on the station’s proximity to the auroral oval and a $k$ value of 0 to 9 is assigned. The $\mathit{aa}$ index is a combination of measurements taken from two mid-latitude stations, in the UK and Australia, since 1868 which, by virtue of being in opposite hemispheres and roughly 10 hours apart in local time, provide a quasi-global measure of geomagnetic activity with particular sensitivity to the substorm current wedge (Lockwood, 2013).

The major disadvantage of $\mathit{aa}$ is that it is compiled from just two stations, but that is necessary in order to generate the series back to 1868, which is its major advantage. Lockwood et al. (2018a) and Lockwood et al. (2018b) corrected $\mathit{aa}$ for a number of factors. Firstly they made allowance for the changing geographic location of the midnight sector auroral oval, due to the secular change in Earth’s intrinsic geomagnetic field (giving different drifts of the geomagnetic poles in the two hemispheres, as observed), which influences the proximity of the stations to the most relevant current system, the nightside auroral electrojet of the substorm current wedge. This improves the intercalibration of the different stations needed to compile the $\mathit{aa}$ series (three have been needed in each hemisphere to make a continuous series since 1868). In addition, they allowed for the time-of-day/time-of-year response pattern of the station (the “station sensitivity”) using a model of how it is influenced by proximity to the auroral oval and by local ionospheric conductivity, thereby reducing the errors introduced by using just two stations. The resulting index, called the “homogeneous $\mathit{aa}$ index”, $\mathit{aa}_{H}$, has been tested by Lockwood et al. (2019) against the $\mathit{am}$ index, generated in a similar way to $\mathit{aa}$ but using rings of 24 mid-latitude stations in both hemispheres (Mayaud (1980), http://isgi.unistra.fr/indices_am.php), and was shown to perform considerably more uniformly in local time than the original $\mathit{aa}$ index. The analysis shown in the present paper uses the $\mathit{aa}_{H}$ data but similar results have been achieved for the $\mathit{am}$ index. The $\mathit{aa}_{H}$ index runs from 1868 to present and definitive $\mathit{am}$ data currently runs from 1959 to 2013. Although $\mathit{am}$ gives a more accurate representation of the instantaneous state of global geomagnetic activity (Lockwood et al., 2019), the advantage of $\mathit{aa}_{H}$ is that it provides an extra century of observations which means that better statistics on large events are obtained.

3 Storm Definition

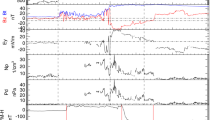
There are no universally agreed-upon criteria to classify geomagnetic storms in geomagnetic time series, with definitions depending on the purpose of the study (Riley et al., 2018). Vennerstrom et al. (2016) defined storms in the 3-hourly $\mathit{aa}$ time series as events in which the maximum value exceeds one of a set of limits which we refer to here as the “upper threshold”. They defined the start and end of a storm as the times when $\mathit{aa}$ rose above and fell below a threshold of twice the mean of the whole dataset ($40~\mbox{nT}$): we here refer to this as the “lower threshold”. Thus in their definition of an event, the start of the storm is where $\mathit{aa}$ first exceeds $40~\mbox{nT}$ prior to the peak, and the end is where it last exceeds $40~\mbox{nT}$ after the peak. Thus multiple upper threshold crossings have the potential to constitute a single storm (see also Figure 1). In the Vennerstrom et al. (2016) definition, $\mathit{aa}$ continuously exceeds the lower threshold in an event and so even a brief drop below it means that a new event is counted as having started. Only storms associated with a sudden storm commencement (SSC) were considered – definitive SSCs are defined by visual searches for sudden increases in the northward component of the field measured at any one of five low-latitude stations. This yielded a set of 2370 storms for the lowest upper threshold they considered ($50~\mbox{nT}$). Kilpua et al. (2015) used 3-hourly $\mathit{aa}$ data, but with an upper threshold of $100~\mbox{nT}$ and a lower threshold of $50~\mbox{nT}$. This gave 2073 storms and performed analysis on cumulatively binned categories of storms larger than a certain value, beginning at $100~\mbox{nT}$ and increasing in increments of $100~\mbox{nT}$ up to $600~\mbox{nT}$. This upper and lower threshold method of storm definition was also employed by Riley and Love (2017) for the $\mathit{Dst}$ index.

Figure 1

Examples of geomagnetic storm definitions using 3-hourly $\mathit{aa}_{H}$ data. The upper threshold determines if the event is included in the analysis. A lower threshold determines the duration of the event. The period defined as a storm, when using an upper and lower threshold, is shown in red. Left: A slight dip below the lower threshold means what an individual observer may regard as the tail of the storm has been cut off. Right: A double peak shape suggests two storms may have been counted together as a single event.

Other approaches include that of Hutchinson, Wright, and Milan (2011) who identified storms in $\mathit{SYM}$–$H$ using a threshold approach of $-80~\mbox{nT}$ and then proceeding to manually inspect individual storms using knowledge of the characteristic storm trace and the solar wind data. This was feasible because the study included only 143 events from a single solar cycle, a relatively small sample compared to that enabled by the $\mathit{aa}_{H}$ dataset.

We follow a similar approach to Kilpua et al. (2015) and Vennerstrom et al. (2016) for storm definition. However, we will follow a more data-informed approach to threshold selection by following the percentile approach (Gonzalez et al., 1994). When categorising $\mathit{Dst}$ storms (in which storms are negative perturbations), Gonzalez et al. (1994) defined the lowest $25\%$ of $\mathit{Dst}$ values as a weak storm, the lowest $8\%$ as a moderate storm, and the lowest $1\%$ as a strong storm. Of course, the issue with this approach is that the percentile-based thresholds will change with the interval considered. This variation will be greatest with short data sequences and very high thresholds (e.g., the top $1\%$ or higher).

Since a strong $\mathit{aa}_{H}$ storm has a positive value, we define a storm to start when the $\mathit{aa}_{H}$ value is greater than the 90th percentile of the full 1868 – 2017 3-hour data sequence. The end of the storm will be the last value greater than the 90th percentile. The 90th percentile of $\mathit{aa}_{H}$ (1868 – 2017) is $40.1~\mbox{nT}$, similar to that used in previous studies. For some parts of the analysis, we have also used an upper threshold to select storms of different peak intensity. As in previous studies, an event must have a peak value over the upper threshold to be selected, but the storm duration is nevertheless measured as the time spent over the lower threshold (i.e., the upper threshold determines whether an event is classed as a storm and the lower threshold determines its duration). Upper and lower thresholds are depicted in Figure 1.

A feature of this approach is that a single measurement that falls just below the lower threshold brings an end to a storm. This is depicted in Figure 1 in which the tail at the end of the storm is cut off. Another feature is that two events occurring close to each other with respect to time will be classed as a single event if the index does not fall back below the lower threshold in the interval between them. This double peak effect is depicted in the plot on the right of Figure 1. While this approach may sometimes disagree with the interpretation of a human observer, it gives a set of objectively defined storms, making our analysis reproducible and readily applicable to the entire dataset.

4 Results

The number of storms in the $\mathit{aa}_{H}$ index can be seen in Figure 2 (Left). The data has been grouped into bins of width $10~\mbox{nT}$. The log–log scale reveals that the distribution of storms follows an approximate power law. This result is in agreement with that from Riley (2012) who found a power law in the occurrence of geomagnetic storms in the $\mathit{Dst}$ index. The sharp drop off associated with a power law can be seen in the probabilities of storm peak intensity revealed by the complementary cumulative distribution function (CCDF) in Figure 3 (Left).

Figure 2

Left: The number of storms as a function of peak intensity on a log–log scale. The data was grouped into equal-size bins of 10 nT. Right: The number of storms as a function of storm duration on a log–log scale plotted using bin width of three hours, the resolution of $\mathit{aa}_{H}$, meaning every possible duration has a unique bin.

Figure 3

Complementary Cumulative Distribution Functions (CCDFs) of peak intensity (left) and durations (right) for all storms in the $\mathit{aa}_{H}$ index.

Similarly, the number of storms as a function of duration has a sharp drop off. Figure 2 (Right) reveals that the decrease is slightly less than a power law. The accompanying CCDF in Figure 3 (Right) shows the drop off in a stepped fashion due to the quantisation of the $\mathit{aa}_{H}$ index into 3-hour data-points.

The variation of mean storm duration with storm intensity, as measured by the upper threshold, is presented in Figure 4. As expected, the general trend is that, as the upper threshold is increased, the mean storm duration also increases. Of course, if storms have a common recovery timescale and thus similar saw-tooth-like profile (see Section 5), storm duration would be expected to increase monotonically with peak intensity. This result is in qualitative agreement with Hutchinson, Wright, and Milan (2011) and Vennerstrom et al. (2016), who noted an increase in storm duration for increasing storm intensities.

Figure 4

Mean storm duration (red line and left axis) and number of storms (blue line and right axis) as a function of increasing storm intensity, as defined by the upper threshold value. Storms have been organised into cumulative intensity bins for the upper threshold. The red line shows how the average duration increases as the upper threshold is increased. Error bars are plus and minus one standard error on the mean. The blue line and right-hand axis show the number of storms in each bin on a log scale.

We find the relation between intensity and duration to be nonlinear, with a plateau in mean duration towards higher thresholds, at a level which selects approximately the top 50 – 100 storms. Yokoyama and Kamide (1997) noted a similar effect in a set of $\mathit{Dst}$ storms and state that storm intensity increases more than linearly with duration.

The above analysis uses cumulative bins of storm intensity, so there are common events within bins. We now separate events using differential peak intensity bins of 70 – 90 nT, 90 – 110 nT, 110 – 150 nT, 150 – 190 nT, 190 – 230 nT, 230 – 300 nT, 300 – 400 nT, and above 400 nT. The number of storms in each bin can be seen in Figure 5 and decreases with intensity. Figure 5 does not represent the distribution function due to unequal bin widths (the distribution function is shown in Figure 2). The bins were chosen to balance the granularity of intensities examined and the number of events in each bin to ensure enough events for the following statistical analysis.

Figure 5

The number of storms in each class of peak storm intensity. Due to unequal bin size, this does not represent a distribution function.

The distribution of the storm durations in each intensity class broadly resembles that of a log-normal distribution. This is shown for storms of all intensity classes in Figure 6. A log-normal distribution is defined by the mean of the logarithm of the values, $\upmu$, and the standard deviation of the logarithm of the values, $\upsigma$. These parameters were found from the observed durations in each intensity class through maximum likelihood estimation (MLE) and used to create a log-normal distribution, plotted in Figure 6 in dark purple. The light purple distribution shows a histogram of the observed data as an estimate of the probability density function (PDF). By eye, the log-normal distribution provides a reasonable first-order match at all intensity thresholds. However, statistical testing suggests the log-normal distribution may not properly capture the high density of storms with 3-hour durations. As this study is primarily interested in larger intensity storms, we focus on using the log-normal fits for the remainder of the study.

Figure 6

Storm durations for each class of peak intensity. The observed probability density function (PDF) of durations is shown in the histogram, while a log-normal with the same mean and width parameters is shown as the purple curve. The intensity classes represented in (a), (b), (c), (d), (e), (f), (g), and (h) are 70 – 90 nT, 90 – 110 nT, 110 – 150 nT, 150 – 190 nT, 190 – 230 nT, 230 – 300 nT, 300 – 400 nT, and above 400 nT, respectively.

We further note here the quantisation of the $\mathit{aa}_{H}$ dataset into 3-hour intervals. The underlying physical phenomenon, that of storm duration, is of course continuous. This issue is commonplace in social and medical science for longitudinal studies through discrete-time survival analysis (Allison, 1982; Singer and Willett, 1993; Carlin et al., 2005). These methods will be investigated in future study. However, here we follow the simpler log-normal approach described above. The reason is twofold. Firstly, it would increase the complexity of the models presented here and it is instructive to begin with this simple and well understood approach. Secondly, for the purposes of the current study, we are not seeking physical understanding through the shape of the distribution function and only require an estimate of the gross properties of the distribution for use as a robust forecast tool.

For each of the peak intensity classes, we have calculated the values of $\upmu$ and $\upsigma$ for the log-normal fits to the duration distributions shown as the black points in Figure 7. The intensity classes are plotted on the $x$-axis at the median value of the intensity of storms in each class. It is clear from the points in the left panel of Figure 7 that $\upmu$ increases as intensity increases, agreeing with the previous results in Figure 4 (i.e., duration increases as intensity increases). The parameter $\upmu$ can be approximated as a function of storm intensity by

$$ \upmu (\text{intensity}) = A \ln (B\ \text{intensity} - C), $$

(1)

where $A$, $B$ and $C$ are free parameters. A least squares fit was implemented, incorporating the 33rd and 67th percentiles (i.e. the 1-sigma range) as the asymmetric uncertainty around the median of each intensity bin and the standard error around $\upmu$. The coefficients $A$, $B$ and $C$ were found to be 0.455, 4.632, 283.143, respectively, and this curve is plotted, along with uncertainty bars, in Figure 7 (left). Although the fit is based on weighted bin-centres of storm intensity, the equation can be used to interpolate for a given value of intensity.

Figure 7

Variation of best-fit log-normal parameters to the observed storm duration PDF as a function of storm intensity. Best-fit curves accounting for uncertainties in both variables are shown, mean storm duration of the log-space (left) and the standard deviation of the log-space (right). The uncertainty bars for storm intensity are the 33rd and 67th percentile (i.e. the 1-sigma range) around the median, for mean duration they are the standard error of the mean and for standard deviation they are the standard error of the standard deviation.

Given the error bars, $\upsigma$ can be approximated by a linear fit to give $\upsigma$ as a function of the peak intensity. Figure 7 (right) shows the best-fit line which has a shallow gradient of $-5.08 \times 10^{-4}$ and $y$-intercept at 0.659. The plot shows that the fit agrees with the points to within the estimated errors for 5 out of the 8 intensity ranges (i.e., $62.5\%$) which is close to the $65\%$ figure expected for the $1\upsigma$ errors employed and hence a linear fit is deemed acceptable for our purposes.

The relations in Figure 7 can be used to produce an ideal log-normal distribution of durations for a given storm peak intensity. This, in turn, can be used to give an estimate of the probability of a storm of a given intensity exceeding a given duration. To test how well this simple model works, we have made a comparison between the probability given by the model and the observed frequency in the dataset. The $\mathit{aa}_{H}$ dataset was split up into two equal-size sets composed of alternating years; a training dataset and a verification dataset. The training set was used to derive coefficients for Equation 1 and the linear fit of $\upsigma$ and thus create the model. The verification dataset was used to compute the observed probabilities, thus ensuring an unbiased comparison. Figure 8 shows the comparison for the probability of storms exceeding 12, 24, and 36 hours as a function of peak intensity. The black line is the observed probability from the verification $\mathit{aa}_{H}$ dataset. The red line is the result of implementation of Equation 1 and expression for $\upsigma$. It is seen that the model gives a generally good match to the observed probability but there are differences in detail. The largest storms (${>}\,400~\mbox{nT}$) are likely to last longer than 24 hours and have a probability of approximately 0.4 of lasting longer than 36 hours. The smallest storms (${<}\,100~\mbox{nT}$) have a low probability (0.2) of lasting longer than 12 hours. There is good agreement with the observed occurrence frequencies.

Figure 8

Comparison of observed and predicted storm durations. Plots show the probability a storm will exceed a certain duration as a function of peak intensity. The red line computes $\upmu$ from Equation 1 and $\upsigma$ from the linear expression and uses these to compute the relevant probabilities. The black line is the observed probability from the training dataset for comparison. The $\mathit{aa}_{H}$ dataset was split into two equal-size sets to avoid bias in the comparison.

To further quantify the agreement between the model and observations we consider the associated reliability diagrams (Jolliffe and Stephenson, 2003), which compare the model predicted probabilities with the observed occurrence rates. We construct the reliability diagram by binning storms according to the model probability, $P_{M}$, of exceeding a given duration. For each model probability bin, we then determine the observed frequential probability, $P_{O}$, as a fraction of events which were actually observed to exceed the given duration. The model is reliable if $P_{M} = P_{O}$, i.e., follows the $y=x$ line on the reliability diagram. A reliability diagram is shown in Figure 9 for storms exceeding durations of 12, 24 and 36 hours. A 5-fold cross validation has been implemented such that independent test and training datasets have been split in five different ways and the analysis carried out on each as shown by the red lines. For all three of the categories shown it is seen that the curves are generally slightly above the $y=x$ line showing a systematic underestimation of storm duration. However, for the analysis on 24 and 36 hour storms the reliability curves become sporadic for larger values of the model probability. This is due to a small sample size of events for which the model gives a large probability of the storm having these durations and hence very few observations with which to compute the frequential probability of the observations. On the whole, where there is sufficient sample size, the model probability and observed probability are in reasonably good agreement. To make this model more reliable it would require modest calibration. A simple approach to this would be to scale the predicted probability by a constant to reduce the systematic underestimation.

Figure 9

Reliability diagrams comparing the model predicted probabilities of storms exceeding 12, 24 and 36 hours with the observed occurrence frequency. A 5-fold cross validation has been carried out and the result of each shown in red. The grey line with a gradient of 1 shows the path of a truly reliable prediction.

5 Superposed Epoch Analysis

Though Yokoyama and Kamide (1997) and Hutchinson, Wright, and Milan (2011) previously conducted a superposed-epoch analysis on geomagnetic storms with the $\mathit{Dst}$ dataset, a study using longer term $\mathit{aa}_{H}$ data is useful to help understand the intensity-duration relations described in the previous sections. Figure 10 shows a superposed-epoch analysis of the storms within each of the peak intensity classes. For each group, the $t=0$ epoch time is taken as the first data point which is on or over the lower threshold.

Figure 10

A superposed-epoch analysis for different storm intensities. The trigger to start an epoch is the first measurement greater than or equal to the lower threshold. The white line represents the median, the pink colour band represents the inter-quartile range and the purple represents the 10th – 90th percentile range. The horizontal dashed line marks the lower threshold. The plots shown are for storms of peak intensity 40 – 60 nT (top left), 60 – 80 nT (top right), 80 – 130 nT (middle left), 130 – 200 nT (middle right), 200 – 400 nT (bottom left) and $400+\mbox{nT}$ (bottom right).

The tendency for more intense storms to have longer durations is once again apparent. The duration of the median for the six bins from least to most intense is 3, 6, 12, 21, 30, and 36 hours, respectively. The smallest storms are almost symmetric in their rise/decay, but with increasing peak intensity the shape becomes increasingly “saw tooth” in nature, with a sudden rise and a long decay. Similarly, the time-of-peak intensity relative to the start of the storm varies with peak intensity. For the lower intensity storms the peak of the median occurs at the same time as the beginning of the storm. As the intensity class increases, the peak of the median storm occurs later and exhibits a more gradual build up towards peak intensity.

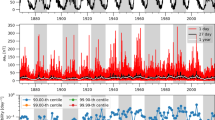
The 27-day solar rotation period (as observed from the Earth) is visible in the superposed-epoch analysis when the time window is extended, as in Figure 11. For a peak intensity bin of less than $200~\mbox{nT}$, the 27-day repeating pattern is found albeit with a much lower intensity in the repeat events. This is suggestive of corotating interaction regions (CIRs, Gosling and Pizzo, 1999), which are known to drive predictable recurrent geomagnetic activity (e.g. Owens et al., 2013).

Figure 11

Superposed-epoch analysis of small (left) and large (right) storms over a 33-day time window, to look for recurrent signatures. Left: Superposed-epoch analysis for storms with peak intensity 80 – 130 nT showing signs of 27-day repeat, indicating the presence of recurrent solar wind structures. Right: Superposed-epoch analysis for storms with peak intensities 300 – 400 nT with no 27-day repeat, indicating a relative absence recurrence.

6 Summary and Conclusions

In this study we have investigated the relationship between geomagnetic storm intensity and duration. We defined storms in the $\mathit{aa}_{H}$ index by upper and lower thresholds where the upper threshold determines whether an event is classed as a storm and the lower threshold determines its duration.

Using this definition, we found that, on average, storm duration increases with storm intensity, as expected, but in a nonlinear fashion. The median durations for the storms with peak intensity in the classes 70 – 90 nT, 90 – 110 nT, 110 – 150 nT, 150 – 190 nT, 190 – 230 nT, 230 – 300 nT, 300 – 400 nT, and above 400 nT were found to be 6, 9, 15, 18, 21, 24, 27 and 33 hours, respectively. This is similar to Vennerstrom et al. (2016) who found in the $\mathit{aa}$ index that the weakest storms have a median duration of 6 hours and the strongest have a median duration of 30 hours. The longest storm was 75 hours which is 18 hours shorter that the 93 hour storm analysed by Vennerstrom et al. (2016).

The distribution of storm duration is approximately log-normal when considering storms with peak intensity above around $150~\mbox{nT}$. The log-normal parameters, $\upmu$ and $\upsigma$, computed for a number of storm intensity classes revealed that $\upmu$ increases monotonically with storm intensity. However, this is not the case for $\upsigma$. Expressions for $\upmu$ and $\upsigma$ as logarithmic and linear functions, respectively, of intensity were found, providing a method to estimate these parameters for a given storm peak intensity. The obtained log-normal distribution can then be used to find the probability of a storm of given intensity lasting longer than a certain duration. This simple model was compared to the observed occurrence probability. Good agreement is found. As expected, more intense storms had a higher probability of lasting longer.

An analysis with reliability diagrams revealed that, while the model tends to underestimate the probability of a storm exceeding a given duration, the reliability curve follows the gradient of the $y=x$ line reasonably well. If the model was to be used operationally, the predicted probabilities could be easily calibrated to match the observed occurrence frequency.

Finally, a superposed-epoch analysis was presented shedding light on the general shape of storms. More intense storms are shown to last longer and have their peak intensity further into the storm. It was observed that 27 day recurrent behaviour becomes less apparent in larger intensity storms, most likely reflecting the sources of the solar wind driving the storm. This is likely the result of corotating interaction regions (CIRs) formed by the interaction of fast and slow solar wind (Richardson, 2004). These structures can be long lasting and repeatedly impact the magnetosphere for many solar rotations but do not cause the very largest geomagnetic storms (Borovsky and Denton, 2006; Tsurutani et al., 2006). For storms with a higher intensity, the repeating pattern disappears. This is due to the dominant driver of very large geomagnetic storms being transient coronal mass ejections (CMEs) (Richardson, Cliver, and Cane, 2001).

Future work could include a discrete-time survival analysis on storm duration. Although this adds complexity, it would provide a more rigorous structure on which to base the work. Another line of research will be to investigate whether the time history of an event could provide further information such as by using an analogue forecast approach.