Goodness of fit tests in stochastic frontier models

Abstract

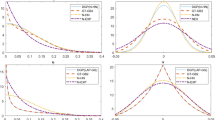
In this paper we discuss goodness of fit tests for the distribution of technical inefficiency in stochastic frontier models. If we maintain the hypothesis that the assumed normal distribution for statistical noise is correct, the assumed distribution for technical inefficiency is testable. We show that a goodness of fit test can be based on the distribution of estimated technical efficiency, or equivalently on the distribution of the composed error term. We consider both the Pearson χ ² test and the Kolmogorov–Smirnov test. We provide simulation results to show the extent to which the tests are reliable in finite samples.

Appendices

Appendix A

In this Appendix we establish Eq. 8 of the text. We write $\bar{g}(\theta_{0} ) = P - \hat{P}$, where P is the (k − 1)-dimensional vector with jth element p _j  = p _j (θ ₀) and $\hat{P}$ is the (k − 1)-dimensional vector with jth element $\hat{p}_{j} = O_{j} /n$. Also we write $V(\theta_{0} ) = \Uppi - PP^{\prime }$ where Π is the diagonal matrix with jth diagonal element equal to p _j . Now we use the fact (e.g. Abadir and Magnus (2005), p. 87) that

$$ [\Uppi - PP^{\prime } ]^{ - 1} = \Uppi^{ - 1} + {\frac{1}{{1 - P^{\prime } \Uppi^{ - 1} P}}}\Uppi^{ - 1} PP^{\prime } \Uppi^{ - 1} $$

(19)

Therefore

$$ n\bar{g}(\theta_{0} )^{\prime } V(\theta_{0} )^{ - 1} \bar{g}(\theta_{0} ) = n(\hat{P} - P)^{\prime } \Uppi^{ - 1} (\hat{P} - P) + {\frac{n}{{1 - P^{\prime } \Uppi^{ - 1} P}}}(\hat{P} - P)^{\prime } \Uppi^{ - 1} PP^{\prime } \Uppi^{ - 1} (\hat{P} - P) $$

(20)

The first term on the right hand side of (20) equals $n\sum\nolimits_{j = 1}^{k - 1} {(\hat{p}_{j} - p_{j} )^{2} /p_{j} } = \sum\nolimits_{j = 1}^{k - 1} {(O_{j} - E_{j} )^{2} /E_{j} }$. For the second term, note that $1 - P^{\prime } \Uppi^{ - 1} P = 1 - \sum\nolimits_{j = 1}^{k - 1} {p_{j} = p_{k} }$ and that $(\hat{P} - P)^{\prime } \Uppi^{ - 1} P = (\hat{P} - P)^{\prime } e_{k - 1}$ (where e _k−1 is a vector of dimension (k − 1) with each element equal to one) = $[(1 - \hat{p}_{k} ) - (1 - p_{k} )] = (p_{k} - \hat{p}_{k} )$. Therefore $n\bar{g}(\theta_{0} )^{\prime } V(\theta_{0} )^{ - 1} \bar{g}(\theta_{0} ) = \sum\nolimits_{j = 1}^{k - 1} {(O_{j} - E_{j} )^{2} /E_{j} + n(p_{k} - \hat{p}_{k} )^{2} /p_{k} } = \sum\nolimits_{j = 1}^{k} {(O_{j} - E_{j} )^{2} /E_{j} }$.

Appendix B

In this Appendix we discuss the goodness of fit test based on quantiles and its relationship to the Pearson test based on actual and expected cell counts. Suppose that we pick (k − 1) probabilities 0 < p ₁ < p ₂ ··· < p _k−1 < 1. Let the corresponding population quantiles be m ₁(θ) < m ₂(θ) ··· < m _k−1(θ), so that P(y ≤ m _j (θ)) = p _j , and let the sample quantiles be $\hat{m}_{1} \le \hat{m}_{2} \cdots \le \hat{m}_{k - 1}$. So now the test will depend on ($\hat{m} - m$), the vector whose jth element equals ($\hat{m}_{j} - m_{j} (\theta )$), and the test statistic equals $n(\hat{m} - m(\hat{\theta }))^{\prime } W(\hat{m} - m(\hat{\theta }))$ with an appropriate choice of W.

To see how this compares to the CMT test, we note that $\sqrt n (\hat{m}_{j} - m_{j} (\theta ))$ is asymptotically normal, and so it must be expressable as an average (plus an asymptotically negligible term). This is the “influence function representation,” which is given by:

$$ \sqrt n (\hat{m}_{j} - m_{j} (\theta )) = {\frac{1}{\sqrt n }}\sum\limits_{i = 1}^{n} {r_{ij} } (\theta ) + o_{p} (1) $$

(21)

where o _p (1) is an asymptotically negligible term (i.e., it converges in probability to zero), and where

$$ r_{ij} (\theta ) = {\frac{1}{{f(m_{j} (\theta ))}}}[p_{j} - 1(y_{i} \le m_{j} (\theta ))] $$

(22)

where f is the pdf of y. See, for example, Ruppert and Carroll (1980), p. 832. Therefore the test based on ($\hat{m} - m$) is equivalent in large samples to the CMT test based on the moment conditions $E[1(y \le m_{j} (\theta )) - p_{j} ], j = 1,2, \ldots k - 1$. This is an overlapping set of cells. However, it is also equivalent to consider the non-overlapping cells: $A_{1} = \{ y\left| {y \le m_{1} } \right.(\theta )\} ,\,A_{2} = \{ y\left| {m_{1} (\theta ) < y \le m_{2} } \right.(\theta )\}$, etc. The resulting test is the CMT test based on observed versus actual cell counts, as discussed in the text.

Appendix C

In this Appendix we derive analytically the variance matrix C used in the conditional moment test, for the case of a normal distribution. We wish to evaluate

$$ C_{11} = E\left( {ss^{\prime } } \right),\quad C_{12} = E\left( {sg^{\prime } } \right),\quad C_{22} = E\left( {gg^{\prime } } \right) $$

(23)

Here s = s(y,θ) is the score function for the normal distribution, given by

$$ s(y,\theta ) = \left[ {\begin{array}{*{20}c} {{\frac{1}{{\sigma^{2} }}}(y - \mu )} \\ {{\frac{ - 1}{{2\sigma^{2} }}} + {\frac{1}{{2\sigma^{4} }}}(y - \mu )^{2} } \\ \end{array} } \right] $$

(24)

and $g = g(y,\theta )$ is the vector whose jth element equals [1(y ∈ A _j ) − p _j ].

It is well known that C ₁₁ is the information matrix for the normal distribution, given by

$$ \left[ {\begin{array}{*{20}c} {{\frac{1}{{\sigma^{2} }}}} & 0 \\ 0 & {{\frac{1}{{2\sigma^{4} }}}} \\ \end{array} } \right] $$

(25)

Also C ₂₂ equals the matrix V(θ) as defined in the discussion following Eq. 6 of the text.

This leaves the submatrix C ₁₂. It is of dimension 2 by (k − 1). We will evaluate in turn the (1,j) and (2,j) elements of this matrix. To do so we make the reasonable assumption that the cells are intervals, so that A _j  = (a, b], where for notational simplicity we do not express the subscript “j” that should appear on a and b.Then element (1,j) of C ₁₂ equals

$$ \begin{aligned} {\frac{1}{{\sigma^{2} }}}E(y - \mu )[1(y \in A_{j} ) - p_{j} ] = {\frac{1}{{\sigma^{2} }}}Ey[1(y \in A_{j} ) - p_{j} ] \\ = & & {\frac{1}{{\sigma^{2} }}}Ey1(y \in A_{j} ) - {\frac{1}{{\sigma^{2} }}}p_{j} \mu \\ = & {\frac{{p_{j} }}{{\sigma^{2} }}}[E(y\left| {a < y \le b) - \mu ]} \right. \\ = & {\frac{1}{{\sigma^{2} }}}\left[ {\varphi \left( {{\frac{a - \mu }{\sigma }}} \right) - \varphi \left( {{\frac{b - \mu }{\sigma }}} \right)} \right], \\ \end{aligned} $$

where “φ“is the standard normal density function. Here we have evaluated the conditional expectation $E\left( {y|a < y \le b} \right) = \mu + {\frac{1}{{p_{j} }}}\left[ {\varphi \left( {{\frac{a - \mu }{\sigma }}} \right) - \varphi \left( {{\frac{b - \mu }{\sigma }}} \right)} \right]$ as in Johnson and Kotz (1970), equation (79), p. 81.

Similarly element (2,j) of C ₁₂ equals

$$ \begin{aligned} E\left[ {{\frac{ - 1}{{2\sigma^{2} }}} + {\frac{1}{{2\sigma^{4} }}}(y - \mu )^{2} } \right][1(y \in A_{j} ) - p_{j} ] \\ = & E\left[ {{\frac{1}{{2\sigma^{4} }}}(y - \mu )^{2} } \right][1(y \in A_{j} ) - p_{j} ] \\ = & {\frac{1}{{2\sigma^{4} }}}E(y - \mu )^{2} 1(a < y \le b) - {\frac{{p_{j} }}{{2\sigma^{4} }}} \\ = & {\frac{1}{{2\sigma^{4} }}}Ey^{2} 1(y \in A_{j} ) + {\frac{1}{{2\sigma^{4} }}}( - 2\mu )Ey1(y \in A_{j} ) + {\frac{1}{{2\sigma^{4} }}}\mu^{2} p_{j} - {\frac{{p_{j} }}{{2\sigma^{4} }}} \\ = & {\frac{1}{{2\sigma^{4} }}}Ey^{2} 1(y \in A_{j} ) - {\frac{\mu }{{\sigma^{4} }}}p_{j} E(y\left| {y \in A_{j} )} \right. + {\frac{{p_{j} \mu^{2} }}{{2\sigma^{4} }}} - {\frac{{p_{j} }}{{2\sigma^{4} }}}, \\ \end{aligned} $$

where $Ey^{2} 1(y \in A_{j} ) = p_{j} \text{var} (y\left| {y \in A_{j} )} \right. + p_{j} \left[ {E(y\left| {y \in A_{j} )} \right.} \right]^{2}$. Furthermore, $Ey^{2} 1(y \in A_{j} ) = p_{j} \sigma^{2} \left\{ {1 - {\frac{b\phi (b) - a\phi (a)}{\Upphi (b) - \Upphi (a)}} - \left[ {{\frac{\phi (b) - \phi (a)}{\Upphi (b) - \Upphi (a)}}} \right]^{2} } \right\} + p_{j} \left[ {\mu - \sigma {\frac{\phi (b) - \phi (a)}{\Upphi (b) - \Upphi (a)}}} \right]^{2}$.