Single photon two-level atom interactions in 1-D dielectric waveguide: quantum mechanical formalism and applications

Abstract

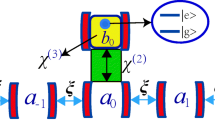
In this paper, we propose an effective model to describe the interactions between a two-level atom and scattered light in a 1-D dielectric waveguide. The proposed formalism allows us to incorporate the effect of changing optical media inside the continuum while demonstrating a non-classical derivation of Fresnel Law. We obtain the transport characteristics of the two-level system, explore its high-Q bandreject filter property and discuss the implications of radiative and non-radiative dissipation. In addition, we apply our formalism to a modified Fabry–Pérot interferometer and show the variation in its spontaneous emission characteristics with changing interferometer length. Finally, we conclude with further remarks on the link between the waveguide and cavity quantum electrodynamics.

Appendices

Appendix 1: Proof of concept

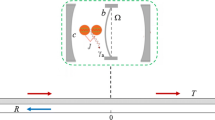
A scattering eigenstate $\mathinner {\left| {E_k}\right\rangle }$, for the Hamiltonian in (1), is given by the equation:

$$\begin{aligned} \begin{aligned} \mathinner {\left| {E_k}\right\rangle }=\int _{-\infty }^{\infty } \mathop {}\mathrm {d}x&\, \Bigg ( e^{ikx} u_R (x) + e^{-ikx} u_L (x) \Bigg ) \phi ^\dag (x) \mathinner {\left| {0,-}\right\rangle } \\&+ e_k \mathinner {\left| {0,+}\right\rangle }, \end{aligned} \end{aligned}$$

(28)

where we denote $e_k$ as the probability amplitude for the excitation of the atom, and $u_R(x)$ and $u_L(x)$ are the complex amplitudes of the right and left moving photons, respectively.

For a photon incident far form the left, $u_R(x)$ and $u_L(x)$ are defined as follows

$$\begin{aligned} \lim _{x \rightarrow \infty } u_R(x) = t, \end{aligned}$$

(29a)

$$\begin{aligned} \lim _{x \rightarrow \infty } u_L(x) = 0, \end{aligned}$$

(29b)

$$\begin{aligned} \lim _{x \rightarrow -\infty } u_R(x) = 1, \end{aligned}$$

(29c)

$$\begin{aligned} \lim _{x \rightarrow -\infty } u_L(x) = r, \end{aligned}$$

(29d)

where r and t are the reflection and transmission coefficients, respectively. It is important to note that, by ansatz, the Fourier coefficient $\bar{u}_R(k^{\prime })$ ($\bar{u}_L(k^{\prime })$) is zero for any $k^{\prime }<-k$ ($k^{\prime }>k$) to divide strictly right-moving and left-moving part of the eigenstate. It is also important to note that the modulations in $u_R(x)$ and $u_L(x)$ happen between $0^-$ and $0^+$ due to the delta-scattering potential $V \delta (x)$.

Solving the eigenvalue equation $\hat{H} \mathinner {\left| {E_k}\right\rangle }=E_k \mathinner {\left| {E_k}\right\rangle }$ and applying the slowly varying field approximation, one obtains the set of equations

$$\begin{aligned} i \hbar v_g (1-t-r) + 2 e_k V^{\prime }&= 0, \end{aligned}$$

(30a)

$$\begin{aligned} i \hbar v_g (1+r - t)&=0, \end{aligned}$$

(30b)

$$\begin{aligned} V^{\prime }t + (\varOmega -E_k) e_k&=0. \end{aligned}$$

(30c)

We can solve them to obtain

$$\begin{aligned} t= \cos b e^{ib},\quad r=i\sin b e^{ib}, \quad e_k = -\frac{ v_g}{V^{\prime }}\sin b e^{ib}, \end{aligned}$$

(31)

where the phase shift is given by $b= \arctan \left( \frac{V^{\prime 2}}{ v_g(\varOmega -E_k)} \right)$, which allows us to redrive the findings of Shen and Fan (2005), Tsoi and Law (2008) using our formalism.

Appendix 2: Sanity checks for the final result

In this appendix, two sanity checks will be performed to show the consistency of (11). The first check is for the case when there is no dielectric material present. For this case, (11) becomes

$$\begin{aligned} r&= i \sin b e^{ib}, \end{aligned}$$

(32a)

$$\begin{aligned} t&= \cos b e^{ib}, \end{aligned}$$

(32b)

$$\begin{aligned} e_k&=-\frac{v_g}{V} \sin b e^{ib}, \end{aligned}$$

(32c)

where the phase shit is $b=\arctan \{ V^2/[v_g(\varOmega -E_k)]\}$, hence resulting in the (31).

The final sanity check is regarding the conservation of probability current, or classically energy. Since there is no non-radiative decay taken into account in these calculations, the sum of transmission and reflection amplitudes is conserved such that

$$\begin{aligned} |r|^2+|t|^2 = 1. \end{aligned}$$

(33)

Note that this can be used as evidence for conservation of energy.