Abstract
A model is developed of a terbium (III) ion doped selenide chalcogenide glass fibre source that provides spontaneous emission within the mid-infrared (MIR) wavelength range. Three numerical algorithms are used to calculate the solution and compare their properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
There are many applications for mid-infrared (MIR) light sources in medicine, biology, environment monitoring, food security and defense. There are many types of light sources potentially available for MIR wavelength range, which include fibre lasers. A large effort has been invested into the development of MIR lanthanide doped fibre lasers. Many pumping schemes have been proposed for this purpose. So far, the success in this field of research is limited to operating wavelengths less than 4 μm. However, the spontaneous emission MIR light fibre sources recently realised using lanthanide ion doped multimode fibres have exceeded the 4 μm barrier and found applications in sensor technology (Starecki et al. 2015; Chahal et al. 2016). Such sources are potentially highly reliable, low cost, and robust. In this contribution using a numerical model we study the luminescence properties of selenide-chalcogenide glass fibres doped with terbium (III) ions applied as wide spectrum spontaneous emission MIR light sources covering the wavelength range stretching from 4 to 5.5 μm. Such a system was shown recently to offer a very simple pumping mechanism (Sojka et al. 2017).
For this purpose we fabricated selenide chalcogenide glass terbium doped multimode fibre and bulk samples and performed absorption and photoluminescence spectrum measurements. From the experimental results using Judd–Ofelt theory and McCumber and Fuchtbauer–Ladenburg theory we extracted the absorption and emission cross section spectra for the relevant transitions and the photoluminescence lifetimes. The details of this procedure are provided in (Sojka et al. 2017). Using an experimentally derived set of parameters we realised a lanthanide doped multimode fibre numerical model based on the rate equations’ approach. Using the model, numerical analysis was performed of the MIR spontaneous emission fibre source, whereby three methods were compared, which calculate numerically a solution of the set of ordinary differential equations. One of them consists in calculating the solution rigorously subject to the given boundary conditions while the other two are based upon an approximate approach, which relies on the assumption of the low intensity of the signal flux. The results show the limitations of the approximate approach.
2 Theory
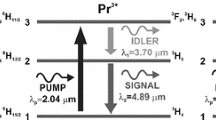
In the case of a pump laser operating at approximately 3.0 μm wavelength and a low Tb3+ doping level a three-level rate equations model of the Tb3+ ion doped into the chalcogenide glass host may be used to calculate the level populations (Fig. 1) (Sojka et al. 2017). Thus in steady state, we obtain a set of three algebraic equations that describe the system (Sojka et al. 2017):
where N is the total dopant ion concentration while the coefficients a21, a22, a23, a31 and a33 are obtained using the rate equations approach (Sojka et al. 2017):
The spatial evolution of the pump and signal photon flux are obtained from a solution of the following equations for the pump (Pele et al. 2016):
and the signal:
where ‘+’ and ‘−’ refer to forward and backward travelling waves, respectively while σxxa, e are the relevant values of emission ‘e’ and absorption ‘a’ cross sections, αx gives the attenuation coefficient, which for the signal wave was calculated by weighing it with respect to the signal spectrum (Pele et al. 2016). The weighting operation is marked with an overstrike symbol and was also applied consistently to the signal emission and absorption cross-section. η is the spontaneous emission coupling factor (Pele et al. 2016), τxr and τxnr are the relevant life times for radiative and non-radiative transitions, respectively. The pump and signal flux ϕp and ϕs are related to the respective power values via: Pp = ϕp*h*υp*A and Ps = ϕs*h*υs*A where A is the fibre cross sectional area, h—Planck’s constant, υp and υs pump and signal frequency, respectively. Equations (1) and (3a, b) are coupled and can be solved numerically in a rigorous manner subject to the relevant boundary conditions imposed at both fibre ends (Sujecki et al. 2010). Alternatively, one can assume that the signal photon flux is negligibly small in (1) and hence \(a_{21} = 0\) and \(a_{22} = - {1 \mathord{\left/ {\vphantom {1 {\tau_{21r} }}} \right. \kern-0pt} {\tau_{21r} }} - {1 \mathord{\left/ {\vphantom {1 {\tau_{21nr} }}} \right. \kern-0pt} {\tau_{21nr} }}\). This assumption allows decoupling of Eqs. (3b) from (1). Thus only Eqs. (1) and (3a) have to be solved in a coupled way whilst Eq. (3b) is solved separately. We consider two techniques in which Eq. (3b) is solved separately from (3a) (in a decoupled way) once the level populations and pump flux distribution are known. In the first technique, the signal wave distribution was calculated separately, in an iterative manner, until the boundary conditions are fulfilled. In the second case, the signal wave distribution carrying out only one pass, like in the case of an amplifier, was calculated whilst assuming zero light intensity for the backward signal wave. Obviously, such a solution does not fulfill the boundary conditions but it leads to a significant simplification of the numerical algorithm at the expense of the calculation accuracy. Therefore the main objective of this paper was to study the limitations of the approximate algorithms and their applicability for the analysis of MIR spontaneous emission light sources.
3 Results
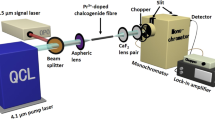
A setup was considered whereby a Tb3+ doped fibre is pumped at one side while the MIR light is collected at the other one (Fig. 2). The values of relevant lifetimes and cross sections were taken from (Sojka et al. 2017). The fibre was unstructured, of 200 μm outside diameter and doped with 0.95 × 1025/m3 Tb3+ ions, i.e. circa 500 ppmw (parts per million by weight). The pump wavelength was 2.95 μm. The attenuation coefficient at the pump wavelength (due to the presence of the OH impurities) is 2 m−1, and the weighted attenuation coefficient calculated according to (Pele et al. 2016) for the signal wave (due to SeH impurities) is 2.7 m−1. The weighted signal emission and absorption cross sections are 6.3 × 10−25 and 6.7 × 10−25 m2, respectively. The reflectivity at the fibre end for chalcogenide selenide glass is assumed to be 0.2 (Sujecki et al. 2010) while η = 0.3. The lifetime of level 3 and 2 (Fig. 1) is 5.8 and 13.1 ms, respectively while the branching ratio of level 3–2 transition is 0.11. The multiphoton transition lifetime for 3–2 and 2–1 transitions is 0.012 and 845 ms, respectively. The confinement factor for pump and cladding was assumed to be equal to 1.
Figure 3 shows the dependence of the threshold gain on the fibre length and of the material gain at the mid infrared wavelength corresponding to the maximum value of emission cross section for the Tb3+ doped fibre on the pump light intensity. These Figures show that for fibre lengths less than 100 mm, the lasing threshold cannot be reached even for very large pump powers. This confirms that for all parameters used in this study the MIR spontaneous emission source cannot reach a lasing threshold, which is consistent with the intended mode of operation of this device.
Figure 4 shows the dependence of the output power (a) and the error of decoupled solution (b) on the pump power for a Tb3+ doped chalcogenide-selenide fibre. The fibre length assumed in these simulations is 100 mm whilst the fibre end reflectivity equals 0.2. The pump wavelength is 2950 nm. Figure 4a shows that all three techniques predict qualitatively the same dependence of the output MIR power on the pump power. In fact it is quite difficult to distinguish between al three curves. Further, there are two distinct regions, which can be identified in the dependence of the MIR output power on the pump power presented in Fig. 4a. For low values of the pump power the MIR output power depends approximately linearly on the pump power (a linear region) while for large values of the pump power the MIR output power saturates to a constant value (a saturation region). Counter intuitively, within the linear region the relative error for both approximate techniques is approximately constant and does not decrease to zero for small pumping powers (Fig. 4b). However, within the saturation region the relative error decreases to zero at large pump powers for the approximate technique, which calculates the solution fulfilling the boundary conditions.
Figure 5 shows the dependence of the calculated relative error of the approximate methods: relative error = |Pexact − Pappr|/Pexact where Pexact is the MIR output power calculated using the rigorous algorithm while Pappr is the value of the output power calculated using the approximate methods. We focus only on the pump powers between 5 and 100 mW, which are most likely to occur in practice. The length of the fibre is 20 mm, which is significantly less than the value required to reach the lasing threshold (Fig. 3). The fibre end-face reflectivity was increased from 0.0002 to 0.2 to study the effect of the feedback on the predicted output power and hence also the calculation error. Figure 5 shows that in accordance with the expectations the error is reduced for low values of the fibre end reflectivity. This effect is particularly pronounced for the single pass approximate approach (Fig. 5b). However, the error for both approximate methods stops decreasing and does not reach zero at low values of the fibre end reflectivity.
The dependence of error of decoupled solution on the pump power calculated at selected values of the fibre end reflectivity R for a Tb3+ doped chalcogenide-selenide fibre for the approximate algorithm calcuating a solution fulfilling the boundary conditions (a) the single pass version of the approximate algorithm (b). The fibre length is 20 mm and the pump wavelength is 2950 nm
Figure 6 shows the dependence of the calculated relative error of the approximate methods on the pump power for selected values of the fibre length. The fibre reflectivity is 0.2 while the pump wavelength is 2950 nm. Figure 6 shows that the error is significantly reduced for short fibres for the approximate technique, which calculates the solution fulfilling the boundary conditions. For the single pass approach however, the error values remain at a relatively constant level of approximately 20%.
The dependence of error of decoupled solution on the pump power calculated at selected values of the fibre length L for a Tb3+ doped chalcogenide-selenide fibre, for the approximate algorithm calculating a solution fulfilling the boundary conditions (a) the single pass version of the approximate algorithm (b). The fibre reflectivity is 0.2 and the pump wavelength is 2950 nm
4 Conclusions
Two approximate algorithms have been compared for analysis of spontaneous emission fibre sources based on decoupling the solution of the equation for the pump wave from the one for the signal wave. As a reference, a method was used that rigorously solves the boundary value problem using a numerical method. The results show that approximate methods predict correctly the shape of the dependence of the MIR output power on the pump power. Thus using the approximate techniques below lasing threshold results in a small but non-negligible calculation errors. Counter intuitively, the values of the relative error do not tend to zero at low pump power values but do so at large values of the pump power for the technique, which calculates an approximate solution fulfilling the boundary conditions.
References
Chahal, R., Starecki, F., Boussard-Pledel, C., Doualan, J.L., Michel, K., Brilland, L., Braud, A., Camy, P., Bureau, B., Nazabal, V.: Fibre evanescent wave spectroscopy based on IR fluorescent chalcogenide fibres. Sens. Actuators B Chem. 229, 209–216 (2016)
Pele, A.L., Braud, A., Doualan, J.L., Starecki, F., Nazabal, V., Chahal, R., Boussard-Pledel, C., Moncorge, B., Camy, P.: Dy3+ doped GeGaSbS fibre at 4.4 μm for optical gas sensing: comparison of simulation and experiment. Opt. Mater. 61, 37–44 (2016)
Sojka, L., Tang, Z., Furniss, D., Sakr, H., Fang, Y., Beres-Pawlik, E., Benson, T.M., Seddon, A.B., Sujecki, S.: Mid-infrared emission in Tb3+ -doped selenide glass fibre. J. Opt. Soc. Am. B 34, 71–79 (2017)
Starecki, F., Charpentier, F., Doualan, J.L., Quetel, L., Michel, K., Chahal, R., Bureau, B., Braud, A., Camy, P., Moizan, V., Nazabal, V.: Mid-IR optical sensor for CO2 detection based on fluorescence absorbance of Dy3+:ga5Ge20Sb10S65 fibres. Sens. Actuators B Chem. 207, 518–525 (2015)
Sujecki, S., Sojka, L., Beres-Pawlik, E., Tang, Z., Furniss, D., Seddon, A.B., Benson, T.M.: Modelling of simple Dy3+ doped chalcogenide glass fibre laser for mid-inrared generation. Opt. Quantum Electron. 42, 69–79 (2010)
Acknowledgements
This Project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 665778 (National Science Centre, Poland, Polonez Fellowship 2016/21/P/ST7/03666).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sujecki, S., Sojka, L., Beres-Pawlik, E. et al. Numerical modelling of Tb3+ doped selenide-chalcogenide multimode fibre based spontaneous emission sources. Opt Quant Electron 50, 416 (2018). https://doi.org/10.1007/s11082-017-1255-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-017-1255-5