1 Introduction

Quantum cascade lasers, for the first time fabricated in the 90-ies (Faist et al. 1994), are one of the most promising compact sources of mid-infrared and terahertz radiation. Since then, many different structure designs have been proposed with the aim of improving performance, achievement of room temperature operation in the mid-infrared range (Page et al. 2001), or to extend the emission spectra to the range of terahertz wavelengths (Köhler et al. 2002).

Design and fabrication of QCL is, without doubt, one of the principal successes of wavefunction engineering. Typical structure of QCL consists of a number of elementary periods, each of which is built of layers of different semiconductors forming quantum wells and barriers, grown with precision up to a single atomic layer. The electric field in QCL device is applied in the direction perpendicular to the semiconductor layers interfaces. The operation of the device mainly depends on the perpendicular electron transport, which is ruled by electron tunneling between subsequent quantum wells and electron scatterings between states belonging to discrete, quantized subbands. Moreover, the radiative emission is achieved between superlattice subband states, hence the emission wavelength of this type of laser is not limited by the materials bandgap, but can be intentionally tuned in a wide range by precise design of constituting layers thicknesses. Precise matching of energy subbands positions, scattering rates, and optical dipole matrix elements are required for this task. To assist with such a challenge, various theoretical models have been developed such as rate equations, Monte Carlo simulations, density matrix models or non-equilibrium Green functions (NEGF) approach.

1.1 MC versus other methods used for QCL modeling

It may be interesting to briefly review various methods that are commonly used in theoretical studies of QCL.

The rate equation method (Donovan et al. 2001; Indjin et al. 2002a, b, 2003, 2004; Chen et al. 2011; Saha and Kumar 2016), often applied to the description of the properties of QCL structures is based on the semiclassical electron transport model (transport dominated by scattering) described by Boltzmann equation, which in fact, is the same physical model as in the MC method. The important point is that the algorithm is easier to implement and less demanding of computational time, at the price of an additional hypothesis about the shape of the electron distribution function, which is usually taken as a Fermi–Dirac distribution, or in even simpler models by using phenomenological values of electron scattering times between subbands.

Models entirely based on density matrix approach have been successfully used by various authors (Willenberg et al. 2003; Kumar and Hu 2009; Weber et al. 2009; Dupont et al. 2010; Terazzi and Faist 2010; Lindskog et al. 2014). Their main advantage, when compared to MC simulations, is proper accounting of electron resonant tunneling through quantum barriers and dephasing processes. However, density matrix models still rely on a number of approximations, such as scattering mechanisms based on Fermi’s golden rule and thermalized subbands.

Iotti and Rossi (2001a) employed density matrix formalism to describe electron transport in QCL and compared with results obtained by MC simulations. They have found that for the typical structures, on a subpicosecond time scale, energy-relaxation and dephasing processes are strong enough to destroy any phase-coherence effect. Consequently, the incoherent (semiclassical) description of stationary charge transport can be justified. For studies of ultrafast phenomena, as for example, time evolution of population inversion, full-quantum description should be used (Iotti and Rossi 2001a, 2003, 2005).

The NEGF method (Wacker 2002; Lee and Wacker 2002; Lee et al. 2006; Banit et al. 2005; Kubis et al. 2009; Schmielau and Pereira 2009; Hałdaś et al. 2011, 2017; Wacker et al. 2013) can provide a fully quantum mechanical treatment of electron transport, where quantum mechanical effects such as coherent tunneling and incoherent scattering effects play an important role. An advantage unique to NEGF method is the ability to capture effects such as dispersive gain and gain linewidth reductions due to correlations. Unfortunately, this approach requires very demanding computations and provides results, the interpretation of which requires additional effort.

Mátyás et al. (2009, 2010b) performed comparative studies of semiclassical ensemble MC and fully quantum mechanical NEGF methods for stationary transport in THz structure. They have found that when all contributing to transport electron states are clearly nondegenerate, the current density and spectral gain profile obtained by the MC method quantitatively agree with NEGF. In the case of bias conditions significantly below threshold, coherent multi-barrier tunneling dominates transport and MC underestimates the current density in this regime. Since, for the purpose of structures design, optimization conditions close or above threshold are studied, the MC modeling is suitable owing to less demanding computations.

When we focus on stationary electron transport in QCL, theoretical description without accounting for the coherent carrier dynamics effects is demonstrated to be sufficient (Iotti and Rossi 2001a) for many cases. That means, that the semiclassical description in the framework of the Boltzmann Transport Equation can be used and the MC technique applied to solve such problems is capable to provide qualitatively and quantitatively reliable description. However, one should be aware (Callebaut et al. 2004) that especially in the case of THz structures, in which relatively thick barriers are used, semiclassical calculations, not taking into account the effect of dephasing, would always result in overestimation of the current density and gain values.

The great advantage of MC modeling is that it relies on well-established material parameters and structure specification and the need to include phenomenological parameters can be reduced or even completely avoided. MC simulation method is relatively intuitive and thus preparation of simulation codes is straightforward. In addition, when MC simulator is developed it can be easily adapted to study different structures. MC methods need higher computational resources than for example rate equation methods, but still they are far less demanding than the need of full quantum transport models. In addition, the results of the modeling can be easily interpreted and they give microscopic insight to elucidate the QCL operation, which often is not easy to be obtained by experiments.

1.2 Examples of MC studies of QCL

Various MC studies aimed to explain measured characteristics of experimentally prepared structures or to give microscopic description of their operation have been reported. Moreover, suggestions for the optimization of structures design or proposal of new structures have been provided. Furthermore, multiple MC studies have been conducted to estimate the importance of electron–electron (e–e) interactions, various screening models, nonequilibrium (hot) phonons, photon emission and other mechanisms.

The QCL structure prepared by Sirtori et al. (1998) has been studied by means of MC modeling by Iotti and Rossi (2000, 2001b) and that research allowed quantitative investigation of the importance of various mechanisms of electron relaxation.

The prototypical design for THz QCL structure proposed by Rochat et al. (1998) was investigated by Köhler et al. (2001), and starting from such studies, two other structures were designed. The first one is based on chirped-superlattice design concept (Tredicucci et al. 1998). Another designed structure using electron–phonon scattering as the depleting mechanism was based on double-quantum well superlattice (Wanke et al. 2001). Subsequent measurements (Köhler et al. 2002) have shown good agreement between predicted and observed results.

A 3.4 THz intersubband laser device (Williams et al. 2003a) has been investigated in several MC studies. Computed by Callebaut et al. (2003) gain is in reasonable agreement with measurements but the current density is underestimated. The observed discrepancies were later explained (Callebaut et al. 2004) by adding impurities scattering mechanism omitted in their first studies. However, on the other hand, this scattering mechanism when included, leads to current and gain values overestimated when compared to experimental data. This discrepancy has been explained as resulting from lack in the semiclassical MC model of dephasing effects. Bonno et al. (2005, 2006) used this structure as a testbed for the MC research of e–e scattering and multi-subband screening models. In other research (Williams et al. 2003b) reasonable agreement of maximal operating temperature has been reported: given by MC simulation \(\sim\)85 K for surface-plasmon waveguide and \(\sim\)160 K for metal-metal waveguide versus experimentally observed values of 92 and 137 K, respectively. In addition, calculations of the gain profile of this structure have been conducted in other research (Jirauschek and Lugli 2009; Jirauschek et al. 2009, 2010).

Jirauschek et al. (2007a) theoretically compared three similar THz QCL structures based on longitudinal-optical phonon scattering depopulation, for which experimental comparison has been performed by Vitiello et al. (2005). The MC simulation demonstrated that it allows to identify the parasitic processes affecting the operation and provided a meaningful explanation of the experimental findings. Calculated inversion peak is higher than experimental estimates, also calculated gain overestimates measurement by about 40%. Authors ascribe this deviation to various effects: absence of broadening mechanisms in modeling, uncertainty of free carrier density in the device, uncertainty in determination of device effective area that is used in calculations. In addition, the shifts of the simulated inversion peak and of the current peak density are ascribed to parasitic resistance in experimental setup or deviations in sample growth processes.

Li and coworkers, in a series of papers (Li et al. 2008a, b, c, d, e, 2009a, b; Li and Cao 2011; Cao et al. 2008), extensively studied various aspects of the performance of THz structures based on resonant phonon depopulation. Agreement between experimental and theoretical results, as well as the influence of various parameters, has been demonstrated. Obtained by simulations (Li et al. 2008b) threshold bias of \({\sim }60\, \hbox {mV/module}\) and threshold current density \({\sim }541\, \hbox {A/cm}^2\) can be compared with measured values of 63.6 mV/module and \(738\, \hbox {A/cm}^2\), respectively. Calculated by Li et al. (2008c) gain peak is slightly higher than measured value, which also leads to wider range of lasing domain: calculated 10.7–13.6 kV/cm versus measured 11.5–13.9 kV/cm. In addition, a blueshift due to the Stark effect in the emission spectra with increased drive current is observed, both in experiment and in simulations.

Multiple MC studies of mid-infrared QCL structure designed by Page et al. (2001), operating at room temperature have been performed. Gao et al. (2006, 2007a) investigated influence of electron leakage to X valleys and compared the performance with other structures (Sirtori et al. 1998, 1999). We would like to notice that this particular structure design has been a basis for fabrication of QCL by Prof. M. Bugajski research group at Institute of Electron Technology, Warsaw, Poland (Kosiel et al. 2009, 2011), and extensively investigated experimentally (Pierściński et al. 2010, 2012; Bugajski et al. 2013, 2014). In collaboration with this project microscopic description of electron behavior (Borowik et al. 2010) and investigation of space-charge effect (Konupek et al. 2011; Borowik et al. 2012) have been performed by MC technique.

Temperature performance and limiting factors for high temperature operation of various designs of THz QCL have been addressed in multiple reports (Jirauschek and Lugli 2008a, b; Li et al. 2009b; Mátyás et al. 2010a; Han and Cao 2010, 2012).

One of proposals in the quest for high temperature operating THz QCL suggested application of novel semiconductor heterostructures with larger LO-phonon frequencies. Structures based on wide bandgap materials GaN/AlGaN, ZnO/MgZnO have been examined by MC simulations (Bellotti et al. 2008, 2009; Bellotti and Paiella 2010).

Fathololoumi et al. (2012) designed a THz structure, for which lasing up to 200 K has been observed. The tunneling barrier thicknesses were determined with the help of simplified density matrix model. In this research, the experimental lasing frequencies and their dependence on applied voltage are shown to be consistent with those deduced from the location of the maxima of gain spectra, calculated by MC simulation. Moreover, the calculated value of peak current is about 10–15% smaller than the experimental one and this discrepancy is explained by uncertainty of interface roughness and possible current leakage through not included in simulations high-energy states.

Further MC studies of similar structures have been conducted (Matyas et al. 2012; Jiang et al. 2014) and modified designs with variable barriers heights have been proposed with aim to increase the maximal operation temperature. Experimental studies (Jiang et al. 2014) have not confirmed operating temperatures superior to that of the reference record. To explain discrepancies between these MC results and experimental measurements several limitations of simulation model have been indicated. First, uncertainty of certain parameters as for example interface roughness, percentage of ionized donors. In addition, effects such as electron leakage to continuum states, tunneling, and aperiodicity of biased QCL structure, which are not included in MC model.

Shi et al. (2012) extracted the heat generation rate from the electron–optical phonon scattering events recorded during the MC simulation and coupled it to the nonlinear heat diffusion equation in a self-consistent manner. The model has been used to investigate the cross-plane temperature distribution throughout a mid-infrared device.

1.3 Goal and organization of the paper

The cited above examples of MC studies confirm that this method is very useful in explaining various physical mechanism governing operation of QCL. Based on such deep understanding of device physics, limiting factors of operation have been demonstrated. In addition, optimizations of existing structures design or new structures designs could be proposed with the aim of increasing maximal operating temperature or extending the emission spectral range.

Recently Jirauschek and Kubis (2014) published review article focused on technical details of various modelling techniques applied to the studies of QCL. The goal of the present paper is to provide more compact review of the research field and applications of the MC technique in this domain.

The paper is organized as follow: in the next section, we briefly describe the MC technique specific to the QCL studies. In the subsequent Sects. 3 and 4, main components of this method such as procedures to find electron states and electron scattering rates due to various scattering mechanisms are described. In addition, we review the influence of these effects on the functioning of QCL. In the Sect. 5, we briefly review types of MC simulations results that are commonly reported. Subsequently, in the Sect. 6 we mention the extension of standard MC simulations, in which also photon generation is considered. Finally, in the Sect. 7 we briefly review available extensions of the MC method focused to include important aspects of these more advanced models. In the summary Sect. 8 we also give our opinion about possible future extension of MC method used for QCL modeling.

2 MC model of QCL operation

Monte Carlo method (Jacoboni and Reggiani 1983; Jacoboni and Lugli 1989) is commonly used to numerically solve Boltzmann Transport Equation in semiconductor devices and materials. The principles of this modeling technique applied to the case of QCL structures and the main components of this theoretical approach are presented below.

Fig. 1
figure 1

Diagram of the standard Monte Carlo program flow

Full size image

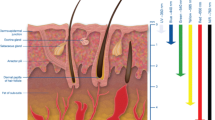
In Fig. 1, we present schematic representation of the typical flow diagram of MC algorithm used in simulations of QCL.

QCL device modeling starts with determination of electron states in the framework of the envelope function theory. An electron is completely characterized by its subband number and its in-plane momentum. The total electron energy can be derived from the subband position and the in-plane kinetic energy. On such basis, scattering rates between these states, due to various interaction mechanisms, may be calculated. Since considered electron transport is only in the direction perpendicular to heterojunctions, it is modeled as a sequence of electron scattering events between discrete energy levels, with simultaneous change of electron kinetic energy in the parallel direction. Movement of simulated particles, only in the reciprocal space, is studied. Probability of electron presence in the real space, in the direction perpendicular to the interfaces, is given by the shape of electron subband wavefunction, thus the motion in the real space is also modeled by discrete scattering events between subbands.

No electric field is intentionally applied in the direction parallel to the interfaces, and the size of device is relatively large, so uniform distribution in layers plane can be expected. Unlike in other types of MC simulations of electronic devices (Jacoboni and Lugli 1989) there is no need to include in the simulation scheme free motion part, because there is no applied field in the free motion directions parallel to layers plane.

MC simulation consists of monitoring the motion of an ensemble of superparticles representing electrons. Random numbers are used to determine, for each electron, the time between scattering events. Common procedure is to use constant time step simulation scheme. Total simulation time is divided into timesteps, which length is chosen in such a way that the total probability of electron scattering during a timestep, due to all possible interactions, is inferior to unity. In a loop over all simulated electron, a random number is taken and compared with calculated scattering probabilities for all scattering mechanisms. If scattering event is selected to happen, then, electron state is changed accordingly to the type of the chosen scattering mechanism. In addition, so-called self-scattering occurs when the random number is higher than the total probability of scattering, and then the electron state is kept unchanged. Usual procedure to speed up the calculations is to calculate the scattering rates prior to the simulation and store them in a look-up table. The scattering rates have to be calculated for each considered mechanisms, all combinations of initial and final subbands, and finally as a function of electron kinetic energy. What’s more, since scattering rates may depend on the electron distribution, which is unknown of the simulation, it may be necessary to recalculate them during simulation procedure. Such self-consistent calculations have to be performed when physical effects such as nonequilibrium phonons, screening by nonequilibrium electron gas, or space-charge effects are considered.

The Pauli Exclusion Principle forbids scattering events to the states that are already occupied by other particles. This effect is usually included to MC simulations using rejection techniques (Lugli and Ferry 1985; Borowik and Thobel 1998; Borowik and Adamowicz 2005). In most of THz lasers structures, electron density is so low that degeneracy of electron gas effect may be omitted. Doping in mid-infrared structures is usually higher, thus this effect may be important in these structures. Some reports (Scarpa et al. 2004) explicitly demonstrate degenerate condition of electron gas in QCL device.

The fundamental adaptation of the standard MC technique, specific to modeling of QCL devices is method of modeling the boundary conditions for electron transport. By these conditions, the structure periodicity should be reflected. In preliminary MC modeling electron states in single QCL period were considered and electron injection/collection was modeled by means of phenomenological parameters (Tortora et al. 1999, 2000; Iotti and Rossi 2000). Periodic boundary conditions were proposed by Iotti and Rossi (2001b) and the following approach is used by most of reported MC studies: only electrons that are present in one period of QCL are used in simulation. However, in the simulation algorithm, the states belonging to the simulated period, and two adjacent periods are used as targets of scattering events. When during the simulation, an electron undergoes transition to a state belonging to one of the adjacent periods, because of the scattering event, this electron is reinjected into the corresponding subband of the central period. The final state of its wavevector that has been determined by the kind of scattering event is conserved. Such transitions can be interpreted as electric current flowing through the modeled structure and, in each moment of the simulation, the electric charge in a period is conserved.

Although the schema, when a single structure period with periodic boundary conditions is modelled, is the most popular one, some authors report that they use more laser periods (Jirauschek 2010a; Jirauschek and Kubis 2014) as elementary cell of simulation.

At the initial stage of calculations, a number of simulation steps have to be performed with the goal to reach electron conditions close to the stationary state, and only then, the procedure collecting results is called. The MC simulation procedure terminates when convergence of the collected results is achieved.

3 Electron subbands and solutions of Schrödinger–Poisson equations

3.1 Electron states in periodic QCL structure

The first component of MC modeling are electron states in QCL structure, which are calculated within the framework of the envelope function theory. This formalism is well established and very popular as it provides a physically meaningful description at relatively low computational cost when compared to ab initio methods. Ben Daniel-Duke approach decomposes electron states to plane waves in direction parallel to heterojunctions and discrete states in perpendicular direction. States in the perpendicular direction are found as solution of Schrödinger equation, in which space dependence of electric potential and effective mass are considered. To be exact, when we consider idealized periodic structure of QCL, always, for sufficiently far distance, the value of energy level is above the maxima of quantum well barriers, as a consequence, strictly speaking there are same unbound states in the structure.

The usual procedure that is used for finding electron states in the QCL structure may be described as follows. Schrödinger equation is solved for limited number of periods, 2\(n+1\), with imposed Dirichlet conditions that wavefunctions vanish at the limits of such modeled structure. Often n = 1 so only 3 periods are considered, but in some reports higher values are used (Jovanović et al. 2004; Jirauschek 2009, 2010b) When energy levels and wavefunctions are found for such system, each wavefunction is assigned to one of structure periods according to probability of electron presence. Then, in order to impose periodicity, the electron states corresponding to the central period are replicated with suitable shift in energy and real space location and these replicated states are used to represent the states of all considered periods.

3.2 Bands nonparabolicity

Schrödinger equation used to find the electron states in QCL structure assumes parabolic dispersion relation. Such approximation may be justified for electron states close to the conduction band valley minimum. However, relevant electron energy levels in the structure may be relatively far from the bottom of the valley, thus to improve the precision of the results, band nonparabolicity should be considered (Jirauschek and Kubis 2014; Vukovic et al. 2014a, b). This is usually introduced by the concept of effective mass depending on energy and dedicated Schrödinger equation solver, accounting to band nonparabolicity has to be used as explained below.

We would like also to notice, that bands nonparabolicity is accounted not only in the solution of the Schrödinger equation. This effect is also included in the formulas defining electron scattering rates and in determination of the electrons kinetic energy after interaction.

3.3 Space-charge effect

Electric potential for which Schrödinger equation is solved consists of repeated quantum wells and barriers defined by the band offset of semiconductor layers and tilted under the action of the applied electric field. Following phenomena that should be considered is modification of electric potential profile caused by nonuniform distribution of electric charge along QCL structure, when separation of dopants and free electrons occurs. This effect is especially important for studies of mid-infrared QCL structures, for which doping level is usually sufficiently high and significant band bending is observed.

To include this space-charge effect, firstly, the electric charge profile has to be determined along the structure. Positions of ionized impurities are given by the structure design while charge of free electrons can be calculated when electron populations on subbands, and shapes of corresponding wavefunctions are known. Then, by the solution of the Poisson equation, electric potential profile induced by the electric charge distribution in the structure is determined. That leads to the need of self-consistent solution of coupled Schrödinger and Poisson equations.

Populations of electron states are not known before completing MC simulation. Approximations (Cassan 2000; Li et al. 2008e) based on Fermi–Dirac statistics are used to determine electron sheet density on subbands and such estimate value is used to solve Schrödinger–Poisson equations self-consistently only once prior to MC simulation (Manenti et al. 2003; Bonno et al. 2005; Li et al. 2008e). Modified algorithm has been proposed (Borowik et al. 2012) and it requires preliminary calculation of subbands populations by rate equation method. More precise studies require self-consistent solution of Schrödinger–Poisson equations and MC simulation of electron population on energy subbands (Jirauschek and Lugli 2009; Jirauschek et al. 2009, 2010). Importance of such approach in studies of bound-to-continuum THz lasers has been demonstrated, in which the nonuniform charge distribution leads to more significant band bending than in comparable resonant phonon depopulation structures.

3.4 \(\varGamma\) and X valleys

In some structures electron transport description may require inclusion of upper valleys and electron leakage from \(\varGamma\) to X valleys has been reported (Gao et al. 2006, 2007a, b, 2008a). In such a case, electron states in upper valleys also have to be found. In these reports the \(\varGamma\) valley states in two adjacent stages have been obtained by solving the Schrödinger equation using the \(\mathbf k \cdot \mathbf{p}\) method and the X valleys ones have been obtained by solving the effective mass equation.

In is worth to notice, that including of electron leakage to X valley allowed Gao et al. (2006) to explain the ability to operate at room temperature of mid infrared QCL (Page et al. 2001) when compared with structures with lower quantum well barriers (Sirtori et al. 1998, 1999). Calculated in this study current density \(J_{th} = 14.4\, \hbox {kA/cm}^2\) is in good agreement with measured \(J_{th} = 16.7\, \hbox {kA/cm}^2\).

3.5 Numerical solutions of the Schrödinger–Poisson equations

There are several numerical methods that are used for solving coupled Schrödinger-Poisson equations in the context of QCL structures studies. The first requirement that is very important is accuracy of the solution, since changes of layers thickness by a few atomic layers significantly modifies electron wavefunctions. In addition, computational cost has to be considered, especially for applications when multiple iterative solutions are required. The simplest technique that is widely used in QCL design work is shooting method (Harrison 2006). Finite difference algorithm may also be used (Juang et al. 1990; Cassan 2000), in which bands nonparabolicity is included in iterative approach (Jovanović et al. 2003; Thobel et al. 2003; Cooper et al. 2010). Other type of numerical method used for such problems is transfer matrix (Ando and Itoh 1987; Jonsson and Eng 1990; Jirauschek 2009).

3.6 Electron states and coherence

We have to admit that there is an issue with presented model, which was initially noticed by Callebaut et al. (2003). The Schrödinger equation is solved for a region of 3 or more structure periods and fully coherent picture of the subbands and corresponding wavefunctions is assumed. Localization and dephasing scatterings are not included in such model. For certain very narrow bias ranges, small anticrossing between levels leads to their interaction, even if these subbands should be weakly coupled due to spatial separation. Obtained electron states are unrealistically extended over wide range of space. Therefore, in the obtained MC results very sharp current spikes appear, which have no physical meaning. In most of reports, they are removed from presented results (Callebaut et al. 2003; Jirauschek et al. 2007a; Jirauschek and Lugli 2008a).

4 Electron scattering mechanisms in MC modeling of QCL

Another theoretical component of MC modeling is calculation of electron scattering rates due to various physical mechanisms. In this section, we enumerate the main ones that are responsible for QCL operation and are commonly used in modeling.

4.1 Electron–phonon scattering

Electric current flowing through QCL structure is owed to scattering between subbands and one of predominant mechanisms is emission of longitudinal optical phonons. Furthermore, operation of resonant phonon THz QCL is based on this interaction process. Electron interactions with LO phonons is the dominant phonon scattering mechanism, acoustic phonons (Nelander and Wacker 2009a) play only a secondary role in QCL.

In most of MC studies bulk optical phonon modes are used, with scattering rates calculated in the framework of Born approximation and Fermi’s golden rule. This well-established approach has been used for studies of two-dimensional electron gas in semiconductor structures. Due to the presence of hetero-interfaces, the electron–phonon scattering may be quite different from that of bulk material. The confining potential changes the electron wavefunctions and the phonons show a multimode dispersion. The validity of bulk phonons approximation on electron transport in the QCL structures has been addressed by Compagnone et al. (2002a, b) and later more detailed investigations have been performed by Gao et al. (2008b, 2008c).

It has been found, that at least for GaAs based structures, the inclusion of phonon confinement enhances the electron-LO scattering rates and consequently the output current. However, the change of obtained current magnitude is relatively small, so the computationally much simpler bulk phonon model can be used.

The second commonly used approximation is assumption about phonons distribution, which is expected to be thermalized with the number of phonons given by the Bose–Einstein distribution. When experimental measures are performed, even though the (external) temperature is controlled, the temperature inside the device in operation may be much higher. Therefore, for fair theory/experiment comparisons, the model should account for such self-heating when calculating phonon population. This is especially important for the cryogenic conditions.

Electron transport down to the subband ladder in quantum cascade is related to high LO-phonon generation. When this is combined with limited thermal conductivity, theoretical concerns of development of transport models including nonequilibrium phonon system are manifested. Rigorous treatment of this problem should include both the electron and phonon coupled Boltzmann Transport Equations (Iotti et al. 2010; Iotti and Rossi 2013). The inclusion of both acoustic and optical modes makes this task quite demanding from computational perspective.

Paulavicius et al. (1998) and later Lü and Cao (2006a) included nonequilibrium polar optical phonons to their studies of resonant phonon THz QCL structure (Liu et al. 2005) using the relaxation time approximation (Lugli et al. 1987; Fischetti and Laux 1988). The evolution of the LO phonon population is followed, and as the number of phonons varies with time, modification of electron–phonon scattering rates should be considered. Over time, LO phonons decay into other modes with phenomenological relaxation time. Significant increase of current density is observed in MC results when hot phonons are included, but only small influence on the population inversion (Lü and Cao 2006a) is noticed. In addition, results obtained by other MC and experimental studies (Iotti et al. 2010; Vitiello et al. 2012; Iotti and Rossi 2013) confirm importance of nonequilibrium phonons in low temperatures. Shi and Knezevic (2014) demonstrated the importance of hot phonons on mid-infrared structure operation mainly in temperatures below 200 K. For chirped superlattices QCL, reported by MC studies (Compagnone et al. 2002a, c) hot phonon influence is negligible. In addition, in some other studies of THz structures, when electron densities are low, the effect of hot-phonons is not important (Jirauschek et al. 2007a; Jirauschek and Lugli 2008a).

4.2 Electron–electron scattering

In the context of electron transport in QCL only the short-range part of the Coulomb interaction (Pines and Bohm 1952) is included, neglecting electron–plasmon scattering, which is justified since electron density is usually low. Short-range e–e scattering is modeled in the framework of Fermi golden rule with Hamiltonian given for screened Coulomb potential.

The modeling of e–e scattering mechanism in MC simulation encounters many difficulties of both technical and theoretical nature. Scattering rates depend on the distribution function, which is an unknown of the simulation, and thus has to be treated in a self-consistent manner, generally using a rejection technique (Goodnick and Lugli 1988). Another issue related to e–e modeling in QCL is that it requires calculation of scattering rates between huge number of scattering states, for which direct evaluation of all needed form-factors may lead to prohibitive computational cost. A technique based on Fourier decomposition of wavefunction (Bonno et al. 2005) can be applied.

Modeling of e–e interactions also requires consideration of distinction between processes when interacting electrons have the parallel or antiparallel spin (Moškova and Moško 1994; Moško et al. 1995). Due to particles indistinguishability exchange effect has to be accounted for in calculation of scattering rates and significantly modifies obtained results (Jirauschek et al. 2009, 2010), especially for bound-to-continuum THz structures design. Intersubband e–e scattering between the closely spaced energy levels in the minibands is the dominant gain broadening mechanism and proper model for the spin-related exchange effect and screening is required to obtain meaningful results of gain profile.

Another issue that should be described is modeling of nonparabolicity in e–e scattering. Bonno and Thobel (2008) proposed MC procedure allowing accounting for this effect. The influence of nonparabolicity on population inversion is found to be small, which leads to conclusion that the high CPU time required by a complete model of nonparabolicity in e–e interactions can be safely avoided. However, when internal quantities such as subband temperatures are investigated, it is highly recommended to consider it.

Important distinction can be noted. Despite the similarity between mid-infrared and THz QCL, there is an important difference in the dynamics of electron transport. When we compare the energy of radiative transitions \(\hbar \omega\) with LO phonon energy \(\hbar \omega _{LO}\) for mid-infrared devices \(\hbar \omega >\hbar \omega _{LO}\) while for THz devices energy levels separation is less than phonon energy. Therefore, such states are strongly coupled, and Coulomb scattering processes can play a prominent role. However, also in mid-infrared structures, the importance of e–e interactions cannot be neglected. Even if pure intersubband transport by e–e scattering is minimal, this mechanism leads to thermalization of electron distribution within subband, as well as pure energy transfer between various subbands (Iotti and Rossi 2001b; Borowik et al. 2012), which significantly modifies the number of electron scattering events and, as a sconsequence, the resulting electron transfer between subbands. Hence, influences all device operating parameters.

4.3 Electron-impurity scattering

Both electron–electron and electron-impurity (e-imp) interaction have nature of Coulomb interaction. Very small subband separation in THz structures makes important the scattering processes for which small energy transition is favored. Those are e–e or e-imp or electron-interface roughness scattering.

Impurity scattering depends on the distance between electron and impurity and is most effective for scattering between subbands whose wavefunctions are spread close to doped layers. One can compare relative importance of e–e and e-imp scattering (Callebaut et al. 2004; Dür et al. 1996). When we consider intersubband processes, e-imp scattering usually dominates over e–e scattering and significantly increases electron gas heating when final subband after scattering lays lower in energy scale than the starting subband. In addition, since e-imp scattering is an elastic process, it does not contribute to intrasubband carrier thermalization.

Callebaut et al. (2004) included e-imp scattering to explain current density of 3.4 THz QCL (Williams et al. 2003a) and obtained \(J = 950\, \hbox {A/cm}^{2}\) which can be compared with experimental value of \(J = 915\, \hbox {A/cm}^{2}\). Calculations (Callebaut et al. 2003) without this scattering mechanism significantly underestimated the current density giving \(J = 580\, \hbox {A/cm}^{2}\). Obtained by this simulation gain slightly exceeded upper limit of measured magnitude, which has been attributed to the neglect by the MC model of wavefunction localization. Similarly, for other studied THz QCL structure (Williams et al. 2001) inclusion of e-imp scattering has been necessary to obtain expected current density.

4.4 Screening

Electron interactions in the presence of other electrons is too complicated to be solved using exact multi-electron Hamiltonian. The treatable modeling consists of the assumption that bare interactions between two particles can be completed by the influence of other electrons through introduced screening effect. Modeling of screening is especially important for Coulomb interactions, for which screened potential is used in interactions Hamiltonian.

Dealing with two-dimensional screening phenomena in multi-subband systems, such as QCL, is a formidable task, requiring huge computational resources for evaluating the dielectric matrix. For this reason, screening has to be treated in an approximate manner.

One of commonly used assumptions is that only the most populated subband contributes to the screening (Bonno et al. 2005; Lü and Cao 2006a). However, it has been shown by Lee and Galbraith (1999) that the use of a single subband dielectric function for modeling intersubband transitions leads to erroneous screened potential matrix elements. These authors argued that in multi-subband systems, one should account for intersubband polarizability, which, in rigorous approach, needs to solve the full \(N_{sb}\times N_{sb}\) equation system. As one can imagine, for case of QCL, this task is numerically intractable owing to the large number of levels.

Bonno et al. (2005) presented approximated model, which, although quite simple, allows describing properly the behavior of both intra- and intersubband matrix elements of the Coulomb potential. In their approach, the screening should be calculated self-consistently during the simulation. That allows to account for the nonequilibrium nature of the distribution, approximated by subband effective temperature.

Lü and Cao (2006b) proposed different approximation of multi-subband screening in QCL. They introduce a modified single subband model, which accounts for different effective temperatures in all subbands.

We can also report some other MC studies, in which other screening models have been mentioned. Callebaut et al. (2004) report to use in their studies of e–e and e-imp scattering another, nonequilibrium, multi-subband screening model (Ando et al. 1982). In addition, dynamic screening model (Maldaque 1978) is reported to be used in some preliminary MC research on QCL (Compagnone et al. 2002a; Callebaut et al. 2003; Manenti et al. 2003).

Nelander and Wacker (2009b) studied various screening models and temperature aspects in QCL structures. With increased temperature, electron screening decrease and that causes an increase of scattering in QCL. When the screening length is of the order of the laser period or longer, the isotropic bulk screening model can be safely used. This situation is common for typical terahertz QCL. They also conclude that screening effect is much more dependent on average subband temperature than on electron redistribution among the different subbands. Mid-infrared laser structures are typically much highly doped, so the screening length is of the order of the layers and microscopic random phase approximation model is necessary. The mentioned work is not based on MC simulations.

Recently, the effect of screening on electron-LO phonon interactions has been studied (Ezhov and Jirauschek 2016) in mid-infrared and THz structures. As the strength of the screening is determined by the electron density it has less importance in THz structures in which usually lower doping is used. It has been reported that screening is responsible for 10–15% reduction of calculated current density and 15% reduction of the output power for mid-infrared structure (Bismuto et al. 2010), when compared to simulations without screening. For THz QCL design (Fathololoumi et al. 2012) inclusion of LO phonon scattering screening reduces current of about 4–7% and optical power of 5–8% depending on temperature. For both compared structures, an agreement with available experimental data is found. However, as it has been admitted, due to the uncertainty of several parameters such as interface roughness values, the significance of comparison with experimental data is limited.

4.5 Alloy scattering

The crystal lattice in ternary materials is not exactly a zinc-blende structure. Atoms are randomly distributed in sites and distorted potential influences electron transport. This mechanism of electron interaction has been commonly used in most of reported MC studies of QCL. However, to our best knowledge there is no systematic MC investigations of the influence of this particular type of interactions.

One can find other theoretical or experimental studies, in which this scattering is studied in more details. Vasanelli et al. (2006) showed that the alloy scattering is a very efficient relaxation mechanism and that the elastic scattering is responsible for 40% of the total scattering rate in investigated GaInAs/AlInAs structure. Regnault et al. (2007) reported calculations of broadening effects in a QCL due to alloy scattering. Kubis et al. (2010) demonstrated optical gain degradation in THz QCL due to the alloy scattering.

4.6 Interface roughness

Interfaces between material layers are not ideally flat to the degree of atomic layer. The roughness depends on the technological process of superlattice growth and thus varies between samples. As a result, this scattering mechanism has to be implemented with help of phenomenological parameters (Ando et al. 1982; Sakaki et al. 1987). The common description of interface roughness is based on two parameters: mean height \(\varDelta\) and correlation length \(\varLambda\) (Leuliet et al. 2006). In simulations of GaAs-based terahertz lasers, often values of around \(\varDelta = 0.1\, \hbox { nm}\) and \(\varLambda = 1\, \hbox {nm}\) are used (Kubis et al. 2008; Nelander and Wacker 2008). For simulations of InGaAs/InAlAs based structures (Mátyás et al. 2011; Singh and Kamoua 2014) experimental results suggests \(\varDelta = 0.06\, \hbox {nm}\) and \(\varDelta \varLambda \approx 1\, \hbox {nm}^2\).

Interface roughness can considerably affect QCL operation (Jirauschek and Lugli 2009; Chiu et al. 2012). The effect of interface roughness on QCL operation is similar to the influence of the impurity scattering. It leads to increased broadening and reduced gain profile height and it strongly depends on the assumed values of \(\varDelta\), \(\varLambda\). The THz structures based on bound-to-continuum design are more sensitive to interface roughness than phonon depopulation based structures. This can be explained by the fact that the wave functions in the minibands tends to be less localized and thus extends over more interfaces (Jirauschek and Lugli 2009).

5 Types of outputs from MC simulations of QCL

For the readers convenience it may be useful to briefly review what kinds of output results are usually obtained by the MC simulations of QCL.

5.1 Electron subbands populations, distribution function and effective temperature

The first parameter that is directly obtained from simulation is electron population or equivalently the electron sheet density \(\sigma _i\) on energy levels, which is directly obtained by just counting during simulation the number of electrons present in the considered subbands. In addition, temporary evolution of this parameter can be extracted, or when the static conditions value is of interest, average over longer simulation time is used to obtain the results with less numerical noise.

Likewise, electron distribution function on each subband \(f_i (\varepsilon )\) can be easily obtained. One can collect during the simulation the number of simulated particles in a grid of energy cells. We can safely assume cylindrical symmetry, thus only the dependence on energy, and not on both wavevector components, is sufficient.

Although the electron distribution function does not always follow the form of Maxwell–Boltzmann or Fermi–Dirac distributions, still such approximation is used with the concept of electron effective temperature. For example, electron effective temperatures have been measured in THz QCL structure (Vitiello et al. 2005), and results of MC simulations have been presented (Jirauschek et al. 2007b). Effective temperature \(T_i\), which may be different in each subband can be calculated as measure of the broadening of the distribution function \(f_i (\varepsilon )\).

5.2 Electron scattering times and current density

MC method also offer very intuitional method of calculation of the electron scattering times between subbands and electron lifetimes on subbands, which is achieved by counting the number of scattering events that occurred during the simulation between the subbands of interest. This method accounts in a natural way of nonequilibrium distribution function.

Similar intuitive concept of calculations is used to obtain the current density flowing through the structure. One just has to count the number of electrons, which during simulation are scattered to adjacent periods and accordingly to assumed periodic conditions are reinjected to corresponding subbands of the central simulated period.

5.3 Optical gain

The first parameter that is commonly used in discussion of the QCL gain performance is the oscillator strength between lasing subbands. When we have the dipole moment \(z_{ud} = \langle u | z | d\rangle\) between wavefunctions and \(\omega _{ud}\) angular frequency between considered states, which is given by levels energy separation, then the dimensionless oscillator strength of transition between upper u and lower d lasing states is given by \(f_{ud} = 2m^* \omega _{ud} | z_{ud} | ^2/\hbar\).

This parameter can be used to calculate the gain peak g, which is given by the expression (Callebaut et al. 2003) \(g = (\sigma _u-\sigma _d ) e^2 f_{ud} / (2\pi L_p c \epsilon _0 n_0 m^* \varDelta \nu )\), where \((\sigma _u-\sigma _d )\) is electron sheet population difference between lasing levels, \(L_p\) is the length of one laser period, \(n_0\) is the refractive index of the media, c is the light velocity, and \(\varDelta \nu\) is the spontaneous emission linewidth (FWHM - full width at half maximum of electroluminescence spectrum below threshold).

It may be interesting to follow the intuitive approach by Hu et al. (2004, 2005), as it partially explains the need of calculation of listed above parameters. Only three parameters determining peak gain: population inversion, oscillator strength and emission linewidth are subject to structure design. It has to be noted that \(\varDelta \nu\) is largely limited by lifetime broadening. To achieve robust laser operation the lifetime of the lower lasing state should be kept as short as possible, which is opposite to the requirement of narrowing the linewidth. Therefore, more attention is paid to optimize two other parameters. When \(\omega _{ud}\) is fixed by expected value of the lasing frequency, the oscillator strength value can be adjusted by designing the value of \(z_{ud}\) which in turn is determined by the spatial overlap of lasing subbands wavefunctions. Thus, spatially vertical radiative transitions are preferred in order to achieve high value of oscillator strength. The population inversion is mainly determined by lifetimes of both lasing states and high values of the inversion can be achieved for short lifetime of lower state, long lifetime of upper state and long lifetime of nonradiative transition from upper to lower state \(\tau _{ud}\). On the other hand \(\tau _{ud}\) can be increased at the cost of reduced oscillator strength. \(\tau _{ud}\) also depends on the electron distribution function (effective temperature) and energy levels separation.

The spontaneous emission linewidth \(\varDelta \nu\) that is used in the above equation determining the optical gain is usually taken as phenomenological parameter extracted from the real devices measurement. We would like to note that, as Li et al. (2009b) demonstrated, the calculations of gain peak require to account for changes of \(\varDelta \nu\) with temperature. Only when \(\varDelta \nu\) broadening with increase of temperature had been included, the agreement with experimental results has been achieved. As it has been demonstrated by Jirauschek and Lugli (2009) \(\varDelta \nu\) also can be extracted from the MC simulations by counting the number of occurring scattering events of intersubband transitions and assuming Lorentzian shape of electron states lifetime broadening. Obtained by such method (Jirauschek et al. 2009) \(\varDelta \nu = 0.85\, \hbox {THz}\) is in good agreement with value of 0.9 THz obtained by electroluminescence measurement (Scalari et al. 2003). Using such more advanced simulations it is possible to calculate the gain spectra, which is obtained by aggregating individual contributions to the gain from all simulated electrons and all possible intersubband transitions. To validate this approach, the ratio of FWHM at 110 and 10 K for 3.5 THz bound-to-continuum structure (Scalari et al. 2003; Faist et al. 2004) has been compared with simulations results (Jirauschek and Lugli 2009). That gives theoretical 1.16 versus experimental 1.18 values respectively. For phonon depopulation structure (Callebaut et al. 2003; Williams et al. 2003a), theoretical magnitude of FWHM of 0.72 THz agrees with experimentally measured 0.88–0.97 THz.

Further development (Jirauschek 2010b) of this method allows extension of the standard MC model of electron transport by self-consistent coupling to photon field generated in the laser structure. We review application of this method in the subsequent section.

6 Electron–photon interactions in MC modeling of QCL

Jirauschek (2010b) demonstrated MC simulation procedure allowing including stimulated emission processes as additional mechanism influencing the electron transport in QCL structure. From computational point of view, it may be treated as an additional scattering process resulting in intersubband electron transitions. It is important to notice, that scattering rates due to stimulated emission depends on the intensity of light inside cavity, and such parameter should be evaluated self-consistently during MC simulation. Iotti and Rossi (2005) proposed to use in MC simulations discrete photon population, but as they noticed, due to statistical fluctuations, it is very difficult to reach satisfactory accuracy of the results. Another approach (Jirauschek 2010b) consists of using classical modes intensities, evaluated over time. In general, multimode light intensities can be evaluated in simulations, however such approach is computationally tedious, so further approximation of single-mode operation is used in the studies (Jirauschek 2010b). One of the main results of such extended MC simulation scheme is the ability to calculate laser optical power. However, the stimulated emission processes also strongly contribute to the calculated current density.

Presented approach has been extended (Jirauschek 2010a) to account for spontaneous emission and black-body radiation, which allowed studies of intrinsic linewidth in resonant phonon THz QCL. It has been demonstrated that thermal photons contribute significantly to linewidth broadening at elevated temperatures. For the investigated structure of 3 THz QCL, a linewidth enhancement factor of \(\alpha \approx\) 0.5 is found, which is in excellent agreement with experimental results (Green et al. 2008).

Mátyás et al. (2011) performed calculations of photon-induced transport in mid-infrared QCL structures (Bai et al. 2010). MC results of optical output power and wall-plug efficiency (WPE) are in very good agreement with experiment: maximum simulated WPE is found 49% versus experimental value of 51%. MC results also allowed to investigate microscopic features that are hard to investigate by experiment, such as intrasubband electron distribution.

Jirauschek et al. (2013, 2015) also used this method to perform the studies of terahertz frequency generation in QCL, which happens when two close radiation frequencies \(\omega _1\) and \(\omega _2\) are used to pump a nonlinear optical medium, generating THz radiation at a frequency \(\omega = \omega _1 - \omega _2\). To validate the model, Jirauschek et al. (2013) obtained by simulations current of 11.7 A, compared with experimental value of 12 A. In addition, emitted powers of two modes 1.55 and 0.6 W are found in agreement with experimental values of 1.2 and 0.8 W. Obtained THz radiation output power of 12 \(\mu\)W and conversion efficiency of \(13\, \mu \hbox {W/W}\) have been compared with values found in experiment of \(8.5\, \mu \hbox {W}\) and \(10\, \mu \hbox {W/W}\). Simulations also confirm experimental estimates of nonlinear susceptibility and the waveguide loss. In other simulations (Jirauschek et al. 2015) power of radiation and conversion efficiency are also in good agreement with available experimental data. In addition, moderate bias dependence of the nonlinear susceptibility is consistent with experimentally observed broad optical bandwidth of the nonlinearity.

Bhattacharya et al. (2012) used different model based on combined MC, density matrix and rate equations approach describing electron–photon interactions and stimulated emission. They demonstrate that inclusion in the model of photon emission process is vital for proper explanation of electron transport, especially for diagonal designs THz QCL structures. They also studied photon modes competition and demonstrated that the convergence of electron populations on subbands is much faster than photon intensity saturation.

7 Quantum transport extensions of semiclassical MC model of QCL

Described in present review MC method is based on semiclassical physical model of electron transport. Several reports should be noticed, in which more sophisticated models, which include quantum extensions to semiclassical MC picture are presented.

As mentioned in Sect. 3.6, the theoretical framework used to describe electron states leads to some fundamental issues, caused by use in modeling electron wave functions unphysically extended over large region of space. To overcome this limitation Callebaut and Hu (2005) proposed a hybrid MC and density matrix simulations model. In their approach, coherent description of electron transport model is used for transport through the injector barrier, and semiclassical model is used inside laser period. The only phenomenological parameter that is needed in this approach is the pure dephasing time. Proposed model was compared with experimental results of THz structures (Williams et al. 2001; Kumar et al. 2004) and full quantum models (Banit et al. 2005) and satisfactory improvement of results was demonstrated.

Another extension for including quantum effect to semiclassical MC modeling was proposed by Matyas et al. (2013). In standard MC approach discrete subbands energies are used and there is no broadening mechanisms included in the Fermi’s golden rule. One of consequences that are reported (Mátyás et al. 2010b) is an underestimation of the simulated currents in the low-bias range. Model based on the replacement of the Dirac delta in Fermi’s golden rule by a Lorentzian function of finite linewidth was implemented. Presented results demonstrate vital importance of the collisional broadening in the correct modeling of the current density in the low-bias conditions. When the lasing regime is considered this effect increases parasitic current and reduces optical gain and output power, which is in reasonable agreement with available experimental data (Kumar et al. 2011; Fathololoumi et al. 2012). In addition, it has been indicated, that inclusion of collisional broadening into MC simulations allowed to notice in power-current curve the feature resembling negative differential resistance that is observed in experiment (Kumar et al. 2011).

Presented above extensions of the MC method allow to enlarge its scope of application to conditions, in which more subtle quantum effects play important role.

8 Summary

8.1 Features of MC modeling of QCL

In present paper, we have reviewed Monte Carlo studies of QCL, based on the semiclassical Boltzmann Equation formalism, assuming that the electron transport is dominated by scattering between, calculated beforehand, fixed quantum states. Therefore, coherent effects are neglected. This approximation, has been discussed, and has been shown to be acceptable in most circumstances. Some notable exceptions include hybrid MC and density matrix models.

Another crucial assumption used in most of the mentioned studies is the ideal periodicity of the structure. Assuming that the basic pattern is infinitely repeated, allows one to consider only a small part of the structure, generally the basic cell and one or a few adjacent cells, reducing drastically the complexity of the device model. Moreover, assuming periodic (“circular”) boundary conditions with immediate reinjection of particles leaving the system, allows overlooking the awkward issue of coupling the device to external circuit through contacts.

This standard approach has been widely used and most of MC simulations share the above-mentioned features and differ essentially by the list of considered scattering mechanisms and details of the evaluation of scattering rates.

This kind of standard model has been proven extremely powerful to study a wide variety of QCL devices, enabling to predict performance, measurable quantities (current, optical power) and giving insight into microscopic behavior, without requiring any adjustable parameters. While the primary applications concerned devices emitting in mid-infrared, MC simulation has also appeared to be successful to describe a variety of terahertz QCL, based on different structures and operation schemes, thereby proving its extreme versatility.

We think that this technique will remain extremely valuable to support the future development of QCL and to help facing the current challenges. Among them, the quest of more compact devices, more widely tunable and operating in a wide temperature range. This last point is of special importance for THz QCL, the applications of which remain limited by the need of cryogenic cooling.

Finally, we think that some other difficulties in comparison of MC results with experimental data, which are mentioned in the paper, should also be listed here: Uncertainty of some important parameters, which are used in simulations as for example, interface roughness parameters that depend on the sample growth process, magnitude of free carrier density in the device that depends on the level of donors ionization, uncertainty of laser effective area that is used in calculations of parameters to be compared with experiments, parasitic resistance in experimental setup, uncertainty of temperature inside modeled device, and many others.

8.2 Possible future extension of MC method used for QCL modeling

In our opinion future research trends in MC modeling might concern the following issues:

Improving the description of the optical field in the cavity and its coupling with carriers. It would be useful to describe multimode behaviors, electromagnetic losses, etc.

Making the model “more self-consistent”, better accounting for the effect of charge redistribution during simulation, for none-quilibrium phonons, for thermal issues and device heating etc.

Coping with some quantum coherent effects. This point is especially embarrassing since the MC method is semiclassical by nature and full account for quantum coherence would certainly require choosing another method, such as NEGF. However, it is possible to account for some quantum effects in an approximate, semi-empirical way: for example finite coherence length of wave function, or finite lifetime of energy levels, tunneling, etc. Various attempts have been made but we think that much remains to be done.

Another basic assumption that remains to be questioned is the infinite periodicity of the structure (Kubis and Vogl 2009). Even if one assumes that the sequence of material layers repeats identically, the periodicity may be broken when the device is under bias, with possible creation of space charge regions. This phenomenon is known to have a profound influence on device behavior (Dhar et al. 2014). The propagation of such domains and the resulting unstable behavior is often mentioned to explain why a QCL device, in some regime, does not work as expected. Of course, the detailed modeling of the whole structure containing hundreds of elementary periods is beyond reach. However, one can envisage dividing the structure into small pieces, which may contain a net electric charge. Each piece could be treated by MC simulation whereas the coupling between them would be described at some approximate level.

A slightly different approach would involve performing a large set of MC simulations for a wide range of configurations and to use them to supply parameters to a rate equation model. In that approach MC model could describe the “local” behavior at the scale of a few laser periods, whereas the global behavior could be described by an approximate method.

Coupling different models is a promising way to study new systems the operation of which involves phenomena occurring on different scales in space and time. The MC simulation being situated in term of complexity between “macroscopic” rate equations techniques and full quantum theories such as NEGF, it appears as an essential component in that context. Interesting example of multiscale simulations is coupling of MC simulations to thermal models (Shi et al. 2012, 2016; Mei et al. 2017) of QCL devices.