Abstract
Numerical modelling of a Pr3+-doped chalcogenide glass fibre laser is presented in this paper. The spectroscopic parameters are extracted from in-house prepared Pr3+ doped selenide-chalcogenide glass samples and used in the modelling. In this contribution, particular attention is paid to a novel resonant pumping scheme. The modelled laser performance is tested as a function of pump wavelength, fibre length, signal wavelength, fibre background loss and output coupler reflectivity. The modelling results show that the proposed resonant pumping scheme, which might be achieved in practice using a high power QCL pump, allows for a significant reduction in the laser threshold and an increase in the laser efficiency. A slope efficiency of 54% is calculated when the fibre losses are brought down to 1 dB/m.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
High power mid-infrared fibre laser sources with emitting wavelengths covering the range stretching from 4 to 5.5 μm offer many applications in remote sensing, medicine and defence (Seddon 2011, 2013; Pollnau and Jackson 2008; Jackson 2012). However, in order to access these wavelengths, low phonon energy host materials are needed. Among the most promising host materials for this wavelength region are chalcogenide glasses (Seddon et al. 2010; Tao et al. 2015). Chalcogenide glasses possess good rare earth ion solubility, high refractive index and can be drawn into fibre. These characteristics make chalcogenide glasses an attractive host material for rare-earth ions (Seddon et al. 2010; Tao et al. 2015). Recent publications show that there is a particularly large interest in mid-infrared fluorescence from the (3F2,3H6) → 3H5 (~3.7–4.2 μm), and 3H5→3H4 (4.3–5.0 μm) transitions of Pr3+ doped selenide glass (Sakr et al. 2014; Sójka et al. 2014; Karaksina et al. 2016a, b; Shpotyuk et al. 2015; Chahal et al. 2016; Shaw et al. 2001). This is because Pr3+ ions in chalcogenide glass have a high pump absorption cross-section, and also because Pr3+ can be pumped with commercially available laser diodes. Despite this, a Pr3+ doped selenide chalcogenide glass fibre laser has not yet been realized. The first problem that stops this technology is the difficulty of manufacturing high purity rare earth doped chalcogenide glasses. Secondly, both the upper and lower laser manifolds possess long lifetimes in comparison to that of the ground state. This tends to cause self-terminating laser operation and makes achieving population inversion difficult. One possible solution to this latter obstacle can be cascading two laser transitions (Quimby et al. 2008). However, the practical realization of cascading is challenging, since it requires the fabrication of two pairs of wavelength-matched fibre gratings in the Pr3+ doped chalcogenide glass fibre. Additionally, significant pump power is required in order to achieve laser action for both transitions. Thus, a potentially better solution is to pump the laser resonantly using a QCL (quantum cascade laser). The low quantum defect of the resonantly pumped praseodymium ions potentially enables the fibre laser to achieve high wall-plug efficiency. Further, the resonant pumping reduces the thermal load due to a low quantum defect. This feature is particularly important for fibres fabricated from low glass transition temperatures like chalcogenide glasses. Currently, high power QCLs operating around 4.1 μm are commercially available (http://www.pranalytica.com; Rauter et al. 2013). Resonant pumping of the Pr3+ ions in low phonon laser crystals using QCLs was suggested in (Ferrier et al. 2009). However, in that study excited state absorption (ESA) was not included in the model which, as the authors themselves note, is a significant shortcoming.
In this contribution, we therefore have paid particular attention to the ESA processes, the inclusion of which is, as we show, essential for predictive modelling. Hence, we extract the ESA spectrum of the 3H5→(3F2,3H6) transition. Then using a complete set of experimentally extracted modelling parameters, including ESA emission and absorption cross-sections, we developed a numerical model of a resonantly pumped Pr3+ selenide fibre laser. Using the model, we study the influence of the ESA on the Pr3+ selenide fibre laser performance and identify the best pumping wavelength for obtaining mid-infrared lasing in a resonantly pumped Pr3+, doped selenide chalcogenide glass fibre laser. Finally, we comprehensively study the laser performance as a function of pump wavelength, fibre length, signal wavelength, fibre background loss, and output coupler reflectivity.
The paper is divided into five sections. After this introduction, Sect. 2 describes the experimental results, which confirm the presence of ESA when pumping resonantly. The procedure used to calculate the ESA cross-section is presented in Sect. 3. In Sect. 4, we develop a numerical model of the resonantly pumped Pr3+ doped chalcogenide glass fibre laser and perform a numerical study of the resonantly pumped fibre laser characteristics. Finally, some conclusions are drawn in Sect. 5.
2 Experimental proof of the presence of ESA
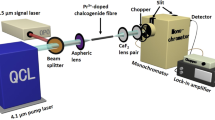
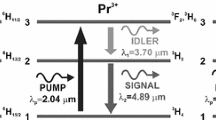
A schematic diagram of the Pr3+ energy level structure in a selenide glass host, and relevant transitions, when pumping with a QCL, are presented in Fig. 1. The details about chalcogenide glass and fibre fabrication are described elsewhere (Sakr et al. 2014; Sójka et al. 2012, 2014; Sujecki et al. 2015; Tang et al. 2015a, b). The ESA describes the absorption from a populated excited state of a system to a higher energy state (Kozak et al. 2006; Gomes et al. 2010; Koepke et al. 1998; Caspary 2003; Quimby and Aitken 2003). In this section, the experimental measurements that were carried out in order to prove the presence of ESA are described. The basic experimental setup for ESA measurement is shown in Fig. 2. The measurements were carried out within the 1.8–2.6 μm spectral range. The detection system consisted of a lock-in amplifier (Model 7270, Signal recovery) room temperature extended InGaAs detector with preamplifier (PDA10D-EC, Thorlabs), a data acquisition card (NI USB-6008 National Instruments) and a computer. The monochromator and data acquisition systems were controlled using in-house developed software based on LabView. A 115 mm long unstructured fibre, of 250 μm diameter, was used in the experiment. A mid-infrared pump at 4.15 μm from a QCL (Model 1101-4150-CW-1500, Pranalytica) was launched into one end of the Pr3+ doped selenide fibre using a Black Diamond lens of focal length f = 5.95 mm. The photoluminescence was collected from the opposite fibre end.
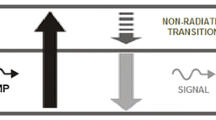
Simplified energy level diagram of Pr3+ in a selenide chalcogenide glass host. The 3H5 level can be populated using optical pumping at a wavelength around 4.15 μm. The ESA from 3H5 to the (3F2,3H6) level is indicated (Wesa). The transition rates depicted in Fig. 1 are defined as follows: the absorption and emission rates Wpa, Wpe, Wsa, Wse of the pump and signal, respectively, Wesa the ESA of the pump from 3H5 → (3F2,3H6), Wese the emission of the pump from (3F2,3H6) → 3H5, W3 = W31 + W32 the spontaneous decay rate of level 3, W21 the spontaneous decay rate of level 2
The presence of the ESA process was proven in the Pr3+ doped selenide fibre by observation of emission centred at a wavelength of 2.4 μm, from the level (3F2,3H6)- >3H4, whilst pumping at a wavelength of 4.15 μm. The measured shape of the 2.4 μm emission is shown in Fig. 3. Therefore the observed emission at around 2.4 μm from the level (3F2,3H6)- >3H4 demonstrates that level (3F2,3H6) is populated by the 4.15 μm pump. The photoluminescence shape at 2.4 μm was measured from the fibre end opposite to the launch end, thus it can be affected by photon trapping (diffusion) and reabsoprtion. A 115 mm long fibre was used in the experiment. Additionally, a sharp cut-off of the spectrum for wavelengths above 2.5 μm can be attributed to the extended InGaAs detector cut-off. These results directly confirm ESA in the Pr3+ doped selenide fibre when pumped at 4.15 μm. Therefore, the ESA should be included in the laser model. To the best of our knowledge this is the first time that experimental evidence has been presented for ESA in a Pr3+ doped selenide fibre whilst resonant pumping at around 4 μm.
3 Calculation of ESA cross section
To evaluate numerically the effect of the ESA on the laser efficiency of the Pr3+ doped selenide fibre, the absorption cross-section related to the 3H5→(3F2,3H6) transition must be known. In this contribution, we estimated the ESA cross-sections using the Judd–Ofelt (J–O) theory, the McCumber method, and the Fuchtbauer–Ladenburg (F–L) equation (Gomes et al. 2010). The rates of spontaneous emission for (3F2,3H6) → 3H5, and 3H5→3H4 transitions were calculated using our Judd–Ofelt parameters for Pr3+ doped selenide glass: Ω2 = 8.156*10-20cm2, Ω4 = 8.08*10-20cm2, Ω6 = 5.70*10-20cm2, which were recalculated after removing Se–H contribution at 4.5 μm from absorption spectra. Taking into consideration the small energy difference between the levels 3F2 and 3H6 it may be assumed that both levels are in thermal equilibrium. Thus, using Boltzmann statistics, the total radiative rate from the combined pair of levels is given by (Caspary 2003; Quimby and Aitken 2003).
where A1 = 166.7 s−1 and A2 = 3131.4 s−1 are the Judd–Ofelt calculated rates from levels 3F2 (fivefold degenerate level) and 3H6 (13-fold degenerate level) and E is the spacing between the levels. E = 600 cm−1 was used in the calculations (Shaw et al. 2001). Values of radiative rates (electronic (Aed), and magnetic (Amd) dipole contribution) and radiative branching ratios obtained from J–O calculations for other transitions in Pr3+ selenide chalcogenide bulk glass are listed in Table 1. Calculated radiative lifetimes, non-radiative lifetimes and total lifetimes for the (3F2,3H6) → 3H5 and 3H5→3H4 transitions are given in Table 2. The multi-phonon non-radiative lifetimes were estimated based upon the data presented in (Shaw et al. 2001). The total fluorescence lifetime is given by a sum of radiative and non-radiative lifetimes. The total fluorescence lifetime is calculated using the following formula:
where τrad and τnr are radiative and non-radiative lifetimes, respectively.
According to the results presented in Tables 1 and 2, the (3F2,3H6) → 3H5, and 3H5→3H4 transitions have a similar strength. Thus, for 2 µm pumping, these transitions are self-terminating. This causes population bottlenecking as a result of the comparatively long lifetime of the (3F2,3H6) → 3H5 transition, and saturation of the laser output. The calculated ESA absorption cross-section is presented in Fig. 3. The maximum cross-section for ESA is equal to 0.90 × 10−24 m2 at λ = 3.76 μm.
ESA cross section was derived using McCumber theory and based on the emission spectrum for the (3F2,3H6) → 3H5 transition that has been reported in (Shaw et al. 2001) and scaled by us using the Fuchtbauer-Ladenburg equation to match the spontaneous emission rate for the (3F2,3H6) → 3H5 transition. This method of extracting ESA from emission measurements using McCumber theory was described by Quimby and Zheng in (Quimby and Zheng 1992). The result of this calculation is shown in Fig. 4a. In Fig. 4b we present both the absorption and emission cross sections of this ESA. Figure 4b shows the characteristic redshift between absorption and emission cross section, which agrees with expectations (Quimby and Zheng 1992).
a ESA cross-section calculated for the transition 3H5→(3F2,3H6) using McCumber theory from the emission spectrum of the (3F2,3H6) → 3H5 transition reported in (Shaw et al. 2001) and b calculated absorption and emission cross-sections for the transition 3H5→(3F2,3H6)
The ground state absorption (GSA) and the ESA absorption of Pr3+ doped selenide glass are compared in Fig. 5. GSA absorption was measured for a 500 ppmw Pr3+ doped selenide bulk sample (Sakr et al. 2014; Sójka et al. 2014). The estimated contribution of the Se–H impurity band to the GSA was removed using Gaussian fitting (Seddon et al. 2016). The cross section values for ESA and GSA are very similar. These results are in reasonable agreement with Judd–Ofelt theory which predicts that both transitions have a similar strength. This further confirms the accuracy of the calculation procedure of ESA that was used in this contribution. The spectral distributions of ESA and GSA cross sections have a significant overlap. As a consequence, both transitions can simultaneously absorb the pump energy at wavelengths between approximately 3.7 and 4.3 μm. Thus, the pump energy populates also the level (3F2,3H6) and significantly depletes the upper laser level 3H5. This behaviour hampers the possibility of establishing population inversion for the 3H5→3H4 transition when pumping resonantly between 3.7 and 4.3 μm. Additionally the presence of ESA can result in higher laser thresholds and lower slope efficiencies.
4 Results and discussion
In order to study the properties of a resonantly pumped Pr3+ doped chalcogenide glass fibre laser, we developed a numerical model. We formulated the rate equations according to the energy-level diagram presented in Fig. 1:
where Ni, i = 1,2,3 are the ion populations of energy levels and the transition rates Wxy are defined in Fig. 1.
In the steady state (\(\frac{{dN_{i} }}{dt} = 0\)), the Eqs. (3–5) reduce to three algebraic equations. The power evolution along the fibre of the pump light Pp and the signal light Ps can be obtained by:
where ‘+’ and ‘−’refer to forward and backward travelling waves, respectively, \(P_{p}^{ \pm } = P_{p}^{ + } + P_{p}^{ - }\);\(P_{s}^{ \pm } = P_{s}^{ + } + P_{s}^{ - }\) and αp, αs, represent the background loss coefficient at pump and signal wavelengths, respectively.
In Eqs. (3–5), the stimulated emission or absorption rates are expressed by:
where Γx is the confinement factor, which defines the fraction of energy that propagates in the core to the total energy that propagates in the fibre (in the core and the cladding), σxy is the absorption or emission cross-section for the xy transition, Px denotes the propagating signal and pump powers, respectively, A is the doping cross section area, h is Planck’s constant, λx is the wavelength of signal or pump and c is the speed of light in free space. Amplified Spontaneous Emission (ASE) was not included in the laser model. According to Quimby ASE can be neglected in the laser model due to fact that for a laser operation the gain is clamped (Quimby et al. 2008). Further model details can be found elsewhere (Sójka et al. 2012; Sujecki et al. 2015).
Figure 6 shows the calculated population inversion for the 3H5→3H4 transition (in ions/m3) as a function of the pump intensity for a Pr3+ ion density equal to 9.46 × 1024 ions/m3 which corresponds to a 500-ppmw Pr3+ doped GeAsGaSe glass. This concentration in a rare earth doped chalcogenide glass does not induce glass crystallisation (Seddon et al. 2010). The pump wavelength is 4.0 μm, while the laser emission takes place at 4.8 μm. In order to explore the ESA contribution, the following two cases were considered: (1) including ESA and (2) with ESA switched off. The results from Fig. 6 show that the pump intensity necessary to render the material transparent without including ESA is 34.9 MW/m2, while, when the ESA is included, it changes to 57.1 MW/m2. We note that the experimentally estimated power damage threshold at 2 μm for Pr3+ doped selenide fibre is in the range of 250 MW/m2; the power damage threshold should increase significantly for longer wavelengths due to better glass transparency (Gattass et al. 2015). Also, it can be seen that the ESA process introduces a large decrease in the value of the population inversion for the 3H5→3H4 transition. For instance, at the pump intensity of 1000 MW/m2, the population inversion is approximately halved. These results show clearly that the ESA should be included in the laser model. The main reason for the strong influence of ESA is the long lifetime of the level (3F2, 3H6), thus a large population builds up easily in this level and does not contribute to the amplification process for the 3H5→3H4 transition.
Figure 7a shows the calculated population inversion (in ions/m3) as a function of the pump intensity for a Pr3+ ion density equal to 9.46 × 1024 ions/m3, for different pump wavelengths. The results from Fig. 7a clearly show that detuning the pump wavelength towards longer wavelengths helps reduce the threshold and increase the population inversion for the 3H5→3H4 transition. Additionally, these results show that the maximum population inversion is achieved at a laser pump wavelength of 4.1–4.15 μm. Therefore the pump wavelength should be selected so that σGSA > σESA between 3.7 and 4.2 μm (see Fig. 4). Note that above 4.2 μm there is strong atmospheric absorption band due to CO2. Thus, pumping above 4.2 μm is not impossible but impractical. Figure 7b shows the calculated material gain at 4.8 μm as a function of the pump intensity and wavelength. The results show that the highest gain can be achieved for pumping at 4.1–4.15 μm. Hence the highest values of gain might be obtained by pumping using an appropriate mid-infrared QCL, and this also should help to overcome the experimentally observed loss of chalcogenide glasses in the range of 4.5 μm due to the Se–H impurity absorption band (Tang et al. 2015a, b).
In order to find optimum laser performance, important parameters such as fibre length, output coupling, signal and pumping wavelength were thoroughly investigated. Firstly, the influence of ESA on the laser performance was investigated. The step index fibre (SIF) structure assumed was a single core, with a radius of 15 µm and numerical aperture equal to 0.4. A fibre with a similar a structure has already been reported in the literature (Tang et al. 2015a, b). This fibre structure should enable efficient optical coupling of the QCL pump laser. The fibre modelled (see Table 3) was multi-moded at 5 μm; in practice a few modes will be guided at 5 µm but through good coupling the number of excited modes can be significantly reduced (Stutzki et al. 2014). The Fundamental Mode (FM) should have the highest confinement factor, i.e. the largest optical overlap with the doping region, therefore in the case of lasing this mode should dominate (Stutzki et al. 2014). The fibre laser resonator structure considered uses fibre Bragg gratings (FBGs). The reflectivity of the input FBG for the pump wavelength was assumed to be 0.05 while the reflectivity of this FBG was assumed to be 0.95 for the signal. The output reflectivity is 0.05 for the signal and for the pump it is 0.95. The level of losses assumed for all the wavelengths considered (i.e. at the pump and emission wavelengths) is 1 dB/m. The parameters used in the modelling are listed in Tables 1, 2, 3 and Figs. 4, 5. These parameters were used in all simulations, unless otherwise stated (Sakr et al. 2014; Sójka et al. 2014; Sujecki et al. 2015).
Figure 8 illustrates the calculated signal output power as a function of fibre length for different pump wavelengths. The pump power was set to 1 W. The laser signal wavelength was set to 4.8 μm. According to numerical simulation this laser emission wavelength (4.8 μm) corresponds to operation at high power. The results presented in Fig. 8 are consistent with the results presented in Fig. 7. Both results prove that by detuning the pump wavelength from the ESA band the laser output power is increased. It can be observed that when fibre length increases the output power steadily decreases. This phenomenon can be attributed to the signal photon flux reabsorption by 3H4→3H5 ground state transition and pump power depletion. Additionally, the laser signal propagating along the fibre is attenuated by the fibre background loss. This causes a reduction in the output power with a further increase in the fibre length. The optical-to-optical efficiencies for 4.8 µm emission with pump wavelengths of 3.9, 4.0, 4.1 and 4.15 µm are 22, 37, 51 and 55% respectively. Note that the Stokes efficiency limit for a pump wavelength of 4.15 μm is ~86% (Quimby 2006). Moreover, from the results presented in Fig. 8, the optimum fibre length can be estimated. It can be observed that the position of maximum output power shifts to a shorter fibre length for longer pump wavelengths. This difference is due to the larger pump cross section for longer pump wavelengths and the weaker ESA contribution which results in a shorter fibre length and correspondingly smaller attenuation loss. The calculated optical-to-optical efficiencies reported in the literature for chalcogenide fibre lasers doped with Pr3+, Dy3+ and Tb3+ were below 45% (Quimby et al. 2008; Sójka et al. 2012; Hu et al. 2015; Falconi et al. 2015, 2016). Therefore resonantly pumping shows a clear advantage in comparison to these previously reported results.
Figure 9 shows the calculated threshold pump power as a function of fibre length for different pump wavelengths. The thresholds for all cases decreases sharply with an increase in the fibre length; they reach the minimum values of 130, 60, 35 and 30 mW for pumping at wavelengths of 3.9, 4.0, 4.1 and 4.15 μm respectively, and then steadily increase with further increasing fibre length. The high pump power threshold for short fibre length can be attributed to insufficient pump power absorption. For longer fibre lengths the ground state absorption of the 3H4→3H5 transition and a background loss in the fibre increases the total cavity loss; thus as a consequence the pump power threshold increases. According to results presented in Figs. 8 and 9 it can concluded that increasing the pump wavelength away from resonance with ESA has a positive effect on the slope efficiency and reduces laser threshold.
In order to estimate the optimum lasing wavelength the output power was calculated as a function of lasing wavelength for various levels of loss (see Fig. 10). The input pump power was 1 W at 4.15 μm, and the fibre length was set to 1 m. It can be observed from Fig. 10 that high output power can be generated by the fibre laser for a spectra region between 4.8 and 5.2 μm. Therefore a Pr3+ doped selenide fibre can be considered as a good candidate for the future construction of a tuneable mid-infrared fibre laser.
In order to illustrate the influence of the output coupling (mirror placed at the opposite end of fibre to the pump launch end) on the laser performance the output power was calculated as a function of output coupler reflectivity. Results are presented in Fig. 11. The optimum fibre length of 1 m deduced from the results shown in Figs. 8 and 9 was used in this simulation, and a 3 dB/m fibre background loss was assumed for all wavelengths. It can be seen that on decreasing the output mirror reflectivity the signal output power increases. The results presented in Fig. 11 show that the highest output power can be achieved for an output mirror reflectivity of 0.05 at 4.8 µm. However, a laser cavity based solely on Fresnel reflection at one of the fibre ends (output coupling around ~20%) can ensure a relatively high output power of around 270 mW. Therefore a simple cavity design, that relies on a highly reflective input mirror and the output reflectivity of 20% provided by Fresnel reflection, can also be used in order to achieve efficient laser operation.
To make a more comprehensive analysis of the proposed fibre laser, the influence of background loss on laser performance is investigated. The background loss is a limiting factor that hampers the possibility of achieving mid-infrared laser action from selenide doped fibres. Selenide glass possesses high optical absorption loss at wavelengths around 4.5 μm due to Se–H glass impurities. However, recently it has been proven that the loss in this spectral region can be reduced to 1.6 dB/m in the host glass by using sophisticated glass purification techniques (Tang et al. 2015a, b). Calculated output power and threshold pump power as a function of fibre background loss are presented in Fig. 12. The fibre length and pump power are set to 1 m and 1 W, respectively. It can be observed that the output power and threshold pump power decrease and increase respectively as the fibre background loss increases. Output power above 100 mW is expected for a fibre loss <5 dB/m. Therefore, in order to obtain efficient laser operation, the fibre loss should be reduced below 5 dB/m.
Calculated output power and threshold pump power as a function of fibre background loss; all other parameters (fibre core size etc.) are given in Table 3
5 Conclusions
The performance of resonantly pumped selenide chalcogenide glass fibre lasers doped with Pr3+ was comprehensively studied. Particular attention was paid to the role of excited state absorption (ESA), which has not been considered previously in the literature on mid-infrared transitions of Pr3+ in selenide chalcogenide glasses. ESA absorption cross section spectra were extracted using McCumber theory. The experimentally extracted parameters formed the basis for the numerical model used in this study. The numerical results showed that ESA had a major influence on the laser performance and that its effect could be reduced by selecting the pump wavelength so that σGSA > σESA. It was also shown that a resonant pumping scheme using a high power QCL is a better solution when compared with the best pumping scheme reported so far. The results obtained showed that resonant pumping allowed for a significant reduction in the laser threshold, and an increase of the laser efficiency. Furthermore, we showed that knowledge of the ESA spectral distribution is indispensable when selecting the optimal wavelength for resonant pumping.
References
Caspary, R.: Applied Rare-Earth Spectroscopy for Fiber Laser Optimization. Shaker, Aachen (2003). ISBN 3-8322-0315-X
Chahal, R., Starecki, F., Boussard-Plédel, C., Doualan, J.-L., Michel, K., Brilland, L., Braud, A., Camy, P., Bureau, B., Nazabal, V.: Fiber evanescent wave spectroscopy based on IR fluorescent chalcogenide fibers. Sensors Actuators B: Chem. 229(28), 209–216 (2016)
Falconi, M. C., Scarcia, W., Palma, G., Chahal, R., Starecki, F., Nazabal, V., Troles, J., Adam, J. L., and Prudenzano, F.: Optimization of Mid-IR microstructured fiber laser based on dysprosium doped chalcogenide glass. In: 17th International Conference on Transparent Optical Networks (ICTON), pp. 1–5 (2015)
Falconi, M.C., Palma, G., Starecki, F., Nazabal, V., Troles, J., Taccheo, S., Ferrari, M., Prudenzano, F.: Design of an efficient pumping scheme for Mid-IR Dy3+:Ga5Ge20Sb10S65 PCF fiber laser. Photon. Technol. Lett. IEEE 28, 1984–1987 (2016)
Ferrier, A., Velázquez, M., Doualan, J.-L., Moncorgé, R.: Spectroscopic investigation and mid-infrared luminescence properties of the Pr3+ -doped low phonon single crystals CsCdBr 3, KpB2Cl5 and Tl3PbBr5. J. Lumin. 129, 1905–1907 (2009)
Gattass, R.R., Thapa, R., Kung, F.H., Busse, L.E., Shaw, L.B., Sanghera, J.S.: Review of infrared fiber-based components. Appl. Opt. 54, F25–F34 (2015)
Gomes, L., Librantz, A.F.H., Jackson, S.D.: Energy level decay and excited state absorption processes in dysprosium-doped fluoride glass. J. Appl. Phys. 107, 053103 (2010). http://www.pranalytica.com
Hu, J., Menyuk, C.R., Wei, C., Shaw, L.B., Sanghera, J.S., Aggarwal, I.D.: Highly efficient cascaded amplification using Pr3+-doped mid-infrared chalcogenide fiber amplifiers. Opt. Lett. 40, 3687–3690 (2015)
Jackson, S.D.: Towards high-power mid-infrared emission from a fibre laser. Nat. Photon. 6, 423–431 (2012)
Karaksina, E.V., Shiryaev, V.S., Kotereva, T.V., Churbanov, M.F.: Preparation of high-purity Pr(3+) doped Ge–Ga–Sb–Se glasses with intensive middle infrared luminescence. J. Lumin. 170(1), 37–41 (2016)
Karaksina, E. V., Shiryaev, V.S., Kotereva, T. V., Velmuzhov, A. P., Ketkova, L.A., Snopatin, G. E.: Preparation of high-purity Pr3+ doped Ge–As–Se–In–I glasses for active mid-infrared optics. J. Lumin. 177, 275–279 (2016) ISSN 0022-2313
Koepke, C., Wiśniewski, K., Grinberg, M., Russell, D.L., Holliday, K., Beall, G.H.: Excited state absorption in Cr3+ -doped gahnite glass ceramics. J. Lumin. 78, 135–146 (1998)
Kozak, M., Goebel, D., Kowalsky, W., Caspary, R.: Excited state absorption spectroscopy for thulium-doped zirconium fluoride fiber. Opt. Commun. 259, 154–157 (2006)
Pollnau, M., Jackson, S.: Advances in mid-infrared fiber lasers. In: Ebrahim-Zadeh, M., Sorokina, I. (eds.) Mid-infrared coherent sources and applications, pp. 315–346. Springer, Netherlands (2008)
Quimby, R.S., Aitken, B.G.: Multiphonon energy gap law in rare-earth doped chalcogenide glass. J. Non-Cryst. Solids 320, 100 (2003)
Quimby, R.S., Shaw, L.B., Sanghera, J.S., Aggarwal, I.D.: Modeling of cascade lasing in dy: chalcogenide glass fiber laser with efficient output at 4.5 μm. Photon. Technol. Lett. IEEE 20, 123–125 (2008)
Quimby, R.S., Zheng, B.: New excited-state absorption measurement technique and application to Pr3+ doped fluorozirconate glass. Appl. Phys. Lett. 60, 1055–1057 (1992)
Quimby, R.S.: Photonics and lasers: an introduction. Wiley, Hoboken (2006)
Rauter, P., Menzel, S., Goyal, A.K., Wang, C.A., Sanchez, A., Turner, G., Capasso, F.: High-power arrays of quantum cascade laser master-oscillator power-amplifiers. Opt. Express 21, 4518–4530 (2013)
Sakr, H., Furniss, D., Tang, Z., Sojka, L., Moneim, N.A., Barney, E., Sujecki, S., Benson, T.M., Seddon, A.B.: Superior photoluminescence (PL) of Pr3+-In, compared to Pr3+-Ga, selenide-chalcogenide bulk glasses and PL of optically-clad fiber. Opt. Express 22, 21236–21252 (2014)
Seddon, A.B.: A prospective for new mid-infrared medical endoscopy using chalcogenide glasses. Int. J. Appl. Glass Sci. 2(3), 177–191 (2011)
Seddon, A.B.: Mid-infrared (IR)—a hot topic: the potential for using mid-IR light for non-invasive early detection of skin cancer in vivo. Phys. Status Solidi B 250(5), 1020–1027 (2013)
Seddon, A.B., Furniss, D., Tang, Z.Q., Sojka, Ł., Benson, T.M., Caspary, R., Sujecki, S.: True mid-infrared Pr3+ absorption cross section in a selenide-chalcogenide host-glass. In: 18th International Conference on Transparent Optical Networks (ICTON) (2016)
Seddon, A., Tang, Z., Furniss, D., Sujecki, S., Benson, T.: Progress in rare-earth-doped mid-infrared fiber lasers. Opt. Express 18, 26704–26719 (2010)
Shaw, L.B., Cole, B., Thielen, P.A., Sanghera, J.S., Aggarwal, I.D.: Mid-wave IR and long-wave IR laser potential of rare-earth doped chalcogenide glass fiber. IEEE J. Quant. Electron. 37, 1127–1137 (2001)
Shpotyuk, Y., Boussard-Pledel, C., Nazabal, V., Chahal, R., Ari, J., Pavlyk, B., Cebulski, J., Doualan, J.L., Bureau, B.: Ga-modified As2Se3–Te glasses for active applications in IR photonics. Opt. Mater. 46, 228–232 (2015)
Sójka, Ł., Tang, Z., Zhu, H., Bereś-Pawlik, E., Furniss, D., Seddon, A.B., Benson, T.M., Sujecki, S.: Study of mid-infrared laser action in chalcogenide rare earth doped glass with Dy3+, Pr3+ and Tb3+. Opt. Mater. Express 2, 1632–1640 (2012)
Sójka, L., Tang, Z., Furniss, D., Sakr, H., Oladeji, A., Bereś-Pawlik, E., Dantanarayana, H., Faber, E., Seddon, A.B., Benson, T.M., Sujecki, S.: Broadband, mid-infrared emission from Pr3+ doped GeAsGaSe chalcogenide fiber, optically clad. Opt. Mater. 36(6), 1076–1082 (2014)
Stutzki, F., Jansen, F., Otto, H.-J., Jauregui, C., Limpert, J., Tünnermann, A.: Designing advanced very-large-mode-area fibers for power scaling of fiber-laser systems. Optica 1, 233–242 (2014)
Sujecki, S., Oladeji, A., Phillips, A., Seddon, A.B., Benson, T.M., Sakr, H., Tang, Z., Barney, E., Furniss, D., Sójka, Ł., Bereś-Pawlik, E., Scholle, K., Lamrini, S., Furberg, P.: Theoretical study of population inversion in active doped MIR chalcogenide glass fibre lasers (invited). Opt. Quant. Electron. 47, 1389–1395 (2015)
Tang, Z., Shiryaev, V.S., Furniss, D., Sojka, L., Sujecki, S., Benson, T.M., Seddon, A.B., Churbanov, M.F.: Low loss Ge-As-Se chalcogenide glass fiber, fabricated using extruded preform, for mid-infrared photonics. Opt. Mater. Express 5, 1722–1737 (2015a)
Tang, Z., Furniss, D., Fay, M., Sakr, H., Sójka, L., Neate, N., Weston, N., Sujecki, S., Benson, T.M., Seddon, A.B.: Mid-infrared photoluminescence in small-core fiber of praseodymium-ion doped selenide-based chalcogenide glass. Opt. Mater. Express 5, 870–886 (2015b)
Tao, G., Ebendorff-Heidepriem, H., Stolyarov, A.M., Danto, S., Badding, J.V., Fink, Y., Ballato, J., Abouraddy, A.F.: Infrared fibers. Adv. Opt. Photon. 7, 379–458 (2015)
Acknowledgements
This research has been partly supported by the European Commission through the framework Seven (FP7) project MINERVA (317803; www.minerva-project.eu). Also we acknowledge COST Action MP 1401 supported by the EU Framework Programme Horizon 2020. LS would like to acknowledge support by the Polish Ministry of Science and Higher Education under the project entitled “Iuventus Plus”, 2016–2018 (project no. IP0441/IP2/2015/73).
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of the Topical Collection on Optical Wave and Waveguide Theory and Numerical Modelling 2016
Guest edited by Krzysztof Anders, Xuesong Meng, Gregory Morozov, Sendy Phang, and Mariusz Zdanowicz.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sójka, L., Tang, Z., Furniss, D. et al. Numerical and experimental investigation of mid-infrared laser action in resonantly pumped Pr3+ doped chalcogenide fibre. Opt Quant Electron 49, 21 (2017). https://doi.org/10.1007/s11082-016-0827-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-016-0827-0