Abstract
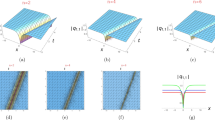
In this paper, we have presented a numerical analysis of the stability of optical bullets (2 + 1), or spatiotemporal solitons (2 + 1), in a planar waveguide with cubic–quintic nonlinearity. The optical spatiotemporal solitons are the result of the balance between the nonlinear parameters, of dispersion (dispersion length, L D) and diffraction (diffraction length, L d) with temporal and spatial auto-focusing behavior, respectively. With the objective of ensure the stability and preventing the collapse or the spreading of pulses, in this study we explore the cubic–quintic nonlinearity with the optical fields coupled by cross-phase modulation and considering several values for the non linear parameter α We have shown the existence of stable light bullets in planar waveguide with cubic–quintic nonlinearity through the study of spatiotemporal collisions of the light bullets.
Similar content being viewed by others
References
Agrawal G.P.: Nonlinear Fiber Optics, 3rd edn. Academic Press, Boston (2001a)
Agrawal G.P.: Applications of Nonlinear Fiber Optics, 1st edn. Academic Press, Boston (2001b)
Akhmediev N., Soto-Crespo J.M.: Generation of a train of three-dimensional optical solitons in a self-focusing médium. Phys. Rev. A 47, 1358–1364 (1993)
Akhmediev N.N., Ankiewicz A.: Solitons: Nonlinear Pulses and Beams. Chapman and Hall, London (1997)
Aleksić, N.B., Skarka, V., Timotijević, D.V., Gauthier, D.: Self-stabilized spatiotemporal dynamics of dissipative light bullets generated from inputs without spherical symmetry in three-dimensional Ginzburg-Landau systems. Phys. Rev. A, 75(6), (2007) (article no. 061802)
Anderson D.: Variational approach to nonlinear pulse propagation in optical fibers. Phys. Rev. A 27, 3135–3145 (1983)
Bergé L.: Self-focusing dynamics of nonlinear waves in media with parabolic-type inhomogeneities. Phys. Plasmas 4, 1227 (1997)
Chen, S.H., Dudley, J.M.: Spatiotemporal nonlinear optical self-similarity in three dimensions. Phys. Rev. Lett., 102(23), (2009) (article no. 233903)
Chiao R.Y., Garmire E., Townes C.H.: Self-trapping of optical beams. Phys. Rev. Lett. 13, 479–482 (1964)
Desyatnikov A., Maimistov A., Malomed B.: Three-dimensional spinning solitons in dispersive media with the cubic–quintic nonlinearity. Phys. Rev. E 61, 3107–3113 (2000)
Enns R.H., Rangnekar S.S.: Bistable spheroidal optical solitons. Phys. Rev. A 45, 3354–3357 (1992)
Fong C.Y., Shen Y.R.: Theoretical Studies on dispersion of nonlinear optical susceptibilites in GaAs, InAs, and InSb. Phys. Rev. B. 12(6), 2325–2355 (1975)
Gorbach, A.V., Skryabin, D.V.: Spatial solitons in periodic nanostructures. Phys. Rev. A, 79(5), (2009) (article no. 053812)
Hayata K., Koshiba M.: Multidimensional solitons in quadratic nonlinear media. Phys. Rev. Lett. 71, 3275–3278 (1993)
Kanashov A.A., Rubenchik A.M.: On diffraction and dispersion effect on three wave interaction. Physica D 4, 122–134 (1981)
Kelley P.: Self-focusing of optical beams. Phys. Rev. Lett. 15, 1005–1008 (1965)
Kivshar Y.S., Agrawal G.P.: Optical Solitons, 1st edn. Academic Press, Boston (2003a)
Kivshar Y.S., Agrawal G.P.: Optical Solitons: From Fibers to Photonic Crystals. Academic Press, San Diego (2003b)
Kolokolo A.A., Skrotski G.V.: Self-compression of spherically symmetric pulses in a nonlinear medium. Optika, I Spektroskopiya 35(5), 898–901 (1973)
Liu X., Qian L.J., Wise F.W.: Generation of optical spatiotemporal solitons. Phys. Rev. Lett. 82, 4631–4634 (1999)
Malomed B.A.: Soliton Management in Periodic Systems. Springer, New York (2006)
Malomed B.A., Drummond P., He H., Berntson A., Anderson D., Lisak M.: Spatiotemporal solitons in multidimensional optical media with a quadratic nonlinearity. Phys. Rev. E 56, 4725–4735 (1997)
Malomed B.A., Mihalache D., Wise F., Torner L.: Spatiotemporal optical solitons. J. Opt. B Quantum Semiclassical Opt. 7(5), R53–R72 (2005)
Marburger J.H.: Self-focusing: theory. Prog. Quantum Electron. 4, 35–110 (1975)
McLeod R., Wagner K., Blair S.: (3 + 1)-dimensional optical soliton dragging logic. Phys. Rev. A 52, 3254–3278 (1995)
Nehmetallah G., Banerjee P.P.: Numerical modeling of spatio-temporal solitons using an adaptive spherical Fourier Bessel split-step method. Opt. Commun. 257, 197–205 (2006)
Rasmussen J.J., Rypdal K.: Blow-up in nonlinear Schroedinger equations. Phys. Scr. 33(6), 481–497 (1986)
Sakaguchi, H,Malomed, B.A.: Channel-guided light bullets. Phys. Rev. A, 75(6), (2007) (article no. 063825)
Sombra A.S.B.: Bistable pulse collisions of the cubic–quintic nonlinear Schrodinger equation. Opt. Commun. 94, 92–98 (1992)
Stegeman G.I., Christodoulides D.N., Segev M.: Optical spatial solitons: historical perspectives. IEEE J. Sel. Top. Quantum Electron. 6, 1419–1427 (2000)
Sukhorukov, A.A., Kivshar, Y.S.: Slow-light optical bullets in arrays of nonlinear Bragg-Grating waveguides. Phys. Rev. Lett., 97(23), (2006) (article no. 233901)
Towers I., Malomed B.A.: Stable (2 + 1)-dimensional solitons in a layered medium with sign-alternating Kerr nonlinearity. J. Opt. Soc. Am. B 19, 537–543 (2002)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Fraga, W.B., Menezes, J.W.M., Sobrinho, C.S. et al. Numerical analysis of the stability of optical bullets (2 + 1) in a planar waveguide with cubic–quintic nonlinearity. Opt Quant Electron 41, 121–130 (2009). https://doi.org/10.1007/s11082-009-9331-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11082-009-9331-0