Abstract
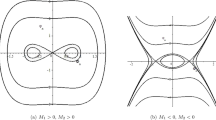
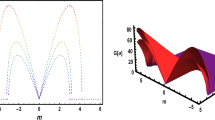
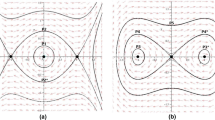
We study numerically the temporal and spatial dynamics of light in Bragg gratings in highly nonlinear photonic crystal fibre for a CW input signal. Our numerical model is based on the plane wave mode solver and a set of nonlinear coupled-mode equations which we solve using a variation of implicit fourth order Runge-Kutta method. We observe not only bistability of the intensity versus transmitted and reflected light but also complex dynamics. We demonstrate that for values of input intensity above the bistable region the steady state may undergo a supercritical Hopf bifurcation. For some ranges of the input intensity we also observe a coexistence of two periodic attractors. The dynamics found, in particular the features in the bifurcation diagram, strongly depend on the parameters of the fibre. Consequently, we suggest that by proper design of the photonic crystal in the cladding we can adjust such nonlinear features of the Bragg gratings as the width of the bistable region, the intensity at which the bifurcation occurs and also the characteristics of the dynamics at high values of input intensity.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Aceves A., De Angelis C., Wabnitz S. (1992). Generation of solitons in a nonlinear periodic medium. Opt. Lett. 17(22): 1566–1568
Antkowiak M., Kotynski R., Panajotov K., Berghmans F., Thienpont H. (2006). Numerical analysis of highly birefringent photonic crystal fibers with Bragg reflectors. Opt. Quantum Electron. 38: 535–545
de Sterke C., Sipe J. (1990). Switching dynamics of finite periodic nonlinear media: a numerical study. Phys. Rev. A 42(5): 2858–2869
de Sterke C.M., Jackson K.R., Robert B.D. (1991). Nonlinear coupled-mode equations on a finite interval: a numerical procedure. J. Opt. Soc. Am. B 8: 403–412
Ebendorff-Heidepriem H., Petropoulos P., Asimakis S., Finazzi V., Moore R., Frampton K., Koizumi F., Richardson D., Monro T. (2004). Bismuth glass holey fibers with high nonlinearity. Opt. Express 12: 5082–5087
Efimov A., Taylor A., Omenetto F., Yulin A., Joly N., Biancalana F., Skryabin D., Knight J., Russell P. (2004). Time-spectrally-resolved ultrafast nonlinear dynamics in small-core photonic crystal fibers: experiment and modelling. Opt. Express 12: 6498–6507
Erdogan T. (1997). Fiber grating spectra. J. Lightwave Technol. 15: 1277–1294
Kotynski R., Antkowiak M., Berghmans F., Thienpont H., Panajotov K. (2005). Photonic crystal fibers with material anisotropy. Opt. Quantum Electron. 37: 253–264
Lee H., Agrawal G.P. (2003). Nonlinear switching of optical pulses on fiber Bragg gratings. IEEE J. Quantum Electron. 39: 508–515
Leon J., Spire A. (2004). Gap soliton formation by nonlinear supratransmission in Bragg media. Phys. Lett. A 327(5–6): 474–480
Leong J.Y.Y., Petropoulos P., Price J.H.V., Ebendorff-Heidepriem H., Asimakis S., Moore R.C., Frampton K.E., Finazzi V., Feng X., Monro T.M., Richardson D.J. (2006). High-nonlinearity dispersion-shifted lead–silicate holey fibers for efficient 1-um pumped supercontinuum generation. J. Lightwave Technol. 24: 183–190
Pelinovsky D., Sargent E.H. (2002). Stable all-optical limiting in nonlinear periodic structures. II. Computations. J. Opt. Soc. Am. B 19: 1873–1889
Winful H., Cooperman G. (1982). Self-pulsing and chaos in distributed feedback bistable optical devices. Appl. Phys. Lett. 40(4): 298–300
Winful H., Marburger J., Garmire E. (1979). Theory of bistability in nonlinear distributed feedback structures. Appl. Phys. Lett. 35: 379–381
Winful H., Zamir R., Feldman S. (1991). Modulational instability in nonlinear periodic structures: implications for “gap solitons”. Appl. Phys. Lett. 58(10): 1001–1003
Yosia S.P., Chao L. (2005). Bistability threshold inside hysteresis loop of nonlinear fiber Bragg gratings. Opt. Express 13: 5127–5135
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Antkowiak, M., Kotyński, R., Panajotov, K. et al. Dynamic characteristics of nonlinear Bragg gratings in photonic crystal fibres. Opt Quant Electron 39, 455–467 (2007). https://doi.org/10.1007/s11082-007-9101-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11082-007-9101-9