Limit cycles at oversteer vehicle

Abstract

Handling and stability properties of automobiles are most often studied from a practical point of view by applying a reduced set of equations, where the forward velocity is kept constant. At studying the full set of equations of a basic nonlinear two-wheel vehicle model, a supercritical Hopf bifurcation is found for an oversteer vehicle. All state variables of the vehicle are involved at small amplitude limit cycles in the vicinity of the Hopf bifurcation point with the steering angle (drive torque) as bifurcation parameter. At the transition to large amplitude relaxation cycles, the cyclic motion of the vehicle may be separated into ‘slow’ longitudinal velocity-related segments, and ‘fast’ vehicle yaw and side slip-related segments, indicating a singular perturbed system. Moreover, Canard phenomenon is observed for both steering angle and drive torque bifurcation parameters.

1 Introduction

Nonlinear stability analysis at the limits of handling of an automobile has become an important issue to increase passive and active safety. Having automated driving in mind, a clear understanding of nonlinear vehicle dynamics is essential to suitably control actuators that will replace the human driver.

When a human driver is controlling the lateral dynamics of the car by steering, it has been shown that the driver may destabilise the motion of the combined nonlinear vehicle–driver system depending on the available preview distance ahead of the vehicle. Then, limit cycles of the steering wheel angle may emerge when following a given trajectory [1,2,3]. However, it is more convenient so far, to consider stability and handling behaviour of the vehicle for specific trajectories only, such as straight-line driving and circular cornering, as stability and steering behaviour are fundamentally related to each other [4]. For linear tyre characteristics of the vehicle model, there is no difference in the stability analysis between the motion in a straight-line or circular curve. It is a well-known result of linear stability analysis, that the steady-state cornering motion will become monotonically unstable for an oversteer vehicle at the critical speed, resulting in a narrowing spiral motion. The loss of stability occurs at zero steering wheel angle, when slowly increasing speed and slowly releasing the steering wheel to maintain steady-state cornering at a constant radius of curvature. For nonlinear tyre characteristics, the limit of stability can still simply be found from (measured) steering characteristics, when the rate of change of steering angle w.r.t. path curvature becomes zero for slowly tightening the steering wheel at constant speed [4].

These findings are based on vehicle speed as given parameter, with longitudinal and lateral dynamics decoupled. Subsequently, this paper accounts for those neglected coupling effects, which require a nonlinear vehicle model with combined longitudinal and lateral tyre forces. As an alternative to accelerator and gear position applied by a driver, the effective torque at the (substitutive) rear wheel is used as input to the vehicle next to the steering angle. The velocity of the centre of gravity of the vehicle, vehicle side slip angle, yaw rate and angular velocity of the rear wheel are used as a minimum set of state variables for a two-wheel vehicle model. Instead of a monotonic loss of stability for the linear oversteer vehicle for steady-state cornering, a Hopf bifurcation has been found for the enhanced nonlinear vehicle model, already noted in [5] for a four-wheel vehicle model, and continued limit cycles are discussed. As a consequence of consideration of longitudinal dynamics in the equations of motion and the influence of longitudinal tyre slip on the lateral tyre force of an oversteer vehicle, the remarkable appearance of Canard phenomenon could be revealed as a main contribution of this paper.

Stability maps with steering angle and the drive torque as bifurcation parameters have been presented in [6] before. In contrast to this study, equilibrium points of an understeer vehicle (without Hopf bifurcation) were considered for continuation, while supercritical Hopf bifurcations have been pointed out for different characteristics of oversteer vehicles in [7]. Results have been thoroughly discussed from a vehicle dynamics point of view, focussing on respective handling diagrams. Longitudinal velocity and steering wheel angle have been chosen as bifurcation parameters, and as a consequence, the influence from longitudinal dynamics has been neglected in [7]. In [8], the importance of the longitudinal velocity in determining the location of bifurcation points has been outlined, which was not yet addressed in [9]. In the latter contribution, destabilization is shown to be caused by a saddle-node bifurcation of a limit-oversteering vehicle, which strongly depends on the saturation of the rear lateral tyre force. As a consequence, a front wheel steering controller was designed to compensate the instability against the nonlinear uncertainty from tyre behaviour; see also [10, 11] for an extension to rear-wheel steering.

Next to [6], longitudinal slip and respective longitudinal vehicle dynamics have been included in [12, 13], resulting in smaller areas of attraction to a stable equilibrium point. As a further extension to bifurcation analysis of equilibrium points, a method to use bifurcation and continuation procedures also for evaluation of vehicle stability during acceleration and braking has been proposed in [14]. A four-wheel vehicle model was introduced in [15] to account for effects from roll moment distribution for both under- and oversteer vehicles on bifurcation locations, neglecting longitudinal dynamics.

The remainder of this paper is organized as follows. The vehicle model with respective tyre/axle characteristics is introduced in Sect. 2, and characteristic handling properties of an oversteer vehicle will be presented. In Sect. 3, the Hopf bifurcation, identified in the previous section, will be addressed, and continued limit cycles discussed in more detail. In the final section, main conclusions will been drawn.

2 Vehicle model and handling properties

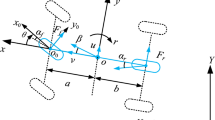
The basic planar two-wheel vehicle model with rear-wheel drive has been chosen to study the motion and stability properties of an automobile, as shown in Fig. 1. The state of the system is represented by the velocity of the vehicle v, the yaw rate ${{\dot{\psi }}}$, the vehicle side slip angle $\beta$, and the angular velocity of the driven rear wheel $\omega _R$. The human driver (or a respective control system) applies a front steering angle $\delta _F$ and a drive torque $M_R$ as input to the vehicle. Thus, the equations of motion of the system read

$$\begin{aligned}&m \dot{v} \cos \beta - m ( {{\dot{\psi }}} + {{\dot{\beta }}} ) v\sin \beta = F_{xR} - F_{yF}\sin \delta _F \end{aligned}$$

(1a)

$$\begin{aligned}&m \dot{v} \sin \beta + m ( {{\dot{\psi }}} + {{\dot{\beta }}} ) v\cos \beta = F_{yR} + F_{yF}\cos \delta _F \end{aligned}$$

(1b)

$$\begin{aligned}&I_{\psi } \ddot{\psi }= l_F F_{yF}\cos \delta _F - l_R F_{yR} \end{aligned}$$

(1c)

$$\begin{aligned}&I_{\omega } {{\dot{\omega }}}_R =M_R - r_R F_{xR} \end{aligned}$$

(1d)

Notation and parameters are given in Table 1.

Fig. 1

Two-wheel vehicle model

For given $v=\mathrm {const.}$, small angles and subsequent linearisation, longitudinal dynamics, (1a), (1d), decouple from lateral dynamics (1b), (1c). To account for coupling effects not only the full set of nonlinear equations in (1) has to be considered, but also the mutual influence of longitudinal and lateral tyre forces. Further, saturation of the tyre forces at large side slip angles needs to be included in the tyre model. Here, the tyre brush model is applied [16].

The lateral slip $\sigma _{yF}$ of the front tyre is derived from kinematic considerations

$$\begin{aligned} \sigma _{yF}= \tan \alpha _F\,\, \text {with}\,\, \tan (\delta _F - \alpha _F) = \frac{v \sin \beta + l_f {{\dot{\psi }}} }{v\cos \beta }\nonumber \\ \end{aligned}$$

(2)

The lateral and longitudinal slip $\sigma _{yR}$ and $\sigma _{xR}$ at the rear tyre read

$$\begin{aligned} \sigma _{yR}= - \frac{v_{syR}}{|r_R \omega _R|} \,\, \text {and}\,\, \sigma _{xR}= - \frac{v_{sxR}}{|r_R \omega _R|} \end{aligned}$$

(3)

with lateral and longitudinal slip velocities $v_{syR}$ and $v_{sxR}$

$$\begin{aligned} v_{syR} = v\sin \beta - l_r {{\dot{\psi }}} \,\,\text {and}\,\, v_{sxR} = v \cos \beta - r_R \omega _R\nonumber \\ \end{aligned}$$

(4)

The absolute slip at front tyre $\sigma _F$, where no longitudinal force appears, as shown in Fig. 1, and at the rear tyre $\sigma _R$,

$$\begin{aligned} \sigma _F=|\sigma _{yF}| \, \, \text {and}\,\, \sigma _R=\sqrt{\sigma _{xR}^2 + \sigma _{yR}^2} \end{aligned}$$

(5)

are input to the tyre brush model [16],

$$\begin{aligned} F_i = \left\{ \begin{array} {ll} \mu _i F_{zi} (3\theta _i \sigma _i - 3 (\theta _i \sigma _i)^2 + (\theta _i \sigma _i)^3 ) &{} \quad \text {for} \quad \sigma _i\le \sigma _{\mathrm {sl}i} \\ \mu _i F_{zi} &{} \quad \text {for} \quad \sigma _i > \sigma _{\mathrm {sl}i} \end{array} \right. \nonumber \\ \end{aligned}$$

(6)

where $F_i$ with $i=F,\,R$ represents the magnitude of the total front and rear tyre/axle force, respectively.

The composite isotropic tyre/axle parameter $\theta _i$

$$\begin{aligned} \theta _i = \frac{2 c_{pi} a_i^2}{3\mu _i F_{zi}} \end{aligned}$$

(7)

includes the constant vertical tyre force $F_{zi}$, resulting from CG position and vehicle weight, the tyre slip stiffness $2 c_{pi} a_i^2$, as well as the maximum tyre force coefficient $\mu _i$, representing tyre–road contact condition. Total sliding of the respective tyre starts at slip $\sigma _{\mathrm {sl}i} = \theta _i^{-1}$ [16].

Lateral and longitudinal tyre/axle force $F_{yi}$ and $F_{xi}$ finally read

$$\begin{aligned} F_{yi} = F_i\frac{\sigma _{yi}}{\sigma _i} \,\, \text {and} \,\, F_{xi} = F_i\frac{\sigma _{xi}}{\sigma _i} \end{aligned}$$

(8)

Parameters of the tyre/axle model are listed in Table 1, and normalized slip characteristics derived with these parameters for the front and rear tyre/axle are shown in Fig. 2.

Table 1 Parameters of vehicle and simplified tyre/axle model

Fig. 2

Normalized slip characteristics of front and rear simplified tyre/axle model

Above all, handling properties of a vehicle are typically evaluated from the steady-state ‘handling diagram’, as shown in Fig. 3, where the steering angle $\delta _F$ (top) and the vehicle side slip angle $\beta$ (centre) are plotted over the normal acceleration of the centre of gravity of the vehicle. The drive torque $M_R$ required to maintain constant velocity is shown at the bottom. Since vehicle side slip angle $\beta$ and yaw rate ${{\dot{\psi }}}$ as well as the steering angle $\delta _F$ are small for sufficiently large radius of curvature $\rho$, and velocity v is constant, the reduced set of equations (1b), (1c) is normally used to study handling properties, see e.g., [16]. Respective curves are denoted ‘pure lateral model’ in Fig. 3 and show a good match with the full vehicle model up to high normal accelerations. Since the mutual influence of longitudinal and lateral tyre forces is not considered in the pure lateral model, differences may be noted at the limits of handling, in particular when inspecting the required steering angle.

Fig. 3

Oversteer vehicle: (top) front steering angle $\delta _F$; (centre) vehicle side slip angle $\beta$; (bottom) drive torque $M_R$; constant radius of curvature $\rho =50$ m; Hopf bifurcation point $\times$: $\delta _F = 2.38^\circ$, $M_R=359.13$ Nm

According to [16], $\partial \delta _F / \partial v =0$ defines the boundary between over- and understeer of the pure lateral model for steady-state cornering at constant radius of curvature $\rho$. Since $\partial \delta _F / \partial v < 0$ in Fig. 3, oversteer handling characteristics are found for the vehicle setup considered in this study. In [4] it has been revealed that

$$\begin{aligned} \phi _F \, \phi _R \left. \frac{\partial \delta _F}{\partial (l/\rho )}\right| _{v=\mathrm {const.}} > 0 \end{aligned}$$

(9)

is required for stable steady-state cornering and positive slopes of the front and rear lateral tyre/axle forces characteristic $\phi _F$ and $\phi _R$ at the respective steady-state side slip angles. Thus, stability properties of the automobile may be directly read off model-based or measured handling diagrams [17], which is very useful from a practical point of view.

Stability in first approximation of vehicle model (1) at steady-state cornering is examined by inspecting the eigenvalues of the system ${\mathbf {M}} \mathrm {\Delta } \varvec{\dot{x}} = {\mathbf {A}} \mathrm {\Delta } \varvec{x} + {\mathbf {B}} \mathrm {\Delta } \varvec{u}$, which results from linearisation, w.r.t. steady-state cornering at varying operating points, with $\varvec{x}=[v,\, {{\dot{\psi }}},$$\beta ,\, \omega _R]^{\mathrm {T}}$ and $\varvec{u}=[\delta _F,\, M_R]^{\mathrm {T}}$. Eigenvalues $\lambda _k$ derive from $\det ({\mathbf {A}} - \lambda {\mathbf {M}}) = 0$, and respective branches of real parts are depicted in Fig. 4.

Fig. 4

Real parts of eigenvalues $\lambda _k$ for the full and pure lateral model: full operational range (top) and detail (bottom); constant radius of curvature $\rho =50$ m; Hopf bifurcation point $\times$: $\delta _F = 2.38^\circ$, $M_R=359.13$ Nm

However, only up to three branches are shown, since eigenvalues and corresponding eigenmodes mostly dominated by wheel speed are below $-200$ 1/s and of less interest. In the vicinity of the critical speed [16], two real eigenvalues combine to a conjugate-complex eigenvalue (oscillatory mode), see also [5], with eigenfrequencies up to 0.5 Hz at the Hopf bifurcation point indicated by $\times$. Inspecting corresponding eigenvectors, all state variables are involved; however, main components are related to vehicle velocity v and wheel speed $\omega _R$. Transient tyre properties, e.g., [16], have been disregarded, since they have only marginal impact on the dynamics of the vehicle in the operational range of interest, but add to the complexity of the model. Nevertheless, the applied tyre model certainly may effect the results [18], and more effort may be spent thereon in the future.

For the sake of comparison, both branches of real parts of the eigenvalues of the pure lateral model are depicted in Fig. 4 as well. As expected, monotonic loss of stability is found in this case. A larger critical speed for the loss of stability can be noticed for the pure lateral model compared with the full vehicle model, basically due to the disregarded mutual influence of longitudinal and lateral tyre/axle forces.

In the next section, the dynamic behaviour of the full vehicle model before and after a loss of stability is assessed by means of numerical continuation of the Hopf bifurcation in more detail. In this way, the effectiveness of actuators on modifying the dynamics of the vehicle can be obtained, if the inputs vary more slowly than the vehicle dynamics. The maximum and minimum control inputs, i.e., bifurcation parameters, result in a range of possible trajectories illustrating the actuator’s capabilities.

3 Numerical analysis of the Hopf bifurcation

3.1 Bifurcation diagram

At the Hopf bifurcation point shown in Fig. 4, a family of periodic solutions bifurcates from the steady-state solutions. This branch of solutions was calculated using the continuation software MatCont [19] and the continuation package Hom [20], using the multiple shooting method Bndsco [21] for solving the boundary value problems. As distinguished bifurcation parameter steering angle $\delta _F$ (and drive torque $M_R$, but not shown here) is used, the remaining parameters are kept fixed.

The bifurcation diagram is displayed in Fig. 5: At the Hopf point, section I, a family of stable periodic solutions with small amplitude is found, which coexists with the unstable steady state (dashed blue line). At $\delta _F = 2.3^\circ$ an almost vertical segment is observed, section II: For an extremely small variation of the parameter $\delta _F$, the diameter of the periodic solution increases strongly. Along this steep part, the tyre forces reach their saturation values. After both tyres experience saturation, the steep segment finishes and for larger periodic oscillations the steering angle decreases quickly, section III, until the velocity component in the longitudinal direction of the vehicle $v_x=v\cos \beta$ approaches zero, after which no more periodic solution can be found.

Fig. 5

Bifurcation diagram for periodic solutions. The solution amplitude is characterized by the smallest value $v_{x,\text {min}}$ of the forward velocity of the vehicle $v_x$. The symbols ‘Sat Rear’ and ‘Sat Front’ indicate periodic orbits, at which the saturation of the respective tyre force occurs first. (Color figure online)

A result similar to Fig. 5 is found with drive torque $M_R$ as bifurcation parameter instead of the steering angle $\delta _F$, however, in contrast to $\delta _F$, amplitudes increase with increasing $M_R$.

The periodic solutions corresponding to the marked points in Fig. 5 are displayed in the $(v, {\dot{\psi }})$-phase plane (top) and $(v, \beta )$-phase plane (bottom) of Fig. 6: Three orbits look very similar and almost agree for larger values of v, while the solution for $\delta _F=0.5^\circ$ significantly differs from the other ones. Along the steep segments at the leftmost parts of the orbits, the solution jumps quickly from the upper branch to the lower one (top).

Fig. 6

Several periodic (full lines) and singular solutions (dashed lines) in the $(v, {\dot{\psi }})$-phase plane (top), and $(v, \beta )$-phase plane (bottom); line colours correspond to markers in Fig. 5. (Color figure online)

Corresponding trajectories of the centre of gravity of the vehicle in the road plane are shown in Fig. 7. Trajectories start at the Hopf bifurcation point. After a period of transition (black lines), limit cycles emerge for $\delta _F=2.3^\circ$ and $\delta _F=0.5^\circ$. The change of the steering angle (as possible action of the driver) from $\delta _F=2.38^\circ$ to $\delta _F=2.3^\circ$ is small from a practical point of view; nevertheless, the steady limit cycle is reached quickly for $\delta _F=2.3^\circ$. The respective limit cycles are indicated by the colours corresponding to Fig. 6 for illustration, before next limit cycles follow (black lines again).

Trajectories found in section I, with increasing cycle times from about 10 to 15 s as the steering angle $\delta _F$ decreases, have almost circular shape. Since the deviations from the steady-state circular path are small, only a slight ‘drift’ of the circular trajectory can be observed. In contrast, for the pure lateral model, a saddle point has been identified in [7], instead of the Hopf bifurcation point, for a similar oversteer vehicle configuration, besides a second saddle that define a basin of attraction of a stable node. Although both models show a fundamentally different loss of stability, monotonic and periodic, resulting motions are similar just after loss of stability, and neglecting longitudinal dynamics is confirmed for section I.

Applying a constant steering angle, when stability is lost close to the Hopf bifurcation point, in the ‘opposite’ direction, no limit cycle will appear, full blue line in Fig. 5. Instead, a steady-steady circular path will result corresponding to the chosen steering angle (and fixed drive torque).

Trajectories found in section III show moderate dynamics for a large part of the cycle time, but fast longitudinal and lateral dynamics at the final part, as shown in Figs. 7 and 8.

When velocity is increased beyond the critical speed, while cornering at constant radius, it is known from experience, that an expert driver may recover stability [16], by steering to a large steering angle for a vehicle with limit oversteer. This can also be concluded from the respective handling diagram. Bifurcation analysis may indicate, that instead of finding and adjusting a stable singular point, a stable limit cycle nearby with slow dynamics may be an alternative to large steering activities.

Fig. 7

Trajectories of the centre of gravity of the vehicle in the road plane. Initial states correspond to Hopf bifurcation point, steering angle $\delta _F=2.3^\circ$ or $\delta _F=0.5^\circ$: black segments starting at (0,0) represent transitions to limit cycles; coloured segments represent one limit cycle corresponding to Fig. 6. (Color figure online)

Fig. 8

Velocity v(t), yaw rate ${\dot{\psi }}(t)$ and $\beta (t)$ of the periodic solutions marked in Fig. 5, starting when the yaw rate ${\dot{\psi }}$ is minimum

3.2 Observations in the regime of exploding solution amplitudes

The most remarkable feature of the periodic solution branch is the almost vertical segment, section II, in the bifurcation diagram, Fig. 5: For a tiny variation of the bifurcation parameter the diameters of the orbits grow significantly and the periodic solutions seem to just change their range for small values of the velocity v; during most of the time all these solutions seem to follow slowly the same trajectory. Most of the tested packages for solving boundary value problems failed to converge in this parameter domain and very small steps had to be used in the continuation method. The largest one of the numerically computed Floquet multipliers, which should have been equal to 1, grew up to 10,000, while the remaining multipliers were less than $10^{-9}$, indicating a very strong contraction of neighbouring solutions. Such a behaviour is frequently observed close to homoclinic solutions, but no nearby saddle point could be found and the periodic orbits continuously increased in size, while they wouldn’t have changed their size when approaching a homoclinic orbit.

Since the motion along the smooth segments of the periodic solutions was quite slow, we suspected, that some kind of singular perturbations causes the strange behaviour: The stiff tyre forces should constrain the wheels to almost slip-free motions. As can be seen in Fig. 8, the yaw rate ${\dot{\psi }}(t)$ varies strongly at the endpoints and behaves regularly in the interior domain, while the velocity component v(t) just displays a kink at the endpoints. Also $\omega _R(t)$ shows a smooth behaviour, while the angle $\beta (t)$ displays similar boundary layers as ${\dot{\psi }}$. One might therefore conclude that v and $\omega _R$ are the ‘slow’ variables and ${\dot{\psi }}$ and $\beta$ are the fast ones. But in this model, we obtain a much better agreement with the predictions from singular perturbation theory, if we consider v as slow variable and $\omega _R$, ${\dot{\psi }}$ and $\beta$ as fast ones.

In singular perturbation theory, one studies problems with the structure

$$\begin{aligned}&\varepsilon \dot{\varvec{x}} = \varvec{f}(\varvec{x}, \varvec{y}, \varepsilon ), \end{aligned}$$

(10)

$$\begin{aligned}&\dot{\varvec{y}} = \varvec{g}(\varvec{x}, \varvec{y}, \varepsilon ), \end{aligned}$$

(11)

where $\varepsilon$ is a small parameter. The fast and slow variables are given by $\varvec{x}$ and $\varvec{y}$, respectively. Setting $\varepsilon =0$ one obtains the reduced problem

$$\begin{aligned} \varvec{0}= & {} \varvec{f}(\varvec{x}, \varvec{y}, 0), \end{aligned}$$

(12)

$$\begin{aligned} \dot{\varvec{y}}= & {} \varvec{g}(\varvec{x}, \varvec{y}, 0), \end{aligned}$$

(13)

which is a differential-algebraic system and governs the slow behaviour. The algebraic equation (12) is solved for the fast variables $\varvec{x}$: $\varvec{x}=\varvec{h}(\varvec{y})$ and the slow dynamics is governed by the reduced equation

$$\begin{aligned} \dot{\varvec{y}} = \varvec{g}(\varvec{h}(\varvec{y}), \varvec{y}, 0). \end{aligned}$$

(14)

Equation (12) need not be solvable for all possible values of $\varvec{y}$; if $\varvec{y}(t)$ approaches a point, where (12) becomes singular, the fast variable usually jumps away from the critical manifold $\varvec{x}=\varvec{h}(\varvec{y})$. Also if the critical manifold becomes unstable, the solutions usually drift quickly away from it.

In our model, the fast dynamics is caused by the large forces acting on the tyres. It would therefore seem reasonable, to regard a common reciprocal of the tyre stiffness parameters as perturbation parameter $\varepsilon$. But one would have to make the tyres infinitely stiff for studying the reduced problem with $\varepsilon =0$.

Instead of explicitly choosing some perturbation parameter $\varepsilon$ and looking for the critical manifold with $\varepsilon =0$, we simply searched for fixed values of the velocity v the stationary values for the fast variables:

$$\begin{aligned} {\dot{\beta }}=0, \qquad \ddot{\psi }=0, \qquad {{\dot{\omega }}}_R = 0. \end{aligned}$$

The corresponding families of partially stationary solutions are displayed by dashed lines in Fig. 6: Along the lower branch of these V-shaped curves we have ${\dot{v}}>0$, whereas at the upper part v decreases; the eigenvalues are stable along the lower part and unstable along the upper part: The periodic solution for $\delta _F=0.5^\circ$ closely follows the corresponding singular solution along the stable lower branch, while the other three displayed periodic solutions follow it also along the unstable upper part, until they jump back to the lower branch.

This type of behaviour was already observed for several nonlinear oscillations, like the Van der Pol-equation, and accurately proven in [22] by geometric singular perturbation theory: Close to the tip of the singular curve a family of periodic orbits grows from a Hopf bifurcation and closely follows the singular curves. The quick increase in the solution amplitudes for tiny variations of parameters is called ‘Canard explosion’ and a corresponding bifurcation diagram is shown in [22] (therein denoted Fig. 7a), which closely resembles the diagram in Fig. 5.

4 Conclusions

Main findings of the analysis of the stability of steady-state cornering of a basic nonlinear two-wheel vehicle model with oversteer characteristic and coupled longitudinal and lateral dynamics are

• A supercritical Hopf bifurcation point has been found when stability is lost at large lateral acceleration. In contrast, an unstable saddle appears [7], for a model that neglects longitudinal effects with longitudinal velocity as a given parameter but similar tyre/axle characteristics.

• Small amplitude limit cycles close to the Hopf bifurcation point emerge with the steering angle (drive torque) as bifurcation parameter, followed by large amplitude relaxation cycles.

• Due to the large tyre forces, the system is singularly perturbed and a ‘Canard explosion’ is observed, during which relaxation oscillations occur.

• Evaluation of the small amplitude limit cycle behaviour by respective phase plots and trajectories of the vehicle motion confirms the use of a pure lateral vehicle model sufficiently close to the loss of stability.

• Nonlinear stability and bifurcation analysis has revealed that a stable limit cycle with small amplitude and slow dynamics may be an attractive alternative to finding and adjusting stable singular points for a human driver or steering robot.

To confirm and extend the results of this paper, the influence of the applied tyre model shall be studied in the future. Also the singular perturbation behaviour needs to be investigated more rigorously.