Abstract
This paper presents an investigation of the collapse of a 325-year-old multi-tiered heritage temple during the 2015 Gorkha earthquake in Kathmandu, Nepal. The research comprises a reconnaissance survey followed by a geotechnical investigation and numerical back-analysis carried out to understand the potential causes of the collapse. The assessment of the structural configuration of the temple indicated seismic vulnerability in the design due to the presence of discontinuous columns over the height of the temple and age-weakened bonding in the masonry walls. The geotechnical investigation revealed the presence of competent soil strata at the location, assisting the survey which indicated no differential or excessive settlement in the foundation. A series of cyclic triaxial tests were conducted on samples recovered during the geotechnical investigation to determine dynamic behaviour of the soil. Further, dynamic analysis of the plinth of the temple under the recorded acceleration–time history indicated a maximum drift percentage of 1.4% and residual relative displacement of 32 mm suggesting the potential reason behind the collapse. The output of this research will support seismic rehabilitation of ancient structures within World Heritage sites across Nepal and effective action plans to safeguard them against future earthquake hazard.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
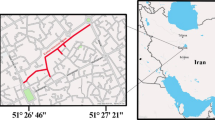
Kathmandu, the capital city of Nepal, is located in the Kathmandu Valley and hosts mediaeval temples that were built centuries ago and is known for their historical and archaeological importance. The city is home to seven UNESCO world heritage monument zones (three Royal or Durbar Squares, i.e. Kathmandu, Patan, Bhaktapur; two Buddhist Stupas, i.e. Swayambhu and Bauddhanath; and two Hindu temples, i.e. Pashupati and Changu Narayan). On 25 April 2015, a very strong earthquake of Mw 7.8 shook the whole of Nepal and some neighbouring areas of India and China at 11:56 am local time; the main shock was followed by several aftershocks. The epicentre of the earthquake was near Barpak village in Gorkha District, 77 km north-west of Kathmandu as shown in Fig. 1a and had an estimated focal depth of 15 km. Figure 1b illustrates acceleration–time history recorded at the Kantipath recording station in Kathmandu which indicates the maximum peak horizontal acceleration of 0.16 g, the bracketed duration of 36.9 s (duration between first and last exceedance from 0.05 g in a recorded motion) and the Fourier Spectrum. The Fourier spectrum indicates predominant periods of 0.44 s, and 5 s, respectively.
The 2015 Gorkha earthquake was the most powerful and devastating earthquakes to hit Nepal since the 1934 Bihar Nepal Earthquake (Mw = 8.1). The main shock (Mw = 7.8) was followed by two major aftershocks (Mw = 6.6 and 6.7). It killed around 8800 people, displaced 2.8 million people, and destroyed 500,000 homes because of the shallow nature of earthquake (Zhao 2016; Gautam and Chaulagain 2016). In addition to the casualties, loss of life and an economic damage, Gautam (2017) reported this earthquake as a cultural catastrophe damaging 403 monuments within Kathmandu’s historical urban infrastructure. Weise et al. (2017) recorded that the earthquake damaged 663 monuments and caused the collapse of 190 other vernacular and historical monuments. Over 70 people were killed during the collapse of one of Kathmandu’s oldest monument, the Kasthamandap (Chiaro et al. 2015; Coningham et al. 2016). Chen et al. (2017) reported the failure of many brick masonry structures due to the heavy masonry materials and lesser strength of bonding materials. Over the years, conservation of historical structures has drawn both national and international concern. The form of many of these structures is symmetrical, having brick masonry as the main load-bearing structural system. Such structures have already suffered minor and major damages due to previous seismic events. This was a result of their low tensile and shear strength as well as brittle failure characteristics in response to seismic forces. Assessment of these structures from a seismic standpoint has now become very important in order to safeguard them from future earthquakes. Huber and Dragoni (1992) suggested to perform a seismic vulnerability study to understand the process of transformation of the heritage structures of Italy for better understanding of effective action against the seismic rehabilitation. Davis et al. (2019) emphasised on development of archaeo-seismological and engineering approaches for identification and classification of the world heritage monuments damaged by the 2015 Gorkha Earthquake. They also suggested lessons of reconstruction and rehabilitations of heritage structures from future earthquake hazards. Kumar et al. (2019) performed reconnaissance surveys within the Pashupati and Changu Narayan sites in Kathmandu after the 2015 Gorkha Earthquake and reported that many of the survived or partially collapsed heritage structures lacked periodic maintenance.
Whilst previous research has focused on the study of historical, cultural and artistic aspects of Nepalese ancient structures (Hutt 2010), little investigation has been carried out to study related structural performances during strong earthquakes. Shakya et al. (2014) developed advanced numerical models to understand the seismic behaviour of Pagoda temples in Nepal and to produce structural component fragility curves that can be used to study the seismic vulnerability of these structures. They reported that damage or degradation in the masonry walls reduces the overall stiffness of the temple structure. Jaishi et al. (2003) conducted finite element analysis to study ten typical multi-tiered temples in Nepal. They reported that the fundamental time period of masonry temples in Nepal is less than 0.6 s. Pan et al. (2018) performed a reconnaissance survey of 68 heritage structures in Kathmandu and stated that more than 70% of the structures studied experienced severe damage to complete collapse during 2015 Gorkha earthquake. Ranjitkar (2000) identified the key issues in terms of safety of heritage structures in safeguarding them from future earthquake damage and also highlighted the weaknesses of these historical temple structures and proposed suggestions for seismic strengthening. Coningham et al. (2019) performed a research involving archaeology, geoarchaeology and the civil engineering in Kathmandu after the 2015 Gorkha Earthquake and emphasised that interdisciplinary collaboration may be able to co-produce and develop a methodology to improve the seismic safety of the world heritage structures. However, investigations of the collapse of these ancient structures based on thorough structural, geotechnical, architectural and archaeological investigation followed by engineering numerical simulations have not been previously undertaken.
This study presents an investigation of the causes of the collapse of the Jaisidewal temple structure by performing a reconnaissance survey, geotechnical investigation of the subsoil profile, numerically modelling the temple plinth structure and analysing it under the prescribed earthquake acceleration–time history recorded during 2015 Gorkha earthquake. In November/December 2017 and May 2018, a team of geotechnical engineers and archaeologists from Durham University and structural engineers from Newcastle University, in partnership with colleagues from Department of Archaeology, Government of Nepal, ICOMOS Nepal and Tribhuvan University, Kathmandu, conducted a reconnaissance survey and geotechnical investigation at the Jaisidewal site with logistical support from the Government of Nepal. To identify potential causes of the collapse, information on the local subsoil profile and the temple plinth internal structure was collected and synthesised to enable a dynamic analysis of the plinth and subsoil.
2 Potential causes of collapse of the Jaisidewal temple
The Jaisidewal temple is located south of Kathmandu’s Hanuman Dhoka Durbar Square monument zone and was a three-storied square tiered temple (Tiwari 2009). It is a Shaivite temple (one of the major traditions within Hinduism) whose superstructure sat on a seven-stepped plinth. Traditionally ascribed a construction date of 1688 CE, its name is linked to Lakshiminarayan Joshi, an influential minister of King Bhupatendra. Jaisidewal is also located within an area thought to contain the early nucleus of Licchavi settlement within the Kathmandu Valley (Prushca 2015). During the 2015 earthquake, the area recorded the collapse of 12 monuments including the Jaisidewal temple, as shown in Fig. 2a and b. The temple was located nearly 80 km from the epicentre of the earthquake. The temple was recorded as having a height 16.3 m and width 7 m. Figure 3a shows the image of temple taken before 25 April 2015. It was made of masonry–timber composite structure, resting on the plinth of height 7.2 m made of brick masonry with a soil and sand filling. A schematic illustration of the temple is shown in Fig. 3b. The masonry–timber structure was primarily composed of two components; load-bearing masonry walls and structural members comprised of columns, beams and struts made of timber. The walls were built with sun-dried bricks on the interior side, fired brick on the exterior side and the middle core was filled with mud and rubble. The brick mortar was a mud mortar that is the typical traditional mortar for temple structures in this region. The local availability and ease of processing mud mortars make it the most energy-efficient building material in the region; however, mud mortars are susceptible to weathering and hence present durability issues (Rashmi et al. 2014). Other problems associated with mud mortars are lack of cohesion and low compressive strength. The masonry walls had a varying thickness, i.e. greater thickness at the plinth level becoming progressively narrower towards the top of the superstructure. The temple geometry was symmetric, thus minimising loading eccentricities and thereby reducing extra moment and shear forces compared to asymmetric construction. This subsequently made the temple less vulnerable to earthquake forces. The temple was supported on the massive plinth, and this plinth provided a rigid base for the temple structure which also helped to redistribute the shear forces and partly absorb the earthquake energy. Archaeological excavation at the plinth level indicated the presence of a massive masonry mat supporting the whole structure (UNESCO 2013). A conical mass distribution resting on a wide base, as shown in Fig. 3a and b, may have helped in distributing shear forces. The concentric support structure with interconnected columns may also have redistributed the shear forces and bending moment that arose during the seismic event; however, as can be seen from Fig. 3b, structural continuity of the columns is not maintained. This reduces the ability of the upper portion of the temple to withstand earthquake lateral forces. The heavy weight of the upper columns made of brick masonry and tiles covering the roof result in the earthquake, generating large inertia forces that need to be resisted. Furthermore, poor connectivity between the multi-layer brick masonry and the timber composites would have further decreased the seismic resistance of the structure. Although this temple survived the 2011 Sikkim–Nepal earthquake and 1934 Bihar–Nepal earthquake, the superstructure portion of the temple having a height equal to 16.3 m collapsed during the 2015 Gorkha earthquake (Fig. 3c), whilst adjacent reinforced concrete structures suffered only minor damage due to the use of modern construction techniques. Similarly, ancient one- and two-storey structures nearby suffered minor-to-major damages due to lower inertia or lower out-of-plane forces in the masonry walls. Hence, the lack of structural continuity of the columns, low bending and shear stiffness of the masonry walls, degradation in bonding between masonry walls and timbers and insufficient timber joints were the most likely primary cause of the collapse of this temple during the 2015 Gorkha Earthquake. However, the response of a structure during an earthquake does not solely depend on the performance of the structure itself but also on the local geology, foundation parameters and earthquake motion characteristics. To obtain the subsurface conditions at the site, during December 2017, a geotechnical investigation was carried out adjacent to the temple plinth.
3 Detailed investigation of subsoil profile
3.1 Geotechnical profile and characterisation of soils at Jaisidewal location
Very limited information was available on the geotechnical properties of soils present within Kathmandu’s World Heritage Site. Hence, a borehole was drilled by cable percussion drilling after careful recording and removal of archaeological materials present via an archaeological trench, located adjacent to temple, excavated to 3.5 m depth, as shown in Fig. 4a. The borehole was drilled from the base of the trench for a further 10 m giving a total depth of investigation of 13.5 m from the ground level. Archaeological excavation was performed to avoid unrecorded destruction of archaeological deposits within the World Heritage Site and also to provide evidence of pre-existing subsurface structures. During drilling, Standard Penetration Tests (SPT) were conducted in the borehole at 1.5-m intervals and soil samples were collected for a program of engineering testing and characterisation. The recorded SPT-N value ranged from 8 to 50 for the full depth of borehole (13.5 m) indicating the presence of soft-to-stiff soil. The soil stratigraphy along with the SPT-N value can be seen in Fig. 4b. These SPT values rate the soil as a Type C Ground Type according to Eurocode 8 (ECN 2003). Beneath the archaeological material, the top 4 m soil is characterised as blackish soft to medium-stiff clay underlain by dense silty fine to very coarse dense sand. A total of 5 disturbed samples and 3 undisturbed samples were collected from the site and then transported to Durham, UK, for laboratory testing.
Particle size distribution analysis and Atterberg limit tests were carried out on the collected soil samples as per BS 1377 (2016). Figure 5 illustrates the gradation curve for the soil samples collected at different depths and shows a uniformly graded shape for all sands. Table 1 shows the details of the percentage of gravel, sand, fines content and Atterberg limits for the site. From Table 1, it can be seen that the clay layer is highly plastic and is underlain by sands with medium-to-low plastic fines soil at deeper depth.
Particle size distribution and enveloping curve (Modified after Tsuchida and Hayashi (1971) for Jaisidewal soils
3.2 Seismic liquefaction feature of soils based on compositional criteria
Seismic liquefaction features of the collected samples were also studied based on the particle size distribution and plasticity characteristics. Figure 5 shows grain size boundary curves indicating the range in which soils are most susceptible to liquefaction as defined by (Tsuchida and Hayashi 1971). From Fig. 5, it can be seen that almost all the curves for the soil samples recovered fall within the range of most liquefiable to potentially liquefiable. Further, the clays (Liquid limit = 54 and Plasticity index = 22) present between 3.5 and 7.5 m are placed in Zone C of the Atterberg limit charts proposed by Seed et al. (2003). This indicates that they are susceptible to strength degradation under the earthquake excitation. In spite of this, evidence of liquefaction at the site was not observed during site visits and has not been reported by other researchers. Neither rotation nor differential settlement of the plinth was observed. This may be due to the absence of groundwater at shallow depth when the earthquake occurred in April 2015. This was the beginning of the summer season in Kathmandu, and groundwater abstraction may have been responsible for artificially lowering the water levels as well as being just before the monsoon.
3.3 Cyclic triaxial tests on Jaisidewal clay
During an earthquake event, soil is subjected to cyclic loading and stress reversal which may cause the degradation of its shear strength. To understand this response, laboratory Cyclic Triaxial Tests (CTX) were carried out on the clay sample retrieved from the depth of 4.7 m from ground level during the boring process as per ASTM D3999 (2011). Three specimens were then recovered from the intact sample for testing. This test evaluates the dynamic characteristics such as shear modulus and damping ratio at high strain level which is essential for back-analysing the cyclic response of soil. Shear modulus represents the stiffness of soil, and damping ratio represents the percentage of energy lost per cycle of vibration. This test was carried out using an electro-mechanical dynamic triaxial apparatus at Geotechnics laboratory in Durham University.
The apparatus consists of a 10-kN-capacity load frame fitted with a dynamic actuator having a double-amplitude displacement of 20 mm and operational frequency range of 0.1–5 Hz. The facility can test soil specimens of dimensions 70 mm diameter and 140 mm height. In order to fit in the cell, the undisturbed samples recovered during drilling works (collected in 80 mm diameter sample tubes) were reduced to 70 mm in diameter by extruding them into a thin-walled 70-mm sample tube. The in situ density (1.86 Mg/m3) and moisture content (31.15%) of the natural state samples were obtained. A total of 5 CTX tests were performed, in which three tests were performed on recovered undisturbed samples and two on reconstituted soil specimen of the same density and moisture content as obtained in situ. The samples were saturated by maintaining constant difference of 5 kPa between cell pressure and back-pressure for the B-value of 0.96. Thereafter, all the samples were isotopically consolidated to a pressure of 100 kPa by increasing cell pressure and maintaining a constant back-pressure. This state of consolidation pressure was selected to simulate the state of the soil at shallow depth and its response under the cyclic loading. Figure 6a and b shows the change in excess pore pressure measured at the base of the sample and change in volume of an undisturbed sample under the confining pressure of 100 kPa during the consolidation stage of testing. The volume change was measured at the top of the sample by back-pressure controller. Following consolidation, each sample was then sheared at shear strain amplitudes of 0.015%, 0.15%, 0.3%, 0.65% and 1% whilst maintaining a constant frequency of 1 Hz in all cases. Each specimen was subjected to 40 cycles of strain-controlled loading. Figure 7a illustrates the peak axial strain (εa = 2%, equivalent to shear strain, γ of 1%) response of an undisturbed soil sample when subjected to cycles after consolidation to 100 kPa. Figure 7b represents the exponential decay in the deviator stress with an increase in the number of cycles and subsequent generation of excess pore water pressure. This indicates the degradation in the strength of soil during cyclic loading. Figure 7c indicates the gradual increase in the excess pore water pressure ratio, ru (ratio of excess pore pressure induced during shearing to the effective confining pressure, 100 kPa) during the cyclic loading where ru reaches to a value of 0.85 at the end of 40 cycles of loading (an ru value of unity would imply liquefaction). Figure 7d indicates the variation of deviator stress with respect to axial strain, i.e. hysteresis loop that depicts the degradation of the stiffness of soil with an increase in the number of cycles under cyclic loading.
3.3.1 Evaluation of dynamic properties
The dynamic properties of soil can be mathematically evaluated considering one hysteresis loop obtained from particular loading cycle as applied during an experimental investigation. Several researchers have indicated the use of different loading cycles to evaluate the dynamic properties of the soils, i.e. tenth cycle, fifth cycle, third cycle and first cycle. This study uses the first cycle of the hysteresis loop for obtaining the dynamic properties of soil (Lanzo et al. 1997; Vucetic et al. 1998). Figure 8 illustrates the typical hysteresis loop indicating the conventional way to determine the dynamic properties of the soil. This method evaluates the dynamic shear modulus (G) of soil from secant Young’s modulus (Esec) obtained by the slope of the line joining the peak of compressive and tensile stress–strain whilst the damping ratio is evaluated from the stored strain energy by a triangle in the first quadrant (considering a symmetrical cyclic for entire loading case).
Figure 9a illustrates the reduction in the shear modulus (G) of soil with an increase in the number of loading cycles (N) and shear strain (γ). This is mainly because of the hysteresis effect of the soil with increasing strain level, thereby dampening the exciting frequency. A modulus reduction curve obtained from CTX was used to represent the degradation of shear modulus of soil with shear strain (γ) in terms of reduction in shear modulus ratio (G/Gmax). Gmax is the maximum shear modulus of soil exhibited at very low shear strain (γ ≤ 5 × 10−6). Since the SPT test was conducted at the site, the maximum shear modulus (Gmax) is estimated by back-calculating the shear wave velocity of soil from SPT-N obtained at the site and using the equation given below:
where ρ is the density of soil in Mg/m3 and Vs is the shear wave velocity of soil in m/sec. The shear wave velocity is derived using the co-relation reported by Seed and Idriss (1982) given below:
Cyclic triaxial test results aG variation with N, bG/Gmax with shear strain γ (%) and c damping ratio with shear strain γ (%) (After Vucetic and Dobry 1991)
The shear wave velocity of the clay layer is obtained as 317 m/sec considering the average SPT-N value of the clay layer as 27. Again this ranks the site as a Type C Ground Type according to Eurocode 8 (ECN 2003). The maximum shear modulus, Gmax, is then calculated as 187 MPa. Figure 10b and c shows the modulus reduction curve and damping ratio curves with increasing shear strain level. It can be observed that obtained curves are closely matching with the results reported by Vucetic and Dobry (1991) for clay of PI = 22.
3.4 Monotonic triaxial test
Monotonic consolidated undrained tests were conducted on the undisturbed samples recovered during the drilling operation. The samples were reduced to 38 mm in diameter and 76 mm in height by extruding them into a thin-walled sample tube. The tests were conducted as per the procedure established in BS: 1377: 2016 at confining pressures of 100 kPa, 200 kPa and 300 kPa to obtain the shear strength parameters of the soil. Figure 10 illustrates the deviator stress–strain response of the soil at different confining pressures. It is observed that the peak deviator stress is dependent on the level of confining pressure and attains peak stress at the axial strain of 5%. Figure 11 illustrates the representation of stresses on p′ − q space where p′ is mean effective stress (p′ = σ1′ + 2σ3′/3) and q is the deviator stress, σ1 − σ3. The response of the soil at different mean effective stresses indicates a normally consolidated soil response. The representation of response of soil in p′ − q space was then used to obtain the critical state parameter, M which is the slope of p′ and q. The critical state friction angle is then obtained by using the expression:
where ϕcs is the critical state friction angle which is the inherent property of the soil. The critical strength friction angle for Jaisidewal clay is 330. It was observed that the shear strength parameter obtained for Jaisidewal clay was comparable with the shear strength parameters corresponding to SPT values (SPT-N: 27) of the Jaisidewal clay recorded during drilling operation as per Tomlinson (1994). Hence, the shear strength parameters required for conducting the numerical simulation explained in the next section are assumed based on the results of SPT-N values obtained during the drilling operation as per Tomlinson (1994).
4 Dynamic behaviour of the Jaisidewal temple plinth
4.1 Details of the numerical modelling and input parameters under static loading
The assessment of the dynamic behaviour of the Jaisidewal temple was carried out under actual acceleration–time history recorded at Kantipath recording station in Kathmandu by USGS. This was done by developing a two-dimensional finite element model (FEM) with the help of a commercial computer program Plaxis2D (Plaxis 2015), as shown in Fig. 12. Plaxis2D can simulate a nonlinear dissipative response of soil subjected to dynamic loading. Owing to the difficulty in the estimation of the mechanical properties of the temple structural components, lack of established research on traditional masonry construction and to simplify the numerical analysis procedure, a lumped mass modelling approach was adopted to model the superstructure of the temple. The subsoil primary comprised clay, medium silty sand and then dense sand extending to 13 m depth. In the absence of boring data beyond this depth, this study assumed dense sand extending to 40 m depth to attain the requirement of numerical modelling. The conventional Mohr–Coulomb elastic-perfectly plastic constitutive relationship was adapted to model the soils, whilst linear elastic model was adopted for the lumped mass and brick masonry. Whilst the Mohr–Coulomb model cannot simulate the cyclic softening or liquefaction of soil subjected to dynamic loading, Mohr–Coulomb model was felt to be appropriate in the present study to model all the soils as it can capture plastic strains during the cyclic loading. Table 2 shows the model parameters and unit weight of soil and masonry chosen in this study. The geotechnical parameters for the soils of the plinths were adopted from Tomlinson (1994) and Bowles (1997) and for the brick masonry from Pejatovik et al. (2019). The soils were assumed to be in a drained state, and cohesion of 0 kPa was assumed. The model uses 15-noded triangular elements, and meshes in Plaxis are automatically generated using a triangulation technique. A mesh optimisation study was carried out to decide the extents of model boundaries which helped in reducing the computational effort. The lateral extent of four times the size of the plinth and the vertical extent of twice the width of the plinth was adopted to avoid any undesirable boundary effect. The lateral boundaries were fixed horizontally, and the base was fixed horizontally and vertically.
The initial stresses were generated for the soil layers by using the Ko procedure available in Plaxis to make the model in equilibrium. Thereafter, the plinth was activated by plastic calculations to capture the response and to simulate the construction procedure. This was followed by analysing the model under lumped mass condition. All the components were activated simultaneously with the assumption that the temple would be constructed, following the ‘bottom-up’ method. Similar methodology was adopted by Kumar et al. (2017). The unit weight of the lumped mass was estimated using the schematic diagram of the temple received from ICOMOS Nepal. The total weight of the temple structure was estimated as 1270 kN assuming the uniform unit weight of the material as 20 kN/m3 as per Sarhosis and Sheng (2014). The settlement of the temple under static loading condition was obtained as 40 mm, as can be seen from Fig. 13.
4.2 Details of dynamic modelling
Dynamic properties of soil were defined in the model as the behaviour of soil is primarily governed by its dynamic properties. An earthquake generates cycles of loading and unloading, forming a hysteresis loop which subsequently dissipates energy by the soil’s damping characteristics. The role of damping in numerical analysis is to reproduce energy losses under dynamic loading. Geotechnical problems can be idealised by assuming the regions remote from the zone of interest extend to infinity, where dynamic wave can propagate in all directions. To model an infinite medium, a numerical model truncates the model boundaries to a finite size with the use of artificial boundaries. Plaxis2D provides viscous boundaries that contain dampers in the normal and shear directions to absorb any undue reflections of seismic waves. In the present study, the viscous boundary condition was assigned to the vertical boundaries and a complaint base condition was applied to the bottom to absorb the incident base. The accuracy of the finite element analysis is dependent on the size of the model and its meshing distribution along the zone of interest. For the convergence of dynamic analysis, the size of elements in the developed model needs to be chosen considering the input motion characteristics and shear wave velocity of the soil. The element size chosen was one-eighth of the wavelength of the shear wave (λs = Vs/f) (Kuhlemeyer and Lysmer 1973). To achieve the required level of accuracy in the dynamic calculation, the time step was chosen such that the input wave should not cross more than one element per time step. The dynamic loading in the form of acceleration–time history was applied after the achievement of equilibrium under the static loading condition. The recorded seismic acceleration–time history was of 300 s duration, and to obtain the response of numerical model under such time history would be computationally expensive. Hence, the acceleration–time history for the bracketed duration (duration between the first and last exceedance of ground acceleration ± 0.05 g), which is of 36.9 s, was obtained from the recorded motion to reduce the computational time, as shown in Fig. 14a. The acceleration–time history was then applied at the base of the soil model, and the response of the plinth in form of spectral acceleration, acceleration and displacements was monitored at three locations.
Figure 14b illustrates the spectral acceleration response obtained at different levels of the plinth. It can be seen that the maximum spectral acceleration lies in the range of 1–1.7 s, whereas the maximum spectral acceleration responses 0.4 g, 0.3 g and 0.15 g were obtained at the plinth top, plinth centre and its base. It is to be noted that Jaishi et al. (2003) reported the predominant period less than 0.6 s for the temples in Nepal without considering the influence of local subsoil condition. Considering the local subsoil condition, the fundamental period of site is subjected to period elongation as can be seen from the present study. Figure 14c indicates the acceleration response which indicated the maximum response of 0.15 g at the plinth top with decreasing response along the plinth base. It is to be noted that the plinth of the temple structure was subjected to a maximum displacement of 300 mm during the motion, and residual displacement of 100 mm was calculated. The residual displacement of 100 mm is very high considering the seismic demand of masonry structures. The rotation of the plinth with respect to dynamic time (ratio of difference in the vertical settlement of two extreme edges of the plinth to the plinth width) is obtained which shows negligible residual inclination at the end of dynamic time, as shown in Fig. 14d. Further, the relative displacement is calculated as the difference of displacement obtained between the plinth top and plinth base showing 32 mm of relative displacement, as shown in Fig. 14e. The drift is also obtained by dividing relative displacement with the height of the plinth, i.e. 7.2 m and expressed as percentage. The maximum percentage drift is recorded as 1.4% which may have caused the collapse of the temple structure. This is in line with the guideline given by Uniform Building Code (1991) limiting the inter-storey drift of 0.4% under seismic condition for the building having time period more than or equal to 0.7 s.
5 Conclusions
This paper presents the results of series of investigations involving reconnaissance survey, laboratory testing and numerical modelling carried out to understand the plausible causes of the collapse of the Jaisidewal temple in Kathmandu during the 2015 Gorkha earthquake. The following conclusions can be drawn from the study:
- 1.
The construction of the temple from the seismic standpoint, i.e. symmetrical geometric configuration to avoid eccentricity, massive plinth to reduce the influence of soft soil underneath, box type structure and conical mass distribution, was beneficial to withstand the seismic forces.
- 2.
The inherent structural configuration in terms of column discontinuity, lesser bending and shear stiffness of the masonry walls, degradation in the bonding between composite structures and insufficient joint strength of the timber may have provided a weak zone to induce the collapse.
- 3.
The preliminary reconnaissance survey ruled out the possibility of seismic soil liquefaction having occurred at the site in spite of the geotechnical investigation indicating the presence of liquefiable soil strata at the site. This is because of the absence of evidence of rotation and differential settlement in the temple’s plinth and adjacent buildings. This is also confirmed by the response of rotation obtained by performing dynamic numerical analysis of the temple plinth.
- 4.
The results of monotonic triaxial and cyclic triaxial testing provide the details of the strength parameters and dynamic properties of the Jaisidewal clay. This would further help in strengthening the base for the ground response analysis.
- 5.
The numerical analysis result indicates the residual relative lateral displacement of 32 mm and maximum drift of 1.4% which may have been responsible for collapse of the temple superstructure.
Hence, an engineering intervention and monitoring system must be employed to safeguard other similar structures existing in Kathmandu from future earthquake hazard, especially interventions and systems sympathetic to the authenticity and traditions of the historical infrastructure of the Kathmandu Valley and the Outstanding Universal Values of the World Heritage Property. Such a thorough investigation in terms of geotechnical and structural performances is pivotal for understanding the mechanism through which damage has occurred and assisting local stakeholders in determining types of strengthening measures which could be adopted to protect these heritage structures from future possible earthquake hazards.
References
ASTM D3999, D3999M–11e1 (2011) Standard Test Methods for the Determination of the Modulus and Damping Properties of Soils Using the Cyclic Triaxial Apparatus. ASTM International, West Conshohocken
Bowles JE (1997) Foundation analysis and design, 5th edn. McGraw-Hill, Inc, New York
British Standards Institution (2016) BS1377-2. Method of test for Soils for civil engineering purposes: Classification tests British Standard, UK
Chen H, Xie Q, Lan R, Li Z, Xu C, Yu S (2017) Seismic damage to school subjected to Nepal Earthquake, 2015. Nat Hazards 88:247–284
Chiaro G, Kiyota T, Pokhrel RM, Goda K, Katagiri T, Sharma K (2015) Reconnaissance report on geotechnical and structural damage caused by the 2015 Gorkha Earthquake, Nepal. Soils Found 55(5):1030–1043
Coningham RAE, Acharya KP, Davis CE, Kunwar RB, Simpson IA, Schmidt A, Tremblay JC (2016) Preliminary results of post-disaster archaeological investigations at the Kasthamandap and within Hanuman Dhoka, Kathmandu Valley UNESCO World Heritage Property (Nepal). Ancient Nepal 191–192:28–51
Coningham RAE, Acharya KP, Barclay CP, Barclay R, Davis CE, Graham C, Hughes PN, Joshi A, Kelly L, Khanal S, Kilic A, Kinnaird T, Kunwar RB, Kumar A, Maskey PN, Lafortune- Bernard A, Lewer N, McCaughie D, Mirnig N, Roberts A, Sarhosis V, Schmidt A, Simpson IA, Sparrow T, Toll DG, Tully B, Weise K, Wilkinson S, Wilson A (2019) Reducing disaster risk to life and livelihoods by evaluating the seismic safety of Kathmandu’s historic urban infrastructure: enabling an interdisciplinary pilot. J Br Acad 7(S2):45–82
Davis C, Coningham RAE, Acharya KP et al (2019) Identifying archaeological evidence of past earthquakes in a contemporary disaster scenario: case studies of damage, resilience and risk reduction from the 2015 Gorkha Earthquake and past seismic events within the Kathmandu Valley UNESCO World Heritage Property (Nepal). J Seismol. https://doi.org/10.1007/s10950-019-09890-7
ECN (2003) Eurocode 8: design of structures for earthquake resistance, Part 5: foundations, retaining structures and geotechnical aspects. European Commission for Standardisation, Brussels
Gautam D (2017) Seismic performance of world heritage sites in Kathmandu valley during Gorkha seismic sequence of April-May 2015. J Performance Constructed Facilities 31:06017003
Gautam D, Chaulagain H (2016) Structural performance and associated lessons to be learned from world earthquakes in Nepal after 25 April 2015 (Mw 7.8) Gorkha earthquake. Eng Fail Anal 68:222–243
Huber A, Dragoni M (1992) The historic and artistic heritage facing the earthquake risk: the Italian case. Nat Hazards 5:269–278
Hutt M (2010) A guide to the art and architecture of the Kathmandu valley. Adroit Publishers, New Delhi
Jaishi B, Ren WX, Zong ZH, Maskey PN (2003) Dynamic and seismic performance of oil multi-tiered temples in Nepal. Eng Struc 25:1827–1839
Kuhlemeyer RL, Lysmer J (1973) Finite element method accuracy for wave propagation problems. J Soil Mech Found Div 99(5):421–427
Kumar A, Patil M, Choudhury D (2017) Soil-structure interaction in a combined pile-raft foundation-a case study. Proc Inst Civil Eng-Geotech Eng 170(2):117–128
Kumar A, Hughes PN, Toll DG, Robin et al (2019). Damage assessment at world heritage Monument zone in Kathmandu valley after 2015 Gorkha Earthquake. In: The XVII European conference on soil mechanics and geotechnical engineering, September 1–6, 2019, Iceland. ISBN 978-9935-9436-1-3. https://doi.org/10.32075/17ecsmge-2019-1018
Lanzo G, Vucetic M, Doroudian M (1997) Reduction of shear modulus at small strains in simple shear. J Geotech Environ Eng 123:1035–1042
Pan Y, Wang X, Guo R, Yuan S (2018) Seismic damage assessment of Nepalese cultural heritage building and seismic retrofit strategies: 25 April 2015 Gorkha (Nepal). Eng Struc 87:80–85
Pejatovik M, Sarhosis V, Milani G (2019) Multi-tiered Nepalese temples: advanced numerical investigations for assessing performance at failure under horizontal loads. Eng Fail Anl 106:104172
Plaxis2D AE.02, Netherlands, Delft, the Netherlands. 2015
Prushca K (2015) Kathmandu valley, 2nd edn. Vajra Books, Kathmandu
Ranjitkar RK (2000) Seismic strengthening of the Nepalese Pagoda: progress report. In: Proceedings of the ICOMOS International Wood Committee (IIWC), earthquake-safe: lessons to be learned from traditional construction, international conference on the seismic performance of traditional buildings 16–18 Nov 2000, Istanbul, Turkey
Rashmi S, Jagadish S, Nethravathi S (2014) Stabilized Mud Mortar. Int J Res Eng Technol 03(18):26–39
Sarhosis V, Sheng Y (2014) Identification of material parameters for low bound strength masonry. Engg. Struct 60:100–110
Seed HB, Idriss IM (1982) Evaluation of liquefaction potential sand deposits based on observation of performance in previous earthquakes. Preprint 81–544, in situ testing to evaluate liquefaction susceptibility, ASCE National Convention, Missouri, pp 81–544
Seed RB, Cetin KO, Moss RES, Kammerer A, Wu J, Pestana J, Riemer M, Sancio RB, Bray JD, Kayen RE, Faris A (2003) Recent advances in soil liquefaction engineering: A unified and consistent framework. Keynote presentation, 26th Annual ASCE Los Angeles Geotechnical Spring Seminar, Long Beach, CA
Shakya M, Varum H, Vicente R, Costa A (2014) Seismic sensitivity analysis of the common structural components of Nepalese Pagoda temples. Bull Earthq Eng 12:1679–1703
Tiwari SR (2009) Temples of Nepal valley. Himal Books, Kathmandu
Tomlinson MJ (1994) Pile design and construction practice, 4th edn. CRC Press, London. ISBN 0-203-47457-0
Tsuchida H, Hayashi S (1971) Estimation of liquefaction potential of sandy soils. In: Proceedings of the third joint meeting, US-Japan panel on wind and seismic effects, UJNR, Tokyo, May 1971; pp 91–109
UNESCO (2013) Revisiting Kathmandu: Safeguarding Living Urban Heritage. In: International symposium, Kathmandu Valley, 25-29 November 2013
Uniform Building Code (1991) International Conference of Building Officials, Whittier, California
Vucetic M, Dobry R (1991) Effect of soil plasticity on cyclic response. J Geotech Eng 117:89–107
Vucetic M, Lanzo G, Doroudian M (1998) Damping at small strain in cyclic simple shear test. J Geotech Geoenviron Eng 124:585–595
Weise K, Gautam D, Rodrigues H (2017) Response and rehabilitation of historic monuments after Gorkha earthquake. In: Gautam D, Rodrigues HFP (eds) Impacts and Insights of the Gorkha Earthquake. Elsevier, Amsterdam, pp 65–94
Zhao B (2016) April 2015 Nepal earthquake: observations and reflection. Nat Hazards 80(2):1405–1410
Acknowledgements
The authors would like to acknowledge the funding received from British Academy’s Global Challenges Research Fund: Cities and Infrastructure Program, to carry out the research titled ‘Reducing Disaster Risk to Life and Livelihoods by Evaluating the Seismic Safety of Kathmandu’s Historic Urban Infrastructure’ (CI70241) and the generous logistical support offered by the Department of Archaeology, Government of Nepal.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kumar, A., Hughes, P.N., Sarhosis, V. et al. Experimental, numerical and field study investigating a heritage structure collapse after the 2015 Gorkha earthquake. Nat Hazards 101, 231–253 (2020). https://doi.org/10.1007/s11069-020-03871-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-020-03871-7